第4章 MATLAB图像处理习题习题

1.归纳一下我们所学过的正交变换有哪些共同特点？在图像处理中怎样应用这些特点？对下面图像(moon.tif)进行傅氏变换并平移到中心点。

(注:先对图像进行灰度格式转换)答：（1）我们所学过的正交变换（傅利叶变换、离散余弦变换、沃尔什变换、哈尔变换）的共同特点有：a．都是将数字图像通过正交函数由空域转变成频域；b．都是在频域（变换域中）完成图像处理，并在空域的复函数和频域的复函数之间建立唯一的对应关系，不仅可以完成空域中的许多处理功能，还能完成在空域难以完成，或完成效果不好的处理功能；c．能保持原函数的奇偶性；d．正交变换是可逆的过程；e．正交变换能使复杂信号的处理简单化（2）根据正交变换的特点，我们可以有效地在图像处理中应用他们，这些应用包括：a．图像边缘检测。

例如利用傅氏变换可以保留图像高频分量而削弱或滤掉低频分量，达到边缘检测的目的。

b．图像恢复。

根据相应的退化模型和知识重建或恢复原始的图像，即将图像退化的过程模型化，并据此采取相反的过程以得到原始的图像。

图像的恢复可在频域内完场。

c．图像重建。

投影函数在空域中转动一个角度后的傅氏变换和它的傅氏变换在转动相同的角度后的结果一样，可以利用这点对图像进行重建。

d．图像压缩：可以直接通过傅里叶系数来压缩数据，比如常用的离散余弦变换。

e．图像去噪。

绝大部分噪音都是图像的高频分量，可以通过低通滤波器来滤除高频噪声。

f．在图像分析和扫描中，用傅里叶描述子描述区域边界点的二维坐标，在纹理分析中，可以用傅里叶频谱的频率特性来描述周期的或者几乎周期的二维图像模式的方向性。

（3）对图像(moon.tif)进行傅氏变换并平移到中心点a．MatLab中所用命令：I = imread('moon.tif');imshow(I);D=double(I)/255;figure,imshow(D);F=fft2(D);figure,imshow(F);%fftshift是位移函数，将左上角的原点移至中心Y=fftshift(F);figure,imshow(Y);b．处理后相应的图像：傅氏变换傅氏变换后移到中心点2. 在图像处理中小波变换的主要用途是什么？对下图进行小波变换。

《数字图像处理》习题参考答案第1 章概述连续图像和数字图像如何相互转换答：数字图像将图像看成是许多大小相同、形状一致的像素组成。

这样，数字图像可以用二维矩阵表示。

将自然界的图像通过光学系统成像并由电子器件或系统转化为模拟图像（连续图像）信号，再由模拟/数字转化器（ADC）得到原始的数字图像信号。

图像的数字化包括离散和量化两个主要步骤。

在空间将连续坐标过程称为离散化，而进一步将图像的幅度值（可能是灰度或色彩）整数化的过程称为量化。

#采用数字图像处理有何优点答：数字图像处理与光学等模拟方式相比具有以下鲜明的特点：1．具有数字信号处理技术共有的特点。

（1）处理精度高。

（2）重现性能好。

（3）灵活性高。

2．数字图像处理后的图像是供人观察和评价的，也可能作为机器视觉的预处理结果。

3．数字图像处理技术适用面宽。

4．数字图像处理技术综合性强。

数字图像处理主要包括哪些研究内容答：图像处理的任务是将客观世界的景象进行获取并转化为数字图像、进行增强、变换、编码、恢复、重建、编码和压缩、分割等处理，它将一幅图像转化为另一幅具有新的意义的图像。

]讨论数字图像处理系统的组成。

列举你熟悉的图像处理系统并分析它们的组成和功能。

答：如图，数字图像处理系统是应用计算机或专用数字设备对图像信息进行处理的信息系统。

图像处理系统包括图像处理硬件和图像处理软件。

图像处理硬件主要由图像输入设备、图像运算处理设备（微计算机）、图像存储器、图像输出设备等组成。

软件系统包括操作系统、控制软件及应用软件等。

$图数字图像处理系统结构图1常见的数字图像处理开发工具有哪些各有什么特点答．目前图像处理系统开发的主流工具为Visual C++（面向对象可视化集成工具）和MATLAB 的图像处理工具箱（Image Processing Tool box）。

两种开发工具各有所长且有相互间的软件接口。

Microsoft 公司的VC++是一种具有高度综合性能的面向对象可视化集成工具，用它开发出来的Win 32 程序有着运行速度快、可移植能力强等优点。

ge 1习题一１。

请说明图像数学表达式 I =f （ x ， y, z ， λ， t)中各参数的含义，该表达式代表哪几种不同种类的图像?图像数学表达式I = f （ x , y , z , λ , t ） 中，(x,y ，z)是空间坐标，λ是波长，t 是时间，I 是光点（x ，y ，z ）的强度（幅度）.上式表示一幅运动 (t) 的、彩色/多光谱 (λ） 的、立体（x ，y ，z ）图像。

２.存储一幅1024x768，256个灰度级的图像需要多少bit ？一幅512x512的32bit 真彩图像的容量为多少bit ？（1）一幅 1024×768，256 个灰度级的图像的容量为:b=1024×768×8 = 6291456 bit（2)一幅 512×512的32位真彩图像的容量为:b=512×512×32=8388608 bit３。

写出“*”标记的像素的4邻域、对角邻域、8邻域像素的坐标（坐标按常规方式确定）４。

简述二值图像、灰度图像与彩色图像的区别?RGB 彩色图像与索引彩色图像有什么区别？５。

简述直方图均衡化的基本原理。

直方图均衡化方法的基本思想是，对在图像中像素个数多的灰度级进行展宽，而对像素个数少的灰度级进行缩减。

从而达到清晰图像的目的.因为灰度分布可在直方图中描述，所以该图像增强方法是基于图像的灰度直方图.６。

在一个线性拉伸中，当a ，b 取何值时，可将双峰直方图的两个峰分别从23和155移到16和240？画出灰度变换函数和两个直方图的形状。

变换函数为：，则16=23a+b ； 240=155a+b于是：a ＝1.7，b ＝－23。

(两个直方图峰值之间距离拉开）７。

图像灰度变换增强有那几种方式，简述其原理.灰度变换、直方图处理、图象的代数运算线性变换和非线性变换，非线性变换包括对数变换和指数变换等８。

说明RGB 模型和HSI 模型各参数的含义.I:表示光照强度或称为亮度，它确定了像素的整体亮度，而不管其颜色是什么。

第2章MATLAB概论1、与其他计算机语言相比较，MA TLAB语言突出的特点是什么？答：起点高、人机界面适合科技人员、强大而简易的作图功能、智能化程度高、功能丰富，可扩展性强.2、MA TLAB系统由那些部分组成？答：开发环境、MATLAB数学函数库、MATLAB语言、图形功能、应用程序接口3、安装MATLAB时，在选择组件窗口中哪些部分必须勾选，没有勾选的部分以后如何补安装？答：在安装MATLAB时，安装内容由选择组件窗口中各复选框是否被勾选来决定，可以根据自己的需要选择安装内容，但基本平台（即MATLAB选项）必须安装.第一次安装没有选择的内容在补安装时只需按照安装的过程进行，只是在选择组件时只勾选要补装的组件或工具箱即可.4、MATLAB操作桌面有几个窗口？如何使某个窗口脱离桌面成为独立窗口？又如何将脱离出去的窗口重新放置到桌面上？答：在MATLAB操作桌面上有五个窗口，在每个窗口的右下角有两个小按钮，一个是关闭窗口的Close 按钮，一个是可以使窗口称为独立的Undock按钮，点击Undock按钮就可以使该窗口脱离桌面称为独立窗口，在独立窗口的view菜单中选择Dock，菜单项就可以将独立的窗口重新防止的桌面上.5、如何启动M文件编辑/调试器？答：在操作桌面上选择“建立新文件”或“打开文件”操作时，M文件编辑/调试器将被启动.在命令窗口中键入edit命令时也可以启动M文件编辑/调试器.6、存储在工作空间中的数组能编辑吗？如何操作？答：存储在工作空间的数组可以通过数组编辑器进行编辑：在工作空间浏览器中双击要编辑的数组名打开数组编辑器，再选中要修改的数据单元，输入修改内容即可.7、命令历史窗口除了可以观察前面键入的命令外，还有什么用途？答：命令历史窗口除了用于查询以前键入的命令外，还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到M文件中.8、如何设置当前目录和搜索路径，在当前目录上的文件和在搜索路径上的文件有什么区别？答：当前目录可以在当前目录浏览器窗口左上方的输入栏中设置，搜索路径可以通过选择操作桌面的file菜单中的Set Path菜单项来完成.在没有特别说明的情况下，只有当前目录和搜索路径上的函数和文件能够被MATLAB运行和调用，如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件，如果没有特别说明，数据文件将存储在当前目录上.9、在MA TLAB中有几种获得帮助的途径？答：（1）帮助浏览器：选择view菜单中的Help菜单项或选择Help菜单中的MATLAB Help菜单项可以打开帮助浏览器.（2）help命令：在命令窗口键入“help”命令可以列出帮助主题，键入“help 函数名”可以得到指定函数的在线帮助信息.（3）lookfor命令：在命令窗口键入“lookfor 关键词”可以搜索出一系列与给定关键词相关的命令和函数.（4）模糊查询：输入命令的前几个字母，然后按Tab键，就可以列出所有以这几个字母开始的命令和函数.注意：lookfor和模糊查询查到的不是详细信息，通常还需要在确定了具体函数名称后用help命令显示详细信息.第3章 MATLAB 数值运算3.1在MA TLAB 中如何建立矩阵⎥⎦⎤⎢⎣⎡194375，并将其赋予变量a ？ 答：在Command Window 窗口输入操作:>> a=[5 7 3;4 9 1]3.2有几种建立矩阵的方法？各有什么优点？ 答：（1）直接输入法，如a=[1 2 3 4]，优点是输入方法方便简捷；（2）通过M 文件建立矩阵，该方法适用于建立尺寸较大的矩阵，并且易于修改； （3）由函数建立，如y=sin(x)，可以由MATLAB 的内部函数建立一些特殊矩阵； （4）通过数据文件建立，该方法可以调用由其他软件产生数据.3.3在进行算术运算时，数组运算和矩阵运算各有什么要求？答：进行数组运算的两个数组必须有相同的尺寸.进行矩阵运算的两个矩阵必须满足矩阵运算规则，如矩阵a 与b 相乘（a*b ）时必须满足a 的列数等于b 的行数.渗釤呛俨匀谔鱉调硯錦。

matlab绘图试题及答案MATLAB绘图试题及答案1. 绘制正弦曲线题目：使用MATLAB绘制函数 \( y = \sin(x) \) 在区间 \([0, 2\pi]\) 上的图像。

答案：```matlabx = 0:0.01:2*pi;y = sin(x);plot(x, y);title('Sin(x) Function');xlabel('x');ylabel('y');```2. 绘制二次函数图像题目：绘制函数 \( y = ax^2 + bx + c \) 在区间 \([-10, 10]\) 上的图像，其中 \( a = 1, b = 2, c = 3 \)。

答案：```matlabx = -10:0.1:10;y = x.^2 + 2*x + 3;plot(x, y);title('Quadratic Function y = x^2 + 2x + 3');xlabel('x');ylabel('y');```3. 绘制柱状图题目：给定一组数据 [10, 20, 30, 40, 50]，使用MATLAB绘制柱状图。

答案：```matlabdata = [10, 20, 30, 40, 50];bar(data);title('Bar Chart');xlabel('Index');ylabel('Value');```4. 绘制散点图题目：给定两组数据 \( x = [1, 2, 3, 4, 5] \) 和 \( y = [2, 4, 6, 8, 10] \)，使用MATLAB绘制对应的散点图。

答案：```matlabx = [1, 2, 3, 4, 5];y = [2, 4, 6, 8, 10];scatter(x, y);title('Scatter Plot');xlabel('x');ylabel('y');```5. 绘制饼图题目：给定一组数据 [10, 20, 30, 40]，使用MATLAB绘制饼图。

第一章1. 什么是图像？如何区分数字图像和模拟图像？模拟图像和数字图像如何相互转换？答：图像是当光辐射能量照在物体上，经过反射或透射，或由发光物体本身发出的光能量，在人的视觉器官中所重现出的物体的视觉信息。

数字图像将图像看成是许多大小相同、形状一致的像素组成。

这样，数字图像可以用二维矩阵表示。

将自然界的图像通过光学系统成像并由电子器件或系统转化为模拟图像（连续图像）信号，再由模拟/数字转化器（ADC）得到原始的数字图像信号。

图像的数字化包括离散和量化两个主要步骤。

在空间将连续坐标过程称为离散化，而进一步将图像的幅度值（可能是灰度或色彩）整数化的过程称为量化。

2. 什么是数字图像处理？答：数字图像处理(Digital Image Processing)是通过计算机对图像进行去除噪声、增强、复原、分割、提取特征等处理的方法和技术。

3. 数字图像处理系统有哪几部分组成？各部分的主要功能和常见设备有哪些？答：一个基本的数字图像处理系统由图像输入、图像存储、图像输出、图像通信、图像处理和分析5个模块组成，如下图所示。

各个模块的作用分别为：图像输入模块：图像输入也称图像采集或图像数字化，它是利用图像采集设备（如数码照相机、数码摄像机等）来获取数字图像，或通过数字化设备（如图像扫描仪）将要处理的连续图像转换成适于计算机处理的数字图像。

图像存储模块：主要用来存储图像信息。

图像输出模块：将处理前后的图像显示出来或将处理结果永久保存。

图像通信模块：对图像信息进行传输或通信。

图像处理与分析模块：数字图像处理与分析模块包括处理算法、实现软件和数字计算机，以完成图像信息处理的所有功能。

4. 试述人眼的主要特性。

答：（1）、人眼的视觉机理。

视网膜上有大量的杆状细胞和锥状细胞，锥状细胞能辨别光的颜色，而杆状细胞感光灵敏度高，但不能辨色。

（2）、人眼的视敏特性。

指人眼对不同波长的光具有不同的敏感程度。

（3）、人眼的亮度感觉。

亮度感觉范围指人眼所能感觉到的最大亮度与最小亮度之间的范围。

第四章图像增强1.简述直方图均衡化处理的原理和目的。

拍摄一幅较暗的图像，用直方图均衡化方法处理，分析结果。

原理：直方图均衡化处理的“中心思想”是把原始图像的灰度直方图从比较集中的某个灰度区间变成在全部灰度范围内的均匀分布。

也就是对图像进行非线性拉伸，重新分配图像像素值，使一定灰度范围内的像素数量大致相同。

把给定图像的直方图分布改变成“均匀”分布直方图分布目的：直方图均衡化是图像处理领域中利用图像直方图对对比度进行调整的方法。

它通常用来增加许多图像的局部对比度，尤其是当图像的有用数据的对比度相当接近的时候。

通过直方图均衡化，亮度可以更好地在直方图上分布。

这样就可以用于增强局部的对比度而不影响整体的对比度，直方图均衡化通过有效地扩展常用的亮度来实现这种功能。

Matlab程序如下：clc;RGB=imread('wxf.jpg'); %输入彩色图像，得到三维数组R=RGB(:,:,1); %分别取三维数组的一维，得到红绿蓝三个分量G=RGB(:,:,2); %为R G B。

B=RGB(:,:,3);figure(1)imshow(RGB); %绘制各分量的图像及其直方图title('原始真彩色图像');figure(2)subplot(3,2,1),imshow(R);title('真彩色图像的红色分量');subplot(3,2,2), imhist(R);title('真彩色图像的红色分量直方图');subplot(3,2,3),imshow(G);title('真彩色图像的绿色分量');subplot(3,2,4), imhist(G);title(' 的绿色分量直方图');subplot(3,2,5),imshow(B);title('真彩色图像的蓝色分量');subplot(3,2,6), imhist(B);title('真彩色图像的蓝色分量直方图');r=histeq(R); %对个分量直方图均衡化，得到个分量均衡化图像g=histeq(G);b=histeq(B);figure(3),subplot(3,2,1),imshow(r);title('红色分量均衡化后图像');subplot(3,2,2), imhist(r);title('红色分量均衡化后图像直方图');subplot(3,2,3),imshow(g);title('绿色分量均衡化后图像');subplot(3,2,4), imhist(g);title('绿色分量均衡化后图像直方图');subplot(3,2,5), imshow(b);title('蓝色分量均衡化后图像');subplot(3,2,6), imhist(b);title('蓝色分量均衡化后图像直方图');figure(4), %通过均衡化后的图像还原输出原图像newimg = cat(3,r,g,b); %imshow(newimg,[]);title('均衡化后分量图像还原输出原图');程序运行结果：原始真彩色图像均衡化后分量图像还原输出原图图1.1 原始图像与均衡化后还原输出图像对比通过matlab仿真，由图1.1比较均衡化后的还原图像与输入原始真彩色图像，输出图像轮廓更清晰，亮度明显增强。

matlab课后习题答案（附图）习题2.1画出下列常见曲线的图形y （1）⽴⽅抛物线3x命令：syms x y;ezplot('x.^(1/3)')(2)⾼斯曲线y=e^(-X^2);命令：clearsyms x y;ezplot('exp(-x*x)')(3)笛卡尔曲线命令：>> clear>> syms x y;>> a=1;>> ezplot(x^3+y^3-3*a*x*y)(4)蔓叶线命令：>> clear>> syms x y;>> a=1ezplot(y^2-(x^3)/(a-x))(5)摆线:()()tsin-=,=-by1命令：>> clear>> t=0:0.1:2*pi;>> x=t-sin(t);>>y=2*(1-cos(t)); >> plot(x,y)7螺旋线命令：>> clear >> t=0:0.1:2*pi; >> x=cos(t); >> y=sin(t); >> z=t;>>plot3(x,y,z)(8)阿基⽶德螺线命令：clear>> theta=0:0.1:2*pi;>> rho1=(theta);>> subplot(1,2,1),polar(theta,rho1)(9) 对数螺线命令：cleartheta=0:0.1:2*pi;rho1=exp(theta);subplot(1,2,1),polar(theta,rho1)(12)⼼形线命令：>> clear >> theta=0:0.1:2*pi; >> rho1=1+cos(theta); >> subplot(1,2,1),polar(theta,rho1)练习2.21. 求出下列极限值（1）nnn n3→命令：>>syms n>>limit((n^3+3^n)^(1/n)) ans = 3（2）)121(lim n n n n ++-+∞→命令：>>syms n>>limit((n+2)^(1/2)-2*(n+1)^(1/2)+n^(1/2),n,inf) ans = 0（3）x x x 2cot lim 0→命令：syms x ；>> limit(x*cot(2*x),x,0) ans = 1/2 （4）)(coslimcm xx ∞→命令：syms x m ； limit((cos(m/x))^x,x,inf) ans = 1（5）)111(lim 1--→exx x命令：syms x>> limit(1/x-1/(exp(x)-1),x,1) ans =(exp(1)-2)/(exp(1)-1) （6）)(2lim x x xx -+∞>> limit((x^2+x)^(1/2)-x,x,inf)ans = 1/2练习2.41. 求下列不定积分，并⽤diff 验证：（1）+x dxcos 1>>Clear >> syms x y >> y=1/(1+cos(x)); >> f=int(y,x) f =tan(1/2*x) >> y=tan(1/2*x); >> yx=diff(y ,x); >> y1=simple(yx) y1 =1/2+1/2*tan(1/2*x)^2 (2)+exdx1clear syms x yy=1/(1+exp(x));f=int(y,x) f =-log(1+exp(x))+log(exp(x)) syms x yy=-log(1+exp(x))+log(exp(x)); yx=diff(y,x); y1=simple(yx) y1 = 1/(1+exp(x)) (3)dx x x ?sin 2syms x yy=x*sin(x)^2; >> f=int(y,x) f =x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2 clearsyms x y y=x*(-1/2*cos(x)*sin(x)+1/2*x)-1/4*cos(x)^2-1/4*x^2; yx=diff(y,x); >> y1=simple(yx) y1 = x*sin(x)^2 (4)xdx ?sec3syms x y y=sec(x)^3;f=int(y,x) f =1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)) clear syms x yy=1/2/cos(x)^2*sin(x)+1/2*log(sec(x)+tan(x)); yx=diff(y,x); y1=simple(yx) y1 =1/cos(x)^32. 求下列积分的数值解 1）dx x-10clearsyms xy=int(x^(-x),x,0,1) y =int(x^(-x),x = 0 .. 1) vpa(y,10) ans =1.291285997 2）xdx e x cos3202?πclearsyms xy=int(exp(2*x)*cos(x)^3,x, clear syms xy=int((1/(2*pi)^(1/2))*exp(-x^2/2),x,0,1) y =7186705221432913/36028797018963968*erf(1/2*2^(1/2))*2^(1/2)*pi^(1/0,2*pi) y =22/65*exp(pi)^4-22/65vpa(ans,10)(3)dx xe21221-π>> clear >> syms x>> y=int(1/(2*pi)^(1/2)*exp(-x^2/2),0,1); >> vpa(y,14) ans =.341344746068552（4）>> clear >> syms x>> y=int(x*log(x^4)*asin(1/x^2),1,3); Warning: Explicit integral could not be found. > In sym.int at 58 >> vpa(y,14) ans = 2.45977212823752（5） >> clear >> syms x1判断下列级数的收敛性，若收敛，求出其收敛值。

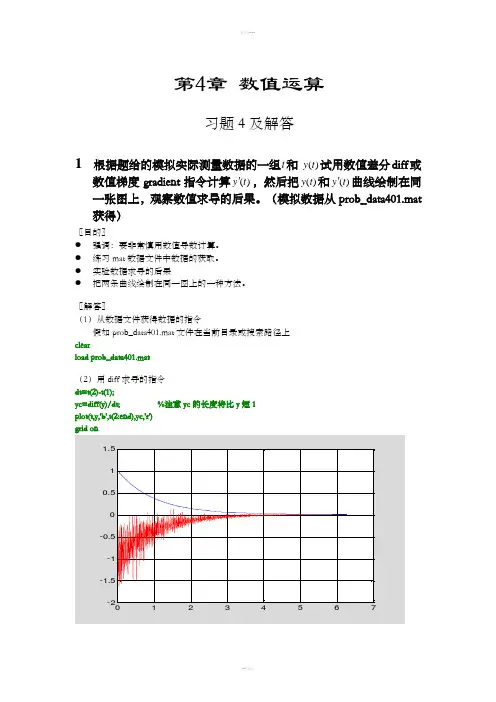
第4章数值运算习题 4 及解答1 根据题给的模拟实际测量数据的一组t和)(t y试用数值差分diff或数值梯度gradient指令计算)(t y'，然后把)(t y和)(t y'曲线绘制在同一张图上，观察数值求导的后果。

（模拟数据从prob_data401.mat 获得）〖目的〗●强调：要非常慎用数值导数计算。

●练习mat数据文件中数据的获取。

●实验数据求导的后果●把两条曲线绘制在同一图上的一种方法。

〖解答〗（1）从数据文件获得数据的指令假如prob_data401.mat文件在当前目录或搜索路径上clearload prob_data401.mat（2）用diff求导的指令dt=t(2)-t(1);yc=diff(y)/dt; %注意yc的长度将比y短1plot(t,y,'b',t(2:end),yc,'r')grid on（3）用gradent 求导的指令（图形与上相似）dt=t(2)-t(1);yc=gradient(y)/dt;plot(t,y,'b',t,yc,'r')grid on〖说明〗● 不到万不得已，不要进行数值求导。

● 假若一定要计算数值导数，自变量增量dt 要取得比原有数据相对误差高1、2个量级以上。

● 求导会使数据中原有的噪声放大。

2 采用数值计算方法，画出dt tt x y x ⎰=0sin )(在]10 ,0[区间曲线，并计算)5.4(y 。

〖提示〗● 指定区间内的积分函数可用cumtrapz 指令给出。

● )5.4(y 在计算要求不太高的地方可用find 指令算得。

〖目的〗● 指定区间内的积分函数的数值计算法和cumtrapz 指令。

● find 指令的应用。

〖解答〗dt=1e-4;t=0:dt:10;t=t+(t==0)*eps;f=sin(t)./t;s=cumtrapz(f)*dt;plot(t,s,'LineWidth',3)ii=find(t==4.5);s45=s(ii)s45 =1.65413 求函数x ex f 3sin )(=的数值积分⎰=π0 )(dx x f s ，并请采用符号计算尝试复算。

数字图像处理习题⼀、判断题（10分）（正确√，错误×）1.图像处理就是对图像信息进⾏加⼯处理，以满⾜⼈的视觉⼼理和实际应⽤的要求（√）2.在MA TLAB中，uint8是⽆符号8位整数（√）3.在MA TLAB中，uint16是⽆符号16位整数（√）4.图像的点运算与代数运算不相同（√）5.点运算也叫灰度级变换（√）6.线性点运算可以改变数字图像的对⽐度（√）7.图像的⼏何变换也叫图像的点运算（×）8.图像的平滑操作实际上是邻域操作（√）9.傅⽴叶变换后的矩阵处在频域上（√）10.傅⽴叶变换后的矩阵处在空域上（×）11.傅⽴叶变换，⼈们可以在空域和频域中同时思考问题（√）12.像素深度是指存储每个像素所⽤的位数（√）13.图像经过变换后，图像的⼤部分能量都集中在中、⾼频段（×）14.图像经过变换后，图像的⼤部分能量都集中在低频段（√）15.直⽅图均衡化也是⼀种⾮线性点运算（√）16.仿射变换是空间变换（√）17.空间变换是频域变换（×）18.边缘检测是将边缘像元标识出来的⼀种图像分割技术（√）19.灰度直⽅图能反映⼀幅图像各灰度级像元占图像的⾯积⽐（√）20.直⽅图均衡是⼀种点运算，图像的⼆值化则是⼀种局部运算（×）21.双边滤波法可⽤于边缘增强（×）22.均值平滑滤波器可⽤于锐化图像边缘（×）23.拉普拉斯算⼦可⽤于图像的平滑处理（×）24.⾼频加强滤波器可以有效增强图像边缘和灰度平滑区的对⽐度（√）25.应⽤傅⽴叶变换的可分离性可以将图像的⼆维变换分解为⾏和列⽅向的⼀维变换（√）26.图像分割可以依据图像的灰度、颜⾊、纹理等特性来进⾏（√）27.图像增强有空域和变换域两类（√）28.加⼤、减⼩对⽐度分别会使图像发⽣亮处更亮，暗处更暗的直观变化（√）29.加⼤、减⼩亮度分别会使图像发⽣亮处更亮，暗处更暗的直观变化（×）30.⼆值图像就是只有⿊⽩两个灰度级（√）31.⼀般来说，图像采样间距越⼤，图像数据量越⼤，质量越好；反之亦然（×）34.⼀般⽽⾔，对于椒盐噪声，均值滤波的效果好于中值滤波（×）35.与⾼斯低通滤波器相⽐，理想低通滤波低通滤波器在图像处理过程中更容易出现振铃(rings)（√）⼆、填空题（20分，1分/空）1.⼀般来说，图像采样间距越⼩，图像数据量_____，质量_____；反之亦然（⼤，⾼）2.若采样4个数，⼤⼩分别为4.56 0.23 7.94 16.55。

一、判断题（10分）（正确√，错误×）1.图像处理就是对图像信息进行加工处理，以满足人的视觉心理和实际应用的要求（√）2.在MATLAB中，uint8是无符号8位整数（√）3.在MATLAB中，uint16是无符号16位整数（√）4.图像的点运算与代数运算不相同（√）5.点运算也叫灰度级变换（√）6.线性点运算可以改变数字图像的对比度（√）7.图像的几何变换也叫图像的点运算（×）8.图像的平滑操作实际上是邻域操作（√）9.傅立叶变换后的矩阵处在频域上（√）10.傅立叶变换后的矩阵处在空域上（×）11.傅立叶变换，人们可以在空域和频域中同时思考问题（√）12.像素深度是指存储每个像素所用的位数（√）13.图像经过变换后，图像的大部分能量都集中在中、高频段（×）14.图像经过变换后，图像的大部分能量都集中在低频段（√）15.直方图均衡化也是一种非线性点运算（√）16.仿射变换是空间变换（√）17.空间变换是频域变换（×）18.边缘检测是将边缘像元标识出来的一种图像分割技术（√）19.灰度直方图能反映一幅图像各灰度级像元占图像的面积比（√）20.直方图均衡是一种点运算，图像的二值化则是一种局部运算（×）21.双边滤波法可用于边缘增强（×）22.均值平滑滤波器可用于锐化图像边缘（×）23.拉普拉斯算子可用于图像的平滑处理（×）24.高频加强滤波器可以有效增强图像边缘和灰度平滑区的对比度（√）25.应用傅立叶变换的可分离性可以将图像的二维变换分解为行和列方向的一维变换（√）26.图像分割可以依据图像的灰度、颜色、纹理等特性来进行（√）27.图像增强有空域和变换域两类（√）28.加大、减小对比度分别会使图像发生亮处更亮，暗处更暗的直观变化（√）29.加大、减小亮度分别会使图像发生亮处更亮，暗处更暗的直观变化（×）30.二值图像就是只有黑白两个灰度级（√）31.一般来说，图像采样间距越大，图像数据量越大，质量越好；反之亦然（×）32.用Matlab开辟一个图像窗口的命令是imshow（×）33.图像尺寸为400*300是指图像的宽为400毫米，高为300毫米（×）34.一般而言，对于椒盐噪声，均值滤波的效果好于中值滤波（×）35.与高斯低通滤波器相比，理想低通滤波低通滤波器在图像处理过程中更容易出现振铃(rings)（√）二、填空题（20分，1分/空）1.一般来说，图像采样间距越小，图像数据量_____，质量_____；反之亦然（大，高）2.若采样4个数，大小分别为4.56 0.23 7.94 16.55。

第4章 MATLAB程序流程控制习题4一、选择题1．下列关于脚本文件和函数文件的描述中不正确的是（)。

A A．函数文件可以在命令行窗口直接运行B．去掉函数文件第一行的定义行可转变成脚本文件C．脚本文件可以调用函数文件D．函数文件中的第一行必须以function开始2．下列程序的输出结果是( ）。

Dy=10；if y==10y=20；elseif y>0y=30enddisp（y)A．1 B．30 C．10 D．203．有以下语句：a=eye（5)；for n=a(2:end,：)for循环的循环次数是（）。

CA．3 B．4 C．5 D．104．设有程序段k=10;whilekk=k—1end则下面描述中正确的是（）。

AA．while循环执行10次B．循环是无限循环C．循环体语句一次也不执行D．循环体语句执行一次5．有以下程序段：x=reshape（1:12,3,4）;m=0;n=0；for k=1：4if x（：，k)<=6m=m+1;elsen=n+1；endend则m和n的值分别是（）。

CA．6 6 B．2 1 C．2 2 D．1 26．调用函数时，如果函数文件名与函数名不一致,则使用（)。

A A．函数文件名B．函数名C．函数文件名或函数名均可D．＠函数名7．如果有函数声明行为“function [x,y,z］=f1（a，b,c）”,则下述函数调用格式中错误的是（）。

BA．x=f1（a,b,c) B．[x,y，z，w]=f1(a,b,c)C．[x，b，z］=f1（a，y,c) D．[a，b]=f1(x,y，z）8．执行语句“fn=@(x）10＊x;"，则fn是（）。

AA．匿名函数B．函数句柄C．字符串D．普通函数9．执行下列语句后，变量A的值是( ）。

D>> f=@（x，y) log（exp（x+y）);〉〉 A=f(22,3);A．22，3B．22 C．3 D．2510．程序调试时用于设置断点的函数是（）。

matlab教材习题答案Matlab是一种广泛应用于科学与工程领域的计算机编程语言和环境。

它具备强大的数值计算和数据可视化功能，被广泛用于数据分析、信号处理、图像处理、机器学习等领域。

对于初学者而言，掌握Matlab的基本语法和常用函数是非常重要的，而教材习题则是帮助学生巩固所学知识的重要资源。

本文将为大家提供一些Matlab教材习题的参考答案，以帮助读者更好地学习和应用Matlab。

1. 基本语法练习题1.1 计算并输出1到10的平方for i = 1:10fprintf('%d的平方是：%d\n', i, i^2);end1.2 计算并输出1到10的阶乘for i = 1:10fact = 1;for j = 1:ifact = fact * j;endfprintf('%d的阶乘是：%d\n', i, fact);end2. 数值计算练习题2.1 求解一元二次方程的根a = 1;b = -3;c = 2;delta = b^2 - 4*a*c;x1 = (-b + sqrt(delta))/(2*a);x2 = (-b - sqrt(delta))/(2*a);fprintf('一元二次方程的根为：%f, %f\n', x1, x2);2.2 求解线性方程组的解A = [1 2; 3 4];B = [5; 6];X = inv(A) * B;fprintf('线性方程组的解为：%f, %f\n', X(1), X(2));3. 数据处理练习题3.1 统计一个数组中的最大值、最小值和平均值data = [1, 2, 3, 4, 5];max_value = max(data);min_value = min(data);average_value = mean(data);fprintf('最大值：%f\n最小值：%f\n平均值：%f\n', max_value, min_value, average_value);3.2 对一个矩阵进行排序matrix = [4 2 3; 1 5 6; 9 8 7];sorted_matrix = sort(matrix);fprintf('排序后的矩阵为：\n');disp(sorted_matrix);4. 图像处理练习题4.1 读取并显示一张图片image = imread('image.jpg');imshow(image);4.2 对一张图片进行灰度化处理gray_image = rgb2gray(image);imshow(gray_image);5. 信号处理练习题5.1 生成并绘制正弦信号t = 0:0.01:2*pi;x = sin(t);plot(t, x);5.2 对一段音频信号进行傅里叶变换[y, fs] = audioread('audio.wav');Y = fft(y);plot(abs(Y));通过以上几个例子，我们可以看到Matlab的强大功能和灵活性。

matlab数字图像处理图像运算+答案实验⼆：图像运算⼀、实验⽬的掌握MATLAB语⾔中图像数据的读取、显⽰与保存⽅法；掌握统计图像灰度直⽅图的⽅法理解直⽅图均衡的原理和作⽤，掌握图像直⽅图均衡化的⽅法理解图像点运算、代数运算、⼏何运算的基本定义和常见⽅法进⼀步熟悉了解MATLAB语⾔的应⽤⼆、知识要点1.数据类型及图像类型间的基本转换函数数据类转换：B = data_class_name(A);2.imhist(H)；%显⽰a的直⽅图histeq(H); %将图像a进⾏直⽅图均衡化adapthisteq(H); %将图像a进⾏直⽅图均衡化3.图像的点运算点运算是通过对图像中每个像素值进⾏计算，改善图像显⽰效果的操作，也称对⽐度增强或对⽐度拉伸或灰度变换。

可以表⽰为B(x,y)=f(A(x,y)).进⾏逐点运算，输⼊映射为输出，不改变图像像素的空间关系。

Y=aX+b %线性点运算Y=X+aX(max(X)-X) %⾮线性点运算4.代数运算代数运算是指对两幅输⼊图像进⾏点对点的加、减、乘或除运算⽽得到输出图像的运算。

四种图像代数运算的数学表达式如下：C(i,j)=A(i,j)+B(i,j) C=imadd(A,B)C(i,j)=A(i,j)-B(i,j) C=imsubtract(A,B);C(i,j)=A(i,j)*B(i,j) C=immultiply(A,B)C(i,j)=A(i,j)/B(i,j) C=imdivide(A,B)5.图像加噪函数imnoise（参阅matlab help）imnoise的语法格式为J = imnoise(I,type)J = imnoise(I,type,parameters)其中J=imnoise(I,type)返回对原始图像I添加典型噪声的有噪图像J。

参数type 和parameters⽤于确定噪声的类型和相应的参数。

J = imnoise(I,'gaussian',m,v) %加⼊均值m,⽅差为v的⾼斯噪声，m默认值0,v默认值0.01J = imnoise(I,'poisson') %加⼊泊松分布的噪声J = imnoise(I,'salt & pepper',d)%加⼊密度为d的椒盐噪声，d的默认值为0.05 J = imnoise(I,'speckle',v) %加⼊均值0,⽅差为v的乘性噪声三、实验内容1、将给定的Couple.bmp图像⽂件读出并显⽰，显⽰其灰度直⽅图，分别⽤histeq、adapthiateq函数将其直⽅图均衡化，观察均衡后的图像及其直⽅图。

数字图像处理及MATLAB实现4武汉理工大学信息学院第4章图像变换(ImageTranform)4.1连续傅里叶变换4.2离散傅里叶变换4.3快速傅里叶变换4.4傅里叶变换的性质4.5图像傅里叶变换实例4.6其他离散变换一、图象变换的引入1.方法：对图象信息进行变换，使能量保持但重新分配。

2.目的：有利于加工、处理[滤除不必要信息(如噪声),加强/提取感兴趣的部分或特征]。

二、方法分类可分离、正交变换:2D-DFT,2D-DCT,2D-DHT,2D-DWT三、用途1.提取图象特征(如):(1)直流分量：f(某,y)的平均值=F(0,0);(2)目标物边缘：F(u,v)高频分量。

2.图像压缩：正交变换能量集中，对集中(小)部分进行编码。

3.图象增强：低通滤波，平滑噪声；高通滤波，锐化边缘。

4.1连续傅里叶变换(ContinuouFourierTranform)1、一维傅立叶变换及其反变换::1F(u)f(某)ej2u某d某f(某)F(u)ej2u某du4.1.1连续傅里叶变换的定义(DefinitionofContinuouFourierTranform)这里f某是实函数，它的傅里叶变换Fu通F常是复函数。

u的实部、虚部、振幅、能量和相位分别表示如下：实部Ruftco2utdt(4.3)虚部Iuftin2utdt(4.4)振幅1FuR2uI2u2(4.5)4.1.1连续傅里叶变换的定义(DefinitionofContinuouFourierTranform)能量相位EuFuR2uI2u2(4.6)(4.7)傅里叶变换可以很容易推广到二维的情形。

设函数f某,y是连续可积的，且fu,v可积，则存在如下的傅里叶变换对：IuuarctanRu4.1连续傅里叶变换的定义(DefinitionofContinuouFourierTranform)Ff(某,y)F(u,v)f(某,y)ej2u某vyd某dy(4.8)F1F(u,v)f(某,y)F(u,v)ej2u某vydudv(4.9)式中u、v是频率变量。

第一章习题3.请指出以下的变量名（函数名、M文件名）中，哪些是合法的？Abc 2004x lil-1 wu_2004 a&b qst.u _xyz 解：合法的变量名有：Abc wu_20044．指令窗操作（1）求[12+2×（7-4）]÷32的运算结果解：>> [12+2*(7-4)]/3^2ans =2（2）输入矩阵A=[1，2，3；4，5，6；7，8，9]，观察输出。

解：>> A=[1,2,3;4,5,6;7,8,9]A =1 2 34 5 67 8 9（3）输入以下指令，观察运算结果；clear;x=-8:0.5:8;y=x';X=ones(size(y))*x;Y=y*ones(size(x));R=sqrt(X.^2+Y.^2)+eps;Z=sin(R)./R;mesh(X,Y,Z);colormap(hot)xlabel('x'),ylabel('y'),zlabel('z')解：7．指令行编辑（1）依次键入以下字符并运行：y1=2*sin(0.3*pi)/(1+sqrt(5))解：>>y1=2*sin(0.3*pi)/(1+sqrt(5))y1 =0.5000(2)通过反复按键盘的箭头键，实现指令回调和编辑，进行新的计算；y2=2*cos(0.3*pi)/(1+sqrt(5))解：>>y2=2*cos(0.3*pi)/(1+sqrt(5))y2 =0.363311.编写题4中（3）的M脚本文件，并运行之。

解：第二章习题1.在指令窗中键入x=1:0.2:2和y=2:0.2:1,观察所生成的数组。

解:>> x=1:0.2:2 x =1.0000 1.2000 1.4000 1.6000 1.80002.0000 >> y=2:0.2:1 y =Empty matrix: 1-by-02．要求在[0，2π]上产生50个等距采样数据的一维数组，试用两种不同的指令实现。

clc,clear,clf,close all;disp('题解4.5,4.6,4.7');pause;echo on;a=[3 4 7 2 9 12],roots(a),pause,b=[1 0 0 0 0 -1],roots(b),pause,c=[-3 -5 -8 -9],poly(c),echo off;disp('题解4.8');pause;echo on;a=[1 2 5 4 3],b=[1],[r,p,k]=residue(b,a)pause,t=0:0.2:10;ys=r(1)*exp(p(1)*t)+r(2)*exp(p(2)*t)+r(3)*exp(p(3)*t)+r(4)*exp(p(4)*t); h=plot(t,ys);set(h,'linewidth',2),echo off;disp('题解4.9,4.10');pause;echo on;R1=randn(8,6),mean(R1),std(R1),pause,mean(R1(:)),std(R1(:)),pause,R=ceil(16*rand(4,6)),a=R(:,[1,2,3,4]),inv(a),echo off;disp('题解4.11');echo on;t=[0:0.05:10];x1=2.*cos(t)+3.*t;y1=2.*sin(t)+3;plot(x1,y1),shg,hold on;x2=3.*cos(t)+3.*t;y2=3.*sin(t)+3;plot(x2,y2),shgx3=4.*cos(t)+3.*t;y3=4.*sin(t)+3;plot(x3,y3),shghold off;pause;figure;plot(x1,y1,x2,y2,x3,y3)echo off;disp('题解4.12');echo on;t=[-2*pi:0.05:2*pi];a=0;x=sin(t);y1=sin(t+a);y2=sin(2.*t+a);y3=sin(3.*t+a);y4=sin(4.*t+a);subplot(2,2,1),plot(x,y1), subplot(2,2,2),plot(x,y2), subplot(2,2,3),plot(x,y3), subplot(2,2,4),plot(x,y4), pause;y11=sin(2.*t);y22=sin(2.*t+pi/3);y33=sin(2.*t+pi/2);y44=sin(2.*t+pi);figure;subplot(2,2,1),plot(x,y11), subplot(2,2,2),plot(x,y22), subplot(2,2,3),plot(x,y33), subplot(2,2,4),plot(x,y44), echo off;disp('题解4.13');pause; echo on;p=[1 -4 0 3 -2 6],x=linspace(-2,8,100);y=polyval(p,x);plot(x,y),pauseaxis([-2 8 -20 20])pause,roots(p),echo off;disp('题解4.14')echo on;z=[0:0.05:10];x=z.*sin(3.*z);y=z.*cos(3.*z);plot3(x,y,z);pause;figure,plot3(x,y,z,'r:')pause;xlabel('x'),ylabel('y'),zlabel('z'), echo off;disp('题解4.15 4.16');echo on;[x,y]=meshgrid(-2:0.1:2,-2:0.1:2); z=x.^2.*exp(-(x.^2+y.^2)); mesh(z);hold on;pause;z1=0.05.*x-0.05.*y+0.1;mesh(z1);echo off;for i=1:41for j=1:41if z(i,j)==z1(i,j)a=z(i,j);plot3(i,j,a,'r+');endendendhold off;disp('题解4.18');pause;type f1.mi=1;a(1)=fzero('f1',-2);for m=-2:1:8b=fzero('f1',m);if abs(a(i)-b)>0.00001i=i+1;a(i)=b;endendapause,echo on,fplot('f1',[-2 8]);shg;hold on,plot(a,0,'ro'),shg,pause,axis([-2 8 -20 20]),grid,hold off;echo off;disp('题解4.18第二问');pause; type f11.mi=1;a(1)=fzero('f11',-2);for m=-2:1:8b=fzero('f11',m);if abs(a(i)-b)>0.00001i=i+1;a(i)=b;endendapause,echo on,fplot('f11',[-2 8]);shg;hold on,plot(a,0,'ro'),shg,pause,axis([-2 8 -20 20]),grid,hold off;echo off;disp('题解4.19');echo on;x=[0:0.05:4];y=f31(x);plot(x,y)echo off;disp('题解420');pause;type f420.mi=1;a(1)=fzero('f420',0.1);for m=0.1:0.1:4b=fzero('f420',m);if abs(a(i)-b)>0.0001i=i+1;a(i)=b;endendapause,echo on,fplot('f420',[0 4]);shg;hold on,plot(a,f420(a),'ro'),shg,pause, axis([0 4 -20 20]),grid,hold off;pause,quad('f420',a(1),a(2)),echo off;disp('题解421');pause;type f421.mecho on[x,y]=ode23('f421',[0 5],1);plot(x,y),shg,pause,p=polyfit(x,y,9),xi=0:0.1:5;yi=polyval(p,xi);plot(x,y,'ro',xi,yi,'b')echo off,disp('题解422');pause;echo onpause,s='magic(3)',pause,eval(s);pause,y(3,:)='magic(3)';y(4,:)='magic(4)';y(5,:)='magic(5)';y,pausefor n=3:5eval(y(n,:));endecho offdisp('题解424');pause;echo one=exp(1);pause,st=sprintf('自然对数底数e=%21.20f',e);disp(st) echo offdisp('题解425');pause;echo on='Jone';student.birthplace='Shanghai';student(2).name='David';student(2).birthplace='Nanjing';student(3).name='Tom';student(3).birthplace='Hangzhou';student,pause,name={'Jone';'David';'Tom'};birthplace={'Shanghai';'Nanjing';'Hangzhou'}; studentt={name;birthplace};studentt,pause,student1=['Jone ';'Shanhai'],student2=['David ';'Nanjing'],student3=['Tom ';'Hongzhou'],echo off调用子程序f1.mfunction y=f1(x)y=x.^5-4*x.^4+3*x.^2-2*x+6;f11.mfunction y=f11(x)y=x.^5-4*x.^4+3*x.^2-2*x+6+x.*sin(x);f31.mfunction f1=f31(x)f1=1./((x-2).^2+0.1)+1./((x-3).^4+0.01);f420.mfunction y=f420(x)y=x.^3-2*(x.^2).*sin(x)+5*x.*cos(x)+1./(x); f421.mfunction yp=f421(x,y)yp=(x.^2)./y-x.*cos(y);。

MATLAB图像处理相关习题实例1：三角函数曲线（1）function shili01h0=figure('toolbar','none','position',[198 56 350 300],'name','实例01'); h1=axes('parent',h0,'visible','off');x=-pi:0.05:pi;y=sin(x);plot(x,y);xlabel('自变量X');ylabel('函数值Y');title('SIN( )函数曲线');grid on实例2：图形的叠加function shili02h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例02');x=-pi:0.05:pi;y1=sin(x);y2=cos(x);plot(x,y1,...'-*r',...x,y2,...'--og');grid onxlabel('自变量X');ylabel('函数值Y');title('三角函数');实例3：双y轴图形的绘制function shili03h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例03');x=0:900;a=1000;b=0.005;y1=2*x;y2=cos(b*x);[haxes,hline1,hline2]=plotyy(x,y1,x,y2,'semilogy','plot');axes(haxes(1))ylabel('semilog plot');axes(haxes(2))ylabel('linear plot');实例4：单个轴窗口显示多个图形function shili04h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例04');t=0:pi/10:2*pi;[x,y]=meshgrid(t);subplot(2,2,1)plot(sin(t),cos(t))axis equalsubplot(2,2,2)z=sin(x)-cos(y);plot(t,z)axis([0 2*pi -2 2])subplot(2,2,3)h=sin(x)+cos(y);plot(t,h)axis([0 2*pi -2 2])subplot(2,2,4)g=(sin(x).^2)-(cos(y).^2);plot(t,g)axis([0 2*pi -1 1])实例5：图形标注function shili05h0=figure('toolbar','none',...'position',[200 150 450 400],...'name','实例05');t=0:pi/10:2*pi;h=plot(t,sin(t));xlabel('t=0到2\pi','fontsize',16);ylabel('sin(t)','fontsize',16);title('\it{从0to2\pi 的正弦曲线}','fontsize',16) x=get(h,'xdata');y=get(h,'ydata');imin=find(min(y)==y);imax=find(max(y)==y);text(x(imin),y(imin),...['\leftarrow最小值=',num2str(y(imin))],...'fontsize',16)text(x(imax),y(imax),...['\leftarrow最大值=',num2str(y(imax))],...'fontsize',16)实例6：饼图的绘制function shili06h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例06');t=[54 21 35;68 54 35;45 25 12;48 68 45;68 54 69];x=sum(t);h=pie(x);textobjs=findobj(h,'type','text');str1=get(textobjs,{'string'});val1=get(textobjs,{'extent'});oldext=cat(1,val1{:});names={'商品一：';'商品二：';'商品三：'};str2=strcat(names,str1);set(textobjs,{'string'},str2)val2=get(textobjs,{'extent'});newext=cat(1,val2{:});offset=sign(oldext(:,1)).*(newext(:,3)-oldext(:,3))/2; pos=get(textobjs,{'position'});textpos=cat(1,pos{:});textpos(:,1)=textpos(:,1)+offset;set(textobjs,{'position'},num2cell(textpos,[3,2]))例7：条形图和阶梯形图function shili07h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例07');subplot(2,2,1)x=-3:0.2:3;y=exp(-x.*x);bar(x,y)title('2-D Bar Chart')subplot(2,2,2)x=-3:0.2:3;y=exp(-x.*x);bar3(x,y,'r')title('3-D Bar Chart')subplot(2,2,3)x=-3:0.2:3;y=exp(-x.*x);stairs(x,y)title('Stair Chart')subplot(2,2,4)x=-3:0.2:3;y=exp(-x.*x);barh(x,y)title('Horizontal Bar Chart')实例8：三维曲线图function shili08h0=figure('toolbar','none',...'position',[200 150 450 400],... 'name','实例08');subplot(2,1,1)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,y1,z1,x,y2,z2,x,y3,z3) grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure1:3-D Plot') subplot(2,1,2)x=linspace(0,2*pi);y1=sin(x);y2=cos(x);y3=sin(x)+cos(x);z1=zeros(size(x));z2=0.5*z1;z3=z1;plot3(x,z1,y1,x,z2,y2,x,z3,y3) grid onxlabel('X轴');ylabel('Y轴');zlabel('Z轴');title('Figure2:3-D Plot')实例09：视角的调整function shili09h0=figure('toolbar','none',...'position',[200 150 450 350],... 'name','实例09);x=-5:0.5:5;[x,y]=meshgrid(x);r=sqrt(x.^2+y.^2)+eps;z=sin(r)./r;subplot(2,2,1)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure1')view(-37.5,30)subplot(2,2,2)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure2')view(-37.5+90,30)subplot(2,2,3)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure3')view(-37.5,60)subplot(2,2,4)surf(x,y,z)xlabel('X-axis')ylabel('Y-axis')zlabel('Z-axis')title('Figure4')view(180,0)实例10：区域图形function shili10h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例10');x=91:95;profits1=[88 75 84 93 77];profits2=[51 64 54 56 68];profits3=[42 54 34 25 24];profits4=[26 38 18 15 4];area(x,profits1,'facecolor',[0.5 0.9 0.6],... 'edgecolor','b',...'linewidth',3)hold onarea(x,profits2,'facecolor',[0.9 0.85 0.7],...'edgecolor','y',...'linewidth',3)hold onarea(x,profits3,'facecolor',[0.3 0.6 0.7],... 'edgecolor','r',...'linewidth',3)hold onarea(x,profits4,'facecolor',[0.6 0.5 0.9],... 'edgecolor','m',...'linewidth',3)hold offset(gca,'xtick',[91:95])set(gca,'layer','top')gtext('\leftarrow第一季度销量')gtext('\leftarrow第二季度销量')gtext('\leftarrow第三季度销量')gtext('\leftarrow第四季度销量')xlabel('年','fontsize',16);ylabel('销售量','fontsize',16);实例11：枝干图function shili11h0=figure('toolbar','none',...'position',[200 150 450 350],...'name','实例11');x=0:pi/20:2*pi;y1=sin(x);y2=cos(x);h1=stem(x,y1+y2);hold onh2=plot(x,y1,'^r',x,y2,'*g');hold offh3=[h1(1);h2];legend(h3,'y1+y2','y1=sin(x)','y2=cos(x)') xlabel('自变量X');ylabel('函数值Y');title('正弦函数与余弦函数的线性组合'); 实例12：罗盘图function shili12h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例12');winddirection=[54 24 65 84256 12 235 62125 324 34 254];windpower=[2 5 5 36 8 12 76 14 10 8];rdirection=winddirection*pi/180;[x,y]=pol2cart(rdirection,windpower); compass(x,y);desc={'风向和风力','北京气象台','10月1日0：00到','10月1日12：00'};gtext(desc)实例13：轮廓图function shili13h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例13');[th,r]=meshgrid((0:10:360)*pi/180,0:0.05:1); [x,y]=pol2cart(th,r);z=x+i*y;f=(z.^4-1).^(0.25);contour(x,y,abs(f),20)axis equalxlabel('实部','fontsize',16);ylabel('虚部','fontsize',16);h=polar([0 2*pi],[0 1]);delete(h)hold oncontour(x,y,abs(f),20)实例14：交互式图形function shili14h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例14');axis([0 10 0 10]);hold onx=[];y=[];n=0;disp('单击鼠标左键点取需要的点');disp('单击鼠标右键点取最后一个点');but=1;while but==1[xi,yi,but]=ginput(1);plot(xi,yi,'bo')n=n+1;disp('单击鼠标左键点取下一个点');x(n,1)=xi;y(n,1)=yi;endt=1:n;ts=1:0.1:n;xs=spline(t,x,ts);ys=spline(t,y,ts);plot(xs,ys,'r-');hold off实例15：变换的傅立叶函数曲线function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren')h=uicontrol('style','slider','position',... [100 10 500 20],'min',1,'max',20)for j=1:20plot(fft(eye(j+16)))set(h,'v alue',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]);movie(m,30)实例16：劳伦兹非线形方程的无序活动function shili15h0=figure('toolbar','none',...'position',[200 150 450 250],...'name','实例15');axis equalm=moviein(20,gcf);set(gca,'nextplot','replacechildren')h=uicontrol('style','slider','position',... [100 10 500 20],'min',1,'max',20)for j=1:20plot(fft(eye(j+16)))set(h,'v alue',j)m(:,j)=getframe(gcf);endclf;axes('position',[0 0 1 1]); movie(m,30)。