三视图中的小正方体计数问题 口诀

由三视图确定小正方体的个数的方法
通过三视图确定小正方体的个数是一种简单而有效的方法，可以用来解决许多复杂的几何问题。

三视图法是一种几何技术，它使用三个平面图来表示一个物体的形状，其中包括正视图、左视图和俯视图。

这三个视图是从不同的角度来看待物体的，可以清楚地显示出物体的三维形状。

例如，如果要确定小正方体的个数，可以使用三视图法。

首先，先找出三个视图，即正视图，左视图和俯视图，仔细观察每个视图中小正方体的位置，数数它们的个数。

然后，根据三个视图中小正方体的位置和数量，计算出小正方体的总数。

根据三视图法，可以通过观察三个视图来确定小正方体的总数，而不需要真正地计算它们的体积。

这一步骤非常实用，可以节省大量的时间和精力。

当然，在使用三视图法之前，需要先熟悉三视图的概念，然后根据实际情况，灵活地运用这一技术来解决实际问题。

只有掌握了这种几何方法，才能解决复杂的几何问题。

总之，三视图法是一种有效的几何方法，可以用来快速确定小正方体的个数。

它可以节省大量的时间和精力，因此被广泛应用于复杂的几何问题的解决中。

数正方形的规律口诀
稿子一
嗨，亲爱的小伙伴们！今天咱们来聊聊数正方形的规律口诀哟！
你知道吗，数正方形这事儿啊，其实挺有趣的。

咱们先看看小的正方形，一个一个的，那数起来简单。

可要是好多正方形堆在一起，就得有点小窍门啦。

比如说，先看最小的那种正方形，一个一个地数清楚。

然后呢，再看看由几个小正方形组成的大一点的正方形。

这时候可别着急，眼睛得放亮。

还有哦，要是图形再复杂点，咱们就一层一层地来。

从里往外，或者从外往里，都可以试试。

其实啊，数正方形就像玩游戏，只要耐心点，多观察，就能找到规律。

比如说，横竖格子数一样的时候，那正方形的总数就有个特别的算法。

总之呢，数正方形别怕麻烦，多练几次，你就会发现其中的乐趣啦！怎么样，是不是觉得没那么难啦？
稿子二
嘿，朋友们！咱们来唠唠数正方形的规律口诀呀！
数正方形，刚开始可能会觉得有点晕乎，但是别慌！咱们慢慢来。

你瞧，如果是一个简单的小方格图，那就从最小的开始数呗。

一个一个，可认真啦。

要是遇到那种大一点的方格图，咱们可以先分分类。

比如说，先数单独的小正方形，再数两个小正方形拼成的，然后三个、四个……
有时候啊，你可以想象自己是个探险家，在这个方格的世界里寻找正方形的宝藏。

而且哦，你还可以边数边做记号，这样就不会乱啦。

还有一个小妙招，要是横竖的格子数量一样，那总数就可以通过一个简单的公式算出来。

是不是很神奇？
反正啊，数正方形就是要细心、耐心，多琢磨琢磨，你肯定能数得又快又准！加油哟，相信你没问题的！。

由三视图判断小正方体个数问题通过小正方体组合图形的三视图,确定组合图形中小正方体的个数,在中考或竞赛中经常会遇到。

解决这类问题如果没有掌握正确的方法，仅仅依赖空间想象去解决，不仅思维难度很大,还很容易出错。

通过三视图计算组合图形的小正方体的个数,关键是要弄清楚这个小正方体组合图形共有多少行、多少列、每行每列中各有多少层,理清了这些行、列、层的数量，小正方体的个数就迎刃而解了.在三视图中，通过主视图、俯视图可以确定组合图形的列数；通过俯视图、左视图可以确定组合图形的行数;通过主视图、左视图可以确定行与列中的最高层数.以上方法可简要地概括为：“主俯看列,俯左看行,主左看层,分清行列层,计数不求人.”一、结果唯一的计数例1在一仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来，如图所示,则这堆正方体货箱共有（)。

A．9箱B．10箱C．11箱D．12箱分析：由三视图可知,这堆货箱共有从前到后3行，从左到右3列。

由左视图：第一行均为1层,第二行最高2层,第三行最高3层；由主视图:第一列、第三列均为1层，第二列(中间列)最高为3层。

故第二行、第二列为2层，第三行第二列为3层，其余皆为1层。

各行、各列小正方体的个数如俯视图中所表示.这堆货箱共有3+1+1+2+1+1=9（箱）。

二、结果不唯一的计数例2（“希望杯”数学邀请赛试题）如图2,是由若干个（大于8个）大小相同的正方体组成的一个几何体的主视图和俯视图,则这个几何体的左视图不可能是(）。

分析：由给出的主视图、俯视图可以看出,该几何体共有2行，3列。

第1列均为1层，第2列最高2层,第3列最高3层。

左视图为A时，第1行、第2行最高均为3层。

几何体中，第1列第1行为1层；第2列第1行、第2行均可为1层或2层，，但不能同时为1层;第3列两行均为3层。

此时，小正方体的个数如俯视图A所示,最少为1+2+1+3+3=10（个），最多为1+2+2+3+3=11个.左视图为B时，第一行均为1层，第二行最高为3层。

思维特训(十八)由三视图巧算正方体个数方法点津·在研究由小正方体搭成的几何体与其三视图的关系时，一般由实物图形可以唯一确定三视图，但反之却要分情况讨论．当条件给出几何体的三个视图或两个视图时，这个几何体不一定是确定的．俯视图确定几何体最底层正方体的个数，主视图和左视图确定几何体的层数、行数及列数．典题精练·类型一由给出的三种视图判断正方体的数量由三视图判断组成原几何体的小正方体的块数的一般解法：(1)数出主视图各列(竖为列)上正方形的个数，将数字分别填在俯视图所对应的列中；(2)再数出左视图各列上正方形的个数，将数字分别填在俯视图所对应的行(横为行)中；(3)在俯视图中的同一个小正方形中，前后两次数字相同的只取一个数，前后两次数字不同的取较小的数，最后将俯视图中各小正方形中的数字相加，所得结果就是组成原几何体的小正方体的总块数．1．由一些大小相同的小正方体组成的几何体的三视图如图18－Y－1所示，那么组成该几何体的小正方体有()图18－Y－1A．4个B．5个C．6个D．7个2．由若干个棱长相等的小正方体搭成的几何体的主视图、左视图、俯视图如图18－Y －2所示，则搭成这个几何体的小正方体有()图18－Y－2A．5个B．6个C．7个D．8个3．如图18－Y－3是由若干个大小相同的小正方体搭成的几何体的三视图，该几何体所用的小正方体的个数是()图18－Y－3A．6 B．4 C．3 D．24．一个几何体由多个完全相同的小正方体组成，它的三视图如图18－Y－4所示，那么组成这个几何体的小正方体的个数为()图18－Y－4A．2 B．3 C．5 D．105．几个棱长为1的小正方体组成的几何体的三视图如图18－Y－5所示，则这个几何体的体积是()图18－Y－5A．4 B．5 C．6 D．76．由完全相同的小立方块搭成的几何体的三视图如图18－Y－6所示，则组成该几何体共用了________个小立方块．图18－Y－6类型二由两种视图判断正方体的数量范围1．已知主视图、俯视图，判断小正方体的数量范围的步骤：在俯视图的方格中标上主视图所看到的小正方体的最高层数，将这些数字填入所在竖列上的每一个方格中，则可得到这个几何体所需最多的小正方体的块数；因为根据俯视图可以确定底层有多少个小正方体，所以方格中的数字最小为1，那么只要将每列上的数字留一个，最高层数不变，其余的均改为1，这样就可以确定最少需要的小正方体的块数．2．已知左视图、俯视图，判断小正方体的数量范围的步骤：在俯视图的方格中标上左视图所看到的小正方体的最高层数，其他步骤同上所述．7．用若干个大小相同的小正方体组合成的几何体的主视图和俯视图如图18－Y－7所示，则下面所给的四个选项中，不可能是这个几何体的左视图的是()图18－Y－7图18－Y－88．如图18－Y－9是由若干个相同的小立方体搭成的几何体的俯视图和左视图，则搭成该几何体的小立方体的个数不可能是()图18－Y－9A．6 B．7 C．8 D．99．一个几何体是由若干个相同的小正方体组成的，其主视图和左视图如图18－Y－10所示，则这个几何体最多可由多少个这样的小正方体组成()图18－Y－10A．12个B．13个C．14个D．18个10．如图18－Y－11是由若干个完全相同的小正方体组成的一个几何体的主视图和左视图，则组成这个几何体的小正方体的个数是()图18－Y－11A．3或4或5 B．4或5C．5或6 D．6或711．用八个同样大小的小立方体搭成一个大立方体，如图18－Y－12①，得到的几何体的三视图如图②所示．若小明从八个小立方体中取走若干个，剩余小立方体保持原位置不动，并使得到的新几何体的三视图仍是图②，则他取走的小立方体最多可以是________个．图18－Y－1212．用小正方体搭成一个几何体，使得其主视图、俯视图如图18－Y－13所示．这样的几何体只有一种吗？(1)它最多需要多少个小正方体？(2)它最少需要多少个小正方体？请分别画出这两种情况下该几何体的左视图．图18－Y－13详解详析1．C[解析] 解决这类问题要做到，一看俯视图，从左至右共有三列，从上到下共有三行；二看主视图，共有三列两行，第一列和第三列上分别只有一层，第二列上有两层，则俯视图中的一、三列上分别只有一个正方体，分别填1(如图①)；三看左视图，共三列两行，第一列和第三列上分别只有一层，第二列上有两层，则俯视图中第一行只有一个正方体，填1，第二行有两个正方体，填2，第三行第二列只有一个正方体，填1，所以在俯视图中每个位置上小正方体的个数如图①所示，搭成这个几何体的小正方体的个数是1＋2＋1＋1＋1＝6，故本题结果选C.相应的几何体如图②所示．2．B[解析] 综合三视图可知，2＋1＋1＋1＝5(个)小正方体，第二层应该有1个小正方体，因此搭成这个几何体的小正方体有5＋1＝6(个)．故选B.3．A 4.C 5.B 6.77.C8.D9．B[解析] 主视图和左视图都为3列，可知该几何体的俯视图有三列三行，最多为3×3个正方形．由主视图可知在俯视图第1，3列的每个正方形内填2，第2列的每个正方形内填1；又由左视图可知，在俯视图的1，3行中(观察者需站在俯视图的左侧看)每个小正方形内都填入2，第2行填1，重叠交叉处数字取小，如图，故这个几何体最多由13个小正方体组成．故选B.10．A11．212．解：这样的几何体不止一种．(1)最多需要6＋6＋2＝14(个)小正方体．左视图如图①.(2)最少需要4＋4＋2＝10(个)小正方体．左视图如图②(左视图不唯一)．。

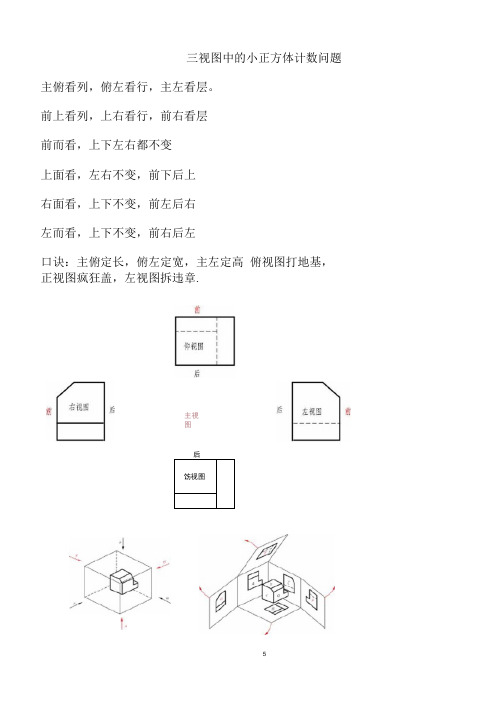
三视图中的小正方体计数问题主俯看列，俯左看行，主左看层。

前上看列，上右看行，前右看层前而看，上下左右都不变上面看，左右不变，前下后上右面看，上下不变，前左后右左而看，上下不变，前右后左口诀：主俯定长，俯左定宽，主左定高俯视图打地基，正视图疯狂盖，左视图拆违章.主視图后饬视图5L 图形 rFRE H Em 是小华从正而、左面、上而看到的，这个物体是由 ____ 块小方块组成的.2•—个几何体是由一些大小相同的小立方块摆成的，如下图是从正而.左而.上而看这个几何体得到的平面图形，那么组成这个几何体所用的小立方块的个数是 _______ • _________ 从正面看3 •如图是某立体图形的俯视图，小正方形中的数字表示在该位置上的小正方体4 •由一些大小相同的小正方体组成的儿何体的俯视图如图所示，其中正方形中a)左右上下块的个数，画出这个几何体的主视图和左视图.从左面看 丛上面看的数字表示在该位置上的小正方体的个数，那么，这个儿何体的左视图是[]5 •如图是一个由多个相同小正方体堆积而成的几何体的俯视图•图中所示数字为该位置小正方体的个数，则这个几何体的主视图是（）6.如图所示，是一个由小立方体搭成的几何体的俯视图，小正方形中数字表示 该位置的小立方块的个数，则它的主视图为（）・叵 2 IT8 •—个由小立方块搭成的几何体如图所示.1 2 13 1该位置的小正方体的个数•请你画出它的主视图和左视图.⑴如图⑶是该几何体的正视图和俯视图，问：这样的几何体的形状确定吗? 如果不确定，那么有多少种情况?(2)如图(b)是该几何体的正视图、左视图和俯视图，问：这样的几何体的形状 确定吗？如果不确定，那么有多少种情况9 •由一些相同的小正方体搭成的几何体的俯视图如右图所示，其中正方形中的数字表示该位置上的小正方体的个数，那么该几何体的左视图是20 •如图所示的几何体是由一些小立方块搭成的, 则这个几何体的俯视图U 如图，由相同的小正方体搭成的几何体的主视图是( )主视方向出田正视国佣视创(a)(D)22•用小正方体搭一个几何体，使它的主视图和俯视图如图所示：（2）搭这样的几何体最少需要 个小正方体，最多需要个小正方体；（2）请你在俯视图的小正方体中用数字表示 当用最多的小正方体搭起的几何体时该位置小正方体的个数；（3）画出其中一种搭成的几何体的左视图・24 •如图是一个由几块相同的小正方体搭成的立体图形的三视图，则这堆立体左视图（2015-深圳模拟> 如图,是由棱长为1的正方体搭成的积木的三视團,则图中棱长为1的正万徉的个数是（>C0B. 5个C. (5个 左视图'・,・！‘■ I ・■-・I主观图 主视图D ・7个图 形 中 的 15•如图，是由一些相同的小正方体搭成的几何体的三视图，搭成这个几何体的小正方体的个数有() 主视图左视图体 有共 小 正 方。

三视图中的小正方体计数问题通过小正方体组合图形的三视图，确定组合图形中小正方体的个数，在中考或竞赛中经常会遇到。

解决这类问题如果没有掌握正确的方法，仅仅依赖空间想象去解决，不仅思维难度很大，还很容易出错。

通过三视图计算组合图形的小正方体的个数，关键是要弄清楚这个小正方体组合图形共有多少行、多少列、每行每列中各有多少层，理清了这些行、列、层的数量，小正方体的个数就迎刃而解了。

在三视图中，通过主视图、俯视图可以确定组合图形的列数；通过俯视图、左视图可以确定组合图形的行数；通过主视图、左视图可以确定行与列中的最高层数。

以上方法可简要地概括为：“主俯看列，俯左看行，主左看层，分清行列层，计数不求人。

”一、结果唯一的计数例1在一仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来，如图所示，则这堆正方体货箱共有（）A．9箱 B．10箱 C．11箱 D．12箱分析：由三视图可知，这堆货箱共有从前到后3行，从左到右3列。

由左视图：第一行均为1层，第二行最高2层，第三行最高3层；由主视图：第一列、第三列均为1层，第二列（中间列）最高为3层。

故第二行、第二列为2层，第三行第二列为3层，其余皆为1层。

各行、各列小正方体的个数如俯视图中所表示。

这堆货箱共有3+1+1+2+1+1=9（箱）。

练习题1．在一仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来（如图），则这堆正方体货箱共有（）A．4箱B．5箱C．6箱D．7箱2．在仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱从三个方向看到的图形画了出来，如图所示，则这堆正方体货箱共有（）A．9箱B．10箱C．11箱D．12箱3．在某仓库里堆放着若干个相同的正方体货箱，管理员将这堆货箱的三视图画了出来（如图），则这堆正方体货箱共有（） A．8箱B．9箱C．10箱D．11箱4．在一个仓库里堆放有若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画出来，如图，则这堆货箱共有（）A．6个B．5个C．4个D．3个5．在一个仓库里堆放有若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画出来，如图，则这堆货箱共有（）A．4个B．5个C．6个D．7个6．在学校教师办公室里堆放着若干个相同的正方体粉笔盒，某同学将这堆粉笔盒的三视图画了出来，如图，则这堆粉笔盒共有（）A．2个B．3个C．4个D．5个7．在抗震救灾某仓库里放着若干个相同的正方体货箱，某摄影记者将这堆货箱的三视图照了出来（如图），则这堆正方体货箱共有（）A．2箱B．3箱C．4箱D．5箱8．在一个仓库里堆积着若干个正方体的货箱，要搬运这些货箱很困难，可是仓库管理员要落实一下箱子的数量，于是就想出一个方法：将这堆货箱分别从正面、左面、上面所看到的平面图形画了出来，如图所示，你能根据这些平面图形帮他清点一下箱子的数量吗？这些正方体货箱的个数为（）A．5 B．6 C．7 D．89．如图是抗争救灾某仓库里放着若干个正方体货箱，某摄影记者将这堆货箱的三视图照了出来，则这堆正方体货箱共有（）A．5箱B．6箱C．7箱D．8箱10．在学校仓库里堆放着若干个盒相同的正方体小粉笔盒，仓库管理员将这堆粉笔盒的三视图画了出来，如图所示，则这堆正方体小粉笔盒共有（）A．11盒B．10盒C．9盒D．8盒11．在一个仓库里堆积着正方体的货箱若干，要搬运这些箱子很困难，可是仓库管理员要落实一下箱子的数量，于是就想出一个办法：将这堆货物的三种视图画了出来，如图，你能根据三视图，帮他清点一下箱子的数量吗？这些正方体箱的个数是（）A．6 B．7 C．8 D．912．在一个仓库里堆积着正方体的货箱若干，要搬运这些箱子很困难，可是仓库管理员要落实一下箱子的数量，于是就想出一个办法：将这堆货物的三种视图画了出来，如图，你能根据三视图，帮他清点一下箱子的数量吗？这些箱子的个数是（）A．9 B．8 C．7 D．613．仓库里堆积着正方体的货箱若干，根据如图所示的三视图可得出箱子的个数是（）A．6 B．7 C．8 D．9二、根据两种视图确定计数范围（结果不唯一的计数）（1）知道几何体的主视图和俯视图例2.如图2，是由若干个（大于8个）大小相同的正方体组成的一个几何体的主视图和俯视图，则这个几何体的左视图不可能是（）。

由三视图,判断小正方体个数问题通过小正方体组合图形的三视图，确定组合图形中小正方体的个数，在中考或竞赛中经常会遇到。

解决这类问题如果没有掌握正确的方法，仅仅依赖空间想象去解决，不仅思维难度很大，还很容易出错。

通过三视图计算组合图形的小正方体的个数，关键是要弄清楚这个小正方体组合图形共有多少行、多少列、每行每列中各有多少层，理清了这些行、列、层的数量，小正方体的个数就迎刃而解了。

在三视图中，通过主视图、俯视图可以确定组合图形的列数；通过俯视图、左视图可以确定组合图形的行数；通过主视图、左视图可以确定行与列中的最高层数。

以上方法可简要地概括为：“主俯看列，俯左看行，主左看层，分清行列层，计数不求人。

”一、结果唯一的计数例1 在一仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来，如图所示，则这堆正方体货箱共有（）。

A．9箱 B．10箱 C．11箱 D．12箱分析：由三视图可知，这堆货箱共有从前到后3行，从左到右3列。

由左视图：第一行均为1层，第二行最高2层，第三行最高3层；由主视图：第一列、第三列均为1层，第二列（中间列）最高为3层。

故第二行、第二列为2层，第三行第二列为3层，其余皆为1层。

各行、各列小正方体的个数如俯视图中所表示。

这堆货箱共有3+1+1+2+1+1=9（箱）。

二、结果不唯一的计数例2（“希望杯”数学邀请赛试题）如图2，是由若干个（大于8个）大小相同的正方体组成的一个几何体的主视图和俯视图，则这个几何体的左视图不可能是（）。

分析：由给出的主视图、俯视图可以看出，该几何体共有2行，3列。

第1列均为1层，第2列最高2层，第3列最高3层。

左视图为A时，第1行、第2行最高均为3层。

几何体中，第1列第1行为1层；第2列第1行、第2行均可为1层或2层，，但不能同时为1层；第3列两行均为3层。

此时，小正方体的个数如俯视图A所示，最少为1+2+1+3+3=10（个），最多为1+2+2+3+3=11个。

由三视图判断小正方体个数问题通过小正方体组合图形的三视图，确定组合图形中小正方体的个数,在中考或竞赛中经常会遇到。

解决这类问题如果没有掌握正确的方法,仅仅依赖空间想象去解决,不仅思维难度很大,还很容易出错。

通过三视图计算组合图形的小正方体的个数,关键是要弄清楚这个小正方体组合图形共有多少行、多少列、每行每列中各有多少层，理清了这些行、列、层的数量,小正方体的个数就迎刃而解了。

在三视图中,通过主视图、俯视图可以确定组合图形的列数；通过俯视图、左视图可以确定组合图形的行数；通过主视图、左视图可以确定行与列中的最高层数.以上方法可简要地概括为：“主俯看列,俯左看行,主左看层,分清行列层，计数不求人。

”一、结果唯一的计数例1在一仓库里堆放着若干个相同的正方体货箱，仓库管理员将这堆货箱的三视图画了出来，如图所示，则这堆正方体货箱共有（）。

A．9箱B．10箱C．11箱D．12箱分析：由三视图可知,这堆货箱共有从前到后3行，从左到右3列。

由左视图：第一行均为1层,第二行最高2层，第三行最高3层；由主视图：第一列、第三列均为1层，第二列(中间列)最高为3层.故第二行、第二列为2层，第三行第二列为3层，其余皆为1层。

各行、各列小正方体的个数如俯视图中所表示。

这堆货箱共有3+1+1+2+1+1=9（箱）。

二、结果不唯一的计数例2（“希望杯”数学邀请赛试题）如图2，是由若干个（大于8个）大小相同的正方体组成的一个几何体的主视图和俯视图，则这个几何体的左视图不可能是（）.分析：由给出的主视图、俯视图可以看出，该几何体共有2行，3列。

第1列均为1层，第2列最高2层，第3列最高3层。

左视图为A时，第1行、第2行最高均为3层。

几何体中，第1列第1行为1层；第2列第1行、第2行均可为1层或2层，，但不能同时为1层；第3列两行均为3层。

此时，小正方体的个数如俯视图A所示，最少为1+2+1+3+3=10（个），最多为1+2+2+3+3=11个。

怎样由三视图确定正方体个数三视图不仅是新教材的一大亮点，也是近些年各省市中考的热点. 学习视图，不仅会画空间几何体的三视图，还应会根据一个空间几何体的三视图，想象出这个简单几何体的形状，若是由小正方体组成的几何体，则要能确定小正方体的个数.例1．由一些大小相同的小正方体组成的几何体的三种视图如图所示，那么组成几何体的小正方体有（ ）个.（A ）4 （B ）5 （C ）6 （D ）7析解：解决这类问题要做到，一看俯视图，从左至右共有三列，从上到下共三行；二看主视图，共有三列两行，第一列和第三列上分别只有一层，第二列上有两层，则俯视图中的一、三列上分别只有一个正方体，分别填1（如图1）；三看左视图，共三列两行，第一列和第三列上分别只有一层，第二列上有两层，则俯视图中第一行只有一个正方体，填1，第二行有两个正方体，填2，第三行第二列只有一个正方体，填1，所以该俯视图上每个小正方体的个数如图1所示，搭成这个几何体的小正方体的个数是1+2+1+1+1=6，故本题结果就选 (C). 相应的几何体如图2所示.图121111 图2例2. 如图是由几个相同的小正方体搭成的几何体的三种视图，则搭成这个几何体的小正方体的个数是 个.析解：先看俯视图，从左至右共有两列，从上到下共两行；再看主视图，共有两列两行，第一列上只有一层，第二列上有两层，则俯视图中的第一列的第一行只有一个正方体，填1（如图3），第二列的第一行、第二行中至少有一行有两个正方体，具体情况再看左视图；左视图共两列两行，第一列有两层，第二列上只有一层，则俯视图中（观察者需站在俯视图的左侧看）第一行的第二列有两个正方体，填2，第二行只有一个正方体，填1，所以该俯视图上每个小主视图 左视图 俯视图正方体的个数如图3所示，搭成这个几何体的小正方体的个数是1+2+1=4，故本题结果就填4. 相应的几何体如图4所示.图4例3．一个几何体是由若干个相同正方体组成的，其主视图和左视图如图5所示，则这个几何体最多可由多少个这样的正方体组成？ （ ）（A ）12个 （B ）13个 （C ）14个 （D ）18个图6111112222解析：主视图和左视图都为3列，可知几何体的俯视图有三列三行，最多为33 的正方形，由主视图可知在俯视图第1、3列每个正方形内填2，第2列每个正方形内填1；又由左视图可知，在俯视图的1、3行中（观察者需站在俯视图的左侧看）每个小正方形内都填入2，第2行填1，重叠交叉处数字取小，如上图，故最多由13个组成. 故选（B ）.点评：由三视图到确定几何体，应根据主视图和俯视图情况分析，再结合左视图的情况定出几何体，最后便可得出这个几何体组合的小正方体个数.名称： U3：由三视图判断几何体描述： （1）由三视图想象几何体的形状，首先，应分别根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，然后综合起来考虑整体形状．（2）由物体的三视图想象几何体的形状是有一定难度的，可以从以下途径进行分析：①根据主视图、俯视图和左视图想象几何体的前面、上面和左侧面的形状，以及几何体的长、宽、高；②从实线和虚线想象几何体看得见部分和看不见部分的轮廓线；③熟记一些简单的几何体的三视图对复杂几何体的想象会有帮助；④利用由三视图画几何体与有几何体画三视图的互逆过程，反复练习，不断总结方法．用三视图确定小正方体的块数的简便方法一、由三个视图确定小正方体的块数例 1 如图所示的是一个由相同的小正方体搭成的几何体的三视图，那么这个几何体是由多少个小正方体搭成的？图5主视图左视图俯视图解析：在三个视图中，俯视图最重要，它可以直接确定底层有几个正方体，再由主视图，左视图确定有几层，每层有几个．一般步骤：1．复制一张俯视图，在俯视图的下方，左方分别标上主视图，左视图所看到的小正方体的最高层数．21 2 12如在横竖方向对应的都是2，则填入2；若方格所对应的横竖方向上的数字不一样，如在横竖方向对应的分别是填入12211 2 1通过上面的两步，我们就能确定每一个方格中的数字（方格中的数字代表所在位置的正方体的块数），从而就能确定这个几何体所需要的小正方体的块数．答案： 2 1 ，这个几何体是由8块小正方体搭成的．1 2 11二、由两个视图确定小正方体的块数根据两个视图一般不能确定一个几何体，但可以确定搭成这样的几何体最多需要多少块？最少需要多少块？1．由主视图，俯视图来确定例2 如图所示的是由一些正方体小木块搭成的几何体的主视图，俯视图．它最多需要多主视图俯视图解析：（1）复制一张俯视图，在俯视图的下方标上主视图所看到的小正方体的最高层数，将这些数字填入所在竖上的每一个方格，则可得到这个几何体所需最多的小正方体的块数．3 2 13 23 23 2 1（2）因为从俯视图可以确定底层有正方体，所以方格中的数字最小为1，那么只要将每列上的数字留一个，其余的均改为1，这样就可以确定最少需要的小正方体的块数．举两种情况如图：3 2 1 1 1 11 1 3 21 1 1 1所以这个几何体最多需要16块，最少需要10块．2．由左视图，俯视图来确定方法跟由主视图，俯视图来确定一样.例3 如图所示的是由一些正方体小木块搭成的几何体的左视图，俯视图，它最多需要多少块？最少需要多少块？左视图俯视图解析：（1）复制一张俯视图，在俯视图的左方标上左视图所看到的小正方体的最高层数，将这些数字填入所在横上的每一个方格，则可得到这个几何体所需最多的小正方体的块数.3 31 1 12 2 2 2（2）因为从俯视图可以确定底层有正方体，所以方格中的数字最小为1，那么只要将每横上的数字留一个，其余的均改为1，这样就可以确定最少需要的小正方体的块数．举两种情况如图：3 3 3 31 1 1 1 1 12 2 1 1 2 1 2 1所以这个几何体最多需要11块，最少需要9块．3．由主视图，左视图来确定由这两个视图来确定小正方体的块数是最难的．例4 如图所示的是由一些正方体小木块搭成的几何体的主视图，左视图，它最多需要多少块？最少需要多少块？主视图左视图解析：（1）取一张3×4的方格纸，在方格纸的下方，左方分别标上主视图，左视图所看到的小正方体的最高层数．然后，在方格纸中填入方格所在横，竖上的较小的数字（如果相同取相同的数字），那么就可确定这个几何体所需最多的小正方体的块数．2 2 1 2 23 2 1 3 21 1 1 1 12 13 2（2）在方格纸中寻找所在横，竖方向上的数字一样的方格，取相同的数字填入方格，这样就可以确定最少需要的小正方体的块数．2 2 23 31 12 13 2所以这个几何体最多需要19块，最少需要8块．通过小正方体组合图形的三视图，确定组合图形中小正方体的个数，在中考或竞赛中经常会遇到．解决这类问题如果没有掌握正确的方法，仅仅依赖空间想象去解决，不仅思维难度很大，还很容易出错．通过三视图确定组合图形的小正方体的个数，关键是要弄清楚这个小正方体组合图形共有多少行、多少列、每行每列中各有多少层，理清了这些行、列、层的数量，再按照上面介绍的方法，小正方体的个数就迎刃而解了．。