高压工艺N阱电阻SPICE模型研究
- 格式:pdf
- 大小:314.12 KB
- 文档页数:6
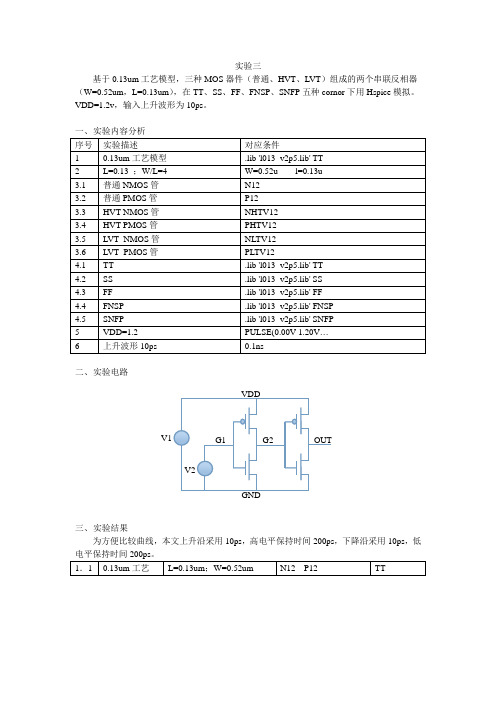
实验三基于0.13um工艺模型,三种MOS器件(普通、HVT、LVT)组成的两个串联反相器(W=0.52um,L=0.13um),在TT、SS、FF、FNSP、SNFP五种cornor下用Hspice模拟。
VDD=1.2v,输入上升波形为10ps。
一、实验内容分析二、实验电路三、实验结果为方便比较曲线,本文上升沿采用10ps,高电平保持时间200ps,下降沿采用10ps,低其中上升沿延时为26ps,下降沿延时为35ps,一个周期的平均功耗为2.184e-0.5 1.2 0.13um工艺L=0.13um;W=0.52um N12 P12 SS其中上升沿延时为26ps,下降沿延时为35ps,一个周期平均功耗为1.998e-05 1.3 0.13um工艺L=0.13um;W=0.52um N12 P12 FF上升沿延时:23ps;下降沿延时:30ps;一周期的平均功耗:2.261e-051.4 0.13um工艺L=0.13um;W=0.52um N12 P12 FNSP上升沿延时:26ps;下降沿延时:37ps 一周期的平均功耗:2.081e-051.5 0.13um工艺L=0.13um;W=0.52um N12 P12 SNFP上升沿延时:26ps;下降沿延时:34ps;一周期的平均功耗:2.118e-052.1 0.13um工艺L=0.13um;W=0.52um NHVT12 PHVT12 TT上升沿延时:37ps;下降沿延时:51ps;一周期的平均功耗:2.305e-052.2 0.13um工艺L=0.13um;W=0.52um NHVT12 PHVT12 SS上升沿延时:48ps;下降沿延时:69ps;一周期的平均功耗:2.247e-05 2.3 0.13um工艺L=0.13um;W=0.52um NHVT12 PHVT12 FF上升沿延时:31ps;下降沿延时:40ps;一周期的平均功耗:2.336e-052.4 0.13um工艺L=0.13um;W=0.52um NHVT12 PHVT12 FNSP上升沿延时:42ps;下降沿延时:60ps;一周期的平均功耗:2.173e-052.5 0.13um工艺L=0.13um;W=0.52um NHVT12 PHVT12 SNFP上升沿延时:36ps;下降沿延时:48ps 一周期的平均功耗:2.345e-053.1 0.13um工艺L=0.13um;W=0.52um NLVT12 PLVT12 TT上升沿延时:22ps ;下降沿延时:27ps;一周期的平均功耗:2.196e-053.2 0.13um工艺L=0.13um;W=0.52um NLVT12 PLVT12 SS上升沿延时:26ps 下降沿延时:33ps 一周期的平均功耗:2.083e-053.3 0.13um工艺L=0.13um;W=0.52um NLVT12 PLVT12 FF上升沿延时:18ps;下降沿延时:22ps;一周期的平均功耗:2.355e-0.53.4 0.13um工艺L=0.13um;W=0.52um NLVT12 PLVT12 FNSP上升沿延时:23ps;下降沿延时:30ps;一周期的平均功耗:2.227e-053.5 0.13um工艺L=0.13um;W=0.52um NLVT12 PLVT12 SNFP上升沿延时:21ps 下降沿延时:26ps 一周期的平均功耗:2.274e-05四、实验结果分析LVT 普通HVT阈值CornerTT 22-27 26-35 37-51SS 26-33 26-35 48-69FF 18-22 23-30 31-40FNSP 23-30 26-37 42-60SNFP 21-26 26-34 36-48功耗分析(e-05)LVT 普通HVT阈值CornerTT 2.196 2.184 2.305SS 2.083 1.998 2.247FF 2.355 2.261 2.336FNSP 2.227 2.081 2.173SNFP 2.274 2.118 2.345经分析,对于该电路的设计而言,可得出以下结论:1.同一阈值不同Corner 中,延时由小到大为:FF,SNFP,TT,FNSP,SS;2.同一Corner不同阈值中,延时由小到大为:LVT,普通,HVT;3.同一阈值不同Corner 中,功耗由小到大为:SS,TT,FNSP,SNFP,FF;4.同一Corner不同阈值中,功耗由小到大为:普通,LVT,HVT;因此,为关键路径选择器件,Corner为FF;阈值为LVT;为非关键路径选择器件,Corner为SS;阈值为普通。


第23卷 第6期 2005年11月应用科学学报JOURNA L OF APP LIE D SCIE NCESV ol.23,N o.6 N ov.2005 收稿日期:2004207218; 修订日期:2004211212基金项目:国家“863”高技术研究发展计划资助项目(2003AA1Z 1400)作者简介:赵 野(1977-),男,辽宁绥中人,博士生,E 2mail :zhaoye @ 文章编号:025528297(2005)0620604206高压功率V DMOST 的SPICE 直流模型赵 野, 孙伟锋, 易扬波, 鲍嘉明(东南大学国家专用集成电路系统工程技术研究中心,江苏南京210096)摘 要:基于高压VDM OST 的物理机理和特殊结构,详细分析、推导了漂移区电阻、埋层电阻、内部节点电压及内部耗尽层宽度随外加偏压变化而变化的情形;采用数值计算的方法,建立了较精确的高压六角型VDM OST 三维物理模型,进而提出了VDM OST 的直流(DC )等效电路模型.该模型由level3NM OS 管、控制源、电容等元件组成,较准确地模拟了高压器件的特性.与以往文献的结果相比,该模型物理概念清晰,准确性高,避免过多工艺参数引入的同时,简化了等效电路.将该模型嵌入SPICE 进行仿真,得到了全电压范围内连续的I 2V 特性曲线,与实际测试结果相比,误差接近5%.关键词:模型;高压集成电路;高压VDM OST;漂移区;等效电路中图分类号:T N710;T N432 文献标识码:AA DC Model of H igh 2V oltage V DMOST for SPICE SimulationZH AO Y e , S UN Wei 2feng , YI Y ang 2bo , BAO Jia 2ming(National ASIC System Engineering Research Center ,Southeast Univer sity ,Nanjing 210096,China )Abstract :An accurate m odel for high 2v oltage hexag on VDM OST is derived based on a three 2dimensional structure and im plemented with SPICE.Drift region resistance ,buried layer resistance ,interior node v oltage and variation of internal capacitance with external applied v oltage are analyzed in detailed.A DC equivalent circuit m odel is als o proposed ,which includes a level 3NM OS transistor ,a controlled s ource and capacitance ,etc .It als o accounts for the quasi 2saturation effect in high v oltage device.This sim ple m odel with a clearphysical concept als o provides easy extraction of inter 2electrode capacitances.The I 2V simulation results are in g ood agreement with experimented results with the DC error approaching 5%within the entire v oltage range ,which can be used in practical applications.K ey w ords :m odel ;H VIC ;high 2v oltage VDM OST;drift region ;equivalent circuit 高压功率VDM OST 广泛用于平板显示驱动(PDP 、LC D 、LE D )以及汽车电子等领域.近年来随着高低压兼容工艺的成熟,高压集成电路(H VIC )应运而生,由于H VIC 集成了低压逻辑控制与高压功率驱动电路,因此得到了越来越广泛的应用.SPICE 是集成电路领域优秀的模拟软件,但是缺乏对高压器件的支持.因此建立准确的、可靠的高压器件SPICE 模型,用于高压集成电路的C AD 设计,成为迫切的需要.传统SPICE 电路宏模型建立在器件的测试结果之上,不能预测器件性能的变化.而基于器件的物理机理和结构提出的模型,能够较准确地预测器件性能的变化,从而进行SPICE 的仿真.文献[1]提出了一种导通电阻模型,其缺陷在于不能准确反映电阻及沟道随外加电压变化的情况;文献[2~6]基于矩形元胞从二维或准三维的角度,建立了VDM OST 的模型,克服了文献[1]的缺陷,但还不能反映器件的三维物理、电学特性;文献[7,8]从器件的结构出发,根据器件的物理特性分别建立了高低压的三维物理模型,并讨论了结构及工艺参数对器件特性的影响,准确地反映了器件的电学特性;但是它们皆是基于对矩形元胞的分析和讨论,并没有针对六角型高压VDM OST 的模型.本文从高压六角型VDM OST 的物理特性和结构出发,利用TS UPRE M 24和ME DICI 模拟结果分析了器件的电流、电场以及内部耗尽层情况,进而推导了漂移区压控电阻、内部节点电压、内部耗尽层宽度随外加偏压变化的情形,建立了较精确的高压六角型VDM OST 漂移区三维物理模型,弥补了模型[7,8]对于六角型元胞的不足;在物理模型基础上提出的VDM OST 等效电路,简单有效,适于工程应用的需要.1 器件结构图1即为高压VDM OST 结构纵向剖面图.从图1中可看出,有一个N +埋层和浓N 型漏连接层,将收集到的漏极电流经由浓N 型漏连接层传输到表面接触端,亦即把漏极电流从表面引出,其工艺与低压C M OS 工艺兼容.图1 H VIC 2VDM OS 纵向剖面图Fig.1 Cross 2section view of H VIC 2VDM OST VDM OST 的M OS 管沟道区是由双扩散形成的,双扩散工艺过程导致器件沟道浓度的不均匀分布.文献[9]已经提出了一个解决沟道不均匀掺杂的数值模型,但形式复杂,工艺参数繁多,不适于工程应用.在沟道尺寸较小的情况下,可以利用level3NM OS 管模型模拟VDM OST 的沟道部分,level3模型中NM OS 管的迁移率调制系数和载流子表面迁移率是两个关键的参数,对整个VDM OST 的导通电阻有重要的影响.图2为栅压等于5V ,漏压等于200V 条件下,ME DICI 模拟的电流、耗尽层的情况,揭示了电流路径以及耗尽层的扩展.由于体区耗尽层的存在,各个区域的厚度、向侧面耗尽的宽度会随着外加电压的变化而变化,亦即漂移区电阻是受外加电压控制的压控电阻.根据模拟的结果将器件的漂移区分为4个部分,如图3所示.在A 区中,电流沿着表面流向两个元胞的中间区域,然后再沿着P 体区与N -外延的P 2N 结耗尽层边缘流向B 区,P 2N 结耗尽层宽度受A 区末端电压V A 的控制,同时在A 区中栅下面的部分会形成积累层,由于这部分的电阻很小,相对于整个导通电阻来说可以忽略不计.在B 区,电流沿着一定的角度(α≈45°)流向漏端,电流所通过的截面和B 区的厚度跟随P 2N 结耗尽层的宽度发生变化,因此流经B 区的电流与V A 和B 区末端电压V B 有关.通过对ME DECI 模拟的结果对照可以看到电流偏转角α不随着器件结构和偏压而变化.在本文所阐述的模型中,认为B 区的掺杂浓度为准中性的,即n ≈N D .C 区的截面为六角型,其高度也与耗尽层宽度有关,因此C 区末端电压V C 也与V A 有关.通过几次深扩散形成的埋层结构,其浓度为非均匀分布,因此其电阻值也为非均匀的.本文采用了与工艺相关的精确的计算方法,利用器件和工艺模拟,得到较精确的电阻值,与实际结果很接近. 通过上述分析,A 、B 、C 区的电阻与各区的压降有关,而各区的压降又与流过该区的电流有关,以电阻作为中间变量,器件的电流电压特性可以通过一组隐含的方程组来描述,因此需要用数值方法来求得最后的结果.器件模型中包含的非线性元件,如压控电阻、压控电容等,可以用压控源或流控源的形式嵌入SPICE.对于非线性电阻可以描述成电压源的506 6期赵 野等:高压功率VDM OST 的SPICE 直流模型形式E RES =i R f (i R ,v R )(1)图2 对图1结构的ME DICI 模拟结果Fig.2 ME DICI simulation of H VIC 2VDMOST图3 VDM OST 单胞剖面图Fig.3 Cross 2section view of VDM OST2 漂移区模型体耗尽层的扩展如图4(a )所示,因为P 2N 结的边界不是平面的,假设在漂移区中的扩展边界斜率为X ′ΠY ′.由图4(b )中可以看到,由于多边形夹角的存在,电流在边角的分布很不均匀,因此在模型中,把电流流经的区域分为可变电阻R A 1区与可变电阻R A 2区(图4(b )中的阴影部分),其中R A 2区看作是半径与高度可变的圆形电阻区,A 区总电阻即为两者电阻的并联值.图4(a ) A 区耗尽层边界近似Fig.4(a) Depletion approximation of Aregion图4(b ) A 区电阻示意图Fig.4(b) Resistance of A region 对于R A 1而言,电流流过的是一个变截面的梯形体电阻,其阻值为R A 1=ρ0L P Y ′X ′ln11-X ′ΠL G (2) 在式(2)中,X ′、Y ′为耗尽层边缘在水平和竖直方向的坐标值.其值分别为X ′=W bd sin45°-(γW j -γ2W j )和Y ′=W bd cos45°+γW j ,γ为横向与纵向扩散的比例系数,其值约为0.8.其中L P 为P 体扩散区的边长,与版图的尺寸一致;L G 为有效栅长;耗尽层宽度是随A 区末端电压V A 变化的,因为P 体区的掺杂浓度很高,N -漂移区浓度相对较低,因此把它当作单边突变结来处理,可得W bd =2ε0εsi (V A -V bi -V S )ΠqN drift (3)其中,V bi 、V S 分别为P 2N 结的内建电势和源端的接触电压.对于R A 2区域,电流通过区域近似为可变截面的1Π6个圆形体电阻,采用与R A 1区同样的方法,积分可得R A 2=∫RAd R A 2=ρ0L G6πY ′X ′ln1+X ′πΠ6L G 1-X ′πΠ6L G(4)A 区的总电阻即为R A 1与R A 2的并联电阻,即R A =(R A 1R A 2)Π(R A 1+R A 2)参照图3所示的单胞结构,考虑其电流路径有一个角度α,所以六角型单胞的B 区电阻可以看作是一个如图5所示的三维结构.根据其几何结构的对称性,可以求得B 区电阻的值.对B 区进行积分,可得积分结果R B =ρ0K 332ln(-2(tan α)2L B +K 1-K 2)(K 1+K 2)(-2(tan α)2L B +K 1+K 2)(K 1-K 2)(5)其中B 区电阻高度606 应 用 科 学 学 报23卷 L B =W h -L G +X ′tan α(6)在式(5)中各个系数的含义如下K 1=2tan α[W h -(L G -X ′)](7)K 2=K 21+4(tan α)2K 3(8)K 3=2W h (L G -X ′)[1-(L G -X ′)](9)其中W h 为单胞宽度,通过以上的分析和计算,B 区的电阻基本表示完毕.分析和计算中不仅考虑了电阻区高度的变化,还考虑了电阻区截面积的变化,因此相对于文献[1]中提到的电阻模型更加精确.图5 B 区电阻示意图Fig.5 Three dimensional view of B region 电流所流过的C 区是一个截面为六角型的柱体,只有其高度随着外加电压的变化而变化,因此相对A 、B 区要简单一些.直接应用电阻率定义即可求解,结果如下R C =3ρ0(L T -L B -Y ′)27L 2A(10)其中L T 是外延的厚度,注意到C 区高度也是一个与耗尽层厚度有关的量,因此这部分电阻也是随电压而变化的.通过以上的推导计算,可以看到,正如引言中所述,A 区末端电压是一个关键变量,只要获得此处的电压,就可以建立关于V A 的方程组,进而求得各区分布的电压及电阻值.3 埋层及连接层电阻在作埋层扩散时,浓度的分布在几次工艺扩散中变化很复杂,与工艺密切相关,需要用器件及工艺模拟进行精确的参数提取.从TS UPRE M 24的模拟结果可以看到,杂质分布的等浓度线近似是一系列与x 轴平行的直线,仅认为沿纵向方向是非均匀掺杂.图6是TS UPRE M 24软件模拟的埋层杂质纵向分布曲线,其分布为高斯分布N D (y ,t )=Q 0πDt exp -y24Dt (11)上式中Q 0为离子注入剂量,D 为扩散系数,t 是扩散时间.对于已经形成的埋层来说t 为常数,则上式可以写成N D (y )=N D 0exp -y2L 2D(12)上式中L D =4Dt ;N D 0=Q 0ΠπDt .横向埋层电阻可以分为两个部分,如图2所示,其长度分别为L bur1和L bur2.埋层总电阻为两部分的电阻之和.这里只关心沿y 方向电阻率的变化,因此电阻率是y 的函数如图7所示,其微分电导是d G bur1=W L bur11ρ(y )d y(13)图6 N +埋层杂质的高斯分布曲线图Fig.6 Distribution of N +impurity buried layer图7 微分法求埋层电阻示意图Fig.7 The schematic of buried layer resistance for calculus对上式从y =0到y =L j 积分区间内积分G bur1=ρ0WL bur1∫Ljexp -y2L 2Dd y(14)其中ρ0=1ΠquN D 0,L j 为埋层杂质在外延中的扩散距离,则其电阻为R bur1=21π1LD 1ρ0L bur1W erfL jL D-1(15) 根据TS UPRE M 24和ME DICI 的模拟结果,可以看到流过埋层电阻的电流都是平行的,沿x 轴正方向不同位置取3个截面A 0、A 1和A 2,通过这几个截面的电流逐渐减小.取微元W ΔL Δy ,再取电流为线性分布,用平均功率法可以得到微元等效电阻I 2DΔR bur2=∫Lbur2x ΔL I D 2ρ(y )d x W Δy(16)706 6期赵 野等:高压功率VDM OST 的SPICE 直流模型由上式可以得到微分电导并积分ΔG bur2=3WΔL ∫Ljd yρ(y )(17)进而可得到这部分的电阻R bur2=231π1L D 1ρ0Lbur1W erfL jL D-1 (18)所以埋层总电阻R burry =R bur1+R bur2 图8所示为浓N +连接层杂质分布的曲线,从图中可以看到,其杂质分布与埋层杂质分布相似,均为高斯分布.因此可以利用与埋层电阻相似的办法求得此部分电阻的值.不过与埋层电阻不同的是,连接层是经过两次扩散形成的,所以实际上是两个电阻的串连.利用图7所示的微元法,可以求得连接层电阻的阻值R C ONT 3=21π1L D 1ρ0L C ONTW C ONTerfL jL D-1(19)上式中各个参数对应连接层形成时的参数值,L C ONT 和W C ONT 与连接层的版图窗口尺寸相对应.所以总的连接层电阻R C ONT =2R C ONT 3(20)图8 浓N +连接层杂质分布曲线图Fig.8 Distribution of N +contact layer4 等效电路从器件物理结构推导而来的电阻方程,代表了该器件的电学特性.根据电压与电流之间的关系可以求得漂移区的电流分别如下I A =V AR A (V A ,V S )(21)I B =V B -V A R B (V A ,V S )(22) 根据电流连续性定理,流过A 、B 和C 区,以及埋层电阻的电流是一致的.以电流作为中间变量,漂移区电压V DR 受外加漏极电压V DS 的控制,可以把漂移区上的电压看作一个受控电压源,而这个控制电压就是漏极电压.通过计算最终可得到外加漏极电压V DS 和漂移区上的电压V DR 之间对应的数值关系.VDM OST 物理模型的等效电路如图9所示.该等效电路包括3个部分:level3NM OS 晶体管模型,用来模拟VDM OST 的沟道区;一个电压控制电压源E ,模拟在漂移区上的电压降,两者串联起来;最后还有栅源和栅漏电容.因为电容对直流特性影响不是很大,所以采用了定值的栅源和栅漏电容.图9 VDM OST 物理模型的直流等效电路Fig.9 DC equivalent circuit of VDM OST physical m odel 等效电路在SPICE 中的测试电路如图10所示.在沟道宽度W =1μm ,漂移区浓度N d =8E14cm -3,栅氧化层厚度T ox =200nm ,沟长L ch =2μm ,外延厚度L T =30μm 条件下的SPICE 仿真结果和流片实测数据如图11所示.通过对比,在线性区模型仿真结果与实测数据基本吻合,在饱和区仿真结果与实测数据也很接近,在全电压范围内的误差接近5%.因为考虑了漂移区电阻的非线性变化,以及level3模型中电压对迁移率的调制效应,I 2V 模拟曲线也显示出模型的准饱和特征与实际测试结果相吻合.图10 导通特性测试电路Fig.10 On 2region characteristics circuit 在模拟中发现,随着漏压和栅压的增加,器件的准饱和效应越来越明显.这是因为当漏压和栅压足够高时,电压对迁移率的调制效应越明显,沟道中载806 应 用 科 学 学 报23卷 图11 直流I2V特性Fig.11 I2V characteristic of simulation and measure流子的迁移率降低,电流变小;同时,体耗尽层扩展导致漂移区中A区的截面变小,电阻也随着增大.当漏压达到足够高时,沟道区发生夹断.在SPICE模型中电子的饱和速度为一定值,因此电流在饱和区内的变化很小,几乎不变.在实际的工程应用中,器件的线性和准饱和特性很重要,本文提出的模型较准确地模拟了线性及准饱和特性,基本满足工程应用的需要,H VIC的C AD设计中.5 结 论本文在高压六角型VDM OST的物理机制下,建立了数值的三维物理模型,进而提出了基于现有仿真平台的等效电路模型.该模型物理概念清晰,简单准确,即避免了过多工艺参数的引入,又简化了等效电路.将该模型嵌入SPICE进行仿真,得到了全电压范围内连续的I2V特性曲线,与实际测试数据相比较,误差接近5%,已能够满足工程应用的需要.通过对内部节点电压的分析,容易求得内部非线性电容随外加偏压变化的情形,为建立瞬态模型提供参考.但是该模型没有考虑沟道漏端电压随栅压和漏压变化的情形,还有待进一步完善.该器件完整的模型将为高压六角型VDM OST的C AD设计提供简单而有效的手段.参考文献:[1] Sun S C,Plummer J D.M odeling of the on2resistance ofLDM OS,VDM OS,and VM OS power transistors[J].IEEET rans on E lectron Devices,1980,E D227(2):356-367. [2] Hu C,Chi M,Patel V M.Optimum design of powerM OSFET’s[J].IEEE T rans E lectron Devices,1984,E D231(10):1693-1700.[3] Victory J,Miller I,Scanchez J,et al.A new physicalpower M OSFET for improved simulation in power electronicdesign[J].IEEE T rans on E lectron Devices,1996,43(1):83-90.[4] Victory J,Scanchez J J,Demassa T A,et al.A staticphysical VDM OS m odel based on the charge2sheet m odel[J].IEEE T rans on E lectron Devices,1996,43(1):157-164.[5] K im Y S,F ossum J G.Physical DM OST m odeling for high2v oltage IC C AD[J].IEEE T rans on E lectron Devices,1990,37(3):797-803.[6] Chung Y,Burk D E.A physically based DM OS transistorm odel implemented in SPICE for advanced power IC C AD[A].International Symposium on P ower SemiconductorDevices&ICs[C].1995.340-345.[7] K im S D,K im I J,Han M K,et al.An accuration on2resistance m odel for low v oltage VDM OS devices[J].S olid2S tate E lectronics,1995,38(2):345-350.[8] Victory J,Mcandrew C C,Thoma R.A three2dimensional,physically based compact m odel for IC VDM OS transistors[J].Microelectronics Journal,1998,29:451-459.[9] Victory J,Scanchez J,Demassa T,et al.Application ofM OS charge2sheet m odel to nonuniform doping along thechannel[J].S olid2S tate E lctron,1995,38(8):1497-1503.(编辑:曹培华)906 6期赵 野等:高压功率VDM OST的SPICE直流模型。

一种用于功率IC的新型SPICE宏模型(英文)
赵野;周玉梅;李海松;孙伟锋
【期刊名称】《半导体学报:英文版》
【年(卷),期】2008(29)2
【摘要】基于规范化分段线性模型技术,建立了高压DMOS器件的SPICE宏模型用于功率集成电路的仿真.从等效电路模型出发,利用Powell算法找到规范化分段线性模型的最佳系数,从而利用节点电压可以直接描述DMOS器件的各种非线性特性.该模型不仅准确性高,而且仿真速度快、收敛性好.最后,给出了仿真与测试的对比结果,证明了模型的有效性和准确性.
【总页数】5页(P229-233)
【关键词】功率IC;SPICE;宏模型;双扩散MOS
【作者】赵野;周玉梅;李海松;孙伟锋
【作者单位】中国科学院微电子研究所;东南大学国家专用集成电路与系统工程技术研究中心
【正文语种】中文
【中图分类】TN402
【相关文献】
1.一种与SPICE程序兼容的新集成运放宏模型 [J], 鲍天保;韩宏伟
2.用于电压反馈放大器的SPICE运算放大器宏模型的开发 [J], Jian
Wang;Tamara Schmitz
3.一种SET的SPICE宏模型及SET/CMOS混合系统仿真研究 [J], 马彦芬;杨晓光;孙铁署
4.一种新颖的功率MOSFET SPICE宏模型 [J], 曾天志;张波;罗萍;蒲奎;赵露
5.一种用于DSCRL绝热电路的新型功率时钟(英文) [J], 罗家俊;李晓民;陈潮枢;仇玉林
因版权原因,仅展示原文概要,查看原文内容请购买。


S p i c e器件模型SPICE的器件模型大全在介绍SPICE基础知识时介绍了最复杂和重要的电路描述语句,其中就包括元器件描述语句。
许多元器件(如二极管、晶体管等)的描述语句中都有模型关键字,而电阻、电容、电源等的描述语句中也有模型名可选项,这些都要求后面配以.MODEL起始的模型描述语句,对这些特殊器件的参数做详细描述。
电阻、电容、电源等的模型描述语句语句比较简单,也比较容易理解,在SPICE基础中已介绍,就不再重复了;二极管、双极型晶体管的模型虽也做了些介绍,但不够详细,是本文介绍的重点,以便可以自己制作器件模型;场效应管、数字器件的模型过于复杂,太专业,一般用户自己难以制作模型,只做简单介绍。
元器件的模型非常重要,是影响分析精度的重要因素之一。
但模型中涉及太多图表,特别是很多数学公式,都是在WORD下编辑后再转为JEPG图像文件的,很繁琐和耗时,所以只能介绍重点。
一、二极管模型:1.1 理想二极管的I-V特性:1.2 实际硅二极管的I-V特性曲线:折线1.3 DC大信号模型:1.4 电荷存储特性:1.5 大信号模型的电荷存储参数Qd:1.6 温度模型:1.7 二极管模型参数表:二、双极型晶体管BJT模型:2.1 Ebers-Moll静态模型:电流注入模式和传输模式两种2.1.1 电流注入模式:2.1.2 传输模式:2.1.3 在不同的工作区域,极电流Ic Ie的工作范围不同,电流方程也各不相同:2.1.4 Early效应:基区宽度调制效应2.1.5 带Rc、Re、Rb的传输静态模型:正向参数和反向参数是相对的,基极接法不变,而发射极和集电极互换所对应的两种状态,分别称为正向状态和反向状态,与此对应的参数就分别定义为正向参数和反向参数。
2.2 Ebers-Moll大信号模型:2.3 Gummel-Pool静态模型:2.4 Gummel-Pool大信号模型:拓扑结构与Ebers-Moll大信号模型相同,非线性存储元件电压控制电容的方程也相同2.5 BJT晶体管模型总参数表:三、金属氧化物半导体晶体管MOSFET模型:3.1 一级静态模型:Shichman-Hodges模型3.2 二级静态模型(大信号模型):Meyer模型3.2.1 电荷存储效应:3.2.2 PN结电容:3.3 三级静态模型:3.2 MOSFET模型参数表:一级模型理论上复杂,有效参数少,用于精度不高场合,迅速粗略估计电路二级模型可使用复杂程度不同的模型,计算较多,常常不能收敛三级模型精度与二级模型相同,计算时间和重复次数少,某些参数计算比较复杂四级模型BSIM,适用于短沟道(<3um)的分析,Berkley在1987年提出四、结型场效应晶体管JFET模型:基于Shichman-Hodges模型4.1 N沟道JFET静态模型:4.2 JFET大信号模型:4.3 JFET模型参数表:五、 GaAs MESFET模型:分两级模型(肖特基结作栅极)GaAs MESFET模型参数表:六、数字器件模型:6.1 标准门的模型语句:.MODEL <(model)name> UGATE [模型参数] 标准门的延迟参数:6.2 三态门的模型语句:.MODEL <(model)name> UTGATE [模型参数] 三态门的延迟参数:6.3 边沿触发器的模型语句:.MODEL <(model)name> UEFF [模型参数] 边沿触发器参数:JKFF nff preb,clrb,clkb,j*,k*,g*,gb* JK触发器,后沿触发DFF nff preb,clrb,clk,d*,g*,gb* D触发器,前沿触发边沿触发器时间参数:6.4 钟控触发器的模型语句:.MODEL <(model)name> UGFF [模型参数] 钟控触发器参数:SRFF nff preb,clrb,gate,s*,r*,q*,qb* SR触发器,时钟高电平触发DLTCH nff preb,clrb,gate,d*,g*,gb* D触发器,时钟高电平触发钟控触发器时间参数:6.5 可编程逻辑阵列器件的语句:U <name> <pld type> (<#inputs>,<#outputs>) <input_node>* <output_node># +<(timing model)name> <(io_model)name> [FILE=<(file name) text value>] +[DATA=<radix flag>$ <program data>$][MNTYMXDLY=<(delay select)valu e>]+[IOLEVEL=<(interface model level)value>]其中:<pld type>列表<(file name) text value> JEDEC格式文件的名称,含有阵列特定的编程数据JEDEC文件指定时,DATA语句数据可忽略<radix flag> 是下列字母之一:B 二进制 O 八进制 X 十六进制 <program data> 程序数据是一个数据序列,初始都为0PLD时间模型参数:七、数字I/O接口子电路:数字电路与模拟电路连接的界面节点,SPICE 自动插入此子电路子电路名(AtoDn和DtoAn)在I/O模型中定义,实现逻辑状态与电压、阻抗之间的转换。
77K温度下MOS器件的SPICE模型实现中期报告
本文介绍了在77K温度下MOS器件SPICE模型实现的进展情况。
SPICE模型是一种在电路仿真软件中广泛使用的模拟模型,用于模拟各种电子元件的性能和行为。
在MOS器件的SPICE模型实现中,需要考虑器件的物理结构和电学特性。
在77K温度下,MOS器件的性能和行为会发生一些变化,因此需要对SPICE模型进行适当的调整和修正。
目前,我们已经开展了一些实验工作,收集了MOS器件在77K温度下的性能数据,并且对这些数据进行了分析和处理。
我们还在建立基于这些数据的SPICE模型,并对模型进行优化和验证。
具体来说,我们已经完成了以下工作:
1. 实验测试:使用特定的测试工具和方法,测试了MOS器件在77K 温度下的性能,包括电流-电压关系、输入输出特性、输出阻抗等。
2. 数据分析:对实验数据进行了分析和处理,研究了MOS器件在低温下的特性和行为。
3. SPICE模型建立:以测试得到的数据为基础,建立了MOS器件在77K温度下的SPICE模型,包括电流源、电容器、电阻器等元件。
4. 优化验证:对SPICE模型进行了优化和验证,确保模型能够准确地模拟MOS器件在77K温度下的性能和行为,提高模拟精度和可靠性。
总体来说,我们已经取得了一定的进展,并且对MOS器件在77K温度下的SPICE模型实现有了更深入的认识。
下一步,我们将继续完善SPICE模型,并进一步优化和验证,以增强其可靠性和应用性。
单光子雪崩二极管SPICE仿真模型的建立和应用
匡华;鞠国豪;徐星;程正喜
【期刊名称】《半导体光电》
【年(卷),期】2024(45)1
【摘要】单光子雪崩二极管(SPAD)作为一种高效的光子探测器件被广泛应用于量子通信和三维成像等领域。
在Cadence中建立了一个SPAD的Spice模型,通过Verilog-A语言,采用两个e指数函数的组合,以连续函数的方式描述了SPAD在盖革模式区等效电阻的动态变化。
这两个e指数函数分别体现了高阻区和低阻区的等效电阻特性,解决了分段电阻模型仿真不收敛的问题。
该Spice模型模拟了SPAD器件在“接收光子-雪崩产生脉冲-淬灭-复位”工作过程中的动态特性和SPAD从正偏到二次击穿的静态I-V特性。
将其应用到4种不同淬灭电路的仿真中,验证了该模型的有效性和稳定性。
【总页数】7页(P42-48)
【作者】匡华;鞠国豪;徐星;程正喜
【作者单位】中国科学院上海技术物理研究所红外探测全国重点实验室;中国科学院大学
【正文语种】中文
【中图分类】TN364.2
【相关文献】
1.SPAD单光子探测器SPICE电路模型的建立与仿真研究
2.基于InGaAs/InP雪崩光电二极管的高速单光子探测器雪崩特性研究
3.单光子雪崩二极管雪崩建立与淬灭的改进模型
4.单光子雪崩二极管行为性仿真建模
5.Zn扩散对InGaAs/InP单光子雪崩光电二极管雪崩击穿概率的影响
因版权原因,仅展示原文概要,查看原文内容请购买。