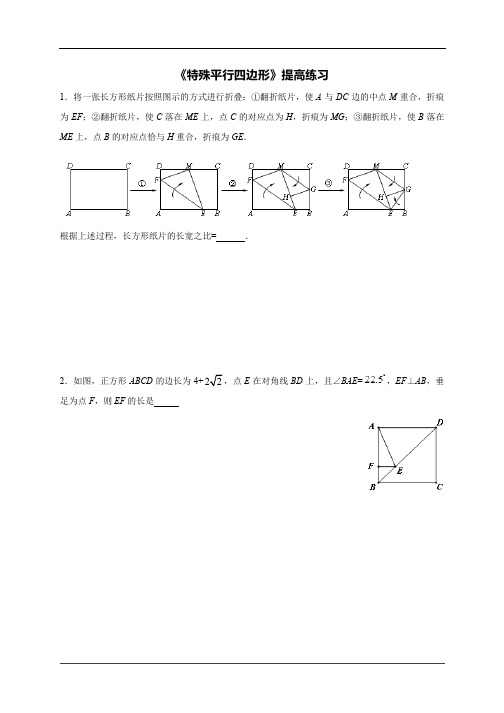
特殊平行四边形提高训练

第十八章第2节《特殊的平行四边形》提高训练卷 (31)一、单选题1．矩形具有而菱形不具有的性质是（ ）A ．两组对边分别平行B ．对角线相等C ．对角线互相垂直D ．两组对角分别相等2．如图，在ABC 中，D 、E 分别是AB 、AC 的中点，16BC =，F 是线段DE 上一点，连接AF 、CF ，4DE DF =，若90AFC ∠=︒，则AC 的长度是（ ）A ．6B ．8C ．10D ．123．如图，Rt △ABC 中，∠ACB ＝90°，AC ＝6，BC ＝8，D 是AB 的中点，E 是BC 的中点，EF ⊥CD 于点F ，则EF 的长是（ ）A ．3B ．4C ．5D ．1254．如图，四边形ABCD 中，∠BAD ＝∠C ＝90°，AB ＝AD ，AE ⊥BC ，垂足是E ，若线段AE ＝4，则四边形ABCD 的面积为（ ）A ．12B ．16C ．20D ．24二、解答题 5．如图，在ABC 中，90ACB ︒∠=，30B ，CE 垂直于AB 于点E ，D 是AB 的中点．（1）求证：AE ED =；（2）若2AC =，求DE 的长．6．如图，在Rt ABC 中，90BAC ∠=︒，AB AC =，点D 是BC 边上一动点，连接AD ，把AD 绕点A 逆时针旋转90°，得到AE ，连接CE ，DE ．点F 是DE 的中点，连接CF ．（1）求证：CF AF =；（2）在不添加任何辅助线的情况下，请直接写出图中所有的等腰直角三角形．7．如图，四边形ABCD 是平行四边形，//DE BF ，且分别交对角线AC 于点E ，F ，连接,BE DF ．若BE DE =，求证：四边形EBFD 是菱形．8．如图，在Rt △ABC 中，∠BAC ＝90°，AD 是边BC 上的中线，过点A 作AE //BC ，过点D 作DE //AB ，DE 与AC ，AE 分别交于点O ，E ，连接EC ．（1）求证：四边形ADCE 是菱形；（2）若AB ＝AO ，OD ＝1，则菱形ADCE 的周长为 ．9．如图，在Rt∆ABC 中，∠ACB ＝90°，AC 的垂直平分线交AB 于点E ，连接CE ，BF//CE 交DE 的延长线于点F ．（1）求证：四边形BCEF 是平行四边形；（2）当∠A 满足什么条件时，四边形BCEF 是菱形？回答并证明你的结论．10．如图，长方形OBCD 的OB 边在x 轴上，OD 边在y 轴上，OB=15，OD=9，在BC 上取一点E ，使△CDE 沿DE 折叠后，点C 落在x 轴上，记作点F ．（1）求点F 的坐标；（2）求点E 的坐标．11．如图，在ABC 中，90,3,4BAC AB AC ︒∠===，点D 是BC 的中点，将ABD △沿AD 翻折得到AED ，联结CE ．（1）求证：//AD CE ；（2）求CE 的长．12．（1）将一张长方形纸片按如图1所示的方式折叠，BC 、BD 为折痕，求CBD ∠的度数；（2）将一张长方形纸片按如图2所示的方式折叠，BC 、BD 为折痕，若115CBD ∠=︒，求A BE ∠'（3）将一张长方形纸片按如图3所示的方式折叠，BC 、BD 为折痕，若CBD α∠=，求A BE '∠'的度数（用含α的式子表示）13．如图，以锐角△ABC 的边AC 、AB 为边向外作正方形ACDE 和正方形ABGF ，连结BE 、CF ． （1）求证：△FAC ≌△BAE ；（2）图中可以通过旋转△BAE 而得到△FAC ，请你说出旋转中心、旋转方向和旋转角的度数．14．已知ABCD 中，点E 在BC 延长线上，连接DE ，180A E ∠+∠=︒（1）如图1，求证：CD DE =；（2）如图2，过点C 作BE 垂线，交于AD 于点F ，求证3BE AF DF =+；（3）如图3，在（2）的条件下，ABC ∠的平分线，交CD 于G ，交CF 于H ，连接FG ，若45FGH ∠=︒，8=CF ，3FD =，求BE 的长．15．如图，矩形ABCD 中，EF 垂直平分对角线BD ，垂足为O ，点E 和F 分别在边AD ，BC 上，连接BE ，DF ．（1）求证：四边形BFDE 是菱形；（2）若AE ＝OF ，求∠BDC 的度数．16．在平行四边形ABCD中，过点D作DE⊥AB于点E，点F在边CD上，DF=BE，连接AF，BF．（1）求证：四边形BFDE是矩形；（2）若CF=9，BF=12，DF=15，求证：AF平分∠DAB．17．如图1，四边形ABCD是正方形，点E是BC的中点，∠AEF=90°，EF交正方形外角的平分线CF于F．（1）求证：AE=EF；（2）若将（1）中的“正方形ABCD”改为“正三角形ABC”（如图2），N是∠ACP的平分线上一点，则当∠AMN=60°时，结论AM=MN是否还成立？请说明理由．18．如图，在矩形ABCD中，AB＝4，BC＝3．将△ACD沿对角线AC翻折得到△ACD′，CD′交AB于点F．（1）判断△ACF的形状，并证明；（2）直接写出线段AF的长．三、填空题19．如图，在矩形ABCD 中，AB=3，BC=4，点,,,E F G H 分别是边,,,AB BC CD AD 的中点，连接,,,AF BG CH DE ，得到一个新的四边形,MNPQ 则四边形MNPQ 的面积为 _____________．20．在平面直角坐标系xOy 中，正方形OABC 的顶点坐标为，则顶点C 的坐标为________． 21．如图，两个长宽分别为7cm 、3cm 的矩形如图叠放在一起，则图中阴影部分的面积是________．22．正方形ABCD 中，E 为BC 上的一点，F 为CD 上的一点，BE+DF=EF ，则∠EAF 的度数是_______．23．如图，已知正方形ABCD 的边长为3，点E 是AB 边上一动点，连接ED ，将ED 绕点E 顺时针旋转90°到EF ，连接DF ，CF ，则DF CF 的最小值______．24．如图，在菱形ABCD 中，E 、F 分别是AC 、BC 的中点，如果EF ＝5，那么菱形ABCD 的周长_____．25．在△ABC 中，点G 是重心，∠BGC =90°，BC =8，那么AG 的长为____．26．如图，在菱形ABCD 中，对角线AC ，BD 相交于点O ，H 为BC 中点，AC ＝6，BD ＝8，则线段OH 的长为_____．27．如图，四边形ABCD 是正方形，AB ＝1，以AB 为对角线作第二个正方形AEBF ，以EB 为对角线作第三个正方形EGBH ，以此类推，则第n 个正方形的面积是_______ ．28．如图，将矩形ABCD 沿DE 折叠，使A 点落在BC 上的F 处，若∠EFB ＝60°，则∠CFD ＝_____．29．如图，AC 是菱形ABCD 的对角线，P 是AC 上的一个动点，过点P 分别作AB 和BC 的垂线，垂足分别是点F 和E ，若菱形的周长是12cm ，面积是6cm 2，则PE +PF 的值是_____cm ．30．如图所示，在矩形ABCD 中，AB a ，BC b ，两条对角线相交于点O ，OB 、OC 为邻边作第1个平行四边形1OBB C ，对角线相交于点1A ，以为11A B 、1AC邻边作第2个平行四边形111A B C C ，对角线相交于1O ；再以11O B 、11O C 为邻边作第3个平行四边形1121O B B C ……此类推，第2020个平行四边形的面积__________．【答案与解析】1．B【解析】矩形的对角线互相平分且相等，菱形的对角线互相平分，互相垂直，并且每一条对角线平分一组对角，据此解答．A 、是菱形的性质，是矩形的性质，故本选项不符合题意；B 、是矩形的性质，不是菱形的性质，故本选项符合题意；C 、是菱形的性质，不是矩形的性质，故本选项不符合题意；D 、矩形、菱形的对角都相等，故本选项不符合题意；故选：B ．此题考查矩形的性质，菱形的性质，熟记各自的性质特征是解题的关键．2．D【解析】先证得DE 是△ABC 的中位线，求出DE=8，及EF=6，再根据90AFC ∠=︒证得AC=2EF 求出答案．∵D 、E 分别是AB 、AC 的中点，∴DE 是△ABC 的中位线，∴DE=12BC=8， ∵4DE DF =，∴DF=2，EF=6，∵90AFC ∠=︒，AE=CE ，∴AC=2EF=12，故选：D ．此题考查三角形中位线的判定及性质定理，直角三角形斜边中线等于斜边一半的性质，熟练掌握各定理并运用解决问题是解题的关键．3．D【解析】根据勾股定理得出AB ，进而利用直角三角形的性质得出：BD=DC=AD=5，利用三角形面积公式解答即可．∵在Rt △ABC 中，∠ACB ＝90°，AC ＝6，BC ＝8，∴10AB ==，∵D 是AB 的中点，∴BD=DC=AD=5，1116812222BDC BAC SS ==⨯⨯⨯=， 连接DE ，∵E 是BC 的中点， ∴162DEC BDC S S ==， ∵115622DEC S DC EF EF ==⨯⨯= ∴125EF = 故选：D ．本题主要考查的是勾股定理，直角三角形斜边上的中线，关键是根据勾股定理解出AB ，进而利用直角三角形的性质解答．4．B【解析】延长CD ，作AF CD ⊥的延长线于点F ，构造出全等三角形，()ABE ADF AAS ≅，即可得到四边形ABCD 的面积就等于正方形AECF 的面积．解：如图，延长CD ，作AF CD ⊥的延长线于点F ，∵AE BC ⊥，∴90AEC AEB ∠=∠=︒，∵AF CD ⊥，∴90AFC ∠=︒，∵90C ∠=︒，∴四边形AECF 是矩形，∴90EAF ∠=︒，∵BAD EAF ∠=∠，∴BAD EAD EAF EAD ∠-∠=∠-∠，即BAE DAF ∠=∠，在ABE △和ADF 中，BAE DAF AEB AFD AB AD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()ABE ADF AAS ≅，∴AE AF =，∴四边形AECF 是正方形，∵ABE ADF S S ，∴216ABCD AECF S S AE ===．故选：B ．本题考查全等三角形的性质和判定，正方形的性质和判定，解题的关键是作辅助线构造全等三角形．5．（1）见解析；（2）１．【解析】（1）根据直角三角形斜边上的中线性质解得CD=BD ，得到30DCB B ==︒∠∠，继而得到60ADC A ∠=∠=︒再根据等腰三角形的判定推出AC=CD ，最后根据等腰三角形的性质解题； （2）先解得30ACE ∠=︒，根据含30°角的直角三角形的性质解得AE 的长，即可解题． （1）证明：在ABC 中，90ACB ︒∠=，D 是AB 的中点，12CD AD BD AB ∴===DCB B ∴∠=∠ 30,90B ACB ∠=︒∠=︒30,180903060DCB A ∴∠=︒∠=︒-︒-︒=︒60ADC B DCB ∴∠=∠+∠=︒A ADC ∴∠=∠AC DC ∴=CE 垂直AB 于点EAE ED ∴=；（2）CE AB ⊥90AEC ∴∠=︒60A ∠=︒30ACE ∴∠=︒12AE AC ∴= 2,AC AE DE ==1DE AE ∴==．本题考查等腰三角形的判定与性质、直角三角形斜边的中线、含30°角的直角三角形、三角形外角的性质、三角形内角和定理等知识，是重要考点，难度一般，掌握相关知识是解题关键． 6．（1）见解析；（2）△ABC ， △ADE ，△ADF ，△AFE【解析】（1）根据90BAC DAE ∠=∠=︒得到BAD CAE ∠=∠再根据已知条件求证ABD ACE ABD ACE ∠=∠≌，再根据题意得∠ABD=∠ACE=45°，进而得到△DCE 为直角三角形，再由点F 是DE 的中点得到CF=AF ；（2）根据等腰直角三角形的性质和定义结合第一问即可得到结果．（1）证明：∵90BAC DAE ∠=∠=︒∴BAC CAD DAE CAD ∠-∠=∠-∠即BAD CAE ∠=∠∵AB AC =，AD AE =∴ABD ACE △≌△，∴ABD ACE ∠=∠∵AB AC =，∴A ABC CB =∠∠∵90BAC ∠=︒∴90ABC ACB ∠+∠=︒，∴45ABC ACB ∠=∠=︒∴45ABD ACE ∠=∠=︒∴90DCE ACB ACE ∠︒=∠+∠=∵点F 是DE 的中点，90DAE DCE ∠=∠=︒ ∴12AF DE =，12CF DE = ∴CF AF =（2）图中所有的等腰直角三角形是：ABC ，ADE ，ADF ，AFE △；此题属于三角形旋转类综合性问题，涉及知识点为三角形全等，直角三角形斜边上的中线为斜边的一半．7．见解析【解析】根据平行四边形的性质，可以得到AD=CB ，AD ∥CB ，从而可以得到∠DAE=∠BCF ，再根据DE ∥BF和等角的补角相等，从而可以得到∠AED=∠CFB ，然后即可证明△ADE 和△CBF 全等，从而可以得到DE=BF ，再根据DE ∥BF ，即可得到四边形EBFD 是平行四边形，再根据BE=DE ，即可得到四边形EBFD 为菱形．证明：∵四边形ABCD 是平行四边形，∴AD=CB ，AD ∥CB ，∴∠DAE=∠BCF ，∵DE ∥BF ，∴∠DEF=∠BFE ，∴∠AED=∠CFB ，在△ADE 和△CBF 中，DAE BCF AED CFB AD CB ∠=∠⎧⎪∠=∠⎨⎪=⎩∴△ADE ≌△CBF （AAS ），∴DE=BF ，又∵DE∥BF，∴四边形EBFD是平行四边形，∵BE=DE，∴四边形EBFD为菱形．本题考查平行四边形的判定和性质、菱形的判定，解答本题的关键是明确题意，找出所求问题需要的条件，利用数形结合的思想解答．8．（1）见解析；（2）【解析】（1）先证四边形ABDE为平行四边形，再证得AE＝CD，得四边形ADCE是平行四边形，然后根据直角三角形斜边上的中线性质得AD＝CD，即可得出结论；（2）先由菱形的性质得AD＝AE＝CE＝CD，AC⊥DE，OA＝OC，再证OD是△ABC的中位线，得AB＝2OD＝2，则AO＝AB＝2，然后由勾股定理求出AD的长即可解决问题．解：（1）证明：∵AE∥BC，DE∥AB，∴四边形ABDE为平行四边形，∴AE＝BD，∵AD是边BC上的中线，∴BD＝CD，∴AE＝CD，∴四边形ADCE是平行四边形，又∵∠BAC＝90°，AD是边BC上的中线，∴AD＝12BC＝CD，∴平行四边形ADCE是菱形；（2）解：∵四边形ADCE是菱形，∴AD＝AE＝CE＝CD，AC⊥DE，OA＝OC，∵BD＝CD，∴OD是△ABC的中位线，∴AB＝2OD＝2，∴AO＝AB＝2，∴AD∴菱形ADCE 的周长＝4AD ＝故答案为：本题考查了平行四边形的判定与性质、菱形的判定与性质、直角三角形斜边上的中线性质以及勾股定理等知识；证得四边形ADCE 为菱形是解题的关键．9．（1）证明见解析；（2）30A ∠=︒，证明见解析【解析】（1）先根据垂直平分线和直角证得DF//BC ，再结合BF//CE ，根据两组对边分别平行的四边形是平行四边形即可证明；（2）根据有一组临边相等的平行四边形是菱形，所以需添加的条件能证明有一组临边相等据此作答．解：（1）证明：∵DF 垂直平分AC ，90ACB ∠=︒，∴DF//BC ，又∵BF//CE ，∴四边形BCEF 是平行四边形；（2）当30A ∠=︒时，四边形BCEF 是菱形，理由是：∵DF 垂直平分AC ，90ACB ∠=︒，30A ∠=︒，∴EA=EC ，1903060∠=︒-︒=︒，∴230A ∠=∠=︒，即3903060∠=︒-︒=︒，∴∆BCE 是等边三角形，∴BC=EC ，由（1）得四边形BCEF 是平行四边形，∴四边形BCEF 是菱形．本题考查菱形的判定定理，平行四边形的判定定理，垂直平分线的性质，等腰三角形的性质．熟练掌握判定定理，并能结合题意选择合适的定理证明是解题关键．10．（1）点F(12，0)；（2）点E(15，4) ．【解析】（1）由四边形OBCD 是长方形可得CD=OB=15、BC=OD=9、∠DOB=∠OBC=900，由折叠的性质可得DF=CD=15，然后运用勾股定理求得OF ，即可确定F 点的坐标；（2）运用线段的和差可得BF=OB-OF=3，再由折叠的性质可得CE=EF, 设BE=x ，则CE= =9-x ，然后运用勾股定理求得x 即可解答．解：（1）∵四边形OBCD 是长方形∴CD=OB=15，BC=OD=9，∠DOB=∠OBC=900由折叠△CDE 得△FDE 可知：DF=CD=15∴12OF∴点F （12，0）；（2）由（1）得OF=12∴BF=OB-OF=15-12=3由折叠可知：CE=EF设BE=x ，则CE=EF=BC-BE=9-x∴()22293x x -=+，解得x=4∴点E （15，4）．本题主要考查了折叠的性质、长方形的性质以及勾股定理的应用，灵活应用相关知识成为解答本题的关键．11．（1）见解析；（2）75 【解析】（1）先根据直角三角形斜边上的中线等于斜边的一半得AD CD BD ==，再由折叠的性质得BD ED =，ADE ADB ∠=∠，再由外角和定理得DCE DEC EDB ADE ADB ∠+∠=∠=∠+∠，则DEC ADE ∠=∠，即可证明结论；（2）利用勾股定理求出BC 的长，由（1）得1522AD BC ==，设DF x =，则52AF x =-，在Rt ABF 和Rt BDF 中，利用勾股定理列式求出x 的值，再根据中位线定理得到2CE DF =即可．解：（1）∵90BAC ∠=︒，D 是BC 中点，∴AD CD BD ==，∵折叠，∴BD ED =，ADE ADB ∠=∠，∵CD BD ED ==，∴DCE DEC ∠=∠，∵DCE DEC EDB ADE ADB ∠+∠=∠=∠+∠，∴22DEC ADE ∠=∠，即DEC ADE ∠=∠，∴//AD CE ；（2）∵90BAC ∠=︒，3AB =，4AC =，∴5BC =，由（1）知1522AD BC ==， 设DF x =，则52AF x =-， ∵折叠，∴AD 是BE 的垂直平分线，在Rt ABF 和Rt BDF 中，222BF AB AF =-，222BF BD DF =-，∴2222AB AF BD DF -=-，即22525924x x ⎛⎫--=- ⎪⎝⎭，解得710x =， ∵D 、F 分别是BC 和BE 的中点， ∴725CE DF ==． 本题考查折叠的性质，中位线定理，直角三角形斜边上中线的性质，解题的关键是掌握这些性质定理进行证明求解．12．（1）90°；（2）50°；（3）1802α︒-【解析】（1）由折叠的性质知ABC A BC ∠∠'=，EBD E BD '∠=∠，即可得到1902CBD ABE ∠=∠=︒； （2）由115CBD ∠=︒计算出18011565ABC EBD ∠+∠=︒-︒=︒，根据ABC A BC ∠∠'=，EBD E BD '∠=∠，即可求出答案；（3）由CBD α∠=求出180ABC EBD α∠+∠=︒-，根据ABC A BC ∠=∠'，EBD E BD '∠=∠计算得出180(2302)6ABA EBE αα''∠+∠=︒-⨯=︒-，再计算36021801802A BE αα''∠=︒--︒=︒-得出答案．（1）由折叠的性质知ABC A BC ∠∠'=，EBD E BD '∠=∠， ∴12A BC ABA '∠'=∠，12E BD E BE '∠'=∠， ∴1902CBD ABE ∠=∠=︒． （2）∵115CBD ∠=︒∴18011565ABC EBD ∠+∠=︒-︒=︒，∵ABC A BC ∠∠'=，EBD E BD '∠=∠，∴652130ABA EBE ''∠+∠=︒⨯=︒，∴18013050A BE ''∠=︒-︒=︒．（3）∵CBD α∠=∴180ABC EBD α∠+∠=︒-∵ABC A BC ∠=∠'，EBD E BD '∠=∠∴180(2302)6ABA EBE αα''∠+∠=︒-⨯=︒-∴36021801802A BE αα''∠=︒--︒=︒-．此题考查折叠的性质：折叠前后的对应角相等，角度的和差计算，掌握图形中各角度之间的位置及和差关系是解题的关键．13．（1）见解析；（2）以点A 为旋转中心，顺时针旋转90°得到△FAC ．【解析】（1）由题意利用正方形的性质得出∠FAC=∠BAE ，AF=AB ，AC=AE ，即可得出△FAC ≌△BAE ； （2）由题意根据旋转前后图形的关系得出旋转中心和旋转角的度数即可．证明：（1）∵四边形ABGF 和四边形ACDE 是正方形，∴AF ＝AB ，AC ＝AE ，∵∠BAF ＝∠CAE ＝90°，∴∠BAF+∠BAC ＝∠CAE+∠BAC 即∠FAC ＝∠BAE ，∵在△FAC 和△BAE 中，AF AB FAC BAE AC AE =⎧⎪∠=∠⎨⎪=⎩，∴△FAC ≌△BAE （SAS ），（2）以点A 为旋转中心，顺时针旋转90°得到△FAC ．本题主要考查旋转的性质以及全等三角形的判定与性质和正方形的性质等知识，根据已知得出∠FAC=∠BAE 是解题的关键．14．（1）证明见解析；（2）证明见解析（3）14【解析】（1）由平行四边形性质可得∠A＋∠DCE=180°，结合已知可得∠DCE=∠E，从而由等角对等边可得CD=DE；（2）过D作DG⊥CE于点G，则由题意可得CE=2CG=2DF，从而得到BE=BC+CE=3DF；（3）由已知可得∠CBG=∠BGC，进一步可得∠HFG=∠FGC，从而可得BC=CG=FC，进而得到BE的值．（1）证明：由题意得：∠A=∠BCD，∠BCD＋∠DCE=180°，∴∠A＋∠DCE=180°，∵∠A＋∠E=180°，∴∠DCE=∠E，∴CD=DE；（2）如图，过D作DG⊥CE于点G，则四边形FDGC为矩形，∴CG=DF，又由（1）可知△DCE是等腰三角形，∴CE=2CG=2DF，∴BE=BC+CE=AF+DF+2DF=AF+3DF；（3）如图，∵四边形ABCD为平行四边形，∴AB∥CD，∴∠ABG=∠BGC，∵BG平分∠ABC，∴设∠ABG=∠CBG=∠BGC=α，∴BC=CG，∵∠FGH=45°，∴∠FGC=45°+α，∵∠BCF=90°，∴∠BHC=∠FHG=90°-α，∴∠HFG=45°+α=∠FGC，∴CG=FC，∴BC=FC=8，由（2）知CE=2DF=6，∴BE=BC+CE=8+6=14．本题考查平行四边形的综合运用，灵活运用平行四边形的性质、平行线的性质、等腰三角形的性质、矩形的性质及有关角的性质是解题关键．15．（1）见解析；（2）60°．【解析】（1）首先判定平行四边形，然后根据对角线互相垂直的平行四边形是菱形进行判定即可；（2）AE＝OF，四边形BFDE是菱形，BE=BF，可证△ABF≌△OBF, ∠ABF=∠OBF, ∠FBO=∠OBF, ∠OBF=30°，即可求解．证明:(1)∵四边形ABCD是矩形,∴ AD∥BC,AD=BC,∴∠EDO=∠OBF,∵EF垂直平分BD,∴BO=DO,∠EOD=∠BOF=90°,∴△DEO=△BFO(ASA)∴OE=OF,∴四边形EBFD是平行四边形,又EF⊥BD,∴四边形EBFD是菱形;(2)∵四边形EBFD是菱形,∴ED=EB又AE＝OF，∠A=∠BOF∴△ABF≌△OBF∴∠ABF=∠OBF,∵∠FBO=∠OBF,∴∠ABF =∠FBO=∠OBF,∴∠OBF=30°∴∠BDC=60°．本题考查了菱形的性质和判定，掌握菱形的性质和判定是解题的关键．16．（1）见解析；（2）见解析【解析】（1）根据平行四边形的性质得出DF∥BE，根据平行四边形的判定得出四边形DEBF为平行四边形，再加上条件∠DEB=90，即可判定矩形；（2）根据矩形的性质求出∠BFC=90°，根据勾股定理求出BC，求出AD=DF，推出∠DAF=∠DFA，求出∠DAF=∠BAF，即可得出答案．证明：（1）∵四边形ABCD为平行四边形，∴DC∥AB，即DF∥BE，又∵DF=BE，∴四边形DEBF为平行四边形又∵DE⊥AB，∴∠DEB=90°，∴四边形DEBF为矩形；（2）∵四边形DEBF为矩形，∴∠BFC=90°，RtΔBCF中CF=9，BF=12，∴=15，∴AD=BC=15，∴AD=DF=15，∴∠DAF=∠DFA，∵AB∥CD，∴∠FAB=∠DFA，∴∠FAB=∠DAF，∴AF平分∠DAB．本题考查了平行四边形的性质和判定，矩形的性质和判定，勾股定理，平行线的性质，角平分线定义的应用，能综合运用性质进行推理是解此题的关键．17．（1）见解析；（2）成立，理由见解析【解析】（1）取AB 的中点M ，连接ME ，利用ASA 证明△AME ≌△ECF ，可得AE=EF ；（2）在AB 上取一点E ，使AE=CM ，连接ME ，利用ASA 即可证明△AEM ≌△MCN ，然后根据全等三角形的对应边相等得出AM=MN ．（1）证明：取AB 的中点M ，连接EM ，∵四边形ABCD 是正方形，AE ⊥EF ，∴∠1＋∠AEB=90°，∠2＋∠AEB=90°，∴∠1=∠2，∵BM=BE ，∠BME=45°，且∠FCG=45°，∴∠AME=∠ECF=135°，AM=CE ，在△AME 和△ECF 中，12AM CEAME ECF ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△AME ≌△ECF(ASA)，∴AE=EF ；（2）解：结论AM=MN 还成立．证明：在边AB 上截取AE=MC ，连接ME ．在正△ABC 中，∠B=∠BCA=60°，AB=BC ．∴∠NMC=180°-∠AMN-∠AMB=180°-60°-（180°-∠B-∠MAE ）=∠MAE ，∵BE=AB-AE=BC-MC=BM ，∴∠BEM=60°，∴∠AEM=120°．∵N 是∠ACP 的平分线上一点，∴∠ACN=60°，∴∠MCN=120°，在△AEM 与△MCN 中，MAE NMC AE MC AEM MCN ∠=∠⎧⎪=⎨⎪∠=∠⎩， ∴△AEM ≌△MCN （ASA ），∴AM=MN ．本题综合考查了正方形、等边三角形的性质及全等三角形的判定和性质，同时考查了学生的归纳能力及分析、解决问题的能力，解题的关键是学会添加辅助线，构造全等三角形解决问题． 18．（1）等腰三角形，证明见解析；（2）258AF =． 【解析】（1）由矩形的性质和折叠的性质，得到∠BAC ＝∠ACD'，然后得到AF=CF ，即可得到结论成立； （2）由题意，设AF=CF=x ，则BF=4-x ，利用勾股定理，即可求出答案．解：（1）△ACF 为等腰三角形，证明如下：∵ 矩形ABCD ，∴ AB ∥CD ．∴∠BAC ＝∠ACD ．又∵ △ACD 沿对角线AC 翻折得到△ACD'，∴ ∠ACD ＝∠ACD'．∴∠BAC ＝∠ACD'．∴ AF ＝CF ．∴△ACF 为等腰三角形（2）在Rt △BCF 中，设AF=CF=x ，则BF=4-x ，由勾股定理，则 222(4)3x x --=， ∴258x =，∴258 AF ．本题考查了矩形的判定和性质，折叠的性质，等腰三角形的判定，勾股定理，解题的关键是熟练掌握所学的知识，正确的进行解题．19．12 5【解析】根据题意，采取割补法，将图中梯形补成与中间的平行四边形一样大小的平行四边形，并找到矩形ABCD与5个小平行四边形的面积关系，即可得出结论．解：如图所示，过A作AK∥DE，交CH的延长线于K，过B作BR∥AF，交DE的延长线于R，过C作CS∥BG，交AF的延长线于S，过D作DT∥CH，交BG的延长线于T，∵H是AD的中点，∴AH=DH，∵AK∥DP，∴∠K=∠DPH，又∵∠AHK=∠DHP，∴△AKH≌△DPH（AAS），∴S△AKH=S△DPH，同理可得，S△BRE=S△AQE，S△CSF=S△BMF，S△DTG=S△CNG，∵AH∥CF，AH=CF，∴四边形AFCH是平行四边形，同理可得，四边形BGDE是平行四边形，∴QM∥PN，QP∥MN，∴四边形MNPQ是平行四边形，∵AK∥QP，AQ∥KP，∴四边形AQPK是平行四边形，又∵E 是AB 的中点，EQ ∥BM ，∴Q 是AM 的中点，∴AQ=MQ ，∴S 四边形AQPK =S 四边形MNPQ ，同理可得，S 四边形BMQR =S 四边形MNPQ ，S 四边形MNCS =S 四边形MNPQ ，S 四边形DTNP =S 四边形MNPQ ，∴S 四边形BMQR =S 四边形MNCS =S 四边形DTNP =S 四边形AQPK =S 四边形MNPQ ，∴S 四边形MNPQ =15S 四边形ABCD =15×3×4=125 故答案为：125本题主要考查了矩形的性质，平行四边形的判定与性质，解决本题的关键是要利用矩形的性质，作出图形中的辅助线构造全等三角形，并找出矩形和平行四边形的面积之间的关系．20．（1-1）【解析】画出符合要求的图形，过A 作AD ⊥x 轴于D ，过C 作CE ⊥x 轴于E ，证明△AOD ≌△OCE ，得到CE=OD=1，可得点C 坐标，同理可得结果．解：如图，过A 作AD ⊥x 轴于D ，过C 作CE ⊥x 轴于E ，∵四边形OABC 是正方形，∴OA=OC ，∠AOC=90°，∴∠COE+∠AOD=90°，又∵∠OAD+∠AOD=90°，∴∠OAD=∠COE ，在△AOD 和△OCE 中，ADO OEC OAD COE OA CO ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△AOD ≌△OCE （AAS ），∴CE=OD=1，∵点C 在第二象限，∴点C的坐标为（1），同理可得：点C1-1），综上：点C 的坐标为：故答案为：（1-1）．本题考查了正方形的性质，全等三角形的判定和性质，解题的关键是找出所有符合条件的正方形，作出辅助线证明全等．21．2877cm ． 【解析】由两个长宽分别为7cm 、3cm 的矩形如图叠放在一起，可证得阴影部分是菱形，然后设BF xcm =，则 D F xcm ，7()AF AD DF x cm ，利用勾股定理可得方程： 2223(7)x x ，则可求得BE 的长，继而求得答案．解：如图：根据题意得：//AD BC ，//BF DE ，∴四边形ABCD 是平行四边形，两个矩形等高，即DH AB =，BEDF S BE AB BF DH ，BE BF ∴=，∴四边形BEDF 是菱形，BF DF ∴=，设BF xcm =，则D F xcm ，7()AF AD DF x cm ，在Rt ABF ∆中，222AB AF BF +=，2223(7)x x ， 解得：297x， 297BE cm ， 2877BEDF S BE AB cm 菱形． 故答案为：2877cm ． 本题考查了菱形的判定与性质以及勾股定理等知识．掌握方程思想的应用是解此题的关键． 22．45°【解析】延长EB 使得BG=DF ，易证△ABG ≌△ADF （SAS ），可得AF=AG ，进而求证△AEG ≌△AEF ，可得∠EAG=∠EAF ，再求出∠EAG+∠EAF=90︒即可解题．解：如图，延长EB 到点G ，使得 BG=DF ，连接AG ，在正方形ABCD 中，∠D=∠ABC=90︒， AB=AD ，∴∠ABG=∠ADF=90︒，在△ABG 和 △ADF 中，AB AD ABG ADF BG DF =⎧⎪∠=∠⎨⎪=⎩，∴△ABG ≌△ADF(SAS) ，∴∠DAF=∠BAG ， AF=AG ，又 ∵EF=DF+BE=BG+BE=EG ，∴ 在△AEG 和 △AEF 中，AE AE GE FE AG AF =⎧⎪=⎨⎪=⎩，∴△AEG ≌△AEF(SSS) ，∴∠EAG=∠EAF ，∵∠DAF+∠EAF+∠BAE=90︒，∴∠BAG+∠EAF+∠BAE=90︒，∴∠EAG+∠EAF=90︒，∴∠EAF=45︒．故答案为：45︒．本题考查了正方形的性质，全等三角形的判定与性质，作出辅助线构造出全等三角形是解决此题的关键．23．【解析】连接BF ，过点F 作FG ⊥AB 交AB 延长线于点G ，易知△AED ≌△GFE （AAS ），F 在BF 的射线上，作点C 关于BF 的对称点C′，由全等三角形的性质可得∠CBF ＝45°，继而求得点C′在AB 的延长线上，进而分析可知当D 、F 、C′三点共线时，DF ＋CF ＝DC′最小，在Rt △ADC′中，由勾股定理即可求解．连接BF ，过点F 作FG ⊥AB 交AB 延长线于点G ，∵将ED 绕点E 顺时针旋转90°到EF ，∴EF ⊥DE ，EF ＝DE ，∴∠DEA ＋∠GEF ＝∠DEA+∠ADE ＝90°∴∠GEF ＝∠ADE又∠A ＝∠EGF ＝90°∴△AED ≌△GFE （AAS ）∴FG ＝EA∵F 在BF 的射线上，作点C 关于BF 的对称点C′∵EG ＝DA ，FG ＝AE∴AE ＝BG∴BG ＝FG∴∠FBG＝45°∴∠CBF＝45°∴点C′在AB的延长线上，当D、F、C′三点共线时，DF＋CF＝DC′最小，在Rt△ADC′中，AD＝3，AC′＝6，∴DC′∴DF＋CF的最小值为故答案为：．．本题考查旋转的性质，全等三角形的判定及其性质，轴对称最短路线问题，解题的关键是将线段的和通过轴对称旋转转化为共线线段即可．24．40【解析】根据三角形的中位线平行于第三边并且等于第三边的一半可得AB＝2EF，然后根据菱形的四条边都相等列式计算即可得解．解：∵E、F分别是AC、BC的中点，∴EF是△ABC的中位线，∴AB＝2EF＝2×5＝10，∴菱形ABCD的周长＝4×10＝40．故答案为：40．本题考查了菱形的性质，三角形的中位线平行于第三边并且等于第三边的一半，熟记性质与定理是解题的关键．25．8【解析】延长AG交BC于D，根据重心的定义，点D为BC的中点，先由直角三角形斜边上的中线等于斜边的一半求得DG的长，再由重心的性质：三角形的重心到一顶点的距离等于到对边中点距离的2倍进行求解即可．解：延长AG交BC于D，∵点G是重心，∴点D为BC的中点，且AG=2DG，∵∠BGC=90°，BC=8，∴DG=12BC=4，∴AG=2DG=8，故答案为：8．本题考查了三角形的重心、直角三角形斜边上的中线性质，熟练掌握三角形的重心定义和性质是解答的关键．26．2.5【解析】先根据菱形的性质得到AC⊥BD，OB＝OD＝12BD＝4，OC＝OA＝12AC＝3，再利用勾股定理计算出BC，然后根据直角三角形斜边上的中线性质得到OH的长．∵四边形ABCD为菱形，AC＝6，BD＝8，∴AC⊥BD，OB＝OD＝12BD＝4，OC＝OA＝12AC＝3，在Rt△BOC中，BC5，∵H为BC中点，∴OH＝12BC＝2.5．故答案为：2.5．本题考查菱形的性质、勾股定理及直角三角形斜边中线的性质，菱形的对角线互相垂直且平分；直角三角形斜边的中线等于斜边的一半；熟练掌握相关性质是解题关键．27．112n - 【解析】由正方形ABCD 的边长为1，求出12AE AF AC ===，1122AH AB ==，分别算出第二个、第三个正方形的面积，即可推导得出答案；∵正方形ABCD 的边长为1，∴1AB =，AC =∴12AE AF AC ===， 1122AH AB ==，∴1正方形=1ABCD S S =，2正方形1222AEBF S S ==⨯=， 3正方形111224HEGB S S ==⨯=, ⋯， ∴112n n S -=． 故答案是：112n - 本题主要考查了正方形的性质，准确分析计算是解题的关键．28．30【解析】根据轴对称和矩形性质，得90EFD A ∠=∠=；结合∠EFB ＝60°，经计算即可得到答案． ∵矩形ABCD 沿DE 折叠，使A 点落在BC 上的F 处∴90EFD A ∠=∠=∵∠EFB ＝60°∴180180609030CFD EFB EFD ∠=-∠-∠=--=故答案为：30．本题考查了轴对称、矩形的性质；解题的关键是熟练掌握轴对称、矩形的性质，从而完成求解．29．2 【解析】连接BP，根据菱形的面积公式和三角形的面积公式得S△ABC＝S△ABP＋S△BPC＝12ABCDS菱形，S△ABP＋S△BPC＝12AB•PE＋12BC•PE把相应的值代入即可．解：连接BP，∵四边形ABCD是菱形，且周长是12cm，面积是6cm2∴AB＝BC＝14×12＝3（cm），∵AC是菱形ABCD的对角线，∴ S△ABC＝S△ABP＋S△BPC＝12ABCDS菱形＝3（cm2），∴S△ABP＋S△BPC＝12AB•PE＋12BC•PE＝3（cm2），∴12×3×PE＋12×3×PF＝3，∴PE＋PF＝3×23＝2（cm），故答案为：2．此题考查菱形的性质，S△ABP＋S△BPC＝S△ABC＝12ABCDS菱形是解题的关键．注意掌握辅助线的作法和数形结合思想的应用．30．20202ab【解析】结合题意，根据矩形性质，得平行四边形1OBB C为菱形，从而依次计算前4个平行四边形的面积，并通过归纳计算规律，即可得到第2020个平行四边形的面积．∵矩形ABCD中，AB a，BC b=，两条对角线相交于点O∴OB OC OA==∵OB、OC为邻边作第1个平行四边形1OBB C∴11OB OC BB CB ===∴平行四边形1OBB C 为菱形∵平行四边形1OBB C ，对角线相交于点1A ，∴1OA BC ⊥，1112BA CA BC ==，111OA A B = ∵OC OA = ∴11122OA AB a == ∴第1个平行四边形1OBB C 面积112BC OA a b =⨯=⨯ ∴第2个平行四边形111A B C C 面积1111122AC A B a b =⨯=⨯ 同理，得第3个平行四边形1121O B B C 面积21111122222a b a b ⎛⎫=⨯⨯=⨯ ⎪⎝⎭第4个平行四边形2221A B C C 面积2221111122222a b a b ⎛⎫⎛⎫⎛⎫=⨯⨯=⨯ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭以此类推，第2020个平行四边形2221A B C C 面积为：10101010202020201112222ab a b ab ⎛⎫⎛⎫⎛⎫⨯== ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 故答案为：20202ab ． 本题考查了数字及图形规律、三角形中位线、幂的乘方、平行四边形、矩形、菱形的知识；解题的关键是熟练掌握数字及图形规律、幂的乘方、平行四边形、矩形的性质，从而完成求解．。

北师大版2019-2020初中数学特殊的平行四边形提升训练题1（附答案）3．如图，将边长为12 cm的正方形ABCD沿其对角线AC剪开，再把ABC沿着AD方向平移，得到△A′B′C′，若两个三角形重叠部分的面积为32 cm2，则它移动的距离AA′等于( )A．4 cm B．8 cm C．6 cm D．4 cm或8 cm11．在数学活动课上，老师让同学们判定一个四边形门框是否为矩形，下面是某合作小组的四位同学的拟订方案，其中正确的是()A．测量对角线是否互相平分B．测量两组对边是否分别相等C．测量一组对角是否为直角D．测量两组对边是否相等，再测量对角线是否相等12．菱形的两条对角线长为6 cm 和8 cm，那么这个菱形的周长为A．40 cm B．20 cm C．10 cm D．5 cm13．在菱形ABCD中，AC、BD为对角线，若AC=4，BD=8，则菱形ABCD的面积是（）A．12 B．16 C．24 D．3214．顺次连接平行四边形各边中点所得的四边形是( )A．平行四边形B．长方形C．任意四边形D．正方形15．如图，在矩形ABCD中，AB=2，E在BC的延长线上，且BD=CE，连接AE，则∠E的度数为（）A．15°B．20°C．30°D．45°16．如图，已知正方形ABCD的边长为2，E是边BC上的动点，BF⊥AE交CD于点F，垂足为点G，连接CG，下列说法：①AG＞GE；②AE=BF；③点G运动的路径长为π；④CG的最小值﹣1．其中正确的说法有（）个．A ．4B ．3C ．2D ．117．矩形，菱形，正方形都具有的性质是（ ）A ．对角线相等B ．对角线互相平分C ．对角线平分一组对角D ．对角线互相垂直18．如图1，点F 从菱形ABCD 的顶点A 出发，沿A→D→B 以1cm/s 的速度匀速运动到点B ，图2是点F 运动时，△FBC 的面积y （cm 2）随时间x （s ）变化的关系图象，则a 的值为( )A ．52B ．2C ．72D ．519．如图，矩形ABCD 中， AC 、BD 相较于点O ，若60AOB ∠=︒， 6AC =，则BC 的长为（ ）．A ．3B ．C ．D ．620．在▱ABCD 中，AB ＝3，BC ＝4，当▱ABCD 的面积最大时，下列结论：①AC ＝5；②∠A+∠C ＝180°；③AC ⊥BD ；④AC ＝BD ．正确的有( )A ．①②③B ．①②④C ．②③④D ．①③④21．设二次函数y=x 2+ax+b 图像与x 轴有2个交点，A(x 1,0)，B(x 2,0)；且0< x 1<1；1< x 2<2,那么（1）a 的取值范围是___________；b 的取值范围是________；则（2）的取值范围是_______.31．如图，在矩形ABCD 中，对角线AC 和BD 相交于点O ，点E 、F 分别是DO 、AO 的中点．若AB=8cm ，BC=4cm ，则△OEF 的周长为 cm ．32．在平面直角坐标系中，正方形ABCD 的位置如图所示，点A 的坐标为（1，0），点D 的坐标为（0，2）．延长CB 交x 轴于点A 1，作正方形A 1B 1C 1C ；则点C 2的坐为 ．33．如图，在矩形ABCD 中，35ABBC =，以点B 为圆心，BC 长为半径画弧，交边AD于点E ，若8AE ED ⋅=，则矩形ABCD 的面积为_______.34．如图，A ，B 两点的坐标分别为（6,0),(0,6)，点P 从点A 出发，沿AB 个单位的速度向终点B 运动；同时动点Q 从点B 出发沿BO 方向以每秒1个单位的速度向终点Q 运动，将△PQO 沿BO 翻折，点P 的对应点为点C ，若四边形QPOC 为菱形，则点C 的坐标为________．35．如图，在菱形ABCD中，，AB的垂直平分线交对角线AC于点F，点E为垂足，连接DF，则的度数为______．36．如图,正方形ABCD,点P是对角线AC上一点,连结BP,过P作PQ⊥BP,PQ交CD于Q,若AP=，CQ=3，则四边形PBCQ的面积为_______.37．已知一个菱形的周长为，有一个内角为，则这个菱形较短的一条对角线长为________．38．如图，已知边长为2的正三角形ABC，两顶点A，B分别在平面直角坐标系的轴、轴的正半轴上滑动，点C在第一象限，连结OC，则OC长的最大值是．39．如图，正方形ABCD的边长是4cm，点G在边AB上，以BG为边向外作正方形GBFE，连接AE、AC、CE，则△AEC的面积是cm2。

特殊平行四边形提高训练一．选择题〔共16 小题〕1．〔2021?灵璧县一模〕如下图，矩形 ABCD 中，AE 平分∠ BAD 交 BC 于 E，∠ CAE=15 °，那么下面的结论：① △ODC 是等边三角形；② BC=2AB；③ ∠ AOE=135°；④ S△AOE=S△COE，其中正确结论有〔〕A．1 个 B．2 个 C．3 个 D．4 个2．〔2021?鄂州一模〕如图，在矩形AOBC 中，点 A 的坐标〔﹣ 2，1〕，点 C 的纵坐标是4，那么 B 、C 两点的坐标分别是〔〕A ．〔，〕、〔﹣，4〕B．〔，3〕、〔﹣，4〕C．〔，3〕、〔﹣，4〕D．〔，〕、〔﹣， 4〕3．〔2021?石峰区模拟〕矩形 ABCD 中，AB=2 ，AD=1 ，点 M 在边 CD 上，假设 AM 平分∠ DMB ，那么 DM 的长是〔〕A．B．C．D．4．〔2021?姜堰区校级模拟〕矩形ABCD中，AB=4，BC=8，矩形CEFG上的点G在CD边，EF=a， CE=2a，连接 BD 、 BF、 DF ，那么△ BDF 的面积是〔〕A．32 B．16 C．82 D． 16+a5．〔2021?灯塔市二模〕如图，在矩形ABCD 中， AB=3 ， DC=2 ，O 是 AD 的中点，连接OB、OC，点 E 在线段 BC 上〔点 E 不与点 B、C 重合〕，过点 E 作 EM ⊥OB 于 M ，EN ⊥ OC 于 N ，那么 EM+EN 的值为〔〕A．6B．1.5 C．D．6．〔2021?肥城市二模〕一个菱形的周长是20cm，两条对角线的比是4： 3，那么这个菱形的面积是〔〕2222A ． 12cmB ．96cmC． 48cm D ．24cm7．〔2021 ?丹东〕过矩形 ABCD 的对角线 AC 的中点 O 作 EF⊥ AC ，交 BC 边于点 E，交 AD 边于点 F，分别连接AE 、 CF．假设 AB=，∠ DCF=30°，那么EF的长为〔〕A．2B．3C．D．8．〔2021?天津一模〕如图，菱形ABCD 的对角线AC 、BD 相交于点O，AC=8 ，BD=6 ，过点 O 作 OH ⊥ AB ，垂足为H，那么点 O 到边 AB 的距离 OH 等于〔〕A．2B．C．D．9．〔2021?和县一模〕如图，菱形ABCD 中，点 O 对角线 AC 的三等分点，连接OB、 OD ，且 OB=OC=OD ． AC=3 ，那么菱形的边长为〔〕A．B．2C．D．10．〔2021?丹东模拟〕如图，在菱形ABCD 中，对角线AC ， BD 相交于点O，点 E 为 BC 的中点，那么以下等式中一定成立的是〔〕A ． AB=BEB ．AC=2AB C． AB=2OE D ．AC=2OE11．〔2021 ?西城区二模〕如图，将正方形OABC 放在平面直角坐标系xOy 中， O 是原点，假设点 A 的坐标为〔 1，〕，那么点C的坐标为〔〕A ．〔，1〕B．〔﹣ 1，〕C．〔﹣，1〕D．〔﹣，﹣1〕12．〔2021 ?桐庐县模拟〕如图，在正方形ABCD 中，对角线AC=6 ，点 P 是对角线 AC 上的一点，过点P 作 PF⊥ AD ，PE⊥ CD ，那么 PF+PE 的值为〔〕A．3B ．3C．2D．613．〔2021 ?本溪二模〕如图，在矩形ABCD 中， AD=2AB ， E、F 分别是 AD 、 BC 的中点，连接 AF 与 BE 、 CE 与 DF 分别交于点M 、 N 两点，那么四边形EMFN 是〔〕A ．正方形B ．菱形C ．矩形D ．无法确定14．〔2021 春?石林县期末〕如图，在正方形ABCD 的外侧，作等边三角形ADE ，连接 CE，与对角线 BD 交于 F，那么∠ BFC 为〔〕A ． 75° B． 70° C． 65° D． 60°15．〔2021 ?铁力市二模〕如图，点 P 是正方形 ABCD 的对角线BD 上一点， PE⊥ BC 于点 E；PF⊥ CD 于点 F，连接 EF ，给出以下五个结论：① AP=EF ；② AP ⊥EF；③∠PFE=∠ BAP ；222④ PD=EC ；⑤ PB +PD =2PA，正确的有〔〕个．A．5B．4C．3D．216．〔2021 ?陕西模拟〕如图，E 是边长为 1 的正方形 ABCD 的对角线BD 上一点，且 BE=BC ，P 为 CE 上任意一点，PQ⊥ BC 于点 Q， PR⊥ BE 于点 R，那么 PQ+PR 的值是〔〕A．B．C．D．二．解答题〔共11 小题〕17．〔2021?咸阳模拟〕如图，矩形 ABCD ，E、 F 在 AB 、 CD 上，且 EF∥ AD ， M 为 EF 的中点，连接 AM 、DM ，求证： AM=DM ．18．〔2021?市南区一模〕：如图，在矩形ABCD 中，点 E 在边 AD 上，点 F 在边 BC上，且 AE=CF ，作 EG∥ FH，分别与对角线BD 交于点 G、 H，连接 EH， FG．（1〕求证：△ BFH ≌△ DEG ；（2〕连接 DF，假设 BF=DF ，那么四边形 EGFH 是什么特殊四边形？证明你的结论．19．〔2021春 ?南京校级月考〕：如图， BE 、 BF 分别是∠ ABC 与它的邻补角∠ ABD 的平分线，AE ⊥BE ，垂足为点 E，AF ⊥ BF ，垂足为点 F，EF 分别交边 AB 、AC 于点 M 和 N ．求证：（1〕四边形 AFBE 是矩形；（2〕 MN= BC ．20．〔2021?安徽模拟〕如图，在△ ABC 中， D 是 BC 边的中点， F， E 分别是 AD 及其延长线上的点， CF∥ BE，连结 BF， CE．〔1〕求证：四边形BFCE 是平行四边形；〔2〕当边 AB 、 AC 满足什么条件时，四边形BECF 是菱形？并说明理由．21．〔2021?十堰模拟〕：如图，在菱形 ABCD 中， F 为边 BC 的中点， DF 与对角线 AC 交于点M ，过 M 作 ME ⊥CD 于点 E，∠ 1=∠ 2．（1〕假设 CE=2，求 BC 的长；（2〕求证： ME=AM ﹣ DF．22．〔2021?东平县一模〕如图，在△ ABC中，∠ ABC=90°，BD为AC的中线，过点C 作CE⊥ BD 于点 E，过点 A 作 BD 的平行线，交CE 的延长线于点F，在 AF 的延长线上截取FG=BD ，连接 BG、DF ．（1〕求证： BD=DF ；（2〕求证：四边形 BDFG 为菱形；（3〕假设 AG=13 ， CF=6 ，求四边形 BDFG 的周长．23．〔2021?南岗区模拟〕如图，在正方形 ABCD 中，点 E 在对角线 AC 上，点 F 在边 BC 上，连接 BE 、DF， DF 交对角线 AC 于点 G，且 DE=DG ．（1〕求证： AE=CG ；（2〕试判断 BE 和 DF 的位置关系，并说明理由．24．〔2021?景德镇校级二模〕如图，在四边形 ABCD 中， AB=BC ，对角线 BD 平分∠ ABC ， P 是BD 上一点，过点 P 作 PM⊥ AD ， PN⊥ CD ，垂足分别为 M ， N．（1〕求证：点 A 与 C 关于直线 BD 对称．（2〕假设∠ ADC=90 °，求证四边形 MPND 为正方形．25．〔2021 ?滕州市模拟〕：如图，正方形ABCD 中，点 E 在 BC 的延长线上， AE 分别交DC， BD 于 F， G，点 H 为 EF 的中点．求证：〔 1〕∠ DAG= ∠ DCG ；〔2〕GC⊥CH ．26．〔2021春 ?丹阳市校级月考〕如图，正方形ABCD 的对角线 AC 、 BD 相交于点O，E 是 AC 上的一点，过点A 作 AG ⊥ BE ，垂足为 G， AG 交 BD 于点 F．（1〕试说明 OE=OF ；（2〕当 AE=AB 时，过点 E 作 EH⊥BE 交 AD 边于 H ，找出与△ AHE 全等的一个三角形加以证明，〔3〕在〔 2〕的条件下假设该正方形边长为1，求 AH 的长．27．〔2021 ?荆州〕如图 1，在正方形 ABCD 中， P 是对角线 BD 上的一点，点 E 在 AD 的延长线上，且 PA=PE， PE 交 CD 于 F．（1〕证明： PC=PE；（2〕求∠ CPE 的度数；（3〕如图 2，把正方形 ABCD 改为菱形 ABCD ，其他条件不变，当∠ ABC=120 °时，连接CE，试探究线段AP 与线段 CE 的数量关系，并说明理由．特殊平行四边形提高训练参考答案与试题解析一．选择题〔共16 小题〕1．〔2021?灵璧县一模〕如下图，矩形 ABCD 中，AE 平分∠ BAD 交 BC 于 E，∠ CAE=15 °，那么下面的结论：① △ODC 是等边三角形；② BC=2AB；③ ∠ AOE=135°；④ S△AOE=S△COE，其中正确结论有〔〕A．1 个 B．2 个C．3 个D．4 个【分析】根据矩形性质求出 OD=OC ，根据角求出∠ DOC=60 °即可得出三角形 DOC 是等边三角形，求出 AC=2AB ，即可判断②，求出∠ BOE=75 °，∠AOB=60 °，相加即可求出∠ AOE ，根据等底等高的三角形面积相等得出S△AOE=S COE．【解答】解：∵四边形ABCD 是矩形，∴∠ BAD=90 °， OA=OC ，OD=OB ， AC=BD ，∴OA=OD=OC=OB ，∵AE 平分∠ BAD ，∴∠ DAE=45 °，∵∠ CAE=15 °，∴∠ DAC=30 °，∵OA=OD ，∴∠ ODA= ∠ DAC=30 °，∴∠ DOC=60 °，∵OD=OC ，∴△ ODC 是等边三角形，∴① 正确；∵四边形 ABCD 是矩形，∴AD ∥ BC ，∠ ABC=90 °∴∠ DAC= ∠ ACB=30 °，∴A C=2AB ，∵AC ＞BC，∴2AB ＞ BC，∴②错误；∵AD ∥BC，∴∠ DBC= ∠ ADB=30 °，∵AE 平分∠DAB ，∠DAB=90 °，∴∠ DAE= ∠ BAE=45 °，∵AD ∥BC，∴∠ DAE= ∠ AEB ，∴∠ AEB= ∠BAE ，∴A B=BE ，∵四边形 ABCD 是矩形，∴∠ DOC=60 °， DC=AB ，∵△ DOC 是等边三角形，∴DC=OD ，∴BE=BO ，∴∠ BOE= ∠BEO=〔180°﹣∠ OBE〕=75°，∵∠ AOB= ∠ DOC=60 °，∴∠ AOE=60 °+75 °=135 °，∴ ③正确；∵OA=OC ，∴根据等底等高的三角形面积相等得出 S△AOE=S COE，∴④正确；应选C．2．〔2021?鄂州一模〕如图，在矩形AOBC 中，点 A 的坐标〔﹣ 2，1〕，点 C 的纵坐标是4，那么 B 、C 两点的坐标分别是〔〕A ．〔，〕、〔﹣，4〕B．〔，3〕、〔﹣，4〕C．〔，3〕、〔﹣，4〕D．〔，〕、〔﹣， 4〕【分析】如过点 A、 B 作 x 轴的垂线垂足分别为F、 M ．过点 C 作 y 轴的垂线交FA 、根据△AOF ∽△ CAE ，△AOF ≌△ BCN ，△ACE ≌△ BOM 解决问题．【解答】解：如图过点 A 、 B 作 x 轴的垂线垂足分别为 F、M ．过点 C 作 y 轴的垂线交 FA、∵点 A 坐标〔﹣ 2， 1〕，点 C 纵坐标为 4，∴A F=1 ， FO=2 ， AE=3 ，∵∠ EAC+ ∠OAF=90 °，∠ OAF+ ∠ AOF=90 °，∴∠ EAC= ∠AOF ，∵∠ E=∠AFO=90 °，∴△ AEC ∽△ OFA，∴，∴EC=，∴点C坐标〔﹣，4〕，∵△ AOF ≌△ BCN ，△ AEC ≌△ BMO ，∴CN=2 ， BN=1 ， BM=MN ﹣ BN=3 ， BM=AE=3 ， OM=EC=，∴点 B 坐标〔，3〕，应选 C．3．〔2021?石峰区模拟〕矩形 ABCD 中，AB=2 ，AD=1 ，点 M 在边 CD 上，假设 AM 平分∠ DMB ，那么 DM 的长是〔〕A．B．C．D．【分析】由矩形的性质得出CD=AB=2 ， AB ∥CD ， BC=AD=1 ，∠ C=90 °，由平行线的性质得出∠ BAM= ∠AMD ，再由角平分线证出∠BAM= ∠ AMB ，得出 MB=AB=2 ，由勾股定理求出 CM ，即可得出DM 的长．【解答】解：∵四边形ABCD 是矩形，∴C D=AB=2 ， AB ∥ CD ， BC=AD=1 ，∠C=90 °，∴∠ BAM= ∠ AMD ，∵AM 平分∠ DMB ，∴∠AMD= ∠AMB ，∴∠ BAM= ∠ AMB ，∴B MB=AB=2 ，∴CM===，∴DM=CD ﹣CM=2 ﹣；应选： D．4．〔2021?姜堰区校级模拟〕矩形ABCD中，AB=4，BC=8，矩形CEFG上的点G在CD边，EF=a， CE=2a，连接 BD 、 BF、 DF ，那么△ BDF 的面积是〔〕A．32 B．16 C．82 D． 16+a【分析】根据两个矩形面积之和加上三角形DGF 面积，减去△ ABD 面积与△ BEF 面积，求出△ BDF 面积即可．【解答】解：根据题意得：△BDF 的面积 =8 ×4+2a?a+×2a〔 4﹣ a〕﹣222﹣×8×4﹣ a〔 2a+8〕 =32+2a +4a﹣ a ﹣ 16﹣ a4a=16；应选： B．5．〔2021?灯塔市二模〕如图，在矩形 ABCD 中， AB=3 ， DC=2 ，O 是 AD 的中点，连接OB、OC，点 E 在线段 BC 上〔点 E 不与点 B、C 重合〕，过点 E 作 EM ⊥OB 于 M ，EN ⊥ OC于 N ，那么 EM+EN 的值为〔〕A．6B．1.5 C．D．【分析】连接 OE，由矩形的性质得出CD=AB=3 ， AD=BC=2 ，∠ A= ∠ D=90 °，由勾股定理得出 OB=OC=，由△OBE的面积+△ OCE的面积=△ OBC的面积，即可得出结果．【解答】解：连接 OE，如下图：∵四边形 ABCD 是矩形，∴C D=AB=3 ， AD=BC=2 ，∠ A= ∠ D=90 °，∵O 是 AD 的中点，∴A O=DO=1 ，∴OB=OC==，∵△ OBE 的面积 +△OCE 的面积 =△ OBC 的面积，∴OB ?EM+ OC?EN= BC?AB ，∴〔EM+EN〕×=×2×3，解得： EM+EN=；应选： D．6．〔2021?肥城市二模〕一个菱形的周长是20cm，两条对角线的比是 4： 3，那么这个菱形的面积是〔〕2222A ． 12cmB ．96cm C． 48cmD ．24cm【分析】先求出菱形的边长，然后设菱形的两对角线分别为8x ， 6x，根据菱形的对角线垂直平分求出两对角线的一半，再利用勾股定理列式求出x，从而得到对角线的长，然后根据菱形的面积等于对角线乘积的一半列式进展计算即可得解．【解答】解：∵菱形的周长是 20cm，∴边长为 20÷4=5cm ，∵两条对角线的比是 4： 3，∴设菱形的两对角线分别为8x， 6x，根据菱形的性质可知，菱形的对角线互相垂直平分，那么对角线的一半分别为4x， 3x，222根据勾股定理得，〔 4x〕+〔 3x〕 =5，解得 x=1 ，所以，两对角线分别为8cm， 6cm，所以，这个菱形的面积=×8×6=24cm 2．应选： D．7．〔2021 ?丹东〕过矩形 ABCD 的对角线边于点 F，分别连接 AE 、 CF．假设AB=AC 的中点 O 作 EF⊥ AC ，交 BC 边于点 E，交 AD ，∠ DCF=30 °，那么 EF 的长为〔〕A．2B．3C．D．【分析】求出∠ ACB= ∠ DAC ，然后利用“角角边〞证明△ AOF 和△ COE 全等，根据全等三角形对应边相等可得OE=OF ，再根据对角线互相垂直平分的四边形是菱形得到四边形AECF第 12 页〔共 31 页〕【解答】解：∵矩形对边AD ∥BC ，∴∠ ACB= ∠ DAC ，∵O 是 AC 的中点，∴AO=CO ，在△ AOF 和△ COE 中，，∴△ AOF ≌△ COE 〔ASA 〕，∴OE=OF ，又∵ EF⊥ AC ，∴四边形 AECF 是菱形，∵∠ DCF=30 °，∴∠ ECF=90 °﹣ 30°=60°，∴△ CEF 是等边三角形，∴E F=CF ，∵AB= ，∴C D=AB= ，∵∠DCF=30 °，∴C F= ÷ =2，∴E F=2 ．应选 A．8．〔2021?天津一模〕如图，菱形ABCD 的对角线AC 、BD 相交于点O，AC=8 ，BD=6 ，过点 O 作 OH ⊥ AB ，垂足为H，那么点 O 到边 AB 的距离 OH 等于〔〕A．2B．C．D．【分析】因为菱形的对角线互相垂直平分，菱形的四边相等，根据面积相等，可求出OH 的长．【解答】解：∵四边形ABCD 是菱形， AC=8 ，BD=6 ，∴B O=3 ， AO=4 ， AO ⊥ BO ，∴AB==5．∵OH⊥AB ，∴AO ?BO= AB ?OH，∴OH=，应选 D．9．〔2021?和县一模〕如图，菱形ABCD 中，点 O 对角线 AC 的三等分点，连接OB、 OD ，且 OB=OC=OD ． AC=3 ，那么菱形的边长为〔〕A．B．2C．D．【分析】由菱形的性质得出AB=BC ，得出∠ BAC= ∠ ACB ，由条件得出OB=OC=AC=1 ，由等腰三角形的性质得出△ BOC∽△ ABC ，得出对应边成比例，即可求出菱形的边长．【解答】解：∵四边形ABCD 是菱形，∴ AB=BC ，∴∠ BAC= ∠ ACB ，∵点 O 对角线 AC 的三等分点，∴OB=OC=AC=1 ，∴∠ BAC= ∠ ACB= ∠ OBC ，∴△ BOC∽△ ABC ，所以，即，2∴BA =3 ，∴BA=；应选： A．10．〔2021?丹东模拟〕如图，在菱形ABCD 中，对角线AC ， BD 相交于点O，点 E 为 BC 的中点，那么以下等式中一定成立的是〔〕A ． AB=BEB ．AC=2AB C． AB=2OE D ．AC=2OE【分析】由菱形的性质以及三角形中位线定理逐项分析即可．【解答】解：∵点 E 为 BC 的中点，∴C E=BE= BC，∵A B=BC ，∴AB=2BE ，应选项A 错误；∵在菱形 ABCD 中，对角线AC ， BD 相交于点O，∴AO=CO=AC ，∴OE 是△ ABC 的中位线，∴OE= AB ，应选项 C 正确；∵AC ≠AB ≠BC，∴AC ≠2AB ≠2OE，应选项B ， D 错误，应选 C．11．〔2021 ?西城区二模〕如图，将正方形OABC 放在平面直角坐标系xOy 中， O 是原点，假设点 A 的坐标为〔 1，〕，那么点C的坐标为〔〕A ．〔，1〕B．〔﹣ 1，〕C．〔﹣，1〕D．〔﹣，﹣1〕【分析】作 AD ⊥轴于 D，作 CE⊥ x 轴于 E，那么∠ ADO= ∠OEC=90 °，得出∠ 1+ ∠ 2=90°，由正方形的性质得出OC=AO ，∠ 1+∠ 3=90 °，证出∠ 3=∠2，由 AAS 证明△OCE≌△ AOD ，OE=AD=， CE=OD=1 ，即可得出结果．【解答】解：作 AD ⊥轴于 D，作 CE⊥x 轴于 E，如下图：那么∠ ADO= ∠ OEC=90 °，∴∠ 1+∠ 2=90°，∵点 A 的坐标为〔 1，〕，∴OD=1 ， AD=，∵四边形 OABC 是正方形，∴∠ AOC=90 °， OC=AO ，∴∠ 1+∠ 3=90°，∴∠ 3=∠ 2，在△ OCE 和△ AOD 中，，∴△ OCE≌△ AOD 〔 AAS 〕，∴OE=AD=，CE=OD=1，∴点 C 的坐标为〔﹣，1〕；应选： C．12．〔2021 ?桐庐县模拟〕如图，在正方形ABCD 中，对角线AC=6 ，点 P 是对角线 AC 上的一点，过点P 作 PF⊥ AD ，PE⊥ CD ，那么 PF+PE 的值为〔〕A．3B ．3C．2D．6【分析】由正方形的性质得出∠PAF=∠ PCE=45 °，证出△ APF 和△ CPE 是等腰直角三角形，得出 PF=AP ， PE=PC，即可得出结论．【解答】解：∵四边形ABCD 是正方形，∴∠ BAD= ∠ BCD=90 °，∠ PAF=∠ PCE=45°，∵P F⊥AD ， PE⊥CD ，∴△ APF 和△CPE 是等腰直角三角形，∴PF=AP， PE=PC，∴PF+PE=〔AP+PC〕=AC=3；应选： A．13．〔2021 ?本溪二模〕如图，在矩形ABCD 中， AD=2AB ， E、F 分别是 AD 、 BC 的中点，连接 AF 与 BE 、 CE 与 DF 分别交于点M 、 N 两点，那么四边形EMFN 是〔〕A ．正方形B ．菱形C ．矩形D ．无法确定【分析】利用矩形的性质与判定方法得出四边形EMFN 是矩形，进而利用等腰直角三角形的性质得出AM=ME ， BM=MF=AM，那么ME=MF，进而求出即可．【解答】解：∵四边形ABCD 为矩形，∴AD ∥ BC ， AD=BC ，∠ EAB= ∠ ABF= ∠ BCD=∠CDA=90 °，又∵ E， F 分别为 AD ， BC 中点， AD=2AB ，∴AE ∥ BF， ED∥ CF， AE=BF=DE=CF=AB=DC，∴∠ ABE= ∠AEB= ∠DEC= ∠ DCE= ∠ DFC=45 °，∴∠ BEN=90 °，又∵ DE BF， AE FC，∴四边形 EMFN 是矩形，∴AM ⊥BE ，BM ⊥ AF，∴AM=ME ， BM=MF=AM，∴ME=MF ，∴四边形 EMFN 是正方形．应选： A．14．〔2021 春?石林县期末〕如图，在正方形ABCD 的外侧，作等边三角形ADE ，连接 CE，与对角线 BD 交于 F，那么∠ BFC 为〔〕A ． 75° B． 70° C． 65° D． 60°【分析】由于四边形ABCD 是正方形，△ADE 是正三角形，由此可以得到CD=DE ，接着利用正方形和正三角形的内角的性质即可求解．【解答】解：∵四边形ABCD 是正方形，∴∠ ADC=90 °， AD=DC ，又∵△ ADE 是正三角形，∴CD=DE ，∠ ADE=60 °，∴△ CDE 是等腰三角形，∠CDE=90 °+60 °=150°，∴∠ ECD= ∠DEC=15 °，∵∠ BDC=45 °，∴∠ CFD=180 °﹣15°﹣45°=120°，∴∠ BFC=60 °，应选 D15．〔2021 ?铁力市二模〕如图，点 P 是正方形ABCD 的对角线BD 上一点， PE⊥ BC 于点 E；PF⊥ CD 于点 F，连接 EF ，给出以下五个结论：① AP=EF ；② AP ⊥EF；③∠PFE=∠ BAP ；222④ PD=EC ；⑤ PB +PD =2PA，正确的有〔〕个．A．5B．4C．3D．2【分析】根据正方形的性质与正方形关于对角线对称可得所给选项的正误．【解答】解：①正确，连接PC，可得PC=EF，PC=PA，∴AP=EF ；②正确；延长AP，交 EF 于点 N ，那么∠ EPN= ∠ BAP= ∠ PCE=∠PFE，可得 AP⊥ EF；③正确；∠ PFE= ∠PCE=∠ BAP ；④错误， PD=222．PF= CE；⑤正确， PB +PD =2PA应选 B．16．〔2021 ?陕西模拟〕如图，E 是边长为 1 的正方形 ABCD 的对角线BD 上一点，且 BE=BC ，P 为 CE 上任意一点，PQ⊥ BC 于点 Q， PR⊥ BE 于点 R，那么 PQ+PR 的值是〔〕A．B．C．D．【分析】连接 BP ，利用面积法求解，PQ+PR 的值等于 C 点到 BE 的距离，即正方形对角线的一半．【解答】解：连接 BP，过 C 作 CM ⊥ BD ，∵S△BCE=S△BPE+S△BPC=BC ×PQ× +BE ×PR×=BC ×〔 PQ+PR〕×=BE ×CM ×，BC=BE ，∴PQ+PR=CM ，∵BE=BC=1 ，且正方形对角线BD=BC=，又∵ BC=CD ， CM ⊥ BD ，∴M 为 BD 中点，又△ BDC 为直角三角形，∴CM= BD=，即 PQ+PR 值是．应选： D．二．解答题〔共11 小题〕17．〔2021?咸阳模拟〕如图，矩形 ABCD ，E、 F 在 AB 、 CD 上，且 EF∥ AD ， M 为 EF 的中点，连接 AM 、DM ，求证： AM=DM ．【分析】由矩形的性质得出AE ∥DF，∠ BAD=90 °，再由 EF∥ AD ，证出四边形AEFD 是矩形，得出 AE=DF ，∠AEM= ∠ DFM=90 °，由 SAS 证明△ AEM ≌△ DFM ，得出对应边相等即可．【解答】证明：∵四边形ABCD 是矩形，∴AE ∥ DF ，∠ BAD=90 °，∵E F∥AD ，∴四边形 AEFD 是矩形，∴A E=DF ，∠ AEM= ∠ DFM=90 °，∵M 为 EF 的中点，∴E M=FM ，在△ AEM 和△DFM 中，，∴△ AEM ≌△ DFM 〔SAS〕，∴AM=DM ．18．〔2021?市南区一模〕：如图，在矩形ABCD 中，点 E 在边 AD 上，点 F 在边 BC上，且 AE=CF ，作 EG∥ FH，分别与对角线BD 交于点 G、 H，连接 EH， FG．（1〕求证：△ BFH ≌△ DEG ；（2〕连接 DF，假设 BF=DF ，那么四边形 EGFH 是什么特殊四边形？证明你的结论．【分析】〔 1〕由平行四边形的性质得出AD ∥BC ，AD=BC ，OB=OD ，由平行线的性质得出∠F BH= ∠ EDG ，∠ OHF= ∠OGE ，得出∠ BHF= ∠ DGE，求出 BF=DE ，由 AAS 即可得出结论；〔2〕先证明四边形EGFH 是平行四边形，再由等腰三角形的性质得出EF⊥ GH ，即可得出四边形 EGFH 是菱形．【解答】〔 1〕证明：∵四边形ABCD 是平行四边形，∴AD ∥ BC ， AD=BC ， OB=OD ，∴∠ FBH= ∠ EDG ，∵AE=CF ，∴BF=DE ，∵EG∥ FH ，∴∠ OHF= ∠ OGE ，∴∠ BHF= ∠ DGE ，在△ BFH 和△ DEG 中，，∴B FH ≌△ DEG 〔 AAS 〕；（2〕解：四边形 EGFH 是菱形；理由如下：连接 DF，如下图：由〔 1〕得： BFH ≌△ DEG ，∴FH=EG ，又∵ EG∥ FH ，∴四边形 EGFH 是平行四边形，∵B F=DF ，OB=OD ，∴EF⊥BD ，∴EF⊥GH ，∴四边形 EGFH 是菱形．19．〔2021春 ?南京校级月考〕：如图， BE 、 BF 分别是∠ ABC 与它的邻补角∠ ABD 的平分线，AE ⊥BE ，垂足为点 E，AF ⊥ BF ，垂足为点 F，EF 分别交边 AB 、AC 于点 M 和 N ．求证：〔1〕四边形AFBE 是矩形；（2〕 MN= BC ．【分析】〔 1〕由 BE 、BE 是角平分线可得∠ EBF 是 90°，进而由条件中的两个垂直可得两个直角，可得四边形 AEBF 是矩形；〔2〕由矩形的 F 质可得∠ 2= ∠ 5 进而利用角平分线的性质可得∠ 1=∠ 5，可得 ME ∥ BC ，进而可得 N 为 AC 中点，根据三角形中位线性质求出即可．【解答】证明：〔 1〕∵ BE、 BF 分别是△ ABC 中∠ B 及它的外角的平分线，∴∠ 1=∠ 2，∠ 3=∠ 4，∵∠ 1+∠ 2+∠ 3+ ∠ 4=180°，∴∠ 2+∠ 3=90°，∵AE ⊥BE，E 为垂足， AF⊥BF， F 为垂足，∴∠ AFB= ∠ AEB=90 °，∴四边形 AEBF 为矩形；〔2〕∵四边形AEBF 为矩形，∴BM=MA=ME，∴∠ 2=∠ 5，∵∠ 2=∠ 1，∴∠ 1=∠ 5，∴ME ∥BC，∵M 是 AB 的中点，∴N 为 AC 的中点，∴MN= BC．20．〔2021?安徽模拟〕如图，在△ ABC 中， D 是 BC 边的中点， F， E 分别是 AD 及其延长线上的点， CF∥ BE，连结 BF， CE．〔1〕求证：四边形BFCE 是平行四边形；〔2〕当边 AB 、 AC 满足什么条件时，四边形BECF 是菱形？并说明理由．【分析】〔 1〕由各件，据AAS 很容易证得：△ BDE ≌△ CDF ；（2〕连接 BF 、CE，由 AB=AC ，D 是 BC 边的中点，可知 AD ⊥ BC ，易证得△ BFD ≌△ CFD ，可得 BF=CF ；又因为〔 1〕中△BDE ≌△ CDF 得 ED=FD ，所以 EF、 BC 互相垂直平分，根据菱形的性质，可得四边形 BECF 是菱形．【解答】〔 1〕证明：∵在△ ABC 中， D 是 BC 边的中点，∴BD=CD ，∵CF∥ BE，∴∠ CFD= ∠ BED ，在△ CFD 和△ BED 中，，∴△ CFD ≌△ BED 〔 AAS 〕，∴C F=BE ，∴四边形 BFCE 是平行四边形；（2〕解：当 AB=AC 时，四边形 BECF 是菱形；理由如下：∵AB=AC ， D 是 BC 边的中点，∴AD ⊥BC，∴EF⊥BC，∴四边形 BECF 是菱形．21．〔2021?十堰模拟〕：如图，在菱形 ABCD 中， F 为边 BC 的中点， DF 与对角线 AC 交于点M ，过 M 作 ME ⊥CD 于点 E，∠ 1=∠ 2．（1〕假设 CE=2，求 BC 的长；（2〕求证： ME=AM ﹣ DF．【分析】〔 1〕根据菱形的性质可得CB=CD ，AB ∥ CD ，然后再证明∠2=∠ ACD ，根据等角对等边可得MC=MD ，根据等腰三角形三线合一的性质可得CD=2CE=4 ，进而可得BC=4 ．〔2〕延长 DF， BA 交于 G，首先证明△CEM ≌△ CFM 可得 ME=MF ，然后再证明△CDF ≌△ BGF 可得 DF=GF ，然后证明∠1=∠ G，根据等角对等边可得GM=CM ，利用线段的和差关系可得结论．【解答】〔 1〕解：∵四边形ABCD 是菱形，∴CB=CD ， AB ∥CD ，∴∠ 1=∠ ACD ．∵∠ 1=∠ 2，∴∠ 2=∠ ACD ，∴MC=MD ．∵ME ⊥CD，∴C D=2CE=4 ，∴B C=CD=4 ；（2〕证明：如图，延长 DF， BA 交于 G，∵四边形 ABCD 是菱形，∴∠ BCA= ∠ DCA ．∵BC=2CF ，CD=2CE ，∴CE=CF ．在△ CEM 和△CFM 中，，∴△ CEM ≌△ CFM 〔 SAS〕，∴ME=MF ．∵AB ∥CD，∴∠ 2=∠ G，∠ GBF= ∠ BCD ，∵F为边 BC 的中点，∵C F=BF ，在△ CDF 和△ BGF 中，，∴△ CDF ≌△ BGF 〔 AAS 〕，∴D F=GF ．∵∠ 1=∠ 2，∠ G=∠ 2，∴∠ 1=∠ G，∴AM=GM=MF+GF=DF+ME，即ME=AM ﹣ DF ．22．〔2021?东平县一模〕如图，在△ ABC 中，∠ ABC=90 °， BD 为 AC 的中线，过点 C 作CE⊥ BD 于点 E，过点 A 作 BD 的平行线，交 CE 的延长线于点 F，在 AF 的延长线上截取FG=BD ，连接 BG、DF ．（1〕求证： BD=DF ；（2〕求证：四边形 BDFG 为菱形；（3〕假设 AG=13 ， CF=6 ，求四边形 BDFG 的周长．【分析】〔 1〕先可判断四边形BGFD 是平行四边形，再由直角三角形斜边中线等于斜边一半，可得 BD=FD ；〔2〕由邻边相等可判断四边形BGFD 是菱形；〔3〕设 GF=x，那么 AF=13 ﹣ x，AC=2x ，在 Rt△ ACF 中利用勾股定理可求出x 的值．【解答】〔 1〕证明：∵∠ABC=90 °， BD 为 AC 的中线，∴BD=AC ，∵AG ∥ BD ， BD=FG ，∴四边形 BGFD 是平行四边形，∵C F⊥ BD ，∴CF⊥ AG ，又∵点 D 是 AC 中点，∴D F= AC ，∴B D=DF ；（2〕证明：∵ BD=DF ，∴四边形 BGFD 是菱形，（3〕解：设 GF=x ，那么 AF=13 ﹣ x， AC=2x ，∵在 Rt△ ACF 中，∠ CFA=90 °，222222∴AF +CF =AC ，即〔 13﹣ x〕 +6=〔 2x〕，解得： x=5 ，∴四边形 BDFG 的周长 =4GF=20 ．23．〔2021?南岗区模拟〕如图，在正方形 ABCD 中，点 E 在对角线 AC 上，点 F 在边 BC 上，连接 BE 、DF， DF 交对角线 AC 于点 G，且 DE=DG ．（1〕求证： AE=CG ；（2〕试判断 BE 和 DF 的位置关系，并说明理由．【分析】〔 1〕先证∠ AED= ∠ CGD ，再证明△ADE ≌△ CDG ，根据全等三角形的对应边相等即可得出结论；〔2〕先证明△AEB ≌△ CGD ，得出对应角相等∠AEB= ∠ CGD ，得出∠ AEB= ∠EGF，即可证出平行线．【解答】解：〔 1〕证明：在正方形ABCD 中，∵AD=CD ，∴∠ DAE= ∠ DCG ，∵DE=DG ，∴∠ DEG= ∠ DGE，∴∠ AED= ∠ CGD ．在△ AED 和△ CGD 中，∴△ AED ≌△ CGD 〔 AAS 〕，∴AE=CG ．（2〕解法一： BE∥ DF ，理由如下：在正方形 ABCD 中， AB ∥CD，∴∠ BAE= ∠DCG ．在△ AEB 和△ CGD 中，∴△ AEB ≌△ CGD 〔 SAS〕，∴∠ AEB= ∠CGD ．∵∠ CGD= ∠ EGF，∴∠ AEB= ∠EGF，∴BE ∥DF．解法二： BE∥ DF，理由如下：在正方形 ABCD 中，∵AD ∥ FC，∴= ．∵CG=AE ，∴AG=CE ．又∵在正方形ABCD 中， AD=CB ，∴= ．又∵∠ GCF= ∠ ECB ，∴△ CGF∽△ CEB ，∴∠ CGF= ∠ CEB ，∴BE ∥DF．24．〔2021?景德镇校级二模〕如图，在四边形 ABCD 中， AB=BC ，对角线 BD 平分∠ ABC ， P 是BD 上一点，过点 P 作 PM⊥ AD ， PN⊥ CD ，垂足分别为 M ， N．（1〕求证：点 A 与 C 关于直线 BD 对称．（2〕假设∠ ADC=90 °，求证四边形 MPND 为正方形．【分析】〔 1〕首先根据角平分线的定义求出∠根据 SAS 证明两个三角形全等，进而得到∠质可得 BD 垂直平分 AC ，进而可得点 A 与ABD= ∠ CBD ，然后在△ ABD 和△ CBD 中，ADB= ∠ CDB ，AD=CD ，根据等腰三角形的性C 关于直线BD 对称；〔2〕首先证明四边形 PMDN 是矩形，再根据角平分线上的点到角两边的距离相等可得PM=PN ，进而可得四边形 MPND 为正方形．【解答】证明：〔 1〕连接 AC ，∵BD 平分∠ ABC ，∴∠ ABD= ∠ CBD ，在△ ABD 和△ CBD 中，，∴△ ABD ≌△ CBD 〔 SAS〕，∴∠ ADB= ∠ CDB ， DA=DC ，∴BD 垂直平分AC ，∴点 A 与 C 关于直线BD 对称；（2〕∵PM⊥AD ，PN⊥CD，∴∠ PMD= ∠ PND=90 °，∵∠ ADC=90 °，∴四边形 PMDN 是矩形，∵∠ ADB= ∠ CDB ，∴BD 平分∠ ADC ，∵PM ⊥ AD ，PN ⊥CD，∴PM=PN ，∴四边形MPND 为正方形．25．〔2021 ?滕州市模拟〕：如图，正方形ABCD 中，点 E 在 BC 的延长线上， AE 分别交DC， BD 于 F， G，点 H 为 EF 的中点．求证：〔 1〕∠ DAG= ∠ DCG ；〔2〕GC⊥CH ．【分析】〔 1〕要证明∠ DAG= ∠ DCG ，需把两角放到两三角形中，证明两三角形△ ADG与△CDG 全等得到，全等的方法是：由 ABCD 为正方形，得到 AD 与 DC 相等，∠ ADB 与∠ CDB 相等，再加上公共边 DG ，利用“SAS 〞得到全等，利用全等三角形的对应角相等得证；〔2〕要证明 GC 与 CH 垂直，需证∠ GCH=90 °，即∠ FCH+ ∠DCG=90 °，方法是：由正方形的对边 AD 与 BE 平行，根据两直线平行，内错角相等得到∠DAF 与∠ E 相等，由〔 1〕得到的∠ DAG 与∠ DCG 相等，等量代换得到∠ E 与∠ DCG 相等，再由 CH 为直角三角形 ECF 斜边上的中线，得到 CH 与 HE 相等都等于斜边 EF 的一半，根据“等边对等角〞得到∠ E 与∠HCE 相等，又∠ FCH+ ∠DCG 等于 90°，等量代换得到∠ FCH+ ∠DCG=90 °，即∠GCH=90 °，得证．【解答】证明：〔 1〕∵ ABCD 为正方形，∴AD=DC ，∠ ADC=90 °，∠ ADB= ∠ CDB=45 °，又DG=DG ，∴△ ADG ≌△ CDG ，∴∠ DAG= ∠ DCG ；（2〕∵ ABCD 为正方形，∴AD ∥BE，∴∠ DAG= ∠ E，又∠ DAG= ∠DCG ，∴∠ E=∠DCG ，∵H 为直角三角形CEF 斜边 EF 边的中点，∴CH=HE= EF，∴∠ HCE= ∠E，∴∠ DCG= ∠ HCE，又∠ FCH+ ∠ HCE=90 °，∴∠ FCH+ ∠ DCG=90 °，即∠ GCH=90 °，∴GC⊥CH ．26．〔2021春 ?丹阳市校级月考〕如图，正方形ABCD 的对角线 AC 、 BD 相交于点O，E 是 AC 上的一点，过点A 作 AG ⊥ BE ，垂足为 G， AG 交 BD 于点 F．（1〕试说明 OE=OF ；（2〕当 AE=AB 时，过点 E 作 EH⊥BE 交 AD 边于 H ，找出与△ AHE 全等的一个三角形加以证明，〔3〕在〔 2〕的条件下假设该正方形边长为1，求 AH 的长．【分析】〔 1〕根据正方形性质得出 AC ⊥BD ， OA=OB ，求出∠ FAO= ∠ EBO，根据 ASA 推出△ AFO ≌△ BEO 即可；（2〕根据正方形性质得出∠ ACB= ∠DAC=45 °，∠ ABE+ ∠ EBC=90 °，求出∠ CBE= ∠AEH ，AE=AB=BC ，证△ BCE≌△ EAH ；〔3〕根据全等三角形的性质推出CE=AH ，即可得出答案．【解答】〔 1〕解：∵四边形ABCD 是正方形，∴AC ⊥ BD ， OA=OB ，∴∠ AOF= ∠ BOE=90 °，∵AG ⊥BE，∴∠ FGB=90 °，∴∠ OBE+ ∠BFG=90 °，∠ FAO+ ∠AFO=90 °，∵∠ AFO= ∠BFG ，∴∠ FAO=∠ EBO ，在△ AFO 和△ BEO 中，，∴△ AFO ≌△ BEO 〔ASA 〕，∴OE=OF ．（2〕△ BCE ≌△ EAH ，证明：∵四边形 ABCD 是正方形，∴∠ ACB= ∠ DAC=45 °，∠ ABE+ ∠EBC=90 °，∵EH⊥BE，∴∠ AEH+ ∠ AEB=90 °，∵A E=AB ，∴∠ ABE= ∠AEB ，∴∠ CBE= ∠ AEH ，∵A E=AB=BC ，在△ BCE 和△ EAH 中，，∴△ BCE ≌△ EAH 〔ASA 〕；（3〕解：∵△ BCE ≌△ EAH ，∴CE=AH ，∵A B=BC=1 ，∴AC= ，∵A E=AB=1 ，∴AH=CE=AC ﹣ AE=﹣1．27．〔2021 ?荆州〕如图 1，在正方形 ABCD 中， P 是对角线 BD 上的一点，点 E 在 AD 的延长线上，且 PA=PE， PE 交 CD 于 F．（1〕证明： PC=PE；（2〕求∠ CPE 的度数；（3〕如图 2，把正方形 ABCD 改为菱形 ABCD ，其他条件不变，当∠ ABC=120 °时，连接CE，试探究线段AP 与线段 CE 的数量关系，并说明理由．【分析】〔 1〕先证出△ ABP ≌△ CBP，得 PA=PC，由于 PA=PE ，得 PC=PE；（2〕由△ABP ≌△ CBP，得∠ BAP= ∠ BCP，进而得∠ DAP= ∠ DCP，由 PA=PC，得到∠DAP= ∠ E，∠ DCP=∠ E，最后∠ CPF=∠ EDF=90 °得到结论；（3〕借助〔 1〕和〔 2〕的证明方法容易证明结论．【解答】〔 1〕证明：在正方形ABCD 中， AB=BC ，∠A BP= ∠ CBP=45 °，在△ ABP 和△ CBP 中，，∴△ ABP ≌△ CBP〔 SAS 〕，∴PA=PC，∵PA=PE，∴P C=PE；（2〕由〔 1〕知，△ABP ≌△ CBP，∴∠BAP= ∠BCP，∴∠ DAP= ∠DCP，∵PA=PE，∴∠DAP= ∠E，∴∠ DCP= ∠ E，∵∠ CFP=∠ EFD 〔对顶角相等〕，∴180°﹣∠ PFC﹣∠ PCF=180 °﹣∠ DFE﹣∠E，即∠ CPF=∠ EDF=90 °；（3〕在菱形 ABCD 中， AB=BC ，∠ ABP= ∠ CBP=60 °，在△ ABP 和△ CBP 中，，∴△ ABP ≌△ CBP〔 SAS 〕，∴P A=PC，∠BAP= ∠BCP，∵PA=PE，∴P C=PE，∴∠ DAP= ∠DCP，∵P A=PC，∴∠ DAP= ∠AEP ，∴∠ DCP= ∠ AEP∵∠ CFP=∠ EFD 〔对顶角相等〕，∴180°﹣∠ PFC﹣∠ PCF=180 °﹣∠ DFE﹣∠ AEP ，即∠ CPF=∠ EDF=180 °﹣∠ ADC=180 °﹣ 120°=60°，∴△ EPC 是等边三角形，∴PC=CE ，∴A P=CE ．第 30 页〔共 31 页〕专业资料整理第 31 页〔共 31 页〕专业资料整理。

2021年度鲁教版八年级数学下册《第6章特殊的平行四边形》章末综合提升训练（附答案）1．在四边形ABCD中，对角线AC和BD交于点O，下列条件能判定这个四边形是菱形的是．（填序号）①．AD∥BC，∠A＝∠C②．AC＝BD，AB∥CD，AB＝CD③．AB∥CD，AC＝BD，AC⊥BD④．AO＝CO，BO＝DO，AB＝BC2．正方形的边长与它的对角线的长度的比值为．3．如图，已知在矩形ABCD中，点E在边BC的延长线上，且CE＝BD，联结AE交BD于点F，如果∠E＝15°，那么∠AFB的度数为．4．如图，菱形ABCD的对角线AC与BD相交于点O．已知AB＝10cm，AC＝12cm．那么这个菱形的面积为cm2．5．我们把两条对角线所成两个角的大小之比是1：2的矩形叫做“和谐矩形”，如果一个“和谐矩形”的对角线长为10cm，则矩形的面积为cm2．6．如图，四边形ABCD为菱形，四边形AOBE为矩形，O，C，D三点的坐标为（0，0），（2，0），（0，1），则点E的坐标为．7．已知正方形ABCD的边长等于4cm，那么边AB的中点E到对角线BD的距离等于cm．8．如图，等边三角形AEF的顶点E，F分别落在矩形ABCD的两邻边BC、CD上，若BE ＝1，CE＝2，则△AEF边长为．9．如图，矩形ABCD的两条对角线相交于点O，∠COB＝2∠AOB，AB＝8，则BC的长是．10．在矩形ABCD中，∠BAD的角平分线交于BC点E，且将BC分成1：3的两部分，若AB＝2，那么BC＝11．已知菱形一组对角的和为240°，较短的一条对角线的长度为4厘米，那么这个菱形的面积为平方厘米．12．已知矩形的两条对角线的夹角为60°，如果一条对角线长为6，那么矩形的面积为．13．已知正方形ABCD的边长为6，点E是边BC的中点．联接AC、DE相交于点F，M、N分别是AC、DE的中点，则MN的长是．14．已知四边形ABCD中，AD∥BC，AC＝BD，如果添加一个条件，即可判定该四边形是矩形，那么所添加的这个条件可以是．15．如图，在菱形ABCD中，对角线AC、BD相交于点O，DE⊥AB，垂足为E，如果AC ＝8，BD＝6，那么DE的长为．16．如图，在直角坐标平面内，矩形ABCD的对角线AC、BD交于原点O，且点A、C都在x轴上，点D的坐标为（4，3），那么点C的坐标为．17．如图，在正方形ABCD中，等边三角形AEF的顶点E、F分别在边BC和CD上，则∠AEB＝度．18．如图，点P在边长为1的正方形ABCD边AD上，连接PB．过点B作一条射线与边DC的延长线交于点Q，使得∠QBE＝∠PBC，其中E是边AB延长线上的点，连接PQ．若PQ2＝PB2+PD2+1，则△P AB的面积为．19．如图，矩形ABCD中，点E在BC边上，点F在CD边上，AE平分∠BAF，且EF⊥AF 于点F．若AB＝5，AD＝4，则EF＝．20．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝4，H是AF的中点，那么CH的长是．21．已知平行四边形ABCD，对角线AC、BD相交于点O，且CA＝CB，延长BC至点E，使CE＝BC，连接DE．（1）当AC⊥BD时，求证：BE＝2CD；（2）当∠ACB＝90°时，求证：四边形ACED是正方形．22．如图，△ABC中，AB＝AC，AD平分∠BAC交BC于点D，AE平分∠BAC的外角，且∠AEB＝90°．求证：四边形ADBE是矩形．23．如图，已知△ABC中，AD是边BC上的中线，过点A作AE∥BC，过点D作DE∥AB，DE与AC、AE分别交于点O、点E，联结EC．（1）求证：四边形ADCE是平行四边形；（2）当∠BAC＝90°时，求证：四边形ADCE是菱形．24．如图，在△ABC中，D是BC边上的一点，E是AD的中点，过A点作BC的平行线交CE的延长线于点F，且AF＝BD，连接BF．（1）求证：BD＝CD；（2）如果AB＝AC，试判断四边形AFBD的形状，并证明你的结论．25．如图，矩形ABCD中，AB＝6，AD＝8，P，E分别是线段AC、BC上的点，且四边形PEFD为矩形．（I）若△PCD是等腰三角形时，求AP的长；（Ⅱ）判断CF与AC有怎样的位置关系并说明理由．26．已知：如图，在△ABC中，AB＝BC，∠ABC＝90°，点D、E分别是边AB、BC的中点，点F、G是边AC的三等分点，DF、EG的延长线相交于点H，连接HA、HC．求证：（1）四边形FBGH是菱形；（2）四边形ABCH是正方形．27．如图，在△ABC中，∠C＝90°，D为边BC上一点，E为边AB的中点，过点A作AF ∥BC，交DE的延长线于点F，连接BF．（1）求证：四边形ADBF是平行四边形；（2）当D为边BC的中点，且BC＝2AC时，求证：四边形ACDF为正方形．28．已知：如图，在正方形ABCD中，点E在边BC上，点F在边CD的延长线上，且BE ＝DF．（1）求∠AEF的度数；（2）如果∠AEB＝75°，AB＝2，求△FEC的面积．29．如图，四边形ABCD中，BD垂直平分AC，垂足为点F，E为四边形ABCD外一点，且∠ADE＝∠BAD，AE⊥AC（1）求证：四边形ABDE是平行四边形；（2）如果DA平分∠BDE，AB＝5，AD＝6，求AC的长．30．如图，已知正方形ABCD的对角线AC、BD交于点O，CE⊥AC与AD边的延长线交于点E．（1）求证：四边形BCED是平行四边形；（2）延长DB至点F，联结CF，若CF＝BD，求∠BCF的大小．31．如图，点E是矩形ABCD的边AD的中点，点P是边BC上的动点，PM⊥BE，PN⊥CE，垂足分别是M、N．求：当AB和AD应满足怎样的数量关系时，四边形PMEN是矩形？请说明理由．32．如图，在平行四边形ABCD中，点E、F分别在AB、CD上，且AE＝CF．（1）求证：DE＝BF；（2）若DF＝BF，求证：四边形DEBF为菱形．33．如图，正方形ABCD中，点E、F分别在边BC、CD上，AE＝AF，AC和EF交于点O，延长AC至点G，使得AO＝OG，连接EG、FG．（1）求证：BE＝DF；（2）求证：四边形AEGF是菱形．34．如图所示，在正方形ABCD中，M是CD的中点，E是CD上一点，且∠BAE＝2∠DAM．求证：AE＝BC+CE．35．已知：如图，在正方形ABCD中，点E为边AB的中点，联结DE，点F在DE上CF ＝CD，过点F作FG⊥FC交AD于点G．（1）求证：GF＝GD；（2）联结AF，求证：AF⊥DE．36．已知：如图，在等边三角形ABC中，过边AB上一点D作DE⊥BC，垂足为点E，过边AC上一点G作GF⊥BC，垂足为点F，BE＝CF，联结DG．（1）求证：四边形DEFG是平行四边形；（2）连接AF，当∠BAF＝3∠F AC时，求证：四边形DEFG是正方形．37．已知：正方形ABCD的边长为厘米，对角线AC上的两个动点E，F．点E从点A，点F从点C同时出发，沿对角线以1厘米/秒的相同速度运动，过E作EH⊥AC交Rt△ACD的直角边于H，过F作FG⊥AC交Rt△ACD的直角边于G，连接HG，EB．设HE、EF、FG、GH围成的图形面积为S1，AE，EB，BA围成的图形面积为S2（这里规定：线段的面积为0）E到达C，F到达A停止．若E的运动时间为x秒，解答下列问题：（1）如图，判断四边形EFGH是什么四边形，并证明；（2）当0＜x＜8时，求x为何值时，S1＝S2；（3）若y是S1与S2的和，试用x的代数式表示y．（如图为备用图）38．我们知道正方形是四条边相等，四个内角都等于90°的四边形．如图1，已知正方形ABCD，点E是边CD上一点，延长CB到点F，使得BF＝DE，作∠EAF的平分线交边BC于点G．求证：BG+DE＝EG．参考答案1．解：①A、∵AD∥BC，∴∠BAD+∠ABC＝180°，∵∠BAD＝∠BCD，∴∠BCD+∠ABC＝180°，∴AB∥CD，∴四边形ABCD是平行四边形；选项①不符合题意；②、∵AB∥CD，AB＝CD，∴四边形ABCD是平行四边形，又∵AC＝BD，∴四边形ABCD是矩形；选项②不符合题意；③、∵AB∥CD，AC＝BD，AC⊥BD，∴四边形ABCD不一定是平行四边形，∴四边形ABCD不一定是菱形；选项③不符合题意；④、∵AO＝CO，BO＝DO，∴四边形ABCD是平行四边形，又∵AB＝BC，∴四边形ABCD是菱形；选项④符合题意；故选：④．2．解：∵四边形ABCD是正方形，∴AB＝BC＝CD＝AD，AC＝BD，∠ABC＝90°，∴AC＝＝＝AB，∴＝；故答案为：．3．解：连接AC交BD于点O，如图所示：∵四边形ABCD是矩形，∴OA＝OC＝AC，OB＝OD＝BD，AC＝BD，∴OB＝OC，∴∠OBC＝∠OCB，∵CE＝BD，∴AC＝CE，∴∠CAE＝∠E＝15°，∴∠OBC＝∠OCB＝∠CAE+∠E＝30°，∴∠AFB＝∠OBC+∠E＝30°+15°＝45°；故答案为：45°．4．解：∵四边形ABCD为菱形，∴AC⊥BD，OA＝OC＝AC＝6cm，OB＝OD，∴OB＝＝＝8（cm），∴BD＝2OB＝16cm，S菱形ABCD＝AC•BD＝×12×16＝96（cm2）．故答案为：96．5．解：∵四边形ABCD是“和谐矩形”，∴OA＝OC，OB＝OD，AC＝BD＝10，∠BAD＝90°，∠CAD：∠BAC＝1：2，∴OA＝OD，∠CAD＝30°，∠BAC＝60°，∴∠ADB＝∠CAD＝30°，∴AB＝BD＝5，AD＝AB＝5，∴矩形ABCD的面积＝AB×AD＝5×5＝25（cm2）；故答案为：25．6．解：∵O，C，D三点的坐标为（0，0），（2，0），（0，1），∴OC＝2，OD＝1，∵四边形ABCD是菱形，∴OA＝OC＝2，OB＝OD＝1，∵四边形AOBE为矩形，∴∠EAO＝∠EBO＝90°，EB＝OA＝2，EA＝OB＝1，∵E在第二象限，∴E点的坐标是（﹣2，﹣1），故答案为：（﹣2，﹣1）．7．解：∵四边形ABCD是正方形，∴AB＝BC＝4cm，∠EBF＝45°，∵EF⊥BD，∴△EBF是等腰直角三角形，∵E是AB的中点，∴EB＝2cm，∴EF＝cm，故答案为：．8．解：设DF＝x，CF＝y，∵四边形ABCD是矩形，∴∠D＝∠C＝∠B＝90°，DC＝AB＝x+y，AD＝BC＝BE+CE＝1+2＝3，∵△AEF是等边三角形，∴AE＝EF＝AF，∴12+（x+y）2＝22+y2＝x2+32，由12+（x+y）2＝22+y2得：y＝，代入22+y2＝x2+32，整理得：3x4+26x2﹣9＝0，解得：x2＝，∴AF2＝x2+32＝，∴AF＝；故答案为：．9．解：∵四边形ABCD是矩形，∴AO＝OC，BO＝OD，AC＝BD，∴OA＝OB，∵∠BOC＝2∠AOB，∠BOC+∠AOB＝180°∴∠AOB＝60°，∴△AOB是等边三角形，∴OA＝OB＝AB＝8，∴AC＝BD＝2AO＝16，则BC＝＝8．故答案是：8．10．解：①如图1中，∵四边形ABCD是矩形，AE平分∠BAD，∴∠BAE＝∠AEB＝45°，∴AB＝BE＝2，当EC＝3BE时，EC＝6，∴BC＝8．②如图2中，当BE＝3EC时，EC＝，∴BC＝BE+EC＝．故答案为8或11．解：如图，∵四边形ABCD是菱形，∠BAD+∠BCD＝240°，∴∠BAD＝∠BCD＝120°，∠ABC＝∠ADC＝60°∵AB＝BC＝AD＝DC，∴△ABC，△ADC是等边三角形，∴AB＝BC＝AC＝4，∴S菱形ABCD＝2•S△ABC＝2××42＝8，故答案为8．12．解：矩形的两条对角线的夹角为：∠1＝60°，∵矩形对角线相等且互相平分，∴△AOB为等边三角形，∴AB＝AO＝AC＝3，在直角△ABC中，AC＝6，AB＝3，∴BC＝，故矩形的面积为：3×3＝9．故答案为：9．13．解：连接BD，∵E是边BC的中点，∴BE＝BC＝3，∵四边形ABCD是正方形，∴M是BD的中点，又N是DE的中点，∴MN＝BE＝1.5，故答案为：1.5．14．解：当AD＝BC或AB∥CD时，四边形ABCD是矩形．理由：∵AD∥BC，∴当AD＝BC或AB∥CD时，四边形ABCD是平行四边形，∵AC＝BD，∴四边形ABCD是矩形．15．解：∵四边形ABCD是菱形，AC＝8，BD＝6，∴AC⊥OD，AO＝AC＝4，BO＝BD＝3，∴由勾股定理得到：AB＝＝5．又∵AC•BD＝AB•DE．∴DE＝4.8．故答案为：4.8．16．解：过点D，作DE⊥OC于点E，∵点D的坐标为（4，3），∴OE＝4，DE＝3，∴OD＝＝5，∵四边形ABCD是矩形，∴OD＝OC＝AC＝BD，∴点C的坐标为（5，0），故答案为：（5，0）．17．解：∵四边形ABCD是正方形，∴AB＝AD，∠B＝∠D＝∠BAD＝90°，在Rt△ABE和Rt△ADF中，，∴△ABE≌△ADF，∴∠BAE＝∠DAF＝（90°﹣60°）÷2＝15°，∴∠AEB＝75°，故答案为75．18．解：∵∠QBE＝∠PBC，∠QBE+∠QBC＝90°，∴∠PBQ＝∠PBC+∠QBC＝90°，∵∠PBC+∠PBA＝90°，∴∠PBA＝∠QBC，在Rt△P AB和Rt△QCB中，，∴△P AB≌△QCB（ASA），∴QC＝P A，设正方形的边长AB＝a，P A＝x，则QC＝x，∴DQ＝DC+QC＝a+x，PD＝AD﹣P A＝a﹣x，在Rt△P AB中，PB2＝P A2+AB2＝x2+a2，∵PQ2＝PB2+PD2+1，∴（a﹣x）2+（a+x）2＝x2+a2+（a﹣x）2+1，解得：2ax＝1，∴ax＝，∵△P AB的面积S＝P A•PB＝ax＝×＝．故答案为：．19．解：∵AE平分∠BAF，且EF⊥AF，∠B＝90°∴EF＝EB在Rt△ABE和Rt△AFE中∴Rt△ABE≌Rt△AFE（HL）∴AF＝AB＝5又∵AD＝4，∠D＝90°∴Rt△ADE中，DF＝＝3∴CF＝5﹣3＝2设EF＝EB＝x，则CE＝4﹣x在Rt△CEF中，22+（4﹣x）2＝x2解得x＝即EF＝故答案为：20．解：过H作HM⊥BE于M，则∠HMC＝90°，∵正方形ABCD和正方形CEFG，∴AB＝BC＝1，EF＝CE＝4，∠B＝∠E＝90°，∴HM∥AB∥FE，∵H为AF大的中点，∴M为BE的中点，∴HM＝（AB+EF）＝（1+4）＝，∵BC＝1，CE＝2，∴BM＝2.5，∴CM＝1.5，在Rt△HMC中，由勾股定理得：CH＝＝，故答案为：．21．（1）证明：∵四边形ABCD是平行四边形，又∵AC⊥BD，∴四边形ABCD是菱形．∴BC＝CD．又∵CE＝BC，∴BE＝2BC，∴BE＝2CD；（2）证明：∵四边形ABCD是平行四边形，∴AD＝BC，AD∥BE，又∵CE＝BC，∴AD＝CE，AD∥CE，∴四边形ACED是平行四边形．∵∠ACB＝90°，∴平行四边形ACED是矩形，又∵CA＝CB，∴CA＝CE，∴矩形ACED是正方形．22．证明：∵AD是∠BAC的平分线，∵AE是∠BAF的平分线，∴∠3＝∠4，∵∠1+∠2+∠3+4＝180°，∴∠2+∠3＝90°，即∠DAE＝90°，∵AB＝AC，∠1＝∠2，∴AD⊥BC，即∠ADB＝90°，∵∠AEB＝90°，∴四边形ADBE是矩形．23．（1）证明：∵AE∥BC，DE∥AB，∴四边形ABDE是平行四边形，∴AE＝BD，∵AD是边BC上的中线，∴BD＝DC，∴AE＝DC，又∵AE∥BC，∴四边形ADCE是平行四边形，（2）∵∠BAC＝90°，AD是边BC上的中线．∴AD＝CD，∵四边形ADCE是平行四边形，∴四边形ADCE是菱形，24．证明：（1）∵AF∥BC，∴∠AFE＝∠DCE，∵E是AD的中点，∴AE＝DE，，∴△AEF≌△DEC（AAS），∵AF＝BD，∴BD＝CD；（2）四边形AFBD是矩形．理由：∵AB＝AC，D是BC的中点，∴AD⊥BC，∴∠ADB＝90°∵AF＝BD，∵过A点作BC的平行线交CE的延长线于点F，即AF∥BC，∴四边形AFBD是平行四边形，又∵∠ADB＝90°，∴四边形AFBD是矩形．25．解：（I）在矩形ABCD中，AB＝6，AD＝8，∠ADC＝90°，∴DC＝AB＝6，∴AC＝＝10，要使△PCD是等腰三角形，①当CP＝CD时，AP＝AC﹣CP＝10﹣6＝4，②当PD＝PC时，∠PDC＝∠PCD，∵∠PCD+∠P AD＝∠PDC+∠PDA＝90°，∴∠P AD＝∠PDA，∴PD＝P A，∴P A＝PC，∴AP＝AC＝5，③当DP＝DC时，如图1，过点D作DQ⊥AC于Q，则PQ＝CQ，∵S△ADC＝AD•DC＝AC•DQ，∴DQ＝＝，∴CQ＝＝，∴PC＝2CQ＝，∴AP＝AC﹣PC＝10﹣＝；所以，若△PCD是等腰三角形时，AP的长为4或5或；（Ⅱ）CF⊥AC，理由如下：如图2，连接PF，DE，记PF与DE的交点为O，连接OC，∵四边形ABCD和PEFD是矩形，∴∠ADC＝∠PDF＝90°，∴∠ADP+∠PDC＝∠PDC+∠CDF，∴∠ADP＝∠CDF，∵∠BCD＝90°，OE＝OD，∴OC＝ED，在矩形PEFD中，PF＝DE，∴OC＝PF，∵OP＝OF＝PF，∴OC＝OP＝OF，∴∠OCF＝∠OFC，∠OCP＝∠OPC，∵∠OPC+∠OFC+∠PCF＝180°，∴2∠OCP+2∠OCF＝180°，∴∠PCF＝90°，∴CF⊥AC．26．证明：（1）∵点F、G是边AC的三等分点，∴AF＝FG＝GC．又∵点D是边AB的中点，∴DH∥BG．同理：EH∥BF．∴四边形FBGH是平行四边形，连接BH，交AC于点O，∴OF＝OG，∴AO＝CO，∵AB＝BC，∠ABC＝90°，∴四边形FBGH是菱形；（2）∵四边形FBGH是平行四边形，∴BO＝HO，FO＝GO．又∵AF＝FG＝GC，∴AF+FO＝GC+GO，即：AO＝CO．∴四边形ABCH是平行四边形．∵AC⊥BH，AB＝BC，∴四边形ABCH是正方形．27．（1）证明：∵AF∥BC，∴∠AFE＝∠BDE，在△AEF与△BED中，，∴△AEF≌△BED，∴AF＝BD，∵AF∥BD，∴四边形ADBF是平行四边形；（2）解：∵CD＝DB，AE＝BE，∴DE∥AC，∴∠FDB＝∠C＝90°，∵AF∥BC，∴∠AFD＝∠FDB＝90°，∴∠C＝∠CDF＝∠AFD＝90°，∴四边形ACDF是矩形，∵BC＝2AC，CD＝BD，∴CA＝CD，∴四边形ACDF是正方形．28．解：（1）由正方形ABCD，得AB＝AD，∠B＝∠ADF＝∠BAD＝90°，在△ABE和△ADF中，，∴△ABE≌△ADF，∴∠BAE＝∠F AD，AE＝AF．∴∠BAD＝∠BAE+∠EAD＝∠F AD+∠EAD＝90°．即得∠EAF＝90°，又∵AE＝AF，∴∠AEF＝∠AFE＝45°．（2）∵∠AEB＝75°，∠AEF＝45°，∴∠BEF＝120°．即得∠FEC＝60°，由正方形ABCD，得∠C＝90°．∴∠EFC＝30°．∴EF＝2EC，设EC＝x．则EF＝2x，BE＝DF＝2﹣x，CF＝4﹣x．在Rt△CEF中，由勾股定理，得CE2+CF2＝EF2．即得x2+（4﹣x）2＝4x2．解得x1＝2﹣2，x2＝﹣2﹣2（不合题意，舍去）．∴EC＝2﹣2，CF＝6﹣2．∴S△CEF＝＝，∴△FEC的面积为．29．（1）证明：∵∠ADE＝∠BAD，∴AB∥DE，∵AE⊥AC，BD⊥AC，AE∥BD，∴四边形ABDE是平行四边形；（2）解：∵DA平分∠BDE，∴∠AED＝∠BDA，∴∠BAD＝∠BDA，∴BD＝AB＝5，设BF＝x，则DF＝5﹣x，∴AD2﹣DF2＝AB2﹣BF2，∴62﹣（5﹣x）2＝52﹣x2，∴x＝，∴AF＝＝，∴AC＝2AF＝．30．（1）证明：∵四边形ABCD是正方形，∴AC⊥DB，BC∥AD，∵CE⊥AC，∴∠AOD＝∠ACE＝90°，∴BD∥CE，∴四边形BCED是平行四边形；（2）解：连接AF，∵四边形ABCD是正方形，∴BD⊥AC，BD＝AC＝2OB＝2OC，即OB＝OC，∴∠OCB＝45°，∵Rt△OCF中，CF＝BD＝2OC，∴∠OFC＝30°，∴∠BCF＝60°﹣45°＝15°．31．解：当AD＝2AB时．四边形PMEN为矩形；理由如下：∵四边形ABCD是矩形，∴∠A＝∠D＝90°，AB＝DC，又∵点E是矩形ABCD的边AD的中点．∴AE＝DE，在△ABE和△CDE中，，∴△ABE≌△DCE（SAS），∴∠AEB＝∠DEC，∵四边形PMEN为矩形，∴∠BEC＝90°，∴∠AEB＝∠DEC＝45°∴AE＝DE＝DC，即AD＝2AB．∴当AD＝2AB时；四边形PMEN为矩形．32．证明：（1）∵四边形ABCD是平行四边形，∴AD＝BC，∠A＝∠C，又∵AE＝CF，∴△ADE≌△CBF，∴DE＝BF；（2）∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD．∵AE＝CF，∴BE＝DF，BE∥DF，∴四边形DEBF是平行四边形．∵DF＝BF，∴平行四边形DEBF是菱形．33．证明：（1）∵四边形ABCD是正方形，∴∠B＝∠D＝90°，AD＝AB，在Rt△ABE和Rt△ADF中，∴Rt△ABE≌Rt△ADF（HL），∴EB＝DF；（2）∵四边形ABCD是正方形，∴BC＝DC，∵EB＝DF，∴EC＝FC，∴AC垂直平分EF，∵AO＝GO，∴四边形AEGF是菱形．34．证明：取BC的中点F，连接AF，过点F作FH⊥AE于H，连接EF．∵四边形ABCD是正方形，∴AB＝AD，∠B＝∠D＝∠C＝90°，∵M是CD的中点，∴BF＝DM，在△ABF和△ADM中，，∴△ABF≌△ADM（SAS），∴∠BAF＝∠DAM，∵∠BAE＝2∠DAM，∴∠BAF＝∠HAF，∵∠AHF＝∠B＝90°，∴∠AFB＝∠AFH，BF＝FH，∴AB＝AH，∴FH＝FC，∵∠FHE＝∠C＝90°，在Rt△CFE和Rt△HFE中，，∴Rt△CFE≌Rt△HFE（HL），∴EH＝CE，∴AE＝AH+HE＝AB+CE＝BC+CE．35．证明：（1）∵四边形ABCD是正方形，∴∠ADC＝90°，∵FG⊥FC，∴∠GFC＝90°，∵CF＝CD，∴∠CDF＝∠CFD，∴∠GFC﹣∠CFD＝∠ADC﹣∠CDE，即∠GFD＝∠GDF，∴GF＝GD．（2）联结CG．∵CF＝CD，GF＝GD，∴点G、C在线段FD的中垂线上，∴GC⊥DE，∴∠CDF+∠DCG＝90°，∵∠CDF+∠ADE＝90°，∴∠DCG＝∠ADE．∵四边形ABCD是正方形，∴AD＝DC，∠DAE＝∠CDG＝90°，∴△DAE≌△CDG，∴AE＝DG，∵点E是边AB的中点，∴点G是边AD的中点，∴AG＝GD＝GF，∴∠DAF＝∠AFG，∠GDF＝∠GFD，∵∠DAF+∠AFG+∠GFD+∠GDF＝180°，∴2∠AFG+2∠GFD＝180°，∴∠AFD＝90°，即AF⊥DE．法2：（1）联结CG交ED于点H．∵四边形ABCD是正方形，∴∠ADC＝90°，∵FG⊥FC，∴∠GFC＝90°，在Rt△CFG与Rt△CDG中，，∴Rt△CFG≌Rt△CDG，∴GF＝GD．（2）∵CF＝CD，GF＝GD，∴点G、C在线段FD的中垂线上，∴FH＝HD，GC⊥DE，∴∠EDC+∠DCH＝90°，∵∠ADE+∠EDC＝90°，∴∠ADE＝∠DCH，∵四边形ABCD是正方形，∴AD＝DC＝AB，∠DAE＝∠CDG＝90°，∵∠ADE＝∠DCH，AD＝DC，∠EAD＝∠GDC．∴△ADE≌△DCG，∴AE＝DG，∵点E是边AB的中点，∴点G是边AD的中点，∵点H是边FD的中点，∴GH是△AFD的中位线，∴GH∥AF，∴∠AFD＝∠GHD，∵GH⊥FD，∴∠GHD＝90°，∴∠AFD＝90°，即AF⊥DE．36．证明：（1）在等边三角形ABC中，∵DE⊥BC，GF⊥BC，∴∠DEF＝∠GFC＝90°，∴DE∥GF，∵∠B＝∠C＝60°，BE＝CF，∠DEB＝∠GFC＝90°，∴△BDE≌△CGF，∴DE＝GF，∴四边形DEFG是平行四边形；（2）在平行四边形DEFG中，∵∠DEF＝90°，∴平行四边形DEFG是矩形，∵∠BAC＝60°，∠BAF＝3∠F AC，∴∠GAF＝15°，在△CGF中，∵∠C＝60°，∠GFC＝90°，∴∠CGF＝30°，∴∠GF A＝15°，∴∠GAF＝∠GF A，∴GA＝GF，∵DG∥BC，∴∠ADG＝∠B＝60°，∴△DAG是等边三角形，∴GA＝GD，∴GD＝GF，∴矩形DEFG是正方形．37．解：（1）四边形EFGH是矩形．理由如下：∵点E从点A，点F从点C同时出发，沿对角线以1厘米/秒的相同速度运动，∴AE＝CF．∵EH⊥AC，FG⊥AC，∴EH∥FG．∵ABCD为正方形，∴AD＝DC，∠D＝90°，∠GCF＝∠HAE＝45°，又∵EH⊥AC，FG⊥AC，∴∠CGF＝∠AHE＝45°，∴∠GCF＝∠CGF，∠HAE＝∠AHE，∴AE＝EH，CF＝FG，∴EH＝FG，∴四边形EFGH是平行四边形，又∵EH⊥AC∴平行四边形EFGH是矩形；（2）∵正方形边长为，∴AC＝16．∵AE＝x，连接BD交AC于O，则BO⊥AC且BO＝8，∴S2＝•AE•BO＝4x．∵CF＝GF＝AE＝x，∴EF＝16﹣2x，∴S1＝EF•GF＝x（16﹣2x）．当S1＝S2时，x（16﹣2x）＝4x，解得x1＝0（舍去），x2＝6．∴当x＝6时，S1＝S2；（3）①当0≤x＜8时，y＝x（16﹣2x）+4x＝﹣2x2+20x．②当8≤x≤16时，AE＝x，CE＝HE＝16﹣x，EF＝16﹣2（16﹣x）＝2x﹣16．∴S1＝（16﹣x）（2x﹣16）．∴y＝（16﹣x）（2x﹣16）+4x＝﹣2x2+52x﹣256．综上，可知y＝．38．证明：∵四边形ABCD是正方形，∴AD＝AB，∠D＝∠ABC＝90°，∴∠ABF＝∠D＝90°，在△ABF与△ADE中，，∴△ABF≌△ADE，∴AE＝AF，∵AG平分∠EAF，∴∠F AG＝∠EAG，∵AG＝AG，∴△EAG≌△F AG，∴EG＝FG＝BF+BG＝DE+BG；。

2021年度人教版八年级数学下册《18.2特殊的平行四边形》同步提升训练（附答案）1．若菱形的两条对角线长分别是6和8，则它的周长为（）A．20B．24C．40D．482．菱形的两条对角线长分别是6和8，则此菱形的周长是（）A．5B．20C．24D．323．如图，在菱形ABCD中，AB＝5，AC＝6，过点D作DE⊥BA，交BA的延长线于点E，则线段DE的长为（）A．B．C．4D．4．如图，菱形ABCD中，过顶点C作CE⊥BC交对角线BD于E点，已知∠A＝134°，则∠BEC的大小为（）A．23°B．28°C．62°D．67°5．边长为5的菱形ABCD按如图所示放置在数轴上，其中A点表示数﹣2，C点表示数6，则BD＝（）A．4B．6C．8D．106．如图，矩形ABCD中，连接AC，延长BC至点E，使BE＝AC，连接DE．若∠BAC＝40°，则∠E的度数是（）A．65o B．60o C．50o D．40°7．如图，矩形ABCD的对角线AC、BD相交于点O，∠ABO＝60°，若矩形的对角线长为6．则线段AD的长是（）A．3B．4C．2D．38．如图，在矩形ABCD中，O为AC中点，EF过O点且EF⊥AC分别交DC于F，交AB 于E，点G是AE中点且∠AOG＝30°，则下列结论正确的个数为（）（1）DC＝3OG；（2）OG＝BC；（3）△OGE是等边三角形；（4）S△AOE＝S矩形ABCD．A．1个B．2个C．3个D．4个9．如图，矩形ABCD的对角线AC，BD交于点O，AB＝6，BC＝8，过点O作OE⊥AC，交AD于点E，过点E作EF⊥BD，垂足为F，则OE+EF的值为（）A．B．C．D．10．如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，那么CH的长是（）A．2.5B．C．D．211．已知平行四边形ABCD，下列条件中，不能判定这个平行四边形为矩形的是（）A．∠A＝∠B B．∠A＝∠C C．AC＝BD D．AB⊥BC12．如图，在边长为4的正方形ABCD中，点M为对角线BD上一动点，ME⊥BC于E，MF⊥CD于F，则EF的最小值为（）A．B．C．2D．113．如图，在正方形ABCD中，边长为2的等边三角形AEF的顶点E、F分别在BC和CD 上，下列结论：①CE＝CF；②∠AEB＝75°；③BE+DF＝EF；④S正方形ABCD＝2+，其中正确的序号是（）A．①②③B．②③④C．①③④D．①②④14．如图，在△ABC中，∠ACB＝90°，边BC在x轴上，顶点A，B的坐标分别为（﹣2，6）和（7，0）．将正方形OCDE沿x轴向右平移，当点E落在AB边上时，点D的坐标为（）A．（，2）B．（2，2）C．（，2）D．（4，2）15．把图1中的菱形沿对角线分成四个全等的直角三角形，将这四个直角三角形分别拼成如图2，图3所示的正方形，则图1中菱形的面积为（）A．6B．24C．26D．1216．如图，正方形ABCD的面积为144，菱形BCEF的面积为108，则S阴影＝（）A．18B．36C．D．17．如图，正方形ABCD中，点E是AD边的中点，BD，CE交于点H，BE、AH交于点G，则下列结论：①∠ABE＝∠DCE；②AG⊥BE；③S△BHE＝S△CHD；④∠AHB＝∠EHD．其中正确的是（）A．①③B．①②③④C．①②③D．①③④18．如图，已知正方形ABCD边长为1，∠EAF＝45°，AE＝AF，则有下列结论：①∠1＝∠2＝22.5°；②点C到EF的距离是﹣1；③△ECF的周长为2；④BE+DF＞EF，其中正确的结论有（）A．4个B．3个C．2个D．1个19．下列判断正确的是（）A．对角线互相垂直的平行四边形是菱形B．两组邻边相等的四边形是平行四边形C．对角线相等的四边形是矩形D．有一个角是直角的平行四边形是正方形20．如图，AC是菱形ABCD的对角线，P是AC上的一个动点，过点P分别作AB和BC的垂线，垂足分别是点F和E，若菱形的周长是12cm，面积是6cm2，则PE+PF的值是cm．21．如图，菱形ABCD的对角线AC，BD相交于点O，过点O作OE⊥BC于点E，若AC ＝6，BD＝8，则OE＝．22．菱形ABCD中，若周长是20cm，对角线AC＝6cm，则对角线BD＝cm．23．已知菱形的周长为20，一条对角线长为8，则菱形的面积为．24．菱形ABCD中，对角线AC长为10cm，BD＝6cm，则菱形ABCD的面积为cm2．25．如图是一张长方形纸片ABCD，已知AB＝8，AD＝7，E为AB上一点，AE＝5，现要剪下一张等腰三角形纸片（△AEP），使点P落在长方形ABCD的某一条边上，则等腰三角形AEP的底边长是．26．如图所示，矩形ABCD的两条对角线相交于点O，∠AOB＝60°，AB＝2，则矩形的对角线AC的长是．27．如图1，直角三角形纸片的一条直角边长为2，剪四块这样的直角三角形纸片，把它们按图2放入一个边长为3的正方形中（纸片在结合部分不重叠无缝隙），则图2中阴影部分面积为．28．如图，已知正方形ABCD的边长为5，点E、F分别在AD、DC上，AE＝DF＝2，BE 与AF相交于点G，点H为BF的中点，连接GH，则GH的长为．29．如图，E为正方形ABCD边BC延长线上一点，且CE＝BD，AE交DC于F，则∠AFC ＝．30．正方形ABCD的边长为4，点M，N在对角线AC上（可与点A，C重合），MN＝2，点P，Q在正方形的边上．下面四个结论中，①存在无数个四边形PMQN是平行四边形；②存在无数个四边形PMQN是菱形；③存在无数个四边形PMQN是矩形；④至少存在一个四边形PMQN是正方形．所有正确结论的序号是．31．已知，如图，菱形ABCD，DE⊥AB于E，且E为AB的中点，已知BD＝4．（1）∠DAB的度数；（2）AC的长；（3）菱形ABCD的面积．32．如图，在△ABC中，AD是BC边上的中线，点E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF．（1）求证：△AEF≌△DEB；（2）若∠BAC＝90°，求证：四边形ADCF是菱形．33．如图，△ABC中，∠BCA＝90°，CD是边AB上的中线，分别过点C，D作BA和BC 的平行线，两线交于点E，且DE交AC于点O，连接AE．（1）求证：四边形ADCE是菱形；（2）若∠B＝60°，BC＝6，求四边形ADCE的面积．34．利用矩形的性质，证明“直角三角形斜边上的中线等于斜边的一半”．已知：如图，；求证：；证明：35．如图，矩形ABCD的对角线AC，BD相交于点O，DE∥AC，CE∥BD．求证：四边形OCED是菱形．36．如图，在矩形ABCD中，E、F分别在AB、CD上，且DE＝BF．求证：四边形DEBF 是平行四边形．37．已知：如图，矩形ABCD的对角线AC、BD相交于点O，CE∥DB，交AB的延长线于点E．求证：AC＝EC．38．如图，四边形ABCD中，对角线AC、BD相交于点O，AO＝OC，BO＝OD，且∠AOB ＝2∠OAD．（1）求证：四边形ABCD是矩形；（2）若∠AOB：∠ODC＝4：3，求∠ADO的度数．39．如图，E、F分别是正方形ABCD中BC和CD边上的点，且AB＝4，CE＝BC，F为CD的中点，连接AF、AE，问△AEF是什么三角形？请说明理由．40．如图，AC为正方形ABCD的对角线，E为AC上一点，且AB＝AE，EF⊥AC，交BC 于F，试说明EC＝EF＝BF．参考答案1．解：如图所示，根据题意得AO＝×8＝4，BO＝×6＝3，∵四边形ABCD是菱形，∴AB＝BC＝CD＝DA，AC⊥BD，∴△AOB是直角三角形，∴AB＝＝＝＝5，∴此菱形的周长为：5×4＝20．故选：A．2．解：如图所示：∵四边形ABCD是菱形，AC＝8，BD＝6，∴AB＝BC＝CD＝AD，OA＝AC＝4，OB＝BD＝3，AC⊥BD，∴AB＝＝＝5，∴此菱形的周长＝4×5＝20；故选：B．3．解：如图．∵四边形ABCD是菱形，AC＝6，∴AC⊥BD，OA＝AC＝3，BD＝2OB，∵AB＝5，∴OB＝＝4，∴BD＝2OB＝8，∵S菱形ABCD＝AB•DE＝AC•BD，∴DE＝＝＝．故选：D．4．解：∵菱形ABCD，∠A＝134°，∴∠ABC＝180°﹣134°＝46°，∴∠DBC＝，∵CE⊥BC，∴∠BEC＝90°﹣23°＝67°，故选：D．5．解：∵A点表示数﹣2，C点表示数6，∴AC＝8，∵AD＝5，∴BD＝2＝6，故选：B．6．解：如图，连接BD，∵矩形ABCD中，∠BAC＝40°，OA＝OB，∴∠ABD＝40°，∠DBE＝90°﹣40°＝50°，∵AC＝BD，AC＝BE，∴BD＝BE，∴△BDE中，∠E＝（180°﹣∠DBE）＝（180°﹣50°）＝65°，故选：A．7．解：∵四边形ABCD是矩形，∴AC＝2AO，BD＝2BO，AC＝BD＝6，∴AO＝OB＝3，∵∠ABO＝60°，∴△AOB是等边三角形，∴AB＝3＝OA，∴AD＝＝＝3，故选：A．8．解：∵EF⊥AC，点G是AE中点，∴OG＝AG＝GE＝AE，∵∠AOG＝30°，∴∠OAG＝∠AOG＝30°，∠GOE＝90°﹣∠AOG＝90°﹣30°＝60°，∴△OGE是等边三角形，故（3）正确；设AE＝2a，则OE＝OG＝a，由勾股定理得，AO＝＝＝a，∵O为AC中点，∴AC＝2AO＝2a，∴BC＝AC＝×2a＝a，在Rt△ABC中，由勾股定理得，AB＝＝3a，∵四边形ABCD是矩形，∴CD＝AB＝3a，∴DC＝3OG，故（1）正确；∵OG＝a，BC＝a，∴OG≠BC，故（2）错误；∵S△AOE＝a•a＝a2，S ABCD＝3a•a＝3a2，∴S△AOE＝S ABCD，故（4）正确；综上所述，结论正确的是（1）（3）（4）共3个．故选：C．9．解：∵AB＝6，BC＝8，∴矩形ABCD的面积为48，AC＝＝10，∴AO＝DO＝AC＝5，∵对角线AC，BD交于点O，∴△AOD的面积为12，∵EO⊥AO，EF⊥DO，∴S△AOD＝S△AOE+S△DOE，即12＝AO×EO+DO×EF，∴12＝×5×EO+×5×EF，∴5（EO+EF）＝24，∴EO+EF＝，故选：C．10．解：如图，连接AC、CF，∵正方形ABCD和正方形CEFG中，BC＝1，CE＝3，∴AC＝，CF＝3，∠ACD＝∠GCF＝45°，∴∠ACF＝90°，由勾股定理得，AF＝＝＝2，∵H是AF的中点，∴CH＝AF＝×2＝．11．解：A、∠A＝∠B，∠A+∠B＝180°，所以∠A＝∠B＝90°，可以判定这个平行四边形为矩形，正确；B、∠A＝∠C不能判定这个平行四边形为矩形，错误；C、AC＝BD，对角线相等，可推出平行四边形ABCD是矩形，故正确；D、AB⊥BC，所以∠B＝90°，可以判定这个平行四边形为矩形，正确；故选：B．12．解：连接MC，如图所示：∵四边形ABCD是正方形，∴∠C＝90°，∠DBC＝45°，∵ME⊥BC于E，MF⊥CD于F∴四边形MECF为矩形，∴EF＝MC，当MC⊥BD时，MC取得最小值，此时△BCM是等腰直角三角形，∴MC＝BC＝2，∴EF的最小值为2；故选：B．13．解：∵四边形ABCD是正方形，∴AB＝AD，∵△AEF是等边三角形，在Rt△ABE和Rt△ADF中，，∴Rt△ABE≌Rt△ADF（HL），∴BE＝DF，∵BC＝DC，∴BC﹣BE＝CD﹣DF，∴CE＝CF，∴①说法正确；∵CE＝CF，∴△ECF是等腰直角三角形，∴∠CEF＝45°，∵∠AEF＝60°，∴∠AEB＝75°，∴②说法正确；如图，连接AC，交EF于G点，∴AC⊥EF，且AC平分EF，∵∠CAF≠∠DAF，∴DF≠FG，∴BE+DF≠EF，∴③说法错误；∵EF＝2，∴CE＝CF＝，设正方形的边长为a，在Rt△ADF中，AD2+DF2＝AF2，即a2+（a﹣）2＝4，解得a＝，则a2＝2+，S正方形ABCD＝2+，故选：D．14．解：如图，设正方形D′C′O′E′是正方形OCDE沿x轴向右平移后的正方形，∵顶点A，B的坐标分别为（﹣2，6）和（7，0），∴AC＝6，OC＝2，OB＝7，∴BC＝9，∵四边形OCDE是正方形，∴DE＝OC＝OE＝2，∴O′E′＝O′C′＝2，∵E′O′⊥BC，∴∠BO′E′＝∠BCA＝90°，∴E′O′∥AC，∴BO′＝3，∴OC′＝7﹣2﹣3＝2，∴当点E落在AB边上时，点D的坐标为（2，2），故选：B．15．解：设图1中分成的直角三角形的长直角边为a，短直角边为b，，得，∴图1中菱形的面积为：×4＝12，故选：D．16．解：如图，由题意，正方形边长为12，∵四边形BCEF是菱形，∴EF∥BC，∵∠BCD＝90°，∴∠CGE＝90°，∵菱形BCEF的面积为108，∴BC•CG＝108，12CG＝108，CG＝108÷12＝9，∵CE＝BC＝12，Rt△CGE中，由勾股定理得：EG＝＝＝3，∴阴影部分三角形AB边上的高＝．∴．故选：C．17．解：∵四边形ABCD是正方形，E是AD边上的中点，∴AE＝DE，AB＝CD，∠BAD＝∠CDA＝90°，∴△BAE≌△CDE（SAS），∴∠ABE＝∠DCE，故①正确；∵四边形ABCD是正方形，∴AD＝DC，∠ADB＝∠CDB＝45°，DH＝DH，∴△ADH≌△CDH（SAS），∴∠HAD＝∠HCD，∵∠ABE＝∠DCE∴∠ABE＝∠HAD，∵∠BAD＝∠BAH+∠DAH＝90°，∴∠ABE+∠BAH＝90°，∴∠AGB＝180°﹣90°＝90°，∴AG⊥BE，故②正确；∵AD∥BC，∴S△BDE＝S△CDE，∴S△BDE﹣S△DEH＝S△CDE﹣S△DEH，即；S△BHE＝S△CHD，故③正确；∵△ADH≌△CDH，∴∠AHD＝∠CHD，∴∠AHB＝∠CHB，∵∠BHC＝∠DHE，∴∠AHB＝∠EHD，故④正确；故选：B．18．解：∵四边形ABCD为正方形，∴AB＝AD，∠BAD＝∠B＝∠D＝90°，在Rt△ABE和Rt△ADF中，，∴Rt△ABE≌Rt△ADF（HL），∴∠1＝∠2，∵∠EAF＝45°，∴∠1＝∠2＝22.5°，所以①正确；连接AC，它们相交于点H，如图，∵Rt△ABE≌Rt△ADF，∴BE＝DF，而BC＝DC，∴CE＝CF，∵AE＝AF，∴AC垂直平分EF，AH平分∠EAF，∴EB＝EH，FD＝FH，∴BE+DF＝EH+HF＝EF，所以④错误；∴△ECF的周长＝CE+CF+EF＝CE+BE+CF+DF＝CB+CD＝1+1＝2，所以③正确；设BE＝x，则EF＝2x，CE＝1﹣x，∵△CEF为等腰直角三角形，∴EF＝CE，即2x＝（1﹣x），解得x＝﹣1，∴BE＝﹣1，Rt△ECF中，EH＝FH，∴CH＝EF＝EH＝BE＝﹣1，∵CH⊥EF，∴点C到EF的距离是﹣1，所以②正确；本题正确的有：①②③；故选：B．19．解：A、对角线互相垂直的平行四边形是菱形，正确；B、两组邻边相等的四边形不一定是平行四边形，错误；C、对角线相等的平行四边形是矩形，错误；D、有一个角是直角的平行四边形是矩形，错误；故选：A．20．解：连接BP，（cm2），∴AB＝BC＝＝3（cm），∴（cm2），∴，∴（cm），故答案为：2．21．解：∵菱形ABCD中，AC＝6，BD＝8，∴OA＝OC＝AC＝3，OB＝BD＝4，AC⊥BD，∴BC＝＝＝5，∵OE⊥BC，∴S△OBC＝×OB×OC＝×BC×OE，∴OE＝＝＝，故答案为：．22．解：如图，∵菱形ABCD的周长是20cm，对角线AC＝6cm，∴AB＝20÷4＝5cm，AO＝AC＝3cm，又∵AC⊥BD，∴BO＝＝＝4cm，∴BD＝2BO＝8cm．故答案为：8．23．解：BD＝8，则BO＝DO＝4，菱形周长为20，则AB＝5，菱形对角线互相垂直平分，∴OA2+OB2＝AB2，AO＝3，AC＝6，故菱形的面积S＝×6×8＝24．故答案为24．24．解：菱形的面积等于两对角线的积的一半，则这个菱形的面积是6×10×＝30cm2．故答案为30．25．解：如图所示：①当AP＝AE＝5时，∵∠BAD＝90°，∴△AEP是等腰直角三角形，∴底边PE＝AE＝5；②当P1E＝AE＝5时，∵BE＝AB﹣AE＝8﹣5＝3，∠B＝90°，∴P1B＝＝4，∴底边AP1＝＝4；③当P2A＝P2E时，底边AE＝5；综上所述：等腰三角形AEP的底边长为5或4或5；故答案为：5或4或5．26．解：∵四边形ABCD是矩形，∴AC＝2AO，BD＝2BO，AC＝BD，∴AO＝OB，∵∠AOB＝60°，∴△AOB是等边三角形，∴AB＝AO＝2，即AC＝2AO＝4，故答案为：4．27．解：由题意可得，直角三角形的斜边长为3，一条直角边长为2，故直角三角形的另一条直角边长为：＝，故阴影部分的面积是：＝4，故答案为：4．28．解：∵四边形ABCD为正方形，∴∠BAE＝∠D＝90°，AB＝AD，在△ABE和△DAF中，∵，∴△ABE≌△DAF（SAS），∴∠ABE＝∠DAF，∵∠ABE+∠BEA＝90°，∴∠DAF+∠BEA＝90°，∴∠AGE＝∠BGF＝90°，∵点H为BF的中点，∴GH＝BF，∵BC＝5、CF＝CD﹣DF＝5﹣2＝3，∴BF＝＝，∴GH＝BF＝，故答案为：．29．解：连接AC，∵四边形ABCD是正方形，∴AC＝BD，∵CE＝BD，∴CE＝AC，∴∠E＝∠CAE，∵AC是正方形ABCD的对角线，∴∠ACB＝45°，∴∠E+∠CAE＝45°，∴∠E＝×45°＝22.5°，在△CEF中，∠AFC＝∠E+∠ECF＝22.5°+90°＝112.5°．故答案为：112.5°．30．解：如图，作线段MN的垂直平分线交AD于P，交AB于Q．∵PQ垂直平分线段MN，∴PM＝PN，QM＝QN，∵四边形ABCD是正方形，∴∠P AN＝∠QAN＝45°，∴∠APQ＝∠AQP＝45°，∴AP＝AQ，∴AC垂直平分线段PQ，∴MP＝MQ，∴四边形PMQN是菱形，在MN运动过程中，这样的菱形有无数个，当点M与A或C重合时，四边形PMQN是正方形，∴①②④正确，故答案为①②④．31．解：（1）∵DE⊥AB于E，且E为AB的中点，∴AD＝BD，∵四边形ABCD是菱形，∴AD＝BA，∴AB＝AD＝BD，∴△ABD是等边三角形，∴∠DAB＝60°；（2）∵BD＝4，△ABD是等边三角形，∴DO＝2，AD＝4，∴AO＝＝2，∴AC＝4；（3）菱形ABCD的面积为：BD•AC＝×4×4＝8．32．证明：（1）∵E是AD的中点，∴AE＝DE，∵AF∥BC，∴∠AFE＝∠DBE，∵∠AEF＝∠DEB，∴△AEF≌△DEB；（2）∵△AEF≌△DEB，∴AF＝DB，∵AD是BC边上的中线，∴DC＝DB，∴AF＝DC，∵AF∥DC，∴四边形ADCF是平行四边形，∵∠BAC＝90°，AD是BC边上的中线，∴AD＝DC，∴▱ADCF是菱形．33．（1）证明：∵DE∥BC，EC∥AB，∴四边形DBCE是平行四边形．∴EC∥DB，且EC＝DB．在Rt△ABC中，CD为AB边上的中线，∴AD＝DB＝CD．∴EC＝AD．∴四边形ADCE是平行四边形．∴ED∥BC．∴∠AOD＝∠ACB．∵∠ACB＝90°，∴∠AOD＝∠ACB＝90°．∴平行四边形ADCE是菱形；（2）解：Rt△ABC中，CD为AB边上的中线，∠B＝60°，BC＝6，∴AD＝DB＝CD＝6．∴AB＝12，由勾股定理得．∵四边形DBCE是平行四边形，∴DE＝BC＝6．∴．34．已知：Rt△ABC中，∠ACB＝90°，CO是斜边AB边上的中线；求证：CO＝AB；证明：如图，延长CO至点E，使CO＝OE，连接AE、BE，∵CO＝OE，点O为AB中点，∴OA＝OC，∴四边形AEBC为平行四边形，∵∠ACB＝90°，∴平行四边形AEBC是矩形，∴CE＝AB，∵CO＝CE，∴CO＝AB；故答案为：Rt△ABC中，∠ACB＝90°，CO是斜边AB边上的中线；CO＝AB．35．证明：∵DE∥AC，CE∥BD，∴四边形OCED是平行四边形，∵矩形ABCD，∴AO＝OC＝OB＝OD＝AC＝BD，∴四边形OCED是菱形．36．证明：∵四边形ABCD是矩形，∴∠A＝∠C＝90°，AD＝BC，在Rt△ADE和Rt△CBF中∴Rt△ADE≌Rt△CBF（HL），∴AE＝CF，∵矩形ABCD中AB＝CD，AB∥CD，∴BE＝DF，BE∥DF，∴四边形DEBF是平行四边形．37．证明：∵四边形ABCD是矩形，∴AC＝DB，AB∥DC，∴DC∥BE，又∵CE∥DB，∴四边形CDBE是平行四边形，∴DB＝CE，∴AC＝CE．38．（1）证明：∵AO＝OC，BO＝OD，∴四边形ABCD是平行四边形，∵∠AOB＝∠DAO+∠ADO＝2∠OAD，∴∠DAO＝∠ADO，∴AO＝DO，∴AC＝BD，∴四边形ABCD是矩形；（2）解：∵四边形ABCD是矩形，∴AB∥CD，∴∠ABO＝∠CDO，∵∠AOB：∠ODC＝4：3，∴∠AOB：∠ABO＝4：3，∴∠BAO：∠AOB：∠ABO＝3：4：3，∴∠ABO＝54°，∵∠BAD＝90°，∴∠ADO＝90°﹣54°＝36°．39．解：∵AB＝4，CE＝BC，∴EC＝1，BE＝3，∵F为CD的中点，∴DF＝FC＝2，∴EF＝＝，AF＝＝，AE＝＝．∴AE2＝EF2+AF2．∴△AEF是直角三角形．40．解：在Rt△AEF和Rt△ABF中，，∴Rt△AEF≌Rt△ABF（HL），∴FE＝FB．∵正方形ABCD，∴∠ACB＝∠BCD＝45°，在Rt△CEF中，∵∠ACB＝45°，∴∠CFE＝45°，∴∠ACB＝∠CFE，∴EC＝EF，∴FB＝EC＝EF．。

2021-2022学年北师大版九年级数学上册《第1章特殊平行四边形》单元能力提升训练（附答案）1．下列说法中，正确的是（）A．两邻边相等的四边形是菱形B．一条对角线平分一组内角的平行四边形是菱形C．对角线垂直且一组邻边相等的四边形是菱形D．对角线垂直的四边形是菱形2．在菱形ABCD中AB＝5，AC＝8，BC边上的高为（）A．1.2B．2.4C．3.6D．4.83．如图，菱形ABCD的边长为2，∠ABC＝45°，则点D的坐标为（）A．（2+）B．（2，2）C．（，2+）D．（4﹣，2）4．如图，矩形ABCD的两条对角线相交于点O，∠AOB＝60°，AC＝8，则AB的长是（）A．4B．5C．6D．85．如图，要使▱ABCD为矩形，则可以添加的条件是（）A．AC⊥BD B．AC＝BD C．∠AOB＝60°D．AB＝BC6．如图，在正方形ABCD中，BD与AC相交于点O．嘉嘉作DP∥OC，CP∥OD，在正方形ABCD外，DP，CP交于点P；淇淇作DP＝OC，CP＝OD，在正方形ABCD外，DP，CP交于点P，两人的作法中，能使四边形OCPD是正方形的是（）A．只有嘉嘉B．只有淇淇C．嘉嘉和淇淇D．以上均不正确7．如图，在矩形ABCD中，AD＝6．对角线AC与BD相交于点O，AE⊥BD，垂足为E，DE＝3BE，则AE的长为（）A．2B．3C．D．38．如图，在菱形ABCD中，对角线AC，BD交于点O，过点A作AE⊥BC，垂足为E，若AC＝，AE＝2，则菱形ABCD的面积为（）A．5B．10C．D．29．如图，已知点E在正方形ABCD的边AB上，以BE为边向正方形ABCD外部作正方形BEFG，连接DF，M、N分别是DC、DF的中点，连接MN．若AB＝17，BE＝7，则MN ＝（）A．25B．C．12D．10．如图，正方形ABCD中，点E，F分别在CD，BC上，且AF⊥BE，垂足为G，则下列结论：①BE＝AF；②∠AFB+∠BEC＝90°；③∠DAF＝∠ABE；④BF＝CE．其中正确的个数是（）A．1个B．2个C．3个D．4个11．如图，矩形ABCD中，对角线AC，BD相交于点O，AD＝2，∠COB＝60°，BF⊥AC，交AC于点M，交CD于点F，延长FO交AB于点E，则下列结论：①FO＝FC；②四边形EBFD是菱形；③△OBE≌△CBF；④MB＝3．其中结论正确的序号是（）A．②③④B．①②③C．①④D．①②③④12．如图，在Rt△ABC中，∠ACB＝90°，AC＝5，BC＝12，D是AB上一动点，过点D 作DE⊥AC于点E，DF⊥BC于点F，连接EF，则线段EF的最小值是．13．如图，四边形ABCD是边长为4的正方形，点E在边CD上，DE＝1；作EF∥BC，分别交AC、AB于点G、F，M、N分别是AG、BE的中点，则MN的长是．14．如图，在四边形ABCD中，BD为对角线，AD∥BC，BC＝AD，∠ABD＝90°，E为AD的中点，连接BE．（1）求证：四边形BCDE为菱形；（2）连接AC，若AC平分∠BAD，BC＝1，求菱形BCDE的面积．15．已知：如图．矩形ABCD中，O是AC与BD的交点，过O点的直线EF与AB、CD的延长线分别相交于点E、F．（1）求证：△BOE≌DOF；（2）当EF与AC满足什么关系时，以A、E、C、F为顶点的四边形是菱形？并给出证明．16．已知：平行四边形ABCD，对角线AC，BD相交于点O．E是AD的中点，连接OE并延长至F使得OE＝EF，连接FD，FC，FC交BD于点G．求证：（1）△FGD≌△CGO；（2）当AB与AC有怎样的数量关系时，四边形FOCD是菱形，并说明理由．17．如图，已知点E是▱ABCD中BC边的中点，连接AE并延长交DC的延长线于点F，连接AC，BF，AF＝BC．（1）求证：四边形ABFC为矩形；（2）若△AFD是等边三角形，且边长为6，求四边形ABFC的面积．18．如图，在▱ABCD中，对角线AC、BD相交于点O，AC⊥BD，过点A作AE⊥BC，交CB延长线于点E，过点C作CF⊥AD，交AD延长线于点F．（1）求证：四边形AECF是矩形；（2）连接OE，若AE＝4，AD＝5，求OE的长．19．如图，AC为矩形ABCD的对角线，BE⊥AC于点E，DF⊥AC于点F．（1）求证：△ABE≌△CDF．（2）求证：四边形BFDE是平行四边形．20．已知：如图，在菱形ABCD中，点E，O，F分别为AB，AC，AD的中点，连接CE，CF，OE，OF．（1）求证：△BCE≌△DCF；（2）当AB与BC满足什么关系时，四边形AEOF是正方形？请说明理由．21．已知：如图，在菱形ABCD中，F为边BC的中点，DF与对角线AC交于点M，过M 作ME⊥CD于点E，∠1＝∠2．（1）若CE＝1，求BC的长；（2）求证：AM＝DF+ME．参考答案1．解：A、∵两邻边相等的平行四边形是菱形，∴选项A不符合题意；B、∵一条对角线平分一组内角的平行四边形是菱形，∴选项B符合题意；C、∵对角线互相平分且一组邻边相等的四边形是菱形，∴选项C不符合题意；D、∵对角线垂直的平行四边形是菱形，∴选项D不符合题意；故选：B．2．解：设AC与BD交于点O，作出BC边的高h，∵四边形ABCD是菱形，∴AO⊥BO，且AC＝2AO，BD＝2BO．在Rt△AOB中利用勾股定理可得BO＝＝4．∴BD＝2BO＝8．∴菱形的面积为BD×AC＝×6×8＝24．设BC变上的高为h，则BC×h＝24，即5h＝24，h＝4.8．故选：D．3．解：过点D作DE⊥x轴，垂足为E．在Rt△CDE中，CD＝2，∴CE＝DE＝，∴OE＝OC+CE＝2+，∴点D坐标为（2+，）．故选：A．4．解：∵四边形ABCD是矩形，∴AO＝AC＝×8＝4，AC＝BD，OB＝BD，∴AO＝OB，∵∠AOB＝60°，∴△AOB是等边三角形，∴AB＝AO＝4，故选：A．5．解：因为有一个角是直角的平行四边形是矩形；对角线相等的平行四边形是矩形，故选：B．6．解：∵四边形ABCD是正方形，∴OD＝OC，OD⊥OC，∵DP∥OC，CP∥OD，∴四边形DOCP是平行四边形，∴DP＝OC，CP＝OD，∴DP＝OC＝CP＝OD，∴平行四边形DOCP是正方形，故嘉嘉正确；∵四边形ABCD是正方形，∴OD＝OC，OD⊥OC，∵DP＝OC，CP＝OD，∴DP＝OC＝CP＝OD，∴四边形DOCP是正方形，故淇淇正确；故选：C．7．解：∵DE＝3BE，∴BD＝4BE，∵四边形ABCD是矩形，∴BO＝DO＝BD＝2BE，∴BE＝EO，又∵AE⊥BO，∴AB＝AO，∴AB＝AO＝BO，∴△ABO是等边三角形，∴∠ABO＝60°，∴∠ADB＝30°，又∵AE⊥BD，∴AE＝AD＝3，故选：D．8．解：∵四边形ABCD是菱形，∴AC⊥BD，OA＝OC＝AC＝，∵AE⊥BC，∴△ABC的面积＝BC×AE＝AC×OB，∴，设BC＝x，则OB＝2x，在Rt△OBC中，由勾股定理得：（x）2﹣（2x）2＝（）2，解得：x＝，∴BC＝，∴菱形ABCD的面积＝BC×AE＝×2＝5；故选：A．9．解：连接CF，∵正方形ABCD和正方形BEFG中，AB＝17，BE＝7，∴GF＝GB＝7，BC＝17，∴GC＝GB+BC＝7+17＝24，∴CF＝＝25，∵M，N分别是DC，DF的中点，∴MN＝CF＝，故选：D．10．解：∵四边形ABCD是正方形，∴∠ABF＝∠C＝90°，AB＝BC，∵BF＝CE，∴△ABF≌△BCE（SAS），∴AF＝BE（①正确），∠BAF＝∠CBE，∠AFB＝∠BEC（②错误），∵∠BAF+∠DAF＝90°，∠ABE+∠EBC＝90°，∴∠DAF＝∠ABE（③正确），∵△ABF≌△BCE，∴BF＝CE（④正确），故选：C．11．解：∵四边形ABCD是矩形，∴AC＝BD，∴OA＝OC＝OD＝OB，∵∠COB＝60°，∴△OBC是等边三角形，∴OB＝BC＝OC，∠OBC＝60°，∵BF⊥AC，∴OM＝MC，∴FM是OC的垂直平分线，∴FO＝FC，故①正确；∵OB＝CB，FO＝FC，FB＝FB，∴△OBF≌△CBF（SSS），∴∠FOB＝∠FCB＝90°，∵∠OBC＝60°，∴∠ABO＝30°，∴∠OBM＝∠CBM＝30°，∴∠ABO＝∠OBF，∵AB∥CD，∴∠OCF＝∠OAE，∵OA＝OC，∠AOE＝∠FOC，∴△AOE≌△COF（ASA），∴OE＝OF，∵OB⊥EF，∴四边形EBFD是菱形，故②正确；∵△OBE≌△OBF≌△CBF，∴③正确；∵BC＝AD＝2，FM⊥OC，∠CBM＝30°，∴BM＝3，故④正确；故选：D．12．解：如图，连接CD．∵∠ACB＝90°，AC＝5，BC＝12，∴AB＝＝＝13，∵DE⊥AC，DF⊥BC，∠C＝90°，∴四边形CFDE是矩形，∴EF＝CD，由垂线段最短可得CD⊥AB时，线段EF的值最小，此时，S△ABC＝BC•AC＝AB•CD，即×12×5＝×13•CD，解得：CD＝，∴EF＝．故答案为：．13．解：连接FM，FC，∵四边形ABCD是正方形，EF∥BC，∴∠BAC＝45°，四边形BCEF为矩形，∴△AFG为等腰直角三角形，BE＝CF，∵M是AG的中点，∴AM＝MG，则FM⊥AG，即△FMC是直角三角形，∵N是FC的中点，∴MN＝FC，∵DE＝1，BC＝DC＝4，∴CE＝3，∴BE＝FC＝，∴MN＝FC＝2.5．故答案为2.5．14．（1）证明：∵E为AD的中点，∴DE＝AE＝AD，∵BC＝AD，∴DE＝BC，∵AD∥BC，∴四边形BCDE是平行四边形，又∵∠ABD＝90°，E为AD的中点，∴BE＝AD＝DE，∴平行四边形BCDE是菱形．（2）解：如图，∵AD∥BC，AC平分∠BAD，∴∠DAC＝∠BCA，∠BAC＝∠DAC，∴∠BCA＝∠BAC，∴AB＝BC＝1，∵BC＝AD，∴AD＝2，∵∠ABD＝90°，∴BD＝＝＝，由（1）得：四边形BCDE为菱形，∵E为AD的中点，∴△BDE的面积＝△ABE的面积，∴菱形BCDE的面积＝2△BDE的面积＝△ABD的面积＝AB×BD＝×1×＝．15．证明：（1）∵四边形ABCD是矩形，∴OB＝OD，∵AE∥CF，∴∠E＝∠F，∠OBE＝∠ODF，在△BOE与△DOF中，，∴△BOE≌△DOF（AAS）；（2）当EF⊥AC时，四边形AECF是菱形．证明：∵△BOE≌△DOF，∴OE＝OF，∵四边形ABCD是矩形，∴OA＝OC，∴四边形AECF是平行四边形，∵EF⊥AC，∴四边形AECF是菱形．16．（1）证明：在△ACD中，点O，E分别为边AC，AD中点，∴OE为△ACD的中位线，∴OE∥CD，，又∵，∴OF∥CD，OF＝CD，∴四边形OCDF为平行四边形，∴FD∥OC，FD＝OC，∴∠GFD＝∠GCO，∠GDF＝∠GOC，∴△FGD≌△HGO（ASA）；（2）解：当时，四边形FOCD是菱形，理由如下：∵四边形ABCD是平行四边形，∴AB＝CD，OC＝AC，∵AB＝AC，∴AB＝CD＝OC，由（1）得：四边形OCDF为平行四边形，∴平行四边形FOCD是菱形，17．（1）证明：∵四边形ABCD是平行四边形，∴AB＝CD，AB∥CD，∴∠BAE＝∠CFE，∵点E是▱ABCD中BC边的中点，∴BE＝CE，∵∠AEB＝∠FEC，∴△ABE≌△FCE（AAS），∴AB＝FC，∵AB∥FC，∴四边形ABFC是平行四边形，又∵AF＝BC，∴平行四边形ABFC为矩形；（2）解：由（1）得：四边形ABFC为矩形，∴∠ACF＝90°，∵△AFD是等边三角形，∴AF＝DF＝6，CF＝DF＝3，∴AC＝＝＝3，∴四边形ABFC的面积＝AC×CF＝3×3＝9．18．证明：（1）∵四边形ABCD是菱形，∴AD∥BC，∵CF∥AE，∴四边形AECF是平行四边形，∵AE⊥BC，∴四边形AECF是矩形；（2）连接OE，在菱形ABCD中，AD＝AB＝BC＝5，AO＝CO，∴∠OEC＝∠OCE，由（1）知，四边形AECF为矩形；∴∠AEC＝90°，∵AE＝4，∴BE＝＝3，∴CE＝3+5＝8，在Rt△AEC中，AE＝4，CE＝8，∴AC＝，∵AO＝CO，∴OE＝AC＝2．19．证明：（1）∵四边形ABCD是矩形，∴AB＝CD，AB∥CD，∴∠BAE＝∠DCF，又∵BE⊥AC，DF⊥AC，∴∠AEB＝∠CFD＝90°，在△ABE和△CDF中，，∴△ABE≌△CDF（AAS）；（2）由（1）得：△ABE≌△CDF，∴BE＝DF，又∵BE⊥AC，DF⊥AC，∴BE∥DF，∴四边形BFDE是平行四边形．20．（1）证明：∵四边形ABCD是菱形，∴∠B＝∠D，AB＝BC＝DC＝AD，∵点E，O，F分别为AB，AC，AD的中点，∴AE＝BE＝DF＝AF，OF＝DC，OE＝BC，OE∥BC，在△BCE和△DCF中，，∴△BCE≌△DCF（SAS）；（2）解：当AB⊥BC时，四边形AEOF是正方形，理由如下：由（1）得：AE＝OE＝OF＝AF，∴四边形AEOF是菱形，∵AB⊥BC，OE∥BC，∴OE⊥AB，∴∠AEO＝90°，∴四边形AEOF是正方形．21．（1）解：∵四边形ABCD是菱形，∴AB∥CD，∴∠1＝∠ACD，∵∠1＝∠2，∴∠ACD＝∠2，∴MC＝MD，∵ME⊥CD，∴CD＝2CE，∵CE＝1，∴CD＝2，∴BC＝CD＝2；（2）证明：如图，∵F为边BC的中点，∴BF＝CF＝BC，∴CF＝CE，在菱形ABCD中，AC平分∠BCD，∴∠ACB＝∠ACD，在△CEM和△CFM中，∵，∴△CEM≌△CFM（SAS），∴ME＝MF，延长AB交DF的延长线于点G，∵AB∥CD，∴∠G＝∠2，∵∠1＝∠2，∴∠1＝∠G，∴AM＝MG，在△CDF和△BGF中，∵，∴△CDF≌△BGF（AAS），∴GF＝DF，由图形可知，GM＝GF+MF，∴AM＝DF+ME．。

2020-2021年人教版八年级数学下册《18.2特殊的平行四边形》同步提升训练（附答案）1．如图，E是平行四边形ABCD边AD延长线上一点，且DE＝AD，连接BE、CE、BD．若AB＝BE，则四边形BCED是（）A．平行四边形B．矩形C．菱形D．正方形2．如图，在平行四边形ABCD中，对角线AC的垂直平分线分别与AD，AC，BC相交于点E，O，F．下列结论正确的个数有（）①四边形AFCE为菱形；②△ABF≌△CDE；③当F为BC中点时，∠ACD＝90°．A．0个B．1个C．2个D．3个3．如图，矩形ABCD中，点E在BC上，且AE平分∠BAC，AE＝CE，BE＝2，则矩形ABCD 的面积为（）A．24B．24C．12D．124．菱形，矩形，正方形都具有的性质是（）A．四条边相等，四个角相等B．对角线相等C．对角线互相垂直D．对角线互相平分5．如图，四边形ABCD为菱形，对角线AC，BD相交于点O，DH⊥AB于点H，连接OH，∠CAD＝25°，则∠DHO的度数是（）A．20°B．25°C．30°D．35°6．如图，正方形ABCD的边长为3，点P为对角线AC上任意一点，PE⊥BC，PQ⊥AB，垂足分别是E，Q，则PE+PQ的值是（）A．B．3C．D．7．已知四边形ABCD是平行四边形，下列说法正确的有（）①当AB＝BC时，它是矩形②AC⊥BD时，它是菱形③当∠ABC＝90°时，它是菱形④当AC＝BD时，它是正方形A．①②B．②C．②④D．③④8．如图，在菱形ABCD中，AC＝2，BD＝2，DH⊥AB于点H，则BH的长为（）A．3B．C．2D．9．如图，点P是Rt△ABC中斜边AC（不与A，C重合）上一动点，分别作PM⊥AB于点M，作PN⊥BC于点N，连接BP、MN，若AB＝6，BC＝8，当点P在斜边AC上运动时，则MN的最小值是（）A．1.5B．2C．4.8D．2.410．在矩形ABCD中，对角线AC、BD相交于点O，AE平分∠BAD交BC于点E，∠CAE ＝15°，连接OE，则下面的结论：其中正确的结论有（）①△DOC是等边三角形；②△BOE是等腰三角形；③BC＝2AB；④∠AOE＝150°；⑤S△AOE＝S△COE．A．2 个B．3个C．4 个D．5个11．在正方形ABCD中，AB＝8，点P是正方形边上一点，若PD＝3AP，则AP的长为．12．在矩形ABCD中，AB＝3，∠ABC的平分线BE交AD所在的直线于点E，若DE＝2，则AD的长为．13．如图，四边形ABCD是一个正方形，E是BC延长线上的一点，且AC＝EC，则∠DAE ＝．14．如图，在正方形ABCD中，AB＝2，点E为边BC中点，P为正方形边上一点，且PB ＝AE，则PE的长为．15．在菱形ABCD中，∠BAD＝108°，AB的垂直平分线交AC于点N，点M为垂足，连接DN，则∠CDN的度数是．16．如图，E是正方形ABCD的边CD的中点，AE的垂直平分线分别交AE、BC于H、G，若CG＝7，则GH的长为．17．已知菱形ABCD的面积是96，对角线AC是12，那么菱形ABCD的周长是．18．如图，正方形ABCD的边长为2，E为对角线AC上一点，且CE＝CB，点P为线段BE 上一动点，且PF⊥CE于F，PG⊥BC于G，则PG+PF的值为．19．如图，正方形ABCD的边长为5，AG＝CH＝4，BG＝DH＝3，连接GH，则线段GH的长为．20．如图，已知正方形ABCD的边长为7，点E，F分别在AD、DC上，AE＝DF＝3，BE 与AF相交于点G，点H为BF的中点，连接GH，则GH的长为．21．如图，在菱形ABCD中，BC＝3，BD＝2，点O是BD的中点，延长BD到点E，使得DE＝BD，连接CE，点M是CE的中点，则OM＝．22．如图，已知▱ABCD的对角线AC、BD交于点O，且∠1＝∠2．（1）求证：▱ABCD是菱形．（2）F为AD上一点，连接BF交AC于E，且AE＝AF，若AF＝3，AB＝5，求AO的长．23．如图，在四边形ABCD中，AB∥DC，AB＝AD，对角线AC，BD交于点O，AC平分∠BAD，过点C作CE⊥AB交AB的延长线于点E，连接OE．（1）求证：∠DAC＝∠DCA；（2）求证：四边形ABCD是菱形；（3）若AB＝，BD＝2，求OE的长．24．如图，已知四边形ABCD为正方形，AB＝3，点E为对角线AC上一动点，连接DE，过点E作EF⊥DE，交BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．（1）求证：矩形DEFG是正方形；（2）探究：CE+CG的值是否为定值？若是，请求出这个定值；若不是，请说明理由．25．如图，△ABC中，D是BC边上的一点，E是AD的中点，过点A作BC的平行线交BE 的延长线于F，且AF＝DC，连接CF．（1）如果AB＝AC，试猜想四边形ADCF的形状，并证明你的结论；（2）△ABC满足什么条件时四边形ADCF为正方形，并证明你的结论．26．如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，垂足为D，AF平分∠CAB，交CD 于点E，交CB于点F．（1）若∠B＝30°，AC＝4，求CE的长；（2）过点F作AB的垂线，垂足为G，连接EG，试判断四边形CEGF的形状，并说明理由．27．四边形ABCD为正方形，点E为线段AC上一点，连接DE，过点E作EF⊥DE，交射线BC于点F，以DE、EF为邻边作矩形DEFG，连接CG．（1）如图，求证：矩形DEFG是正方形；（2）若AB＝2，CE＝2，求CG的长；（3）当线段DE与正方形ABCD的某条边的夹角是40°时，直接写出∠EFC的度数．28．如图，过△ABC边AC的中点O，作OE⊥AC，交AB于点E，过点A作AD∥BC，与BO的延长线交于点D，连接CD，CE，若CE平分∠ACB，CE⊥BO于点F．（1）求证：①OC＝BC；②四边形ABCD是矩形；（2）若BC＝3，求DE的长．参考答案1．解：∵四边形ABCD是平行四边形，∴AD∥BC，AD＝BC，AB＝DC，∴DE∥BC，∵DE＝AD，∴DE＝BC，∴四边形BCED是平行四边形，∵AB＝BE，∴BE＝DC，∴▱BCED是矩形，故选：B．2．解：∵四边形ABCD为平行四边形，∴AD∥BC，AD＝BC，AB＝CD，∠B＝∠D，AB∥CD，∴∠EAC＝∠FCA，∵EF垂直平分AC，∴OA＝OC，EA＝EC，∴∠EAC＝∠ECA，∴∠FCA＝∠ECA，在△AOE和△COF中，，∴△AOE≌△COF（ASA），∴OE＝OF，∴四边形AFCE为平行四边形，∵EF垂直平分AC，∴平行四边形AFCE是菱形，①正确；∴AE＝CF，∴BF＝DE，在△ABF和△CDE中，，∴△ABF≌△CDE（SAS），②正确；∵四边形AFCE是菱形，∴AF＝CF，∵F为BC的中点，∴BF＝CF，∴AF＝CF＝BC，∴∠BAC＝90°，∵AB∥CD，∴∠ACD＝∠BAC＝90°，③正确；正确的个数有3个，故选：D．3．解：∵四边形ABCD是矩形，∴∠B＝90°，∴∠BAC+∠BCA＝90°，∵AE平分∠BAC，AE＝CE，∴∠BAE＝∠EAC＝∠ECA，∴∠BAE+∠EAC+∠ECA＝90°，∴∠BAE＝∠EAC＝∠ECA＝30°，∴AE＝CE＝2BE＝4，AB＝2，∴BC＝BE+CE＝6，∴矩形ABCD面积＝AB×BC＝2×6＝12；故选：C．4．解：菱形，矩形，正方形都具有的性质为对角线互相平分．故选：D．5．解：如图：∵四边形ABCD是菱形，∴OD＝OB，AB∥CD，BD⊥AC∵DH⊥AB，∴DH⊥CD，∠DHB＝90°，∴OH为Rt△DHB的斜边DB上的中线，∴OH＝OD＝OB，∴∠HDO＝∠DHO，∵DH⊥CD，∴∠GDO+∠ODC＝90°，∵BD⊥AC，∴∠ODC+∠DCO＝90°，∴∠HDO＝∠DCO，∴∠DHO＝∠DCA，∵四边形ABCD是菱形，∴DA＝DC，∴∠CAD＝∠DCA＝25°，∴∠DHO＝25°，故选：B．6．解：∵四边形ABCD是正方形，∴∠CAB＝45°，∠B＝90°．∵PE⊥BC，PQ⊥AB，∴∠PQB＝∠PEB＝90°．∴∠PQB＝∠PEB＝∠B＝90°．∴四边形PQBE为矩形．∴PE＝BQ．∵PQ⊥AB，∠CAB＝45°，∴△P AQ为等腰三角形．∴PQ＝AQ．∴PE+PQ＝BQ+AQ＝AB＝3．故选：B．7．解：①若AB＝BC，则▱ABCD是菱形，选项说法错误；②若AC⊥BD，则▱ABCD是菱形，选项说法正确；③若∠ABC＝90°，则▱ABCD是矩形，选项说法错误；④若AC＝BD，则▱ABCD是矩形，选项说法错误；故选：B．8．解：在菱形ABCD中，AC＝2，BD＝2，∴AO＝CO＝AC＝，BO＝DO＝BD＝，∴AB＝＝＝3，∵DH×AB＝AC×BD，∴DH＝＝2，∴BH＝＝＝2，故选：C．9．解：∵∠ABC＝90°，AB＝6，BC＝8，∴AC＝＝＝10，∵PM⊥AB，PN⊥BC，∠C＝90°，∴四边形BNPM是矩形，∴MN＝BP，由垂线段最短可得BP⊥AC时，线段MN的值最小，此时，S△ABC＝BC•AB＝AC•BP，即×8×6＝×10•BP，解得：BP＝4.8，即MN的最小值是4.8，故选：C．10．解：∵AE平分∠BAD，∴∠BAE＝∠DAE＝45°，∴∠AEB＝45°，∴△ABE是等腰直角三角形，∴AB＝BE，∵∠CAE＝15°，∴∠ACE＝∠AEB﹣∠CAE＝45°﹣15°＝30°，∴∠BAO＝90°﹣30°＝60°，∵矩形ABCD中：OA＝OB＝OC＝OD，∴△ABO是等边三角形，△COD是等边三角形，故①正确；∴OB＝AB，∠ABO＝∠AOB＝60°，∴OB＝BE，∴△BOE是等腰三角形，故②正确；∵∠OBE＝∠ABC﹣∠ABO＝90°﹣60°＝30°＝∠ACB，∴∠BOE＝（180°﹣30°）＝75°，BC＝AB，故③错误；∴∠AOE＝∠AOB+∠BOE＝60°+75°＝135°，故④错误；∵AO＝CO，∴S△AOE＝S△COE，故⑤正确；故选：B．二．填空题（共11小题）11．解：当点P在AD上时，∵PD＝3AP，PD+AP＝8，∴AP＝2，当点P在AB上时，∵PD2＝AP2+AD2，∴9AP2＝AP2+64，∴AP＝2，综上所述：AP＝2或2，故答案为2或2．12．解：如图1，当点E在AD上时，∵四边形ABCD是矩形，∴∠A＝90°，AD∥BC，∴∠AEB＝∠CBE，∵BE平分∠ABC，∴∠ABE＝∠CBE，∴∠ABE＝∠AEB，∴AE＝AB＝3，∵DE＝2，∴AD＝AE+DE＝3+2＝5；如图2，当点E在AD的延长线上时，同理AE＝3，∴AD＝AE﹣DE＝3﹣2＝1．故答案为：5或1．13．解：∵四边形ABCD是正方形，∴∠ACB＝45°，AD∥BC，∵AC＝EC，∴∠E＝∠CAE，∵∠ACB＝∠E+∠CAE＝2∠E，∴∠E＝∠ACB＝22.5°，∵AD∥BC，∴∠DAE＝∠E＝22.5°．故答案为：22.5°．14．解：当点P在AD边上时，∵PB＝AE，点E为边BC中点，∴点P为边AD中点，∴PE＝AB＝2；当点P在CD边上时，∵PB＝AE，点E为边BC中点，∴点P为边CD中点，∴PE＝＝＝．所以PE的长为：2或．故答案为：2或．15．解：如图，连接BN，∵在菱形ABCD中，∠BAD＝108°，∴AD＝AB，∠ABC＝72°，∠CAB＝54°，∵AB的垂直平分线交AC于点N，∴AN＝NB，∴∠CAB＝∠ABN＝54°，∴∠CBN＝72°﹣54°＝18°，在△DCN和△BCN中，，∴△DCN≌△BCN（SAS），∴∠CDN＝∠CBN＝18°，故答案为：18°．16．解：如图，连接AG，GE，∵AE的垂直平分线分别交AE、BC于H、G，∴AG＝GE，AH＝HE，AH⊥HE，设AD＝CD＝BC＝AB＝2a，∵点E是CD的中点，∴CE＝DE＝a，∵AG2＝AB2+BG2，GE2＝EC2+GC2，∴4a2+（2a﹣7）2＝a2+49，∴a1＝4，a2＝0（舍去），∴EC＝DC＝4，AD＝8，∴GE＝＝＝，AE＝＝＝4，∴HE＝2，∴GH＝＝＝3，故答案为：3．17．解：∵四边形ABCD是菱形，∴BO＝OD＝BD，AO＝OC＝AC＝6，AC⊥BD，AB＝BC＝CD＝AD，∴AC•BD＝96，∴BD＝16，∴BO＝8，∴AB＝＝＝10，∴菱形的周长＝4×10＝40．故答案为：40．18．解：连接CP，BD，交AC于M，∵四边形ABCD为正方形，BC＝2，∴BD⊥AC，垂足为M，BM＝MC＝BC＝，∵S△BCE＝CE•BM，S△PCE＝CE•PF，S△BCP＝BC•PG，S△BCE＝S△PCE+S△BCP，∴CE•BM＝CE•PF+BC•PG，∵BC＝CE，∴BM＝PF+PG，∴PG+PF＝．故答案为．19．解：如图，延长BG交CH于点E，在△ABG和△CDH中，，∴△ABG≌△CDH（SSS），∴∠1＝∠5，∠2＝∠6，∵AG＝CH＝4，BG＝DH＝3，AB＝5，∴AG2+BG2＝AB2，∴∠AGB＝∠CHD＝90°，∴∠1+∠2＝90°，∠5+∠6＝90°，又∵∠2+∠3＝90°，∠4+∠5＝90°，∴∠1＝∠3＝∠5，∠2＝∠4＝∠6，在△ABG和△BCE中，，∴△ABG≌△BCE（ASA），∴BE＝AG＝4，CE＝BG＝3，∠BEC＝∠AGB＝90°，∴GE＝BE﹣BG＝4﹣3＝1，同理可得HE＝1，在Rt△GHE中，GH＝＝＝，故答案为：．20．解：∵四边形ABCD是正方形，∴AB＝DA，∠BAE＝∠ADF＝90°，在△BAE和△ADF中，，∴△BAE≌△ADF（SAS），∴∠ABE＝∠DAF，∵∠ABE+∠BEA＝90°，∴∠DAF+∠BEA＝90°，∴∠AGE＝90°，∴∠BGF＝90°，∵点H为BF的中点，∴GH＝BF，又∵BC＝CD＝7，DF＝3，∠C＝90°，∴CF＝4，∴BF＝＝＝，∴GH＝，故答案为：．21．解：连接OC，∵四边形ABCD是菱形，∴BC＝CD＝3，BO＝OD＝1，∴CO⊥BD，∴OC＝，∵DE＝BD＝2，在Rt△EOC中，CE＝，∵点M是CE的中点，∴OM＝，故答案为：．22．（1）证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠2＝∠ACB，∵∠1＝∠2，∴∠1＝∠ACB，∴AB＝CB，∴▱ABCD是菱形．（2）解：由（1）得：▱ABCD是菱形，∴BC＝AB＝5，AO＝CO，∵AD∥BC，∴∠AFE＝∠CBE，∵AE＝AF＝3，∴∠AFE＝∠AEF，又∵∠AEF＝∠CEB，∴∠CBE＝∠CEB，∴CE＝BC＝5，∴AC＝AE+CE＝3+5＝8，∴AO＝AC＝4．23．（1）证明：∵AB∥DC，∴∠OAB＝∠DCA，∵AC平分∠BAD，∴∠OAB＝∠DAC，∴∠DAC＝∠DCA；（2）证明：∵∠DAC＝∠DCA，AB＝AD，∴CD＝AD＝AB，∵AB∥DC，∴四边形ABCD是平行四边形，∵AD＝AB，∴▱ABCD是菱形；（3）解：∵四边形ABCD是菱形，∴OA＝OC，OB＝OD，BD⊥AC，∵CE⊥AB，∴OE＝OA＝OC，∵BD＝2，∴OB＝BD＝1，在Rt△AOB中，由勾股定理得：OA＝＝＝2，∴OE＝OA＝2．24．解：（1）如图，作EM⊥BC于M，EN⊥CD于N，∴∠MEN＝90°，∵点E是正方形ABCD对角线上的点，∴EM＝EN，∵∠DEF＝90°，∴∠DEN＝∠MEF，∵∠DNE＝∠FME＝90°，在△DEN和△FEM中，，∴△DEN≌△FEM（ASA），∴EF＝DE，∵四边形DEFG是矩形，∴矩形DEFG是正方形；（2）CE+CG的值是定值，定值为6，理由如下：∵正方形DEFG和正方形ABCD，∴DE＝DG，AD＝DC，∵∠CDG+∠CDE＝∠ADE+∠CDE＝90°，∴∠CDG＝∠ADE，在∴△ADE和△CDG中，，∴△ADE≌△CDG（SAS），∴AE＝CG，∴CE+CG＝CE+AE＝AC＝AB＝×3＝6是定值．25．解：（1）四边形ADCF为矩形，理由如下：∵AF＝DC，AF∥BC，∴四边形AFCD为平行四边形，∴AF＝CD，又∵E为AD的中点，AF∥BD，∴AE＝DE，∠AFE＝∠DBE，在△AEF和△DEB中，∴△AEF≌△DEB（AAS），∴BD＝AF，∴BD＝CD，又∵AB＝AC，∴AD⊥BC，∴∠ADC＝90°，∴平行四边形AFCD为矩形；（2）当△ABC为等腰直角三角形时，四边形ADCF为正方形；理由：∵△ABC为等腰直角三角形，D为BC中点，∴AD⊥BC，AD＝BC＝BD＝CD，∴平行四边形ADCF为矩形，∴矩形ADCF为正方形．26．解：（1）∵∠ACB＝90°，∠B＝30°，∴∠CAB＝60°，∵CD⊥AB，∴∠ADC＝90°，∴∠ACD＝30°，∵AF平分∠CAB，∴∠CAF＝∠BAF＝30°，∴CE＝AE，过点E作EH⊥AC于点H，∴CH＝AH∵AC＝4，∴CH＝2，∴CE＝；（2）∵FG⊥AB，FC⊥AC，AF平分∠CAB，∴∠ACF＝∠AGF＝90°，CF＝GF，在Rt△ACF与Rt△AGF中，，∴Rt△ACF≌Rt△AGF（HL），∴∠AFC＝∠AFG，∵CD⊥AB，FG⊥AB，∴CD∥FG，∴∠CEF＝∠EFG，∴∠CEF＝∠CFE，∴CE＝CF，∴CE＝FG，∴四边形CEGF是菱形27．（1）证明：作EP⊥CD于P，EQ⊥BC于Q，∵∠DCA＝∠BCA，∴EQ＝EP，∵∠QEF+∠FEC＝45°，∠PED+∠FEC＝45°，∴∠QEF＝∠PED，在Rt△EQF和Rt△EPD中，，∴Rt△EQF≌Rt△EPD（ASA），∴EF＝ED，∴矩形DEFG是正方形；（2）如图2中，在Rt△ABC中，AC＝AB＝4，∵EC＝2，∴AE＝CE，∴点F与C重合，此时△DCG是等腰直角三角形，易知CG＝2；（3）①如图3，当DE与AD的夹角为40°时，∠DEC＝45°+40°＝85°，∵∠DEF＝90°，∴∠CEF＝5°，∵∠ECF＝45°，∴∠EFC＝130°，②如图4，当DE与DC的夹角为40°时，∵∠DEF＝∠DCF＝90°，∴∠EFC＝∠EDC＝40°，综上所述，∠EFC＝130°或40°．28．（1）证明：①∵CE平分∠ACB，∴∠OCE＝∠BCE，∵BO⊥CE，∴∠CFO＝∠CFB＝90°，在△OCF与△BCF中，，∴△OCF≌△BCF（ASA），∴OC＝BC；②∵点O是AC的中点，∴OA＝OC，∵AD∥BC，∴∠DAO＝∠BCO，∠ADO＝∠CBO，在△OAD与△OCB中，，∴△OAD≌△OCB（ASA），∴AD＝BC，∵AD∥BC，∴四边形ABCD是平行四边形，∵OE⊥AC，∴∠EOC＝90°，在△OCE与△BCE中，，∴△OCE≌△BCE（SAS），∴∠EBC＝∠EOC＝90°，∴四边形ABCD是矩形；（2）解：∵四边形ABCD是矩形，∴AD＝BC＝3，∠DAB＝90°，AC＝BD，∴OB＝OC，∵OC＝BC，∴OC＝OB＝BC，∴△OBC是等边三角形，∴∠OCB＝60°，∴∠ECB＝OCB＝30°，∵∠EBC＝90°，∴EB＝EC，∵BE2+BC2＝EC2，BC＝3，∴EB＝，EC＝2，∵OE⊥AC，OA＝OC，∴EC＝EA＝2，在Rt△ADE中，∠DAB＝90°，∴DE＝＝＝．。

特殊的平行四边形（能力提高训练）一、选择题：1、如图，矩形ABCD 中，AB ＝3，BC ＝5.过对角线交点O 作OE ⊥AC 交AD 于E ，则AE 的长是（ ）A.1.6B.2.5C.3D.3.42、如图，菱形纸片ABCD 中，∠A=60°，折叠菱形纸片ABCD ，使点C 落在DP （P 为AB 中点）所在的直线上，得到经过点D 的折痕DE ．则∠DEC 的大小为( ) A ．78 B ．75° C ．60° D ．45°3、如图，在边长为2的正方形ABCD 中，M 为边AD 的中点，延长MD 至点E ，使ME=MC ，以DE 为边作正方形DEFG ，点G 在边CD 上，则DG 的长为（ ） A ．B ．C ．D ．4、如图，菱形OABC 在平面直角坐标系中的位置如图所示，∠AOC ＝45°，OC则点B 的坐标为（ ）1) B.(1，1)D.(15、如图，正方形ABCD 内有两条相交线段MN 、EF ，M 、N 、E 、F 分别在边AB 、CD 、AD 、BC 上.小明认为：若MN ＝EF ，则MN ⊥EF ；小亮认为: 若MN ⊥EF ，则MN ＝EF .你认为（ ） A.仅小明对 B.仅小亮对 C.两人都对 D.两人都不对6、如图所示，正方形ABCD 的面积为12，△ABE 是等边三角形，点E 在正方形ABCD 内，在对角线AC 上有一点P ，使PD +PE 的和最小，则这个最小值为（ ）C.3二、填空题：7、如图，在矩形ABCD 中，AB=3，AD=4，点P 在AD 上，PE ⊥AC 于E ，PF ⊥BD 于F ，则PE+PF ＝ 。

E DCBA O第1题图第3题图第2题图第4题图第5题图A E PBC第6题图第7题图8、如图，将边长为8cm 的正方形ABCD 折叠，使点D 落在BC 边的中点E 处，点A 落在F 处，折痕为MN ，则线段CN 的长是＿＿＿.9、如图，菱形ABCD 中，对角线AC ，BD 相交于点O ，H 为AD 边中点，菱形ABCD 的周长为24，则OH 的长等于＿＿＿.10、如图，将两张长为8，宽为2的矩形纸条交叉，使重叠部分是一个菱形，容易知道当两张纸条垂直时，菱形的周长有最小值8，那么菱形周长的最大值是＿＿＿.11、如图，矩形ABCD 中,AC 、BD 相交于O ,AE 平分∠BAD 交BC 于E ,若∠CAE =15°，则∠BOE ＝ 。