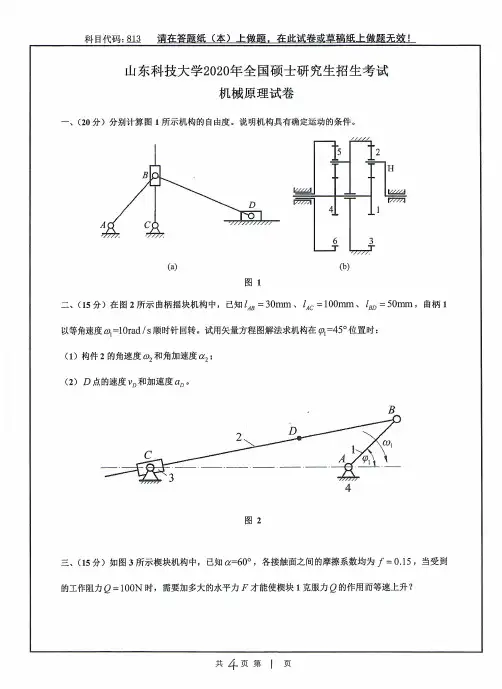
山东科技大学结构力学2004--2020年考研初试真题

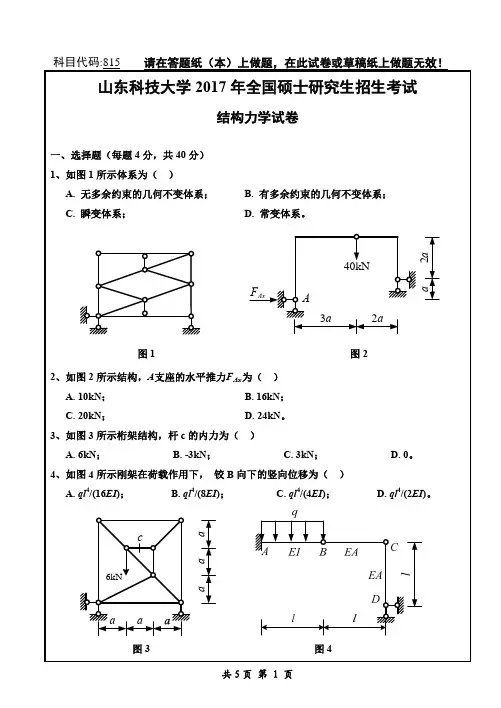
D.常变体系。

图1图2、如图2所示结构，杆1的轴力FF P； B.-2F P；F P/2； D.-1.12F P。

、如图3所示结构，当其高度h增加时，水平支座反力F Ax（）A.增大；B.减少；C.不变；D.不确定。

图3图44、如图4所示结构，在给定荷载作用下，BA为（）A．F P l；B．F P l/2；C．F P l/4；D．F P l/8。

5、机动法作静定梁影响线应用的原理为（）A.变形条件；B.平衡条件；C.虚功原理；D.叠加原理。

共4页第1页C.0.05rad；D.0.06rad。

图5图66所示结构，可视为多余约束的三根链杆是（）、6、7； B.3、6、8；6、7； D.5、6、7。

7所示结构，梁式杆EI=常数，桁架杆常数，杆AB的轴力为（）拉力； B.压力；零； D.无法确定。

图7图8、如图8所示结构，截面C的剪力影响线在处的竖标y E的绝对值为（）A.1；B.l；0.5； D.0.5l。

二、填空题（共20分，每题4分）、如图9所示体系的计算自由度W=①。

、用力法计算图10所示结构时，取A、B支座反力为基本未知量：X1，X2。

当EI1增大时，力法方程中∆1P②。

（填不变、增大或减小）共4页第2页共4页第3页图9图103、如图11所示结构，已知I 1/I 2=K ，则|M AB |/|M DC |=③。

4、如图12所示结构，已知力偶矩M =16kN·m ，则杆端弯矩M DA =④。

（顺时针为正）图11图125、如图13所示结构，各杆EI =常数，忽略杆件轴向变形，M CA =⑤。

图13图14三、计算题（共100分，每题20分）1、如图14所示刚架，忽略杆件轴向变形。

绘制刚架的剪力图，并求C 点的竖向位移ΔC V 。

2、如图15所示桁架，计算指定杆件1、2、3的轴力。

3、用力法计算图16所示刚架，并作出刚架的弯矩图。

已知I /A =10。

共4页第4页图15图164、用位移法计算图17所示刚架，并作出刚架的弯矩图。

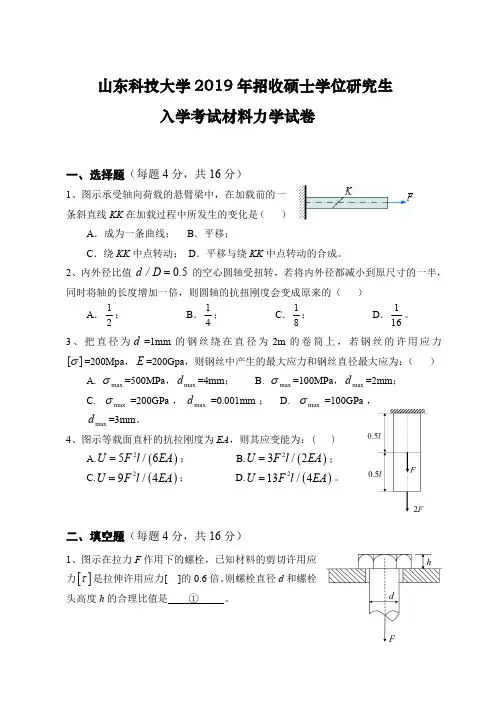
山东科技大学2019年招收硕士学位研究生入学考试材料力学试卷一、选择题（每题4分，共16分）1、图示承受轴向荷载的悬臂梁中，在加载前的一条斜直线KK 在加载过程中所发生的变化是（）A ．成为一条曲线；B ．平移；C ．绕KK 中点转动；D ．平移与绕KK 中点转动的合成。

2、内外径比值05d /D .=的空心圆轴受扭转，若将内外径都减小到原尺寸的一半，同时将轴的长度增加一倍，则圆轴的抗扭刚度会变成原来的（）A ．21；B ．41；C ．81；D ．161。

3、把直径为d =1mm 的钢丝绕在直径为2m 的卷筒上，若钢丝的许用应力][σ=200Mpa ，E =200Gpa ，则钢丝中产生的最大应力和钢丝直径最大应为：（）A.max σ=500MPa ，max d =4mm ； B.max σ=100MPa ，max d =2mm ；C.max σ=200GPa ，max d =0.001mm ；D.max σ=100GPa ，max d =3mm 。

4、图示等载面直杆的抗拉刚度为EA ，则其应变能为：()A.()25/6U F l EA =； B.()23/2U F l EA =；C.()29/4U F l EA =；D.()213/4U F l EA =。

二、填空题（每题4分，共16分）1、图示在拉力F 作用下的螺栓，已知材料的剪切许用应力[]τ是拉伸许用应力[]的0.6倍。

则螺栓直径d 和螺栓头高度h 的合理比值是①。

2、螺栓受轴向的最大拉力F max =6kN ，最小拉力F min =5kN 作用；螺栓直径d =12mm ，则其交变应力的循环特征r ＝②，应力幅值a σ＝③MPa ，平均应力m σ＝④MPa 。

3、已知图（a ）所示梁C 截面的转角()2/8c Fl EI θ=，则图（b ）所示梁B 截面的挠度为⑤。

4、图示梁的A、B、C、D 四点中，单向应力状态的点是⑥，纯剪应力状态的点是⑦，在任何截面上应力均为零的点是⑧。

l图图11 所示桁架的杆1、的轴力。

a /3a /3a /3图12分）用力法计算图所示刚架，并作出弯矩图和剪力图。

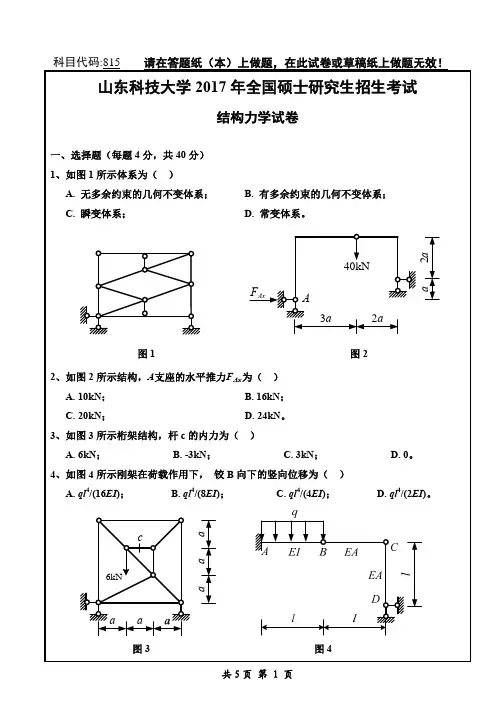
已知A =1.5ABCllEIEIF PEAD图13图15D.常变体系。

图1图2、如图2所示结构，杆1的轴力FF P； B.-2F P；F P/2； D.-1.12F P。

、如图3所示结构，当其高度h增加时，水平支座反力F Ax（）A.增大；B.减少；C.不变；D.不确定。

图3图44、如图4所示结构，在给定荷载作用下，BA为（）A．F P l；B．F P l/2；C．F P l/4；D．F P l/8。

5、机动法作静定梁影响线应用的原理为（）A.变形条件；B.平衡条件；C.虚功原理；D.叠加原理。

C.0.05rad；D.0.06rad。

图5图66所示结构，可视为多余约束的三根链杆是（）、6、7； B.3、6、8；6、7； D.5、6、7。

7所示结构，梁式杆EI=常数，桁架杆常数，杆AB的轴力为（）拉力； B.压力；零； D.无法确定。

图7图8、如图8所示结构，截面C的剪力影响线在处的竖标y E的绝对值为（）A.1；B.l；0.5； D.0.5l。

二、填空题（共20分，每题4分）、如图9所示体系的计算自由度W=①。

、用力法计算图10所示结构时，取A、B支座反力为基本未知量：X1，X2。

当EI1增大时，力法方程中∆1P②。

（填不变、增大或减小）图9图103、如图11所示结构，已知I1/I2=K，则|M AB|/|M DC|=③。

4、如图12所示结构，已知力偶矩M=16kN·m，则杆端弯矩M DA=④。

（顺时针为正）图11图125、如图13所示结构，各杆EI=常数，忽略杆件轴向变形，M CA=⑤。

图13图14三、计算题（共100分，每题20分）1、如图14所示刚架，忽略杆件轴向变形。

绘制刚架的剪力图，并求C点的竖向位移ΔC V。

2、如图15所示桁架，计算指定杆件1、2、3的轴力。

山东科技大学805弹性力学2004--2019年考研真题
一、概念题（每题10分，共40分）
1、简述弹性力学基本假定中小变形假定有何意义？
2、检验弹性力学问题中应力分量是否为正确解答的条件有哪些？
3、何谓最小势能原理，基于这一原理的两种近似解法是什么？
4、满足什么条件的位移是几何可能的位移，它与真实的位移有何不同？
二、写出下列问题边界条件（固定边界不写）（共20分）
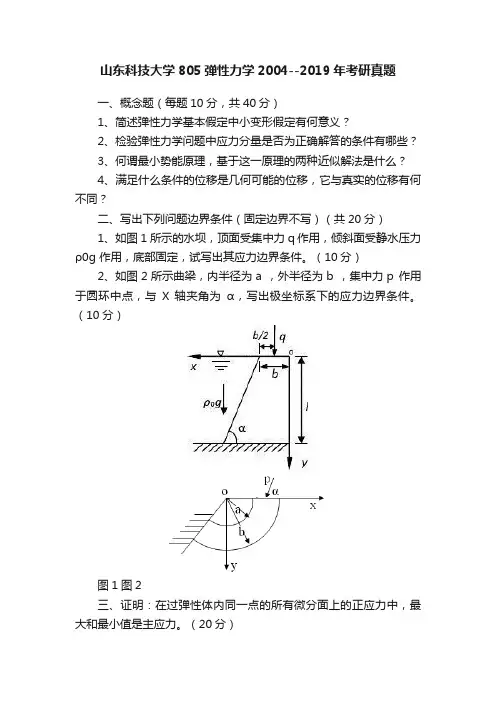
1、如图1所示的水坝，顶面受集中力q 作用，倾斜面受静水压力ρ0g 作用，底部固定，试写出其应力边界条件。

（10分）
2、如图2所示曲梁，内半径为a ，外半径为b ，集中力p 作用于圆环中点，与X 轴夹角为α，写出极坐标系下的应力边界条件。

（10分）
图1图2
三、证明：在过弹性体内同一点的所有微分面上的正应力中，最大和最小值是主应力。

（20分）
四、已知6个应变分量为x σ，y σ，z σ，xy τ，yz τ，zx τ，其中z yz zx σττ===0，试写出应力张量不变量，并导出主应力的公式。

（20分）
五、（20分）一圆截面杆件两端作用扭矩，如图3所示，其位移分量为c bz ay zy u +++-=θ，f dx ez zx v +-+=θ，k ey bx w +--=，设坐标原点O 位移固定，试按照下列转动位移边界条件分别确定待定系数a ,b ,c ,d ,e ,f 和k 。

（1）微分线段d z 在xOz 和yOz 平面内不能转动；（2）微分线段d x 和d y 在xOy 平面内不能转动。

，有一对渐开线标准外*20,1,*0.25,a h c ︒==齿宽B=50mm 第1页
F,试四、（15分）在图示的缓冲器中，若已知各楔块接触面间的磨擦系数f及弹簧的压力
s
求当楔块2、3被等速推开及等速恢复原位时力F的大小、该机构的效率以及此缓冲器正、反行程均不至发生自锁的条件。

α=︒，五、（15分）已知一对渐开线标准外啮合圆柱直齿轮传动的模数m=5mm，压力角20
中心距a=350mm，传动比i12=9/5，试求：①两轮的齿数；②小齿轮分度圆直径、齿顶圆直径、基圆直径、分度圆上的齿厚和齿槽宽；③小齿轮齿廓曲线在齿顶圆上的曲率半径和齿顶圆压力角。

六、（20分）在图示的变速传动轮系中，已知Z1=Z4=30,Z2=Z5=30,Z3=Z6=90，A、B为两个制动器，分别计算固定齿轮3时的传动比i1H和固定齿轮6时的传动比i1H。

第2页
分）已知凸轮以等角速度逆时针回转，基圆半径r0=20mm
δ=
时，推杆等加速等减速上升10mm；120
δ=︒︒时，推杆近休。

试以作图法设时，推杆等速回程10mm；300~360
计一个对心对动尖顶推杆盘形凸轮机构凸轮的轮廓曲线，并简述凸轮机构受到的冲击情况。

分）某内烯机的曲柄输出力距M d随曲柄转角ϕ的变化曲线如图所示，其运动周期。