5.2圆的对称性(1)课件ppt苏科版九年级上
- 格式:ppt
- 大小:1.52 MB
- 文档页数:17


圆的对称性学习目标1.理解圆的轴对称性和中心对称性;2.利用圆的旋转不变性,研究圆心角、弧、弦之间相互关系定理及其简单应用;3.通过观察、比较、操作、推理、归纳等活动,发展空间观念、推理能力及概括问题的。
重点难点重点中心对称性及相关性质难点运用圆心角、弧、弦之间的关系解决有关问题。
学生活动过程教师导学过程一、自主学习(独学)任务1:什么是中心对称图形?圆是中心对称图形吗?结论:圆是图形,是它的对称中心。
任务2:⑴在两张透明纸片上,分别作半径相等的⊙O和⊙'O;⑵在⊙O和⊙'O中,分别作相等的圆心角∠AOB、∠'''AO B,连接AB、''A B;⑶将两张纸片叠在一起,使⊙O与⊙O'重合(如图)⑷固定圆心,将其中一个圆旋转某个角度,使得OA与OA'重合。
在操作的过程中,你有什么发现。
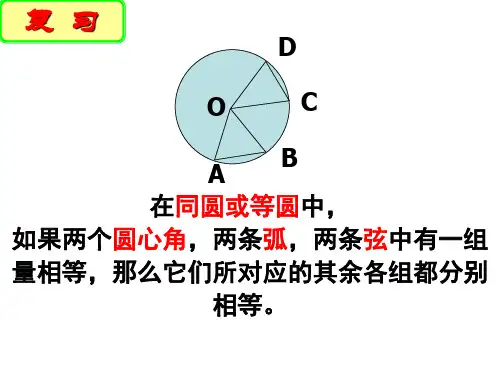
结论:在同圆或等圆中任务3:上面的命题反映了在同圆或等圆中,圆心角、弧、弦的关系,对于这三个量之间的关系,你还有什么思考?你有什么结论你能够用文字语言把你的发现表达出来吗?结论:在同圆或等圆中想一想:在上面的结论中,为什么一定要添加条件“在同圆或等圆中.......”?小检测:如图,已知⊙O、⊙O'半径相等,AB、CD分别是⊙O、⊙O'的两条弦填空:(1)若AB=CD,则,,;(2)若AB= CD,则,,;(3)若∠AOB=∠CO'D,则,,;任务4.在圆心角、弧、弦这三个量中,角的大小可以用度数刻画,弦的大小可以用长度刻画,那么如何来刻画弧的大小呢?结论:︵︵二、合作探究1.对学:任务1:什么是中心对称图形?圆是中心对称图形吗?任务4.在圆心角、弧、弦这三个量中,角的大小可以用度数刻画,弦的大小可以用长度刻画,那么如何来刻画弧的大小呢?2.群学:任务2:⑴在两张透明纸片上,分别作半径相等的⊙O和⊙'O;⑵在⊙O和⊙'O中,分别作相等的圆心角∠AOB、∠'''AO B,连接AB、''A B⑶将两张纸片叠在一起,使⊙O与⊙O'重合⑷固定圆心,将其中一个圆旋转某个角度,使得OA与OA'重合。






5.2圆的对称性(1)教案备课时间: 主备人:一、学习目标:1、经历探索圆的中心对称性及有关性质的过程2、理解圆的中心对称性及有关性质3、会运用圆心角、弧、弦之间的关系解决有关问题 重点:理解圆的中心对称性及有关性质难点:运用圆心角、弧、弦之间的关系解决有关问题 二、知识准备:1、什么是中心对称图形?2、我们采用什么方法研究中心对称图形? 三、学习内容:1、按照下列步骤进行小组活动:⑴在两张透明纸片上,分别作半径相等的⊙O 和⊙O '⑵在⊙O 和⊙O '中,分别作相等的圆心角∠AOB 、∠'''B O A ,连接AB 、''B A ⑶将两张纸片叠在一起,使⊙O 与⊙O '重合(如图)⑷固定圆心,将其中一个圆旋转某个角度,使得OA 与OA '重合 在操作的过程中,你有什么发现,请与小组同学交流 _______________________________________________2、上面的命题反映了在同圆或等圆中,圆心角、弧、弦的关系,对于这三个量之间的关系,你还有什么思考?请与小组同学交流.你能够用文字语言把你的发现表达出来吗? 3、圆心角、弧、弦之间的关系:在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等4、试一试:如图,已知⊙O 、⊙O '半径相等,AB 、CD 分别是⊙O 、⊙O '的两条弦填空:(1)若AB=CD ,则 ,(2)若AB= CD ,则 ,(3',则 ,5么如何来刻画弧的大小呢?’’C ︵ ︵弧的大小:圆心角的度数与它所对的弧的度数相等例1、如图,AB、AC、BC都是⊙O的弦,∠AOC=∠BOC∠ABC与∠BAC相等吗?为什么?例题2、已知:如图,AB是⊙O的直径,点C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AE=BF,AC与BD相等吗?为什么?四、知识梳理:1、在同圆或等圆中,如果两个圆心角、两条弧、两条弦中有一组量相等,那么它们所对应的其余各组量都分别相等;2、圆心角的度数与它所对的弧的度数相等。
