双逻辑斯蒂曲线拟合 python

逻辑斯蒂回归是一种常用的分类算法，用于将数据分为两个或多个类别。

在二分类问题中，逻辑斯蒂回归可以用于对数据进行二分，然后根据概率来确定新样本属于哪一类。

然而，在多分类问题中，逻辑斯蒂回归的应用相对复杂一些。

本文将讨论Python中逻辑斯蒂回归的多分类问题。

二、逻辑斯蒂回归的多分类问题1. 二分类问题的逻辑斯蒂回归在二分类问题中，逻辑斯蒂回归通过计算样本属于某一类的概率来进行分类。

具体来说，逻辑斯蒂回归使用sigmoid函数将线性函数的输出转换为概率值，然后根据概率值进行分类。

这种方法在二分类问题中表现良好，并且在Python中有很多成熟的库可以直接调用。

2. 多分类问题的逻辑斯蒂回归在多分类问题中，逻辑斯蒂回归的思想是类似的，但实现起来相对复杂一些。

常见的方法有一对多（One-vs-Rest）和一对一（One-vs-One）两种。

三、Python中逻辑斯蒂回归多分类的实现1. 使用sklearn库进行多分类逻辑斯蒂回归在Python中，sklearn库提供了方便易用的多分类逻辑斯蒂回归接口。

通过调用库中的相关函数，可以很方便地实现逻辑斯蒂回归的多2. 使用TensorFlow进行多分类逻辑斯蒂回归TensorFlow是一个强大的机器学习框架，可以用于实现逻辑斯蒂回归的多分类问题。

通过构建神经网络模型，可以实现复杂的多分类问题。

四、案例分析1. 使用sklearn库进行多分类逻辑斯蒂回归的案例以某个实际的数据集为例，我们可以使用sklearn库中的多分类逻辑斯蒂回归模型，对数据进行处理和训练，并进行预测和评估。

2. 使用TensorFlow进行多分类逻辑斯蒂回归的案例以同样的数据集为例，我们可以使用TensorFlow构建多分类逻辑斯蒂回归模型，训练和测试模型，并与sklearn库的结果进行对比分析。

五、总结多分类逻辑斯蒂回归在Python中有多种实现方法，可以根据实际情况选择合适的工具和方法。

在实际应用中，需要充分了解不同方法的特点和适用场景，以便选择合适的方案。

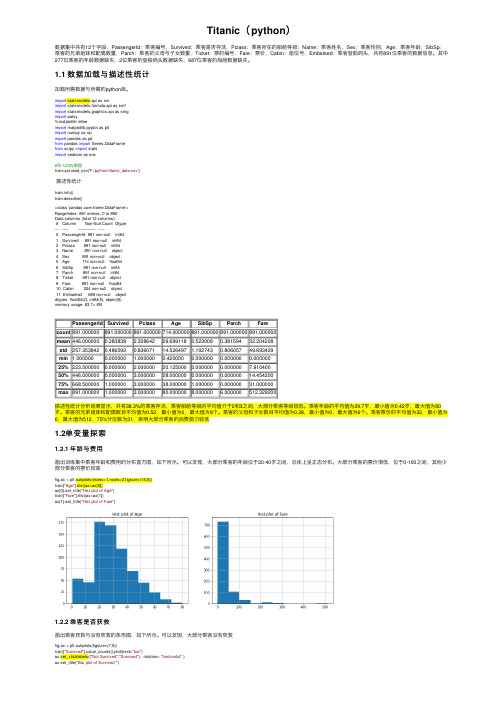
Titanic（python）数据集中共有12个字段，PassengerId：乘客编号，Survived：乘客是否存活，Pclass：乘客所在的船舱等级；Name：乘客姓名，Sex：乘客性别，Age：乘客年龄，SibSp：乘客的兄弟姐妹和配偶数量，Parch：乘客的⽗母与⼦⼥数量，Ticket：票的编号，Fare：票价，Cabin：座位号，Embarked：乘客登船码头，共有891位乘客的数据信息。

其中277位乘客的年龄数据缺失，2位乘客的登船码头数据缺失，687位乘客的船舱数据缺失。

1.1 数据加载与描述性统计加载所需数据与所需的python库。

import statsmodels.api as smimport statsmodels.formula.api as smfimport statsmodels.graphics.api as smgimport patsy%matplotlib inlineimport matplotlib.pyplot as pltimport numpy as npimport pandas as pdfrom pandas import Series,DataFramefrom scipy import statsimport seaborn as sns#导⼊CSV数据train=pd.read_csv('F:/python/titanic_data.csv')描述性统计()train.describe()<class 'pandas.core.frame.DataFrame'>RangeIndex: 891 entries, 0 to 890Data columns (total 12 columns):# Column Non-Null Count Dtype--- ------ -------------- -----0 PassengerId 891 non-null int641 Survived 891 non-null int642 Pclass 891 non-null int643 Name 891 non-null object4 Sex 891 non-null object5 Age 714 non-null float646 SibSp 891 non-null int647 Parch 891 non-null int648 Ticket 891 non-null object9 Fare 891 non-null float6410 Cabin 204 non-null object11 Embarked 889 non-null objectdtypes: float64(2), int64(5), object(5)memory usage: 83.7+ KBPassengerId Survived Pclass Age SibSp Parch Farecount891.000000891.000000891.000000714.000000891.000000891.000000891.000000mean446.0000000.383838 2.30864229.6991180.5230080.38159432.204208std257.3538420.4865920.83607114.526497 1.1027430.80605749.693429min 1.0000000.000000 1.0000000.4200000.0000000.0000000.00000025%223.5000000.000000 2.00000020.1250000.0000000.0000007.91040050%446.0000000.000000 3.00000028.0000000.0000000.00000014.45420075%668.500000 1.000000 3.00000038.000000 1.0000000.00000031.000000max891.000000 1.000000 3.00000080.0000008.000000 6.000000512.329200描述性统计分析结果显⽰，共有38.3%的乘客存活，乘客船舱等级的平均值介于2和3之间，⼤部分乘客等级较低。

logistic 函数程序一、logistic 函数的定义与特性1.逻辑斯蒂函数的定义逻辑斯蒂函数（logistic function）是一种非线性函数，其定义如下：f(x) = 1 / (1 + exp(-αx + β))其中，α和β 是参数，exp 是自然对数的底（约等于2.71828）。

2.逻辑斯蒂函数的图像特征逻辑斯蒂函数的图像具有以下特点：- 当x 趋近于负无穷时，f(x) 趋近于0；- 当x 趋近于正无穷时，f(x) 趋近于1；- f(x) 的图像关于直线x = β 对称；- f(x) 的图像在x = β 处取得最小值，最小值为1/2；- f(x) 的图像在x 轴上方部分为凸函数，下方部分为凹函数。

3.逻辑斯蒂函数的应用场景逻辑斯蒂函数在以下场景中有广泛应用：- 生物种群数量模型；- 神经网络中的激活函数；- 机器学习中的分类与回归问题。

二、logistic 函数在编程中的实现1.Python中的logistic函数库在Python中，可以使用scipy库中的sigmoid函数来实现logistic函数：```pythonfrom scipy.special import expitdef logistic_function(x, alpha, beta):return expit(alpha * x + beta)```2.其他编程语言中的logistic函数实现在其他编程语言中，可以通过类似的公式实现logistic函数。

例如，在Java中：```javapublic class LogisticFunction {public static double logistic(double x, double alpha, double beta) {return Math.exp(alpha * x + beta) / (1 + Math.exp(alpha * x + beta));}}```三、logistic 函数的参数调节与优化1.参数α的影响α控制着logistic函数的曲率，α越大，曲率越小，函数越平缓。

在Python中，常用的曲线拟合方法主要有以下几种：1. **Numpy的polyfit函数**：这是一个用于进行多项式拟合的函数，可以方便地拟合出一条曲线。

```pythonimport numpy as npx = np.array([0, 1, 2, 3, 4, 5])y = np.array([0, 0.8, 0.9, 0.1, -0.8, -1])# 使用numpy的polyfit进行拟合，这里我们选择2次多项式coeffs = np.polyfit(x, y, 2)# 打印出拟合后的曲线方程的系数print(coeffs)```2. **SciPy库的curve_fit函数**：这个函数是用于拟合用户自定义函数或者SciPy内置函数的。

相对于numpy的polyfit，它更加灵活，可以拟合更复杂的函数形式。

```pythonfrom scipy.optimize import curve_fitimport numpy as np# 定义一个自定义的函数形式，例如一个正弦函数def func(x, a, b, c):return a * np.sin(b * x) + c# 初始化参数的初始猜测值p0 = [1.0, 1.0, 1.0]# 使用curve_fit进行拟合params, params_covariance = curve_fit(func, x, y, p0)# 打印出拟合后的参数值print(params)```3. **Scikit-learn库的LinearRegression**：这是用于线性回归的函数，可以方便地进行线性拟合。

如果需要更复杂的模型，可以使用其他回归函数，如PolynomialRegression（多项式回归）、Ridge（岭回归）、Lasso（套索回归）等。

```pythonfrom sklearn.linear_model import LinearRegression# 使用LinearRegression进行拟合model = LinearRegression()model.fit(x, y)# 打印出拟合后的斜率和截距print(model.coef_) # 斜率print(model.intercept_) # 截距```以上就是Python中进行曲线拟合的一些常用方法。

python参数曲线拟合摘要：1.曲线拟合简介2.Python 参数曲线拟合方法3.示例：使用Python 进行曲线拟合4.结论正文：曲线拟合是数据分析中的一种重要技术，用于在数据集上找到最佳拟合函数，该函数可以表示数据之间的关系。

在Python 中，有多种方法可以实现曲线拟合，包括使用内置函数、第三方库等。

Python 参数曲线拟合方法主要包括以下几种：1.使用scipy.optimize 库中的curve_fit 函数。

这个函数可以用于拟合任意给定数据点的函数，包括线性、多项式、指数等。

curve_fit 函数接受两个参数：需要拟合的数据点坐标和拟合函数。

例如，拟合一个线性函数y = a * x + b，可以通过以下代码实现：```pythonfrom scipy.optimize import curve_fitimport numpy as npxdata = np.array([0, 1, 2, 3, 4, 5])ydata = np.array([0, 1, 4, 9, 16, 25])popt, pcov = curve_fit(lambda x, a, b: a * x + b, xdata, ydata)print(popt) # 输出：[1.2.]print(pcov) # 输出：[[ 0.00000000e+00 0.00000000e+00][ 0.00000000e+00 9.99999999e-01]] ```2.使用scikit-learn 库中的PolynomialFeatures 和LinearRegression。

这个方法可以用于拟合多项式函数，例如y = a * x^2 + b * x + c。

首先，需要安装scikit-learn 库，然后通过以下代码进行拟合：```pythonfrom sklearn.linear_model import LinearRegressionfrom sklearn.preprocessing import PolynomialFeaturesx_data = np.array([0, 1, 2, 3, 4, 5])y_data = np.array([0, 1, 4, 9, 16, 25])poly = PolynomialFeatures(degree=2, include_bias=False)x_data_poly = poly.fit_transform(x_data.reshape(-1, 1))model = LinearRegression()model.fit(x_data_poly, y_data)print(model.coef_) # 输出：[0.1.2.]print(model.intercept_) # 输出：0.0```3.使用matplotlib 库绘制拟合曲线。

一、概述在数据分析和机器学习中，经常会遇到对一组数据进行拟合曲线的需求。

而多项式函数在拟合曲线中有着广泛的应用，其中Python作为一种流行的编程语言，拥有强大的数学计算能力，为我们提供了多种方法来进行多项式函数的拟合。

本文将介绍如何使用Python进行多项式函数的拟合，让我们深入探讨这一有趣而又实用的主题。

二、多项式函数的概念及应用多项式函数是一种常见的数学函数形式，其表达式为f(x) = a0 + a1x + a2x^2 + ... + anx^n，其中a0, a1,..., an为多项式的系数。

多项式函数可以用来拟合各种类型的数据，从简单的二次函数到高阶的多项式函数都可以被用来逼近实际数据分布。

在实际应用中，多项式函数的拟合能够帮助我们理解数据的趋势和规律，同时也能够用于预测未来的数据走势，因此在数据分析和机器学习领域有着广泛的应用。

三、Python中的多项式函数拟合Python作为一种功能强大的编程语言，提供了多种方法来进行多项式函数的拟合。

以下将介绍使用Numpy和Scipy两个库来进行多项式函数的拟合。

1. Numpy库Numpy是Python中用于数值计算的一个重要库，它提供了多种工具和函数来进行数组操作和数学计算。

在Numpy中，我们可以使用polyfit()函数来进行多项式函数的拟合。

其用法为np.polyfit(x, y, deg)，其中x为自变量的取值，y为因变量的取值，deg为要拟合的多项式的阶数。

通过调用polyfit()函数，我们可以得到多项式的系数，从而得到拟合曲线。

2. Scipy库Scipy是Python中用于科学计算的一个库，提供了许多数学、科学和工程计算中常用的函数和工具。

在Scipy中，我们可以使用polyfit()函数来进行多项式函数的拟合，其用法与Numpy中的polyfit()函数类似。

Scipy还提供了curve_fit()函数来进行非线性拟合，通过传入自定义的多项式函数及初始参数，可以得到更加灵活和准确的拟合结果。

逻辑斯蒂回归代码逻辑斯蒂回归是基于逻辑斯蒂函数的二分类算法，可以用于预测某个事件发生的概率。

而逻辑斯蒂回归的代码实现也并不复杂，下面就介绍一下逻辑斯蒂回归代码的实现方法。

1. 数据集的准备首先需要准备一个用于训练和测试的数据集，其中包含了特征和相应的分类标签。

可以使用Python中的Pandas库来处理数据集。

下面展示了一个简单的数据集的准备代码：``` pythonimport pandas as pddataset = pd.read_csv("dataset.csv")X = dataset.iloc[:, :-1].valuesy = dataset.iloc[:, -1].values```其中，X变量包含了特征信息，y变量则包含了分类标签。

这样就可以开始训练了。

2. 创建逻辑斯蒂回归模型使用Python中的Scikit-Learn库来训练逻辑斯蒂回归模型。

下面展示了基本的模型创建代码：``` pythonfrom sklearn.linear_model import LogisticRegressionclf = LogisticRegression()clf.fit(X_train, y_train)```其中，clf是逻辑斯蒂回归模型的对象。

使用fit()方法来对模型进行训练，传入的参数为训练数据集X_train和标签y_train。

3. 测试模型的准确性训练完模型之后，需要对模型进行测试，以检验模型的准确性。

下面是测试代码：``` pythony_pred = clf.predict(X_test)from sklearn.metrics import accuracy_scoreaccuracy = accuracy_score(y_test, y_pred)print("Accuracy:", accuracy)```其中，y_pred为模型对测试集进行预测的结果，accuracy_score()函数用于计算预测和实际分类之间的准确性比较得分。

一、背景介绍1.1 Python在数据分析领域的应用1.2 指数曲线拟合在数据预测中的重要性二、指数曲线拟合的基本原理2.1 指数曲线的表达式及特点2.2 最小二乘法在指数曲线拟合中的应用三、Python中的指数曲线拟合方法3.1 使用SciPy库进行指数曲线拟合3.2 使用NumPy库进行指数曲线拟合四、实例分析4.1 选择合适的数据集4.2 数据预处理4.3 完成指数曲线拟合4.4 结果展示及分析五、指数曲线拟合在实际应用中的意义5.1 预测和趋势分析5.2 数据挖掘和商业决策支持六、总结与展望6.1 总结指数曲线拟合的优势和局限性6.2 展望指数曲线拟合在未来的发展方向七、参考文献Python 多种指数曲线拟合一、背景介绍1.1 Python在数据分析领域的应用随着大数据时代的到来，数据分析和挖掘在各个领域中的应用愈发广泛。

Python作为一种简单易学、功能强大的编程语言，被广泛应用于数据分析领域。

其丰富的数据处理库和科学计算库，使得Python成为数据分析和挖掘的重要工具之一。

1.2 指数曲线拟合在数据预测中的重要性指数曲线拟合是一种常用的数据拟合方法，它可用于描述一些数据集合的增长或衰减趋势。

在实际应用中，我们经常需要利用已有的数据来预测未来的趋势，指数曲线拟合可以较好地完成这一任务。

掌握Python中的指数曲线拟合方法对于进行数据预测具有重要意义。

二、指数曲线拟合的基本原理2.1 指数曲线的表达式及特点指数曲线的一般表达式为： y = a * exp(b * x) + c，其中a、b、c为拟合参数，exp为自然对数的底数e的指数函数。

指数曲线具有自变量的指数幂函数形式，在描述一些增长或衰减的数据时具有较好的拟合效果。

2.2 最小二乘法在指数曲线拟合中的应用在进行指数曲线拟合时，常常需要使用最小二乘法来确定拟合参数。

最小二乘法是一种通过使得实际观测值与拟合值的残差平方和最小来确定参数的优化方法，对于拟合过程具有重要的意义。

python拟合曲线求方程Python是一种高级编程语言，其具有强大的科学计算和数据分析功能。

在Python中，使用NumPy和SciPy等库可以进行拟合曲线求方程的操作。

1. 数据准备首先需要准备数据，以便进行拟合曲线求方程的操作。

可以使用Python中的NumPy库生成随机数据或导入外部数据文件。

例如，下面是一个生成随机数据的示例代码：```import numpy as np# 生成x轴数据x = np.linspace(0, 10, 100)# 生成y轴数据y = 2 * x + 1 + np.random.randn(100) * 0.5```上述代码中，使用`np.linspace()`函数生成了一个包含100个元素、范围为0到10的一维数组作为x轴数据；使用`2 * x + 1`生成了理想情况下的y轴数据，并加入了一些随机噪声。

2. 拟合曲线接下来需要使用Python中的SciPy库进行拟合曲线操作。

SciPy提供了多种拟合曲线函数，如多项式拟合、指数拟合、对数拟合等等。

这里以多项式拟合为例。

```from scipy.optimize import curve_fit# 定义多项式函数def func(x, a, b, c):return a * x ** 2 + b * x + c# 拟合曲线popt, pcov = curve_fit(func, x, y)# 输出拟合结果print(popt)```上述代码中，使用`curve_fit()`函数对数据进行拟合，其中第一个参数是拟合函数，第二个参数是x轴数据，第三个参数是y轴数据。

在这里定义了一个二次多项式函数，并将其作为拟合函数传入`curve_fit()`函数中。

`popt`和`pcov`分别是拟合系数和协方差矩阵。

3. 输出结果最后需要将拟合结果输出。

可以将拟合曲线绘制出来，并输出方程式。

```import matplotlib.pyplot as plt# 绘制原始数据plt.scatter(x, y)# 绘制拟合曲线plt.plot(x, func(x, *popt), 'r-', label='fit')# 输出方程式print('y = %.2f * x^2 + %.2f * x + %.2f' % tuple(popt))# 显示图像plt.show()```上述代码中，使用Matplotlib库绘制了原始数据和拟合曲线，并输出了方程式。

Python曲线拟合计算曲率引言在科学研究和工程领域中，曲线拟合和曲率计算是常见的任务。

本文将介绍使用P yt ho n进行曲线拟合和计算曲率的方法。

1.什么是曲线拟合？曲线拟合是指根据一组给定的数据点，通过适当的数学模型来拟合并生成一条曲线，以近似表示这组数据点的特征和趋势。

2.曲线拟合的常用方法2.1多项式拟合多项式拟合是指使用多项式函数来拟合数据点。

通过调整多项式的阶数，可以得到更高阶的拟合曲线，从而更好地适应数据点。

2.2最小二乘拟合最小二乘拟合是指通过最小化实际数据点与拟合曲线的误差平方和来确定拟合曲线的参数。

它可以应用于各种拟合问题，并且在数学上有明确的解析解。

2.3样条曲线拟合样条曲线拟合是指使用一系列小段连续的多项式函数来逼近给定的数据点。

样条曲线具有较好的平滑性和适应性，可以更好地处理数据中的噪声和不规则性。

3. Py thon中的曲线拟合3.1使用N u m p y库进行多项式拟合N u mp y库是P yt ho n中用于科学计算的核心库之一，它提供了多项式拟合的功能。

通过调用`nu mp y.po ly fi t`函数，可以实现对一组数据点的多项式拟合。

3.2使用S c i p y库进行最小二乘拟合S c ip y库是一个开源的P yt ho n科学计算库，其中拥有丰富的拟合函数。

通过调用`s ci py.op ti mi ze.c ur ve_f it`函数，可以进行最小二乘拟合，并得到拟合曲线的参数。

3.3使用S c i p y库进行样条曲线拟合S c ipy库中的`sc ipy.in te rp ol at e`模块提供了样条曲线拟合的功能。

通过调用`s ci py.i nt e rp ol at e.sp lr ep`和`s ci py.i nt er po lat e.s pl ev`函数，可以实现对数据点的样条曲线拟合。

4.曲线拟合后的曲率计算曲率是指曲线弯曲程度的度量，计算曲率有助于理解曲线形状的变化。