2018阿式圆完整版

中考数学最值——阿氏圆问题（点在圆上运动）（PA+k·PB型最值）【问题背景】与两个定点距离之比为一个不为0的常数的点的轨迹是一个圆，这个圆为阿氏圆。

这个定理叫阿波罗尼斯定理。

【知识储备】①三角形三边关系：两边之和大于第三边；两边之差小于第三边。

②两点之间线段最短。

③连接直线外一点和直线上各点的所有线段中，垂线段最短。

【模型分析】①条件：已知A、B为定点，P为 O上一动点，OPOB=k（0＜k＜1）。

②问题：P在何处时，PA+k·PB的值最小。

③方法：连接OP，OB，在OB上取点C，使OCOP =k，可得△POC∽△BOP，所以CPPB=OPOB=k，所以得CP=k·PB。

所以PA+k·PB=PA+CP≥AC，当P为AC与 O的交点时，PA+k·PB的最小值为AC。

总结：构造母子三角形相似若能直接构造△相似计算的，直接计算，不能直接构造△相似计算的，先把k提到括号外边，将其中一条线段的系数化成，再构造△相似进行计算。

【经典例题】已知∠ACB=90°，CB=4,CA=6，⊙C半径为2，P为圆上一动点.（1）求12AP BP+的最小值为。

（2）求13AP BP+的最小值为。

【巩固训练】练习1：如图，点A、B在⊙O 上，且OA=OB=6，且OA⊥OB，点C是OA的中点，点D在OB 上，且OD=4，动点P在⊙O 上，则2PC+PD的最小值为；练习2：如图，在Rt△ABC中，∠ACB=90°，D为AC的中点，M为BD的中点，将线段AD绕A点任意旋转（旋转过程中始终保持点M为BD的中点），若AC=4，BC=3，那么在旋转过程中，线段CM长度的取值范围是__________。

练习3：Rt △ABC 中，∠ACB=90°，AC=4，BC=3，点D 为△ABC 内一动点，满足CD=2，则AD+32BD 的最小值为_______.练习4：如图，菱形ABCD 的边长为2，锐角大小为60°，⊙A 与BC 相切于点E ，在⊙A 上任取一点P ，则PB+23PD 的最小值为________.练习5：如图，已知菱形ABCD 的边长为4，∠B=60°，圆B 的半径为2，P 为圆B 上一动点，则PD+21PC 的最小值为_________.练习6：如图，等边△ABC 的边长为6，内切圆记为⊙O ，P 是圆上动点，求2PB+PC 的最小值.值。

专题2.6 阿氏圆阿氏圆问题问题：求解“AP nPB+”类加权线段和最小值方法：①定：定系数，并确定是半径和哪条线段的比值②造：根据线段比，构造母子型相似③算：根据母子型结论，计算定点位置④转：“AP nPB+”问题+”转化为“AP PM关键：①可解性：半径长与圆心到加权线段中定点距离比等于加权系数②系数小于1：内部构造母子型③系数大于1：外部构造母子型【典例1】阅读以下材料，并按要求完成相应的任务．已知平面上两点A、B，则所有符合＝k（k＞0且k≠1）的点P会组成一个圆．这个结论最先由古希腊数学家阿波罗尼斯发现，称阿氏圆．阿氏圆基本解法：构造三角形相似．【问题】如图1，在平面直角坐标系中，在x轴，y轴上分别有点C（m，0），D（0，n），点P是平面内一动点，且OP＝r，设＝k，求PC+kPD的最小值．阿氏圆的关键解题步骤：第一步：如图1，在OD上取点M，使得OM：OP＝OP：OD＝k；第二步：证明kPD＝PM；第三步：连接CM，此时CM即为所求的最小值．下面是该题的解答过程（部分）：解：在OD上取点M，使得OM：OP＝OP：OD＝k，又∵∠POD＝∠MOP，∴△POM∽△DOP．任务：（1）将以上解答过程补充完整．（2）如图2，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，D为△ABC内一动点，满足CD＝2，利用（1）中的结论，请直接写出AD+BD的最小值．【变式1-1】如图，在Rt△ABC中，∠ABC＝90°，AB＝6，BC＝9，⊙B的半径为3，点P是⊙B上一点，连接AP，CP，则AP+CP的最小值为．【变式1-2】如图，在Rt△ABC中，∠ACB＝90°，CB＝4，CA＝6，⊙C半径为2，P为圆上一动点，连接AP，BP，则AP+BP的最小值为（）A．B．6 C．2 D．4【变式1-3】如图，在正方形ABCD中．AB＝8，点P是正方形ABCD内部的一点，且满足BP＝4，则PD+PC的最小值是（）A．6 B．8 C．10 D．12【变式1-4】如图，已知抛物线y＝﹣x2+x+3与x轴交于A，B两点（A在点B的左侧），与y轴交于点C，⊙O与x轴交于点E（2，0），点P是⊙O上一点，连接CP，BP，求BP+CP的最小值．【变式1-5】（西峡县期末）如图，在△ABC中，∠A＝90°，AB＝AC＝4，点E、F分别是边AB、AC的中点，点P是以A为圆心、以AE为半径的圆弧上的动点，则的最小值等于（）A．4B．C．D．【变式1-6】（2022春•长顺县月考）如图，在Rt△ABC中，∠ACB＝90°，AC ＝6，BC＝8，D、E分别是边BC、AC上的两个动点，且DE＝4，P是DE的中点，连接P A，PB，则P A+PB的最小值为．【变式1-7】（龙凤区期末）如图，在Rt△ABC中，∠C＝90°，AC＝9，BC＝4，以点C为圆心，3为半径做⊙C，分别交AC，BC于D，E两点，点P是⊙C上一个动点，则P A+PB的最小值为．【变式1-8】如图，在Rt△ABC中，∠ACB＝90°，AC＝4，BC＝3，点D为△ABC内一动点，且满足CD＝2，则AD+BD的最小值为．【变式1-9】如图，正方形ABCD的边长为4，E为BC的中点，以B为圆心，BE为半径作⊙B，点P是⊙B上一动点，连接PD、PC，则PD+PC的最小值为．【典例2】如图，在扇形AOB中，∠AOB＝90°，OA＝4，C，D分别为OA，OB的中点，点P是上一点，则2PC+PD的最小值为．【变式2-1】如图，在扇形COD中，∠COD＝90°，OC＝3，点A是OC中点，OB ＝2，点P是为CD上一点，则PB+2PA的最小值为．【变式2-2】（梁溪区校级期中）如图，⊙O与y轴、x轴的正半轴分别相交于点M、点N，⊙O半径为3，点A（0，1），点B（2，0），点P在弧MN上移动，连接P A，PB，则3P A+PB的最小值为．【变式2-3】（溧阳市一模）如图，在⊙O中，点A、点B在⊙O上，∠AOB＝90°，OA＝6，点C在OA上，且OC＝2AC，点D是OB的中点，点M是劣弧AB上的动点，则CM+2DM的最小值为．【变式2-4】如图，边长为4的正方形，内切圆记为圆O，P为圆O上一动点，则P A+PB的最小值为．。

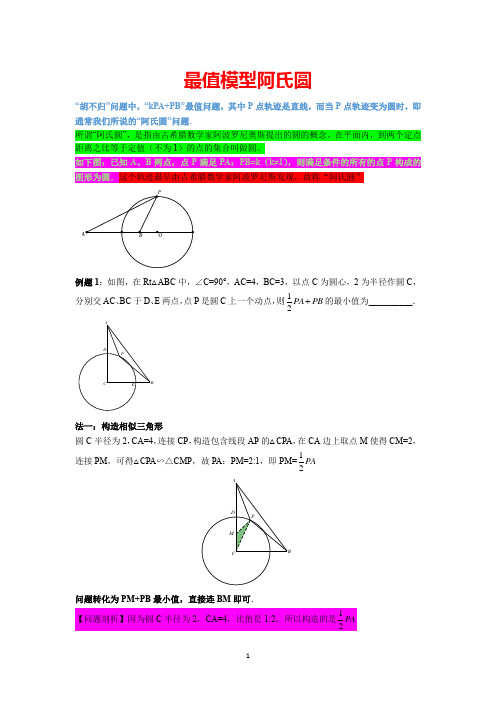
最值模型阿氏圆“胡不归”问题中，“kPA+PB”最值问题，其中P 点轨迹是直线，而当P 点轨迹变为圆时，即通常我们所说的“阿氏圆”问题．所谓“阿氏圆”，是指由古希腊数学家阿波罗尼奥斯提出的圆的概念。

在平面内，到两个定点距离之比等于定值（不为1）的点的集合叫做圆。

如下图：已知A 、B 两点，点P 满足PA ：PB=k （k≠1），则满足条件的所有的点P 构成的图形为圆．这个轨迹最早由古希腊数学家阿波罗尼斯发现，故称“阿氏圆”例题1：如图，在Rt △ABC 中，∠C=90°，AC=4，BC=3，以点C 为圆心，2为半径作圆C ，分别交AC 、BC 于D 、E 两点，点P 是圆C 上一个动点，则12PA PB 的最小值为__________．法一：构造相似三角形圆C 半径为2，CA=4，连接CP ，构造包含线段AP 的△CPA ，在CA 边上取点M 使得CM=2，连接PM ，可得△CPA ∽△CMP ，故PA ：PM=2:1，即PM=12PA问题转化为PM+PB 最小值，直接连BM 即可．EABC DP法二：阿氏圆模型P 点轨迹圆的圆心C 点和A 点在直线AC 上，故所求M 点在AC 边上，考虑到PM ：PA=1:2，例题2：如图 1 所示，⊙O 的半径为R ，点 A 、B 都在⊙O 外 ，P 为⊙O 上一动点，已知R=25OB ，连接 PA 、PB ，则当“PA+25PB ”的值最小时，P 点的位置如何确定？解决办法：如图2，在线段 OB 上截取OC 使 OC=25R ，△BPO ∽△PCO 则有25PB=PC 。

“PA+25PB ”的最小值可以转化为“PA+PC ”的最小值，其中与A 与C 为定点，P 为动点，故当 A 、P 、C 三点共线时，“PA+PC ”值最小。

问题转化为“PA+PC ”最小值，直接连AC 即可。

【技巧总结】计算PA k PB +的最小值时，利用两边成比例且夹角相等构造母子型相似三角形问题：在圆上找一点P 使得PA k PB +的值最小，解决步骤具体如下： 1. 如图，将系数不为1的线段两端点与圆心相连即OP ，OB2. 计算出这两条线段的长度比OPk OB = 3. 在OB 上取一点C ，使得OC k OP =，即构造△POM△△BOP ，则PCk PB=，PC k PB =4. 则=PA k PB PA PC AC ++≥，当A 、P 、C 三点共线时可得最小值。

阿氏圆知识点总结1. 定义和特点阿氏圆是一种特殊类型的圆，它可用来解决一些几何问题。

与普通的圆不同，阿氏圆的圆周上的任何一段圆弧都与圆心之外一点的连线成一个特定的恒定角度。

在阿氏圆内，存在两个特定的点，一个是内圆心，一个是外圆心。

这两个点与圆上的任意一点连成的线段呈现出恒定的夹角。

这些特点使得阿氏圆在数学和工程领域有着广泛的应用。

2. 阿氏圆的历史阿氏圆是由17世纪的意大利数学家乔万尼·贝尔努利所提出的。

他的研究成果被认为是建立了航空学的良好基础，为后来的飞行器设计和控制系统提供了有力支持。

阿氏圆之所以被命名为“阿氏”是因为乔万尼·贝尔努利的英文名是“Giovanni Alfonso”而被称为“Giovanni Alfonso”.3. 构造方法阿氏圆的构造方法有多种，其中最常见的是利用平行直线和圆相交的关系来构造。

具体方法如下：- Step 1：在平面上选择一条直线作为基准线。

- Step 2：在基准线上选择一个点作为内圆心。

- Step 3：从内圆心开始画一条半直线，使得它和基准线成一个特定的角度。

- Step 4：通过内圆心，将这条半直线上每一个点与基准线的交点作为初始圆上的一个点。

- Step 5：连接初始圆上的点和内圆心，得到阿氏圆。

4. 基本性质阿氏圆是一种精美的几何图形，它具有许多基本性质，其中最为重要的包括以下几点：- 周长和半径：由于阿氏圆上的任意一段弧都与外圆心的连线成一个特定的角度，因此，圆周上的每一小段都是等长的。

此外，阿氏圆的半径大小也是不固定的，但是半径越大，圆周上的弧长越大。

- 角度恒定性：阿氏圆上任何一条弧都与外圆心的连线成一个恒定的角度。

这个角度也被称为阿氏角，它在阿氏圆上是始终不变的。

5. 应用领域阿氏圆由于其独特的特点，被广泛应用于航空航天、船舶和汽车制造、导弹制导系统、机械制造等领域。

在飞机设计中，利用阿氏圆可精确控制机体的姿态，提高飞行性能和飞行安全。

阿氏圆定理（全称：阿波罗尼斯圆定理），具体的描述：一动点P到两定点A、B的距离之比等于定比m：n，则P点的轨迹，是以定比m：n内分和外分定线段AB的两个分点的连线为直径的圆．这个轨迹最先由古希腊数学家阿波罗尼斯发现，该圆称为阿波罗尼斯圆，简称阿氏圆．
定理读起来和理解起来比较枯燥，阿氏圆题型也就是大家经常见到的PA+KPB，（K≠1）p 点的运动轨迹是圆或者圆弧的题型。

初中数学解决阿氏圆问题，要熟练掌握母子型相似三角形的性质和构造方法。

构造母子三角形相似也就是解决阿氏圆题型的核心武器！
方法看起来复杂，其实核心就是构造母子三角形相似，也有人称之为美人鱼相似，不论怎样称呼，方法都是一样的那就是构造母子三角形相似！精髓就是母子三角形相似！
那么我们先来看一个阿氏圆题型的例题，结合视频讲解，加上自己的总结分析，相信大家看了本文的题型后，初中阿氏圆题型就可以踩在脚下了，也不枉小编辛苦整理一番苦心了！。

阿氏圆最值问题(超完整)一、定点在圆外--向圆内找点构造相似1.如图，在Rt ΔABC 中，∠ACB =90°，CB =7，AC =9，以C 为圆心、3为半径作⊙C ，P 为⊙C 上一动点，连接AP 、BP ，则13AP +BP 的最小值为( )A.7B.52C.4+10D.2132.如图，在ΔABC 中，BC =6，∠BAC =60°，则2AB +AC 的最大值为 ．3.【新知探究】新定义：平面内两定点A ，B ，所有满足PA PB=k (k 为定值)的P 点形成的图形是圆，我们把这种圆称之为“阿氏圆”【问题解决】如图，在ΔABC 中，CB =4，AB =2AC ，则ΔABC 面积的最大值为 ．4.如图，已知菱形ABCD 的边长为8，∠B =60°，圆B 的半径为4，点P 是圆B 上的一个动点，则PD -12PC 的最大值为 ．5.如图，正方形ABCD的边长为4，E为BC的中点，以B为圆心，BE为半径作⊙B，点P是⊙B上一动点，连接PD、PC，则PD+12PC的最小值为 ．6.如图所示的平面直角坐标系中，A(0,4)，B(4,0)，P是第一象限内一动点，OP=2，连接AP、BP，则BP+12AP的最小值是 ．7.如图，边长为4的正方形，内切圆记为圆O，P为圆O上一动点，则2PA+PB的最小值为 ．8.已知：等腰RtΔABC中，∠ACB=90°，AC=BC=8，O是AB上一点，以O为圆心的半圆与AC、BC均相切，P为半圆上一动点，连PC、PB，如图，则PC+22PB的最小值是 ．9.如图，在RtΔAOB中，∠AOB=90°，OA=3，OB=2，⊙O的半径为1，M为⊙O上一动点，求AM+12BM的最小值．10.如图，在RtΔABC中，∠ACB=90°，CB=4，CA=6，圆C的半径为2，点P为圆上一动点，连接AP，BP．求①AP+12BP；②2AP+BP；③13AP+BP；④AP+3BP的最小值．11.如图，在平面直角坐标系中，A(2,0)、B(0,2)、C(4,0)、D(3,2)，P是ΔAOB外部的第一象限内一动点，且∠BPA=135°，则2PD+PC的最小值是 ．12.如图，在平面直角坐标系xOy中，A(6,-1)，M(4,4)，以M为圆心，22为半径画圆，O为原点，P是⊙M上一动点，则PO+2PA的最小值为 ．二、定点在圆内--向外找点构造相似13.如图，⊙O与y轴、x轴的正半轴分别相交于点M、点N，⊙O半径为3，点A(0,1)，点B(2,0)，点P在弧MN上移动，连接PA，PB，则3PA+PB的最小值为 ．14.如图，在⊙O 中，点A 、点B 在⊙O 上，∠AOB =90°，OA =6，点C 在OA 上，且OC =2AC ，点D 是OB 的中点，点M 是劣弧AB 上的动点，则CM +2DM 的最小值为 ．15.如图，扇形AOB 中，∠AOB =90°，OA =6，C 是OA 的中点，D 是OB 上一点，OD =5，P 是AB上一动点，则PC +12PD 的最小值为 ．16.问题提出：如图1，在等边ΔABC 中，AB =12，⊙C 半径为6，P 为圆上一动点，连接AP ，BP ，求AP +12BP 的最小值．(1)尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP ，在CB 上取点D ，使CD=3，则有CD CP =CP CB=12，又∵∠PCD =∠BCP ，∴ΔPCD ∽ΔBCP ，∴PD BP=12，∴PD =12BP ，∴AP +12BP =AP +PD ．请你完成余下的思考，并直接写出答案：AP +12BP 的最小值为．(2)自主探索：如图3，矩形ABCD 中，BC =7，AB =9，P 为矩形内部一点，且PB =3，13AP +PC 的最小值为．(3)拓展延伸：如图4，扇形COD 中，O 为圆心，∠COD =120°，OC =4，OA =2，OB =3，点P 是CD上一点，求2PA +PB 的最小值，画出示意图并写出求解过程．17.⊙O 半径为2，AB ，DE 为两条直线．作DC ⊥AB 于C ，且C 为AO 中点，P 为圆上一个动点．求2PC +PE 的最小值．18.问题提出：如图1，在Rt ΔABC 中，∠ACB =90°，CB =4，CA =6，⊙C 半径为2，P 为圆上一动点，连接AP 、BP ，求AP +12BP 的最小值．(1)尝试解决：为了解决这个问题，下面给出一种解题思路：如图2，连接CP ，在CB 上取点D ，使CD =1，则有CD CP =CP CB =12，又∵∠PCD =∠BCP ，∴ΔPCD ∽ΔBCP ．∴PD BP =12，∴PD =12BP ，∴AP +12BP =AP +PD ．请你完成余下的思考，并直接写出答案：AP +12BP 的最小值为　37　．(2)自主探索：在“问题提出”的条件不变的情况下，13AP +BP 的最小值为 ．(3)拓展延伸：已知扇形COD 中，∠COD =90°，OC =6，OA =3，OB =5，点P 是CD上一点，求2PA +PB 的最小值．三、一内一外提系数19.如图，在ΔABC中，∠ABC=90°，AB=2BC=6，BD=1，P在以B为圆心3为半径的圆上，则AP+6PD的最小值为 ．20.如图，正方形ABCD边长为4，L是CD的中点，Y在⊙C上，|2LY-YA|的最大值是 ，22LY+YA的最小值是 四、真题演练21.如图，AB是⊙O的直径，C为⊙O上一点，作CE⊥AB于点E，BE=2OE，延长AB至点D，使得BD=AB，P是弧AB(异于A，B)上一个动点，连接AC、PE．(1)若AO=3，求AC的长度；(2)求证：CD是⊙O的切线；(3)点P在运动的过程中是否存在常数k，使得PE=k∙PD，如果存在，求k的值，如果不存在，请说明理由．22.如图1，在平面直角坐标系中，抛物线与x轴分别交于A、B两点，与y轴交于点C(0,6)，抛物线的顶点坐标为E(2,8)，连结BC、BE、CE．(1)求抛物线的表达式；(2)判断ΔBCE的形状，并说明理由；(3)如图2，以C为圆心，2为半径作⊙C，在⊙C上是否存在点P，使得BP+12EP的值最小，若存在，请求出最小值；若不存在，请说明理由．23.如图1，在平面直角坐标系中，直线y=-5x+5与x轴，y轴分别交于A，C两点，抛物线y=x2+bx+c经过A，C两点，与x轴的另一交点为B．(1)求抛物线解析式及B点坐标；(2)如图2，若P点是半径为2的⊙B上一动点，连接PC、PA，当点P运动到某一位置时，PC+12PA的值最小，请求出这个最小值，并说明理由．24.如图1，抛物线y=ax2+(a+3)x+3(a≠0)与x轴交于点A(4,0)，与y轴交于点B，在x轴上有一动点E(m，0)(0<m<4)，过点E作x轴的垂线交直线AB于点N，交抛物线于点P，过点P作PM⊥AB于点M．(1)求a的值和直线AB的函数表达式；(2)设ΔPMN的周长为C1，ΔAEN的周长为C2，若C1C2=65，求m的值；(3)如图2，在(2)条件下，将线段OE绕点O逆时针旋转得到OE′，旋转角为α(0°<α<90°)，连接E′A、E′B，求E′A+23E′B的最小值．25.如图1，在平面直角坐标系xOy 中，点M 在x 轴的正半轴上，⊙M 交x 轴于A 、B 两点，交y 轴于C 、D 两点，且C 为AE的中点，AE 交y 轴于G 点，若点A 的坐标为(-2,0)，AE =8．(1)求点C 的坐标；(2)连接MG 、BC ，求证：MG ⎳BC ；(3)如图2，过点D 作⊙M 的切线，交x 轴于点P ．动点F 在⊙M 的圆周上运动时，OF PF的比值是否发生变化？若不变，求出比值；若变化，说明变化规律．26.如图，在平面直角坐标系中，抛物线y =-x 2+bx +c 交x 轴于点A 和C (1,0)，交y 轴于点B (0,3)，抛物线的对称轴交x 轴于点E ，交抛物线于点F ．(1)求抛物线的解析式；(2)将线段OE 绕着点O 沿顺时针方向旋转得到线段OE ，旋转角为α(0°<α<90°)，连接AE ′，BE ′，求BE ′+13AE ′的最小值；27.如图，抛物线y=-x2+bx+c与直线AB交于A(-4,-4)，B(0,4)两点，直线AC:y=-12x-6交y轴于点C．点E是直线AB上的动点，过点E作EF⊥x轴交AC于点F，交抛物线于点G．(1)求抛物线y=-x2+bx+c的表达式；(2)连接GB，EO，当四边形GEOB是平行四边形时，求点G的坐标；(3)①在y轴上存在一点H，连接EH，HF，当点E运动到什么位置时，以A，E，F，H为顶点的四边形是矩形？求出此时点E，H的坐标；②在①的前提下，以点E为圆心，EH长为半径作圆，点M为⊙E上一动点，求12AM+CM它的最小值．。

专题28最值模型之阿氏圆模型最值问题在中考数学常以压轴题的形式考查，“阿氏圆”又称“阿波罗尼斯圆”，主要考查转化与化归等的数学思想。

在各类考试中都以高档题为主，中考说明中曾多处涉及。

本专题就最值模型中的阿氏圆问题进行梳理及对应试题分析，方便掌握。

【模型背景】已知平面上两点A 、B ，则所有满足PA =k ·PB （k ≠1）的点P 的轨迹是一个圆，这个轨迹最早由古希腊数学家阿波罗尼斯发现，故称“阿氏圆”。

【模型解读】如图1所示，⊙O 的半径为r ，点A 、B 都在⊙O 外，P 为⊙O 上一动点，已知r =k ·OB ，连接PA 、PB ，则当“PA +k ·PB ”的值最小时，P 点的位置如何确定？如图2，在线段OB 上截取OC 使OC =k ·r ，则可说明△BPO 与△PCO 相似，即k ·PB =PC 。

故本题求“PA +k ·PB ”的最小值可以转化为“PA +PC ”的最小值，其中与A 与C 为定点，P A 、P 、C 三点共线时，“PA +PC ”值最小。

如图3所示：注意区分胡不归模型和阿氏圆模型：在前面的“胡不归”问题中，我们见识了“k ·PA +PB ”最值问题，其中P 点轨迹是直线，而当P 点轨迹变为圆时，即通常我们所说的“阿氏圆”问题．【最值原理】两点之间线段最短及垂线段最短解题。

例1．（2023·山东·九年级专题练习）如图，在Rt ABC 中，90ACB ∠=︒，4CB =，6CA =，圆C 半径为2，P 为圆上一动点，连接,2,1A A P P P P B B +最小值__________．13BP AP +最小值__________．，例3．（2023·广东·九年级专题练习）如图，菱形ABCD的边长为2，锐角大小为60︒，A与BC相切于点E，在A上任取一点P，则32PB PD+的最小值为___________．例4．（2023·湖北武汉·九年级校考阶段练习）如图，在边长为例5．（2023·浙江·一模）问题提出：如图1，在等边△ABC中，AB＝9，⊙C半径为3，P为圆上一动点，连结AP，BP，求AP+13BP的最小值(1)尝试解决：为了解决这个问题，下面给出一种解题思路，通过构造一对相似三角形，将13BP转化为某一条线段长，具体方法如下：(请把下面的过程填写完整)如图2，连结CP，在CB上取点D，使CD＝1，则有13== CD CP CP CB又∵∠PCD＝∠△∽△∴13=PDBP∴PD＝13BP∴AP+13BP＝AP+PD∴当A，P，D三点共线时，AP+PD取到最小值请你完成余下的思考，并直接写出答案：AP+13BP的最小值为．(2)自主探索：如图3，矩形ABCD中，BC＝6，AB＝8，P为矩形内部一点，且PB＝4，则12AP+PC的最小值为．(请在图3中添加相应的辅助线)(3)拓展延伸：如图4，在扇形COD中，O为圆心，∠COD＝120°，OC＝4．OA＝2，OB＝3，点P是CD上一点，求2PA+PB例6．（2022·湖北·九年级专题练习）（1）如图1，已知正方形ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上的一个动点，求12PD PC +4PC +的最小值，12PD PC -的最大值．（2）如图2，已知正方形ABCD 的边长为9，圆B 的半径为6，点P 是圆B 上的一个动点，求23PD PC +的最小值，23PD PC -的最大值，23+PC PD 的最小值．（3）如图3，已知菱形ABCD 的边长为4，=60B ∠︒，圆B 的半径为2，点P 是圆B 上的一个动点，求12PD PC +的最小值和12PD PC -的最大值．6+PC PD 的最小值例7．（2022·湖北武汉·模拟预测）【新知探究】新定义：平面内两定点A ,B ，所有满足PA PB=k (k 为定值)的P 点形成的图形是圆，我们把这种圆称之为“阿氏圆”，【问题解决】如图，在△ABC 中，CB =4，AB =2AC ，则△ABC 面积的最大值为_____．轴交于课后专项训练＝A．62B．43．（2022·湖北·九年级专题练习）如图，已知正方形ABCD的边长为4，⊙B的半径为2，点P是⊙B上的一个动点，则PD﹣12PC的最大值为_____．内切于的取值范围为5．（2023·湖南·九年级专题练习）如图，边长为最小值为．6．（2023上·四川成都·九年级校考期中）如图，已知EC AE＝，G是射线CN上的动点，同时在:2:1为．若点H运动轨迹与射线7．（2023·广西·南宁市一模）如图，在平面直角坐标系中，A(2，0)、B(0，2)、C(4，0)、D(3，2)，P是AOB外部的第一象限内一动点，且∠BPA＝135°，则2PD+PC的最小值是_____．9．（2023秋·浙江温州·九年级校考期末）如图，在边长为分别是11．（2022·江苏·苏州九年级阶段练习）如图，正方形ABCD的边长为4，点E为边AD上一个动点，点F在边CD上，且线段EF＝4，点G为线段EF的中点，连接BG、CG，则BG+12CG的最小值为_____．12．（2023·四川成都·九年级专题练习）在ABC中，AB=9，BC=8，∠ABC=60°，⊙A的半径为6，P是A上一动点，连接PB，PC，则32PC PB+的最小值_____________PB的最小值_______=6014．（2023·黑龙江哈尔滨·模拟预测）已知：（1）初步思考：如图1，在PCB ∆中，已知2PB =，BC=4，N 为BC 上一点且1BN =，试说明：12PN PC =（2）问题提出：如图2，已知正方形ABCD 的边长为4，圆B 的半径为2，点P 是圆B 上的一个动点，求12PD PC+的最小值．（3）推广运用：如图3，已知菱形ABCD 的边长为4，∠B ﹦60°，圆B 的半径为2，点P 是圆B 上的一个动点，求12PD PC -的最大值．图1图2图3的三个顶点的距离分别为(1)如图2，在55⨯的网格中，每个小正方形的边长均为1，点A ，B 、C 、D 、E 均在小正方形的格点上，则点D 是ABC 关于点______的勾股点；若点F 在格点上，且点E 是ABF △关于点F 的勾股点，请在方格纸中画出ABF △；(2)如图3，菱形ABCD 中，AC 与BD 交于点O ，点E 是平面内一点，且点O 是ABE 关于点E 的勾股点．D17．（2023·重庆大渡口·九年级统考阶段练习）如图线为x轴、y轴，建立如图所示的平面直角坐标系，连接并与矩形的两边交于点E和点F已知平面上两点）的点的轨迹是一个圆，这个轨迹最早由古希腊数学家阿波罗尼斯发现，故称第1步：一般将含有k 的线段PB 两端点分别与圆心O 相连，即连接OB 、OP ；第2步：在OB 上取点C ，使得2OP OC OB =⋅，即OC OP OP OB=，构造母子型相似OCP △∽OPB △（图2）；第3步：连接AC ，与圆O 的交点即为点P （图3）．【问题解决】如图，O 与y 轴、x 轴的正半轴分别相交于点M 、点N ，O 半径为，点()0,2A ，点3,02B ⎛⎫ ⎪⎝⎭，点的任意一点，为半径画圆，交。

第7节 阿氏圆知识与方法1.阿氏圆：设A 、B 是平面上的两个定点，若平面内的动点P 满足PA PBλ=（0λ>且1λ≠），则点P 的轨迹是圆，该圆叫做阿氏圆.2．考题中常用的阿氏圆性质：（1）圆心位置：当1λ>时，圆心M 在AB 的延长线上；当01λ<<时，圆心M 在BA 的延长线上.（2）半径公式：21dr λλ=-，其中d 为两定点A 、B 之间的距离.（3）找定点：如右图所示，设圆M 的半径为r ，对于圆M 外任意一点A ，连接AM 交圆M 于点N ，则在线段MN 上必定存在点B ，使得对于圆M 上任意一点P ，都有PAPB λ=，可以根据2MA MB r ⋅=找到点B MA MBλ=求出λ.典型例题【例题】已知两个定点()2,0A -，()4,0B ，若动点C 满足2CB CA =，则点C 的轨迹方程为______.【解析】设(),C x y ，因为2CB CA =()()2222422x y x y -+=++，化简得：()22416x y ++=【答案】()22416x y ++=变式1 已知圆()22:416M x y ++=，点()2,0A -，若x 轴上的定点B 满足对圆M 上的任意一点C ，都有PA PBλ=恒成立，其中λ为常数，则点B 的坐标为______，常数______.【解析】设(),0B a ，()00,C x y ，则()2200416x y ++=，所以()22200001648y x x x =-+=--，故()()()2222000000022222200000002448442828x y CA x x x x x CBx ax a x x a x a x a y ++++----+--+--+ 要使CA CB 为定值，应有24428a a-=+-， 解得：4a =或2-（舍去），所以点B 的坐标为()2,0-， 此时0044116162CA x CBx -==-，即12λ=.解法2：如图，由阿氏图性质，点B 在MA 的延长线上，且2MA MB r ⋅=，所以216MB =，故8MB =，显然()4,0M -，从而点B 的坐标为()4,0，12MA MBλ==.【答案】()2,0-，12变式2 在ABC 中，6AB =，2BC AC =，则ABC 的面积的最大值为______. 【解析】解法1：设AB c =，BC a =，AC b =，则6c =，2a b =，由余弦定理，22222536cos 24a b c b C ab b +--==， 所以222221536sin sin 1cos 124ABCb Sab C b C b C b b ⎛⎫-===-- ⎪⎝⎭()()4222242225360361194014492092561644b b b b b b -+=-=--+=--+⨯所以当25b =ABC 的面积取得最大值12.解法2：以AB 中点O 为原点建立如图1所示的平面直角坐标系， 则()3,0A -，()3,0B ，设(),C x y ，因为2BC AC =()()2222323x y x y -+++，化简得：()22516x y ++=()0y ≠所以点C 的轨迹是以5,0M -为圆心，4为半径的圆（不含与x 轴的交点)，如图1，由图可知，()max 164122ABC S=⨯⨯=. 解法3：由2BC AC =可知点C 的轨迹是阿氏圆，设圆心为M ，半径为r ，如图2，由阿氏圆性质，22264121d r λλ⨯===--，结合图形可得()max 164122ABC S =⨯⨯=.【答案】12变式 3 在平面直角坐标系中，已知点()4,0B ，()1,4D ，C 为圆()22:416M x y ++=上的动点，则2CB CD +的最小值为______.【解析】先根据阿氏圆性质，找到与点()4,0B 对应的圆M 内的定点A ， 由2MA MB r ⋅=可得2MA =所以()2,0A -，且对于圆M 上的任意一点C ， 都有2CB MB CAMA==，从而2CB CA =所以()2222CB CD CA CD CA CD +=+=+，如图，由图可知当点C 在圆M 上运动到如图所示位置时，CA CD +取得最小值， 且最小值为()()2221045AD --+-=，所以2CB CD +的最小值为10.【答案】10变式 4 在平面直角坐标系中，已知点()4,0B ，()4,2D -，C 为圆()22:416M x y ++=上的动点，则2CB CD -的最大值为______.【解析】先根据阿氏圆性质，找到与点()4,0B 对应的圆M 内的定点A ， 由2MA MB r ⋅=可得2MA =，所以()2,0A -，且对于圆M 上的任意一点C ， 都有2CB MB CAMA==，从而2CB CA =所以()2222CB CD CA CD CA CD +=+=+，如图，由图可知当点C 在圆M 上运动到如图所示位置时，CA CD -取得最大值， 且最大值为2AD =2CB CD -的最大值为42 【答案】2变式5 已知抛物线2:4C y x =的焦点为F ，P 为C 上的动点，Q 为圆()22:54M x y -+=上的动点，则22PF PQ QF ++的最小值为______.【解析】由题意，()5,0M ，如图，作PN ⊥抛物线C 的准线1x =-于N ， 由抛物线定义，|PF PN =所以2222PF PQ QF PN PQ QF ++=++接下来根据阿氏圆性质，在圆M 内找到与F 对应的定点A ，由4MA MF ⋅=和4MF =可得1MA =， 所以()4,0A ，且2QF MF QAMA=，故2QF QA =，从而)222PF PQ QF PN PQ QA ++=++，如图，显然当P 为原点，点的坐标为()3,0时，PN PQ QA ++取得最小值5， 所以22PF PQ QF ++的最小值为10.【答案】10强化训练1.（★★★）已知圆22:9O x y +=，点()5,0B -，在直线OB 上存在不同于点B 的定点A ，满足对于圆O 上任意一点P ，都有PA PB是常数λ，则点A 的坐标为____，λ= ______.【解析】由阿氏圆性质，点A 在线段OB 上，且29OA OB r ⋅==，所以95OA =，从而9,05A ⎛⎫- ⎪⎝⎭，35OA OBλ==【答案】9,05A ⎛⎫- ⎪⎝⎭，35λ=2.（★★★）在ABC 中，4AB =，sin :sin 5:3B A =，则ABC S 的最大值为______.【解析】5sin :sin 5:3:5:33AC B A b a BC =⇒=⇒=⇒点C 的轨迹是阿氏圆，设圆心为T ，半径为r ，如图，由阿氏圆性质，225415341513d r λλ⨯===-⎛⎫- ⎪⎝⎭， 由图可知()max 11151542242ABC SAB r =⋅⋅=⨯⨯=.【答案】1523.（★★★★）设P 为圆()22:34C x y +-=上一动点，()0,1B -，()1,0M ，则2PB PM +的最小值为______. 【解析】先根据阿氏圆性质，找到与点()0,1B -对应的圆C 内的定点A ， 由2CA CB r ⋅=可得1CA =，从而2PB CB PACA==，所以2PB PA =，故(2222PB PM PA PM PA PM +=+=+显然当点P 位于如图所示位置时，PA PM +取得最小值，显然()0,3C ，所以()0,2A ，故PA PM +的最小值为5AM =2PA PM +的最小值为5【答案】54.（★★★★）设P 为圆()22:316C x y +-=上一动点，()0,13A -，()1,2M ，则4PA PM -的最大值为______.【解析】先根据阿氏圆性质，找到与点()0,13A -对应的圆C 内的定点B ，由|2CA CB r ⋅=可得1CB =， 所以()0,2B ，且4PA CA PBCB=，所以4PA PB =，从而()4444PA PM PB PM PB PM -=-=-， 显然当点P 位于如图所示位置时，PB PM -最大， 且最大值为1BM =，所以4PA PM -的最大值为4.【答案】45.（★★★★）在ABC 中，3BC =，2AB AC =，则BC BA ⋅的取值范围是______. 【解析】因为2AB AC =，所以点A 的轨迹是阿氏圆，设圆心为M ，显然点M 在BC 的延长线上，由题意，圆M 的半径22232121d r λλ⨯===-- 设MC m =，则()34MC MB m m ⋅=+=，解得：1m =或4-（舍去）， 所以4M B =，又cos 3cos BC BA BC BA B BA B ⋅=⋅⋅=⋅ 且cos BA B ⋅表示BA 在BC 方向上的投影，如图，当A 在圆M 上（不含A 、B 、C 共线的情形）运动的过程中，()cos 2,6BA B ⋅∈，故()6,18BC BA ⋅∈.【答案】()6,186.（★★★★）已知ABCD 是边长为3的正方形，其所在平面内的点P 、Q 满足2PA PB =，2QA QB =，则PQ AD ⋅的最小值为______.【解析】以A 为原点建立如图所示的平面直角坐标系，则()3,0B ，设(), P x y ，因为2PA PB =，所以()222223x y x y +-+化简得：()2214x y ++=，即点P 的轨迹是以()1,0C -为圆心，2为半径的圆，同理，点Q 的轨迹是圆()222:44C x y -+=，如图，当P 、Q 分别位于如图所示位置时，PQ 在AD 方向上的投影反向最大，且投影为4-，此时PQ AD ⋅最小，从而()()min3412PQ AD⋅=⨯-=-【答案】12-7.（★★★★）阿波罗尼斯（约公元前262-190年）证明过这样一个命题：平面内到两个定点的距离之比为常数k （0k >且1k ≠）的点的轨迹是圆，后人将此圆称为阿氏圆．若平面内两定点A 、B 间的距离为4，动点P 满足3PA =，则动点P 的轨迹所围成的图形的面积为___，PA PB ⋅的最大值是______. 【解析】由题意，点P 的轨迹是阿氏圆，其半径()223423131dr λλ⨯===--212S r ππ==；如图，设阿圆的圆心为M ，由阿氏圆性质，12MA MB ⋅=，又4MA MB -=，所以6MA =，2MB =，当点P 位于图中0P 处时，PA 、PB 都最长且同向，显然此时PA PB ⋅最大， 所以PA PB ⋅的最大值为()()0023623224163P A P B ⋅=⨯=+.【答案】12π，24163+8.（★★★★）已知椭圆22:143x y C +=的右焦点为F ，上顶点为A ，点P 在圆22:6O x y +=上，点Q 在椭圆C 2PA PQ QF +-的最小值为______.【解析】由题意，(3A ，()1,0F ，设椭圆C 的左焦点为1F ，则()11,0F -，且14QF QF +=所以14QF QF =-，()1122424PA PQ QF PA PQ QF PA PQ QF +-+--++-① 如图，先由阿氏圆性质，找到圆外与A 对应的定点B ，(36230,23OA OB OB B ⋅==⇒=⇒， 所以2PB OB PAOA==2PB PA =，124PA PQ QF PB PQ QF +-=++-， 显然当P 、Q 分别位于图中0P 、0Q 处时，1PB PQ QF ++取得最小值，且最小值等于1BF易求得113BF =2PA PQ QF +-134.134。