当前位置：文档之家 › 第十七章 非线性电路简介

第十七章 非线性电路简介

  • 格式：doc
  • 大小：1.92 MB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

第十七章 非线性电路简介

第十七章 非线性电路简介

i
u1 = f1 ( i )
u2 = f 2 ( i )
充气二极管
u = f (i )
0
u
③ 并联： 并联： 压控型电阻 i = g(u)
i
i1
i2
u
a、解析法： 、解析法：
KVL: KCL:
u1
u2
u = u1 = u2
i = i1 + i2 = g1 ( u) + g 2 ( u) = g ( u)
IS
u ①当 I S = 1 Α 时， = f (1 ) = 101 V u = f (i ) u 当 I S = 3 Α 时， = f ( 3 ) = 309 V
f ( 3 ) ≠ 3 f (1 ) ，齐性定理不成立。 齐性定理不成立。 不成立
②
f ( I 1 + I 2 ) = 100 ( I 1 + I 2 ) + ( I 1 + I 2 ) 2
压控型电阻 ②压控型电阻
i = g (u)
i
i0
“N形”特性曲线，隧道二极 形 特性曲线， 管
电阻中的电流是电阻两端电压的 单值函数，反函数不一定单值。 单值函数，反函数不一定单值。 反之， u 每一个 u 对应唯一的 i 。反之， 对同一个 i ，可能有多个 u 与之 对应。 对应。
注意到随 的变化，切线斜率时正时负，负时为负电阻， 注意到随 u 的变化，切线斜率时正时负，负时为负电阻，此段 为有源，且为单向性元件。测取这些元件的伏安特性时， 为有源，且为单向性元件。测取这些元件的伏安特性时，必须 改变一个电压，测一个电流，不能反。 变电压源 变电压源) 改变一个电压，测一个电流，不能反。(变电压源
u = UQ i = IQ

电路理论课件第17章非线性电路

电路理论课件第17章非线性电路

非线性电路的应用
01
02
03
信号处理
非线性电路可以用于信号 处理，如音频压缩、噪声 消除等。
通信系统
非线性电路在通信系统中 用于调制解调、信号放大 等。
自动控制系统
非线性电路在自动控制系 统中用于实现非线性控制 逻辑和算法。
02
非线性元件
非线性元件 非线性电阻
总结词
非线性电阻是指电阻值随输入电 压的非线性变化的电子元件。
通过观察仿真得到的电压、电流波形， 分析非线性元件对电路性能的影响。
参数分析
分析仿真结果中的元件参数，如电阻、 电容、电感等，了解其在非线性条件 下的变化情况。
性能评估
根据仿真结果，评估非线性电路的性 能指标，如频率响应、稳定性等。
优化设计
通过对仿真结果的分析，对非线性电 路的设计进行优化，提高其性能或降 低成本。
仿真实验步骤
1. 建立电路模型
根据非线性电路的原理图，在 仿真软件中建立相应的电路模
型。
2. 设置仿真参数
选择适当的仿真算法、时间步 长、精度等参数。
3. 运行仿真
设置好参数后，启动仿真过程 ，观察仿真结果。
4. 结果分析
对仿真结果进行分析，验证非 线性电路的工作原理和特性。
仿真结果分析
波形分析
03
非线性电路的分析方法
非线性电路的分析方法
• 请输入您的内容
04
非线性电路的稳定性分 析
静态稳定性分析
分析方法
通过求解系统的平衡点，判断平衡点的稳定性。
平衡点的求解方法
通过设置系统的输入信号为0，然后求解系统的状态方程。
平衡点的稳定性判断
通过判断平衡点的导数矩阵的行列式和迹的正负来判断。

第十七章 非线性电路简介

第十七章 非线性电路简介

第十七章非线性电路简介非线性元件中的电压和电流之间的关系是非线性的，有时不能用函数是来表示，要靠对应的曲线来表征其特征，这一特点是分析非线性电路的困难所在。

与线性电路的一个根本区别就是不能使用叠加定理和齐性定理。

但是分析非线性电路的基本依据仍然是KCL、KVL和元件的特性方程。

一、基本要求1、掌握非线性电阻元件的电特性；2、掌握含非线性电阻电路方程的建立；3、掌握非线性电路的计算方法—图解法和小信号分析法。

二、重点和难点重点：1. 非线性元件的特性；2. 非线性电路的小信号分析法；难点：非线性电阻电路方程的列写。

三、学时安排共计4学时四、基本内容§17.1 非线性电阻1．非线性电路在线性电路中, 线性元件的特点是其参数不随电压或电流而变化。

如果电路元件的参数随着电压或电流而变化, 即电路元件的参数与电压或电流有关, 就称为非线性元件, 含有非线性元件的电路称为非线性电路。

实际电路元件的参数总是或多或少地随着电压或电流而变化, 所以严格说来, 一切实际 电路都是非线性电路。

但在工程计算中，可以对非线性程度比较弱的电路元件做为线性元件来处理, 从而简化电路分析。

而对许多本质因素具有非线性特性的元件，如果忽略其非线性特性就将导致计算结果与实际量值相差太大而无意义。

因此，分析研究非线性电路具有重要的工程物理意义。

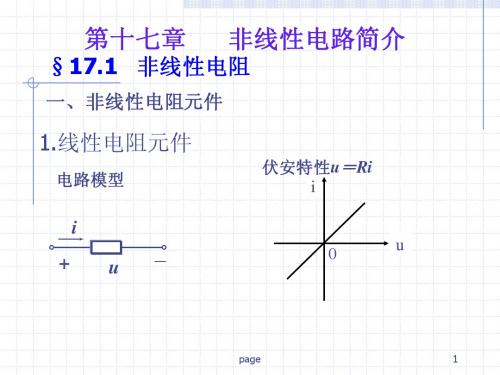
2．非线性电阻线性电阻元件的伏安特性可用欧姆定律来表示, 即Ri u =, 在 i u -平面上它是通过坐标原点的一条直线。

非线性电阻元件的伏安关系不满足欧姆定律, 而是遵循某种特定的非线性函数关系。

非线性电阻在电路中符号如图 17.1（a ）所示 。

图 17.1(a) 图 17.1 (b) 图 17.1 (c)（1）电流控制型电阻： 非线性电阻元件两端电压是其电流的单值函数, 它的伏安特性可用下列函数关系表示：)(i f u =其典型的伏安特性如图17.1（b ）所示 , 从其特性曲线上可以看到: 对于同一电压值, 与之对应的电流可能是多值的。

第17章 非线性电路

第17章 非线性电路

①+
i1 G1
i3
u3
− i 3 + i4 + i5 = 0 − i4 − i 2 − I s = 0
3 i3 = 5 u 3
② i4 − + +
u5
u4
−
③
Is
+
Us
1 i5 = 15 u 5 5
−i
将下列式子代入方程
i4 = 10 u 1 3 4
−
5
u 3 = u n1 − u n 2
u4 = un2 − un3
代入方程 U s + us (t ) = Rsi + u
得
US+ uS(t )= RS [IQ + ∆ i(t) ]+ UQ + ∆ u(t)
又US= RSIQ + UQ为直流工作状态
1 u S ( t ) = RS ∆ i ( t ) + ∆ U ( t ) = RS ∆ i ( t ) + ∆i ( t ) Gd = RS ∆i ( t ) + Rd ∆i ( t )
i '1
i2 = f 2 (u )
u'
u
10
page
七、含有一个非线性电阻元件电路的求解 先求出线性含源电阻网络的戴维宁等效电路， 先求出线性含源电阻网络的戴维宁等效电路，再用图解法求解
a
线性 含源 电阻 网络
a i i
+
u
−
R + U −
0 0
+
u
−
b
左右一端口网络分别满足以下关系式： i u=f(i) u =U 0− R0i U0 两关系式同时满足两条伏安特性交点，即 R0 U Q =U 0− R0 I Q U =f(I ) I

电路课件非线性电路简介

电路课件非线性电路简介
第十七章 非线性电路简介
主要内容：
❖ 简要介绍非线性电路元件 ❖ 举例说明非线性电路方程建立方法 ❖ 介绍分析非线性电路的一些常用方
法，如小信。
17-1 非线性电阻
❖ 含非线性元件的电路称非线性电路。 ❖ 实际电路严格说非线性。
❖ 非线性程度较微弱电路元件，作线性元件 处理不会带来本质差异。
❖ (2) 当i=2sin(314t) A时
u=[100×2sin(314t)+8sin3(314t)] V
=[206sin(314t)-2sin(942t)] V
电压u含3倍频率分量，可见，用非线性电阻可产生频 率不同于输入频率的输出，称倍频作用。
❖ (3) 设 u12=f(i1+i2)，则
u12=100(i1+i2)+(i1+i2)3 =100(i1+i2)+(i13+i23)+(i1+i2)×3i1i2 =100i1+i13+100i2+i23+(i1+i2)×3i1i2
i2=10 A时： u2=(100×10+103) =2000 V i3=10 mA 时 ： u3=[100×10×10-3+(10×10-3)3]=(1+10-6)
V
❖ 从上述结果可见，如作为100Ω线性电阻，电 流i不同时，引起误差不同，当17电-1 非流线性较电阻小-8时， 引起的误差不大。
例17-1 （2）
可得
i=i1=i2 u=u1+u2
u=f1(i1)+f2(i2)=f(i) ❖ 对所有i，有
f(i)=f1(i1)+f2(i2)
17-1 非线性电阻 -10

第十七章非线性电路简介

第十七章非线性电路简介

Io
Uo （Uo，Io）称为静态工作点
6
17-2 非线性电容和非线性电感
一、非线性电容 定义：如果一个电容元件的库伏特性是一条通过原点的直 线，则此电容为线性电容，否则为非线性电容。 符号： 类型： q = f ( u ) 压控型
u = h ( q ) 荷控型 f = h -1 单调型
非线性电容及q－u特性曲线
(a) 解： 1、作出大信号电路
(b)
1 is − u − u2 = 0 R3
10 − 3u − u 2 = 0
u>0
u>0
17
u* = 2 V
2、作出小信号电路，其中小信号电阻为
1 1 = df (u ) d 2 (u ) du u *= 2 du u *= 2
=
1 2u u*= 2
1 = Ω 4
3
2、压控型电阻元件 i = g(u) 为单值函数
如隧道二极管
3、单调型电阻元件
（既是流控型又是压控型）
u = f (i) ，i = g(u) f=g-1 双向元件：
如果电阻元件的伏安特性对称于坐标系的原点，则称之为双向元件 一切线性电阻元件都是双向元件。大多数非线性电阻元件是非双向元件。 非线性电阻元件的电压和电流之间的关系可用非线性代数方程f(u, i) = 0来 描述。
以u*表示当 ∆is = 0时方程的解，即
u* is − − f (u*) = 0 R2
14
输入激励由is 至is +∆ is的变化，导致电压u*改变为 u=u*+∆ u。因此，有
1 (is + ∆ is ) − (u * + ∆ u ) − f (u * + ∆ u ) = 0 R2

第17章非线性电路(丘关源)


4-5
四、非线性电阻元件的电阻表示方法(参数)
——静态电阻 R 和动态电阻 Rd 1.静态电阻(直流电阻) R R=工作点 Q 的电压 u 与电流 i 之比
R u i
Q

i
= tan
u
2. 动态电阻(交流电阻)Rd
Rd=工作点 Q 的斜率
Rd du di
= tan
注意:(1)工作点不同， R 和Rd就不同。 (2) Rd 有可能会出现“负电阻”情况。
il1

R1 il1 + R2(il1- il2) = Us 20il21/3 -R2(il1- il2)=0
即为所求回路ቤተ መጻሕፍቲ ባይዱ流方程
4-22
例3 电路图中非线性电阻的伏安特性关系为: u3=20i31/2。 试列写支路电流法方程。 i
1
R1
解： u1= R1 i1 u2= R2i2 u3=20i31/2
o o
Ro
u
i +
Q u
UQ
Uo
该直线与非线性元件u~i关系曲线的交点=Q点
4-25
2.求Q点时非线性电阻的动态 电导Gd或动态电阻Rd
Gd di du uQ
Ro
Uo + u
i +
或
Rd
du
i
di
Q
uS(t)
3.画出Q点处的小信号等效电路 ——小信号源单独作用, 直流激 励源=0时的电路
U n3 Is
i1=G1(un1-us) i2=G2(un1-un3) i3=5(un1-un2)3 i4=10(un2-un3)1/3 i5=15un21/5
G1
u5

非线性电路简介


例1 电路如图所示，其中 非线性电阻的伏安特性关系
为u3 20i31 2。试列出电路方程。
i1
R1
+
u1
+
i2
解 非线性电阻特性:
i3 +
U s il1
u2 R2 il2
u3
u1 u2 Us u2 u3 0
u1 R1il1 u2 R2 (il1 il 2 ) u3 20il122
解 改变U0就改变工作点。若信号电压比U0小许多，则在一定
U0下，非线性电容可作为线性电容处理，其
Cd
dq ku du
可见， U0不同，Cd值不同，调节U0可改变Cd的大小，而
达到调谐的目的。
二、非线性电感
1. 韦安特性
i h( ) 或 ＝f (i)
磁通控制电感
电流控制电感
非线性电感的电路符号和 i 特性曲线如图所示。
i
u
L
P
O
i
2.静态电感L和动态电感Ld
静态电感
L
i
|P
tg
动态电感
Ld
d
di
|P
tg
注：
电感也可以是单调型的，但 带有铁芯的电感具有回线形 状，如图示。
P
O
i
ψ
i
O
§17-3 非线性电路的方程
由于基尔霍夫定律对于线性电路和非线性电路均适用， 所以线性电路方程与非线性电路方程的差别仅由于元件特 性的不同而引起。对于非线性电阻电路列出的方程是一组 非线性代数方程，而对含有非线性储能元件的电路列出的 方程是一组非线性微分方程。
（1）电流控制型 （2）电压控制型 （3）单调型
（1）电流控制型

17-非线性电路


律，而遵循某种特定的非线性函数关系。
u=f(i) i=g(u)
A.2.非线性电阻的分类
①流控型电阻 电阻两端电压是其电流的单值
函数。 i
u=f(i)
特点
+
u-
i
a)对每一电流值有唯一的电压
与之对应。
b)对任一电压值则可能有 多个电流与之对应 。
S形 o
u
如：充气二极管等
②压控型电阻 通过电阻的电流是其两端电压
P

④静态电感L和动态电感Ld
L
i
Ld

d
di

o
i
17.3 非线性电路的方程
方法：
• 列写非线性电路方程的依据仍然是KCL、 KVL和元件伏安特性。
• 对于非线性电阻电路列出的方程是一组 非线性代数方程。
• 对于含有非线性储能元件的动态电路列 出的方程是一组非线性微分方程 。
例 电路中非线性电阻的特性，
②对压控型和流控型非线性电阻，伏安特性曲线
的下倾段 Rd 为负，因此，动态电阻具有“负电 阻”性质。
例 一非线性电阻的伏安特性 u 100i i3
求 i1 = 2A， i2 = 10A时对应的电压 u1，u2；
解
u1

100 i1

i3
1

208V
u2
100i2

i3
2

2000V
B.非线性电容
①符号 ②库伏特性
i
+
u
-
非线性电容元件的库伏特性不是一条通过原
点的直线，而遵循某种特定的非线性函数关系。
q=f(u) u=h(q)

第17章 非线性电路简介


ψ 静态电感: 静态电感: L = i
dψ 动态电感： 动态电感： Ld = di
三、非线性电路分析 1、电路定理 1）KVL，KCL KVL， 2）元件端口特性 2、分析方法 1）图解法 2）分段线性化 3）小信号分析法
§ 17.2
非线性电阻的串联、 非线性电阻的串联、并联电路
一、非线性电阻的串联 i + + u (i) − + 1 u2 ( i ) u
∴ ∆i = Gd * ∆u 或 ∆u = R d * ∆i
由此可得其等效电路： 由此可得其等效电路：
RS
i
Us Ri
△i
i(u) P U 0 Us
+
− uS(t) Rd
+
△u
−
I0 o
u
此电路称为非线性电阻在工作点P(U0, I0) 此电路称为非线性电阻在工作点 处的小信号等效电路。 处的小信号等效电路。 称为小信号分析方法。 上述分析方法 称为小信号分析方法。
+ i2
u1 −
+
u2 −
i = i1 + i2 u = u1 = u2
i
i ' i2
' i1 o
'
i (u)
i1 ( u)
i '1
i2 ( u)
同一压下将电流 相加。 相加。
u'
u
三、含有一个非线性电阻元件电路的求解 a
线性 含源 电阻 网络
a i i
+
u
−
Ri + Us −
+
u b
−
b i
Us Ri
di Gd = du
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第十七章 非线性电路简介17．1 基本概念17．1．1 非线性元件与非线性电路 1． 非线性电阻（1） 定义：线性电阻的电压、电流关系是i u -平面上一条过原点的直线，否则称为非线性电阻，用函数)(i u u =或)(u i i =来表示。

（2） 分类：根据电压与电流的函数关系，非线性电阻可以区别成:电压控制型（电流是电压的单值函数，简称压控型）、电流控制型（电压是电流的单值函数，简称流控型）、单调型（电压是电流的单调函数）。

2． 非线性电感（1） 定义：线性电感的磁链、电流关系是-ψ平面上一条过原点的直线，否则称为非线性电感，用函数)()(ψψψi i i ==或来表示。

（2） 分类：根据磁链与电流的函数关系，非线性电感可以区别成：电源控制型（磁链是电流的单值函数，简称流控型）、磁链控制型（电流是磁链的单值函数，简称链控型）、单调型（磁链是电流的单调函数）。

3． 非线性电容（1） 定义：线性电容的电荷、电压关系是u q -平面上一条过原点的直线，否则称为非线性电容，用函数)()(q u u u q q ==或来表示。

（2） 分类：根据电荷与电压的函数关系，非线性电容可以区别成：电压控制型（电荷是电压的单值函数，简称压控制）、电荷控制型（电压是电荷的单值函数，简称荷控制）、单调型（电荷是电压的单调函数）。

4． 非线性电路及其工作点用非线性方程描述的电路称为非线性电路，通常是指含有非线性元件的电路；不含动态元件的非线性电路称为非线性电阻电路，描述非线性电阻电路的方程是非线性代数方程；含有动态元件的非线性电路称为非线性动态电路，描述非线性动态电路的方程是非线性微分方程。

工作点：非线性电路的直流解称为工作点，它对应特性曲线上的一个确定位置。

5． 非线性元件的静态参数和动态参数（1） 静态参数：工作点与原点相连的直线的斜率，即：静态电阻：)()(Q i Q u R Q=，静态电感：)()(Q i Q L Q ψ=，静态电容：)()(Q u Q q C Q = 。

（2） 动态参数当信号在工作点的足够小的邻域内变化时，可用工作点处的切线近似代替非线性曲线，切线的斜率定义为非线性元件的动态参数。

动态电阻：QQddidu R =，动态电感：Q Qddid L ψ=，动态电容：QQddudq C =。

17．1．2 简单非线性电阻电路的计算这里指含一个等效非线性电阻的电路，介绍两种方法：1． 解析法。

步骤如下：（1） 将非线性电阻元件的线性电路用戴维南或诺顿等效电路代替。

（2） 对等效后的电路列出KCL 或KVL 方程，并利用非线性电阻的电压、电流关系求出非线性电阻支路的电压或电流。

（3） 根据替代定理，用电压源或电流源替代非线性电阻，求出其他支路的电压或电流。

2． 曲线相交法。

步骤如下：（1）、（3）同解析法中（1）、（3）（2）在同一坐标系中作出线性部分与非线性部分的特性曲线，它们的交点就是工作点),(00I U Q 。

17．1．3 非线性电路方程的列写 1. 非线性电阻电路方程的列写根据非线性电阻的类型选择分析方法，使非线性电阻的控制量作为方程的待求变量。

（1） 如果非线性电阻都是压控的，宜列写结点电压方程或支路电压方程，割集电压方程； （2） 如果非线性电阻都是流控的，宜列写回路电流方程或支路电流方程；（3） 如果非线性电阻一部分是压控的，另一部分是流控的，宜列写混合法方程；（4） 如果非线性电阻是单调的，则列何种方程均可，取决于其它分析需要。

非线性电阻电路方程是非线性代数方程，通常用数值分析法进行求解。

2. 动态电路状态方程的列写非线性动态电路状态方程的编写步骤类似于前面第十五章中已介绍过的线性电路的状态方程所采用的步骤。

其状态变量一般是这样选取的：(1) 当动态元件为线性，电阻为非线性时，一般仍取L c i u 或为状态变量；(2) 当动态元件为非线性时，一般选电荷q 或磁链ψ为状态变量。

说明：非线性动态电路状态方程的标准形式的列写很困难，有时不可能。

17．1．4 小信号分析法小信号分析法是工程上分析非线性电路的一个重要方法。

它的实质就是将非线性电路分别对直流偏置和交流小信号进行线性化处理，然后按线性电路分析方法进行计算的一种方法。

一般步骤是：1、 尽量把电路中线性部分化简，令直流电源作用，求出非线性电路的工作点),(00I U Q ；2、 根据特性方程求出非线性元件在工作点处的动态参数，即d R 、d G 、d L 和d C ；3、 用动态参数表示非线性元件，画出小信号等效电路；4、 令小信号电源作用，求出小信号响应u ∆、i ∆，根据待分析的内容，选择不同的分析方法：对于电阻电路，采用前面介绍过的各种电阻电路的分析方法；对于正弦稳态电路，采用相量法分析；对于一阶动态电路，采用时域分析法；对于复杂动态电路，采用复频域分析法。

5、 电路的全解：u U u ∆+=0，i I i ∆+=0。

17．1．5 分段线性化分析法分段线性化方法（又称折线法），是用若干个直线段近似代替非线性的特性曲线，相当于用若干个线性电路模型代替非线性电路模型，从而将非线性电路问题近似化为线性电路问题来求解。

对如图17-1（a ）所示的采用分段线性化表示非线性电阻的i u -曲线，每段折线都可用戴维南等效电路来代替，如图17-1（b ）所示。

u U 为折线与0轴的交点，R 即为这条线段的斜率。

理想二极管的符号及伏安特性如图17-2所示，实际二极管正向特性及等效电路如图17-3所示。

A)(117a-图UαtgR=u+-)(117b-图V/uUV/u217-图317-图17．2 重点、难点分析17．2．1 本章重点1.非线性元件的特性，非线性电路方程的列写。

2.简单非线性电阻电路的计算。

3.小信号法分析非线性电路。

17．2．2 本章难点1．小信号分析法是本章的重点，也是难点。

首先采用的前提是当输入的交流信号的幅度相对偏置直流电源的幅度足够小。

另外，小信号分析法的关键是正确作出小信号的等效电路，注意小信号的等效电路应与原来的非线性电路具有相同的拓扑结构。

另外，当给定的非线性电路的偏置电源发生改变，小信号等效电路也随之发生改变。

2．分段线性化方法也是本章的难点之一。

分段线性化法是把非线性电路转化成一系列电路结构相同而参数不等的线性电路来处理，而每个线性电路可以用熟知的线性电路的分析方法独立地进行分析计算，但必须考虑非线性元件折线段的所有组合。

检验是一个非常重要而必不可少的步骤，只有通过检验才能去除掉虚解，获得电路的真实解。

17．3 典型例题例17-1 电路如图17-4所示，其中非线性电阻1R 的伏安关系为211121.0u u i +=，非线性电阻2R 的伏安关系为)1(202-=Tu u eI i ，试列出电路的结点电压方程。

2417-图解题指导：若非线性电阻均为压控型，宜用结点电压法，割集电压法及支路电压法列写方程；若均为流控型，宜用回路电流方程或支路电流方程；若一部分为压控型，一部分为流控型，则宜用混合方程。

解 根据KCL 和KVL 得：2321211232121,n n n n S S u u u u u u u I i i I i i =-===-=+电阻元件的VAR 为：333022211)1(21.02u G i e I i u u i Tu u =-=+= 将上述方程中的非结点电压变量消去，可得下列结点电压方程133)(01)(0211)1()1(21.02121S n u u u S u u u n n I u G eI I e I u u Tn n Tn n =--=-++--例17-2 如图17-5所示电路中，非线性电阻的特性方程分别为33211sin ,i u i u ==，试列出电路的网孔方程。

517-图s U 2s U解 网孔电流的参考方向如图所示，则∏I -=i i i 3 对各网孔列写KVL 方程，并考虑各元件的VAR ，可得下列的网孔电流方程：22121)sin()sin(S S u i R i i u i i i -=+--=-+∏∏I ∏I例17-3 如图17-6所示电路中，设)V A,(311单位：U I =，)A V,(322单位：I u =。

试列出求解21I U 及的二元方程组。

617-图3+-V解 对结点①列出KCL 方程 0331=-+I I ⑴对回路1l 列KVL 方程0224=-+U U ⑵将 )(11)(214213I I U U U I -⨯=+=及311U I = 322I U = 代入⑴、⑵式得关于1U 及2I 的二元方程组⎩⎨⎧-=--=++232323132131I I U I U U 例17-4 如图17-7所示非线性电路，已知：非线性电感32L i =ψ，非线性电容313c u q =，非线性电阻21i u=，S u R 与1为线性元件，试编写电路的状态方程。

717-图U u解 以ψ与q 为状态变量编写电路的状态方程。

电路方程由两部分组成，即：（1） 电路元件特性方程：非线性元件的，有：2131323iu u q i c L ===ψ 线性元件的有：L R i R u 11=（2） KVL KCL 和方程结点1方程 i i i c L += ⑴回路方程 S c L R U u u u =++1 ⑵u u c = ⑶将元件特性方程代入式⑴、⑵、⑶，并消去状态变量，得⎪⎭⎪⎬⎫+==++-6231271227123113131qdt dq U q dt d R S ψψψ 整理后得⎪⎭⎪⎬⎫-=+--=--6232712271231313131q dt dq U q dt d S ψψψ 例17-5 图17-8(a)所示D 为一理想二极管，求?=IK 3K 6D )(817a -图U DR )(817b -图解题指导：求解此类题目时必须先判断二极管是否导通，一旦导通，则用短路线代之；若为截止，则等效于断开。

解 断开二极管，求余下的线性有源一端口电路的戴维南等效电路，得出Ω==K 100,V 5.2eq oc R U 作出等效电路如图17-8(b)所示。

由此可见，二极管两端加的是正向电压（正向偏置），D导通，所以A 25mA 025.01005.2μ====eq oc R U I例17-6 如图17-9(a)所示电路，元件A 的伏安特性为：⎩⎨⎧+=102I U00>≤I I ，求I 、1I U 及。

8)(917a -图R U解：此题为非线性电阻电路，先求非线性元件A 以外的有源二端网络的戴维南等效电路。

得出 V 3=oc U ，Ω=1eq R 作出等效电路如图17-9(b)所试。

虚线以左的线性有源支路可用一直线方程来表示其伏安特性I U -=3 ⑴ 虚线以右的非线性元件的伏安特性为⎩⎨⎧+=12I U00>≤I I ⑵ 由⑴、⑵式即可解出U 、I 1=I ，A 2-=I （舍去） 所以：V 2=U返回到图17-9(a)中求1I ，A 11122121=+-=+-=I U I 总的解答为：A 1=I 、V 2=U 、A 11=I例17-7 电路如图17-10(a)所示，非线性电阻元件R 的伏安特性如图17-10(b)所示。