2015年北京市17区二模试题第16题汇编—找规律

2015北京中考数学二模各区29题（含答案）昌平29. 在平面直角坐标系xOy 中，给出如下定义：形如()()2y a x m a x m =-+-与()()2y a x m a x m =---的两个二次函数的图象叫做“兄弟抛物线”． （1）试写出一对兄弟抛物线的解析式 与 ； （2）判断二次函数2y x x =-与232y x x =-+的图象是否为兄弟抛物线，如果是，求出a 与m 的值，如果不是，请说明理由；（3）若一对兄弟抛物线各自与x 轴的两个交点和其顶点构成直角三角形，其中一个抛物线的对称轴为直线2x =且开口向上，请直接写出这对兄弟抛物线的解析式．备用图朝阳29.如图，顶点为A （－4,4）的二次函数图象经过原点（0,0），点P 在该图象上，OP 交其对称轴l 于点M ，点M 、N 关于点A 对称，连接PN ，ON .（1）求该二次函数的表达式；（2）若点P 的坐标是（－6,3），求△OPN 的面积； （3）当点P 在对称轴l 左侧的二次函数图象上运动时，请解答下面问题：① 求证：∠PNM ＝∠ONM ；② 若△OPN 为直角三角形，请直接写出所有符合 条件的点P 的坐标.丰台29.对某一个函数给出如下定义：如果存在实数M ，对于任意的函数值y ，都满足y M ≤，那么称这个函数是有上界函数，在所有满足条件的M 中，其最小值称为这个函数的上确界．例如，图中的函数是有上界函数，其上确界是2． （1）分别判断函数1y x=-（0x ＜）和23y x =-（2x ＜） 是不是有上界函数？如果是有上界函数，求其上确界； （2）如果函数2y x =-+ （,a x b b a ≤≤＞）的上确界是b ，且这个函数的最小值不超过21a +，求a 的取值范围；（3）如果函数222y x ax =-+（15x ≤≤）是以3为上确界的 有上界函数，求实数a 的值.怀柔29. 阅读理解：学习了三角形全等的判定方法:“SAS ”，“ASA ”，“AAS ”，“SSS ”和直角三角形全等的判定方法“HL ”后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”即“SSA ”的情形进行研究．我们不妨将问题用符号语言表示为：在△ABC 和△DEF 中，AC =DF ，BC =EF ，∠A =∠D . 初步探究：如图1，已知AC=DF, ∠A =∠D ,过C 作CH ⊥射线AM 于点H ，对△ABC 的CB 边进行分类，可分为“CB<CH ，CB=CH ，CH<CB<CA ，”三种情况进行探究．深入探究： 第一种情况，当BC<CH 时，不能构成△ABC 和△DEF ．第二种情况，（1）如图2，当BC=CH 时，在△ABC 和△DEF 中，AC =DF ，BC =EF ，∠A =∠D ，根据 ，可以知道Rt △ABC ≌Rt △DEF ．HNANA第三种情况，（2）当CH<BC<CA 时，△ABC 和△DEF 不一定全等．请你用尺规在图1的两个图形中分别补全△ABC 和△DEF,使△DEF 和△ABC 不全等（表明字母，不写作法，保留作图痕迹）．（3）从上述三种情况发现，只有当BC=CH 时，才一定能使△ABC ≌△DEF ． 除了上述三种情况外，BC 边还可以满足什么条件，也一定能使△ABC ≌△DEF ？写出结论,并利用备用图证明.石景山29．对于平面直角坐标系xOy 中的点(),P m n ，定义一种变换：作点(),P m n 关于y 轴对称的点'P ，再将'P 向左平移()0k k >个单位得到点'k P ，'k P 叫做对点(),P m n 的k 阶“ℜ”变换．（1）求()3,2P 的3阶“ℜ”变换后3'P 的坐标；（2）若直线33y x =-与x 轴，y 轴分别交于,A B 两点，点A 的2阶“ℜ”变换后得到点C ，求过,,A B C 三点的抛物线M 的解析式； （3）在（2）的条件下，抛物线M 的对称轴与x 轴交于D ，若在抛物线M 对称轴上存在一点E ，使得以,,E D B 为顶点的三角形是等腰三角形，求点E 的坐标．房山29.如图1，若抛物线L 1的顶点A 在抛物线L 2上，抛物线L 2的顶点B 也在抛物线L 1上(点A 与点B 不重合)，我们把这样的两抛物线L 1、L 2互称为“友好”抛物线. （1）一条抛物线的“友好”抛物线有_______条.A . 1 B. 2 C. 3 D. 无数 （2）如图2，已知抛物线L 3：2284y x x =-+与y 轴交于点C ，点C 关于该抛物线对称轴的对称点为D ，请求出以点D 为顶点的L 3的“友好”抛物线L 4的表达式;（3）若抛物线21()y a x m n =-+的“友好”抛物线的解析式为22()y a x h k =-+,请直接写出1a 与2a 的关系式为 .ANH图2图1平谷29．定义：如图1，平面上两条直线AB 、CD 相交于点O ，对于平面内任意一点M ，点M 到直线AB 、CD 的距离分别为p 、q ，则称有序实数对（p ，q ）是点M 的“距离坐标”．根据上述定义，“距离坐标”为（0,0）点有1个，即点O ． （1）“距离坐标”为（1，0）点有 个；（2）如图2，若点M 在过点O 且与直线CD 垂直的直线l 上时，点M 的“距离坐标”为（p ，q ），且∠BOD =120°．请画出图形，并直接写出p ，q 的关系式； （3）如图3，点M 的“距离坐标”为（1，且∠AOB =30°，求OM 的长．顺义29．如图，在平面直角坐标系xOy 中，抛物线223y x bx c =-++与x 轴交于A ，B 两点，其中B （6，0），与y 轴交于点C （0，8），点P 是x 轴上方的抛物线上一动点（不与点C 重合）． （1）求抛物线的表达式；（2）过点P 作PD ⊥x 轴于点D ，交直线BC 于点E ，点E 关于直线PC 的对称点为'E ，若点'E 落在y 轴上（不与点C 重合），请判断以P ，C ，E ，'E 为顶点的四边形的形状， 并说明理由； （3）在（2）的条件下直接写出点P 的坐标．图1O D C B A 图2 图3备用图西城29．对于平面直角坐标系xOy 中的点P 和图形G ，给出如下定义：在图形G 上若存在两点M ，N ，使△PMN 为正三角形，则称图形G 为点P 的τ型线，点P 为图形G 的τ型点， △PMN 为图形G 关于点P 的τ型三角形．（1）如图1，已知点(0,A ，(3,0)B ，以原点O 为圆心的⊙O 半径为1．在A ，B两点中，⊙O 的τ型点是____，画出并回答⊙O 关于该τ型点的τ型三角形；（画 出一个即可）（2）如图2，已知点(0,2)E ，点(,0)F m （其中m ＞0）．若线段EF 为原点O 的τ型线，且线段EF 关于原点O 的τ，求m 的值； （3）若(0,2)H -是抛物线2y x n =+的τ型点，直接写出n 的取值范围．东城29．定义：如果一条直线能够将一个封闭图形的周长和面积平分，那么就把这条直线称作这个封闭图形的等分线。

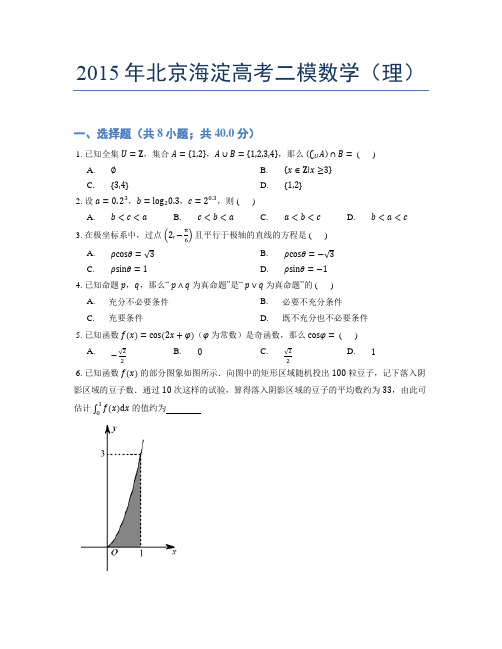
北京各区二模理科数学分类汇编函数充要(2015届西城二模) 3．设命题p ：函数在R上为增函数；命题q：函数为奇函数．则下列命题中真命题是(D)(2015届西城二模)7．若“ x ＞1 ”是“不等式成立”的必要而不充分条件，则实数a的取值范围是（A）A．a ＞3 B．a ＜3 C．a ＞4 D．a ＜4(2015届西城二模)14．如图，正方形ABCD 的边长为2，O 为AD 的中点，射线OP 从OA 出发，绕着点O 顺时针方向旋转至OD，在旋转的过程中，记，OP 所经过的在正方形ABCD内的区域（阴影部分）的面积S ＝f （x），那么对于函数f （x）有以下三个结论：①；②任意，都有③任意其中所有正确结论的序号是．答案：①②(2015届海淀二模)答案：（2）D （4）A （7）C (2015届东城二模) （2）设4log a =π，14log b =π，4c =π，则a ，b ，c 的大小关系是（D ）（A ） b c a>> （B ）a c b >> （C ） a b c >> （D ）b a c >>(2015届东城二模) （5）已知p ，q 是简单命题，那么“p q ∧是真命题”是“p ⌝是真命题”的（D ）（A ）充分而不必要条件 （B ）必要而不充分条件 （C ）充分必要条件 （D ）既不充分也不必要条件 (2015届东城二模) （7）定义在R 上的函数()f x 满足)()6(x f x f =+.当)1,3[--∈x 时，2)2()(+-=x x f ,当)3,1[-∈x 时，x x f =)(，则(1)(2)(3)(2015)f f f f ++++=（A ）（A ）336 （B ）355 （C ）1676 （D ）2015(2015届丰台二模) 2．“a =0”是“复数i za b =+(a ，b ∈R)为纯虚数”的(A) 充分不必要条件 (B) 必要不充分条件 (C) 充分必要条件 (D) 既不充分也不必要条件 “复数i z a b =+(a ，b ∈R)为纯虚数”成立的充分不必要条件是(A) a =0，b ≠0(B) a =0(C) b =0(D) a =0，b =2(2015届丰台二模) 4．函数1,0,()2cos 1,20x f x x x ≥=--π≤<⎪⎩的所有零点的和等于(A) 1-2π (B)312π-(C)1-π(D)12π-(2015届昌平二模) 4. “||2b <是“直线y b =+与圆2240x y y +-=相交”的（A ）A ．充分不必要条件 B. 必要不充分条件 C ．充要条件 D. 既不充分也不必要条件 (2015届昌平二模) 7. 已知函数()y f x =（x ∈R ）是奇函数，其部分图象如图所示,则在(2,0)-上与函数()f x 的单调性相同的是（ D ）A.21y x =+ B. 2log y x= C.(0)(0)x x e x y e x -⎧≥⎪=⎨<⎪⎩ D. cos y x =框图(2015届西城二模)4．执行如图所示的程序框图，若输入的，则输出的s 属于（A ）6,aA ． {1‚ 2}B ．{1‚ 3}C ．{2 ‚ 3}D ．{1‚ 3‚ 9}(2015届昌平二模) 5. 在篮球比赛中，某篮球队队员投进三分球的个数如表所示： 右图是统计上述6名队员在比赛中投进的三分球总数s 的程序框图，则图中的判断框内应填入的条件是（A. 6i < B. 7i < C. 8i < D. 9i <12．执行如图所示的程序框图，则输出的结果是 ．向量(2015届西城二模) 2．已知平面向量，则实数k ＝（D ）A ．4B ．－4C ．8D ．－8(2015届东城二模)（13）已知非零向量,a b 满足||1=b ，a 与-b a 的夹角为120，则||a 的取值范围是 ．答案：]332,0( (2015届丰台二模)6．平面向量a 与b的夹角是3π，且1a =，2b =，如果AB a b =+，3AC a b =-，D 是BC 的中点，那么AD =(A)(B)(C) 3 (D) 6(2015届昌平二模) 12.如图,在菱形ABCD 中,1AB =,60DAB ∠=,E 为CD 的中点,则AB AE ⋅的值是 . 答案：1不等式线性规划(2015届西城二模)5．某生产厂商更新设备，已知在未来x 年内，此设备所花费的各种费用总和y （万元）与x 满足函数关BCDEA系，若欲使此设备的年平均花费最低，则此设备的使用年限x 为（B ）A ．3B ．4C ．5D ．6(2015届东城二模)（10）已知正数,x y 满足x y xy +=，那么x y +的最小值为 ．答案：4(2015届东城二模)（6）若实数y x ,满足不等式组330101x y x y y +-≤⎧⎪-+≥⎨⎪≥-⎩，，，则2||z x y =+的取值范围是（D ）（A ）[1,3]- （B ）[1,11] （C ）]3,1[ （D ）]11,1[-(2015届丰台二模)7．某生产厂家根据市场调查分析，决定调整产品生产方案，准备每周（按5天计算）生产A ，B ，C 三种产品共15吨（同一时间段内只能生产一种产品），已知生产这些产品每吨所需天数和每吨产值如下表：(A) 30 (B) 40 (C) 47.5 (D) 52.5某生产厂家根据市场调查分析，决定调整产品生产方案，准备每周（按5天计算）生产A ，B ，C 三种产品共15吨（同一时间段内只能生产一种产品），且C 种产品至少生产5吨，已知生产这些产品每吨所则每周最高产值是(A) 40 (B) 42.5(C) 45(D) 50说明：这两个题没有本质区别，主要差一句话（且C 种产品至少生产5吨），这句话意味着什么？考题希望交给学生遇到问题应如何思考。

2015北京中考二模选择题、填空题压轴题汇总一．选择题：【2015海淀二模】1.如右图所示，点Q 表示蜜蜂，它从点P 出发，按 照着箭头所示的方向沿P →A →B →P →C →D →P 的路径匀速飞行，此飞行路径是一个以直线l 为对称轴的轴对称图形，在直线l 上的点O 处（点O 与点P 不重合）利用仪器测量了∠POQ 的大小．设蜜蜂飞行时间为x ，∠POQ 的大小为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是（ ）A B C D【2015西城二模】2．在平面直角坐标系xOy 中，点M 的坐标为(,1)m ．如果以原点为圆心，半径为1的⊙O 上存在点N ，使得45OMN ∠=︒，那么m 的取值范围是（ ） A ．1-≤m ≤1 B. 1-＜m ＜1 C. 0≤m ≤1 D. 0＜m ＜1【2015东城二模】3. 如图，矩形ABCD 中，AB =3，BC =4，动点P 从A 点出发，按A →B →C 的方向在AB 和BC 上移动，记P A =x ，点D 到直线P A 的距离为y ，则y 关于x 的函数图象大致是（ ）A ．B ．C ．D ．【2015朝阳二模】4. 如图，矩形ABCD 中，E 为AD 中点，点F 为BC 上 的动点（不与B 、C 重合）．连接EF ，以EF 为直径的圆分别交BE ，CE 于点G 、H . 设BF 的长度为x ，弦FG 与FH 的长度和为y ，则下列图象中， 能表示y 与x 之间的函数关系的图象大致是（ ）A B CDDBACPQO【2015丰台二模】5．如图，点N 是以O 为圆心，AB 为直径的半圆上的动点，（不与点A ，B 重合），AB =4，M 是OA 的中点，设线段MN 的长为x ，△MNO 的面积为y ，那么下列图象中，能表示y 与x 的函数关系的图象大致是（ ）A B C D【2015石景山二模】6．在平面直角坐标系中，四边形ABCD 是菱形，其中点B的坐标是（0,2），点D 的坐标是（34，2），点M 和点N 是两个动点，其中点M 从点B 出发沿BA 以每秒1个单位的速度做匀速运动，到点A 后停止，同时点N 从B 点出发沿折线BC →CD 以每秒2个单位的速度做匀速运动，如果其中一点停止运动，则另一点也停止运动，设M 、N 两点的运动时间为x ，BMN 的面积是y ，下列图象中能表示y 与x 的函数关系的图象大致是（ ）AB CD【2015房山二模】7. 如图，在矩形A BCD 中，AB =2，点E 在边AD 上，∠ABE =45°，BE=DE ，连接BD ，点P 在线段DE 上，过点P 作PQ∥BD 交BE 于点Q ，连接QD ．设PD =x ，△PQD 的面积为y ，则能表示y 与x 函数关系的图象大致是（）A B C D【2015平谷二模】8．在平行四边形ABCD 中，点P 从起点B 出发，沿BC ，CD 逆时针方向向终点D 匀速运动．设点P 所走过的路程为x ，则线段AP ，AD的函数关系的图象大致如下图，则AB 边上的高是( )A ．3B ．4C ．5D ．6【2015门头沟二模】9．在平面直角坐标系中，四边形OABC 是矩形，点B 的坐标为（4，3）．平行于对角线AC 的直线m 从原点O 出发，沿x 轴正方向以每秒1个单位长度的速度运动，设直线m 与矩形OABC 的两边分别交于点M ，N ，直线m 运动的时间为t （秒）．设△OMN 的面积为S ，那么能反映S 与t 之间函数关系的大致图象是( )A B C D【2015昌平二模】10.如图，正方形ABCD 的边长为5，动点P 的运动路线为AB →BC ，动点Q 的运动路线为BD ．点P 与Q 以相同的均匀速度分别从A ，B 两点同时出发，当一个点到达终点停止运动时另一个点也随之停止．设点P 运动的路程为x ，△BPQ 的面积为y ，则下列能大致表示y 与x 的函数关系的图象为（ ）【2015怀柔二模】11．小丽早上从家出发骑车去上学，途中想起忘了带昨天晚上完成的数学作业，于是打电话让妈妈马上从家里送来，同时小丽也往回骑，遇到妈妈后停下说了几句话，接着继续骑车去学校．设小丽从家出发后所用时间为t ，小丽与学校的距离为S ．下面能反映S 与t 的函数关系的大致图象是（ ）y xOM AB C Nm【2015顺义二模】12．如图，大小两个正方形在同一水平线上，小正方形从图①的位置开始，匀速向右平移，到图③的位置停止运动．如果设运动时间为x ，大小正方形重叠部分的面积为y ，则下列图象中，能表示y 与x 的函数关系的图象大致是（ ）【2015通州二模】13．如图，火车匀速通过隧道（隧道长等于火车长）时，火车进入隧道的时间x 与火车在隧道内的长度．．．．．．y 之间的关系用图象描述大致是（ ）A ．B ．C ．D ．二．填空题：【2015海淀二模】1.五子棋是一种两人对弈的棋类游戏，规则是：在正方形棋盘中，由黑方先行，白方后行，轮流弈子，下在棋盘横线与竖线的交叉点上，直到某一方首先在任一方向（横向、竖向或者是斜着的方向）上连成五子者为胜．如图，这一部分棋盘是两个五子棋爱好者的对弈图．观察棋盘，以点O 为原点，在棋盘上建立平面直角坐标系，将每个棋子看成一个点，若黑子A 的坐标为（7，5），则白子B 的坐标为______________；为了不让白方获胜，此时黑方应该下在坐标为______________的位置处．C.B.A.D.图③图②图①第10题图【2015西城二模】2．如图，在平面直角坐标系xOy 中，点D 为直线2y x =上且在第一象限内的任意一点，1DA ⊥x 轴于点1A ，以1DA 为边在1DA 的右侧作正方形111A B C D ；直线1OC 与边1DA 交于点2A ，以2DA 为边在2DA 的右侧作正方形222A B C D ；直线2OC 与边1DA 交于点3A ，以3DA 为边在3DA 的右侧作正方形333A B C D ，……，按这种方式进行下去，则直线1OC 对应的函数表达式为 ，直线3OC 对应的函数表达式为 .【2015东城二模】3．如图，已知A 1，A 2，……，A n ，A n ＋1在x 轴上，且OA 1＝A 1A 2＝A 2A 3＝……＝A n A n ＋1＝1，分别过点A 1，A 2，……，A n ，A n ＋1作x 轴的垂线交直线y ＝x 于点B 1，B 2，……，B n ，B n ＋1，连接A 1B 2，B 1A 2，A 2B 3，B 2A 3，……，A n B n ＋1，B n A n ＋1，依次相交于点P 1，P 2，P 3，……，P n ，△A 1B 1P 1，△A 2B 2P 2，……，△A n B n P n 的面积依次为S 1，S 2，……，S n ，则S 1=，S n = ．【2015朝阳二模】4．如果一个平行四边形一个内角的平分线分它的一边为1:2的两部分，那么称这样的平行四边形为“协调平行四边形”，称该边为“协调边”．当“协调边”为3时，它的周长为 ． 【2015丰台二模】5．如图，在平面直角坐标系xOy 中，直线l 的表达式是y ＝x ，点A 1坐标为(0，1)，过点A 1作y 轴的垂线交直线l 于点B 1，以原点O 为圆心，OB 1长为半径画弧交y 轴于点A 2；再过点A 2作y 轴的垂线交直线l 于点B 2，以原点O 为圆心，OB 2长为半径画弧交y 轴于点A 3，…，按此做法进行下去，点B 4的坐标为 ，2015OA = ．【2015石景山二模】6．在平面直角坐标系xOy 中，我们把横，纵坐标都是整数的点叫做整点，已知在函数()50050<<+-=x x y 上有一点()n m P ,（,m n 均为整数），过点P 作x PA ⊥轴于点A ，y PB ⊥轴于点B ，当2=m 时，矩形PAOB 内部（不包括边界）有47个整点，当3=m 时，矩形PAOB 内部有92个整点，当4=m 时，矩形PAOB 内部有_____个整点，当=m ________时，矩形PAOB 内部的整点最多．33【2015房山二模】7．正方形111A B C O ，2221A B C C ，3332A B C C ，…，按如图所示的方式放置．点1A ，2A ，3A ，…，和点1C ，2C ，3C ，…，分别在直线1y x =+和x 轴上，则点B 1的坐标是_________;点B n 的坐标是 ．（用含n 的代数式表示）【2015平谷二模】8．在平面直角坐标系中，点A,B,C 的坐标分别为()1,0，()0,1，()1,0-．一个电动玩具从坐标原点O 出发，第一次跳跃到点P 1，使得点P 1与点O 关于点A 成中心对称；第二次跳跃到点P 2，使得点P 2与点P 1关于点B 成中心对称；第三次跳跃到点P 3，使得点P 3与点P 2关于点C 成中心对称；第四次跳跃到点P 4，使得点P 4与点P 3关于点A 成中心对称；第五次跳跃到点P 5，使得点P 5与点P 4关于点B 成中心对称；.…照此规律重复下去．则点P 3的坐标为 ；点P n 在y 轴上，则点P n 的坐标为 ．【2015门头沟二模】9．在平面直角坐标系xOy 中，矩形OABC 如图放置，动点P 从（0，3）出发，沿所示方向运动，每当碰到矩形的边时反弹，反弹时反射角等于入射角，当点P 第2次碰到矩形的边时，点P 的坐标为 ；当点P 第6次碰到矩形的边时，点P 的坐标为 ；当点P 第2015次碰到矩形的边时，点P 的坐标为____________.【2015昌平二模】10. 如图所示，是一张直角三角形纸片，其中有一个内角为30︒，最小边长为2，点D 、E 分别是一条直角边和斜边的中点，先将纸片沿DE 剪开，然后再将两部分拼成一个四边形，则所得四边形的周长是 ．【2015怀柔二模】11.已知等腰△ABC 中，AD⊥BC 于点D ，且AD=BC ，则△ABC 底角的度数为__________．21xy OA BC【2015顺义二模】12．如图，在平面直角坐标系xOy 中，点1A ，2A ，3A ，…，n A在x 轴的正半轴上，且1=2OA ，212OA OA =，322OA OA =，…，12n n OA OA -=，点1B ，2B ，3B ，…，n B 在第一象限的角平分线l 上，且11A B ，22A B ，…，n n A B 都与射线l 垂直， 则1B 的坐标是_ _____， 3B 的坐标是_ _____，n B 的坐标是_ _____．【2015通州二模】13．若x 是不等于1的实数，我们把11x -称为x 的差倒数，如2的差倒数是1112=--，－1的差倒数为11112=-（-），现已知，x 1=13-，x 2是x 1的差倒数，x 3是x 2的差倒数，x 4是x 3的差倒数，……，依次类推，则x 2015= .2015北京中考二模选择题、填空题压轴题汇总参考答案：一．选择题：1.D2.A3.B4.D5.D6.D7.C8.B9.C 10.B 11.B 12.C 13.B二．填空题：1. （5,1）； （3,7）或（7,3）2. 23y x = 1415y x =3.16；24+2n n 4. 8或105. （） 20142 6. 135；25． 7.()111B ， ,()121,2n n n B -- 8. （0，﹣2）；（0,0）或（0,﹣2）9. （7,4） （0,3） （1,4） 10. 8或 11. 45o或75o或15o12. 1A （1，1），3A （4，4），11n n n A --（2,2） 13.34。

北京各区二模理科数学分类汇编
排列组合二项式
(2015届西城二模)13．现有6 人要排成一排照相，其中甲与乙两人不相邻，且甲不站在两端，则不同的排法有 种．（用数字作答）答案：288
(2015届海淀二模
)
答案：14
(2015届东城二模)
（9）
若1)n
x 的二项展开式中各项的二项式系数的和是64，则n = ，展开式中的常数项
为 ．（用数字作答）答案：6，15
(2015届昌平二模) 13. 某班举行联欢会由5个节目组成，演出顺序有如下要求：节目甲必须和节目乙相邻，且节目甲不能排在第一个和最后一个，则该班联欢会节目演出顺序的编排方案共有___________种.（用数字作答）答案：36。

北京各区二模理科数学分类汇编三角(2015届西城二模)11．已知角α的终边经过点（－3，4），则cos α＝ ；cos 2α＝ ．答案：257,53-- (2015届西城二模)15．（本小题满分13 分）在锐角△ABC 中，角 A ，B ，C 所对的边分别为a ，b ，c ，已知a，b ＝3，32sin sin 7=+A B ．（Ⅰ） 求角A 的大小； （Ⅱ） 求△ABC 的面积．（Ⅰ）解：在ABC ∆中，由正弦定理sin sin a b AB=， ……………… 2分得3sin sin AB=3sin B A =， ……………… 3分sin B A +=，解得sin 2A =……………… 5分因为ABC ∆为锐角三角形，所以π3A =. ……………… 6分 （Ⅱ）解：在ABC ∆中，由余弦定理222cos 2b c a A bc+-=， ……………… 8分得219726c c+-=，即2320c c -+=，解得1c = 或 2c =. ……………… 10分当1c =时，因为222cos 2014c b Baca +-==-<， 所以角B 为钝角，不符合题意，舍去. ……………… 11分当2c =时，因为222cos 20c b B aca +-==>，且b c >，b a >， 所以ABC ∆为锐角三角形，符合题意.所以ABC ∆的面积11sin 3222S bc A ==⨯⨯. ……………… 13分(2015届海淀二模)答案：B(2015届海淀二模)（15）（共13分）解：（Ⅰ）因为a A =， 所以22222b c a a bc+-=. ………………3分因为 5c =，b =所以23404930a a +-⨯=.解得：3a =，或493a =-（舍）. ………………6分（Ⅱ）由（Ⅰ）可得：cos 3A ==.所以21cos 22cos 13A A =-=. ………………9分 因为3a =，5c =，b =，所以2221cos 23a cb B ac +-==. ………………11分所以cos2cos A B =. ………………12分 因为 c b a >>，所以 (0,)3A π∈.因为 (0,)B ∈π，所以2B A ∠=∠. ………………13分另解：因为(0,)A ∈π，所以sin 3A ==.由正弦定理得：sin 3B = 所以sin 3B =.所以sin 22sin 333A B =⨯==. ………………12分 因为 c b a >>，所以 (0,)3A π∈，(0,)2B π∈.所以 2B A ∠=∠. ………………13分(2015届东城二模) （1）23sin()6π-=（C ） （A）-（B ）12-（C ）12（D(2015届东城二模) （15）（本小题共13分）已知函数2sin 22sin ()sin x x f x x-=．（Ⅰ）求()f x 的定义域及其最大值；（Ⅱ）求()f x 在(0,π)上的单调递增区间．（15）（共13分）解：（Ⅰ）由sin 0x ≠，得xk k ≠π(∈)Z ．所以()f x 的定义域为{|}x x k k ∈≠π,∈R Z ． …………………2分因为2sin 22sin ()sin x x f x x-=，2cos 2sin x x =-)4x π=+， …………………6分所以()f x的最大值为 …………………7分（Ⅱ）函数cos y x =的单调递增区间为[22k k π+π,π+2π]（k ∈Z ）由224k x k ππ+π≤+≤π+2π，x k k ≠π(∈)Z ，且(0,x ∈π)，所以()f x 在(0,π)上的单调递增区间为3[,4ππ)． ……13分(2015届昌平二模) 11. 在ABC ∆中，若a =b =5π6B ∠=，则边c =__________. 答案：1(2015届昌平二模) 15. (本小题满分13分) 已知函数()sin()(0,0,||,)2f x A x A x ωϕωϕπ=+>><∈R 的部分图象如图所示. （I ）求函数()f x 的解析式；（II ）求函数()()()123g x f x f x ππ=+-+ 的单调递增区间.解：（I ）由题意可知，2A =,39412T π=，得T =π,2T ωπ==π，解得2=ω.()2sin(2)233f ϕππ=⨯+=， 即2232k k ϕππ+=+π,∈Z ，||2ϕπ<，所以 6ϕπ=-，故()2sin(2)6f x x π=-. ……………7分(II)ππππ()2sin(2(+)-)-2sin(2(+)-)12636g x x x =π2sin2-2sin(2+)2=2sin22cos2)4x x x -x =x =π-由222,242k x k k πππ-+π≤-≤+π∈Z,,88k x k k π3π-+π≤≤+π∈Z. 故()g x 的单调递增区间是[,],88k k k π3π-+π+π∈Z..……………13分(2015届丰台二模)15.（本小题共13分） 在△ABC 中，30A ︒=，52=BC ，点D 在AB 边上，且BCD ∠为锐角，2CD =，△BCD 的面积为4．（Ⅰ）求cos BCD ∠的值； （Ⅱ）求边AC 的长． 15.（本小题共13分） 解：（Ⅰ）因为1sin 42BCDS BC CD BCD ∆=⋅⋅∠=， 所以552sin =∠BCD ．因为BCD ∠为锐角，所以cos BCD∠==． ……………………6分 （Ⅱ）在BCD ∆中，因为BCD BC CD BC CD DB∠⋅⋅-+=cos 2222，所以4=DB ． 因为222BC CD DB=+，所以︒=∠90CDB ．所以ACD ∆为直角三角形． 因为30A ︒=，所以24AC CD ==，即4AC =． ……………………13分。

北京各区二模理科数学分类汇编概率统计(2015届西城二模)16．（本小题满分13 分）某厂商调查甲、乙两种不同型号电视机在10 个卖场的销售量（单位：台），并根据这10 个卖场的销售情况，得到如图所示的茎叶图．为了鼓励卖场，在同型号电视机的销售中，该厂商将销售量高于数据平均数的卖场命名为该型号电视机的“星级卖场”．（Ⅰ）当a ＝b ＝3时，记甲型号电视机的“星级卖场”数量为m ，乙型号电视机的“星级卖场”数量为n ，比较m ，n 的大小关系；（Ⅱ）在这10 个卖场中，随机选取2 个卖场，记X 为其中甲型号电视机的“星级卖场”的个数，求X 的分布列和数学期望．（Ⅲ）若a ＝1，记乙型号电视机销售量的方差为s2，根据茎叶图推断b为何值时，s2达到最小值．（只需写出结论）16．（本小题满分13分）（Ⅰ）解：根据茎叶图，得甲组数据的平均数为101014182225273041432410+++++++++=，………1分乙组数据的平均数为1018202223313233334326.510+++++++++=. …………2分由茎叶图，知甲型号电视机的“星级卖场”的个数5m=，………………3分乙型号电视机的“星级卖场”的个数5n=，所以m n=. ………………4分（Ⅱ）解：由题意，X的所有可能取值为0，1，2，………………5分且0255210C C2(0)C9P X===，1155210C C5(1)C9P X===，2055210C C2(2)C9P X===，…………8分所以X的分布列为：X0 1 2P295929………………9分所以252()0121999E X=⨯+⨯+⨯=. ………………10分（Ⅲ）解：当b=0时，2s达到最小值．………………13分(2015届海淀二模)答案：A(2015届海淀二模)（16）（共13分）解：（Ⅰ）20名女生掷实心球得分如下：5，6，7，7，7，7，7，7，8，8，8，9，9，9，9，9，9，9，10，10．所以中位数为8，众数为9．………………3分（Ⅱ）X的可能取值为0，1，2．………………4分73 5 5 284 5 519 7 8 乙甲()21222033095C P X C ===；()1112822048195C C P X C ===；()2822014295C P X C ===；………………10分 （Ⅲ）略. ………………13分 评分建议：从平均数、方差、极差、中位数、众数等角度对整个年级学生掷实心球项目的情况进行合理的说明即可；也可以对整个年级男、女生该项目情况进行对比；或根据目前情况对学生今后在该项目的训练提出合理建议.(2015届东城二模) （4）甲、乙两名同学8次数学测验成绩如茎叶图所示，12,x x 分别表示甲、乙两名同学8次数学测验成绩的平均数，12,s s 分别表示甲、乙两名同学8次数学测验成绩的标准差，则有（B ）（A ）12x x >，12s s < （B ）12x x =，12s s <（C ）12x x =，12s s = （D ）12x x <，12s s >(2015届东城二模) （16）（本小题共13分）某校高一年级开设A ，B ，C ，D ，E 五门选修课，每位同学须彼此独立地选三门课程，其中甲同学必选A 课程，不选B 课程，另从其余课程中随机任选两门课程．乙、丙两名同学从五门课程中随机任选三门课程．（Ⅰ）求甲同学选中C 课程且乙同学未选中C 课程的概率；（Ⅱ）用X 表示甲、乙、丙选中C 课程的人数之和，求X 的分布列和数学期望．（16）（共13分）解：（Ⅰ）设事件A 为“甲同学选中C 课程”，事件B 为“乙同学选中C 课程”．则1223C 2()C 3P A ==，2435C 3()C 5P B ==． 因为事件A 与B 相互独立，所以甲同学选中C 课程且乙同学未选中C 课程的概率为224()()()()[1()]3515P AB P A P B P A P B ==-=⨯=． …………………4分（Ⅱ）设事件C 为“丙同学选中C 课程”．1=6,a则2435C 3()C 5P C ==．X 的可能取值为：0,1,2,3．1224(0)()35575P X P ABC ===⨯⨯=． (1)()()()P X P ABC P ABC P ABC ==++2221321232035535535575=⨯⨯+⨯⨯+⨯⨯=． (2)()()()P X P ABC P ABC P ABC ==++2322231333335535535575=⨯⨯+⨯⨯+⨯⨯=． 23318(3)()35575P X P ABC ===⨯⨯=． X 为分布列为：420331814028()0123757575757515E X =⨯+⨯+⨯+⨯==．………13分(2015届昌平二模) 5. 在篮球比赛中，某篮球队队员投进三分球的个数如表所示：右图是统计上述6名队员在比赛中投进的三分球总数s A. 6i < B. 7i < C. 8i < D. 9i <(2015届昌平二模) 16. （本小题满分13分）某大学志愿者协会有10名同学，成员构成如下表，其中表中部分数据不清楚，只知道从这10名同学中随机抽取一位，抽到该名同学为“数学专业．．．．”的概率为25.现从这10名同学中随机选取3名同学参加社会公益活动（每位同学被选到的可能性相同）.（I ） 求,m n 的值；（II ）求选出的3名同学恰为专业互不相同的男生．．的概率； （III ）设ξ为选出的3名同学中“女生或数学专业．．．．．．．”的学生的人数，求随机变量ξ的分布列及其数学期望E ξ.16. (本小题满分13分)解：（I ）设事件A ：从10位学生中随机抽取一位，抽到该名同学为“数学专业”． 由题意可知，“数学专业”的学生共有(1)m +人． 则12()105m P A +==． 解得 3m =．所以1n =． …………… 4分（II ）设事件B ：从这10名同学中随机选取3名同学为专业互不相同的男生．则123331011()12C C P B C +==． ……………7分 （III ）由题意，ξ的可能取值为0，1，2，3． 由题意可知，“女生或数学专业”的学生共有7人．所以333101(0)120C P C ===ξ，1273310217(1)12040C C P C ====ξ， 21733106321(2)12040C C P C ====ξ，37310357(3)12024C P C ====ξ． 所以ξ的分布列为所以 012312040402410E =⨯+⨯+⨯+⨯=ξ． ……………13分(2015届丰台二模) 16.（本小题共13分）长时间用手机上网严重影响着学生的健康，某校为了解A ，B 两班学生手机上网的时长，分别从这两个班中随机抽取6名同学进行调查，将他们平均每周手机上网时长作为样本数据，绘制成茎叶图如图所示（图中的茎表示十位数字，叶表示个位数字）．如果学生平均每周手机上网的时长超过21小时，则称为“过度用网”．（Ⅰ）请根据样本数据，估计A ，B 两班的学生平均每周上网时长的平均值；（Ⅱ）从A 班的样本数据中有放回地抽取2个数据，求恰有1个数据为“过度用网”的概率；（Ⅲ）从A 班、B 班的样本中各随机抽取2名学生的数据，记“过度用网”的学生人数为ξ，写出ξ的分布列和数学期望ξE ．(2015届昌平二模) 16. （本小题满分13分）某大学志愿者协会有10名同学，成员构成如下表，其中表中部分数据不清楚，只知道从这10名同学中随机抽取一位，抽到该名同学为“数学专业．．．．”的概率为25.现从这10名同学中随机选取3名同学参加社会公益活动（每位同学被选到的可能性相同）. （I ） 求,m n 的值；（II ）求选出的3名同学恰为专业互不相同的男生．．的概率；（III ）设ξ为选出的3名同学中“女生或数学专业．．．．．．．”的学生的人数，求随机变量ξ的分布列及其数学期望E ξ. 解：（I ）设事件A ：从10位学生中随机抽取一位，抽到该名同学为“数学专业”．A 班B 班 0 1 2 39 1 0 73 41 1 62 57由题意可知，“数学专业”的学生共有(1)m +人． 则12()105m P A +==． 解得 3m =．所以1n =． …………… 4分（II ）设事件B ：从这10名同学中随机选取3名同学为专业互不相同的男生．则123331011()12C C P B C +==． ……………7分 （III ）由题意，ξ的可能取值为0，1，2，3． 由题意可知，“女生或数学专业”的学生共有7人．所以333101(0)120C P C ===ξ，1273310217(1)12040C C P C ====ξ， 21733106321(2)12040C C P C ====ξ，37310357(3)12024C P C ====ξ． 所以ξ的分布列为 所以1721721012312040402410E =⨯+⨯+⨯+⨯=ξ． ……………13分。

北京各区二模理科数学分类汇编立几(2015届西城二模) 8．在长方体，点M 为AB 1 的中点，点P 为对角线AC 1上的动点，点Q 为底面ABCD 上的动点（点P ，Q 可以重合），则MP ＋PQ 的最小值为（ ）(2015届西城二模) 17．（本小题满分14 分）如图 1，在边长为4 的菱形ABCD 中，AB DE BAD ⊥=∠,600于点E ，将△ADE 沿DE折起到△A 1D E 的位置，使A 1D ⊥DC ，如图 2．⑴ 求证：A 1E ⊥平面BCDE ；⑵ 求二面角E —A 1B —C 的余弦值；⑶ 判断在线段EB 上是否存在一点P ，使平面A 1DP ⊥A 1BC ？若存在，求出的值；若不存在，说明理由．17．（本小题满分14分）（Ⅰ）证明：因为D E BE ⊥,//BE DC ,所以DE DC ⊥, ……………… 1分 又因为1A D DC ⊥，1A D DE D =,所以DC ⊥平面1A DE ， ……………… 2分所以1DC A E ⊥. ……………… 3分 又因为1A E DE ⊥,DCDE D =,所以1A E ⊥平面B C D E .……………… 4分（Ⅱ）解：因为1A E ⊥平面B C D E ，D E BE ⊥，所以1,,A E DE BE 两两垂直，以1,,EB ED EA 分别为x 轴、y 轴和z 轴，如图建立空间直角坐标系， ……………… 5分易知DE= 则1(0,0,2)A ，(2,0,0)B，C，(0,D ，EA 1BCD所以1(2,0,2)BA =-,BC =.平面1A BE 的一个法向量为0,1,0n =（）， ……………… 6分 设平面1A BC 的法向量为(,,)m x y z =,由10BA m ⋅=，0BC m ⋅=,得220,20.x z x -+=+=⎧⎪⎨⎪⎩令 1y =,得(3,1,m =-. ……………… 8分所以7cos ,7||||m n m n m n ⋅<>==⋅.由图，得二面角1E A B C--的为钝二面角，所以二面角1E A B C --的余弦值为7-. ……………… 10分（Ⅲ）结论：在线段EB 上不存在一点P ，使平面1A DP ⊥平面1A BC . ……………… 11分 解：假设在线段EB 上存在一点P ，使平面1A DP ⊥平面1A BC .设(,0,0)P t （02t ≤≤），则1(,0,2)A P t =-,1(0,2)A D =-，…………… 12分 设平面1A DP 的法向量为111(,,)p x y z =，由10A D p ⋅=，10A P p ⋅=，得111120,20.z tx z-=-=⎧⎪⎨⎪⎩令 12x =，得所以)p t =. ……………… 13分因为平面1A DP ⊥平面1A BC ，所以0m p ⋅=，即0+=，解得3t =-. 因为02t ≤≤，所以在线段EB 上不存在点P ，使得平面1A DP ⊥平面1A BC . ……………… 14分(2015届海淀二模)A 1EC答案：C(2015届海淀二模)（17）（共14分） （Ⅰ）证明：连结BD 交AC 于点O ，连结OM .因为 //AB CD ，2AB CD =，所以2BO ABDO CD ==. 因为 2BM MP =，所以2BMPM =. 所以 BM BOPM DO=. 所以 //OM PD . ………………2分 因为 OM ⊂平面MAC ，PD ⊄平面MAC ，所以 //PD 平面MAC . ………………4分（Ⅱ）证明：因为 平面PAD⊥平面ABCD ，AD AB ⊥，平面PAD 平面ABCD AD =，AB ⊂平面ABCD ，所以AB ⊥平面PAD . ………………6分 因为 PA ⊂平面PAD ，所以 AB PA ⊥. ………………7分 同理可证：AD PA ⊥.因为 AD ⊂平面ABCD ，AB ⊂平面ABCD ，AD AB A =，所以PA ⊥平面ABCD . ………………9分（Ⅲ）解：分别以边,,AD AB AP所在直线为,,x y z轴，建立如图所示的空间直角坐标系.由MBD C O A PEFA22AB AD AP CD ====得(0,0,0)A ，(0,2,0)B ，(2,1,0)C ，(2,0,0)D ，(0,0,2)P ，则(2,1,0)AC =u u u r，(0,2,2)PB =-u u r.由（Ⅱ）得：PA⊥平面ABCD .所以 平面ABCD 的一个法向量为(0,0,1)n =r. ………………10分设PMPBλ=(01)λ≤≤，即P M P λ=u u u r u u r .所以(0,2,22)AM AP PB λλλ=+=-u u u r u u u r u u r.设平面AMC 的法向量为(,,)m x y z =u r，则 0,0,m AC m AM ⎧⋅=⎪⎨⋅=⎪⎩u r uuu r ur uuu r 即20,2(22)0.x y y z λλ+=⎧⎨⋅+-⋅=⎩令1xλ=-，则22y λ=-，2z λ=-.所以(1,22,2)m λλλ=---u r. ………………12分因为 二面角B AC M--的余弦值为23，所以23=，解得12λ=.所以 PM PB的值为12. ………………14分(2015届东城二模)（17）（本小题共14分） 如图，三棱柱ABC DEF -的侧面BEFC 是边长为1的正方形，侧面BEFC ⊥侧面ADEB ，4AB =，60DEB ∠=，G 是DE 的中点．（Ⅰ）求证：CE ∥平面AGF ；（Ⅱ）求证：GB⊥平面BEFC ；（Ⅲ）在线段BC 上是否存在一点P ，使二面角P GE B --为45，的长；若不存在，说明理由．（17）（共14分）（Ⅰ）证明：连接CD 与AF 相交于H ，则H 为CD 的中点，连接HG ．因为G 为DE 的中点， 所以HG ∥CE ． 因为CE⊄平面AGF ，HG ⊂平面AGF ，A所以CE ∥平面AGF ． ………4分（Ⅱ）证明：1BE=，2GE =，在△GEB 中，60GEB ∠=，BG =．因为222BG BE GE +=，所以GBBE ⊥．因为侧面BEFC⊥侧面ADEB ，侧面BEFC侧面ADEB BE =，GB ⊂平面ADEB ，所以GB⊥平面BEFC ． ………8分（Ⅲ）解：,,BG BE BC 两两互相垂直，建立空间直角坐标系B xyz -．二面角为．假设在线段BC 上存在一点P ，使平面BGE 的法向量(0,0,1)=m，设(0,0,),[0,1]P λλ∈．G (0,1,0)E ．所以()GP λ=，(,0)GE =．设平面PGE 的法向量为(,,)x y z =n ，则0,0.GPGE ⎧⋅=⎪⎨⋅=⎪⎩n n所以0,0.z y λ⎧+=⎪⎨+=⎪⎩令1z=，得y λ=，x =，所以PGE 的法向量为,1)λ=n ．因为1⋅=m n ，所以112=，解得[]0,1λ=，故BP =． 因此在线段BC 上存在一点P ，使二面角P GE B --为45，且BP=. ………14分(2015届昌平二模) 6 一个几何体的三视图如图所示，则这个几何体的体积为A.B.C.D.(2015届丰台二模) 5(A) 6(B)29(C) 3 (D)23(2015届丰台二模)17.（本小题共14分）如图所示，在四棱柱1111D C B A ABCD -中，⊥1AA 底面A B C D ，BD AC⊥于O,且124AA OC OA ===，点M 是棱1CC 上一点．（Ⅰ）如果过1A ，1B ，O 的平面与底面ABCD 交于直线l ，求证：//l AB ；（Ⅱ）当M 是棱1CC 中点时，求证：1AO DM ⊥； （Ⅲ）设二面角1A BD M--的平面角为θ，当cos 25θ=时，求CM 的长．（Ⅲ）原题：设二面角1A BD M --的余弦值为25，求CM 的长．（要舍一解）17.（本小题共14分）证明：（Ⅰ）因为1111D C B A ABCD -是棱柱，所以BAB A 11侧 视图正视图俯视图俯视图正视图OMD 1C 1B 1A 1DCBA是平行四边形．所以AB B A //11．因为⊄11B A 平面ABCD ，⊂AB 平面ABCD ，所以//11B A 平面ABCD ．因为平面O B A 11平面ABCD l =，所以11//B A l ． 所以AB l //．………………4分（Ⅱ）因为DB AC ⊥于O ，如图建立空间直角坐标系．因为41=AA ，且24OC AO ==，所以(0,0,0)O ，(4,0,0)C ，(2,0,0)A -，1(2,0,4)A -．因为M 是棱1CC 中点，所以(4,0,2)M ． 设(0,,0)D b ，所以(4,,2)DM b =-，1(2,0,4)OA =-．所以08081=++-=⋅．所以1AO DM ⊥． ……………………8分 （Ⅲ）设(0,,0)D b ，(0,,0)B c ，平面BD A 1的法向量为),,(z y x m =，又因为1(2,,4)AD b =-，1(2,,4)AB c =-，所以1102402400m A D x by z x cy z m A B ⎧⋅=+-=⎧⎪⇒⎨⎨+-=⋅=⎩⎪⎩．因为c b≠，所以0=y ，令1z =，则2x =，所以(2,0,1)m =．设),0,4(h M ，所以(4,,)MD b h =--，(4,,)MB c h =--． 设平面MBD 的法向量为111(,,)n x y z =，所以 111111400400x by hz n MD x cy hz n MB ⎧-+-=⋅=⎧⎪⇒⎨⎨-+-=⋅=⎩⎪⎩．因为c b ≠，所以10y =，令11z =，则14h x =-，所以(,0,1)4hn =-．B又因为cos θ=， 所以2cos ,m n<>=，即125m nn m⋅==解得3h=或76h =． 所以点(4,0,3)M 或7(4,0,)6M ．所以3CM =或76CM =． ……………………14分(2015届昌平二模) 17. (本小题满分14分)如图，已知等腰梯形ABCD 中，1//,2,2AD BC AB AD BC E ===是BC 的中点，AE BD M =，将BAE ∆沿着AE 翻折成1B AE ∆，使平面1B AE ⊥平面AECD .（I ） 求证：1CD B DM ⊥平面；（II ）求二面角1D AB E --的余弦值； （III ）在线段1BC 上是否存在点P ，使得//MP 平面1B AD ，若存在，求出11B PB C的值；若不存在，说明理由.17. (本小题满分14分) ( I ) 由题意可知四边形ABED 是平行四边形，所以MEAM =，故AE M B ⊥1.又因为,AB BE M AE =为的中点,所以BM AE ⊥,即.DMAE ⊥AD //BC 又因为, 2.AD CE ==所以四边形ADCE 是平行四边形.所以//.AE CD 故CD DM ⊥.因为平面⊥AE B 1平面AECD , 平面 AE B 1平面AEAECD =,1B M ⊂平面AECD所以⊥MB 1平面AECD .1.B M AE ⊥因为⊂CD平面AECD , 所以⊥M B 1CD .因为M M B MD =1 , MD 、⊂M B 1平面MD B 1,所以⊥CD平面MD B 1. ……………5分(II) 以ME 为x 轴, MD 为y轴, 1MB 为z 轴建立空间直角坐标系，则)0,3,2(C , )3,0,0(1B , )0,0,1(-A ,)0,3,0(D .平面E AB 1的法向量为)0,3,0(=→MD .设平面A DB 1的法向量为),,(z y x m =→, 因为)3,0,1(1=→AB ，)0,3,1(=→AD ,⎪⎩⎪⎨⎧=+=+0303y x z x , 令1=z 得, )1,1,3(-=→m .所以55,cos >=<→→MD m , 因为二面角E AB D --1为锐角, 所以二面角E AB D --1的余弦值为55. ……………10分 (III) 存在点P ,使得//MP 平面1B AD . ……………11分 法一: 取线段1BC 中点P ，1B D 中点Q ，连结,,MP PQ AQ . 则//PQ CD ，且1=2PQ CD . 又因为四边形AECD 是平行四边形，所以//AE CD .因为M 为AE 的中点，则//AM PQ .所以四边形AMPQ 是平行四边形，则//MP AQ .又因为AQ ⊂平面1AB D ,所以//MP 平面1AB D .所以在线段C B 1上存在点P ，使得//MP 平面AD B 1，2111=C B P B . ……………14分 法二：设在线段C B 1上存在点P ，使得//MP 平面AD B 1,设11B P B C λ=,(10≤≤λ),C ，因为11MP MB B P =+.所以(2)MP λ=.因为//MP 平面AD B 1, 所以0MP m ⋅=, 所以033332=-++-λλλ, 解得21=λ, 又因为MP ⊄平面AD B 1, 所以在线段C B 1上存在点P ，使得//MP 平面AD B 1，2111=C B P B ．……………14分。

2015北京中考数学二模试题28题汇编及答案28．如图1，在△ABC中，AB=AC，∠ABC =α，D是BC边上一点，以AD为边作△ADE，使AE=AD，DAE∠+BAC∠=180°．（1）直接写出∠ADE的度数（用含α的式子表示）；（2）以AB，AE为边作平行四边形ABFE，①如图2，若点F恰好落在DE上，求证：BD=CD；②如图3，若点F恰好落在BC上，求证：BD=CF．图1 图2 图328．正方形ABCD的边长为3，点E，F分别在射线DC，DA上运动，且DE=DF．连接BF，作EH⊥BF所在直线于点H，连接CH.（1）如图1，若点E是DC的中点，CH与AB之间的数量关系是；（2）如图2，当点E在DC边上且不是DC的中点时，（1）中的结论是否成立？若成立给出证明；若不成立，说明理由；（3）如图3，当点E，F分别在射线DC，DA上运动时，连接DH，过点D作直线DH 的垂线，交直线BF于点K，连接CK，请直接写出线段CK长的最大值．28. 如图1，在ABC Rt △中，90ACB ∠=︒，E 是边AC 上任意一点(点E 与点A ，C 不重合)，以CE 为一直角边作ECD Rt △，90ECD ∠=︒，连接BE ，AD . (1) 若CA CB =，CE CD =，①猜想线段BE ，AD 之间的数量关系及所在直线的位置关系，直接写出结论； ②现将图1中的ECD Rt △绕着点C 顺时针旋转锐角α，得到图2，请判断①中的结论是否仍然成立，若成立，请证明；若不成立，请说明理由；(2) 若8CA =，6CB =，3CE =，4CD =，ECD Rt △绕着点C 顺时针旋转锐角α，如图3，连接BD ，AE ，计算22BD AE +的值.28． 已知△ABC 是锐角三角形，BA =BC ，点E 为AC 边的中点，点D 为AB 边上一点，且∠ABC =∠AED =α．（1）如图1，当α=40°时，∠ADE = °；（2） 如图2，取BC 边的中点F ，联结FD ，将∠AED 绕点E 顺时针旋转适当的角度β(β<α)，得到∠MEN ，EM 与BA 的延长线交于点M ， EN 与FD 的延长线交于点N ． ①依题意补全图形；②猜想线段EM 与EN 之间的数量关系，并证明你的结论．图3EAC图1 图228．如图1，点O 为正方形ABCD 的中心．（1）将线段OE 绕点O 逆时针方向旋转︒90，点E 的对应点为点F ，连结EF ，AE ，BF ，请依题意补全图1；（2）根据图1中补全的图形，猜想并证明AE 与BF 的关系；（3）如图2，点G 是OA 中点，△EGF 是等腰直角三角形，H 是EF 的中点，︒=∠90EGF，AB =2=GE ，△EGF 绕G 点逆时针方向旋转α角度，请直接写出旋转过程中BH 的最大值．ECCBH EFGODA图1图228．数学活动课上，老师提出这样一个问题:如果AB=BC,∠ABC=60°,∠APC=30°,连接PB，那么P A、PB、PC之间会有怎样的等量关系呢？经过思考后，部分同学进行了如下的交流：小蕾：我将图形进行了特殊化，让点P在BA延长线上（如图1），得到了一个猜想: P A2+PC2=PB2 .小东：我假设点P在∠ABC的内部，根据题目条件，这个图形具有“共端点等线段特点，可以利用旋转解决问题，旋转△P AB后得到△P′CB ,并且可推出△PBP′ ,△PCP′分别是等边三角形、直角三角形，就能得到猜想和证明方法.这时老师对同学们说，请大家完成以下问题：（1）如图2，点P在∠ABC的内部，①P A=4，PC=PB= .②用等式表示P A、PB、PC之间的数量关系，并证明.（2）对于点P的其他位置，是否始终具有②中的结论？若是，请证明；若不是，请举例说明.图1 图228．如图，△ABC中，∠BAC=90°，AB=AC，边BA绕点B顺时针旋转α角得到线段BP，连结PA，PC，过点P作PD⊥AC于点D．（1）如图1，若α=60°，求∠DPC的度数；（2）如图2，若α=30°，直接写出∠DPC的度数；（3）如图3，若α=150°，依题意补全图，并求∠DPC的度数．EF OA BCD28.在△ABC 中，AB ＝BC=2，∠ABC ＝90°，BD 为斜边AC 上的中线，将△ABD 绕点D 顺时针旋转α(0°＜α＜180°)得到△EFD ，其中点A 的对应点为点E ，点B 的对应点为点F . BE 与FC 相交于点H .（1）如图1，直接写出BE 与FC 的数量关系：____________; （2）如图2，M 、N 分别为EF 、BC 的中点.求证：MN = 22FC ;（3）连接BF ，CE ，如图3，直接写出在此旋转过程中，线段BF 、CE 与AC 之间的数量关系： .28.如图，在平行四边形ABCD 中，AB =5，BC =12，对角线交于点O ，∠BAD 的平分线交BC 于E 、交BD 于F ，分别过顶点B 、D 作AE 的垂线，垂足为G 、H ，连接OG 、OH ． （1）补全图形； （2）求证：OG =OH ；（3）若OG ⊥OH ，直接写出∠OAF 的正切值．图3CDD图2图1ABPCBCPA图2图1图328．对某一种四边形给出如下定义：有一组对角相等而另一组对角不相等的凸四边形叫做“等对角四边形”．（1）已知：如图1，四边形ABCD 是“等对角四边形”，∠A ≠∠C ，∠A =70°，∠B =80°．则∠C = 度，∠D = 度． （2）在探究“等对角四边形”性质时：小红画了一个“等对角四边形ABCD ”（如图2），其中∠ABC =∠ADC ，AB =AD ，此时她发现CB =CD 成立．请你证明此结论；（3）已知：在“等对角四边形ABCD ”中，∠DAB =60°，∠ABC =90°，AB =5，AD =4．求对角线AC 的长．28．如图1，在△ABC 中，CA =CB ，∠ACB =90°，D 是△ABC 内部一点，∠ADC =135°，将线段CD 绕点C 逆时针旋转90°得到线段CE ，连接DE ． （1）① 依题意补全图形；② 请判断∠ADC 和∠CDE 之间的数量关系，并直接写出答案．（2）在（1）的条件下，连接BE ，过点C 作CM ⊥DE ，请判断线段CM ，AE 和BE 之间的数量关系，并说明理由．（3）如图2，在正方形ABCD 中，AB =2，如果PD =1，∠BPD =90°，请直接写出点A到BP 的距离．图1 图2DAB CPDC AB图1图228．如图①，∠MON =60°，点A ，B 为射线OM ，ON 上的动点（点A ，B 不与点O 重合），且AB =34，在∠MON 的内部、△AOB 的外部有一点P ，且AP =BP ，∠APB =120°． （1）求AP的长；（2）求证：点P 在∠MON 的平分线上；（3）如图②，点C ，D ，E ，F 分别是四边形AOBP 的边AO ，OB ，BP ，P A 的中点，连接CD ，DE ，EF ，FC ，OP ．当A B ⊥OP 时，请直接．．写出四边形CDEF 周长的值．图① 图②OO答案28．(本小题满分7分) （1）∠ADE=90α︒-．…………………………………………………………… ……………………….…1分（2）①证明：∵四边形ABFE 是平行四边形， ∴AB ∥EF ．∴EDC ABC α∠=∠=． …………………………….……2分 由（1）知，∠ADE =90α︒-，∴90ADC ADE EDC ∠=∠+∠=︒． …………………...……3分 ∴AD ⊥BC ． ∵AB =AC ， ∴BD =CD ．……………………………………………………………………………………..……………4分 ②证明：∵AB =AC ，∠ABC =， ∴C B α∠=∠=．∵四边形ABFE 是平行四边形，∴AE ∥BF , AE =BF ． ∴EAC C α∠=∠=．……………………………………………………………………………………………5分由（1）知，2DAE α∠=， ∴DAC α∠=．…………………………………………………………………………………………………6分 ∴DAC C ∠=∠．α∴AD =CD ． ∵AD =AE =BF ， ∴BF =CD ． ∴BD =CF ．………………………………………………………………………………………………………7分28．解：（1）CH=AB ． ………………………………… 1分 （2）结论成立．………………………………… 2分 证明：如图11，连接BE ． 在正方形ABCD 中，AB=BC=CD=AD ，∠A=∠BCD=∠ABC=90°． ∵ DE=DF ， ∴ AF=CE ．在△ABF 和△CBE 中，,,,AB CB A BCE AF CE =⎧⎪∠=∠⎨⎪=⎩∴ △ABF ≌△CBE ．∴ ∠1=∠2．……………………………………………………………………3分 ∵ EH ⊥BF ，∠BCE =90°，∴ H ，C 两点都在以BE 为直径的圆上． ∴ ∠3=∠2． ∴ ∠3=∠1．∵ ∠3+∠4=90°，∠1+∠HBC =90°， ∴ ∠4=∠HBC ．∴ CH=CB ．………………………………………………………………… 5分 ∴ CH=AB ．………………………………………………………………… 6分 （3）3．………………………………………………………………………7分28．（1）①解： BE AD =，BE AD ⊥；……2分 ②BE AD =，BE AD ⊥仍然成立；证明：设BE 与AC 的交点为点F ，BE 与AD 的交点为点G ，如图1. ∵90ACB ECD ∠=∠=︒， ∴ACD BCE ∠=∠. 在ACD △和BCE △中，,,,AC BC ACD BCE CD CE =⎧⎪∠=∠⎨⎪=⎩∴ACD BCE △≌△.∴AD BE =，CAD CBE ∠=∠.……3分∵BFC AFG ∠=∠，90BFC CBE ∠+∠=︒， ∴90AFG CAD ∠+∠=︒. ∴90AGF ∠=︒. ∴BE AD ⊥.……4分（2）证明：设BE 与AC 的交点为点F ，BE 的延长线与AD 的交点为点G ，如图2. ∵90ACB ECD ∠=∠=︒， ∴ACD BCE ∠=∠.∵8CA =，6CB =，3CE =，4CD =，∴43CA CD CB CE ==. ∴ACD BCE △∽△.……5分∴CAD CBE ∠=∠.∵BFC AFG ∠=∠，90BFC CBE ∠+∠=︒，∴90AFG CAD ∠+∠=︒. ∴90AGF ∠=︒. ∴BG AD ⊥.……6分 ∴90AGE BGD ∠=∠=︒.∴222AE AG EG =+，222BD BG DG =+. ∴222222BD AE AG EG BG DG +=+++. ∵222AG BG AB +=，222EG DG ED +=，∴22222222125BD AE AB ED CA CB CD CE +=+=+++=.……7分28. 解：（1）°70ADE ∠=；…….1分（2）①见右图；…….2分②EM EN =．…….3分 证明：∵ABC AED α∠=∠=，BAC BAC ∠=∠． ∴°902EDA ACB α∠=∠=-．∵BA BC =， ∴ACB BAC ∠=∠，即EDA BAC ∠=∠． ∴EA ED = . …….4分 ∵E 是AC 中点，∴EA EC =． ∴EA EC ED ==． ∴点,,A D C 在以AC 为直径的圆上．∴°90ADC ∠=．. …….5分 而°°°°180180(90)9022EAM EAD αα∠=-∠=--=+．∵点F 是BC 中点，∴FD FB =．∴FDB ABC α∠=∠=． ∴°°909022EDN EDA ADN EDA FDB ααα∠=∠+∠=∠+∠=-+=+.∴EAM EDN ∠=∠．…….6分 ∵ ∠AED 绕点E 顺时针旋转适当的角度，得到∠MEN ， ∴ ∠AED=∠MEN ，∴∠AED - ∠AEN=∠MEN -∠AEN ，即 ∠MEA=∠NED ． ∴ ΔEAM ≌ΔEPN ． ∴ EM=EN ．…….7分28．解：（1）正确画出图形；………………1分（2）延长EA 交OF 于点H ，交BF 于点G …2分 ∵O 为正方形ABCD 的中心， ∴OB OA =，∠AOB ＝90……3分∵OE 绕点O 逆时针旋转90角得到OF ∴OF OE =∴∠AOB ＝∠EOF ＝90∴∠EOA ＝∠FOB ……4分 在△EOA 和△FOB 中，OF OE =，OB OA =，∠EOA ＝∠FOB ，∴△EOA ≌△FOB ∴BF AE =.……5分 ∴∠OEA ＝∠OFB ∵∠OEA +∠OHA ∴∠OFB +∠FHG =90 ∴AE ⊥BF ……6分（3）BH 的最大值为25+……8分28. （1）①72；……………………………………………………………………………1分②222PB PC PA =+. …………………………………………………………2分证明：作∠PBP ′＝∠ABC ＝60°，且使BP ′＝BP ，连接P ′C 、P ′P . ……………3分∴∠1＝∠2. ∵AB ＝CB ，∴△ABP ≌△CBP ′. …………………………4分 ∴PA ＝P ′C ，∠A ＝∠BCP ′. 在四边形ABCP 中，∵∠ABC ＝60°，∠APC ＝30°， ∴∠A ＋∠BCP ＝270°.∴∠BCP ′＋∠BCP ＝270°.∴∠PCP ′＝360°－(∠BCP ′＋∠BCP )＝90°. ……………………………………5分 ∵△PBP ′是等边三角形. ∴PP ′＝PB .在Rt △PCP ′中，222''P P PC C P =+.……………………………………………6分 ∴222PB PC PA =+.（2）点P 在其他位置时，不是始终具有②中猜想的结论，举例： 如图，当点P 在CB 的延长线上时，结论为222PC PB PA =+.（说明：答案不惟一）……………………………………………………………………………………………7分28．解：（1）∵边BA 绕点B 顺时针旋转α角得到线段BP ， ∴BA = BP ，∵α=60°，∴△ABP 是等边三角形，..................................1分 ∴∠BAP =60º，AP = AC ， 又∵∠BAC =90°，∴∠PAC =30º，∠ACP =75º，∵PD⊥AC于点D，∴∠DPC=15º．....................................................................2分（2）结论：∠DPC=75º．..................................................3分（3）画图.............................................................................4分过点A作AE⊥BP于E．∴∠AEB=90º，∵∠ABP=150°，∴∠1=30º，∠BAE=60º，又∵BA= BP，∴∠2=∠3=15º，∴∠PAE=75º，∵∠BAC=90°，∴∠4=75º，∴∠PAE=∠4，∵PD⊥AC于点D，∴∠AEP=∠ADP =90º，∴△APE≌△APD，..............................................................5分∴AE= AD，在Rt△ABE中，∠1=30º，∴12AE AB=，又∵AB=AC，∴1122AE AD AB AC ===，∴AD=CD，又∵∠ADP=∠CDP=90º，∴△ADP≌△CDP，.............................................................6分∴∠DCP=∠4=75º，∴∠DPC=15º．.......................................................................7分4123EDBAC PEBC P321EAPC BD28.（1）=BE CF ． ………………………………………………………………2分 （2）证明：如图2，∵AB =BC ，∠ABC =90°，BD 为斜边中线 ∴BD =AD =CD =12AC ，BD ⊥AC∵ △EFD 是由△ABD 旋转得到的，∴DE =DF =DB =DC ，∠EDF =∠ADB =∠BDC =90° ∴∠EDF +∠BDF =∠BDC +∠BDF ，即∠BDE =∠FDC ∴△BDE ≌△FDC ∴BE =FC 且∠1=∠2 又∵∴ ,即…………………………………………3分 连接BF ，取BF 中点G ，连接MG 、NG . ∵M 为EF 中点，G 为BF 中点，N 为BC 中点 ∴MG ∥BE ，MG =12BE ；NG ∥FC ，NG =12FC 又∵EB =FC ，BE ⊥FC ∴MG =NG ，∠MGN =90° ∴△MGN 为等腰直角三角形∴MN =22FC …………………………………………………………………5分 （3） ……………………………………………………………7分28．解：（1）………………………………∠3=∠4FHE FDE ︒==90∠∠BE CF ⊥222BF CE AC +=B图2………… 1分 （2）证明：如图，延长AE 、DC 交于点P ．∵ 四边形ABCD 是平行四边形， ∴ AD //BC ，AB //CD ． ∴∠DAE =∠AEB，∠BAE =∠DPA ． ……………………………………… 2分∵ AE 平分∠ BAD ， ∴ ∠ DAE =∠ BAE ，∴ ∠ BAE =∠ AEB ，∠ DAE =∠ DPA ． ∴BA =BE，DA =DP ， ……………………………………………………… 3分又 ∵ BG ⊥ AE ，DH ⊥ AE ， ∴G为AE中点，H为AP中点． …………………………………………… 4分又 ∵O 为AC 中点，AD =BC ， ∴ ()()111222OG CE BC BE AD AB ==-=-， ()()111222OH CP DP CD AD AB ==-=- ． …………………………… 5分∴OG =OH ． ………………………………………………………………… 6分 （3）717． ……………………………………………………………………………… 7分28．解：（1）∠D =80°， (1)B∠C =130°； (2)（2）①如图2，连接BD ， ∵AB =AD ，∴∠ABD =∠ADB ．………………………………………………3 ∵∠ABC =∠ADC ，∴∠ABC ﹣∠ABD =∠ADC ﹣∠ADB ． ∴∠CBD =∠CDB ．∴CB =CD ．………………………………………………………4 （3）（Ⅰ）如图，当∠ADC =∠ABC =90°时，延长AD ，BC 相交于点E ， ∵∠ABC =90°，∠DAB =60°，AB =5， ∴AE =10．∴DE =AE ﹣AD =10﹣4═6．……………………………………5 ∵∠EDC =90°，∠E =30°，∴CD∴AC=2 (6)（Ⅱ）如图，当∠BCD =∠DAB =60°时，过点D 作DM ⊥AB 于点M ，DN ⊥BC 于点N ， ∵DM ⊥AB ，∠DAB =60°，AD =4， ∴AM =2，DM=2∴BM =AB ﹣AM =5﹣2=3．………………………………………7 ∵四边形BNDM 是矩形， ∴DN =BM =3，BN =DM∵∠BCD =60°， ∴CN∴BC =CN +BN∴AC=2……………………………………………………8 即AC28．（本小题满分7分）解：（1）① 依题意补全图形（如图）；…………………………………………1分 ② ∠ADC +∠CDE =180°．……………………………………………2分 （2）线段CM ，AE 和BE 之间的数量关系是AE =BE +2CM ，理由如下： ∵ 线段CD 绕点C 逆时针旋转90°得到线段CE ， ∴ CD =CE ，∠DCE =90°． ∴ ∠CDE =∠CED =45°．又∵ ∠ADC =135°， ∴ ∠ADC +∠CDE =180°，∴ A 、D 、E 三点在同一条直线上.∴ AE =AD +DE . …………………………………………………………3分 又∵ ∠ACB =90°，AAMDABCE∴∠ACB－∠DCB=∠DCE－∠DCB，即∠ACD=∠BCE．又∵AC=BC，CD=CE，∴△ACD≌△BCE．∴AD=BE．………………………………………………………………4分∵CD=CE，∠DCE=90°，CM⊥DE．∴DE=2CM．…………………………………………………………5分∴AE=BE+2CM．……………………………………………………6分（3）点A到BP的距离为．…………………………………………7分。