布尔向量与五种八卦图的构图原理

外八卦、内八卦、十爻立体八卦、八爻平面八卦外八卦、内八卦、十爻立体八卦、八爻平面八卦论后天八卦中卦数的千年谬误（转录）一、外八卦说到《八卦》懂易经的人都会想到先天八卦和后天八卦，其实八卦并不只有先后天八卦，还有几种不常见的八卦图，由于流传的不是很广泛，所以知道的人不多。

我目前也只掌握四种八卦图，每种八卦都有具体的应用方法按习惯称呼有：外八卦、内八卦、十爻立体八卦、八爻平面八卦。

先说外八卦，什么叫做外八卦呢？，是相对于内八卦而言。

外八卦就是传统的先天八卦，是由太极生两仪、两仪生四象、四象生八卦而来。

因为外八卦是由上、中、下三个爻横向紧密联合在一起的，所以代表总体规律。

它的生成图是这样的：先天八卦是由阳爻与阴爻按照一阳和一阴的顺序相互重合三次而来，卦与卦之间是靠上、中、下三个爻横向紧密联合在一起的，是自然生成的顺序，毫无人为的因素。

并且，八个卦之间的阴阳比例分配的非常平均，是成倍的增长，构成了一个相对平衡稳定的系统。

因为卦与卦之间是靠上、中、下三个爻按一固定的顺序联合在一起的，每卦之间的关系是间断性的连接，但又是一个不可分割的整体，而内部之间的联系并不紧密。

故此可表示事物的外部规律和总体规律。

在预测时主要用于宏观预测和总体规律的预测。

外八卦图如下：上、中、下三个爻全是阳爻的卦是乾卦，乾卦代表天在上。

上、中、下三个爻全是阴爻的卦是坤卦，坤卦代表地在下。

下面是阳爻，上面也是阳爻，中间是阴爻，是离卦，代表太阳，位置在东方，亦代表火，代表光明。

下面是阴爻，中间是阳爻，上面是阴爻，卦名叫坎，代表月亮，也代表水。

乾、坤、离、坎四个卦，就是天、地、日、月四个象。

下面一爻是阳爻，上面两爻是阴爻，这个卦名为震。

“震为雷”，它代表的是雷电、动能，在八卦图上，它的位置放在东北角上。

在震卦的对面西南角上的一个卦是：下面一爻是阴爻，上面两爻是阳爻，这个卦名是巽，代表宇宙的气，代表风。

另外在图的西北角上，下面两爻是阴爻，上面一爻是阳爻，形成：艮卦，代表山，它的对宫卦是：下面两爻是阳爻，上面一爻是阴爻，名兑卦，又叫作泽，代表海洋江河。

布尔巴基学派布尔巴基学派，又称为布尔巴基学派数学原理，是20世纪初数学的一个重要学派。

这个学派的名字来自于其创立者大卫·卢特维格·布尔巴基，他是一位德国数学家。

布尔巴基学派致力于建立数学的严格基础，并将其发展成为一套严密的形式逻辑体系。

这种基础是从集合论、逻辑和范畴论等领域出发的。

布尔巴基学派的一个核心目标是剥离数学于直观经验和直观直观直观直观概念，而通过形式系统和严格的逻辑来分析和构建数学体系。

他们认为，数学的基础不应该依赖于人类的感官体验或直观直观直观直观直观直观直观直观直观直观直观直观直观直观化抽象思维，而应该建立在逻辑和形式之上。

布尔巴基学派采用的一种重要的工具是严格的形式逻辑，主要是一阶谓词逻辑。

这种逻辑强调符号和符号之间的关系，并依赖于形式的推理和推理规则。

他们使用形式逻辑来建立数学中的定义、定理和证明，并通过推理规则来推导和证明数学结论。

布尔巴基学派还引入了范畴论的思想。

范畴论是一种研究数学结构和结构之间关系的数学理论。

布尔巴基学派将数学结构看作是对象和箭头之间的关系，并通过定义和研究范畴，来研究数学结构之间的映射和变换。

范畴论提供了一种统一的语言，使得不同的数学分支可以以一种更加通用的方式来进行交流和研究。

总结而言，布尔巴基学派通过建立严格的形式逻辑和抽象的数学体系，剥离了数学的直观和直观直观直观直观直观直观直观直观直观直观直观直观直观直观直观直观直观直观直观直观直观化抽象思维，为数学的发展提供了稳定的基础，并对现代数学产生了重大影响。

布尔巴基学派的数学原理奠定了数学的基础，成为了数学思想的重要里程碑。

易经的数学原理与结构易经是中国古代的一本典籍，被誉为中国古代文化的瑰宝之一。

在易经中，有许多数学原理和结构隐藏其中，这些原理和结构既体现了古代中国人的智慧，也反映了他们对自然界规律的深刻理解。

首先，易经中的八卦图就是一个很好的例子。

八卦图是由八个卦（乾、坤、震、巽、坎、离、艮、兑）组成的，每个卦由三个爻组成。

在这个结构中，我们可以发现一些有趣的数学规律。

首先是八卦图中的对称性。

如果我们将八卦图细分为上下两部分，可以发现上部和下部的结构是完全对称的。

这种对称性反映了古代中国人对阴阳平衡的追求。

其次是八卦图中的旋转对称性。

如果我们将八卦图按照某个方向旋转180度，我们会发现旋转后的八卦图与原来的八卦图是一样的。

这种旋转对称性在数学中被称为旋转群，它是对称性的一种重要表现形式。

除了八卦图，易经中还有许多数学原理。

例如，易经中的“易数”包含了一些与数学相关的概念。

易数中有一个重要的原理是“变化”。

易经认为世界万物都处于变化之中，变化的规律是可以被预测和把握的。

这种观念在现代数学中有着广泛的应用，例如混沌理论中就包含了一种描述系统变化的数学模型。

易经中的“卦变”也与数学中的变化规律相对应，它描述了八卦之间的相互转换关系。

这种描述方式与数学中的变换群有着一定的相似性。

此外，易经中的“五行”理论也与数学有着密切的联系。

易经认为世界万物都可以归纳为五行（木、火、土、金、水），这五行之间存在着一种相克相生的关系。

在数学中，这个原理可以被类比为矩阵乘法。

矩阵乘法可以描述不同维度之间的变换和相互作用，而五行原理则可以用来描述不同事物之间的相互作用关系。

总之，易经中的数学原理和结构揭示了古代中国人对自然界规律的深刻理解。

这些原理和结构在当代数学中仍然具有一定的启示意义，对于我们更好地理解自然界的规律和探索数学的应用具有重要的价值。

因此，我们应该继续研究和传承易经中的数学思想，为推动科学技术的发展做出更多的贡献。

易经的数学智慧易经是中国古代一部重要的典籍，被誉为中华文化的瑰宝。

它是一种哲学体系，涵盖了广泛的领域，包括数学。

易经中蕴含着丰富的数学智慧，这些智慧不仅仅是数学知识的应用，更是对数学思维的深刻理解和应用。

1. 数字的含义和象征意义易经中的八卦图是由阴阳两种状态组成的八个卦象，每个卦象都有特定的含义和象征意义。

八卦图中的数字1和0分别代表阴和阳，它们是二进制数的基础。

易经通过这种二进制的表示方式，将阴阳的变化和数学联系起来，揭示了数字的深层含义。

2. 数字的变化规律易经中的八卦图展示了阴阳的变化规律，这种变化可以用数学方法来描述。

八卦图中的每个卦象都有三个爻，每个爻可以是阴或阳。

阴爻用0表示，阳爻用1表示。

通过对八卦图中的爻进行变换，可以得到不同的卦象，这种变换的规律可以用二进制数的加法和减法来表示。

这种数学方法的应用，使得易经中的卦象变化成为了一种数学模型。

3. 数学与易经的相互影响数学和易经之间存在着相互影响的关系。

易经中的数学智慧为数学提供了新的思维方式和应用场景，而数学的发展也为易经的研究提供了更多的工具和方法。

数学和易经的相互影响促进了两者的发展，为人们提供了更深入的理解和应用。

4. 数学在易经中的应用易经中的数学智慧不仅仅是理论上的探讨，更是应用于实际生活中的问题。

例如，易经中的八卦图可以用来解决决策问题。

通过对八卦图的变换和组合，可以得到不同的卦象，每个卦象都有特定的含义和象征意义。

人们可以根据自己的问题和情况，选择相应的卦象进行解读和分析，从而做出更明智的决策。

5. 数学智慧的启示易经中的数学智慧给我们带来了很多启示。

首先，易经告诉我们，数学不仅仅是一门学科，更是一种思维方式。

数学思维可以帮助我们更好地理解和解决问题。

其次，易经告诉我们，数学是与生活密切相关的。

数学的应用不仅仅局限于学术领域，更可以用来解决实际生活中的问题。

最后，易经告诉我们，数学是一门美的学科。

数学的规律和变化可以给人们带来美的享受和思考。

周易研究1997年第3期(总第三十三期)伏羲卦图中的布尔代数侯维民1701年,德国哲学家莱布尼茨忽然宣称他与鲍威特(中国名白晋)用二进制序数破译了伏羲卦图(八卦图与六十四卦图)的数学秘密。

莱布尼茨在该图中发现,用阴爻“22”与阳爻“—”可以表示万有的这一配列顺序,竟可以与他在数学上的新发明即以0与1表示一切数的二进制序数互相印证。

由此他说:伏羲已先我得到二进制序数的关键。

然而,莱布尼茨这一震惊中外的发现仅是伏羲卦图蕴含的一少部分内容。

笔者发现伏羲卦图无论在卦的符号上,还是在图的结构上都与1847年创立,目前仍在蓬勃发展的“布尔代数”一致。

这一事实说明伏羲卦图不仅蕴含着二进制数原理,而且蕴含了“布尔代数”的基本模型。

本文首先简介了布尔代数的基础知识,接着论证了伏羲八卦、六十四卦分别与三维、六维布尔代数结构的一致性。

一、布尔代数简介布尔代数是以英国数学家乔治・布尔(Geo rge・Boo le,1813～1864)命名的一种代数系统。

它由一个非空集合B和定义在B上的二元运算+与・构成。

它们满足下列条件: (1)运算+和・都是交换的;(2)每一个运算对于另一个运算而言都是分配的;(3)对于运算+和・,有互异的零元素0和单位元素1,使得对于所有Α∈B,恒有Α+0=Α,Α・1=Α;(4)对于每个Α∈B,都存在一个元素Α∈B,这个元素称为Α的补元素,它满足Α+Α=1,Α・Α=0。

这个代数系统记作(B、・、+、　、0、1)。

利用布尔代数的+、・,可以诱导出B的一种偏序关系:Α≤ΒΖΑ+Β=Β(或Α・Β=Α)。

由于对于所有的Α∈B,均有Α+0=Α,Α・1=Α,可知0是B的最小元,1是B的最大元。

由两个元素组成的集合B2={0,1}上的布尔代数最常用到,B2上的+,・,　的定义为:0+0=0, 0+1=1, 1+0=1, 1+1=1;0・0=0,0・1=0,1・0=0,1・1=1;(1)0=1,1=0。

这个代数系统记作(B2,・,+,-,0,1)。

布尔巴基学派三个基本数学结构在数学史上，布尔巴基学派（Boole-Schrder School）是一个重要的学派，它在数学结构中所做的贡献十分重大。

这个学派的名称来源于它的两位创始人：查尔斯布尔（Charles Boole）和爱德华施罗德（Edward Schrder），他们在19世纪后期提出并完善了布尔巴基学派三个基本数学结构。

布尔巴基学派在数学方面作出了巨大贡献，它的三个基本数学结构是极其重要的，它们是：布尔代数、再现法和强制逻辑。

首先，布尔代数是布尔巴基学派的最关键的结构，它是数学逻辑术语的实现，也是一种发展自欧几里德算术的抽象代数学系统。

也就是说，它是建立在欧几里德算术的基础上的，它可以用来编码逻辑表达式，并以一种形式进行推理。

它的本质是用0和1来表示各种逻辑关系，充分利用了“真”和“假”这两个概念，可以用来实现数学逻辑思维的比较和判断。

布尔代数非常重要，因为它有助于推动数学研究的发展，使计算机技术飞速发展，改变了人们的思维方式。

其次是再现法，它是一种推理方法，可以从真实的物理世界中提取出纯数学的概念，也可以将人类的抽象思维转化为实实在在的实物。

这对数学研究和数学教育都有很大的支持，因为它极大地改变了我们理解数学的方式，使数学概念变得清晰明了，同时也更容易被其他学科所接受。

最后，强制逻辑是布尔巴基学派在数学结构中提出的另一项基本概念。

它是以著名的“布尔巴基定理”（Boole-Schrder Theorem）为基础的，它揭示了逻辑思维的本质。

它利用符号逻辑，引入了各种概念，如真、假、条件、操作、数字等，以更深入的方式描述了数学逻辑的本质，提高了人们对数学的理解和使用。

布尔巴基学派给数学史上留下了重大痕迹，它的三个基本数学结构为数学研究提供了新思路，对数学结构的研究也有很大的推动。

布尔巴基学派的三个基本数学结构都发挥了重要作用，深刻影响了数学研究的发展，包括计算机技术和逻辑思维等。

布尔巴基学派的成就和贡献使它闪耀着光芒，在数学史上占据着重要的地位。

布尔巴基数学原理布尔巴基数学原理（The Bourbaki Approach to Mathematics）是一种以严格陈述和抽象理论为基础的数学研究方法。

布尔巴基是法国一支数学派别的名称，他们提出的方法被称为“布尔巴基数学”，也被称为现代数学。

布尔巴基数学主张抽象代数学，拓扑学与数学分析的统一，所进行的思想运算、符号的运用、命题的表述与证明均借助严谨的数理逻辑。

布尔巴基数学重视抽象思维，是一种以抽象定义、推理与严格证明为主要工具的数学方法，不过这种方法是建立在数学分支的应用基础上的。

该方法追求的是数学知识的系统、显明、紧凑和严谨的呈现，而不是从具体的实例入手，而是从定义和性质出发展开讨论。

因此，布尔巴基数学的在陈述上具有特殊的形式，传统的问题、定理和证明被转化为宏观定义、定理与证明中的微观成分，构成了一个复杂的数学体系。

它的学习要求我们具有高度的严谨性、逻辑性以及抽象思维能力。

具体来说，它要求我们：1.准确理解各种符号与数学概念的意义；2.熟练掌握形式化推理的各种规则；3.具有严格的证明习惯，如清晰的句法、合理的换行和确定的引用等；4.熟悉各种数学分支的背景、发展和主要问题。

总之，布尔巴基数学的目标是使数学的使用和发展更加清晰、严谨。

它要求我们重新审视数学的定义、推理、证明和结论，并从更加抽象和一般化的角度来理解抽象概念的基本性质。

布尔巴基数学已经成为现代数学的一个重要分支，在不同的数学分支中都产生了广泛的应用。

它促进了数学的内部协作，改善了数学的公共阅读和讨论，并推动了数学的交叉学科发展。

尤其是在现代数学的理论研究中，它的成果已经为整个学科提供了一个坚实的基础。

八卦的数学基础
八卦的数学基础可以追溯到古代中国的易经（又称《周易》）。

易经是一本包含八卦的经典著作，八卦由三个连续的线条组成，每个线条可以是阳（实线）或阴（虚线）。

八卦包括乾（天）、坤（地）、震（雷）、巽（风）、离（火）、坎（水）、艮（山）和兑（泽）。

八卦在易经中被用来描述自然现象和人类行为，并且被认为是一种预测和解读未来的工具。

在数学上，八卦被用来表示二进制数。

每个八卦可以看作是一个三位二进制数，阳线对应1，阴线对应0。

通过排列不同的八卦，可以表示不同的二进制数。

在数学中，八卦还与对称性和变换有关。

八卦的排列方式可以产生不同的对称性和变换，比如旋转、镜像等。

这些对称性和变换在数学中有广泛的应用，特别是在几何学和群论中。

八卦的数学基础包括二进制表示、对称性和变换等概念。

这些概念在数学和其他领域中都具有重要的意义。

古代河图洛书的排列原理及九宫格八卦图河、洛是宋代理学家对宇宙的解释,既是宇宙时空模型图,又是宇宙的数学模型。

《系辞上传》云:“河出图,洛出书,圣人则之。

”河是黄河;洛是洛水。

想传伏羲时有龙马出于黄河、其背有旋毛如星点,后一、六,前二、七,左三、八,右四、九,中五、十,称为龙图,伏羲取其法以画八卦生蓍法。

又大禹治水时,有神龟出于洛水,其背有裂纹,前九,后一,左三,右七、中五,前右二,前左四,后右六,后左八。

其纹如字,禹取其法而作《尚书·洪范九畴》。

后人据此绘“河图”、“洛书”二图,以释“河出图,洛出书,圣人则之”诸语。

图中白点表示奇数(阳),即天数,黑点表示偶数(阴),即地数。

此图根据《系辞上传》所说的“天一地二,天三地四,天五地六,天七地八,天九地十”,按“天数一、三、五、七、九和地数二、四、六、八、十排列,排成“一、六居下,二、七居上,三、八居左,四、九居右,五、十居中”的方位。

洛书则以一至九数,排成“戴九履一,左三右七,二、四为肩,六、八为足,五居中央的“龟形”方位,即取龟为象。

图中白点为奇数(阳),黑点为偶数(阴),奇为天数,偶为地数。

河图数字的总和为55,而55则由天数1、3、5、7、9与地数2、4、6、8、10相加而成,其中1、2、3、4、5是“生数”,它们分别与代表五行金、木、水、火、土的5相加,生出6、7、8、9、10五个“成数”。

河图的数字分布实际上也是一种方位分布,即1、6配水,位北,图中列于下:2、7配火居南,列于上;3、8配木居东列于左,4、9配金居西列于右,5、10配土居中央,为地。

其数字排列所显示的是地的“方之象”,即地之方的简明而形象的数学表现。

而洛书全部数字之和为45,从其排列方式上看,如下表所示。

纵、横、斜名方数字相加之和为15,45又恰是15的3倍,显然是一个直径为15的球体在平面上的数学描绘,因此,《周髀经解》称:“洛书者,圆之象也。

”可见,河图显示的是地之方,洛书显示的是天之圆。

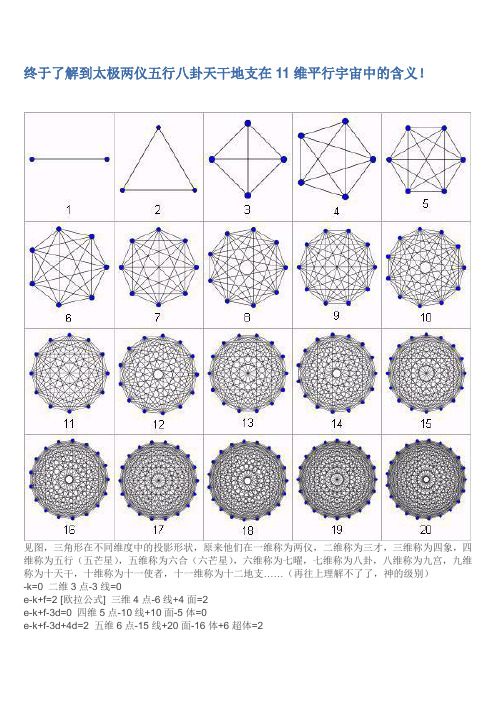
终于了解到太极两仪五行八卦天干地支在11维平行宇宙中的含义！见图，三角形在不同维度中的投影形状，原来他们在一维称为两仪，二维称为三才，三维称为四象，四维称为五行（五芒星），五维称为六合（六芒星），六维称为七曜，七维称为八卦，八维称为九宫，九维称为十天干，十维称为十一使者，十一维称为十二地支……（再往上理解不了了，神的级别）-k=0 二维3点-3线=0e-k+f=2 [欧拉公式] 三维4点-6线+4面=2e-k+f-3d=0 四维5点-10线+10面-5体=0e-k+f-3d+4d=2 五维6点-15线+20面-16体+6超体=2e-k+f-3d+4d-5d=0 六维7点-21线+35面-35体+21超体-7五维体=0e-k+f-3d+4d-5d+6d=2 七维8点-28线+56面-70体+56超体-28五维体+8六维体=2e-k+f-3d+4d-5d+6d-7d=0 八维9点-36线+84面-126体+126超体-84五维体+36六维体-9七维体=0 e-k+f-3d+4d-5d+6d-7d+8d=2 九维10点-45线+120面-210体+252超体-210五维体+120六维体-45七维体+10八维体=2e-k+f-3d+4d-5d+6d-7d+8d-9d=0 十维11点-55线+165面-330体+462超体-462五维体+330六维体-165七维体+55八维体-11九维体=0e-k+f-3d+4d-5d+6d-7d+8d-9d+10d=2 十一维12点-66线+220面-495体+792超体-924五维体+792六维体-495七维体+220八维体-66九维体+12十维体=2莫非四象就是四面体（四象其实是4顶点或4面？）三角形的二维投影，而五行是10面5体（五行就是五体？）四维三角形的二维投影，神圣六芒星是20面16体6超体（六芒=六超体？）五维三角形的二维投影，八卦是56面70体56超体（估计64卦就是56超体即复合卦加上8顶点或8六维体即纯卦的组合）28五维体8六维体的七维三角形的二维投影，十天干是10点120面（天干地支相乘不就是120吗？）210体252超体210五维体120六维体45七维体10八维体三角形的二维投影），12地支是220面495体792超体924五维体792六维体495七维体220八维体66九维体12十维体（每个地支代表一个十维体？）的二维投影？看来太极两仪三才四象五行六合七曜八卦九宫十天干十二地支是各维度空间的位置坐标啊？难道是上古的外星人或者更高维度的生命传授给中国人的？仔细看我第一张图的3号小图，这是什么？如果你没看懂，肯定脱口而出这是个正方形套十字架，或者说是4个直角三角形，高深一点的人说是四象限，或者青龙白虎朱雀玄武等等。

排列图的原理与应用范围原理排列图是一种用于显示对象之间关系的图表，通过排列对象的位置和方向来表示它们之间的连接和顺序关系。

排列图的原理基于以下几个核心概念：1.节点（Node）：节点是排列图中的基本单位，表示一个对象或事物。

每个节点在图中都有一个唯一的标识符和对应的位置坐标。

2.连接线（Edge）：连接线用于连接两个节点，表示它们之间的关联关系。

每条连接线都有起始节点和目标节点，可以是单向或双向连接。

3.方向性（Directionality）：排列图可以是有向的或无向的。

有向图中，连接线有一个确定的起点和终点，表示一个有明确方向的关联关系；无向图中，连接线没有明确的方向，表示两个节点之间的关系是相互的。

4.位置布局（Layout）：排列图中的节点通过位置布局来表示它们之间的顺序关系。

常见的布局方式包括线性排列、层次排列、圆形排列等。

应用范围排列图作为一种可视化方法，广泛应用于各个领域。

以下是排列图的一些常见应用范围：1. 数据结构与算法排列图可以用于可视化展示各种数据结构和算法的执行过程，帮助理解和优化算法的效率。

例如，可以使用排列图来展示二叉树的结构和遍历方式，有向图的拓扑排序等。

2. 组织关系图排列图可以用于展示企业组织的层级关系和人员之间的联系。

通过排列图，可以清晰地表示不同职位之间的上下级关系和沟通路径，有助于优化组织架构和提升沟通效率。

3. 流程图排列图可以用于表示复杂的流程和事务的执行过程。

通过排列图，可以清晰地展示各个步骤之间的依赖关系和执行顺序，有助于发现潜在瓶颈和优化流程。

4. 知识图谱排列图可以用于构建和展示知识图谱，帮助理清知识之间的逻辑关系和联系。

通过排列图，可以将知识点和概念组织起来，并展示它们之间的层级关系和相互作用。

5. 网络拓扑图排列图可以用于表示计算机网络的拓扑结构和设备之间的连接关系。

通过排列图，可以清晰地展示网络设备之间的层级关系、网络拓扑的结构和路径选择。

２０１９年第５期Ｎｏ．５　２０１９ＪＯＵＲＮＡＬＯＦ　ＡＮＨＵＩ　ＶＯＣＡＴＩＯＮＡＬ　ＣＯＬＬＥＧＥ　ＯＦ　ＥＬＥＣＴＲＯＮＩＣＳ　＆　ＩＮＦＯＲＭＡＴＩＯＮ　ＴＥＣＨＮＯＬＯＧＹ安徽电子信息职业技术学院学报第１８卷（总第１０４期）Ｇｅｎｅｒａｌ　Ｎｏ．１０４　Ｖｏｌ．１８摘 要：在图形处理操作中引用布尔运算可以使简单的基本图形组合产生新的形体。

在平面设计中，两个图形的关系可以细分为分离、相接、覆叠、透叠、重合、组合、剪缺、差叠等8种关系。

通过3个典型图标的绘制来解析布尔运算的使用技巧，便于平面设计学习者更加快速、准确、高效的绘制基本图标。

关键词：布尔运算；图标；Potoshop中图分类号：TP39 文献标识码：A布尔运算绘制图标技巧解析高敏钦（福建农业职业技术学院，福建 福州 350000）Technical Parsing of Drawing Icons Using Boolean Operations[文章编号] １６７１－８０２Ｘ（２０１９）０５－００３６－０３（一）　利用布尔运算绘制灯泡图标灯泡图标的绘制涉及到的布尔运算主要有相减、相接、结合以及剪缺，绘制灯泡主要是要注意交接处的自然过渡的处理，具体步骤如下：１．新建一个长宽相同（１５ｃｍ＊１５ｃｍ）的画布，新建两条上下左右居中的参考线。

２．选择椭圆工具在画布上绘制一个正圆，选择“添加到形状区域”，在正面下面绘制一个矩形，形成灯泡的初步形状，如图２－１所示。

３．圆形与矩形交接的地方需要自然的过度，这里要用到的是矩形和圆形相切的原理，需要选择“添加到形状区域”绘制一个矩形，然后选择“从形状区域减去”，绘制一个圆形与刚刚绘制的矩形相切，并慢慢调整矩形的位置，使得灯泡和底座过渡自然，如图２－２所示。

４．复制刚才绘制的矩形和圆形，移动到左侧，利用自由变换工具翻转调整位置即可得到左侧灯泡的自然过渡。

（二）利用布尔运算绘制心形图标心形图标的绘制涉及到的布尔运算主要是相接、结合以及覆叠，绘制心形图标的要点是图形的对称性以及圆形和矩形交接处的自然过渡，具体步骤如下：１．　新建一个长宽相同（１５ｃｍ＊１５ｃｍ）的画布，新建两条上下左右居中的参考线。

统一构图的基本原理有统一构图（Unified Modelling Language，UML）是一种软件工程领域常用的建模语言，用于描述和设计系统、软件和其他应用程序的结构、行为和交互。

UML是一种通用的标准化建模语言，它提供了一种统一的模型化方式，可以帮助开发人员在软件开发过程中进行系统分析、设计和交流。

UML使用图形符号表示模型的各个元素，包括类、对象、关系、行为、状态等信息，通过这些图形符号可以对系统进行更加直观和清晰的描述。

统一构图的基本原理包括如下几个方面：1. 用例建模：用例是用来描述系统功能的，它描述了系统与用户之间的交互过程。

用例建模是统一构图的第一步，它可以帮助开发人员更好地理解用户的需求和期望，从而设计出更好的系统架构。

2. 类建模：类是面向对象编程的基本概念，它描述了具有相似属性和行为的一组对象。

类建模是统一构图的核心部分，通过类图可以清晰地表示系统的结构和关系。

在类图中可以定义类的属性、方法、关联关系、继承关系等，以及类之间的各种关系和依赖。

3. 对象建模：对象是类的实例，通过对象建模可以以更加具体和实际的方式描述系统的行为和交互。

对象建模是基于类建模的，它可以描述一组对象的状态和行为，以及对象之间的消息传递和协作关系。

4. 时序建模：时序建模是用来描述系统中各个对象之间的消息传递和交互顺序的。

时序图可以清晰地表示对象之间的时序关系，帮助开发人员更好地理解系统的行为和交互过程。

时序图是统一构图中很重要的一部分，通常与用例图、类图等结合使用。

5. 状态建模：状态建模是用来描述一个对象在不同状态之间的转变和行为的。

状态图可以表示状态之间的转变条件、事件触发和相应的动作。

状态建模可以帮助开发人员更好地理解系统的状态和行为规则，从而设计出更加合理和健壮的系统。

6. 活动建模：活动建模是用来描述系统中各个任务和活动的执行过程的。

活动图可以清晰地表示活动的流程和执行顺序，帮助开发人员更好地理解系统的流程和交互过程。