植树问题
- 格式:doc
- 大小:75.50 KB
- 文档页数:10

植树问题:植树问题三要素:植树路线:(1)总路线长度(1)封闭路线(2)间隔长(株距)(2)不封闭路线(3)棵数植树问题可分为三类:一、不封闭的路线:1、两端都植树:树的棵数=间隔个数(段数) + 12、一端植,另一端不植:树的棵数=间隔个数(段数)3、两端都不植树:树的棵数=间隔个数(段数) - 1间隔个数=全长÷间隔长度例1:有一行树,从第一棵树到最后一棵树的距离为120米,并且每两棵树之间的距离为3米,求这行树共有多少棵?两端都植树:树的棵数=间隔个数(段数)间隔个数=全长÷间隔长度120÷3=40(个) 40+1=41(棵)答:这行树共有41棵。
练习:1.一条路长3000米,在路的一旁从头至尾每隔40米栽1棵树,需要栽树多少棵?2.在一条长1000米的公路的一旁,每隔5米栽一棵树,两端栽树,要栽多少棵树?3.在一条长240米的水渠边植树,每隔30米植一棵,两端栽树,共植树多少棵?例2:在一条长1200米的公路的一旁,每隔4米栽一棵杨树,一端栽树,要栽多少棵?2、一端植,另一端不植:树的棵数=间隔个数间隔个数=全长÷间隔长度解:1200÷4=300(棵)答:要栽300棵杨树。
练习:1.小刚家门口到公路边有一条小路,长60米,小刚要在小路一旁每隔5米栽一棵树,家门口不栽,一共要栽多少棵树?2.学校计划要在一条小道旁每隔5米放一个垃圾桶,如果小道的另一端不放,一共可以放15个垃圾桶,问这条小道有多长?3、两端都不植树:树的棵数=间隔个数 - 1例3:两楼之间相距80米,在两楼之间每隔8米栽一棵柳树,共栽了几棵树? 间隔个数=全长÷间隔长度解:80÷8=10(个) 10-1=9(棵)答:共栽了9棵柳树练习:1. 在一条长1200米的公路的两旁,每隔6米栽一棵树,两端不栽树,要栽多少棵树?2.李师傅要把一根长12米的木头锯成4段,锯一次要2分钟,李师傅要用多少分钟能锯完?例题:园林计划在一条路的两边植树,为了不挡视线,路的两端不用植,现在42棵树,每隔5米植一棵,这条路多长?1、一条小路两端不放花,在中间以相等 的距离摆了22盆鲜花,两盆之间相距6米,这条小路长多少米?2.在两个大楼之间的一段200米长的空地上栽了一排树,一共49棵。


五年级下册植树问题一.两端植树问题,棵数=段数+11.从小芳家到东胜广场的路上一边一共安有28个路灯(两端都安),每相邻两个路灯之间的距离都是 150 米。
从小芳家到东胜广场有多远?2.中山路上一条电车路线长 9000米,从起点到终点共设有16个车站。
平均每相邻两个车站之间的距离是多少米?3.元旦期间,某景区在一条长 120 米的长廊一侧挂下灯笼,相邻灯笼之间间隔是8米,长廊两端都挂了。
一共要准备多少个灯笼?4.街道路口处有一种路障石,这些路障石在一条直线上,相邻两个路障石之间的距离是1.5米,这个路口共设置了 12 个路障石(两端都设置),这个路口宽多少米?5.五(1)班有48名同学,做广播体操时排成两列纵队,每列纵队长 46 米。
每列纵队前后两名同学之间的距离是多少米?6.王叔叔到某写字楼的21 层办事,不巧停电。
如果从1层走到4层需要 54 秒,那么以同样的速度从1层走到 21层,需要多少秒才能到达?二.两端都不植树问题,棵数=段数-11.有两棵树相距505米,要在这两棵树之间安装路灯,每隔5米安装一盏。
一共要安装多少盏路灯?2.过年时,爷爷在大门口挂起了彩灯,绳子一共长6m,每隔0.2m 挂一盏彩灯(两端都不挂),一共挂了多少盏彩灯?3.一条甬路长 42 米,绿化队准备把6棵树苗在甬路的一侧均匀地栽成一行(两端都不栽)。
求每相邻两棵树苗之间的距离。
4.工人师傅要把15米长的圆钢切割成3米长的小段,切割一次要 25 秒。
一共需要多少秒?5.两棵柳树相隔165 m,要在这两棵柳树之间等距离地种植32棵桃树,第1棵桃树到第25 棵桃树之间的距离是多少米?6.冬冬家所在的小区有一个长方形的电动车车棚,小区物业计划沿着车棚的长边安装11个电动车充电电源(两端都不安),每相邻两个电源之间间隔0.9米。
现在要将间隔改为1.2米,那么只需要安装多少个充电电源?三.一端植树,另一端不植树(或者封闭图形),棵数=段数。
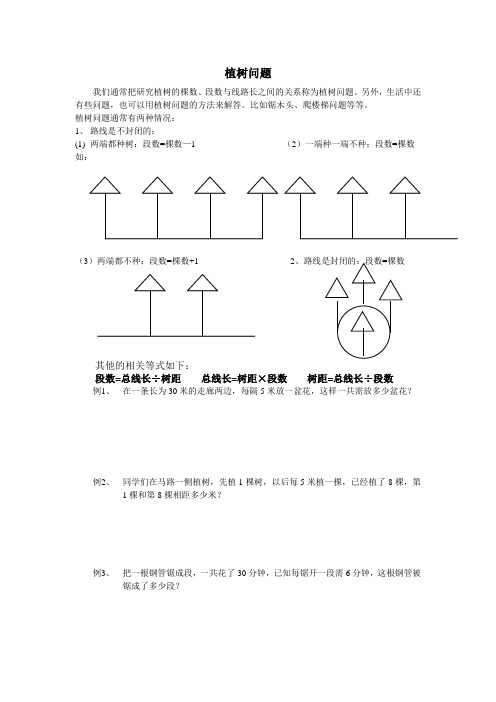
植树问题
我们通常把研究植树的棵数、段数与线路长之间的关系称为植树问题。
另外,生活中还有些问题,也可以用植树问题的方法来解答。
比如锯木头、爬楼梯问题等等。
植树问题通常有两种情况:
1、路线是不封闭的:
(1)两端都种树:段数=棵数—1 (2)一端种一端不种:段数=棵数如:
(3)两端都不种:段数=棵数+1 2
其他的相关等式如下:
段数=总线长÷树距总线长=树距×段数树距=总线长÷段数
例1、在一条长为30米的走廊两边,每隔5米放一盆花,这样一共需放多少盆花?
例2、同学们在马路一侧植树,先植1棵树,以后每5米植一棵,已经植了8棵,第1棵和第8棵相距多少米?
例3、把一根钢管锯成段,一共花了30分钟,已知每锯开一段需6分钟,这根钢管被锯成了多少段?。

植树问题(间隔问题)植树问题一、概念在一段路线上,每隔一定的距离种一棵树,一共可以种多少棵树,像这类型问题都是植树问题。
这段路线的长度就叫总长,相邻两棵树之间的距离就叫每段长,树把路线分成很多个间隔,叫段数;一共种了多少棵树叫棵数。
植树问题就是研究总长、每段长、段数、棵数四者之间的关系,在不同情况下,四者的关系都会不同。
解题关键就在于,分析是哪种把握情况及四者间关系。
思考方法就是画图初步判断属哪种情况及四者的关系(一般画最简单的情况,如种一棵或两棵来帮助理解)二、类型:(一)、非封闭路线1、非封闭路线两端都种树拓展:上楼梯问题段数=棵数-1 总长=段数×每段长例1、在一条长1000米的公路一边栽树,每隔4米栽一棵树,如果公路的起点和终点都栽树,问一共可以栽多少棵树?分析:由“如果公路的起点和终点都栽树”这句话我们就可以判断,它是属于非封闭路线两端都种树的情况;总长=1000米,每段长=4米,求棵数;要求棵数,必须先求段数,而要求段数,我们可以用这个公式“段数=总长÷每段长”2、非封闭路线一端种树段数=棵数总长=段数×每段长3、非封闭路线两端都不种树拓展:锯木问题段数=棵数+1 总长=段数×每段长例:两幢楼房相隔16米,每隔2米种一棵树,一共种多少棵树分析:种树的路线上,两端是楼房,不能种树,这时,段数会等于棵树+1,而题目告诉了我们总长(16米),每段长(2米),就可以求出段数(16÷2=8段),即棵数是:8+1=9棵练习:1.有一条2000米的公路,在路一边每相隔50米埋设一根路灯杆,从头到尾需要埋设路灯杆多少根?2.某大学从校门口的门柱到教学楼墙根,有一条1000米的甬路,每边相隔8米栽一棵白杨,可以栽白杨多少棵?1、在一条长300米的公路两边种树,每隔4米种一棵,一共可以种多少棵树?2、一条路上每隔10米有一根电线杆,连两端共有24棵,这条路有多长?7.马路的每边相隔7米有一棵国槐,小军乘无轨电车3分看到马路的一边有国槐151棵,无轨电车每小时行多少千米?8、一个老人以等速在公路上散步,从第一根电线杆走到第12根电线杆用了12分钟,这个老人用同样的速度走24分钟,应走到第几根电线杆?10、有一条道路,左边每隔5米种一棵杨树,右边每隔6米种一棵柳树,两端都种上树,共有5处杨树与柳树相对。

植树问题(一)以植树为内容,研究植树的棵树、棵与棵之间的距离(棵距)和需要植树的总长度(总长)等数量间关系的问题,称为植树问题。
植树问题在生活中很有实际运用价值,其基本数量关系和解题的要点是:1、植树问题的基本数量关系:每段距离×段数=总距离。
2、在直线上植树要根据以下几种情况,弄清棵数与段数间的关系:(1)在一段距离中,两端都植树,棵数=段数+1;(2)在一段距离中,两端都不植树,棵数=段数-1;(3)在一段距离中,一端不植树,棵数=段数。
3.在封闭曲线上植树,棵数=段数。
例 1 :有一条长1000米的公路,在公路的一侧从头到尾每隔25米栽一棵树苗,一共需要准备多少棵树苗?分析:先将全长1000米的公路每25米分成一段,一共分成多少段?种树的总棵树和分成的段数的关系是棵数=段数+1。
解 1000÷25+1=41(棵)。
答:一共需要准备41棵树苗。
做一做1、学校有一条长60米的走道,计划在道路一旁栽树。
每3米栽一棵。
(1)如果两端都各栽一棵树,那么共需多少棵树苗?(2)如果两端都不栽树,那么共需多少棵树苗?(3)如果只有一端栽树,那么共需多少棵树苗?例2:公园的一个湖的周长是1800米,在这个湖的周围每隔20米种一棵柳树。
需要柳树多少棵?练习:1、工程队打算在长96米,宽36米的长方形工地的四周打水泥桩,要求四角各打一根,并且每相邻两根的距离是4米,共要打水泥桩多少根?2、一个长方形的池塘长120米、宽28米,在池塘边每隔2米种一棵树,一共需要种多少棵树?3、圆形滑冰场,周长400米,每隔40米装一盏灯。
再在相邻两盏灯之间放3盆花,问共需装几盏灯?放几盆花?例3:在一段路边每隔50米埋设一根路灯杆,包括这段路两端埋设的路灯杆,共埋设了9根。
这段路长多少米?解:这是两端都栽的情形,所以“段数”=9-1=8。
这段路长为50×(9-1)=400(米)。
答:这段路长400米。
植树问题知识植树问题是一种研究总长、间隔长、间隔数、棵数等数量关系的问题。
在生活和生产中,常见的爬楼梯、锯木头、剪绳子、立电线杆、装灯、敲钟等实际问题也有与植树问题相同的数量关系。
植树问题的公式包括:1. 两端要栽:间隔数=总长÷间距;总长=间距×间隔数;棵数=间隔数+1;间隔数=棵数-1(类似问题有:竖电线杆,两端插旗)。
2. 两端不栽:间隔数=总长÷间距;总长=间距×间隔数;棵数=间隔数-1;间隔数=棵数+1(类似问题有:锯木头,剪铁丝)。
3. 一端栽一端不栽:间隔数=总长÷间距;总长=间距×间隔数;棵数=间隔数;间隔数=棵数(类似问题有:敲钟听声,上楼时间)。
4. 封闭的图形(例如围成一个圆形、椭圆形):总长÷间距=间隔数;棵数=间隔数。
5. 过桥问题:总长=车身长+车间距×车间隔数+桥(路长);速度=总长÷时间。
此外,方阵问题也是一个重要的知识点。
方阵问题主要研究实心方阵和空心方阵的特点和数量关系。
方阵的基本特点是任何一层的每边上物体数相等,相邻两层边长差2,相邻两层圈长差8。
实心方阵的总物体数是边长的平方,空心方阵的总物体数是实心物体总数减去空心部分物体总数。
最后,爬楼梯和敲钟问题也是植树问题的延伸。
爬楼梯问题需要考虑楼层高度和时间的关系,敲钟问题需要考虑敲钟次数和时间的关系。
这些问题的解决思路与植树问题类似,需要利用数量关系进行计算。
以上是植树问题的相关知识,包括植树问题的公式、方阵问题、爬楼梯和敲钟问题的解决方法等。
通过学习和掌握这些知识点,可以更好地解决生活中的实际问题。
植树问题一、不封闭植树问题公式:棵树=段数+1.学校在校园一条长30米的小路一侧栽树,每隔5米栽一棵,两端都栽,共栽树多少棵?2.在一条长300米的公路两边栽树,从头到尾每隔4米栽一棵,这样一共要栽多少棵树?二、封闭植树问题公式:棵树=段数1.公园沿人工湖植树一周,每隔6米栽一棵树。
已知人工湖周长540米,共栽树多少棵?2.公园内有一个人工湖,周长为120米,现在沿湖边等距修10个长9米的花台,相邻两个花台间的距离是多少米?三、植树问题公式:棵树=段数-1练习题:1、在一条马路2旁植树,每隔3米植一颗,植到头还剩3棵;每隔2.5米植一颗,植到头还缺少37棵,这条马路的长度?2、植树节到了,老师叫同学们在一个小村庄的道路上种树。
一端植树,一端不植树。
道路有100米长,每隔2米种一棵。
问:(1)、要植树多少棵?(2)、每棵苗苗要50元,需要多少钱?3、四年级植树b棵,比三年级植树的3倍少15棵,三年级植树()棵4、有一条公路长900米,在公路的一侧从头到尾每隔10米栽一根电线杆,可栽多少根电线杆?5、城中小学在一条大路边从头至尾栽树28棵,每隔6米栽一棵。
这条大路长多少米?6、同学们做早操。
21个同学排成一排,每相邻两个同学之间的距离相等,第一个人到最后一个人的距离是40米,相邻两个人之间相隔多少米?7、一个鱼塘的周长是1500米,沿鱼塘周围每隔6米栽一棵杨树,需要种多少棵杨树?8、在圆形的水池边,每隔3米种一棵树,共种树60棵,这个水池的周长是多少米?9、在一块长80米,宽60米的长方形地的周围种树,每隔4米种一棵,一共要种多少棵?10、在一条长300米的公路一旁栽树,每隔5米栽一棵,这样一共要栽多少棵?11、在一条公路一旁从头至尾植树36棵,每相邻两棵之间隔8米,这条公路长多少米?12、在圆形的水池边,每隔3米种一棵树,共种树60棵,这个水池的周长是多少米?13、在一条长400米的公路两旁,每隔4米植一棵树,共植树多少棵?14、在相距120米的两楼之间栽树,每隔12米栽一棵,共栽树多少棵?15、小朋友们植树,先植一棵树,以后每隔3米植一棵,已经植了9棵。
植树问题的五种公式在做植树问题时,总是有同学出错,分不清间隔数与栽树的棵树之间的关系,结果不是多一就是少一。
植树问题有以下几种情况,分别列举如下。
1单边植树(两端都植)棵数=总距离÷间隔长+1总距离=间隔长×(棵数-1)间隔长=总距离÷(棵数-1)【例1】在一条长80米的小路一旁种树,每隔16米种一棵树,两端都种,一共可以种多少棵树?解:棵数=总距离÷间隔长+1=80÷16+1=6(棵)答:可以种6棵树。
【例2】在一条小路一旁种树,每隔16米种一棵树,两端都种,一共种了6棵数,这条小路有多长?解:总距离=间隔长×(棵数-1)=16×(6-1)=80(米)答:这条小路长80米。
2单边植树(只植一端)棵数=总距离÷间隔长总距离=间隔长×棵数间隔长=总距离÷棵数【例1】小明的爸爸在房前的小路一旁栽树,小路长100米,每5米栽一棵树(第一棵树距离房子也是5米),小明的爸爸一共栽了多少棵树?解:棵数=总距离÷间隔长=100÷5=20(棵)答:小明的爸爸一共栽了20棵数。
【例2】小熊家门口有一条小路,从门口开始在小路一侧每隔5米种一棵树,一共种了20棵数,这条小路长多少?解:总距离=间隔长×棵数=5×20=100(米)答:这条小路长100米。
3单边植树(两端都不值)棵数=总距离÷间隔长-1总距离=间隔长×(棵数+1)间隔长=总距离÷(棵数+1)【例1】在一条长1500米的公路一侧架设电线杆,每隔50米架设一根。
若公路两端都不架设,一共需要架设多少根电线杆?解:杆数=总距离÷间隔长-1=1500÷50-1=29(个)答:一共需要架设29根电线杆。
【例2】在两栋楼之间栽树,每隔4米栽一棵,一共栽了5棵,这两栋楼相距多少米?解:总距离=间隔长×(棵数+1)=4×(5+1)=24(米)答:这两栋楼相距24米。
教师备课录备课人:课题数学广角课时授课日期教学目标 1. 使学生通过生活中的事例,经历探究两端要栽植树的数学规律的过程,初步体会解决植树问题的方法。
2. 初步培养学生从实际植树问题中探索规律以及找出解决问题的有效方法的能力。
3. 让学生感受数学在日常生活中的广泛应用,培养学生的应用意识和解决问题的能力。
教学重点用解决植树问题的方法解决实际问题。
教学难点两端栽树棵数与间隔数之间的关系课前准备投影教学流程一、创设情境师:同学们,看老师手里拿着什么?(植树模型)问:你们知道植树有什么好处吗?师:对,植树不仅可以美化环境,净化空气,而且,植树还有很多数学问题值得我们去研究。
这节课我们就来研究植树中的数学问题,好吗?(板书课题)二、探究新知:(一)出示例一师:同学们,请允许我先提出一个问题。
小黑板出示例1:同学们在全长100米的小路一边植树,每隔5米栽一棵(两端要栽)。
一共需要多少棵树苗?师:请同学们先仔细看读,如果又不明白的地方,可以大声地提出来,我们一起讨论研究。
(1)“两端”是指什么?(出示模型解释)“两端要栽”是怎么栽树的?(板书)(2)“每隔5米是什么意思?(是指两棵树之间的距离是5米。
两棵树之间的距离,我们称作两颗之间的间隔(板书)也叫段。
(3)同学们还看到别的什么东西有间隔吗?2、猜猜答案师:那么根据题目中的信息,请同学们猜一猜一共有需要多少棵树苗?3、简单验证师:现在出现了三种答案,而且每种答案都有不少的支持者,设计意图通过谈论植树节的话题引入内容,调动学生的积极性,并渗透植树环保教育。
通过讲解,初步让学生体会到两端的意义。
到底哪种答案是正确的呢?咱们可不可以画图或线段图模拟实际种一种树?如果从图上一棵一棵种到1000米,数一数,是不是就能知道到底谁的答案是正确的了呢?3、简单验证,发现规律。
(1)画图实际种一种。
演示:我们用这条线段表示这条小路。
“两端要种”,我们从小路的这头开始,先在头儿上种上一棵,然后隔5米再种一棵,再隔5米再种一棵,再隔5米再种一棵,照这样一棵一棵的种下去……(2)学生同桌讨论画一画,。
(3)学生汇报,小结规律先种15米,还是每隔5米种一棵,画图种一种,看种了多少棵?比一比,看谁画得快种的好。
(板书:3段4棵)跟上面一样,再种25米看一看,这次你又分了几段,种了几棵?(板书:5段6棵)任意选择一段距离再种一种,看这次你又分了几段,种了几棵?从中你发现了什么?(板书:2段3棵;7段8棵;10段11棵。
)规律:两端要种:棵树=段数+1)(板书)4、应用规律,解决问题。
师:应用这个规律,前面这个问题,能不能解决了?那个答案是正确的?1000÷5=200 这里的200指什么?200 +1=201 为什么还要+1?师:这个“秘方”好不好?5、小结:通过简单的例子,发现了规律,应用这个规律解决了这个复杂的问题。
以后,再遇到“两端要种”求棵树,知道该怎么做了吗?三、巩固规律1、出示“做一做”学生独立完成。
2、汇报,再由板演着组织同学讨论,教师参与其中)。
指名板演(看情况,因为有两种方法解决)。
生:同学们,你们对我的算式有什么问题要提吗?……或许(是举手,生点到)师:谢谢,终于关注到我了。
师:请问38-1=35,求出了什么?生:间隔数渗透思维方法的教学,即先得出一般规律,再解决复杂的问题。
接着让学生提问。
若提不到一下问题,老师提问。
师:35ⅹ6=180是求出什么?为什么?生:……师:哦,我明白了,35个间隔数的长度就是从第一棵到第二棵树的长度。
生:同学们赞同我的算式吗?……那饿就做对了。
师:这位同学表现的真好,掌声鼓励。
……谢谢你对学习的贡献。
四、解决问题师:同学们,利用植树问题中的规律还可以解决一些类似的生活活动中的问题。
1、学校运动会上,在笔直的跑道的一侧插彩旗,每隔6米插一面(两端要插)。
这条跑道长60米,一共要插多少面彩旗?(学生独立完成。
)学生独立完成,指名说说答案,纠正答案。
师:这道题是不是应用植树问题的规律解决的?师:看来,应用植树问题的规律,不仅仅能解决植树的问题,生活中很多类似的现象也能用植树问题的规律。
2、一座楼房每上一层要走18个台阶,到小明家要走64个台阶,。
小明家住在几楼?五、全课总结通过今天的学习,你有哪些收获?通过实例巩固本节课的内容,加深学生的印象。
通过不一样的题型拓展学生的思维。
板书设计:植树问题两端都有:棵树=段数+1点数=间隔数+1 数棵段数关系3 2 棵树=段数+1 8 711 10课后反思教师备课录备课人:课题数学广角课时授课日期教学目标教学目标:1、用线段图分析实际生活中的数学问题。
2、培养学生运用数学知识正确解决实际问题的能力。
3、感受数学在日常生活中的广泛应用。
教学重点正确解答实际生活问题。
教学难点正确解答实际生活问题。
课前准备课件教学流程一、引入新课生活中的数学问题真有趣,稍不认真分析,就会算错。
上节课我们学习了植树问题中两端都有的情况,现在请你们看下面一副图。
(出示例2主题图)1、大象馆和猩猩馆相距60米,绿化队要在两馆间的小路两旁栽树,相邻两棵树之间的距离是3米。
一共要栽几棵树?2.找学生读题,理解题意。
3.在小组里交流,并汇报。
4.小路的两端都是场馆,还需不需要栽树呢?师:这是属于哪种情况呢(两端都没有,板书)师:两端都没有,段数和棵树之间有什么样的关系呢?(棵数=段数– 1)师:我们一起来验证一下,这个结论是否正确。
二、合作探究两端都没有1.小组合作,提供通道。
(1)画一画(2)摆一摆(3)说一说师:请你们选择你最喜欢的一种方法来验证。
2.展示小组研究成果,发现规律,验证前面的猜测。
小结:同学们太了不起了,通过举简单的例子,自己又发现了“两端不种”的规律:棵树=段数-1。
如果“两端不种”求棵树,你会做了吗?3.做一做。
设计意图通过谈话激发学生的学习兴趣,有意识地渗透新知识。
这个环节的设计主要为了鼓励学生带着有思考价值的数学问题展开研究和讨论。
教师在与学生的交流中正确引导学生。
①在一条长2000米的路的一侧种树,每隔10米种一棵(两端不种)。
一共需要多少棵树苗?(学生独立完成)②师:同学们注意看,这道题发生了什么变化?问:“两侧种树”是什么意思?实际要种几行树?小结:今天我们研究了植树问题的另一种情况。
两端不种:棵树=段数—1。
以后同学们在做题的时候,一定要注意分清是“两端要种”还是“两端不种”。
三、回归生活,实际应用1.一根木头长8米,每2米锯一段。
一共要锯几次?(学生独立完成。
)问:为什么要—1?这相当于今天学习的植树问题中的那种情况?2.我们身边类似的数学问题。
①看,这一列共有几个同学?(4个)如果每相邻两个同学的距离是1米,从第1个同学到最后一个同学的距离是多少米?如果这一列共有10个同学呢?100个同学呢?②这一列还是4个同学,如果每相邻两个同学之间的距离是2米,从第一个同学到最后一个同学的距离是多少米呢?3.在一条路的一侧种树,每隔6米种一棵,一共种了41棵树。
从第1棵树到最后一棵树的距离是多少米?四、全课总结通过今天的学习,你有哪些收获?将总结规律的自主权交给学生,并在此基础上进行练习,既巩固知识,同时注重提升。
板书设计:植树问题两端都没有:棵树=段数-1点数=间隔数-1 数棵段数关系3 4 棵树=段数+1 8 911 12课后反思教师备课录备课人:课题数学广角课时 3 授课日期教学目标1、通过观察、操作及交流活动,探索并认识封闭线路上间隔排列中的简单规律,并能将这种认识应用到解决类似的实际问题之中。
2、培养学生观察能力、操作能力以及与人合作的能力。
3、让学生经历探索规律的过程,激发学生探索的欲望。
教学重点让学生具体分析,建立模型、正确解答实际问题教学难点让学生具体分析,建立模型、正确解答实际问题课前准备课件教学流程一、情境导入(课件出示)猜谜:十九乘十九,黑白两对手,有眼看不见,无眼难活久。
(打一棋类名称)二、探索新知1.教学每边摆放3粒棋子的方法。
(1)课件出示围棋格子图,最外层每边能放3个棋子。
最外层可以摆放多少个棋子?(2)抢答:读题后,让学生口算出答案。
(3)动手验证:请学生分小组按要求摆放棋子,验证刚才答案。
(4)汇报交流(着重请学生说出方法。
)可能会出现以下方法:3×2+2=8 2×4=83×3-1=8 3×4-4=8直接点数。
2.教学每边摆放4粒棋子的方法。
(1)课件出示围棋格子图,最外层每边能放4个棋子。
最外层可以摆放多少棋子?(2)动手操作:请学生分小组按要求摆放棋子,写出算式。
(3)游戏:让一学生当“小老师”,其余学生当“围棋子”,请小老师邀请“围棋子”按上题要求站在老师设计的大棋盘上。
(4)汇报交流(着重请学生说出方法)设计意图用谜语引入,从学生的已有经验出发,激发学生的学习兴趣。
培养学生良好的兴趣爱好让每位学生都参与活动,通过抢答、验证、分析、交流等一系列活动,借助围棋盘探讨封闭曲线(方阵)中的植树问题,进一步体会数学在日常生活中的广泛应用,学生在亲身“经历”的过程中实现知识能力乃至生命的同步发展。
教师随学生回答,用课件出示摆放方法。
(5)你们最喜欢哪种方法?为什么?3.教学每边摆放5粒棋子的方法。
(1)课件出示围棋格子图,最外层每边能放5个棋子。
最外层可以摆放多少棋子?(2)动手操作:请学生分小组按要求摆放棋子,写出算式。
(3)汇报交流。
(教师随学生回答,用课件出示摆放方法。
)(4)你们最喜欢哪种方法?和同桌说一说。
三、总结规律(1)师:你觉得再用棋子摆,方便吗?你能根据前面我们摆放的方法,填写下列表格,总结出规律吗?(小组合作完成)每边放的个数最外层总数3456…18发现规律:_________________________________(2)教学例3:出示围棋格子图。
问:围棋盘的最外层每边都能放19个棋子,最外层一共可以摆放多少个棋子?(2)总结规律::教师随着学生的回答板书:间隔数×边数=最外层的总数(3)学生根据规律,独立完成例3。
四、运用规律1.如果最外层每边能放100个,最外层一共可以摆放多少个棋子?如果最外层每边能放200个,最外层一共可以摆放多少个棋子?如果最外层每边能放300个,最外层一共可以摆放多少个棋子?拓展思维:如果一个五边形,怎么算?一个三角形呢?(集体口答)2.做第121页第三题。
3.请你参加:12名学生在操场上做游戏,大家围成一个正方形,每边人这一游戏的方法,激发了学生的兴趣,不仅使学生学到了摆放方法,让每个学生参与活动,把所学知识运动到游戏中。
充分相信学生,放手让学生分析问题、解决问题,以学生为主归纳问题;教师在关键之处疏通点拨,引导学生加深理解,做到以学生为主体。