2015北师大附中初二(上)期中数学

北京市师范大学南山附属学校中学部2015-2016年度八年级数学上学期期中试题 15-16年度上学期八年级数学期中考试选择题（本大题共10题，每小题3分，共30分）在平面直角坐标系中，点A （2,5）与点B 关于x 轴对称，则点B 的坐标是（ ）A. (5-，2-)B. (2-，5-)C. (2-，5)D. (2，5-) 下列四组数据中，不能作为直角三角形的三边长的是（ ）A. 7，24，25B. 6，8，10C. 9，12，15D. 3，4，6 数3π，3.14，722，3，16-，8，∙∙302.0，⋅⋅⋅-1010010001.0（相邻两个1之间的0的个数逐渐加1）中，无理数的个数为 （ ）A. 1B. 2C. 3D. 4下列各式中，正确的是 （ ） A. 416±= B.416=± C. 3273-=- D. 4)4(2-=-下列函数中，y 随x 增大而减小的是（ ）A. 1-=x yB.x y 21= C. 12-=x y D. 32+-=x y 点P 在第二象限内，P 到x 轴的距离是4，到y 轴的距离是3，那么点P 的坐标为（ ）A. 4(-，)3B.3(-，)4-C. 3(-，)4D. 3(，)4- 如图，数轴上点P 表示的数可能是（ ） A. 7 B. 2.3- C. 7- D. 10-8. 已知函数32)1(-+=m x m y 是正比例函数，且图像在第二、四象限内，则m 的值是（ ）A. 2B. 2-C. 2±D. 21-已知：5=a ，72=b ，且b a b a +=+，则b a -的值为（ ） A. 2或12 B. 2或12- C. 2-或12 D. 2-或12-10. 如图，在矩形ABCD 中，AB=4，BC=3，点P 从起点B 出发，沿BC 、CD 逆时针方向向终点D 匀速运动。

设点P 所走过路程为x ，则线段AP 、AD 与矩形的边所围成的图形（上面部分）面积为y ，则下列图像中能大致反映y 与x 函数关系的是（ ）A B C D填空题（本大题共5小题，每小题3分，共15分）16的平方根 。

桑水初中数学试卷桑水出品2015-2016年第一学期八年级期中联考数学试卷第一部分 选择题（本部分共12小题，每小题3分，共36分。

每小题给出4个选项，其中只有一个是正确．．的） 1．数3π，3.14159，115，2.3•， 3.747747774-⋅⋅⋅（相邻两个4之间的7的个数逐次加1）中，无理数的个数为 （ ）.A.2B.3C.4D.52．下列各组数分别是三角形三边的长，能构成直角三角形边的是( )． A.5，13，13 B. 13 D. 15，25，35 3．下列运算中，正确的是 （ ） A.1251144251= B.4)4(2±=- C.6)6(2-=-- D.2095141251161=+=+ 4．一个三角形的三边长分别是3，4，5，则这个三角形最长边上的高是（ ）. A.512 B .310 C .25D . 4 5．若点P 在x 轴的下方, y 轴的右方, 到每条坐标轴的距离都是3,则点P 的坐标为（ ）. A .(3,3)； B .(-3,3)； C .(-3,-3)； D .(3,-3). 6．函数23y x =-+的图象不经过（ ）A ．第一象限B ．第二象限C ．第三象限D ．第四象限 7．1a -与32a -是某正数的两个平方根，则实数a 的值是（ ）. A.2 B.43C. 1D.-2 8．如右图，如果半圆的直径恰为直角三角形的一条直角边，那么半圆的面积为（ ） A ．24cm π B ．26cm π C ．212cm π D ．224cm π 9．若5)3(82++=-a xa y 是一次函数，则=a （ ）桑水yxO C 1 B 2A 2 C 3B 1A 3B 3A 1C 2第16题OxyB 'MBAA ．±3B ．22C ．3-D ．310．把正比例函数y=2x 图象向上平移3个单位，得到图象解析式是（ ） A ．y=2x-3 B.y=2x+3 C.y=3x-2 D.y=3x+211．一次函数y=kx+b 的图像经过点(),1m 和()1,m -其中m>1，则,k b 应满足条件（ ） A .k>0,b>0 B .k>0,b<0 C . k<0,b>0 D .k<0,b<012．正方形A 1B 1C 1O ，A 2B 2C 2C 1，A 3B 3C 3C 2，…按如图所示的方式放置．点A 1，A 2，A 3，…和点C 1，C 2，C 3，…分别在直线y kx b =+(k ＞0)和x 轴上，已知点B 1(1，1)，B 2(3，2)， 则B 6的坐标是（ ）A ．()63,32B ．()65,32C ．()63,64D ．()65,64第二部分 非选择题填空题（答案必须写在答题卡上。

2015-2016学年河南省北大附中分校八年级（上）期中数学试卷一．选择题（共10题，30分）1．（3分）如果点P（x，y）满足xy=0，那么点P必定在（）A．原点上B．x轴上C．y轴上D．坐标轴上2．（3分）横坐标和纵坐标都是正数的点在（）A．第一象限B．第二象限C．第三象限D．第四象限3．（3分）下列说法正确的是（）A．﹣81的平方根是±9B．任何数的平方是非负数，因而任何数的平方根也是非负数C．任何一个非负数的平方根都不大于这个数D．2是4的平方根4．（3分）的平方根是（）A．±12 B．12 C．﹣12 D．±5．（3分）在下列长度的各组线段中，能组成直角三角形的是（）A．5，6，7 B．5，12，13 C．1，4，9 D．5，11，126．（3分）若一个三角形的三边长的平方分别为：32，42，x2则此三角形是直角三角形的x2的值是（）A．42B．52C．7 D．52或77．（3分）如果△ABC的三边分别为m2﹣1，2 m，m2+1（m＞1）那么（）A．△ABC是直角三角形，且斜边长为m2+1B．△ABC是直角三角形，且斜边长为2mC．△ABC是直角三角形，但斜边长需由m的大小确定D．△ABC不是直角三角形8．（3分）等式成立的条件是（）A．x≥1 B．x≥﹣1 C．﹣1≤x≤1 D．x≥1或x≤﹣19．（3分）下列各等式成立的是（）A．4×2=8B．5×4=20C．4×3=7D．5×4=2010．（3分）函数y=kx的图象经过点P（3，﹣1），则k的值为（）A．3 B．﹣3 C．D．﹣二．填空题（共8题，24分）11．（3分）某农舍的大门是一个木制的矩形栅栏，它的高为2m，宽为1.5m，现需要在相对的顶点间用一块木棒加固，木板的长为．12．（3分）已知直角三角形两直角边长分别是5cm、12cm，其斜边上的高是．13．（3分）36的倒数的算术平方根的相反数是．14．（3分）的最小值是，此时a的取值是．15．（3分）的平方根为．16．（3分）6×（﹣2）=．17．（3分）把化成最简二次根式是．18．（3分）点A（x1，﹣5），B（2，y2），若（1）A、B关于x轴对称，则x1=，y2=；（2）A、B关于y轴对称，则x1=，y2=；（3）A、B关于原点对称，则x1=，y2=．三．解答题（共6题，66分）19．（12分）计算题（1）（﹣）+÷．（2）÷（﹣）×．20．（10分）小强到某海岛上去探宝，登陆后先往东走10千米，又往北走2千米，遇到障碍后又往西走3千米，再折向北走到4千米处往东拐，仅走1千米便找到宝藏，问登陆点到宝藏埋藏点的直线距离是多少千米？21．（10分）已知直角三角形的两条直角边的长分别为、4，求它的周长和面积．22．（10分）写出如图中△ABC各顶点的坐标且求出此三角形的面积．23．（12分）一商贩在市场销售土豆．为了方便，他带了一些零钱备用．按市场价售出一些后，又降价出售．土豆千克数与他手中持有的钱数（含备用零钱）的关系如图，结合图象回答：（1）商贩自带的零钱有多少元？（2）降价前他每千克土豆出售的价格是多少？（3）降价后他按每千克0.8元将剩余土豆售完，这时他手中的钱（含备用零钱）是62元，问他一共带了多少千克土豆？24．（12分）某移动通讯公司开设两种业务．“全球通”：先缴50元月租费，然后每通话1分钟，再付0.4元，“神州行”：不缴纳月租费，每通话1分钟，付话费0.6元（通话均指市话）．若设一个月内通话x分钟，两种方式的费用分别为y1和y2元．（通话时不足1分钟的按1分钟计算，如3分20秒按4分钟收费）（1）写出y1、y2与x之间的函数关系式；（2）在同一坐标系下做出以上两个函数的图象；（3）一个月内通话多少分钟，两种费用相同；（4）某人估计一个月内通话300分钟，应选择哪种合算？2015-2016学年河南省北大附中分校八年级（上）期中数学试卷参考答案与试题解析一．选择题（共10题，30分）1．（3分）如果点P（x，y）满足xy=0，那么点P必定在（）A．原点上B．x轴上C．y轴上D．坐标轴上【解答】解：∵xy=0，∴x和y中至少有一个为0，当x为0时，点P在y轴上；当y为0时，点P在X轴上；当x和y都为0时，点p在原点．综上点P一定在坐标轴上，故选D．2．（3分）横坐标和纵坐标都是正数的点在（）A．第一象限B．第二象限C．第三象限D．第四象限【解答】解：横坐标和纵坐标都是正数的点符合第一象限内点的坐标符号，故点在第一象限．故选：A．3．（3分）下列说法正确的是（）A．﹣81的平方根是±9B．任何数的平方是非负数，因而任何数的平方根也是非负数C．任何一个非负数的平方根都不大于这个数D．2是4的平方根【解答】解：A：由于负数没有平方根，故A选项错误；B：任何数的平方为非负数，正确；但只有非负数才有平方根，且平方根有正负之分（0的平方根为0）．故选项B错误；C：任何一个非负数的平方根都不大于这个数，不一定正确，如：当0＜a＜1时，a＞a2，故选项错误；D：2的平方是4，所以2是4的平方根，故选项正确．故选：D．4．（3分）的平方根是（）A．±12 B．12 C．﹣12 D．±【解答】解：∵表示144的算术平方根，即12，∴的平方根为．故选：D．5．（3分）在下列长度的各组线段中，能组成直角三角形的是（）A．5，6，7 B．5，12，13 C．1，4，9 D．5，11，12【解答】解：A、因为52+62≠72，所以不能组成直角三角形；B、因为52+122=132，所以能组成直角三角形；C、因为12+42≠92，所以不能组成直角三角形；D、因为52+112≠122，所以不能组成直角三角形．故选：B．6．（3分）若一个三角形的三边长的平方分别为：32，42，x2则此三角形是直角三角形的x2的值是（）A．42B．52C．7 D．52或7【解答】解：根据勾股定理的逆定理列出方程解则可，有42是斜边或者x2是斜边两种情况．当42是斜边时，32+x2=42，x2=42﹣32=7；当x2是斜边时，x2=32+42=52，故选：D．7．（3分）如果△ABC的三边分别为m2﹣1，2 m，m2+1（m＞1）那么（）A．△ABC是直角三角形，且斜边长为m2+1B．△ABC是直角三角形，且斜边长为2mC．△ABC是直角三角形，但斜边长需由m的大小确定D．△ABC不是直角三角形【解答】解：∵（m2﹣1）2+（2 m）2=（m2+1）2，∴三角形为直角三角形，且斜边长为m2+1，A、△ABC是直角三角形，且斜边长为m2+1，正确；B、△ABC是直角三角形，且斜边长为2m，错误；C、△ABC是直角三角形，但斜边长需由m的大小确定，错误；D、△ABC是直角三角形，错误．故选：A．8．（3分）等式成立的条件是（）A．x≥1 B．x≥﹣1 C．﹣1≤x≤1 D．x≥1或x≤﹣1【解答】解：∵，∴，解得：x≥1．故选：A．9．（3分）下列各等式成立的是（）A．4×2=8B．5×4=20C．4×3=7D．5×4=20【解答】解：A、4×2=8×5=40，故选项错误；B、5×4=20=20，故选项错误；C、4×3=12=12，故选项错误；D、5×4=20=20，故选项正确．故选：D．10．（3分）函数y=kx的图象经过点P（3，﹣1），则k的值为（）A．3 B．﹣3 C．D．﹣【解答】解：∵函数y=kx的图象经过点P（3，﹣1），∴3k=﹣1，∴k=﹣．故选：D．二．填空题（共8题，24分）11．（3分）某农舍的大门是一个木制的矩形栅栏，它的高为2m，宽为1.5m，现需要在相对的顶点间用一块木棒加固，木板的长为 2.5m．【解答】解：设矩形的长为am，宽为bm，对角线长为cm，根据勾股定理可得：c2=a2+b2，故c==2.5m．故木板的长为2.5m．故答案为：2.5m．12．（3分）已知直角三角形两直角边长分别是5cm、12cm，其斜边上的高是．【解答】解：根据勾股定理，斜边长为=13cm，根据面积相等，设斜边上的高为xcm，列方程得：×5×12=×13•x，解得：x=，故答案为为cm．13．（3分）36的倒数的算术平方根的相反数是﹣．【解答】解：∵36的倒数是，∴36的倒数的算术平方根是，∴36的倒数的算术平方根的相反数是﹣；故答案为：﹣．14．（3分）的最小值是2，此时a的取值是﹣1．【解答】解：根据二次根式有意义的条件知，a+1≥0，解得a≥﹣1，当a=﹣1时，的最小值是2，故答案为2，﹣1．15．（3分）的平方根为±2．【解答】解：∵4的立方等于64，∴64的立方根等于4．4的平方根是±2，故答案为：±2．16．（3分）6×（﹣2）=﹣48．【解答】解：6×（﹣2）=﹣12=﹣48．故答案为：﹣48．17．（3分）把化成最简二次根式是．【解答】解：原式==．故答案为：．18．（3分）点A（x1，﹣5），B（2，y2），若（1）A、B关于x轴对称，则x1=2，y2=5；（2）A、B关于y轴对称，则x1=﹣2，y2=﹣5；（3）A、B关于原点对称，则x1=﹣2，y2=5．【解答】解：（1）∵A、B关于x轴对称，∴横坐标相等，纵坐标互为相反数，则x1=2，y2=5；（2）∵A、B关于y轴对称，∴横坐标互为相反数，纵坐标相等，则x1=﹣2，y2=﹣5；（3）∵A、B关于原点对称，∴横坐标相反数，纵坐标互为相反数，则x1=﹣2，y2=5．故答案为：（1）2，5；（2）﹣2，﹣5；（3）﹣2，5．三．解答题（共6题，66分）19．（12分）计算题（1）（﹣）+÷．（2）÷（﹣）×．【解答】解：（1）原式=2﹣+=2；（2）原式=×==．20．（10分）小强到某海岛上去探宝，登陆后先往东走10千米，又往北走2千米，遇到障碍后又往西走3千米，再折向北走到4千米处往东拐，仅走1千米便找到宝藏，问登陆点到宝藏埋藏点的直线距离是多少千米？【解答】解：过点B作BD⊥AC于点D，根据题意可知，AD=8﹣3+1=6千米，BD=2+6=8千米，在Rt△ADB中，由勾股定理得AB=10千米．即登陆点到宝藏处的距离为10千米．21．（10分）已知直角三角形的两条直角边的长分别为、4，求它的周长和面积．【解答】解：∵直角三角形的两条直角边的长分别为、4，∴直角三角形的斜边长===，∴周长为=+4+=5+，面积=××4=10．22．（10分）写出如图中△ABC各顶点的坐标且求出此三角形的面积．【解答】解：根据图形得：A（2，2）、B（﹣2，﹣1）、C（3，﹣2），三角形的面积是5×4﹣6﹣2.5﹣2=9.5．23．（12分）一商贩在市场销售土豆．为了方便，他带了一些零钱备用．按市场价售出一些后，又降价出售．土豆千克数与他手中持有的钱数（含备用零钱）的关系如图，结合图象回答：（1）商贩自带的零钱有多少元？（2）降价前他每千克土豆出售的价格是多少？（3）降价后他按每千克0.8元将剩余土豆售完，这时他手中的钱（含备用零钱）是62元，问他一共带了多少千克土豆？【解答】解：（1）由图象可知，当x=0时，y=10．答：农民自带的零钱是10元．（2）设降价前每千克土豆价格为k元，则农民手中钱y与所售土豆千克数x之间的函数关系式为：y=kx+10，∵当x=30时，y=46，∴46=30k+10，解得k=1.2．答：降价前每千克土豆价格为1.2元．（3）设他一共带了x千克土豆，根据题意得：0.8（x﹣30）+46=62，解得：x=50．答：农民一共带了50千克土豆．24．（12分）某移动通讯公司开设两种业务．“全球通”：先缴50元月租费，然后每通话1分钟，再付0.4元，“神州行”：不缴纳月租费，每通话1分钟，付话费0.6元（通话均指市话）．若设一个月内通话x分钟，两种方式的费用分别为y1和y2元．（通话时不足1分钟的按1分钟计算，如3分20秒按4分钟收费）（1）写出y1、y2与x之间的函数关系式；（2）在同一坐标系下做出以上两个函数的图象；（3）一个月内通话多少分钟，两种费用相同；（4）某人估计一个月内通话300分钟，应选择哪种合算？【解答】解：（1）y1=50+0.4x；y2=0.6x；（2）画图如下：（3）令y 1=y 2，则50+0.4x=0.6x ， 解得x=250．所以通话250分钟两种费用相同； （4）y 1，=170，y 2，=180， 170＜180，所以选择“全球通”的通讯方式便宜．赠送初中数学几何模型【模型一】“一线三等角”模型： 图形特征：60°60°60°45°45°45°运用举例：1.如图，若点B 在x 轴正半轴上，点A (4，4)、C (1，－1)，且AB ＝BC ，AB ⊥BC ，求点B 的坐标；2.如图，在直线l 上依次摆放着七个正方形（如图所示），已知斜放置的三个正方形的面积分别是1、2、3，正放置的四个正方形的面积依次是1S 、2S 、3S 、4S ，则14S S += ．ls 4s 3s 2s 13213. 如图，Rt △ABC 中，∠BAC =90°，AB =AC =2，点D 在BC 上运动（不与点B ，C 重合），过D 作∠ADE =45°，DE 交AC 于E ． （1）求证：△ABD ∽△DCE ；（2）设BD =x ，AE =y ，求y 关于x 的函数关系式，并写出自变量x 的取值范围； （3）当△ADE 是等腰三角形时，求AE 的长．B4.如图，已知直线112y x =+与y 轴交于点A ，与x 轴交于点D ，抛物线212y x bx c =++与直线交于A 、E 两点，与x 轴交于B 、C 两点，且B 点坐标为 (1，0)。

首师大附中2015-2016学年第一学期期中考试初二年级数学第I 卷（共24分）一、选择题（本题共8小题，每小题3分，共24分。

每题所列选项只有一个最符合题意） 1.下图中的轴对称图形有（ ）A.（1），（2）B.（1），（4）C.（2），（3）D.（3），（4） 2.点P （4，5）关于x 轴对称点的坐标是（ ）A.（-4，-5）B.（-4，5）C.（4，-5）D.（5，4） 3.下面计算正确的是（ ）A.633)(x x = B.2446a a a =⋅ C.2224)()(n m mn mn =-÷- D.2523a a a =+4.已知，，65==+xy y x 则22y x +的值是（ ）A.1B.13C.17D.255.如图，在△ABE 中，∠A=105°，AE 的垂直平分线MN 交BE 于点C ，且AB=CE ，则∠B 的度数是（ ）A.45°B.60°C.50°D.55°6.已知2)8()16(-=+-y a y y ，则a 的值是（ ）A.8B.16C.32D.647.如图，点P 为∠AOB 内一点，点M ，N 分别是射线OA ，OB 上一点，当△PMN 的周长最小时，∠OPM=50°， 则∠AOB 的度数是（ ）A.55°B.50°C.40°D.45°8.如图，在等腰Rt △ABC 中，∠BAC=90°，AD ⊥BC 于点D ，∠ABC 的平分线分别交AC 、AD 于点E 、F 两点，M 为EF 的中点，延长AM 交BC 于点N ，连接DM 。

下列结论：①DF=DN ；②AE=CN ；③△DMN 是等腰三角形；④∠BMD=45°，其中正确的结论个数是（ ）A.1个B.2个C.3个D.4个第II 卷二、填空题（本大题共6小题，每小题3分，共18分）9.已知1=+y x ，则222121y xy x ++=____________10.若12+-kx x 是完全平方式，则k=_________ 11.已知，22=nx则nn x x 2223)()(-的值为________12.若)()3(2q x x x -+-的乘积中不含2x 项，则q =______13.如图，已知△ABC 为等边三角形，点D 、E 在BC 的延长线上，G 是AC 上一点，且CG=CD ，F 是GD 上一点，且DF=DE ，则∠E=_______14.如图，在平面直角坐标系中，点A 的横坐标为-1，点B 在X 轴的负半轴上，AB=AO ，∠ABO=30°，直线MN 经过原点O ，点A 关于直线MN 的对称点A 1在x 轴的正半轴上，点B 关于直线MN 的对称点为B 1，则∠AOM 的度数为_____；点B 1的纵坐标为_______三、解答题（本大题共6小题，每小题5分，共30分） 15.计算（1）)2()48(2342y x y x y x -÷- （2）2)1()32()23(--+-x x x16因式分解（1）y x xy y 22396+- （2）3)2()2(+-+a a17.化简求值（1）若02910422=+-+-b b a a ，求22ab b a +的值（2）先化简，再求值：2)12()1(5)23()23(-----+x x x x x ，其中31-=x四、解答题（本大题共2答题，18题4分，19题6分，共10分） 18.△ABC 在平面直角坐标系中的位置如图所示 （1）作出△ABC 关于y 轴对称的△AB 1C 1；（2）点P 在x 轴上，且点P 到点B 与点C 1的距离之和最小，直接写出点P 的坐标为______19.已知x ≠1，计算4323221)1)(1(1)1)(1(1)1)(1(x x x x x x x x x x x -=++--=++--=+-，，（1）观察以上各式并猜想:__________)1)(1(2=+⋅⋅⋅+++-nx x x x （n 为正整数） （2）根据你的猜想计算：①_______)222221)(21(5432=+++++- ②_________222232=+⋅⋅⋅+++n （n 为正整数） ③________)1)(1(2979899=+++⋅⋅⋅+++-x x x x xx（3）通过以上规律请你进行下面的探索： ①______))((=+-b a b a②________))((22=++-b ab a b a ③_______))((3223=+++-b ab b a a b a五、解答题（共3大题，20题5分，21题6分，22题7分，共18分）20.阅读下面材料：小聪遇到这样一个有关角平分线的问题：如图1，在△ABC 中，∠A=2∠B ，CD 平分∠ACB ，AD=2.2，AC=3.6求BC 的长.小聪思考：因为CD 平分∠ACB ，所以可在BC 边上取点E ，使EC=AC ，连接DE. 这样很容易得到△DEC ≌△DAC ，经过推理能使问题得到解决（如图2）. 请回答：（1）△BDE 是_________三角形.（2）BC 的长为__________.参考小聪思考问题的方法，解决问题： 如图3，已知△ABC 中，AB=AC, ∠A=20°，BD 平分∠ABC,BD=2.3,BC=2.求AD 的长.21．在等边△ABC 外侧作直线AP ，点B 关于直线AP 的对称点为D ，连接BD,CD ，其中CD 交直线AP 于点E ．（1）依题意补全图1； （2）若∠PAB=30°，求∠ACE 的度数；（3）如图2，若60°<∠PAB <120°，判断由线段AB,CE,ED 可以构成一个含有多少度角的三角形，并证明.22.如图1，已知A （0，a ），B （b ，0）且228204b b a a -=+-（1）A 、B 两点的坐标为A________、B________； （2）如图2，连接AB ，若点D （0，-6），DE ⊥AB 于点E ，B 、C 关于y 轴对称，M 是线段DE 上的一点，且DM=AB ，连接AM ，试判断AC 与AM 之间的位置和数量关系，并证明你的结论；（3）如图3，在（2）的条件下，若N 是线段DM 上的一个动点，P 是MA 延长线上的一点，且DN=AP ，连接PN 交图1ABCPABCP图2AB C D 图3y轴于点Q，过点N作NH⊥y轴于点H，当N点在线段DM上运动时，△MQH的面积是否为定值？若是，请写出这个值；若不是，请说明理由。

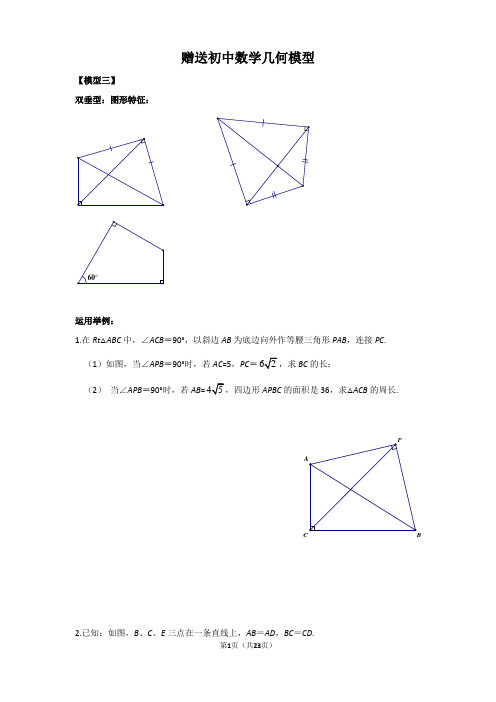
赠送初中数学几何模型【模型三】双垂型：图形特征：60°运用举例：1.在Rt△ABC中，∠ACB＝90°，以斜边AB为底边向外作等腰三角形PAB，连接PC. （1）如图，当∠APB＝90°时，若AC=5，PC＝62，求BC的长；（2）当∠APB＝90°时，若AB=45APBC的面积是36，求△ACB的周长.P 2.已知：如图，B、C、E三点在一条直线上，AB＝AD，BC＝CD.（1）若∠B＝90°，AB＝6，BC＝23，求∠A的值；（2）若∠BAD＋∠BCD＝180°，cos∠DCE＝35，求ABBC的值.3.如图，在四边形ABCD中，AB=AD，∠DAB=∠BCD=90°，（1）若AB=3，BC+CD=5，求四边形ABCD的面积（2）若p= BC+CD，四边形ABCD的面积为S，试探究S与p之间的关系。

DBC2015-2016学年北京市教院附中八年级（上）期中数学试卷一．用心选一选：（每小题3分，共30分）1．（3.00分）下列各式是因式分解且完全正确的是（）A．ab+ac+d=a（b+c）+d B．x3﹣x=x（x2﹣1）C．（a+2）（a﹣2）=a2﹣4 D．a2﹣1=（a+1）（a﹣1）2．（3.00分）医学研究发现一种新病毒的直径约为0.000043毫米，则这个数用科学记数法表示为（）A．0.43×10﹣4B．0.43×104C．4.3×10﹣5D．0.43×1053．（3.00分）下列各式（1﹣x），，，+x，，其中分式共有（）个．A．2 B．3 C．4 D．54．（3.00分）多项式9a2x2﹣18a3x3﹣36a4x4各项的公因式是（）A．a2x2 B．a3x3C．9a2x2D．9a4x45．（3.00分）如图，用三角尺可按下面方法画角平分线：在已知的∠AOB的两边上分别取点M、N，使OM=ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP．可证得△POM≌△PON，OP平分∠AOB．以上依画法证明△POM≌△PON根据的是（）A．SSS B．SAS C．AAS D．HL6．（3.00分）甲、乙二人做某种机械零件，已知甲每小时比乙多做6个，甲做90个所用的时间与乙做60个所用的时间相等．如果设甲每小时做x个零件，那么下面所列方程中正确的是（）A．=B．=C．=D．=7．（3.00分）如图，已知△ABC，则甲、乙、丙三个三角形中和△ABC全等的是（）A．只有乙B．甲和乙C．只有丙D．乙和丙8．（3.00分）下列各式中，正确的是（）A．=B．+=C．=D．=9．（3.00分）如图，正方形ABCD的边长为4，将一个足够大的直角三角板的直角顶点放于点A处，该三角形板的两条直角边与CD交于点F，与CB延长线交于点E，四边形AECF的面积是（）A．16 B．12 C．8 D．410．（3.00分）在数学活动课上，小明提出这样一个问题：如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB的度数是（）A．35°B．45°C．55°D．65°二．细心填一填：（每小题3分，共24分）．11．（3.00分）计算：20042﹣20032=．12．（3.00分）40==（2a﹣1b）3=．13．（3.00分）如果分式的值为0，那么x的值为．14．（3.00分）将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕，则∠CBD的度数为．15．（3.00分）计算：﹣=．16．（3.00分）如图，AC、BD相交于点O，∠A=∠D，请你再补充一个条件，使得△AOB≌△DOC，你补充的条件是．17．（3.00分）如图点P是∠BAC的平分线AD上一点，PE⊥AC于点E．已知PE=3，则点P到AB的距离是．18．（3.00分）在平面直角坐标系中，已知点A（1，2），B（5，5），C（5，2），存在点E，使△ACE和△ACB全等，写出所有满足条件的E点的坐标．三.用心做一做（19、20题每题3分，21、22、23题每题4分，共26分）19．（3.00分）因式分解：4a2﹣32a+64．20．（3.00分）计算：（ab﹣2）﹣2•（a﹣2）3（结果写成分式）21．（4.00分）计算：（1）（2）（+）÷．22．（4.00分）解分式方程：（1）（2）．23．（4.00分）先化简，，并任选一个你喜欢的数x代入求值．四．应用题（本题5分）24．（5.00分）列方程解应用题：甲乙两站相距1200千米，货车与客车同时从甲站出发开往乙站，已知客车的速度是货车速度的2.5倍，结果客车比货车早6小时到达乙站，求客车与货车的速度分别是多少？五、作图题（本题2分）25．（2.00分）画图（不用写作法，要保留作图痕迹）尺规作图：求作∠AOB的角平分线OC．六、解答题：（28题5分，其他每题4分，共17分）26．（4.00分）已知，如图，在△AFD和△CEB中，点A，E，F，C在同一直线上，AE=CF，DF=BE，AD=CB．求证：AD∥BC．27．（4.00分）已知：如图，AB=AD，AC=AE，且BA⊥AC，DA⊥AE．求证：（1）∠B=∠D．（2）AM=AN．28．（5.00分）如图，已知∠1=∠2，P为BN上的一点，PF⊥BC于F，PA=PC．求证：∠PCB+∠BAP=180°．29．（4.00分）已知：在平面直角坐标系中，△ABC的顶点A、C分别在y轴、x 轴上，且∠ACB=90°，AC=BC．（1）如图1，当A（0，﹣2），C（1，0），点B在第四象限时，则点B的坐标为；（2）如图2，当点C在x轴正半轴上运动，点A在y轴正半轴上运动，点B在第四象限时，作BD⊥y轴于点D，试判断与哪一个是定值，并说明定值是多少？请证明你的结论．四、附加题30．（3.00分）以如图方格纸中的3个格点为顶点，有多少个不全等的三角形（）A．6 B．7 C．8 D．9八、填空题（共1小题，每小题1分，满分1分）31．（1.00分）考察下列命题：（1）全等三角形的对应边上的中线、高线、角平分线对应相等；（2）两边和其中一边上的中线对应相等的两个三角形全等；（3）两边和第三边上的中线对应相等的两个三角形全等；（4）两角和其中一角的角平分线对应相等的两个三角形全等；（5）两角和第三角的角平分线对应相等的两个三角形全等；（6）两边和其中一边上的高线对应相等的两个三角形全等；（7）两边和第三边上的高线对应相等的两个三角形全等；其中正确的命题是（填写序号）．九、解答题（共1小题，满分0分）32．我们知道假分数可以化为带分数．例如：．在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．例如：，这样的分式就是假分式；，这样的分式就是真分式．类似的，假分式也可以化为带分式（即整式与真分式和的形式）．例如：；．（1）将分式化为带分式；（2）若分式的值为整数，求x的整数值．2015-2016学年北京市教院附中八年级（上）期中数学试卷参考答案与试题解析一．用心选一选：（每小题3分，共30分）1．（3.00分）下列各式是因式分解且完全正确的是（）A．ab+ac+d=a（b+c）+d B．x3﹣x=x（x2﹣1）C．（a+2）（a﹣2）=a2﹣4 D．a2﹣1=（a+1）（a﹣1）【解答】解：A、没把多项式转化成几个整式积的形式，故A错误；B、还可以再分解，故B错误；C、整式的乘法，故C错误；D、把一个多项式转化成几个整式积的形式，故D正确；故选：D．2．（3.00分）医学研究发现一种新病毒的直径约为0.000043毫米，则这个数用科学记数法表示为（）A．0.43×10﹣4B．0.43×104C．4.3×10﹣5D．0.43×105【解答】解：将0.000 043用科学记数法表示为4.3×10﹣5．故选：C．3．（3.00分）下列各式（1﹣x），，，+x，，其中分式共有（）个．A．2 B．3 C．4 D．5【解答】解：中的分母含有字母是分式．故选A．4．（3.00分）多项式9a2x2﹣18a3x3﹣36a4x4各项的公因式是（）A．a2x2 B．a3x3C．9a2x2D．9a4x4【解答】解：9a2x2﹣18a3x3﹣36a4x4中∵系数的最大公约数是9，相同字母的最低指数次幂是a2x2，∴公因式是9a2x2．故选：C．5．（3.00分）如图，用三角尺可按下面方法画角平分线：在已知的∠AOB的两边上分别取点M、N，使OM=ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP．可证得△POM≌△PON，OP平分∠AOB．以上依画法证明△POM≌△PON根据的是（）A．SSS B．SAS C．AAS D．HL【解答】解：∵OM=ON，OP=OP，∠OMP=∠ONP=90°∴△OPM≌△OPN所用的判定定理是HL．故选：D．6．（3.00分）甲、乙二人做某种机械零件，已知甲每小时比乙多做6个，甲做90个所用的时间与乙做60个所用的时间相等．如果设甲每小时做x个零件，那么下面所列方程中正确的是（）A．=B．=C．=D．=【解答】解：设甲每小时做x个零件，则乙每小时做（x﹣6）个零件，由题意得，=．故选：D．7．（3.00分）如图，已知△ABC，则甲、乙、丙三个三角形中和△ABC全等的是（）A．只有乙B．甲和乙C．只有丙D．乙和丙【解答】解：在△ABC和乙三角形中，有两边a、c分别对应相等，且这两边的夹角都为50°，由SAS可知这两个三角形全等；在△ABC和丙三角形中，有一边a对应相等，和两组角对应相等，由AAS可知这两个三角形全等，所以在甲、乙、丙三个三角形中和△ABC全等的是乙和丙，故选：D．8．（3.00分）下列各式中，正确的是（）A．=B．+=C．=D．=【解答】解：A、，不能再化简，故本选项错误；B、+=+=，故本选项错误；C、=，故本选项错误；D、=，故本选项正确；故选：D．9．（3.00分）如图，正方形ABCD的边长为4，将一个足够大的直角三角板的直角顶点放于点A处，该三角形板的两条直角边与CD交于点F，与CB延长线交于点E，四边形AECF的面积是（）A．16 B．12 C．8 D．4【解答】解：∵四边形ABCD为正方形，∴∠D=∠ABC=90°，AD=AB，∴∠ABE=∠D=90°，∵∠EAF=90°，∴∠DAF+∠BAF=90°，∠BAE+∠BAF=90°，∴∠DAF=∠BAE，在△AEB和△AFD中∴△AEB≌△AFD（ASA），∴S=S△AFD，△AEB∴它们都加上四边形ABCF的面积，可得到四边形AECF的面积=正方形的面积=16．故选：A．10．（3.00分）在数学活动课上，小明提出这样一个问题：如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB的度数是（）A．35°B．45°C．55°D．65°【解答】解：过点E作EF⊥AD，∵DE平分∠ADC，且E是BC的中点，∴CE=EB=EF，又∠B=90°，且AE=AE，∴△ABE≌△AFE，∴∠EAB=∠EAF．又∵∠CED=35°，∠C=90°，∴∠CDE=90°﹣35°=55°，即∠CDA=110°，∠DAB=70°，∴∠EAB=35°．故选：A．二．细心填一填：（每小题3分，共24分）．11．（3.00分）计算：20042﹣20032=4007．【解答】解：原式=（2004+2003）×（2004﹣2003）=4007．故答案为：4007．12．（3.00分）40=1=4（2a﹣1b）3=．【解答】解：40=1；===4；（2a﹣1b）3=8a﹣3b3=．故答案为：1；4；．13．（3.00分）如果分式的值为0，那么x的值为2．【解答】解：由题意得：x2﹣4=0，且x+2≠0，解得：x=2，故答案为：2．14．（3.00分）将一张长方形纸片按如图所示的方式折叠，BC，BD为折痕，则∠CBD的度数为90°．【解答】解：∵一张长方形纸片沿BC、BD折叠，∴∠ABC=∠A′BC，∠EBD=∠E′BD，而∠ABC+∠A′BC+∠EBD+∠E′BD=180°，∴∠A′BC+∠E′BD=180°×=90°，即∠CBD=90°．故答案为：90°．15．（3.00分）计算：﹣=2．【解答】解：﹣，=，=，=2．故答案为：2．16．（3.00分）如图，AC、BD相交于点O，∠A=∠D，请你再补充一个条件，使得△AOB≌△DOC，你补充的条件是AO=DO或AB=DC或BO=CO．【解答】解：添加AO=DO或AB=DC或BO=CO后可分别根据ASA、AAS、AAS判定△AOB≌△DOC．故填AO=DO或AB=DC或BO=CO．17．（3.00分）如图点P是∠BAC的平分线AD上一点，PE⊥AC于点E．已知PE=3，则点P到AB的距离是3．【解答】解：∵P是∠BAC的平分线AD上一点，PE⊥AC于点E，PE=3，∴点P到AB的距离=PE=3．故答案为：3．18．（3.00分）在平面直角坐标系中，已知点A（1，2），B（5，5），C（5，2），存在点E，使△ACE和△ACB全等，写出所有满足条件的E点的坐标（1，5）或（1，﹣1）或（5，﹣1）．【解答】解：如图所示：有3个点，当E在E、F、N处时，△ACE和△ACB全等，点E的坐标是：（1，5），（1，﹣1），（5，﹣1），故答案为：（1，5）或（1，﹣1）或（5，﹣1）．三.用心做一做（19、20题每题3分，21、22、23题每题4分，共26分）19．（3.00分）因式分解：4a2﹣32a+64．【解答】解：4a2﹣32a+64=4（a2﹣8a+16）=4（a﹣4）2．20．（3.00分）计算：（ab﹣2）﹣2•（a﹣2）3（结果写成分式）【解答】解：（ab﹣2）﹣2•（a﹣2）3（结果=a﹣2b4•a﹣6=a﹣8b4=．21．（4.00分）计算：（1）（2）（+）÷．【解答】解：（1）原式=••，=﹣2；（2）原式=•=．22．（4.00分）解分式方程：（1）（2）．【解答】解：（1）去分母得：x+3=4x，移项合并得：3x=3，解得：x=1；（2）去分母得：x2+2x+1﹣4=x2﹣1，解得：x=1，经检验x=1是增根，分式方程无解．23．（4.00分）先化简，，并任选一个你喜欢的数x代入求值．【解答】解：原式=…（2分）=…（3分）=x﹣1．…（4分）任选一个非﹣1，1，﹣2的数代入求值，给（1分）．当x=2，原式=x﹣1=1．四．应用题（本题5分）24．（5.00分）列方程解应用题：甲乙两站相距1200千米，货车与客车同时从甲站出发开往乙站，已知客车的速度是货车速度的2.5倍，结果客车比货车早6小时到达乙站，求客车与货车的速度分别是多少？【解答】解：设货车速度为x千米/小时，则客车速度为2.5x千米/小时，根据题意得：=+6，解得x=120，经检验：x=120是原方程的解且符合实际．2.5×120=300（千米/小时），答：货车速度为120千米/小时，客车速度为300千米/小时．五、作图题（本题2分）25．（2.00分）画图（不用写作法，要保留作图痕迹）尺规作图：求作∠AOB的角平分线OC．【解答】解：如图所示：．六、解答题：（28题5分，其他每题4分，共17分）26．（4.00分）已知，如图，在△AFD和△CEB中，点A，E，F，C在同一直线上，AE=CF，DF=BE，AD=CB．求证：AD∥BC．【解答】解：∵AE=CF，∴AE+EF=CF+EF，即AF=CE，在△ADF和△CBE中，，∴△ADF≌△CBE（SSS），∴∠A=∠C，则AD∥BC．27．（4.00分）已知：如图，AB=AD，AC=AE，且BA⊥AC，DA⊥AE．求证：（1）∠B=∠D．（2）AM=AN．【解答】证明：（1）∵BA⊥AC，DA⊥AE，∴∠BAC=∠DAE=90°，在△ABC与△ADE中，，∴△ABC≌△ADE（SAS），∴∠B=∠D；（2）∵△ABC≌△ADE，∴AB=AD，∵∠BAC=∠DAE，∴∠BAM=∠DAN，在△ABM与△ADN中，，∴△ABM≌△ADN（ASA），∴AM=AN．28．（5.00分）如图，已知∠1=∠2，P为BN上的一点，PF⊥BC于F，PA=PC．求证：∠PCB+∠BAP=180°．【解答】证明：如图，过点P作PE⊥BA于E，∵∠1=∠2，PF⊥BC于F，∴PE=PF，∠PEA=∠PFB=90°，在Rt△PEA与Rt△PFC中，∴Rt△PEA≌Rt△PFC（HL），∴∠PAE=∠PCB，∵∠BAP+∠PAE=180°，∴∠PCB+∠BAP=180°．29．（4.00分）已知：在平面直角坐标系中，△ABC的顶点A、C分别在y轴、x 轴上，且∠ACB=90°，AC=BC．（1）如图1，当A（0，﹣2），C（1，0），点B在第四象限时，则点B的坐标为（3，﹣1），；（2）如图2，当点C在x轴正半轴上运动，点A在y轴正半轴上运动，点B在第四象限时，作BD⊥y轴于点D，试判断与哪一个是定值，并说明定值是多少？请证明你的结论．【解答】（1）解：过B作BE⊥x轴于E，则∠BEC=∠ACB=∠AOC=90°，∴∠1+∠2=90°，∠1+∠OAC=90°，∴∠2=∠OAC，在△AOC和△CEB中∵，∴△AOC≌△CEB（AAS），∴OA=CE，OC=BE，∵A（0，﹣2），C（1，0），∴OA=CE=2，OC=BE=1，∴OE=1+2=3，∴点B的坐标为（3，﹣1 ）；（2）结论：，证明：作BE⊥x轴于E，∴∠1=90°=∠2，∴∠3+∠4=90°，∵∠ACB=90°，∴∠5+∠3=90°，∴∠5=∠4，在△CEB和△AOC中，∵∴△CEB≌△AOC，∴AO=CE，∵BE⊥x轴于E，∴BE∥y轴，∵BD⊥y轴于点D，EO⊥y轴于点O，∴BD∥OE，∴四边形OEBD是矩形，∴EO=BD，∴OC﹣BD=OC﹣EO=CE=AO，∴．四、附加题30．（3.00分）以如图方格纸中的3个格点为顶点，有多少个不全等的三角形（）A．6 B．7 C．8 D．9【解答】解：如图所示：△ABC、△BFD、△BFE、△BHC、△BHD、△BOC、△BOD、△BOE故选：C．八、填空题（共1小题，每小题1分，满分1分）31．（1.00分）考察下列命题：（1）全等三角形的对应边上的中线、高线、角平分线对应相等；（2）两边和其中一边上的中线对应相等的两个三角形全等；（3）两边和第三边上的中线对应相等的两个三角形全等；（4）两角和其中一角的角平分线对应相等的两个三角形全等；（5）两角和第三角的角平分线对应相等的两个三角形全等；（6）两边和其中一边上的高线对应相等的两个三角形全等；（7）两边和第三边上的高线对应相等的两个三角形全等；其中正确的命题是1，2，3，4，5（填写序号）．【解答】解：（1）全等三角形的对应边上的中线、高线、角平分线对应相等，正确；（2）两边和其中一边上的中线对应相等的两个三角形全等，正确；（3）两边和第三边上的中线对应相等的两个三角形全等，正确；（4）两角和其中一角的角平分线对应相等的两个三角形全等，正确；（5）两角和第三角的角平分线对应相等的两个三角形全等，正确；（6）两边和其中一边上的高线对应相等的两个三角形全等，错误；（7）两边和第三边上的高线对应相等的两个三角形全等，正确；故答案为：1，2，3，4，5．九、解答题（共1小题，满分0分）32．我们知道假分数可以化为带分数．例如：．在分式中，对于只含有一个字母的分式，当分子的次数大于或等于分母的次数时，我们称之为“假分式”；当分子的次数小于分母的次数时，我们称之为“真分式”．例如：，这样的分式就是假分式；，这样的分式就是真分式．类似的，假分式也可以化为带分式（即整式与真分式和的形式）．例如：；．（1）将分式化为带分式；（2）若分式的值为整数，求x的整数值．【解答】解：（1）==1﹣；（2）==2﹣，当为整数时，也为整数，∴x+1可取得的整数值为±1，±3，∴x的可能整数值为0，﹣2，2，﹣4．。

题号总分得分三二一一、选择题（每小题3分，共36分）1.一个直角三角形的两边长分别为3和4，则以第三边为边长的正方形的面积是（）A.25B.12C.7D.7或252.下列说法错误的是（）A.（-1）2√=1 B.2的平方根是±2√C.（-1）3√=-1 D.ab √=a √·b√3.点P 在第二象限，且到x 轴的距离是4，到y 轴的距离为3，则点P 的坐标为（）A.（-4，3） B.（-3，-4） C.（-3，4） D.（3，-4）4.如图数轴上的点A、B 表示的数分别为-1和3√，点B 关于点A 的对称点为点C，则点C 所表示的数为（）A.-2-3√B.-1-3√C.-2+3√D.1+3√5.已知关于x 的一次函数y =5x +b 图象经过第一、二、三象限，则b 的值可能是（）A.-2B.-1C.0D.26.下列说法正确的有（）①若a 、b 、c 为△ABC 的三边，且a 2-b 2=c 2，则△ABC 为直角三角形②在Rt△ABC 中，a =13，b =23，c =5√3，则13、23、5√3为一组勾股数③2√2是有理数④无理数都是无限小数⑤任何一个数的平方的算术平方根都是它本身A.1个B.2个C.3个D.4个7.已知y =-12x +b 的图象经过P 1（x 1，y 1）、P 2（x 2，y 2）两点，下列判断正确的是（）A.y 1<y 2B.y 1>y 2C.若x 1<x 2，则y 1>y 2D.若x1<x 2，则y 1<y 28.下列各数中，与3√的积为有理数的是（）A.2√B.32√C.23√D.2-3√9.点P 坐标为（2-a ，3a +6），且点P 到两坐标轴的距离相等，则点P 的坐标为（）A.（3，3） B.（3，-3）C.（6，-6）D.（3，3）或（6，-6）10.已知等腰三角形周长为20，则底边长y 关于腰长x 的函数图象是（）A BC D11.在一次函数y =kx +b 的图象中，y 随x 的增大而减小，且kb <0,则正确的图象是（）A BC D12.如图，每个小正方形的边长为1，A、B、C 是小正方形的顶点，则∠ABC 的度数为（）A.90°B.60°C.45°D.30°八数（北师大）（A ）第1页（共6页）第一学期期中素质考试（A ）八年级数学（北师大版）（本试题满分120分，考试时间90分钟。

2014-2015学年北京市教育学院附中八年级（上）期中数学试卷一．用心选一选：（每小题3分，共30分）1．（3.00分）下列图形中，是轴对称图形的是（）A．B．C．D．2．（3.00分）下列各式中，正确的是（）A．=B．+=C．=D．=3．（3.00分）如图，△ABC中，AB的垂直平分线交AC于D，如果AC=5cm，BC=4cm，那么△DBC的周长是（）A．6 cm B．7 cmC．8 cm D．9 cm4．（3.00分）下列因式分解结果正确的是（）A．15a3+10a2=5a（3a2+2a） B．9﹣4x2=（3+4x）（3﹣4x）C．a2﹣10a﹣25=（a﹣5）2D．a2﹣3a﹣10=（a+2）（a﹣5）5．（3.00分）如图，用三角尺可按下面方法画角平分线：在已知的∠AOB的两边上分别取点M、N，使OM=ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP．可证得△POM≌△PON，OP平分∠AOB．以上依画法证明△POM≌△PON根据的是（）A．SSS B．SAS C．AAS D．HL6．（3.00分）甲、乙二人做某种机械零件，已知甲每小时比乙多做6个，甲做90个所用的时间与乙做60个所用的时间相等．如果设甲每小时做x个零件，那么下面所列方程中正确的是（）A．=B．=C．=D．=7．（3.00分）如图，已知△ABC，则甲、乙、丙三个三角形中和△ABC全等的是（）A．只有乙B．甲和乙C．只有丙D．乙和丙8．（3.00分）如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别是C，D．下列结论中正确的有（）（1）ED=EC；（2）OD=OC；（3）∠ECD=∠EDC；（4）EO平分∠DEC；（5）OE⊥CD；（6）直线OE是线段CD的垂直平分线．A．3个 B．4个 C．5个 D．6个9．（3.00分）如图，正方形ABCD的边长为4，将一个足够大的直角三角板的直角顶点放于点A处，该三角形板的两条直角边与CD交于点F，与CB延长线交于点E，四边形AECF的面积是（）A．16 B．12 C．8 D．410．（3.00分）在数学活动课上，小明提出这样一个问题：如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB的度数是（）A．35°B．45°C．55°D．65°二．细心填一填：（每小题3分，共24分）．11．（3.00分）计算：20142﹣20132=．12．（3.00分）点A（2，﹣1）关于x轴对称的点的坐标是．13．（3.00分）如果分式的值是零，那么x的值是．14．（3.00分）计算：﹣=．15．（3.00分）如图，AC、BD相交于点O，∠A=∠D，请你再补充一个条件，使得△AOB≌△DOC，你补充的条件是．16．（3.00分）如图点P是∠BAC的平分线AD上一点，PE⊥AC于点E．已知PE=3，则点P到AB的距离是．17．（3.00分）在平面直角坐标系中，已知点A（1，2），B（5，5），C（5，2），存在点E，使△ACE和△ACB全等，写出所有满足条件的E点的坐标．18．（3.00分）如图，正方形ABCD的边长为2，M、N分别为AB、AD的中点，在对角线BD上找一点P，使△MNP的周长最小，则此时PM+PN=．三.用心做一做（每题5分，共35分）19．（5.00分）因式分解：4a2﹣32a+64．20．（5.00分）．21．（5.00分）如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC．求证：AD=BC．22．（5.00分）解方程：﹣=1．23．（5.00分）先化简：后，再选择一个你喜欢的x 值代入求值．24．（5.00分）如图，AB=AD，BC=DE，且BA⊥AC，DA⊥AE，你能证明AM=AN吗？25．（5.00分）a，b分别代表铁路和公路，点M、N分别代表蔬菜和杂货批发市场．现要建中转站O点，使O点到铁路、公路距离相等，且到两市场距离相等．请用尺规画出O点位置，不写作法，保留作图痕迹．四.解答题（26题5分，27题各6分，共11分）26．（5.00分）如图，已知∠1=∠2，P为BN上的一点，PF⊥BC于F，PA=PC．求证：∠PCB+∠BAP=180°．27．（6.00分）如下图，在△ABC中，AP平分∠CAB（∠CAB＜60°）（1）如图（1）点P在BC上，若∠CAB=42°，∠B=32°，确定AB，AC，PB之间的数量关系，并证明．（2）如图（2），点P在△ABC内，若∠CAB=2α，∠ABC=60°﹣α，且∠CBP=30°，求∠APC的度数（用含α的式子表示）．2014-2015学年北京市教育学院附中八年级（上）期中数学试卷参考答案与试题解析一．用心选一选：（每小题3分，共30分）1．（3.00分）下列图形中，是轴对称图形的是（）A．B．C．D．【解答】解：A、不是轴对称图形，故A错误；B、是轴对称图形，故B正确；C、不是轴对称图形，故C错误；D、不是轴对称图形，故D错误．故选：B．2．（3.00分）下列各式中，正确的是（）A．=B．+=C．=D．=【解答】解：A、，不能再化简，故本选项错误；B、+=+=，故本选项错误；C、=，故本选项错误；D、=，故本选项正确；故选：D．3．（3.00分）如图，△ABC中，AB的垂直平分线交AC于D，如果AC=5cm，BC=4cm，那么△DBC的周长是（）A．6 cm B．7 cmC．8 cm D．9 cm【解答】解：∵DE是AB的垂直平分线，∴AD=BD，∵AC=5cm，BC=4cm，∴△DBC的周长是：BD+CD+BC=AD+CD+BC=AC+BC=5+4=9（cm）．故选：D．4．（3.00分）下列因式分解结果正确的是（）A．15a3+10a2=5a（3a2+2a） B．9﹣4x2=（3+4x）（3﹣4x）C．a2﹣10a﹣25=（a﹣5）2D．a2﹣3a﹣10=（a+2）（a﹣5）【解答】解：A、15a3+10a2=5a2（3a+2），故此选项错误；B、9﹣4x2=（3+2x）（3﹣2x），故此选项错误；C、a2﹣10a﹣25无法因式分解，故此选项错误；D、a2﹣3a﹣10=（a+2）（a﹣5），正确．故选：D．5．（3.00分）如图，用三角尺可按下面方法画角平分线：在已知的∠AOB的两边上分别取点M、N，使OM=ON，再分别过点M、N作OA、OB的垂线，交点为P，画射线OP．可证得△POM≌△PON，OP平分∠AOB．以上依画法证明△POM≌△PON根据的是（）A．SSS B．SAS C．AAS D．HL【解答】解：∵OM=ON，OP=OP，∠OMP=∠ONP=90°∴△OPM≌△OPN所用的判定定理是HL．故选：D．6．（3.00分）甲、乙二人做某种机械零件，已知甲每小时比乙多做6个，甲做90个所用的时间与乙做60个所用的时间相等．如果设甲每小时做x个零件，那么下面所列方程中正确的是（）A．=B．=C．=D．=【解答】解：设甲每小时做x个零件，则乙每小时做（x﹣6）个零件，由题意得，=．故选：D．7．（3.00分）如图，已知△ABC，则甲、乙、丙三个三角形中和△ABC全等的是（）A．只有乙B．甲和乙C．只有丙D．乙和丙【解答】解：在△ABC和乙三角形中，有两边a、c分别对应相等，且这两边的夹角都为50°，由SAS可知这两个三角形全等；在△ABC和丙三角形中，有一边a对应相等，和两组角对应相等，由AAS可知这两个三角形全等，所以在甲、乙、丙三个三角形中和△ABC全等的是乙和丙，故选：D．8．（3.00分）如图，点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，垂足分别是C，D．下列结论中正确的有（）（1）ED=EC；（2）OD=OC；（3）∠ECD=∠EDC；（4）EO平分∠DEC；（5）OE⊥CD；（6）直线OE是线段CD的垂直平分线．A．3个 B．4个 C．5个 D．6个【解答】解：∵点E是∠AOB的平分线上一点，EC⊥OA，ED⊥OB，∴EC=ED，故（1）正确；在Rt△OCE和Rt△ODE中，，∴Rt△OCE≌Rt△ODE（HL），∴OD=OC，∠ECD=∠EDC，故（2）（3）正确；∴EO平分∠DEC，故（4）正确；∵OC=OD，OE平分∠AOB，∴OE⊥CD，故（5）正确；直线OE是线段CD的垂直平分线，故（6）正确；综上所述，6个结论都正确．故选：D．9．（3.00分）如图，正方形ABCD的边长为4，将一个足够大的直角三角板的直角顶点放于点A处，该三角形板的两条直角边与CD交于点F，与CB延长线交于点E，四边形AECF的面积是（）A．16 B．12 C．8 D．4【解答】解：∵四边形ABCD为正方形，∴∠D=∠ABC=90°，AD=AB，∴∠ABE=∠D=90°，∵∠EAF=90°，∴∠DAF+∠BAF=90°，∠BAE+∠BAF=90°，∴∠DAF=∠BAE，在△AEB和△AFD中∴△AEB≌△AFD（ASA），∴S=S△AFD，△AEB∴它们都加上四边形ABCF的面积，可得到四边形AECF的面积=正方形的面积=16．故选：A．10．（3.00分）在数学活动课上，小明提出这样一个问题：如图，∠B=∠C=90°，E是BC的中点，DE平分∠ADC，∠CED=35°，则∠EAB的度数是（）A．35°B．45°C．55°D．65°【解答】解：过点E作EF⊥AD，∵DE平分∠ADC，且E是BC的中点，∴CE=EB=EF，又∠B=90°，且AE=AE，∴△ABE≌△AFE，∴∠EAB=∠EAF．又∵∠CED=35°，∠C=90°，∴∠CDE=90°﹣35°=55°，即∠CDA=110°，∠DAB=70°，∴∠EAB=35°．故选：A．二．细心填一填：（每小题3分，共24分）．11．（3.00分）计算：20142﹣20132=4027．【解答】解：20142﹣20132=（2014+2013）×（2014﹣2013）=4027．故答案为：4027．12．（3.00分）点A（2，﹣1）关于x轴对称的点的坐标是（2，1）．【解答】解：点A（2，﹣1）关于x轴对称的点的坐标是（2，1），故答案为：（2，1）．13．（3.00分）如果分式的值是零，那么x的值是5．【解答】解：依题意得x﹣5=0且x+2≠0．解得x=5．故答案是：5．14．（3.00分）计算：﹣=．【解答】解：原式==．故答案为：．15．（3.00分）如图，AC、BD相交于点O，∠A=∠D，请你再补充一个条件，使得△AOB≌△DOC，你补充的条件是AO=DO或AB=DC或BO=CO．【解答】解：添加AO=DO或AB=DC或BO=CO后可分别根据ASA、AAS、AAS判定△AOB≌△DOC．故填AO=DO或AB=DC或BO=CO．16．（3.00分）如图点P是∠BAC的平分线AD上一点，PE⊥AC于点E．已知PE=3，则点P到AB的距离是3．【解答】解：∵P是∠BAC的平分线AD上一点，PE⊥AC于点E，PE=3，∴点P到AB的距离=PE=3．故答案为：3．17．（3.00分）在平面直角坐标系中，已知点A（1，2），B（5，5），C（5，2），存在点E，使△ACE和△ACB全等，写出所有满足条件的E点的坐标（1，5）或（1，﹣1）或（5，﹣1）．【解答】解：如图所示：有3个点，当E在E、F、N处时，△ACE和△ACB全等，点E的坐标是：（1，5），（1，﹣1），（5，﹣1），故答案为：（1，5）或（1，﹣1）或（5，﹣1）．18．（3.00分）如图，正方形ABCD的边长为2，M、N分别为AB、AD的中点，在对角线BD上找一点P，使△MNP的周长最小，则此时PM+PN=2．【解答】解：∵DN=AM=AN=1，∠A=90°，∴由勾股定理求出MN=，即MN值一定，∴要使△MNP的周长最小，只要MP+NP最小即可，过N作NG⊥BD交BD于G，交CD于F，连接MF交BD于P，∵四边形ABCD是正方形，∴∠NDB=∠FDB=∠ADC=45°，∴∠DNG=∠DFG=90°﹣45°=45°，∴∠DNG=∠NDG，∠DFG=∠FDG，∴NG=DG=FG，即N、F关于BD对称，∴PN=PF，∴MP+NP=MP+PF=MF，即此时的PN+PM的值最小，∵BD⊥NF，NG=FG，∴DN=DF=1=AM，∵四边形ABCD是正方形，∴AM∥DF，∴四边形AMFD是平行四边形，∴MF=AD=2，即MP+NP=2，故答案为：2．三.用心做一做（每题5分，共35分）19．（5.00分）因式分解：4a2﹣32a+64．【解答】解：4a2﹣32a+64=4（a2﹣8a+16）=4（a﹣4）2．20．（5.00分）．【解答】解：原式=+=x+x﹣1=2x﹣1．21．（5.00分）如图，已知：在△AFD和△CEB中，点A、E、F、C在同一直线上，AE=CF，∠B=∠D，AD∥BC．求证：AD=BC．【解答】证明：∵AD∥BC，∴∠A=∠C，∵AE=CF，∴AE+EF=CF+EF，即AF=CE，∵在△ADF和△CBE中，∴△ADF≌△CBE（AAS），∴AD=BC．22．（5.00分）解方程：﹣=1．【解答】解：方程两边同乘（x+1）（x﹣1），得（x+1）2﹣4=（x+1）（x﹣1），整理得2x﹣2=0，解得x=1．检验：当x=1时，（x+1）（x﹣1）=0，所以x=1是增根，应舍去．∴原方程无解．23．（5.00分）先化简：后，再选择一个你喜欢的x值代入求值．【解答】解：原式=（2分）=（4分）=（5分）=；（7分）当x=3时，原式=．（9分）注：本题答案不唯一，只要x的取值不为0、2、4，计算正确均可得分．24．（5.00分）如图，AB=AD，BC=DE，且BA⊥AC，DA⊥AE，你能证明AM=AN吗？【解答】证明：∵BA⊥AC，DA⊥AE，∴∠BAC=∠DAE=90°，在Rt△ABC和Rt△ADE中，，∴Rt△ADE≌Rt△ABC，∴∠E=∠C，AC=AE，∴在△ACM和△AEN中，∴△ACM≌△AEN（ASA），∴AM=AN．25．（5.00分）a，b分别代表铁路和公路，点M、N分别代表蔬菜和杂货批发市场．现要建中转站O点，使O点到铁路、公路距离相等，且到两市场距离相等．请用尺规画出O点位置，不写作法，保留作图痕迹．【解答】解：点O或O′就是所求的点．四.解答题（26题5分，27题各6分，共11分）26．（5.00分）如图，已知∠1=∠2，P为BN上的一点，PF⊥BC于F，PA=PC．求证：∠PCB+∠BAP=180°．【解答】证明：如图，过点P作PE⊥BA于E，∵∠1=∠2，PF⊥BC于F，∴PE=PF，∠PEA=∠PFB=90°，在Rt△PEA与Rt△PFC中，∴Rt△PEA≌Rt△PFC（HL），∴∠PAE=∠PCB，∵∠BAP+∠PAE=180°，∴∠PCB+∠BAP=180°．27．（6.00分）如下图，在△ABC中，AP平分∠CAB（∠CAB＜60°）（1）如图（1）点P在BC上，若∠CAB=42°，∠B=32°，确定AB，AC，PB之间的数量关系，并证明．（2）如图（2），点P在△ABC内，若∠CAB=2α，∠ABC=60°﹣α，且∠CBP=30°，求∠APC的度数（用含α的式子表示）．【解答】解：（1）AB﹣AC=PB；证明：在AB上截取AD，使AD=AC．连PD（如图1）∵AP平分∠CAB，∴∠1=∠2在△ACP和△ADP中，，∴△ACP≌△ADP（SAS），∴∠C=∠3．∵△ABC中，∠CAB=42°，∠ABC=32°，∴∠C=180°﹣∠CAB﹣∠ABC=180°﹣42°﹣32°=106°．∴∠3=106°．∴∠4=180°﹣∠3=180°﹣106°=74°，∠5=∠3﹣∠ABC=106°﹣32°=74°．∴∠4=∠5．∴PB=DB．∴AB﹣AC=AB﹣AD=DB=PB．（2）延长AC至M，使AM=AB，连接PM，BM．（如图2）∵AP平分∠CAB，∠CAB=2α，∴∠1=∠2=•2α=α．在△AMP和△ABP中，，∴△AMP≌△ABP（SAS），∴PM=PB，∠3=∠4．∵∠ABC=60°﹣α，∠CBP=30°，∴∠4=（60°﹣α）﹣30°=30°﹣α．∴∠3=∠4=30°﹣α．∵△AMB中，AM=AB，∴∠AMB=∠ABM=（180°﹣∠MAB）÷2=（180°﹣2α）÷2=90°﹣α．∴∠5=∠AMB﹣∠3=（90°﹣α）﹣（30°﹣α）=60°．∴△PMB为等边三角形．∵∠6=∠ABM﹣∠ABC=（90°﹣α）﹣（60°﹣α）=30°，∴∠6=∠CBP．∴BC平分∠PBM．∴BC垂直平分PM．∴CP=CM．∴∠7=∠3=30°﹣α．∴∠ACP=∠7+∠3=（30°﹣α）+（30°﹣α）=60°﹣2α．∴△ACP中，∠APC=180°﹣∠1﹣∠ACP=180°﹣α﹣（60°﹣2α）=120°+α．。