【数学】江苏省宿迁市马陵中学2014-2015学年高二(下)期中考试

宿迁市三校2014-2015学年第二学期第二次质量检测高二数学试题一、填空题〔5′×14=70′〕1．}1|{},1|{2+==+==x y y B x y x A ，如此=B A _____________． 2．函数123--=Xxy 的定义域为_______________． 3．给出如下各对函数：①22)()(,)(x x g x x f ==，②12)(,12)(-=+=x x g x x f ，③11)(-⋅+=x x x f 1)(,2-=x x g ，④x x x g x f )21()(,2)(==-，其中是同一函数的是______________〔写出所有符合要求的函数序号〕4．假设1)12(2+=+x x f ，如此=)0(f _______________．5．1>x ，如此x x c b x a )32(,)23(,log 132===-从大到小的排列应为________________． 6．函数x x x f ++=12)(的值域是_______________．7．5)(357++++=dx cx bx ax x f ，其中a 、b 、c 、d 为常数，假设7)7(-=-f ，如此=)7(f ______________．8．函数)32(log 221-+=x x y 的单调递减区间是_____________．9．“不等式012>+-ax ax 对一切实数x 都成立〞的充要条件是_____________． 10．假设ABC ∆的三边长分别为a 、b 、c ，其内切圆的半径为r ，如此=∆ABC S r c b a )(21++，类比平几中的这一结论，写出立几中的一个结论为____________________．11．i z +=1，如此=++211z z _______________． 12．假设C z ∈，且1|22|=-+i z ，如此|22|i z --的最小值是________________．13．假设)2(log ax y a -=在]3,0[上是x 的增函数，如此a 的取值范围是______________．14．实数t s x ,,满足s t x =+98，且s x ->，如此tx st x t s x +++++1)(2的最小值为_______________．二、解答题〔90′〕15．〔14′〕}02|{},1,1{2=+-=-=b ax x x B A ，假设φ≠B ，且A B A = ，求a 、b 的值．16．〔14′〕设命题p ：函数x c y =在R 上单调递减，命题q ：不等式1|2|>-+c x x 的解集为R ，假设q p ∨为真，q p ∧为假，求实数c 的取值范围．17．〔15′〕在函数)1(log >=a x y a 的图象上有A 、B 、C 三点，横坐标分别为,4,2,++m m m 其中1>m ．⑴求ABC ∆的面积)(m f S =的表达式；⑵求)(m f S =的值域．18．〔15′〕某上市股票在30天内每股的交易价格P 〔元〕与时间t 〔天〕所组成的有序数对),(P t 落在如下图中的两条线段上，该股票在30天内的日交易量Q 〔万股〕与时间t 〔天〕的局部数据如下表所示．第t 天 4 10 16 22⑴根据提供的图象，写出该种股票每股交易价格P 〔元〕与时间t 〔天〕所满足的函数关系式； ⑵根据表中数据确定日交易量Q 〔万股〕与时间t 〔天〕的一次函数关系式；⑶用y 〔万元〕表示该股票日交易额，写出y 关于t 的函数关系式，并求这30天中第几天日交易额最大，最大值为多少？19．〔16′〕函数)1(52)(2>+-=a ax x x f⑴假设)(x f 的定义域和值域均是],1[a ，求实数a 的值；⑵假设)(x f 在]2,(-∞上是减函数，且对任意的]1,1[,21+∈a x x ，总有|)()(|21x f x f -≤4，求实数a 的取值范围．20．〔16′〕函数)(x f 的定义域为}0|{≠=x x D ，且满足对于任意D x x ∈21,，有)()()(2121x f x f x x f +=．⑴求)1(f 的值；⑵判断)(x f 的奇偶性并证明；Q 〔万股〕 36 30 24 18⑶如果)62()13(,1)4(-++=x f x f f ≤3，且)(x f 在),0(+∞上是增函数，求x 的取值范围．高二数学〔文科〕质量检测试卷参考答案1．}1|{≥x x ； 2．]3,0(； 3．④； 4．45； 5．a c b >>； 6．),2[+∞- 7．17； 8．),1(+∞ 9．40<≤a10．假设三棱锥BCD A -四个面的面积分别为4321,,,S S S S ，其内切球的半径为r ，如此 r S S S S V BCD A )(314321+++=- 11．i -； 12．3； 13．)32,0(； 14．6； 15．⎩⎨⎧==⎩⎨⎧=-=⎩⎨⎧==101111b a b a b a 或或16．21:,10:><<c q c p ，综上),1[]21,0(+∞ ⑴p 真q 假 如此210≤<c⑵p 假q 真 如此1≥c17．⑴)1(4)2(log 22>++=m mm m S a ⑵)441(log 2mm S a ++=，∵1>a ，∴S 在),1(+∞ 5954144112=+<++<mm ，∴59log 0a S <<，值域)59log ,0(a 18．⑴*∈⎪⎪⎩⎪⎪⎨⎧≤<+-≤<+=N t t t t t P ,3020810200251⑵*∈≤<+-=N t t t Q ,300,40 ⑶*∈⎪⎪⎩⎪⎪⎨⎧≤<+-≤<++-=N t t t t t t t y ,302032012101,2008065122，当15=t 时，125max =y 万元，1203202012400101=+⨯-⨯<y ，∴第15天日交易额最大为125万元． 19．对称轴a x =，∵]2,(-∞∴2≥a ，∵1)1(=-+a a ，02)1(1≤-=--a a 11≥-a ，∴在]1,1[+a ，a a f x f 26521)1()(max -=+-==5)()(2min +-==a a f x f ，∴412)5()26(22≤+-=+---a a a a0322≤--⇒a a 31≤≤-⇒a ，又2≥a ，∴32≤≤a20．⑴0 ⑵令121-==x x ，如此0)1(2)1()1()1(=-⇒-+-=f f f f 0)1(=-⇒f ， 021 x =aa+1 1 0 1 2再令,11-=x x x =2，如此)()()1()(x f x f f x f =+-=-，偶 ⑶),0()64()]62)(13[(+∞≤-+f x x f )0,(-∞ 64)}62)(13([|≤-+⇒x x 64616664[2≤--≤-⇒x x ⎪⎪⎪⎩⎪⎪⎪⎨⎧≠-≠-≤≤-⇒≤--∈⇒≥+-⇒7333151532035830298322x x x x x R x x x 且 ∴]5,3()3,31()31,37[ ---。

2014-2015学年江苏省宿迁市宿豫中学高二（下）期中数学试卷（理科）一、填空题：（本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．）1．（5分）函数f（x）＝e x sin x的导数f′（x）＝．2．（5分）曲线y＝sin x在点（）处的切线方程为．3．（5分）已知向量与垂直，则实数k的值为．4．（5分）用反证法证明命题：“三角形的内角中至少有一个内角不大于60°”时，假设部分的内容应为．5．（5分）若函数f（x）＝x3+x2+mx+2是R上的单调函数，则实数m的取值范围为．6．（5分）在空间直角坐标系中，已知点A（1，0，2），B（1，﹣3，1），点M 在y轴上，且M到A与到B的距离相等，则M的坐标是．7．（5分）已知“凡是9的倍数的自然数都是3的倍数”和“自然数n是9的倍数”，根据三段论推理规则，我们可以得到的结论是．8．（5分）奇函数f（x）＝ax3+bx2+cx在x＝﹣1处有极值，则3a+b+c的值为．9．（5分）观察下列等式：，，，…，照此规律，计算1×2+2×3+…+n（n+1）＝（n∈N*）．10．（5分）已知函数f（x）＝x3﹣3ax（a∈R），若直线x+y+m＝0对任意的m∈R 都不是曲线y＝f（x）的切线，则a的取值范围为．11．（5分）如图为函数f（x）＝ax3+bx2+cx+d的图象，f′（x）为函数f（x）的导函数，则不等式x•f′（x）＜0的解集为．12．（5分）利用数学归纳法证明“”，从n＝k推导n＝k+1时原等式的左边应增加的项数是项．13．（5分）已知可导函数f（x）（x∈R）的导函数f′（x）满足f′（x）＞f（x），则不等式ef（x）＞f（1）e x的解集是．14．（5分）已知函数，当x＞1时，不等式k（x﹣1）＜xf（x）+2g′（x）+3恒成立，则整数k的最大值为．二、解答题：（本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．）15．（14分）若函数f（x）＝x3﹣px2+（m﹣1）x+2m2﹣m+1在区间（﹣2，0）内单调递减，且在（﹣∞，﹣2）及（0，+∞）内单调递增，求实数p、m的值．16．（14分）如图，在五面体ABCDEF中，F A⊥平面ABCD，AD∥BC∥FE，AB ⊥AD，M为EC的中点，（I）求异面直线BF与DE所成的角的大小；（II）证明平面AMD⊥平面CDE．17．（14分）已知函数f（x）＝bx，g（x）＝lnx．（1）若f（x）的图象与g（x）的图象相切于点P（x0，y0），求x0及b的值；（2）f（x）＝g（x）在[1，m]上有解，求b的范围．18．（16分）如图，在半径为30cm的半圆形（O为圆心）铝皮上截取一块矩形材料ABCD，其中点C、D在圆弧上，点A、B在两半径上，现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设矩形的边长BC＝xcm圆柱的体积为Vcm3．（1）写出体积V关于x的函数关系式；（2）当x为何值时，才能使做出的圆柱形罐子体积V最大？19．（16分）已知数列{a n}的前n项和为S n，通项公式为．（Ⅰ）计算f（1），f（2），f（3）的值；（Ⅱ）比较f（n）与1的大小，并用数学归纳法证明你的结论．20．（16分）已知函数f（x）＝lnx+，其中a为大于零的常数．（1）若函数f（x）在区间[1，+∞）内不是单调函数，求a的取值范围；（2）求函数f（x）在区间[e，e2]上的最小值．2014-2015学年江苏省宿迁市宿豫中学高二（下）期中数学试卷（理科）参考答案与试题解析一、填空题：（本大题共14小题，每小题5分，共计70分．请把答案填写在答题卡相应位置上．）1．（5分）函数f（x）＝e x sin x的导数f′（x）＝e x sin x+e x cos x．【解答】解：f′（x）＝e x sin x+e x cos x．故答案为：e x sin x+e x cos x．2．（5分）曲线y＝sin x在点（）处的切线方程为．【解答】解：依题意得y′＝cos x，因此曲线y＝sin x在点（）处的切线的斜率等于，相应的切线方程是y﹣＝（x﹣），即，故答案为：．3．（5分）已知向量与垂直，则实数k的值为﹣5．【解答】解：因为与垂直，∴，所以﹣1+k+6＝0，∴k＝﹣5．故答案为﹣5．4．（5分）用反证法证明命题：“三角形的内角中至少有一个内角不大于60°”时，假设部分的内容应为三角形的三个内角都大于60°．【解答】证明：用反证法证明命题：“三角形的内角中至少有一个内角不大于60°”时，应假设命题的否定成立，而命题“三角形的内角中至少有一个内角不大于60°”的否定是：三角形的三个内角都大于60°，故答案为三角形的三个内角都大于60°．5．（5分）若函数f（x）＝x3+x2+mx+2是R上的单调函数，则实数m的取值范围为[，+∞）．【解答】解：f′（x）＝3x2+2x+m；∵f（x）在R上是单调函数；∴f′（x）≥0对于x∈R恒成立；∴△＝4﹣12m≤0；∴．∴实数m的取值范围为[，+∞）．故答案为：．6．（5分）在空间直角坐标系中，已知点A（1，0，2），B（1，﹣3，1），点M 在y轴上，且M到A与到B的距离相等，则M的坐标是（0，﹣1，0）．【解答】解：设M（0，y，0）由12+y2+4＝1+（y+3）2+1可得y＝﹣1故M（0，﹣1，0）故答案为：（0，﹣1，0）．7．（5分）已知“凡是9的倍数的自然数都是3的倍数”和“自然数n是9的倍数”，根据三段论推理规则，我们可以得到的结论是自然数n是3的倍数．【解答】解：由演绎推理三段论可得“三段论”推理出一个结论，则这个结论是：“自然数n是3的倍数”．故答案为：自然数n是3的倍数．8．（5分）奇函数f（x）＝ax3+bx2+cx在x＝﹣1处有极值，则3a+b+c的值为0．【解答】解：∵f（x）＝ax3+bx2+cx，∴f′（x）＝3ax2+2bx+c，∵f（x）＝ax3+bx2+cx在x＝﹣1处有极值，∴f′（﹣1）＝0，∴3a﹣2b+c＝0，又f （x ）是奇函数，∴b ＝0，∴3a +b +c ＝0，故答案为：0．9．（5分）观察下列等式：，，，…，照此规律，计算1×2+2×3+…+n （n +1）＝ （n ∈N *）． 【解答】解：∵，，，…照此规律，1×2+2×3+…+n （n +1）＝故答案为： 10．（5分）已知函数f （x ）＝x 3﹣3ax （a ∈R ），若直线x +y +m ＝0对任意的m ∈R都不是曲线y ＝f （x ）的切线，则a 的取值范围为 ．【解答】解：f （x ）＝x 3﹣3ax （a ∈R ），则f ′（x ）＝3x 2﹣3a若直线x +y +m ＝0对任意的m ∈R 都不是曲线y ＝f （x ）的切线，直线的斜率为﹣1，f ′（x ）＝3x 2﹣3a ＝﹣1没有实数解，则3a ﹣1＜0，则a 的取值范围为即答案为． 11．（5分）如图为函数f （x ）＝ax 3+bx 2+cx +d 的图象，f ′（x ）为函数f （x ）的导函数，则不等式x •f ′（x ）＜0的解集为 ．【解答】解：由图可知：±是函数f（x）＝ax3+bx2+cx+d的两个极值点，且a＞0即±是导函数f′（x）的两个零点，导函数的图象如图，由图得：不等式x•f′（x）＜0的解集为：．故答案为：．12．（5分）利用数学归纳法证明“”，从n＝k推导n＝k+1时原等式的左边应增加的项数是2k项．【解答】解：由题意，n＝k时，最后一项为，n＝k+1时，最后一项为∴由n＝k变到n＝k+1时，左边增加了，增加2k项．故答案为：2k．13．（5分）已知可导函数f（x）（x∈R）的导函数f′（x）满足f′（x）＞f（x），则不等式ef（x）＞f（1）e x的解集是（1，+∞）．【解答】解：令g（x）＝，则＝，因为f'（x）＞f（x），所以g′（x）＞0，所以，函数g（x）＝为（﹣∞，+∞）上的增函数，由ef（x）＞f（1）e x，得：，即g（x）＞g（1），因为函数g（x）＝为（﹣∞，+∞）上的增函数，所以，x＞1．所以，不等式ef（x）＞f（1）e x的解集是（1，+∞）．故答案为（1，+∞）．14．（5分）已知函数，当x＞1时，不等式k（x﹣1）＜xf（x）+2g′（x）+3恒成立，则整数k的最大值为4．【解答】解：因为当x＞1时，不等式k（x﹣1）＜xf（x）+2g′（x）+3恒成立，即k（x﹣1）＜xlnx+2（x﹣2）+3对一切x∈（1，+∞）恒成立，亦即k＜＝对一切x∈（1，+∞）恒成立，所以不等式转化为k＜对任意x＞1恒成立．设p（x）＝，则p′（x）＝，令r（x）＝x﹣lnx﹣2（x＞1），则r′（x）＝1﹣＝＞0所以r（x）在（1，+∞）上单调递增．因为r（3）＝3﹣ln3﹣2＝1﹣ln3＜0，r（4）＝4﹣ln4﹣2＝2﹣2ln2＞0，所以r（x）＝0在（1，+∞）上存在唯一实根x0，且满足x0∈（3，4），当1＜x＜x0时，r（x）＜0，即p′（x）＜0；当x＞x0时，r（x）＞0，即p′（x）＞0．所以函数p（x）＝在（1，x0）上单调递减，在（x0，+∞）上单调递增，又r（x0）＝x0﹣lnx0﹣2＝0，所以lnx0＝x0﹣2．所以[p（x）]min＝p（x0）＝＝＝x0﹣1+2∈（4，5），所以k＜[p（x）]min＝x0﹣1+2∈（4，5）故整数k的最大值是4．故答案为：4二、解答题：（本大题共6小题，共计90分．请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．）15．（14分）若函数f（x）＝x3﹣px2+（m﹣1）x+2m2﹣m+1在区间（﹣2，0）内单调递减，且在（﹣∞，﹣2）及（0，+∞）内单调递增，求实数p、m的值．【解答】解：由f（x）＝x3﹣px2+（m﹣1）x+2m2﹣m+1，得f'（x）＝3x2﹣2px+m﹣1，因为f（x）在区间（﹣2，0）内单调递减，且在区间（﹣∞，﹣2）及（0，+∞）内单调递增，所以f'（x）＝3x2﹣2px+m﹣1＝0 的两个根是﹣2，0，所以，解得：．16．（14分）如图，在五面体ABCDEF中，F A⊥平面ABCD，AD∥BC∥FE，AB ⊥AD，M为EC的中点，（I）求异面直线BF与DE所成的角的大小；（II）证明平面AMD⊥平面CDE．【解答】解：分别以AB、AD、AF为x轴、y轴、z轴，建立空间直角坐标系，如图所示设AB＝1，依题意得B（1，0，0），C（1，1，0），D（0，2，0）E（0，1，1），F（0，0，1），M（，1，）（I）＝（﹣1，0，1），＝（0，﹣1，1）∴•＝﹣1×0+0×（﹣1）+1×1＝1||＝＝，||＝＝可得cos＜，＞＝＝＝∵＜，＞的范围是[0，π]，∴＜，＞＝所以异面直线BF与DE所成的角的大小为．（II）∵＝（，1，），＝（﹣1，0，1），∴•＝×（﹣1）+1×0+×1＝0，得⊥，同理可得：•＝0，得⊥∵AM、DM是平面AMD内的相交直线，∴CE⊥平面AMD又∵CE⊂平面CDE，∴平面AMD⊥平面CDE．17．（14分）已知函数f（x）＝bx，g（x）＝lnx．（1）若f（x）的图象与g（x）的图象相切于点P（x0，y0），求x0及b的值；（2）f（x）＝g（x）在[1，m]上有解，求b的范围．【解答】解：（1）f（x）＝bx，g（x）＝lnx的导数为，∴，∴；（2）∵，即y＝b与在[1，m]上有交点，∵，∴m≤e时h（x）在[1，m]上递增，；m＞e时h（x）在[1，e]上递增，在[e，m]上递减且h（x）＞0，，综上可得，m≤e时，；m＞e时，．18．（16分）如图，在半径为30cm的半圆形（O为圆心）铝皮上截取一块矩形材料ABCD，其中点C、D在圆弧上，点A、B在两半径上，现将此矩形铝皮ABCD卷成一个以BC为母线的圆柱形罐子的侧面（不计剪裁和拼接损耗），设矩形的边长BC＝xcm圆柱的体积为Vcm3．（1）写出体积V关于x的函数关系式；（2）当x为何值时，才能使做出的圆柱形罐子体积V最大？【解答】解：（1）连结OC，因为BC＝x，所以，设圆柱底面半径为r，则，即π2r2＝900﹣x2，所以，其中0＜x＜30．…（7分）（2）由，得，又在上V′＞0，在上V′＜0，所以，在上是增函数，在上是减函数，所以，当时，V有最大值..…（16分）19．（16分）已知数列{a n}的前n项和为S n，通项公式为．（Ⅰ）计算f（1），f（2），f（3）的值；（Ⅱ）比较f（n）与1的大小，并用数学归纳法证明你的结论．【解答】解：（Ⅰ）由已知，，；（3分）（Ⅱ）由（Ⅰ）知f（1）＞1，f（2）＞1；当n≥3时，猜想：f（n）＜1．（4分）下面用数学归纳法证明：（1）由（Ⅰ）当n＝3时，f（n）＜1；（5分）（2）假设n＝k（k≥3）时，f（n）＜1，即，那么＝＝＝，所以当n＝k+1时，f（n）＜1也成立．由（1）和（2）知，当n≥3时，f（n）＜1．（9分）所以当n＝1，和n＝2时，f（n）＞1；当n≥3时，f（n）＜1．（10分）20．（16分）已知函数f（x）＝lnx+，其中a为大于零的常数．（1）若函数f（x）在区间[1，+∞）内不是单调函数，求a的取值范围；（2）求函数f（x）在区间[e，e2]上的最小值．【解答】解：f′（x）＝（x＞0）…（2分）（1）由已知，得f′（x）在[1，+∞）上有解，即a＝在（1，+∞）上有解，又∵当x∈（1，+∞）时，＜1，所以a＜1．又a＞0，所以a的取值范围是（0，1）…（6分）（2）①当a≥时，因为f′（x）＞0在（e，e2）上恒成立，这时f（x）在[e，e2]上为增函数，所以当x＝e时，f（x）min＝f（e）＝1+…（8分）②当0＜a≤时，因为f′（x）＜0在（e，e2）上恒成立，这时f（x）在[e，e2]上为减函数，所以，当x＝e2时，f（x）min＝f（e2）＝2+，…（10分）③当＜a＜时，令f′（x）＝0得，x＝∈（e，e2），又因为对于x∈（e，）有f′（x）＜0，对于x∈（，e2）有f′（x）＞0，所以当x＝时，f（x）min＝f（）＝ln+1﹣…（14分）综上，f（x）在[e，e2]上的最小值为f（x）min＝…（16分）。

高二数学（理）期中考试复习一 、填空题1.已知()2,a i b i a b R i+=+∈，其中i 为虚数单位，则a b += . 2.用反证法证明命题“如果x<y ，那么51x >51y ”时，假设的内容应该是 ．3．已知7)(a x +的展开式中，4x 的系数是-280，则a = ．4.函数()f x =的定义域为 ．5.已知i 为虚数单位，复数2i1iz +=-，则 | z | ＝ . 6.学校召开学生代表大会，高二年级的3个班共选6名代表，每班至少1名，代表的名额分配方案种数是 ．7.在△AOB 的边OA 上有5个点，边OB 上有6个点，加上O 点共12个点，以这12个点为顶点的三角形有 个.8. 设某种动物有出生算起活20岁以上的概率为0.8，活到25岁以上的概率为0.4.现有一个20岁的这种动物，问它能活到25岁以上的概率是_______________．9. 设函数f(x)=x(e x +ae -x ),x ∈R ，是偶函数，则实数a =________________ 10. 已知函数⎩⎨⎧<≥+=0,10,1)(2x x x x f ,则满足不等式)x (f )x (f 212>-的x 的范围是____11．观察式子：213122+<，221151233++<，222111712344+++<，，则可归纳出式子为 ． 12．在平面上，若两个正三角形的边长的比为1：2，则它们的面积比为1：4，类似地，在空间内，若两个正四面体的棱长的比为1：2，则它们的体积比为 . 13.若20122012012012(12)()x a a x a x x R -=+++∈,则20121222012222a a a +++的值为 . 14. 已知实数0≠a ，函数⎩⎨⎧≥--<+=1,21,2)(x a x x a x x f ，若)1()1(a f a f +=-，则a 的值为 。

2014宿迁市高二数学第二学期期终考试文科试卷（带答案苏教版）一、填空题（本大题共14小题,每小题5分,计70分） 1.设集合{0,1,2}A =，{1,2,3}B =，则A B ⋂＝ ▲ ．2.函数()lg(1)f x x =+的定义域为 ▲ ．3.函数()3cos(2)3f x x π=+的最小正周期为 ▲ ．4.把函数2sin y x =的图象向左平移3π个单位得到的函数解析式为 ▲ ． 5.等比数列{}n a 中，若33=a ，246=a ，则7a 的值为 ▲ ． 6.不等式21122x +≤的解为 ▲ ． 7.ABC ∆中，sin cos a bA B=，则B = ▲ ． 8.已知实数,x y 满足20,0,1,x y x y x -+≥⎧⎪+≥⎨⎪≤⎩则2z x y =+的最小值是 ▲ ． 9.ABC ∆中，3,5,7,AB AC BC ===则AB AC ⋅= ▲ ．10.若命题“2,(1)10x R x a x ∃∈+-+<”是真命题，则实数a 的取值范围是 ▲ ．11.设函数()f x 是定义在R 上的奇函数，若当(0,)x ∈+∞时，()lg f x x =，则满足()0f x >的x 的取值范围是 ▲ ．12.设n S 是公差不为零的等差数列{}n a 的前ｎ项和，若137920,,,a a a a =且成等比数列，则10S = ▲ ．13.若320sin 20tan =+m ，则m 的值为 ▲ ． 14.如图为函数()1)f x x <<的图象，其在点(())M t f t ， l l y 处的切线为，与轴和直线1=y 分别交于点P 、Q ，点N （0，1），若△PQN 的面积为b 时的点M 恰好有两个，则b 的取值范围为 ▲ ． 二、解答题（本大题共6小题，计80分. 请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．）15.已知向量()()1,2,3,4-=a =b ． （1）若()()3//k -+a b a b ，求实数k 的值； （2）若()m ⊥-a a b ，求实数m 的值．16.已知c b a ,,分别是ABC ∆中角C B A ,,的对边，且222sin sin sin sin sin A C B A C +-=. （1）求角B 的大小；（2）若ABC ∆b =a c +的值；17.若函数2()(2)2f x x a x b =-++++，2log (1)2f =，且()()2g x f x x =-为偶函数. （１） 求函数()f x 的解析式；（２） 若函数()f x 在区间[,)m +∞的最大值为33m -，求m 的值.18.已知某公司生产某品牌服装的年固定成本为10万元，每生产千件需另投入2.7万元，设该公司年内共生产该品牌服装x 千件并全部销售完，每千件的销售收入为()R x 万元，且⎪⎪⎩⎪⎪⎨⎧>-≤<-=)10(31000108)100(3018.10)(22x x xx x x R ．（1）写出年利润W （万元）关于年产品x （千件）的函数解析式；（2）年产量为多少千件时，该公司在这一品牌服装的生产中所获年利润最大？ （注：年利润=年销售收入－年总成本）高二年级数学试题（文）参考答案一、填空题（本大题共14小题,每小题5分,计70分） 1. {1,2} 2. (1,)-+∞ 3. π4. 2sin()3y x π=+5. 486. (,1]-∞-7. 4π8. 1-9. 152-10. 3 <1a or a >- 11. (1,0)(1,)-⋃+∞ 12. 110 13. 414. 18,427⎛⎫ ⎪⎝⎭二、解答题（本大题共6小题，计90分. 请在答题卡指定区域内作答，解答时应写出文字说明、证明过程或演算步骤．） 15.已知向量()()1,2,3,4-=a =b ． （1）若()()3//k -+a b a b ，求实数k 的值； （2）若()m ⊥-a a b ，求实数m 的值．解：（１）3(0,10)-=-a b ，(13,24)k k k +=+-+a b ，因为(3)-a b ∥()k ＋a b ， 所以10300k --=，所以13k =-.（２）(3,24)m m m -=---a b ，因为()m ⊥-a a b ，所以32(24)0m m ----=，所以1m =-.16.已知c b a ,,分别是ABC ∆中角C B A ,,的对边，且222sin sin sin sin sin A C B A C +-= （１） 求角B 的大小； （２） 若ABC ∆的面积为4，且b =a c +的值. 解：(1) π3B =.⑵ 因为△ABC，所以1sin 2ac B =，所以3ac =．因为b2222cos b a c ac B =+-，所以22a c ac +-＝3，即2()3a c ac +-＝3． 所以2()a c +＝12，所以a ＋c＝．17.若函数2()(2)2f x x a x b =-++++，2log (1)2f =，且()()2g x f x x =-为偶函数.（３） 求函数()f x 的解析式；（４） 求函数()f x 在区间[,)m +∞的最大值为33m -，求m 的值. 解：（1）2()23f x x x =-++；（2）当2max 1,()2333m f x m m m ≥=-++=-，可得5m = 当max 1,()433m f x m <==-，可得1.3m =- 综合得15 3m or =-18. 已知某公司生产某品牌服装的年固定成本为10万元，每生产千件需另投入2.7万元，设该公司年内共生产该品牌服装x 千件并全部销售完，每千件的销售收入为()R x 万元，且⎪⎪⎩⎪⎪⎨⎧>-≤<-=)10(31000108)100(3018.10)(22x x x x x x R ．（1）写出年利润W （万元）关于年产品x （千件）的函数解析式；（2）年产量为多少千件时，该公司在这一品牌服装的生产中所获年利润最大？ （注：年利润=年销售收入－年总成本）解：（1）当0<x≤10时，10301.8)7.210()(3--=+-=x x x x xR W 当x >10时，x xx x xR W 7.23100098)7.210()(--=+-= ⎪⎪⎩⎪⎪⎨⎧>--≤<--=∴107.2310009810010301.83x x x x x x W ……………5分 （2）①当0<x≤10时，由;0,)9,0(.90101.82>'∈==-='W x x x W 时且当得 当(9,10),0;x W '∈<时∴当x=9时，W 取最大值，且6.3810930191.83max =-⨯-⨯=W ……………10分 ②当x>10时，W=98387.2310002987.231000=⨯-≤⎪⎭⎫⎝⎛+-x x x x当且仅当max 10001002.7,,38.39x x W x ===即时 综合①、②知x=9时，W 取最大值．所以当年产量为9千件时，该公司在这一品牌服装生产中获利最大． ……………15分 19.已知数列{}n a 是等差数列，n S 为其前n 项和，且满足254,25S S ==，数列{}n b 满足11n n n b a a +=⋅，n T 为数列{}n b 的前n 项和．（1）求数列{}n a 的通项公式；（2）若对任意的n *N ∈，不等式8(1)n n T n λ<+⋅-恒成立，求实数λ的取值范围； （3）是否存在正整数,m n (1)m n <<，使得1,,m n T T T 成等比数列？若存在，求出所有,m n 的值；若不存在，请说明理由．解：（1）11,2a d ==21n a n ∴=-（2）①当n 为偶数时，要使不等式8(1)n n T n λ<+⋅-恒成立，即需不等式(8)(21)8217n n n n nλ++<=++恒成立．828n n+≥，等号在2n =时取得． ∴此时λ需满足25λ<． ②当n 为奇数时，要使不等式8(1)n n T n λ<+⋅-恒成立，即需不等式(8)(21)8215n n n n nλ-+<=--恒成立． 82n n -是随n 的增大而增大， 1n ∴=时82n n -取得最小值6-．∴此时λ需满足21λ<-．综合①、②可得λ的取值范围是21λ<-．（3）11,,32121m n m nT T T m n ===++，若1,,m n T T T 成等比数列，则21()()21321m nm n =++，即2244163m n m m n =+++．…12分 （法一）由2244163m n m m n =+++， 可得2232410m m n m -++=>， 即22410m m -++>， ------------------------14分∴11m <<+． 又m ∈N ，且1m >，所以2m =，此时12n =． 因此，当且仅当2m =， 12n =时，数列{}n T 中的1,,m n T T T 成等比数列．-------- 16分（法二）因为1136366n n n=<++，故2214416m m m <++，即22410m m --<，20.已知a 为实数，函数()(1)xf x ax e =+，函数1()1g x ax=-，令函数()()()F x f x g x =⋅. （１） 若1,a =求函数()f x 的极小值；（２） 当1,2a =-解不等式()1F x <； （３） 当0,a <求函数()F x 的单调减区间. （1）/()(2),xf x x e =+令/()02f x x =⇒=-当(2,),()x f x ∈-+∞递增；当(,2),()x f x ∈-∞-递减； 故()f x 的极小值为2(2)f e --=-（2）由2()2x x F x e x -=+ 可得2/2()0(2)x x e F x x =-<+ 故()F x 在(,2),(2,)-∞--+∞递减当2x <-时()0,F x < 故当2x <-时()1F x < 当2x >-时(0)1,F =，由()1(0)0F x F x <=⇒> 综合得：原不等式的解集为(,2)(0,)x ∈-∞-⋃+∞（3）22/221()(1)x a x a F x e ax -++=-，令/()0F x =得2221a x a += ①当12a <-时，/()0F x <，减区间为11(,),(,)a a-∞+∞②当102a -<<时，减区间为11(,),(,),()a a a a-∞-+∞ ③当12a =-时，减区间为(,2),(2,)-∞--+∞19.已知数列{}n a 是等差数列，n S 为其前n 项和，且满足254,25S S ==，数列{}n b 满足11n n n b a a +=⋅，n T 为数列{}n b 的前n 项和．（1）求数列{}n a 的通项公式；（2）若对任意的n *N ∈，不等式8(1)n n T n λ<+⋅-恒成立，求实数λ的取值范围； （3）是否存在正整数,m n (1)m n <<，使得1,,m n T T T 成等比数列？若存在，求出所有,m n 的值；若不存在，请说明理由．20.已知a 为实数，函数()(1)xf x ax e =+，函数1()1g x ax=-，令函数()()()F x f x g x =⋅. （４） 若1,a =求函数()f x 的极小值；（５） 当1,2a =-解不等式()1F x <； （６） 当0,a <求函数()F x 的单调减区间.。

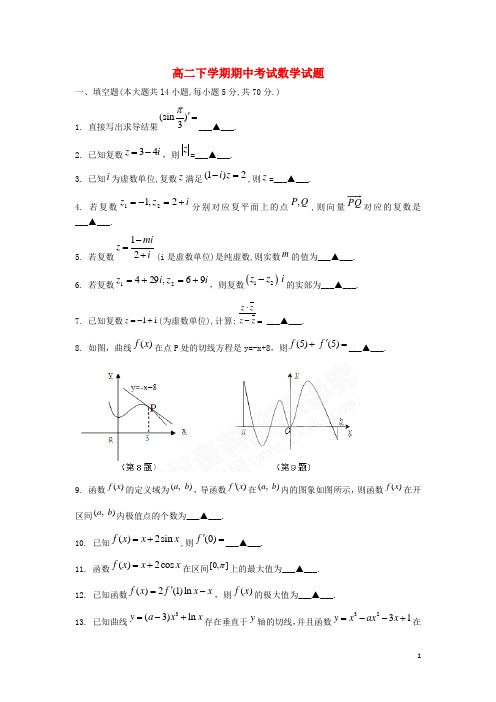
高二下学期期中考试数学试题一、填空题(本大题共l4小题,每小题5分,共70分.)1. 直接写出求导结果(sin)3π'=___▲___.2. 已知复数34z i=-，则z=___▲___.3. 已知i为虚数单位,复数z满足(1)2i z-=,则z=___▲___.4. 若复数izz+=-=2,121分别对应复平面上的点QP,,则向量PQ对应的复数是___▲___.5. 若复数12mizi-=+(i是虚数单位)是纯虚数,则实数m的值为___▲___.6. 若复数iziz96,29421+=+=，则复数()12z z i-的实部为___▲___.7. 已知复数1iz=-+(为虚数单位),计算:z zz z⋅-=___▲___.8. 如图，曲线)(xf在点P处的切线方程是y=-x+8，则(5)f+(5)f'=___▲___.9. 函数()f x的定义域为(,)a b，导函数()f x'在(,)a b内的图象如图所示，则函数()f x在开区间(,)a b内极值点的个数为___▲___.10. 已知()2sinf x x x=+,则(0)f'=___▲___.11. 函数()2cosf x x x=+在区间[0,]π上的最大值为___▲___.12. 已知函数()2(1)lnf x f x x'=-，则()f x的极大值为___▲___.13. 已知曲线3(3)lny a x x=-+存在垂直于y轴的切线，并且函数3231y x ax x=--+在[1,2]上单调递增，则a 的取值范围为___▲___.14. )(x f ,)(x g 分别是定义在R 上的奇函数和偶函数，当0<x 时,0)(')()()('>+x g x f x g x f ，且0)3(=-g ，则不等式0)()(<x g x f 的解集是___▲___.二、解答题(本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤)15. 设5221)(23+--=x x x x f ，当[2,2]x ∈-时，()0f x m ->恒成立，求实数m 的取值范围．16.已知函数f(x)=321ax bx cx +++的导函数为()f x '，()y f x '=的图象如图所示请写出f(x)单调区间若a=1,试求函数f(x)的解析式，并求出函数f(x)的极值及取极值时的相应的x 的值17. 已知z ∈C ，z1 = 2z i +，z2 =2zi -。

2014-2015学年江苏省宿迁市高二（下）期中数学试卷一、填空题：本大题共14小题，每小题5分，共计70分，请把答案填写在答题卡相应位置上．1．（5分）函数f（x）＝lg（2x﹣1）的定义域为．2．（5分）已知全集U＝{1，2，3}，集合A＝{1}，集合B＝{1，2}，则A∪∁U B ＝．3．（5分）已知函数y＝a x﹣2+1（a＞0，a≠1），不论常数a为何值，函数图象恒过定点．4．（5分）已知幂函数y＝f（x）的图象过点＝．5．（5分）已知函数则的值为．6．（5分）已知a，b∈R，若2a＝5b＝100，则＝．7．（5分）关于x的方程x2+2（a﹣1）x+2a+6＝0的两根为α，β，且满足0＜α＜1＜β，则a的取值范围是．8．（5分）已知f是有序数对集合M＝{（x，y）|x∈N*，y∈N*}上的一个映射，正整数数对（x，y）在映射f下对应的为实数z，记作f（x，y）＝z．对于任意的正整数m，n（m＞n），映射f由下表给出：则使不等式f（2，x）≤3的解集为．9．（5分）已知函数f（x）＝log2（x+2）+x﹣5存在唯一零点x0，则大于x0的最小整数为．10．（5分）函数的值域为．11．（5分）生活中常用的十二进位制，如一年有12个月，时针转一周为12个小时，等等，就是逢12进1的计算制，现采用数字0～9和字母A、B共12个计数符号，这些符号与十进制的数的对应关系如下表；例如用十二进位制表示A+B＝19，照此算法在十二进位制中运算A×B＝．12．（5分）已知函数f（x）＝（a≠±1）在区间（0，1]上是减函数，则a的取值范围是．13．（5分）已知大于1的任意一个自然数的三次幂都可写成连续奇数的和．如：若m是自然数，把m3按上述表示，等式右侧的奇数中含有2015，则m＝．14．（5分）已知定义在R上的函数f（x）既是奇函数，又是周期函数，且周期为．当时，（a、b∈R），则f（1）+f（2）+…+f（100）的值为．二、解答题：本大题共6小题，15-17每小题14分，18-20每小题14分，共计90分．请在答题卡指定的区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．（14分）已知命题A＝{x|x2﹣2x﹣8＜0}，B＝．（1）若A∩B＝（2，4），求m的值；（2）若B⊆A，求m的取值范围．16．（14分）已知z为复数，z+2i为实数，且（1﹣2i）z为纯虚数，其中i是虚数单位．（1）求复数z；（2）若复数z满足，求|ω|的最小值．17．（14分）某商场欲经销某种商品，考虑到不同顾客的喜好，决定同时销售A、B两个品牌，根据生产厂家营销策略，结合本地区以往经销该商品的大数据统计分析，A品牌的销售利润y1与投入资金x成正比，其关系如图1所示，B 品牌的销售利润y2与投入资金x的算术平方根成正比，其关系如图2所示（利润与资金的单位：万元）．（1）分别将A、B两个品牌的销售利润y1、y2表示为投入资金x的函数关系式；（2）该商场计划投入5万元经销该种商品，并全部投入A、B两个品牌，问：怎样分配这5万元资金，才能使经销该种商品获得最大利润，其最大利润为多少万元？18．（16分）（1）找出一个等比数列{a n}，使得1，，4为其中的三项，并指出分别是{a n}的第几项；（2）证明：为无理数；（3）证明：1，，4不可能为同一等差数列中的三项．19．（16分）已知定义在R上的函数f（x）＝ln（e2x+1）+ax（a∈R）是偶函数．（1）求实数a的值；（2）判断f（x）在[0，+∞）上的单调性，并用定义法证明；（3）若f（x2+）＞f（mx+）恒成立，求实数m的取值范围．20．（16分）已知函数f（x）＝x2﹣1，g（x）＝|x﹣a|．（1）当a＝1时，求F（x）＝f（x）﹣g（x）的零点；（2）若方程|f（x）|＝g（x）有三个不同的实数解，求a的值；（3）求G（x）＝f（x）+g（x）在[﹣2，2]上的最小值h（a）．2014-2015学年江苏省宿迁市高二（下）期中数学试卷参考答案与试题解析一、填空题：本大题共14小题，每小题5分，共计70分，请把答案填写在答题卡相应位置上．1．（5分）函数f（x）＝lg（2x﹣1）的定义域为．【解答】解：∵函数f（x）＝lg（2x﹣1），∴2x﹣1＞0，解得x＞；∴f（x）的定义域为（，+∞）．故答案为：（，+∞）．2．（5分）已知全集U＝{1，2，3}，集合A＝{1}，集合B＝{1，2}，则A∪∁U B ＝{1，3}．【解答】解：∵全集U＝{1，2，3}，集合A＝{1}，集合B＝{1，2}，∴∁U B＝{3}，则A∪∁U B＝{1，3}，故答案为：{1，3}3．（5分）已知函数y＝a x﹣2+1（a＞0，a≠1），不论常数a为何值，函数图象恒过定点（2，2）．【解答】解：∵y＝a x﹣2+1，∴当x﹣2＝0时，x＝2，此时y＝1+1＝2，即函数过定点（2，2）．故答案为：（2，2）4．（5分）已知幂函数y＝f（x）的图象过点＝．【解答】解：设f（x）＝x n，n是有理数，则∵幂函数的图象过点∴＝2n，即2﹣2＝2n，可得n＝﹣2∴幂函数表达式为f（x）＝x﹣2，可得f（3）＝3﹣2＝故答案为：5．（5分）已知函数则的值为．【解答】解：函数则＝f（log3）＝f（﹣3）＝2﹣3＝．故答案为：．6．（5分）已知a，b∈R，若2a＝5b＝100，则＝．【解答】解：a，b∈R，若2a＝5b＝100，∴a＝log2100＝＝，b＝log5100＝＝，∴＝（lg2+lg5）＝，故答案为：．7．（5分）关于x的方程x2+2（a﹣1）x+2a+6＝0的两根为α，β，且满足0＜α＜1＜β，则a的取值范围是．【解答】解：依题意，函数f（x）＝x2+2（a﹣1）x+2a+6＝的两个零点α，β满足0＜α＜1＜β，且函数f（x）过点（0，4），则必有，即：，解得：﹣3．故答案为：（﹣3，﹣）8．（5分）已知f是有序数对集合M＝{（x，y）|x∈N*，y∈N*}上的一个映射，正整数数对（x，y）在映射f下对应的为实数z，记作f（x，y）＝z．对于任意的正整数m，n（m＞n），映射f由下表给出：则使不等式f（2，x）≤3的解集为{1，2}．【解答】解；根据题意得出：f（2，x）＝∴不等式f（2，x）≤3可以转化为：或即﹣1≤x≤2或x∈∅，x∈N*，∴解集为{1，2}故答案为：{1，2}9．（5分）已知函数f（x）＝log2（x+2）+x﹣5存在唯一零点x0，则大于x0的最小整数为3．【解答】解：∵函数f（x）＝log2（x+2）+x﹣5，∴函数f（x）在（﹣2，+∞）上单调递增，∵f（2）＝log24+2﹣5＝﹣1＜0，f（3）＝log25+3﹣5＝log25﹣2＝log2＞0，∴根据函数零点存在性定理得出；f（x）在（2，3）上有一个零点，且存在唯一零点，故大于x0的最小整数为3，故答案为：3．10．（5分）函数的值域为（﹣∞，﹣2]∪[10，+∞）．【解答】解：∵函数，∴y＝2+，x∈[0，3]且x≠2，∵﹣2≤x﹣2≤1，x﹣2≠0∴≤﹣4或≥8∴y≤﹣2或y≥10，故答案为：（﹣∞，﹣2]∪[10，+∞）11．（5分）生活中常用的十二进位制，如一年有12个月，时针转一周为12个小时，等等，就是逢12进1的计算制，现采用数字0～9和字母A、B共12个计数符号，这些符号与十进制的数的对应关系如下表；例如用十二进位制表示A+B＝19，照此算法在十二进位制中运算A×B＝92．【解答】解：把十二进制数化为十进制数，则B（12）＝11，A（12）＝10，∴B（12）×A（12）＝11×10＝110＝9×121+2×120＝92；故答案为：92．12．（5分）已知函数f（x）＝（a≠±1）在区间（0，1]上是减函数，则a的取值范围是（﹣1，0）∪（1，3]．【解答】解：∵f（x）＝（a≠±1）在区间（0，1]上是减函数，∴或，解得﹣1＜a＜0或1＜a≤3，∴a的取值范围是：（﹣1，0）∪（1，3]，故答案为：（﹣1，0）∪（1，3]．13．（5分）已知大于1的任意一个自然数的三次幂都可写成连续奇数的和．如：若m是自然数，把m3按上述表示，等式右侧的奇数中含有2015，则m＝45．【解答】解：由题意，从23到m3，从3开始的连续奇数共2+3+4+…+m＝个，2015＝3+2（n﹣1），所以n＝1007，即2015是从3开始的第1007个奇数，当m＝44时，从23到443，从3开始的连续奇数共＝989个当m＝45时，从23到453，从3开始的连续奇数共＝1034个故m＝45，故答案为：45．14．（5分）已知定义在R上的函数f（x）既是奇函数，又是周期函数，且周期为．当时，（a、b∈R），则f（1）+f（2）+…+f（100）的值为．【解答】解：∵定义在R上的函数f（x）是奇函数，∴f（0）＝0，∵当时，（a、b∈R），∴a＝0，即当时，f（x）＝﹣bx（a、b∈R），∵函数f（x）的周期为，f（1）＝f（）＝f（﹣），f（2）＝f（）＝f（），f（3）＝f（+）＝f（0）＝0f（4）＝f（3+1）＝f（1）＝f（﹣），…f（100）＝f（99+1）＝f（1）＝f（﹣）＝﹣f（），∴f（1）+f（2）+…+f（100）＝f（1）＝，∵定义在R上的函数f（x）既是奇函数，又是周期函数，且周期为，∴f（﹣）＝﹣f（）＝﹣1+，f（﹣）＝f（﹣）＝f（）＝1﹣，∴﹣1＝1﹣，求解b＝∴f（1）+f（2）+…+f（100）＝f（1）＝﹣f（）＝＝，故答案为：．二、解答题：本大题共6小题，15-17每小题14分，18-20每小题14分，共计90分．请在答题卡指定的区域内作答，解答时应写出文字说明、证明过程或演算步骤．15．（14分）已知命题A＝{x|x2﹣2x﹣8＜0}，B＝．（1）若A∩B＝（2，4），求m的值；（2）若B⊆A，求m的取值范围．【解答】解：化简得A＝{x|﹣2＜x＜4}，B＝{x|m﹣3＜x＜m}．（1）∵A∩B＝（2，4），∴m﹣3＝2且m≥4，则m＝5．（2）∵B⊆A，即，解得1≤m≤4．∴m的取值范围是[1，4]．16．（14分）已知z为复数，z+2i为实数，且（1﹣2i）z为纯虚数，其中i是虚数单位．（1）求复数z；（2）若复数z满足，求|ω|的最小值．【解答】解：（1）设z＝a+bi（a，b∈R），则z+2i＝a+（b+2）i，因为z+2i为实数，所以有b+2＝0①…2分（1﹣2i）z（1﹣2i）（a+bi）＝a+2b+（b﹣2a）i，因为（1﹣2i）z为纯虚数，所以a+2b＝0，b﹣2a≠0，②…4分由①②解得a＝4，b＝﹣2．…6分故z＝4﹣2i．…7分（2）因为z＝4﹣2i，则＝4+2i，…8分设ω＝x+yi，（x，y∈R），因为，即（x﹣4）2+（y﹣2）2＝1…10分又|ω|＝，故|ω|最小值即为原点到圆（x﹣4）2+（y﹣2）2＝1上的点距离的最小值，因为原点到点（4，2）的距离为＝，又因为圆的半径r＝1，原点在圆外，所以|ω|的最小值即为2﹣1．…14分．17．（14分）某商场欲经销某种商品，考虑到不同顾客的喜好，决定同时销售A、B两个品牌，根据生产厂家营销策略，结合本地区以往经销该商品的大数据统计分析，A品牌的销售利润y1与投入资金x成正比，其关系如图1所示，B 品牌的销售利润y2与投入资金x的算术平方根成正比，其关系如图2所示（利润与资金的单位：万元）．（1）分别将A、B两个品牌的销售利润y1、y2表示为投入资金x的函数关系式；（2）该商场计划投入5万元经销该种商品，并全部投入A、B两个品牌，问：怎样分配这5万元资金，才能使经销该种商品获得最大利润，其最大利润为多少万元？【解答】解：（1）因为A品牌的销售利润y1与投入资金x成正比，设y1＝k1x（x＞0），又过点（2，0.5），解得，所以；B品牌的销售利润y2与投入资金x的算术平方根成正比，设y2＝k2（x＞0），又过点（4，1.5），即有1.5＝2k2，解得k2＝，所以y2＝（x＞0）；（2）设总利润为y，投入B品牌为x万元，则投入A品牌为（5﹣x）万元，则，令，则＝，当时，即时，投入A品牌为：，．答：投入A品牌万元、B品牌万元时，经销该种商品获得最大利润，最大利润为万元．18．（16分）（1）找出一个等比数列{a n}，使得1，，4为其中的三项，并指出分别是{a n}的第几项；（2）证明：为无理数；（3）证明：1，，4不可能为同一等差数列中的三项．【解答】解：（1）取一个等比数列{a n}：首项为1、公比为，则，…2分则令＝4，解得n＝5，所以a 1＝1，，a5＝4．…4分（2）证明：假设是有理数，则存在互质整数h、k，使得，…5分则h2＝2k2，所以h为偶数，…7分设h＝2t，t为整数，则k2＝2t2，所以k也为偶数，则h、k有公约数2，这与h、k互质相矛盾，…9分所以假设不成立，所以是有理数．…10分（3）证明：假设1，，4是同一等差数列中的三项，且分别为第n、m、p项且n、m、p互不相等，…11分设公差为d，显然d≠0，则，消去d得，，…13分由n、m、p都为整数，所以为有理数，由（2）得是无理数，所以等式不可能成立，…15分所以假设不成立，即1，，4不可能为同一等差数列中的三项．…16分．19．（16分）已知定义在R上的函数f（x）＝ln（e2x+1）+ax（a∈R）是偶函数．（1）求实数a的值；（2）判断f（x）在[0，+∞）上的单调性，并用定义法证明；（3）若f（x2+）＞f（mx+）恒成立，求实数m的取值范围．【解答】19．解：（1）因为f（x）是定义在R上的偶函数，所以f（1）＝f（﹣1），即ln（e2+1）+a＝ln（e﹣2+1）﹣a，即2a＝＝﹣2，得a＝﹣1，…2分当a＝﹣1时，f（x）＝ln（e2x+1）﹣x，对于∀x∈R，f（﹣x）＝ln（e﹣2x+1）+x＝ln（e2x+1）﹣x＝f（x），综上a＝﹣1 …4分（2）f（x）在[0，+∞）上是单调增函数，…5分证明如下：设x1，x2为[0，+∞）内的任意两个值，且x1＜x2，则＝因为0≤x1＜x2，所以x2﹣x1＞0，x2+x1＞0，所以，所以，所以，所以，所以f（x1）﹣f（x2）＜0，即f（x1）＜f（x2），所以f（x）在[0，+∞）上是单调增函数．…10分（3）f（x）在[0，+∞）上是单调增函数，且是偶函数，又，所以，…12分令，则t∈（﹣∞，﹣2]∪[2，+∞），所以|mt|＜t2﹣2，恒成立，…14分因为，关于|t|在[2，+∞）上单调递增，所以，所以|m|＜1恒成立，所以﹣1＜m＜1．…16分．20．（16分）已知函数f（x）＝x2﹣1，g（x）＝|x﹣a|．（1）当a＝1时，求F（x）＝f（x）﹣g（x）的零点；（2）若方程|f（x）|＝g（x）有三个不同的实数解，求a的值；（3）求G（x）＝f（x）+g（x）在[﹣2，2]上的最小值h（a）．【解答】解：（1）当a＝1时，，令F（x）＝0得，当x≥1时，x2﹣x＝0，x＝1（x＝0舍去）当x＜1时，x2+x﹣2＝0，x＝﹣2（x＝1舍去）所以当a＝1时，F（x）的零点为1，﹣2，（2）方程|f（x）|＝g（x），即|x2﹣1|＝|x﹣a|，变形得（x2+x﹣a﹣1）（x2﹣x+a﹣1）＝0，从而欲使原方程有三个不同的解，即要求方程x2+x﹣a﹣1＝0 (1)与x2﹣x+a﹣1＝0 (2)满足下列情形之一：（I）一个有等根，另一个有两不等根，且三根不等（II）方程（1）、（2）均有两不等根且由一根相同；对情形（I）：若方程（1）有等根，则△＝1+4（a+1）＝0解得代入方程（2）检验符合；若方程（2）有等根，则△＝1﹣4（a﹣1）＝0解得代入方程（1）检验符合；对情形（II）：设x0是公共根，则，解得x0＝a代入（1）得a＝±1，a＝1代入|f（x）|＝g（x）检验得三个解为﹣2、0、1符合a＝﹣1代入|f（x）|＝g（x）检验得三个解为2、0、﹣1符合故|f（x）|＝g（x）有三个不同的解的值为或a＝±1．（3）因为G（x）＝f（x）+g（x）＝x2﹣1+|x﹣a|＝，①当时，G（x）在上递减，在上递增，故G（x）在[﹣2，2]上最小值为②当时G（x）＝x2﹣x﹣1+a，在上递减，在上递增，故G（x）在[﹣2，2]上最小值为③当时，G（x）在[﹣2，a]上递减，当x∈[a，2]时递增，故此时G（x）在[﹣2，2]上的最小值为综上所述：。

2015～2016学年度第二学期期中调研测试高二数学参考答案本试卷包含填空题（第1题—第14题）和解答题（第15题—第20题）两部分，共4页．本卷满分160分，考试时间为120分钟．一、填空题：本大题共14小题，每小题5分，共70分. 请把答案填写在答题卡相应的位置．．．．．．．．上．. 1.设集合{}54321，，，，=A ，{}8,7542，，，=B ，则=B A {}5,4,22.复数i 32-的实部是 23.函数)2ln(1)(x x x f -+-=的定义域为 [)2,1 4.设幂函数()为实数ααx x f =)(的图像经过点()8,4，则幂函数的解析式为)(x f 23x5. 已知函数⎩⎨⎧<≥+=-4 ,24,32)(1x x x x f x ，则[]=)3(f f 116. 计算()=+-32272lg 4lg 32lg 12 7. 用反证法证明命题“设,a b 是实数，则方程30x ax b ++=至少有一个实根”时，要做的反设是 （4） （填序号）（1）．方程30x ax b ++=恰好有两个实根 （2）．方程30x ax b ++=至多有一个实根（3）．方程30x ax b ++=至多有两个实根 （4）．方程30x ax b ++=没有实根8.已知函数52lg )(-+=x x x f 的零点在区间()1,+k k ()z k ∈，则=k 29.已知函数)(x f y =是定义在R 上的奇函数，当0>x 时，72)(2-=x x f ， 则-)2(f 1-10.已知212+=a ，函数x x f a log )(=，若正实数n m ,满足)()(n f m f >， 则n m ,的大小关系是 n m >11.若复数z 满足i z z 423+=-，其中i 为虚数单位，则复数z12. 已知函数)(1)()1(x f x f x f +=+，且1)1(=f ，则=)10(f 101 13.将全体正整数排成一个三角形数阵：51 41 31 21 1101 9 8 765 4321按照以上的排列规律，第20行第2个数是 19214.已知函数⎪⎩⎪⎨⎧>-≤+-=1,21211,22)(x x x x f x ，若存在实数21x x <，使得()()21x f x f =， 则)(12x f x 的取值范围是 ()10,0二、解答题: 本大题共6小题，15—17每小题14分，18—20每小题16分，共计90分．请在答题卡指定的区域内作答．．．．．．．．．．．，解答时应写出文字说明，证明过程或演算步骤． 15设集合{}|13A x x =-<<，{}m x x B >=|．（1）若1-=m ，求集合A 在B 中的补集；（2）若B B A = ，求实数m 的取值范围．（1）{}31|<<-=x x A ………………2分1-=m∴{}1|->=x x B ………………4分∴集合A 在B 中的补集为{}3|≥x x ………………7分（2） B B A =∴B A ⊆………………10分又 {}31|<<-=x x A ，{}m x x B >=|∴实数m 的取值范围是1-≤m ………………14分16.已知复数i z +-=21，i z z 5521+-=（其中i 为虚数单位）（1）求复数2z ；（2）若复数])1()32)[(3(223i m m m z z -+---=所对应的点在第四象限，求实数m 的取值范围。