高一数学两个变量的线性相关
- 格式:pdf
- 大小:1.09 MB
- 文档页数:9





人教版高一数学必修三第二章统计目录2.1.1 简单随机抽样(新授课)2.1.2 系统抽样(新授课)2.1.3 分层抽样(新授课)2.2.1用样本的频率分布估计总体分布(2课时)(新授课) 2.2.2用样本的数字特征估计总体的数字特征(2课时)(新授课) 2.3.1变量之间的相关关系(新授课)2.3.2两个变量的线性相关(第一课时)(新授课)2.3.2两个变量的线性相关(第二课时)(新授课)2.3.2生活中线性相关实例(第三课时)(新授课)第二章统计单元检测题(一)第二章统计单元检测题(一)参考答案第二章统计单元检测题(二)第二章统计单元检测题(二)参考答案第二章统计单元检测题(三)第二章统计单元检测题(三)参考答案第二章统计一、课程目标:本章主要介绍最基本的获取样本数据的方法,以及集中从样本数据中提取信息的统计方法,其中包括用样本估计总体分布、数字特征和线性回归等内容。
本章通过实际问题,进一步介绍随机抽样、样本估计总体、线性回归的基本方法。
二、学习目标:1、随机抽样(1)能从现实生活或其他学科中提出具有一定价值的统计问题。
(2)结合具体的实际问题情境,理解随机抽样的必要性和重要性。
(3)在参与解决统计问题的过程中,学会用简单随机抽样从总体中抽取样本;通过对实例的分析,了解分层抽样和系统抽样方法。
(4)通过试验、查阅资料、设计调查问卷等方法收集数据。
2、用样本估计总体(1)通过实例体会分布的意义和作用,在表示样本数据的过程中,学会列频率分布彪、花频率分布直方图、频率折线图、茎叶土,体会它们各自的特点。
(2)通过实例理解样本数据标准差的意义和作用,学会计算数据样本差。
(3)能根据实际问题的需求合理地选取样本,从样本数据中提取基本的数字特征,并做出合理的解释。
(4)进一步体会用样本估计总体的思想。
(5)会用随机抽样的基本方法和样本估计总体的思想,解决一些简单的实际问题。
(6)形成对数据处理过程进行初步评价的意识。

变量间的相关关系讲义变量间的相关关系讲义一、基础知识梳理知识点1:变量之间的相关关系两个变量之间的关系可能是确定的关系(如:函数关系),或非确定性关系。
当自变量取值一定时,因变量也确定,则为确定关系;当自变量取值一定时,因变量带有随机性,这种变量之间的关系称为相关关系。
相关关系是一种非确定性关系,如长方体的高与体积之间的关系就是确定的函数关系,而人的身高与体重的关系,学生的数学成绩好坏与物理成绩的关系等都是相关关系。
注意:两个变量之间的相关关系又可分为线性相关和非线性相关,如果所有的样本点都落在某一函数曲线的附近,则变量之间具有相关关系(不确定性的关系),如果所有样本点都落在某一直线附近,那么变量之间具有线性相关关系,相关关系只说明两个变量在数量上的关系,不表明他们之间的因果关系,也可能是一种伴随关系。
点睛:两个变量相关关系与函数关系的区别和联系相同点:两者均是两个变量之间的关系,不同点:函数关系是一种确定的关系,如匀速直线运动中时间t与路程s的关系,相关关系是一种非确定的关系,如一块农田的小麦产量与施肥量之间的关系,函数关系是两个随机变量之间的关系,而相关关系是非随机变量与随机变量之间的关系;函数关系式一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系。
知识点2.散点图.1.在考虑两个量的关系时,为了对变量之间的关系有一个大致的了解,人们常将变量所对应的点描出来,这些点就组成了变量之间的一个图,通常称这种图为变量之间的散点图。
2.从散点图可以看出如果变量之间存在着某种关系,这些点会有一个集中的大致趋势,这种趋势通常可以用一条光滑的曲线来近似,这种近似的过程称为曲线拟合。
3.对于相关关系的两个变量,如果一个变量的值由小变大时,另一个变量的的值也由小变大,这种相关称为正相关,正相关时散点图的点散布在从左下角到由上角的区域内。
如果一个变量的值由小变大时,另一个变量的值由大变小,这种相关称为负相关,负相关时散点图的点散步在从左上角到右下角的区域。

高一数学常用公式及结论必修1: 一、集合1、集合三要素:确定性,互异性,无序性 3. 元素与集合的关系:属于∈ 不属于:∉ 空集:φ5.集合A 有n 个元素,则子集有2n 个;真子集有2n –1个;非空子集有2n –1个;非空真子集有2n –2个;6.常用数集:自然数集:N 正整数集:*N 整数集:Z 有理数集:Q 实数集:R 二、函数1、复合函数的单调性: 同增异减2、二次函数y = ax 2 +bx + c (0a ≠)的性质(1)、顶点坐标公式:⎪⎪⎭⎫ ⎝⎛--a b ac a b 44,22, 对称轴:a bx 2-=, (2).二次函数的解析式的三种形式(1)一般式2()(0)f x ax bx c a =++≠; (2)顶点式2()()(0)f x a x h k a =-+≠; (3)两根式12()()()(0)f x a x x x x a =--≠. 三、指数与指数函数 1、幂的运算法则:(1)a m • a n = a m + n , (2)n m n m a a a -=÷, (3)( a m ) n = a m n (4)( ab ) n = a n • b n(5) n n nb a b a =⎪⎭⎫⎝⎛ (6)a 0 = 1 ( a ≠0) (7)n n a a 1=-(8)m nmna a= (9)mnmn aa1=-(10)3、指数函数y = a x (a > 0且a ≠1)的性质:(1)定义域:R ; 值域:( 0 , +∞) (2)图象过定点(0,1)4.指数式与对数式的互化: log b a N b a N =⇔=(0,1,0)a a N >≠>. 四、对数与对数函数 1对数的运算法则:(1)a b = N <=> b = log a N (2)log a 1 = 0(3)log a a = 1 (4)log a a b = b (5)a log a N = N(6)log a (MN) = log a M + log a N (7)log a (NM) = log a M -- log a N(8)log a N b = b log a N (9)换底公式:log a N =aNb b log log (10)推论 log log m n a a nb b m=. (11)log a N =a N log 1 (12)常用对数:lg N = log 10 N (13)自然对数:ln A = log e A (e = 2.71828…)2、对数函数y = log a x (a > 0且a ≠1)的图像与性质:(1)定义域:( 0 , +∞) ; 值域:R (2)图象过定点(1,0)五、幂函数y = x a 的图象:(1) 根据 a 的取值画出函数在第一象限的简图 .例如: y = x 2 21x x y == 11-==x xy 六.图象平移:左加右减,上加下减必修3:(1)、平均值:nx x x x n+++= 21(2)、8、两个变量的线性相关(1)、概念:(1)回归直线方程:y a b x ∧∧∧=+必修4 一、三角函数与三角恒等变换2、同角三角函数公式 sin 2α+ cos 2α= 1 ααcos tan =3、二倍角的三角函数公式sin2α= 2sin αcos α cos2α=2cos 2α-1 = 1-2 sin 2α= cos 2α- sin 2αααα2tan 1tan 22tan -= 4、降幂公式 22cos 1cos 2αα+= 22cos 1sin 2αα-=5、两角和差的三角函数公式sin (α±β) = sin αcos β土cos αsin β cos (α±β) = cos αcos β干sin αsin β()βαβαβαtan tan 1tan tan tan ±=±6、两角和差正切公式的变形:tan α±tan β= tan (α±β) (1干tan αtan β) ααtan 1tan 1-+=ααtan 45tan 1tan 45tan ︒-+︒= tan (4π+α) ααtan 1tan 1+-=ααtan 45tan 1tan 45tan ︒+-︒= tan (4π-α)7、两角和差正弦公式的变形(合一变形)()ϕααα++=+sin cos sin 22b a b a (其中ab =ϕtan )8、三角函数的诱导公式 “奇变偶不变,符号看象限。


高一数学必修三导学稿使用时间:2014-5 编号:编制人:张永柱田娟备课组长:责任领导:班级:小组:姓名:小组评价:教师评价:§7相关性学习目标:1.通过收集有关数据,分析两个变量之间的关系,正确判断两个变量之间的关系是函数关系还是其他关系,从直观上认识两个变量之间的相关关系与函数关系的区别,知道两个变量的相关关系是一种不确定关系。
2.会画出散点图,并会利用散点图来判断两个变量之间的关系。
3.从实际问题分析两个变量具有相关关系时,拟合直线的几种认识。
一.预习导引:1.两个变量之间的关系,常见的有两类:一类是具有确定的函数关系,如⑴()⑵(),另一类是两个变量存在一定的关系,但却不具备函数关系所要求的确定性,它们之间的关系是带有一定的随机性的,如⑶()像这一类关系,我们称为相关关系。
2.什么是散点图?什么是曲线拟合?3.什么是线性相关?什么是非线性相关?什么是不相关?p的表中的数据4.案例分析:课本48(1)根据表中的数据,制成散点图,你能从散点图中发现身高与右手的一拃长之间的近似关系吗?(2)如果近似成线性关系,请画出一条直线来近似的表现这种关系。
(3)如果一个学生的身高是188cm,你能估计他的一拃大概有多长吗?二.探究交流:1.下列说法中是相关关系的是()A.光照时间和果树的单位的面积产量。
B.正方形的边长和它的周长。
C.球的半径和它的表面积。
D.在公路上行驶的汽车,行驶时间与路程。
2(1) 画出散点图(2) 由散点图判断变量x 与y 之间的关系。
归纳:相关关系的判断方法:三.随堂训练:1.下列两个变量之间的关系不是函数关系的是( )A .正方体的棱长与体积。
B .单产为常数时,土地面积与产量。
C .日照时间与水稻的亩产量。
D .电压一定时,电流与电阻。
2.对变量,x y 有观测数据(,i i x y ) (i =1,2,…,10),得散点图1;对变量,u v 有观测数据(,i i u v )(i =1,2,,10),得散点图2,由这个散点图可以判断。

[核心必知]1.预习教材,问题导入根据以下提纲,预习教材P84~P91,回答下列问题.(1)两个变量之间除了函数关系还有其他关系吗?提示:相关关系.(2)当两个变量呈负相关关系时,散点图有什么特点?提示:当两个变量之间呈负相关关系时,散点图中的点散布的位置是从左上角到右下角的区域.(3)求回归直线方程的主要方法是什么?提示:求回归直线方程的主要方法是最小二乘法.2.归纳总结,核心必记(1)变量之间的相关关系变量与变量之间的关系常见的有两类:一类是确定性的函数关系,变量之间的关系可以用解析式表示;另一类是相关关系,变量之间有一定的联系,但不能完全用解析式来表达.(2)两个变量的线性相关①散点图将各数据在平面直角坐标系中的对应点画出来,得到表示两个变量的一组数据的图形,这样的图形叫做散点图.②正相关在散点图中,点散布在从左下角到右上角的区域,对于两个变量的这种相关关系,我们将它称为正相关.③负相关在散点图中,点散布在从左上角到右下角的区域,对于两个变量的这种相关关系,我们将它称为负相关.④线性相关关系、回归直线如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫做回归直线,这条直线的方程叫做回归直线方程,简称回归方程.(3)回归直线方程 ①回归直线方程假设我们已经得到两个具有线性相关关系的变量的一组数据(x 1,y 1),(x 2,y 2),…,(x n ,y n ),则所求回归方程是y ^=b ^x +a ^,其中b ^是回归方程的斜率,a ^是截距.其中⎩⎪⎨⎪⎧b ^=∑i =1n (x i -x )(y i -y )∑i =1n (x i-x )2=∑i =1nx i y i -n x y ∑i =1nx 2i -n x2,a ^=y -b ^x -.②最小二乘法通过求Q =(y 1-bx 1-a )2+(y 2-bx 2-a )2+…+(y n -bx n -a )2 的最小值而得出回归直线的方法,即使得样本数据的点到回归直线的距离的平方和最小的方法叫做最小二乘法.[问题思考](1)任意两个统计数据是否均可以作出散点图?提示:可以,不管这两个统计量是否具备相关性,以一个变量值作为横坐标,另一个作为纵坐标,均可画出它的散点图.(2)任何一组数据都可以由最小二乘法得出回归直线方程吗?提示:用最小二乘法求回归直线方程的前提是先判断所给数据具有线性相关关系(可利用散点图来判断),否则求出的回归直线方程无意义.(3)根据a ^=y -b ^x 及回归直线方程y ^=b ^x +a ^,判断点(x ,y )与回归直线的关系是什么?提示:由a ^=y -b ^x 得y =b ^x +a ^,因此点(x ,y )在回归直线上.[课前反思]通过以上预习,必须掌握的几个知识点:(1)相关关系: ; (2)散点图: ; (3)回归直线方程及求回归直线方程的方法步骤:.瑞雪兆丰年,这不禁使我们想到这样一句谚语:“冬天麦盖三层被,来年枕着馒头睡”,意思是冬天“棉被”盖得越厚,春天小麦就长得越好.[思考1] 下雪与小麦丰收有关系吗?提示:有关系,但这种关系具有不确定性.[思考2]若把下雪量和小麦产量看作两个变量,则这两个变量之间的关系是确定的吗?若不是确定的,那会是什么关系?名师指津:这两个变量之间的关系是不确定的,这两个变量之间的关系是相关关系.[思考3]怎样理解两个变量之间的关系?名师指津:两个变量间的关系分为三类:(1)确定性的函数关系,如正方形的边长与面积的关系;(2)相关关系,变量间确实存在关系,但又不具备函数关系所要求的确定性,它们的关系是带有随机性的,这种关系就是相关关系,例如,某位同学的“物理成绩”与“数学成绩”之间的关系;(3)不相关,即两个变量间没有任何关系.讲一讲1.下列关系中,属于相关关系的是________.①人的身高与视力的关系;②做自由落体运动的物体的质量与落地时间的关系;③降雪量与交通事故的发生率之间的关系.[尝试解答]续表相关关系与函数关系区别函数关系是一种确定的关系,而相关关系是两个变量间一种不完全确定的关系.函数关系是一种因果关系,而相关关系不一定是因果关系,也可能是伴随关系.练一练1.在下列两个变量的关系中,哪些是相关关系?①正方形边长与面积之间的关系;②作文水平与课外阅读量之间的关系;③人的身高与年龄之间的关系;解:两变量之间的关系有三种:函数关系、相关关系和不相关.①正方形的边长与面积之间的关系是函数关系.②作文水平与课外阅读量之间的关系不是严格的函数关系,但是具有相关性,因而是相关关系.③人的身高与年龄之间的关系既不是函数关系,也不是相关关系,因为人的年龄达到一定时期身高就不发生明显变化了,因而他们不具备相关关系.下表为某地搜集到的新房屋的销售价格y(单位:万元)和房屋的面积x(单位:m2)的数据:[思考1]点?此图称为什么图形?名师指津:能,如图所示,此图称为散点图.[思考2]从散点图看应怎样描述房屋的销售价格与房屋面积之间的变化关系?名师指津:从大体上看,面积越大,销售价格越高,但不是正比例函数关系.[思考3]怎样认识散点图?名师指津:(1)散点图与相关性的关系:散点图形象地反映了各对数据的密切程度.根据散点图中点的分布趋势分析两个变量之间的关系,可直观地判断并得出结论.(2)散点图与正、负相关性的关系:如果散点图中的点散布在从左下角到右上角的区域内,称这两个变量正相关,即两个变量具有相同的变化趋势;如果散点图中的点散布在从左上角到右下角的区域内,称这两个变量负相关,即两个变量具有相反的变化趋势.讲一讲2.下表是某地的年降雨量与年平均气温,判断两者是相关关系吗?求回归直线方程有意义吗?[尝试解答]以x轴为年平均气温,y轴为年降雨量,可得相应的散点图,如图所示:因为图中各点并不在一条直线附近,所以两者不具有相关关系,求回归直线方程也是没有意义的.用散点图判断两个变量x与y的相关关系(1)判断两个变量x和y间是否具有线性相关关系,常用的简便方法就是绘制散点图,如果图上发现点的分布从整体上看大致在一条直线附近,那么这两个变量就是线性相关的,注意不要受个别点的位置的影响.(2)画散点图时应注意合理选择单位长度,避免图形过大或偏小,或者是点的坐标在坐标系中画不准,使图形失真,导致得出错误结论.练一练2.对变量x,y有观测数据(x i,y i)(i=1,2,…,10),得散点图①;对变量u,v有观测数据(u i,v i)(i=1,2,…,10),得散点图②.由这两个散点图可以判断()A.变量x与y正相关,u与v正相关B.变量x与y正相关,u与v负相关C.变量x与y负相关,u与v正相关D.变量x与y负相关,u与v负相关解析:选C在从散点图来看,图①中的点自左上方向右下方分布,说明变量x与y负相关;图②中的点自左下方向右上方分布,说明u与v正相关.观察知识点2中的背景实例.[思考]根据表格中的数据,能否估计出房屋面积为120 m2时的销售价格?如何估计?名师指津:能.可根据散点图作出一条直线,求出直线方程,再进行预测.根据两个变量的取值,画出散点图后作出一条直线,利用最小二乘法求出此直线方程,代入相关数据即可对另一个变量取值进行估计.讲一讲3.一般来说,一个人脚掌越长,他的身高就越高,现对10名成年人的脚掌长x 与身高y 进行测量,得到数据(单位均为 cm)作为一个样本如下表所示:(1)散点在一条直线附近,试求“身高”与“脚掌长”之间的线性回归方程y ^=b ^x +a ^;(2)若某人的脚掌长为26.5 cm ,试估计此人的身高. (参考数据:∑i =110(x i -x )(y i -y )=577.5,∑i =110(x i -x )2=82.5)[尝试解答] (1)记样本中10人的“脚掌长”为x i (i =1,2,…,10),“身高”为y i (i =1,2,…,10),则b ^=∑i =110(x i -x )(y i -y )∑i =110(x i -x )2=577.582.5=7, ∵x =x 1+x 2+…+x 1010=24.5,y =y 1+y 2+…+y 1010=171.5,∴a ^=y -b ^x =0.∴y ^=7x . (2)由(1)知y ^=7x ,则当x =26.5时, y ^=7×26.5=185.5(cm). 故估计此人的身高为185.5 cm.用线性回归方程估计总体的一般步骤(1)作出散点图,判断散点是否在一条直线附近;(2)如果散点在一条直线附近,用公式求出a ^,b ^,并写出线性回归方程(否则求出的回归方程是没有意义的);(3)根据线性回归方程对总体进行估计. 练一练3.2016年元旦前夕,某市统计局统计了该市2015年10户家庭的年收入和年饮食支出的统计资料如下表:(1)(2)若某家庭年收入为9万元,预测其年饮食支出. (参考数据:∑i =110x i y i =117.7,∑i =110x 2i =406)解:(1)由题意可计算得:x =6,y =1.83,x 2=36, x y =10.98,又∵∑i =110x i y i =117.7,∑i =110x 2i =406,∴b =∑i =110x i y i -10x y∑i =110x 2i -10x2≈0.17,a =y -b x =0.81,∴y ^=0.17x +0.81.∴所求的回归方程为y ^=0.17x +0.81.(2)当x =9时,y ^=0.17×9+0.81=2.34(万元),可估计该年收入为9万元的家庭每年饮食支出约为2.34万元.——————————————[课堂归纳·感悟提升]———————————————1.本节课的重点是会作两个有关联变量的数据的散点图,会利用散点图认识变量间的相关关系,能根据给出的线性回归方程系数公式建立线性回归方程.难点是了解相关关系、线性相关、回归直线的概念,了解最小二乘法的思想.2.本节课要掌握以下几类问题: (1)准确区分相关关系与函数关系,见讲1.(2)会利用散点图判断两个变量间的相关关系,见讲2. (3)掌握用线性回归方程估计总体的一般步骤,见讲3. 3.本节课的易错点有两个:(1)区分不清相关关系与函数关系,如讲1;(2)求回归直线方程中易出现计算错误,如讲3.课下能力提升(十四)[学业水平达标练]题组1变量间的相关关系1.下列两个变量之间的关系,哪个不是函数关系()A.正方体的棱长和体积B.圆半径和圆的面积C.正n边形的边数和内角度数之和D.人的年龄和身高解析:选D A、B、C都是函数关系,对于A,V=a3;对于B,S=πr2;对于C,g(n)=(n-2)π.而对于年龄确定的不同的人可以有不同的身高,∴选D.2.下列语句所表示的事件中的因素不具有相关关系的是()A.瑞雪兆丰年B.上梁不正下梁歪C.吸烟有害健康D.喜鹊叫喜,乌鸦叫丧解析:选D选项A,B,C中描述的变量间都具有相关关系,而选项D是迷信说法,没有科学依据.题组2散点图3.下列图形中,两个变量具有线性相关关系的是()解析:选B线性相关关系要求两个变量的散点图大致在一条直线上,且不是函数关系.4.如图是两个变量统计数据的散点图,判断两个变量之间是否具有相关关系?解:不具有相关关系,因为散点图散乱地分布在坐标平面内,不呈线形. 5.某种产品的广告费支出x 与销售额y 之间有如下对应数据(单位:百万元):(1)画出散点图;(2)从散点图中判断销售金额与广告费支出成什么样的关系?解:(1)以x 对应的数据为横坐标,以y 对应的数据为纵坐标,所作的散点图如图所示:(2)从图中可以发现广告费支出与销售金额之间具有相关关系,并且当广告费支出由小变大时,销售金额也大多由小变大,图中的数据大致分布在某条直线的附近,即x 与y 成正相关关系.题组3 线性回归方程的求法及应用6.下列有关回归方程y ^=b ^x +a ^的叙述正确的是( ) ①反映y ^与x 之间的函数关系; ②反映y 与x 之间的函数关系; ③表示y ^与x 之间的不确定关系;④表示最接近y 与x 之间真实关系的一条直线. A .①② B .②③ C .③④ D .①④解析:选D y ^=b ^x +a ^表示y ^与x 之间的函数关系,而不是y 与x 之间的函数关系.且它所反映的关系最接近y 与x 之间的真实关系.故选D.7.设有一个回归方程为y ^=-1.5x +2,则变量x 增加一个单位时( ) A .y 平均增加1.5个单位 B .y 平均增加2个单位 C .y 平均减少1.5个单位 D .y 平均减少2个单位解析:选C ∵两个变量线性负相关,∴变量x 增加一个单位,y 平均减少1.5个单位. 8.某产品的广告费用x 与销售额y 的统计数据如下表:根据上表可得回归方程y ^=b ^x +a ^中的b ^为9.4,据此模型预报广告费用为6万元时销售额为( )A .63.6万元B .65.5万元C .67.7万元D .72.0万元解析:选B 样本中心点是(3.5,42),则a ^=y -b ^x =42-9.4×3.5=9.1,所以回归直线方程是y ^=9.4x +9.1,把x =6代入得y ^=65.5,故选B.9.已知工厂加工零件的个数x 与花费时间y (h)之间的线性回归方程为y ^=0.01x +0.5,则加工200个零件大约需要________小时.解析:将200代入线性回归方程y ^=0.01x +0.5,得y =2.5. 答案:2.510.有人统计了同一个省的6个城市某一年的人均国民生产总值(即人均GDP)和这一年各城市患白血病的儿童数量,如下表:(1)(2)通过计算可知这两个变量的回归直线方程为y ^=23.25x +102.15,假如一个城市的人均GDP 为12万元,那么可以断言,这个城市患白血病的儿童一定超过380人,请问这个断言是否正确?解:(1)根据表中数据画散点图,如图所示.从图中可以看出,在6个点中,虽然第一个点离这条直线较远,但其余5个点大致分布在这条直线的附近,所以这两个变量具有线性相关关系.(2)上述断言是错误的,将x =12代入y ^=23.25x +102.15得y ^=23.25×12+102.15=381.15>380,但381.15是对该城市人均GDP 为12万元的情况下所作的一个估计,该城市患白血病的儿童可能超过380人,也可能低于380人.[能力提升综合练]1.(2014·湖北高考)根据如下样本数据得到的回归方程为y ^=bx +a ,则( ) A .a >0,b >0 B .a >0,b <0 C .a <0,b >0 D .a <0,b <0解析:选B 由表中数据画出散点图,如图,由散点图可知b <0,a >0,选B.2.已知变量x ,y 之间具有线性相关关系,其散点图如图所示,则其回归方程可能为( )A.y ^=1.5x +2B.y ^=-1.5x +2 C.y ^=1.5x -2 D.y ^=-1.5x -2解析:选B 设回归方程为y ^=bx +a ,由散点图可知变量x 、y 之间负相关,回归直线在y 轴上的截距为正数,所以b <0,a >0,因此方程可能为y ^=-1.5x +2.3.在2015年5月1日,某市物价部门对本市的5家商场某商品的一天销售量及其价格进行了调查,5家商场的售价x 元和销售量y 件之间的一组数据如下表所示:y ^=-3.2x +a (参考公式:回归方程y ^=bx +a ,a =y -b x ),则a =( )A .-24B .35.6C .40.5D .40解析:选D 价格的平均数是x =9+9.5+10+10.5+115=10,销售量的平均数是y =11+10+8+6+55=8,由y ^=-3.2x +a 知b =-3.2,所以a =y -b x =8+3.2×10=40,故选D.4.设某大学的女生体重y (单位:kg)与身高x (单位: cm)具有线性相关关系,根据一组样本数据(x i ,y i )(i =1,2,…,n ),用最小二乘法建立的回归方程为y ^=0.85x -85.71,则下列结论中不正确的是( )A .y 与x 具有正的线性相关关系B .回归直线过样本点的中心(x ,y )C .若该大学某女生身高增加1 cm ,则其体重约增加0.85 kgD .若该大学某女生身高为170 cm ,则可断定其体重必为58.79 kg解析:选D 由于回归直线的斜率为正值,故y 与x 具有正的线性相关关系,选项A 中的结论正确;回归直线过样本点的中心,选项B 中的结论正确;根据回归直线斜率的意义易知选项C 中的结论正确;由于回归分析得出的是估计值,故选项D 中的结论不正确.5.假设学生在初中的英语成绩和高一英语成绩是线性相关的.现有10名学生的初中英语成绩(x )和高一英语成绩(y )如下:解析:将x =71,y =72.3,b ^=1.22,代入y =b ^x +a ^,得a ^=72.3-1.22×71=-14.32. 答案:y ^=1.22x -14.326.对某台机器购置后的运行年限x (x =1,2,3,…)与当年利润y 的统计分析知x ,y 具有线性相关关系,回归方程为y ^=10.47-1.3x ,估计该台机器最为划算的使用年限为________年.解析:当年利润小于或等于零时应该报废该机器,当y =0时,令10.47-1.3x =0,解得x ≈8,故估计该台机器最为划算的使用年限为8年.答案:87.一项关于16艘轮船的研究中,船的吨位区间为[192,3 246](单位:吨),船员的人数5~32人,船员人数y 关于吨位x 的回归方程为y ^=9.5+0.006 2x ,(1)若两艘船的吨位相差1 000,求船员平均相差的人数; (2)估计吨位最大的船和最小的船的船员人数.解:(1)设两艘船的吨位分别为x 1,x 2 ,则船员人数为y ^1,y ^2, y ^1-y ^2=9.5+0.006 2x 1-(9.5+0.006 2x 2) =0.006 2×1 000≈6, 即船员平均相差6人.(2)当x =192时,y ^=9.5+0.006 2×192≈11, 当x =3 246时,y ^=9.5+0.006 2×3 246≈30.即估计吨位最大和最小的船的船员数分别为11人和30人.8.某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:(1)求回归直线方程y =b x +a ,其中b =-20;(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入-成本)解:(1)由于x =16(x 1+x 2+x 3+x 4+x 5+x 6)=8.5,y =16(y 1+y 2+y 3+y 4+y 5+y 6)=80.所以a ^=y -b ^x =80+20×8.5=250, 从而回归直线方程为y ^=-20x +250. (2)设工厂获得的利润为L 元,依题意得L =x (-20x +250)-4(-20x +250)=-20x 2+330x -1 000 =-20(x -8.25)2+361.25.当且仅当x =8.25时,L 取得最大值, 故当单价定为8.25元时,工厂可获得最大利润。
高一数学所有知识点及其公式大全数学作为一门理科学科,对于高中学生来说是必修的科目之一。
在高一数学学习中,掌握并熟练运用各种知识点和公式是至关重要的。
下面将为大家详细介绍高一数学的所有知识点及其相应的公式。
一、函数与方程1. 函数:函数是一种特殊的关系,它将一个自变量的值映射到一个因变量的值。
函数通常用f(x)或y表示,其中x为自变量,y为因变量。
2. 相关系数:相关系数用于衡量两个变量之间的线性关系强弱,其取值范围为-1至1。
相关系数趋近于1时表示正相关,趋近于-1时表示负相关,趋近于0时表示无相关。
3. 一次函数:一次函数是最简单的线性函数,表达式为y = kx + b,其中k为斜率,b为截距。
4. 二次函数:二次函数是一种特殊的非线性函数,表达式为y = ax²+ bx + c,其中a、b、c为常数。
5. 幂函数:幂函数是形如y = x^a的函数,其中a为常数。
6. 对数函数:对数函数是幂函数的反函数,表达式为y = logₐx,其中a为底数。
7. 幂函数与对数函数的关系:幂函数与对数函数是互为反函数的关系,即y = a^x与y = logₐx 是一对反函数。
8. 指数函数:指数函数是以底数为常数的指数形式表示的函数,表达式常为y = a^x,其中a为底数。
9. 三角函数:三角函数包括正弦函数、余弦函数和正切函数等,它们是数学中常用的特殊函数。
10. 方程与不等式:方程和不等式是数学中常见的表示关系的符号体系,可用于求解各种实际问题。
二、数列与数列的运算1. 等差数列:等差数列是一种具有公差的数列,其中相邻两个项之间的差值是恒定的。
2. 等差数列的通项公式:等差数列的通项公式为an = a₁ + (n-1)d,其中a₁为首项,d为公差,n为项数。
3. 等比数列:等比数列是一种具有公比的数列,其中相邻两个项之间的比值是恒定的。
4. 等比数列的通项公式:等比数列的通项公式为an = a₁ * r^(n-1),其中a₁为首项,r为公比,n为项数。
高一数学导学案课题:变量间的相关关系编写人:审核人:时间:【学习目标: 】【知识与技能目标】(1)通过收集现实问题中两个有关联变量的数据认识变量间的相关关系。
(2)知道最小二乘法和回归分析的思想;(3)能根据线性回归方程系数公式建立线性回归方程或根据给出的数据,应用图形计算器建立线性回归方程.【过程与方法目标】通过对变量之间的关系的学习了解从总的变化趋势来看变量之间存在某种关系,但这种关系又不能用确定的函数关系精确表达出来,也让学生了解变量之间的不确定性关系是很普遍的,帮助学生树立科学的辨证唯物主义观点,感受自然的辩证法。
(1)通过对本课的学习,学会关注社会,关注生活,进一步学会观察、比较、归纳、分析等一般方法的运用。
【情感、态度与价值观】(1)通过观察生活中的例子,能直接找出变量之间的函数关系引出到无法直接找出变量之间的函数关系,即变量之间的相关关系,激发求知欲。
(2)通过感受生活中实际问题转化为数学问题,学会查找资料,收取信息,学会用统计知识对实际问题进行数学分析【重点和难点】:重点:利用散点图直观认识两个变量之间的线性关系,根据给出的线性回归方程的系数公式建立线性回归方程。
难点:回归思想的建立,变量之间相关关系的理解。
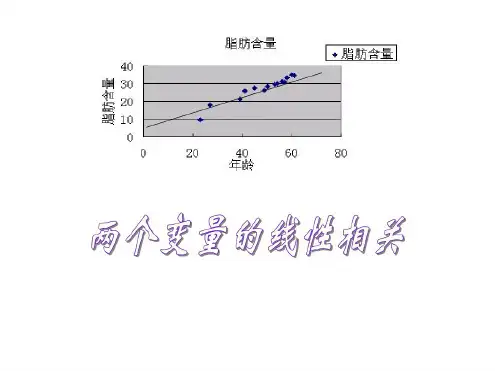
【课前预习导读】自学课本P84~P91内容【预习提示】:1.什么是相关关系?相关关系和函数关系有什么联系与区别?2.两个变量成正相关或者负相关的时候,散点图有什么特点?3..下列图中两变量是否具有相关关系?【课堂自主导学】探究任务:回归直线及其方程观察上面两个散点图,图中点的分布具有什么共同特征?新知:回归直线概念_____________________________________________________________________ 结合“人体脂肪与年龄的相关关系”这一实例可以推断出,如果可以求出这条直线的方程(回归方程),那么我们就可以比较清楚的了解年龄与体内脂肪含量的相关性。
2-3-1变量之间的相关关系2-3-2 两个变量的线性相关一、选择题1.对于给定的两个变量的统计数据,下列说法正确的是() A.都可以分析出两个变量的关系B.都可以用一条直线近似地表示两者的关系C.都可以作出散点图D.都可以用确定的表达式表示两者的关系[答案] C[解析]给出一组样本数据,总可以作出相应的散点图,但不一定分析出两个变量的关系,更不一定符合线性相关或有函数关系.2.下列两个变量之间的关系,哪个不是函数关系()A.正方体的棱长和体积B.圆半径和圆的面积C.正n边形的边数和内角度数之和D.人的年龄和身高[答案] D[解析]A、B、C都是函数关系,对于A,V=a3;对于B,S=πr2;对于C,g(n)=(n-2)π.而对于年龄确定的不同的人可以有不同的身高,∴选D.3.下列变量之间的关系是函数关系的是()A.一次函数y=ax+b,其中a,b是已知常数,取b为自变量,因变量是b2-4aB.施肥量和小麦亩产量C .降雨量和交通事故发生率D .学习时间和学习成绩 [答案] A[解析] 一般地说,在一定范围内,在其它条件相同的情况下,施肥量加大,小麦亩产量会增加,它们正相关,但不具有函数关系;同理C 、D 也没函数关系,而A 中,∵a ,b 为已知常数,当b 确定时,b 2-4a 也随之确定且有唯一值与之对应,∴A 为函数关系.4.由一组样本数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )得到的回归直线方程y ^=bx +a ,那么下面说法不正确的是( )A .直线y ^=bx +a 必经过点(x -,y -)B .直线y ^=bx +a 至少经过点(x 1,y 1),(x 2,y 2),…,(x n ,y n )中的一个点C .直线y ^=bx +a 的斜率为∑i =1nx i y i -n x - y-∑i =1nx 2i -n x-2D .直线y ^=bx +a 和各点(x 1,y 1),(x 2,y 2),…,(x n ,y n )的偏差∑i =1n[y i -(bx i +a )]2是该坐标平面上所有直线与这些点的偏差中最小的直线.[答案] B[解析] 由a =y -b x 知y ^=y -b x +bx ,∴必定过(x ,y )点.回归直线方程对应的直线是与样本数据距离最小的,但不一定过原始数据点,只须和这些点很接近即可.5.设有一个回归方程为y^=2-1.5x,则变量x增加一个单位时()A.y平均增加1.5个单位B.y平均增加2个单位C.y平均减少1.5个单位D.y平均减少2个单位[答案] C[解析]y^2-y^1=2-1.5(x+1)-2+1.5x=-1.5.6.如图是具有相关关系的两个变量的一组数据的散点图和回归直线,去掉哪个点后,剩下的5个点数据的相关系数最大?()A.D B.E C.F D.A[答案] C[解析]第F组数据距回归直线最远,所以去掉第F组后剩下的相关系数最大.7.以下关于线性回归的判断,正确的有________个.()①若散点图中所有点都在一条直线附近,则这条直线为回归直线②散点图中的绝大多数点都线性相关,个别特殊点不影响线性回归,如图中的A,B,C点.③已知回归直线方程为y^=0.50x-0.81,则x=25时,y的估计值为11.69④回归直线方程的意义是它反映了样本整体的变化趋势A.0个B.1个C.2个D.3个[答案] D[解析]能使所有数据点都在它附近的直线不止一条,而据回归直线的定义知,只有按最小二乘法求得回归系数a,b得到的直线y^=ax+b才是回归直线,∴①不对;②正确;将x=25代入y^=0.50x-0.81,解得y^=11.69,∴③正确;④正确,∴选D.8.为了考察两个变量x和y之间的线性相关性,甲、乙两个同学各自独立地作10次和15次试验,并且利用线性回归方法,求得回归直线分别为l1和l2.已知在两个人的试验中发现对变量x的观测数据的平均值恰好相等,都为s,对变量y的观测数据的平均值也恰好相等,都为t.那么下列说法正确的是()A.直线l1和l2有交点(s,t)B.直线l1和l2相交,但是交点未必是点(s,t)C.直线l1和l2由于斜率相等,所以必定平行D.直线l1和l2必定重合[答案] A[解析]由题意,结合回归直线易知只有选项A符合已知条件.9.下表是某同学记录的某地方在3月1日~3月12日的体检中的发烧人数,并给出了散点图.下列说法:①根据此散点图,可以判断日期与发烧人数具有线性相关关系.②根据此散点图,可以判断日期与发烧人数具有一次函数关系.其中正确的是()A.②B.①C.①②D.都不正确[答案] B[解析]由散点图可以判断日期与发烧人数具有正相关关系,但不是函数关系,更不是一次函数关系,因为所有点不在一条直线上,而是在一条直线附近.10.过(3,10),(7,20),(11,24)三点的回归直线方程是()A.y^=1.75+5.75xB.y^=-1.75+5.75xC.y^=5.75+1.75xD.y^=5.75-1.75x[答案] C[解析]求过三点的回归直线方程,目的在于训练求解回归系数的方法,这样既可以训练计算,又可以体会解题思路,关键是能套用公式.代入系数公式得b^=1.75,a^=5.75.代入直线方程,求得y^=5.75+1.75x.故选C.二、填空题11.下列关系:(1)炼钢时钢水的含碳量与冶炼时间的关系;(2)曲线上的点与该点的坐标之间的关系;(3)柑橘的产量与气温之间的关系;(4)森林的同一种树木,其横断面直径与高度之间的关系.其中具有相关关系的是________.[答案](1)(3)(4)[解析](1)炼钢的过程就是一个降低含碳量进行氧化还原的过程,除了与冶炼时间有关外,还要受冶炼温度等其他因素的影响,故具有相关关系.(2)曲线上的点与该点的坐标之间的关系是一一对应的,即是一种确定性关系.(3)柑橘的产量除了受气温影响以外,还要受肥量以及水分等因素的影响,故具有相关关系.(4)森林的同一种树木,其横断面直径随高度的增加而增加,但是还受树木的疏松及光照等因素的影响,故具有相关关系.12.(2011·辽宁高考)调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y 具有线性相关关系,并由调查数据得到y对x的回归直线方程:y^=0.254x+0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加________万元.[答案]0.254[解析]由于y^=0.254x+0.321知,当x增加1万元时,年饮食支出y增加0.254万元.14.改革开放30年以来,我国高等教育事业迅速发展,对某省1990~2000年考大学升学百分比按城市、县镇、农村进行统计,将1990~2000年依次编号为0~10,回归分析之后得到每年考入大学的百分比y与年份x的关系为:城市:y^=2.84x+9.50;县镇:y^=2.32x+6.67;农村:y^=0.42x+1.80.根据以上回归直线方程,城市、县镇、农村三个组中,________的大学入学率增长最快.按同样的增长速度,可预测2010年,农村考入大学的百分比为________%.[答案]城市10.2[分析]增长速度可根据回归直线的斜率来判断,斜率大的增长速度快,斜率小的增长速度慢.[解析]通过题目中所提供的回归方程可判断,城市的大学入学率增长最快;2010年农村考入大学的百分比为0.42×20+1.80=10.2.三、解答题15.某种产品的广告费支出x 与销售额y 之间有如下对应数据(单位:百万元)(1)(2)从散点图中判断销售金额与广告费支出成什么样的关系? [解析] (1)以x 对应的数据为横坐标,以y 对应的数据为纵坐标,所作的散点图如下图所示:(2)从图中可以发现广告费支出与销售金额之间具有相关关系,并且当广告费支出由小变大时,销售金额也大多由小变大,图中的数据大致分布在某条直线的附近,即x 与y 成正相关关系.16.某个服装店经营某种服装,在某周内获纯利y (元),与该周每天销售这种服装件数x 之间的一组数据关系见表已知∑i =17x 2i =280,∑i =17y 2i =45209,∑i =17x i y i =3487.(1)求x -,y -;(2)求回归方程.[解析] (1)x -=17×(3+4+5+6+7+8+9)=6, y -=17×(66+69+73+81+89+90+91)=5597. (2)b ^=3487-7×6×5597280-7×36=194∴a ^=5597-194×6=71914,∴所求回归方程为y ^=194x +71914.17.某工厂对某产品的产量与成本的资料分析后有如下数据:(2)求成本y 与产量x 之间的线性回归方程. [解析] (1)散点图如下:(2)设成本y 与产量x 的线性回归方程为y ^=b ^x +a ^, x -=2+3+5+64=4,y -=7+8+9+124=9.b^=∑i=1nx i y i-n x-y-∑i=1nx2i-n x-2=1110=1.1,a^=y--b^x-=9-1.1×4=4.6.所以,回归方程为y^=1.1x+4.6.18.下面是世界上10名男网球选手的身高(x)与体重(y)的情况.(1)(2)你能从散点图中发现身高与体重近似成什么关系吗?(3)若近似成线性关系,请画出一条直线来近似地表示这种线性关系;(4)若某名男网球运动员的身高是172 cm,请预测他的体重.[解析](1)散点图如图:(2)由图可见,图中的数据点大致分布在一条直线附近,当身高数据由小到大变化时,体重数据也由小变大,因此身高与体重近似成线性相关关系.(3)直线如图所示.(4)根据所画直线可预测当身高是172 cm时,其体重约为61 kg.[点评]第(3)问中的直线不是唯一的,当然不同的近似直线将直线影响第(4)问的预测结果.。
相关系数[学习目标]了解相关系数的计算公式,会由r 值的大小判断两随机变量线性相关程度的大小. [知识链接]当r =1或-1时,两个变量的相关性如何答 当r =1时,两个变量完全正相关;当r =-1时,两个变量完全负相关. [预习导引]1.相关系数r 的计算假设两个随机变量的数据分别为(x 1,y 1),(x 2,y 2),…,(x n ,y n ),则变量间线性相关系数r 的计算公式为r =l xyl xx l yy=∑ni =1(x i -x -)(y i -y -)∑n i =1(x i -x -)2∑n i =1(y i -y -)2=∑ni =1x i y i -nx -y -∑ni =1x 2i -nx -2∑ni =1y 2i -ny -22.误差表达式Q (a ,b )=∑ni =1[y i -(a +bx i )]2=l yy +n [y --(a +bx -)]2+l xx(b -l xy l xx )-l 2xyl xx, Q min =l yy (1-r 2)(Q ≥0). 3.相关系数r 的性质 (1)r 的取值范围为[-1,1];(2)|r |值越大,误差Q 越小,变量之间的线性相关程度越高; (3)|r |值越接近0,Q 越大,变量之间的线性相关程度越低.要点一 利用相关系数检验两变量间的相关性例1 现随机抽取了某中学高一10名在校学生,他们入学时的数学成绩(x )与入学后第一次考试的数学成绩(y )如下: 学生号1 2 3 4 5 6 7 8 9 10 x 120 108 117 104 103 110 104 105 99 108 y84648468696869465771请问:这10名学生的两次数学成绩是否具有线性关系 解 x -=110(120+108+…+99+108)=,y -=110(84+64+…+57+71)=68,∑10i =1x 2i =1202+1082+…+992+1082=116 584, ∑10i =1y 2i =842+642+…+572+712=47 384, ∑10i =1x i y i =120×84+108×64+…+99×57+108×71=73 796. 所以相关系数为r =73 796-10××68(116 584-10×)(47 384-10×682)≈ 6.由此可看出这10名学生的两次数学成绩具有较强的线性相关关系.规律方法 利用相关系数r 进行判断相关关系,需要应用公式计算出r 的值,由于数据较大,需要借助计算器.跟踪演练1 假设关于某种设备的使用年限x (年)与所支出的维修费用y (万元)有如下统计资料:x 2 3 4 5 6 y已知∑5i =1x 2i =90,∑5i =1y 2i =,∑5i =1x i y i =.(1)求x -,y -;(2)对x ,y 进行线性相关性检验. 解 (1)x -=2+3+4+5+65=4.y -=错误!=5.(2)∑5i =1x i y i -5x -y -=-5×4×5=, ∑5i =1x 2i -5x -2=90-5×42=10, ∑5i =1y 2i -5y -2=-125=, 所以r =错误!≈.|r |≈>,所以x 与y 之间具有很强的线性相关关系. 要点二 线性回归分析例2 已知某地每单位面积菜地年平均使用氮肥量x (kg)与每单位面积蔬菜年平均产量y (t)之间的关系有如下数据:(1)求x 与y 之间的相关系数,并检验是否线性相关;(2)若线性相关,求蔬菜产量y 与使用氮肥量x 之间的线性回归直线方程,并估计每单位面积施氮肥150 kg 时,每单位面积蔬菜的年平均产量. 解 (1)列出下表,并用科学计算器进行相关计算:x -=1 51515=101,y -=错误!≈,∑15i =1x 2i =161 125,∑15i =1y 2i =1 ,∑15i =1x i y i =16 . 故蔬菜产量与施用氮肥量的相关系数 r =16 -15×101×(161 125-15×1012)(1 -15×)≈ 3.所以蔬菜产量与施用氮肥量之间存在着线性相关关系. (2)设所求的线性回归方程为y =a +bx ,则b =∑15i =1x i y i -15x -y -∑15i =1x 2i -15x -2=16 -15×101×161 125-15×1012≈ 7, a =y --bx -≈- 7×101= 3, ∴线性回归方程为y = 3+ 7x .∴当每单位面积施氮肥150 kg 时,每单位面积蔬菜年平均产量为 3+ 7×150≈(t).规律方法 在研究两个变量之间的关系时,应先进行相关性检验,若具备线性相关关系再求线性回归方程.如果本身两个变量不具备线性相关关系,即使求出线性回归方程也是毫无意义的,而且用其估计和预测的量也是不可信的.跟踪演练2 为分析学生初中升学的数学成绩对高一数学学习的影响,在高一年级随机抽取10名学生,了解他们的入学成绩和高一期末考试数学成绩如下表:入学成绩(x ) 63 67 45 88 81 71 52 99 58 76 高一期末成绩(y )65785282928973985675(1)画出散点图;(2)对变量x 与y 进行相关性检验,如果x 与y 之间具有线性相关关系,求出线性回归方程;(3)若某学生入学的数学成绩为80分,试估计他在高一期末考试中的数学成绩.解 (1)散点图如图所示.(2)由题可得x -=70,y -=76,∑10i =1(x i -x -)·(y i -y -)=1 894, ∑10i =1(x i -x -)2=2 474, ∑n i =1 (y i -y -)2=2 056, 因此可得相关系数为r =∑10i =1(x i -x -)(y i -y -)∑10i =1 (x i -x -)2·∑10i =1 (y i -y -)2= 1 8942 474× 2 056≈ 8>,所以入学数学成绩与高一期末考试数学成绩存在线性相关关系. 设线性回归方程为y =a +bx ,则b =∑10i =1 (x i -x -)(y i -y -)∑10i =1(x i -x -)2=1 8942 474≈ 56, a =y --bx -=76- 56×70= 8. 因此所求的线性回归方程是y = 8+ 56x .(3)若某学生入学的数学成绩为80分,代入(2)中的方程可求得y = 8+ 56×80≈84,即这名学生在高一期末考试中的数学成绩的预测值为84分.1.对于回归分析,下列说法错误的是( )A .在回归分析中,变量间的关系若是非确定关系,那么因变量不能由自变量唯一确定B .线性相关系数可以是正的,也可以是负的C .回归分析中,如果r 2=1,说明x 与y 之间完全相关D .样本相关系数r ∈(-1,1) 答案 D解析 相关系数r 的范围是[-1,1].2.一唱片公司欲知打歌费用x (十万元)与唱片销售量y (千张)之间的关系,从其所发行的唱片中随机抽取了10张,得如下的资料:∑10i =1x i =28,∑10i =1x 2i =, ∑10i =1y i =75,∑10i =1y 2i =,∑10i =1x i y i =237,则y 与x 的相关系数r 的绝对值为__________. 答案解析 由公式r =∑ni =1x i y i -nx -y -∑n i =1x 2i -nx -2∑n i =1y 2i -ny -2得|r |=.3.若线性回归方程中的回归系数b =0,则相关系数r =__________. 答案 0 解析 相关系数r =∑ni =1(x i -x -)(y i -y -)∑n i =1 (x i -x -)2∑n i =1(y i -y -)2与b =∑n i =1(x i -x -)(y i -y -)∑ni =1(x i -x -)2的分子相同.4.有5组数据如下:x 1 2 3 4 10 y3410512将这组数据中的哪一组去掉后,另外的4组数据具有较强的线性相关性解作出散点图如图所示.观察散点图,可以发现A,B,D,E四个点大致在某条直线附近,具有较强的线性相关关系,故应将点C(3,10)去掉.对相关系数r的理解(1)判断变量之间的线性相关关系,一般用散点图,但在作图中,由于存在误差,有时很难判断这些点是否分布在一条直线的附近,从而就很难判断两个变量之间是否具有线性相关关系,此时就必须利用线性相关系数来判断.(2)|r|越接近1,它们的散点图越接近一条直线,这时用线性回归模型拟合这组数据的效果就越好.(3)相关系数r只能描述两个变量之间的变化方向及密切程度,不能揭示二者之间的本质联系.(4)相关系数r可以定量地反映出变量间的相关程度,明确的给出有无必要建立两变量间的回归方程.一、基础达标1.下列说法不正确的是( ) A.回归分析中,变量x和y都是普通变量B.变量间的关系若是非确定性关系,那么因变量不能由自变量唯一确定C.线性相关系数可能是正的,也可能是负的D.如果线性相关系数是负的,y随x的增大而减少答案A解析在回归分析中的两个变量是具有相关关系的两个变量.2.通过相关系数来判断两个变量相关关系的强弱时,相关系数的绝对值越大,用线性回归模型拟合样本数据的效果就越好,如果相关系数r∈[,1],则两个变量( )A.负相关很强B.相关性一般C.正相关很强D.两变量之间几乎没有关系答案C3.对四对变量y和x进行线性相关检验,已知n是观测值组数,r是相关系数,且已知:①n=7,r= 3 ②n=15,r= 2 ③n=17,r= 1④n=3,r= 0则变量y和x具有线性相关关系的是( ) A.①和② B.①和④ C.②和④ D.③和④答案B解析相关系数r的绝对值越大,变量x,y的线性相关关系越强,故选B. 4.对变量x,y有观测数据(x i,y i)(i=1,2,…,10),得散点图①:对变量u,v有观测数据(u,v i)(i=1,2,…,10),得散点图②.由这两个散点图可以判i断( )A.变量x与y正相关,u与v正相关B.变量x与y正相关,u与v负相关C .变量x 与y 负相关,u 与v 正相关D .变量x 与y 负相关,u 与v 负相关 答案 C解析 在图①中,所有点都在一条直线的附近,且直线的斜率为负值,所以变量x 与y 负相关;同理,变量u 与v 正相关,故选C.5.设两个变量x 和y 之间具有线性相关关系,它们的相关系数是r ,y 关于x 的回归直线的斜率是b ,纵轴上的截距是a ,则下列说法正确的是__________. ①b 与r 的符号相同 ②a 与r 的符号相同 ③b 与r 的符号相反 ④a 与r 的符号相反 答案 ①解析 因为b >0时,两变量正相关,此时r >0;b <0时,两变量负相关,此时r <0.6.部门所属的10个工业企业生产性固定资产价值与工业增加值资料如下表(单位:百万元):根据上表资料计算的相关系数为__________. 答案 8解析 x -=3+3+5+6+6+7+8+9+9+1010=.y -=15+17+25+28+30+36+37+42+40+4510=.∴r =∑10i =1(x i -x -)(y i -y -)∑10i =1 (x i -x -)2∑10i =1 (y i -y -)2= 8.7.维尼纶纤维的耐热水性能的好坏可以用指标“缩醛化度”y 来衡量,这个指标越高,耐水性能也越好,而甲醛浓度是影响缩醛化度的重要因素,在生产中常用甲醛浓度x (克/升)去控制这一指标,为此必须找出它们之间的关系,现安排一批实验,获得如下数据:求相关系数r . 解 列表如下x -=1687=24,y -=错误!,r =l xyl xx l yy =∑7i =1x i y i -7x - y -∑7i =1x 2i -7x -2∑7i =1y 2i -7y -2=错误!=.由此可知,甲醛浓度与缩醛化度之间有很强的线性相关关系. 二、能力提升8.变量X 与Y 相对应的一组数据为(10,1),,2),,3),,4),(13,5);变量U 与V 相对应的一组数据为(10,5),,4),,3),,2),(13,1).r 1表示变量Y 与X 之间的线性相关系数,r 2表示变量V 与U 之间的线性相关系数,则( ) A .r 2<r 1<0B .0<r 2<r 1C .r 2<0<r 1D .r 2=r 1答案 C解析 由线性相关系数公式知r =∑ni =1(x i -x -)(y i -y -)∑ni =1(x i -x -)2∑n i =1(y i -y -)2.∵X -=U -=,Y -=V -=3,X i =U i (i =1,2,…,5),Y i =V 6-i (i =1,2,…,5),∴∑5i =1(X i -X -)2·∑5i =1 (Y i -Y -)2=∑5i =1 (U i -U -)2·∑5i =1(V i -V -)2. 令∑5i =1(X i -X -)(Y i -Y -)=A =(10-X -)(1-Y -)+-X -)(2-Y -)+-X -)(3-Y -)+-X -)(4-Y -)+(13-X -)(5-Y -),∑5i =1(U i -U -)(V i -V -)=B =(10-U -)(5-V -)+-U -)(4-V -)+-U -)(3-V -)+-U -)(2-V -)+(13-U -)(1-V -),∴A >0,B <0,∴r 1>0,r 2<0. 9.相关系数是度量( )A .两个变量之间线性相关关系的强度B .散点图是否显示有意义的模型C .两个变量之间是否存在因果关系D .两个变量之间是否存在关系 答案 A解析 系数来衡量两个变量之间线性相关关系的强弱.10.去年一轮又一轮的寒潮席卷全国,某商场为了了解某品牌羽绒服的月销售量y (件)与月平均气温x (℃)之间的关系,随机统计了某4个月的月销售量与当月平均气温、数据如下表:月销售量y (件) 24 33 40 55由表中数据算出线性回归方程y =bx +a 中的b ≈-2.气象部门预测下个月的平均气温约为 6 ℃,据此估计,该商场下个月羽绒服的销售量的件数约为__________. 答案 46解析 x -=10,y -=38,a =38-(-2)×10=58, ∴回归方程为y =-2x +58. 当x =6 ℃时,y =46.11.5个学生的数学和物理成绩如表:学生学科 A B C D E 数学 80 75 70 65 60 物理7066686462试用散点图和相关系数r 判断它们是否有线性相关关系,若有,是正相关还是负相关解 法一 涉及两个变量:数学成绩与物理成绩,可以以数学成绩为自变量,考察因变量物理成绩的变化趋势.以x 轴表示数学成绩,y 轴表示物理成绩,可得相应的散点图.由散点图可见,两者之间具有线性相关关系且是正相关. 法二 列表:i x i y i x 2i y 2i x i y i 1 80 70 6 400 4 900 5 600 275665 6254 3564 9503 70 684 900 4 624 4 760 4 65 64 4 225 4 096 4 160 5 60 62 3 600 3 844 3 720 ∑35033024 75021 82023 190∴r =∑5i =1x i y i -5x -y -(∑5i =1x 2i -5x -2)(∑5i =1y 2i -5y -2)=23 190-23 100250×40=>0.∴两变量具有相关关系且正相关.12.下列是水稻产量与施化肥量的一组观测数据:施化肥量 15 20 25 30 35 40 45 水稻产量320330360410460470480(1)将上表中的数据制成散点图,并计算相关系数r .(2)你能从散点图中发现施化肥量与水稻产量近似成什么关系吗该结论与相关系数r 的计算一致吗 解 (1)散点图如下:列表:i x i y i x 2i y 2i x i y i 1 15 320 225 102 400 4 800 2 20 330 400 108 900 6 600 3 25 360 625 129 600 9 000 430410900168 10012 300535460 1 225211 60016 100 640470 1 600220 90018 800 745480 2 025230 40021 600∑210 2 8307 000 1 171 90089 200∴r=∑7i=1xiyi-7x-y-(∑7i=1x2i-7x-2)(∑7i=1y2i-7y-2)=错误!≈.(2)从图中可以发现施化肥量与水稻产量具有线性相关关系,当施化肥量由小到大变化时,水稻产量也由小变大,图中的数据点大约分布在一条直线的附近,因此施化肥量和水稻量近似成线性正相关关系.又由于r=>0,故散点图与r的计算一致.三、探究与创新13.某运动员训练次数与运动成绩之间的数据关系如下:次数x3033353739444650成绩y3034373942464851(1)作出散点图;(2)求出回归方程;(3)计算相关系数并进行相关性检验;(4)试预测该运动员训练47次及55次的成绩.解(1)作出该运动员训练次数x与成绩y之间的散点图,如下图所示,由散点图可知,它们之间具有线性相关关系.(2)列表计算:由上表可求得x -=,y -=,∑8i =1x 2i =12 656, ∑8i =1y 2i =13 731,∑8i =1x i y i =13 180, ∴b =∑8i =1x i y i -8x -y -∑8i =1x 2i -8x -2≈ 5,a =y --bx -=- 88,∴线性回归方程为y = 5x - 88.(3)计算相关系数r = 7,因此运动员的成绩和训练次数两个变量有较强的相关关系.(4)由上述分析可知,我们可用线性回归方程y = 5x - 88作为该运动员成绩的预报值.将x =47和x =55分别代入该方程可得y =49和y =57.故预测该运动员训练47次和55次的成绩分别为49和57.。