线性代数2016-2017-2本科授课计划表 共17周
- 格式:doc
- 大小:45.00 KB
- 文档页数:1

线性代数基础学习计划第一篇:线性代数基础学习计划线性代数基础学习计划学习目标掌握常见低阶行列式的值的求解方法,理解矩阵的三个重要概念(即伴随、转置、可逆),熟练掌握矩阵的乘法法则;理解向量的相关性及线性表示,会找出给定向量组的极大无关组;掌握方程组的解的结构及其理解基础解系的概念,会判断基础解系,会用方程组来解决向量组的相关性问题。
特征值和特征向量在基础阶段可以不复习,把主要精力放在向量组和方程组上,因为这是线代的核心和考试重点。
适合人群考研数学基础阶段学习计划的设计定位,主要是针对在本科阶段数学学习中基础薄弱的同学,同时适合于广大在职考研人士。
此计划特别注重基础知识的学习和掌握,对于有一定基础的考生而言,按照计划循序渐进,夯实基础,为考研数学的最终成功迈出最为重要的一步课程介绍(学习方法)新东方在线网络课程线性代数部分由考研数学辅导名师尤承业老师主讲,共有十五课时,线性代数部分在研究生入学考试中约占22%的比重,因此,我们应该特别重视对这部分的学习和掌握。
线性代数是研究生入学考试里面概念性最强的学科,因此,做好考研数学试卷里面的线性代数部分,重心应该放在切实理解线性代数的基本理论。
新东方网络课程主要针对基础中等和薄弱的考生设计,我们对考研数学的每一章节都进行了全面认真的安排,基本按照基础知识讲解,典型例题分析的步骤进行,使得同学们一方面可以掌握考研所要求的知识点,另一方面可以对考研典型题目有基本了解和掌握。
课程所讲授内容覆盖了所有的考研知识点,时间安排合理,注重循序渐进,善于发掘考研数学的内在要求,并针对要求进行详细讲授。
参考书目(掌握程度)本科阶段所用教材及其相关习题数学复习全书(李永乐、李正元)考研数学(新东方考研数学培训教材)线性代数线性代数考试题型不多,计算方法比较初等,但是往往计算量比较大,导致很多同学对线性代数感到棘手,同时从理论的角度出发,线性代数的很多概念和性质比较复杂和抽象,所以同学们必须要注意各部分内容之间的密切联系。

XXX财经大学
本科课程教学进度计划表2015—2016学年度第二学期
学院XXX学院
教学系
其他院系
(课程组)
主讲教师张三
填表日期:2015年9月10 日
教务处制表
XXX大学本科课程教学进度计划表
2015 —2016学年度第二学期
主讲教师张三职称讲师学历研究生学位_博士_ 主授专业古代文学
课程名称大学语文课程编号00000. 班级A01 学生人数50
总学时48 学时,其中课堂讲授46学时;实验(上机)教学0 学时;其它教学(讨论、见习等) 2 学时;机动0学时实习实训(包括课程实习、课程实训、课程设计等)0 周
教材(名称、主编、出版社、出版时间等)《大学语文》,江西科学技术出版社,2011年7月
成绩考核说明及要求:期末闭卷考试或课程论文
其成绩评定方法:平时成绩占30%,期末考试占70%
考试题型:填空题、选择题、计算题、简答题、应用题、
考试时间:110分钟
系主任(签字):教学院长(签字):年月日年月日。

关于2016-2017学年第一学期期末考试工作安排的通知各教学院(部):根据学校本学期教学工作安排,现将我校2016-2017学年第一学期期末考试工作的有关事项通知如下:一、专业课程期末考试1、各教学院第19周前的专业课程考试务必安排在每周一下午进行(晚上不安排),第19周的专业课程考试安排在1月4日—1月6日(周三、周四、周五)进行,且专业课程考试工作应于2017年1月6日前完成。
各教学院在安排专业课程考试时请按照“各教学院期末考试场地安排表”安排地点(见附件一),考试场地不得占用上课教室,各教学院应加强联络,实现资源共享,避免不必要的冲突。
为确保教室使用不发生冲突,各教学院必须通过教务管理系统办理教室借用手续,具体操作为:进入教务管理系统的智能排课—教学场地—教学场地调度中输入借用信息,并到教务处办理纸质教室借用申请。
2、各教学院请于11月30日前上交规范样式的期末专业课程考试安排表。
(见附件二)二、公共课课程考试1、请体育部于12月9日前将体育课考试安排报教务处备案,并通知各教学院。
2、请外国语学院和数理学院于12月5日前将“大学英语”和“高等数学”的A、B试卷送交教务处。
3、公共课程考试时间安排见附表三,具体考试安排另行通知。
教务处2016年11月22日附表一:2016年11月21日—1月11日各教学院期末考试场地安排注意:1.考试必须安排在规定的标准化考场进行,各教学院可相互协商,共享资源,确因场地因素可安排在其它考场。
2.各教学院安排场地时请在教务管理系统中核实。
附表二:期末考试安排表规范样式(Excel表)注意:各教学院请按照考试日期排序,日期相同请按照考试时间排序。
附表三:2016—2017第一学期公共课程考试安排表声明:此资源由本人收集整理于网络,只用于交流学习,请勿用作它途。
如有侵权,请联系,删除处理。

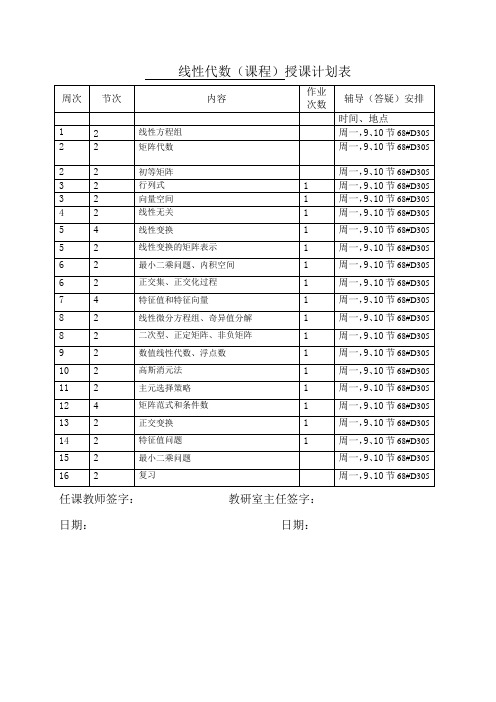
《线性代数》课程教学大纲第一篇:《线性代数》课程教学大纲《线性代数》课程教学大纲课程编码:414002(A)课程英文名称:Linear Algebra 先修课程:微积分适用专业:理科本科专业总学分:3.5 总学时:56讲课学时 56 实验学时 0实习学时 0一、课程性质、地位和任务课程名称:线性代数线性代数是我校计算机科学与技术专业的一门重要基础课。
它不但是其它后继专业课程的基础,而且是科技人员从事科学研究和工程设计必备的数学基础。
通过本课程的教学,使学生获得矩阵、行列式、向量、线性方程组、二次型等方面的基本知识,掌握处理离散问题常用的方法,增强学生“用”数学的意识,培养学生“用”数学的能力。
二、课程基本要求1.了解行列式的定义和性质,掌握利用行列式的性质及展开法则,掌握三、四阶行列式的计算法,会计算简单的n阶行列式;理解和掌握克拉默(Cramer)法则。
2.理解矩阵概念并掌握矩阵的线性运算、乘法、转置及其运算规律;理解逆矩阵的概念,掌握逆矩阵存在的条件,掌握求逆矩阵的方法;掌握对称矩阵的性质;了解分块矩阵及其运算。
3.理解n维向量、向量组线性相关与线性无关的概念;了解有关向量组线性相关、线性无关的重要结论;理解向量组的最大线性无关组与向量组的秩的概念;了解n维向量空间、子空间、基底、维数、坐标等概念;掌握齐次线性方程组有非零解的充要条件及非齐次线性方程组有解的充要条件;会求齐次线性方程组的基础解系、通解;掌握非齐次线性方程组的解的结构,会求非齐次线性方程组的通解;了解向量的内积、正交和向量的长度等概念;会利用施密特(Schmidt)方法把线性无关的向量组正交规范化。
4.掌握Gauss消元法;掌握用Gauss消元法求线性方程组通解的方法;掌握用初等变换求齐次线性方程组和非齐次线性方程组解的方法。
5.掌握矩阵的特征值与特征向量的概念,会求矩阵的特征值与特征向量;理解相似矩阵的概念、性质及矩阵可相似对角化的充要条件。
(三)《线性代数》课程简介及教学大纲一、课程简介1.课程编号:JA01032.课程名称:线性代数3.开课学院:数学课程组4.学时:345.类别:必修6.先修课程:无7.课程简介:《线性代数》课程是高等学校经济管理类和理工类本科各专业学生的一门必修的重要基础理论课,属于基础数学类课程。
是大部分经济管理类和理工类课程的必备基础。
通过本课程的学习,要使学生掌握行列式、矩阵、线性方程组、向量空间、矩阵特征值特征向量及二次型等基本概念、基本理论和基本运算技能,为学习后继课程和进一步获得数学知识奠定必要的数学基础。
在课程的教学过程中,要通过各个教学环节培养学生具有比较熟练的运算能力和综合运用所学知识去分析问题和解决问题的能力。
Course Code:JA0103Name of Course:Linear AlgebraFaculty: Mathematics Course GroupCredit Hours: 34Classification: Compulsory coursePrerequisite:NoneCourse Outline:Linear Algebra is a compulsory basic theory course for undergraduate students who are major in Economic Management or Science and Engineering. It is a part of fundamental mathematic courses and is a necessary foundation for most Economic Management and Science and Engineering courses.Through studying this course, the students will gain basic concepts, basic theories, and basic computing ability on determination, matrix, linear algebraic equations, vector space, the eigenvalue and eigenvector of matrix, quadratic etc. These are key to understanding the subsequent courses and further study in mathematics.In the process of teaching the course, we will gradually train the students through various teaching methods to gain skilled operational capability and the ability to analyze and solve problems through comprehensive use of the learned knowledge.二、课程教学大纲1. 课程编号:JA0103 5. 先修课程:无2. 课程类别:基础数学类,必修 6. 课内总学时:343. 开课学期:第一学年二学期 7. 实验/上机学时:4. 适用专业:各工科、管理类专业 8. 执笔人:柳金甫,安玉冉1.课程教学目的《线性代数》课程是高等学校经济管理类和理工类本科各专业学生的一门必修的重要基础理论课,属于基础数学类课程。
新编线性代数课程设计一、课程目标知识目标:1. 理解线性代数的基本概念,掌握矩阵、行列式、向量组的运算及其性质;2. 掌握线性方程组的求解方法,包括高斯消元法、克莱姆法则等;3. 了解线性空间、线性变换及其基本性质,掌握线性变换矩阵的求法。
技能目标:1. 能够运用矩阵、行列式、向量组等工具解决实际问题,提高数学建模能力;2. 能够熟练运用线性方程组的求解方法解决实际问题,提高问题求解能力;3. 能够运用线性空间和线性变换的概念,分析并解决简单的几何问题。
情感态度价值观目标:1. 培养学生严谨、认真的学习态度,激发学生对线性代数的兴趣;2. 培养学生团队合作意识,提高学生沟通与交流能力;3. 引导学生认识到线性代数在自然科学、社会科学等领域的广泛应用,培养学生的应用意识。
本课程针对高中年级学生,充分考虑学生已具备一定的数学基础和抽象思维能力,通过本课程的学习,使学生掌握线性代数的基本知识和方法,提高数学素养,为后续相关课程打下坚实基础。
课程目标具体、可衡量,便于教学设计和评估。
在教学过程中,注重理论联系实际,培养学生的实际应用能力。
二、教学内容1. 矩阵与行列式:矩阵的运算、行列式的性质与计算、矩阵的逆、克莱姆法则;2. 向量组:线性组合与线性表示、向量组的线性相关性、向量组的秩、极大线性无关组;3. 线性方程组:高斯消元法、克莱姆法则、齐次线性方程组、非齐次线性方程组;4. 线性空间:线性空间的定义与性质、基、维数、坐标、子空间;5. 线性变换:线性变换的定义与性质、线性变换的矩阵表示、特征值与特征向量、对角化。
教学内容根据课程目标进行选择和组织,以教材为依据,注重科学性和系统性。
教学大纲明确以下安排和进度:第一周:矩阵与行列式;第二周:向量组;第三周:线性方程组;第四周:线性空间;第五周:线性变换。
三、教学方法针对线性代数课程特点,结合课程目标和教学内容,采用以下教学方法:1. 讲授法:以教师为主导,系统地讲解线性代数的基本概念、性质、定理及方法。