2019高中数学 第一章1.3 二项式定理 1.3.2“杨辉三角”与二项式系数的性质高效演练

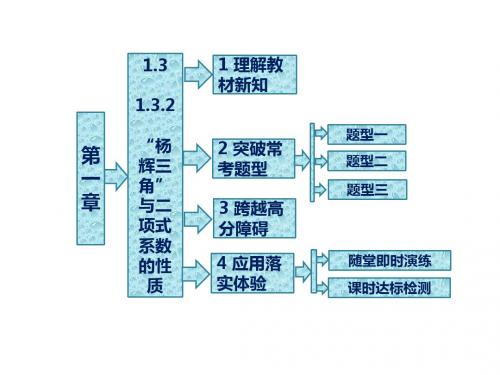
1.3.2 “杨辉三角”与二项式系数的性质
【学习目标】
1．结合“杨辉三角”体会二项式系数的性质． 2．会求二项展开式中二项式系数最大的项． 3. 会对n
b a )(+中的b a ,赋值解决和的问题.
【复习】
1. 二项式定理：
2. 二项展开式的通项： 公式中的r n
C 叫做 【探究活动与知识点梳理】
（三）、二项式系数的性质：
①性质1： ，即
直线 将函数r n
C r f =)( ,},,2,1,0{n r ∈的图象分成对称的两部分，它是图象的对称轴. ②性质2：
当 时，二项式系数是逐渐增大的；
当 时，二项式系数是逐渐减小的；
当n 是偶数时，第 项的二项式系数最大；
当n 是奇数时，第 项的二项式系数最大.
③性质3： ， 即
④ ，
即
【例题及练习】
例1. 画出函数r
C r f 6)(= ,}6,543,2,1,0{，，r ∈的图象.
例2. 试证明：在n
b a )(+的展开式中，奇数项的二项式系数的和等于偶数项的二项式系数的和.
练习：
1. 当n 为偶数时，n
b a )(+的二项式系数的最大值是
当n 为奇数时，n
b a )(+的二项式系数的最大值是
2. =+++1111311111C C C
3. =+++++++++++++1
1
221101210n n n n n n
n
n n n C C C C C C C C
4. =++++n n n n n C C C C 420。

2018-2019学年高中数学第一章计数原理1.3 二项式定理1.3.2“杨辉三角”与二项式系数的性质高效演练新人教A版选修2-3编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（2018-2019学年高中数学第一章计数原理1.3 二项式定理1.3.2“杨辉三角”与二项式系数的性质高效演练新人教A版选修2-3）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为2018-2019学年高中数学第一章计数原理1.3 二项式定理1.3.2“杨辉三角”与二项式系数的性质高效演练新人教A版选修2-3的全部内容。

1.3。

2“杨辉三角"与二项式系数的性质A级基础巩固一、选择题1．(1＋x）2n＋1（n∈N*）的展开式中,二项式系数最大的项所在的项数是（）A．n,n＋1 B．n－1，nC．n＋1，n＋2 D．n＋2,n＋3解析：因为2n＋1为奇数，所以展开式中间两项的二项式系数最大，中间两项的项数是n ＋1，n＋2。

答案：C2．设（x2＋1）(2x＋1)9＝a0＋a1（x＋2)＋a2(x＋2）2＋…＋a11（x＋2)11,则a0＋a1＋a2＋…＋a11的值为（）A．－2 B．－1 C．1 D．2解析：令等式中x＝－1可得a0＋a1＋a2＋…＋a11＝(1＋1)×（－1）9＝－2,故选A。

答案：A3．已知（1－2x)n展开式中，奇数项的二项式系数之和为64，则（1－2x）n（1＋x）展开式中含x2项的系数为（）A．71 B．70 C．21 D．49解析:因为奇数项的二项式系数和为2n－1，所以2n－1＝64，n＝7，因此（1－2x)n(1＋x）展开式中含x2项的系数为C27(－2）2＋C错误!(－2）＝70。

1．3.2 “杨辉三角”与二项式系数的性质知识点“杨辉三角”与二项式系数的性质(a ＋b )n的展开式的二项式系数，当n 取正整数时可以表示成如下形式：1．杨辉三角的特点(1)在同一行中每行两端都是1，与这两个1等距离的项的系数□01相等． (2)在相邻的两行中，除1外的每一个数都等于它“肩上”两个数的□02和，即C r n ＋1＝□03C r －1n＋C rn .2．二项式系数的性质(1)要区分二项式系数与二项式项的系数的区别，二项式系数是指C0n，C1n，…，C n n是组合数，而二项式项的系数是指该项除字母以外的常数部分，与二项式系数有关，但不一定等于二项式系数．(2)在求二项式系数时常用赋值法．如－1,0,1等，赋值法体现了函数思想f(x)＝(ax＋b)n＝a0＋a1x＋a2x2＋…＋a n x n，f(1)＝a0＋a1＋a2＋…＋a n.在解题时要注意审题，恰当赋值．(1)杨辉三角的每一斜行数字的差成一个等差数列．( )(2)二项式展开式的二项式系数和为C1n＋C2n＋…＋C n n.( )(3)二项式展开式中系数最大项与二项式系数最大项相同．( )答案 (1)× (2)× (3)× 2．做一做(1)⎝⎛⎭⎪⎫x －1x 11的展开式中二项式系数最大的项是第________项． (2)若(a ＋b )n的展开式中只有第5项的二项式系数最大，则n ＝________.(3)已知(a －x )5＝a 0＋a 1x ＋a 2x 2＋…＋a 5x 5，若a 2＝80，则a 0＋a 1＋a 2＋…＋a 5＝________. 答案 (1)6和7 (2)8 (3)1解析 (1)由n ＝11为奇数，则展开式中第11＋12项和第11＋12＋1项，即第6项和第7项的二项式系数相等，且最大．(2)由二项式系数的性质可知，第5项为二项展开式的中间项，即二项展开式有9项，故n ＝8.(3)展开式的通项为T r ＋1＝(－1)r C r 5·a5－r·x r ，令r ＝2，则a 2＝(－1)2C 25·a 3＝80，所以a＝2.则(2－x )5＝a 0＋a 1x ＋a 2x 2＋…＋a 5x 5，令x ＝1，得a 0＋a 1＋…＋a 5＝1.探究1 杨辉三角的有关问题例 1 如图所示，在杨辉三角中，斜线AB 上方箭头所示的数组成一个锯齿形的数列：1,2,3,3,6,4,10，…，记这个数列的前n 项和为S n ，求S 19.[解] 由题图知，数列中的首项是C 22，第2项是C 12，第3项是C 23，第4项是C 13，…，第17项是C 210，第18项是C 110，第19项是C 211.∴S 19＝(C 12＋C 22)＋(C 13＋C 23)＋(C 14＋C 24)＋…＋(C 110＋C 210)＋C 211 ＝(C 12＋C 13＋C 14＋…＋C 110)＋(C 22＋C 23＋C 24＋…＋C 211) ＝(2＋10)×92＋C 312＝274. 拓展提升解决与杨辉三角有关的问题的一般思路[跟踪训练1] (1)如图数表满足：①第n 行首尾两数均为n ；②图中的递推关系类似杨辉三角，则第n (n ≥2)行的第2个数是________；(2)将杨辉三角中的奇数换成1，偶数换成0，得到如图所示的三角数表．从上往下数，第1次全行的数都为1的是第1行，第2次全行的数都为1的是第3行，…，第n 次全行的数都为1的是第________行；第61行中1的个数是________．答案 (1)n 2－n ＋22(2)2n－1 32解析 (1)由图中数字规律可知，第n 行的第2个数是[1＋2＋3＋…＋(n －1)]＋1＝n (n －1)2＋1.(2)观察可得第1行，第3行，第7行，第15行，全行都为1，故第n 次全行的数都为1的是第2n－1行；∵n ＝6⇒26－1＝63，故第63行共有64个1，递推知第62行共有32个1，第61行共有32个1.探究2 二项展开式的系数和问题 例2 在(2x －3y )10的展开式中，求： (1)各项的二项式系数的和；(2)奇数项的二项式系数的和与偶数项的二项式系数的和； (3)各项系数之和；(4)奇数项系数的和与偶数项系数的和． [解] 在(2x －3y )10的展开式中：(1)各项的二项式系数的和为C 010＋C 110＋…＋C 1010＝210＝1024. (2)奇数项的二项式系数的和为C 010＋C 210＋…＋C 1010＝29＝512， 偶数项的二项式系数的和为C 110＋C 310＋…＋C 910＝29＝512.(3)设(2x －3y )10＝a 0x 10＋a 1x 9y ＋a 2x 8y 2＋…＋a 10y 10(*)，各项系数之和即为a 0＋a 1＋a 2＋…＋a 10，由于(*)是恒等式，故可用“赋值法”求解．令(*)中x ＝y ＝1，得各项系数之和为(2－3)10＝(－1)10＝1.(4)奇数项系数的和为a 0＋a 2＋a 4＋…＋a 10，偶数项系数的和为a 1＋a 3＋a 5＋…＋a 9. 由(3)知a 0＋a 1＋a 2＋…＋a 10＝1.①令(*)中x ＝1，y ＝－1，得a 0－a 1＋a 2－a 3＋…＋a 10＝510.②①＋②得2(a 0＋a 2＋…＋a 10)＝1＋510，故奇数项系数的和为12(1＋510)；①－②得2(a 1＋a 3＋…＋a 9)＝1－510,故偶数项系数的和为12(1－510)．拓展提升求展开式的各项系数之和常用赋值法．“赋值法”是求二项式系数常用的方法，根据题目要求，灵活赋给字母不同的值．一般地，要使展开式中项的关系变为系数的关系，令x ＝0可得常数项，令x ＝1可得所有项系数之和，令x ＝－1可得偶次项系数之和与奇次项系数之和的差，而当二项展开式中含负值项时，令x ＝－1则可得各项系数绝对值之和．[跟踪训练2] 设(2－3x )100＝a 0＋a 1x ＋a 2x 2＋…＋a 100·x 100，求下列各式的值． (1)a 0；(2)a 1＋a 2＋a 3＋a 4＋…＋a 100； (3)a 1＋a 3＋a 5＋…＋a 99；(4)(a 0＋a 2＋…＋a 100)2－(a 1＋a 3＋…＋a 99)2； (5)|a 0|＋|a 1|＋…＋|a 100|.解 (1)令x ＝0，则展开式为a 0＝2100. (2)令x ＝1，可得a 0＋a 1＋a 2＋…＋a 100＝(2－3)100，(*) 所以a 1＋a 2＋…＋a 100＝(2－3)100－2100.(3)令x ＝－1，可得a 0－a 1＋a 2－a 3＋…＋a 100＝(2＋3)100.与(2)中(*)式联立相减得a 1＋a 3＋…＋a 99＝(2－3)100－(2＋3)1002.(4)原式＝[(a 0＋a 2＋…＋a 100)＋(a 1＋a 3＋…＋a 99)]·[(a 0＋a 2＋…＋a 100)－(a 1＋a 3＋…＋a 99)]＝(a 0＋a 1＋a 2＋…＋a 100)·(a 0－a 1＋a 2－a 3＋…＋a 98－a 99＋a 100) ＝[(2－3)(2＋3)]100＝1100＝1. (5)因为T r ＋1＝(－1)r C r 1002100－r·(3)r x r，所以a 2k －1<0(k ∈N *)．所以|a 0|＋|a 1|＋|a 2|＋…＋|a 100| ＝a 0－a 1＋a 2－a 3＋…＋a 100 ＝(2＋3)100.探究3 求二项展开式中的最大项问题 例3 已知在的展开式中，各项系数和与它的二项式系数和的比为32.(1)求展开式中二项式系数最大的项； (2)求展开式中系数最大的项． [解] 令x ＝1，则展开式中各项系数和为(1＋3)n ＝22n. 又展开式中二项式系数和为2n. ∴22n2n ＝2n＝32，n ＝5. (1)∵n ＝5，展开式共6项，∴二项式系数最大的项为第三、四两项，拓展提升1.二项式系数的最大项的求法求二项式系数的最大项，根据二项式系数的性质对(a ＋b )n中的n 进行讨论． (1)当n 为奇数时，中间两项的二项式系数最大． (2)当n 为偶数时，中间一项的二项式系数最大． 2．展开式中系数的最大项的求法求展开式中系数的最大项与求二项式系数最大项是不同的，需要根据各项系数的正、负变化情况进行分析．如求(a ＋bx )n(a ，b ∈R )的展开式中系数的最大项，一般采用待定系数法．设展开式中各项系数分别为A 0，A 1，A 2，…，A n ，且第r ＋1 项最大，应用⎩⎪⎨⎪⎧A r ≥A r －1，A r ≥A r ＋1，解得r ，即得出系数的最大项．[跟踪训练3] 已知二项式⎝ ⎛⎭⎪⎫12＋2x n .(1)若展开式中第5项，第6项，第7项的二项式系数成等差数列，求展开式中二项式系数最大项的系数；(2)若展开式中前三项的二项式系数和等于79，求展开式中系数最大的项． 解 (1)由题意，得C 4n ＋C 6n ＝2C 5n ， ∴n 2－21n ＋98＝0，∴n ＝7或n ＝14.当n ＝7时，展开式中二项式系数最大的项是T 4和T 5，T 4的系数为C 37×⎝ ⎛⎭⎪⎫124×23＝352，T 5的系数为C 47×⎝ ⎛⎭⎪⎫123×24＝70.故展开式中二项式系数最大项的系数分别为352，70.当n ＝14时，展开式中二项式系数最大的项是T 8，∵T 8的系数为C 714×⎝ ⎛⎭⎪⎫127×27＝3432.故展开式中二项式系数最大项的系数为3432. (2)由题意知C 0n ＋C 1n ＋C 2n ＝79， 解得n ＝12或n ＝－13(舍去)． 设展开式中第r ＋1项的系数最大，由于⎝ ⎛⎭⎪⎫12＋2x 12＝⎝ ⎛⎭⎪⎫1212·(1＋4x )12，则⎩⎪⎨⎪⎧C r12·4r≥C r －112·4r －1，C r 12·4r ≥C r ＋112·4r ＋1，∴9.4≤r ≤10.4.又r ∈{0,1,2，…，12}，∴r ＝10，∴系数最大的项为T 11，且T 11＝⎝ ⎛⎭⎪⎫1212·C 1012·(4x )10＝16896x 10.1．(2－x )8展开式中不含x 4项的系数的和为( ) A ．－1 B ．0 C ．1 D ．2 答案 B 解析∴展开式中x 4项的系数为C 88＝1.又∵(2－x )8展开式中各项系数和为(2－1)8＝1， ∴展开式中不含x 4项的系数的和为0.2．在⎝ ⎛⎭⎪⎫2x－3x n (n ∈N *)的展开式中，所有的二项式系数之和为32，则所有系数之和为( )A ．32B ．－32C ．0D ．1 答案 D解析 由题意得2n ＝32，得n ＝5.令x ＝1，得展开式所有项的系数之和为(2－1)5＝1.故选D.3．若(1－2x )2019＝a 0＋a 1x ＋…＋a 2019x2019(x ∈R )，则a 12＋a 222＋…＋a 201922019的值为( )A ．2B ．0C ．－2D ．－1 答案 D 解析 (1－2x )2019＝a 0＋a 1x ＋…＋a 2019x2019，令x ＝12，则⎝⎛⎭⎪⎫1－2×122019＝a 0＋a 12＋a 222＋…＋a 201922019＝0，其中a 0＝1，所以a 12＋a 222＋…＋a 201922019＝－1.4．如图所示的数阵叫“莱布尼茨调和三角形”，他们是由正整数的倒数组成的，第n 行有n 个数且两端的数均为1n (n ≥2)，每个数是它下一行左右相邻两数的和，如：11＝12＋12，12＝13＋16，13＝14＋112，…，则第n (n ≥3)行第3个数字是________．答案2n (n －1)(n －2)(n ∈N *，n ≥3)解析 杨辉三角形中的每一个数都换成分数，就得到一个如题图所示的分数三角形，即为莱布尼茨三角形．∵杨辉三角形中第n (n ≥3)行第3个数字是n C 2n －1，则“莱布尼茨调和三角形”第n (n ≥3)行第3个数字是1n C 2n －1＝2n (n －1)(n －2). 5．在二项式(2x －3y )9的展开式中，求： (1)二项式系数之和； (2)各项系数之和； (3)所有奇数项系数之和； (4)系数绝对值的和．解 设(2x －3y )9＝a 0x 9＋a 1x 8y ＋a 2x 7y 2＋…＋a 9y 9. (1)二项式系数之和为C 09＋C 19＋C 29＋…＋C 99＝29. (2)各项系数之和为a 0＋a 1＋a 2＋…＋a 9， 令x ＝1，y ＝1，∴a 0＋a 1＋a 2＋…＋a 9＝(2－3)9＝－1. (3)由(2)知a 0＋a 1＋a 2＋…＋a 9＝－1， 令x ＝1，y ＝－1，可得：a 0－a 1＋a 2－…－a 9＝59，将两式相加除以2可得：a 0＋a 2＋a 4＋a 6＋a 8＝59－12，即为所有奇数项系数之和．(4)解法一：|a 0|＋|a 1|＋|a 2|＋…＋|a 9|＝a 0－a 1＋a 2－…－a 9，令x ＝1，y ＝－1，则|a 0|＋|a 1|＋|a 2|＋…＋|a 9|＝a 0－a 1＋a 2－…－a 9＝59.解法二：|a 0|＋|a 1|＋|a 2|＋…＋|a 9|即为(2x ＋3y )9展开式中各项系数和，令x ＝1，y ＝1得：|a 0|＋|a 1|＋|a 2|＋…＋|a 9|＝59.。