圆的垂径定理习题及答案

垂径定理练习题及答案一、选择题1. 在一个圆中，如果一条直径的端点与圆上一点相连，这条线段的中点与圆心的距离是直径的（）A. 一半B. 半径B. 直径D. 无法确定2. 垂径定理指出，如果一条线段是圆的直径，那么它与圆上任意一点连线所形成的直角三角形的斜边是（）A. 直径B. 半径C. 线段D. 无法确定3. 圆内接四边形的对角线互相平分，且其中一条对角线是圆的直径，那么这个四边形是（）A. 平行四边形B. 矩形C. 菱形D. 无法确定4. 如果圆的半径为r，那么圆的直径是（）A. 2rB. rC. r的平方D. 2r的平方二、填空题1. 垂径定理告诉我们，如果一条线段是圆的直径，那么它与圆上任意一点连线所形成的直角三角形的斜边是______。

2. 圆的内接四边形中，如果对角线互相平分，且其中一条对角线是圆的直径，那么这个四边形的对角线长度相等，等于______。

3. 已知圆的半径为5cm，那么圆的直径是______。

三、解答题1. 已知一个圆的半径为7cm，圆内有一点P，连接点P和圆心O，得到线段OP。

如果OP的长度为4cm，求点P到圆上任意一点的距离。

2. 一个圆的直径为14cm，圆内接四边形ABCD，其中AC为直径。

已知AB=6cm，求BC的长度。

四、证明题1. 证明：如果一个三角形是直角三角形，且斜边是圆的直径，那么这个三角形的外接圆的直径是这个三角形的斜边。

2. 证明：如果一个圆的内接四边形的对角线互相平分，且其中一条对角线是圆的直径，那么这个四边形的对角线长度相等。

答案：一、选择题1. A2. A3. B4. A二、填空题1. 直径的一半2. 圆的直径3. 10cm三、解答题1. 点P到圆上任意一点的距离是3cm（利用勾股定理，OP为直角三角形的一条直角边，半径为斜边，另一直角边为点P到圆上任意一点的距离）。

2. BC的长度是8cm（利用圆内接四边形的性质，对角线互相平分，且AC是直径，所以BD=7cm，再利用勾股定理求BC）。

1《圆》练习题（垂径定理, 弧、弦、圆心角, 圆周角）一、选择题1.已知在⊙O 中, 弦AB 的长为8厘米, 圆心O 到AB 的距离为3厘米, 则⊙O 的半径是（ ）A. 3厘米B. 4厘米C. 5厘米D. 8厘米2.半径等于12的圆中, 垂直平分半径的弦长为（ ）A. B. C. D.3.如图1, 在⊙O 中, ∠ABC=50°, 则∠AOC 等于（ ）A. 50°B. 80°C. 90°D. 100°4.如图2, AB 是⊙O 的直径, ∠ABC=30°, 则∠BAC =（ ）A. 90°B. 60°C. 45°D. 30°5.如图3, △ABC 内接于⊙O, 连结OA.OB, 若∠ABO ＝25°, 则∠C 的度数为（ ）．A. 55°B. 60°C. 65°D. 70°6.如图4, 四边形ABCD 内接于⊙O, 若它的一个外角∠DCE=70°, 则∠BOD=( )A. 35°B.70°C. 110°D.140°7、如图5, △ABC 内接于⊙O, AD ⊥BC 于点D, AD=2cm, AB=4cm, AC=3cm, 则⊙O 的直径是（ ）A. 2cmB. 4cmC. 6cmD. 8cm8、如图6, BD 是⊙O 的直径, 圆周角∠A = 30(, 则∠CBD 的度数是（ ）A. 30(B. 45(C. 60(D. 80(9、如图7, AB 为⊙O 的直径, C ．D 是⊙O 上的两点, ∠BAC=30º, AD=CD, 则∠DAC 的度数是（ ）A. 30ºB. 60ºC. 45ºD. 75º10、圆内接四边形ABCD 中, ∠A ∶∠B ∶∠C ∶∠D 可以是（ ）A. 1∶2∶3∶4B. 1∶3∶2∶4C. 4∶2∶3∶1D. 4∶2∶1∶3AB O C图1 图2 O 30D B C A O D CBA 图3 图4图6图7图52二、填空题11.如图8, ∠A 是⊙O 的圆周角, ∠A=40°, 则∠OBC 的度数为_______.12.如图9, AB 是⊙O 的直径, 点D 在⊙O 上∠AOD=130°, BC ∥OD 交⊙O 于C, 则∠A= .13、如图10, ⊙O 的直径AB=8cm, C 为⊙O 上的一点, ∠BAC=300, 则BC= .14、如图，量角器外沿上有A 、B 两点，它们的读数分别是70°、40°，则∠1的度数为 .三、解答题: 15、.如图, AB 、CD 是⊙O 的两条弦, 延长AB 、CD 交于点P, 连结AD 、BC 交于点E ． , , 求 的度数．16.如图所示, AB 是⊙O 的一条弦, OD ⊥AB , 垂足为C, 交⊙O 于点D , 点E 在⊙O 上。

2013中考全国100份试卷分类汇编圆的垂径定理1、（2013年潍坊市）如图，⊙O 的直径AB=12，CD 是⊙O 的弦，CD ⊥AB ，垂足为P ，且BP ：AP=1:5,则CD 的长为（ ）.A.24B.28C.52D.542、(2013年黄石)如右图，在Rt ABC 中，90ACB ∠= ，3AC =，4BC =，以点C 为圆心，CA 为 半径的圆与AB 交于点D ，则AD 的长为（ ）A.95B. 245C. 185D. 523、(2013河南省)如图，CD 是O 的直径，弦AB CD ⊥于点G ，直线EF 与O 相切与点D ，则下列结论中不一定正确的是（ ）A. AG ＝BGB. AB ∥BFC.AD ∥BCD. ∠ABC ＝ADC4、（2013•泸州）已知⊙O 的直径CD=10cm ，AB 是⊙O 的弦，AB⊥CD，垂足为M ，且AB=8cm ，则AC 的长为（ ） A. cm B. cm C. cm 或cm D. cm 或cm5、（2013•广安）如图，已知半径OD 与弦AB 互相垂直，垂足为点C ，若AB=8cm ，CD=3cm ，则圆O 的半径为（ ）A. cmB. 5cmC. 4cmD. cm6、（2013•绍兴）绍兴市著名的桥乡，如图，石拱桥的桥顶到水面的距离CD 为8m ，桥拱半径OC 为5m ，则水面宽AB 为（ ）7、（2013•温州）如图，在⊙O中，OC⊥弦AB于点C，AB=4，OC=1，则OB的长是（）A. B. C. D.8、（2013•嘉兴）如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EC．若AB=8，CD=2，则EC的长为（）A. 2B.C.D.9、（2013•莱芜）将半径为3cm的圆形纸片沿AB折叠后，圆弧恰好能经过圆心O，用图中阴影部分的扇形围成一个圆锥的侧面，则这个圆锥的高为（）A. B. C. D. 3210、（2013•徐州）如图，AB是⊙O的直径，弦CD⊥AB，垂足为P．若CD=8，OP=3，则⊙O的半径为（）A. 10B. 8C. 5D. 311、(2013浙江丽水)一条排水管的截面如图所示，已知排水管的半径OB=10，水面宽AB=16，则截面圆心O到水面的距离OC是A. 4B. 5C.6D.812、（2013•宜昌）如图，DC 是⊙O直径，弦AB⊥CD于F，连接BC，DB，则下列结论错误的是（）A. B. AF=BF C. OF=CF D. ∠DBC=90°13、（2013•毕节地区）如图在⊙O中，弦AB=8，OC⊥AB，垂足为C，且OC=3，则⊙O的半径（）A. 5B. 10C. 8D. 614、（2013•南宁）如图，AB是⊙O的直径，弦CD交AB于点E，且AE=CD=8，∠BAC=∠BOD，则⊙O 的半径为（）A. 4B. 5C. 4D. 315、（2013年佛山）半径为3的圆中，一条弦长为4，则圆心到这条弦的距离是（）A.3B.4C.5D.716、（2013甘肃兰州4分、12）如图是一圆柱形输水管的横截面，阴影部分为有水部分，如果水面AB宽为8cm，水面最深地方的高度为2cm，则该输水管的半径为（）A．3cm B．4cm C．5cm D．6cm17、（2013•内江）在平面直角坐标系xOy中，以原点O为圆心的圆过点A（13，0），直线y=kx﹣3k+4与⊙O交于B、C两点，则弦BC的长的最小值为．18、（13年安徽省4分、10）如图，点P是等边三角形ABC外接圆⊙O上的点，在以下判断中，不．正确．．的是（）19、（2013•宁波）如图，AE是半圆O的直径，弦AB=BC=4，弦CD=DE=4，连结OB，OD，则图中两个阴影部分的面积和为．图20 图21 图2220、（2013•宁夏）如图，将半径为2cm的圆形纸片折叠后，圆弧恰好经过圆心O，则折痕AB的长为 cm．21、（2013•包头）如图，点A、B、C、D在⊙O上，OB⊥AC，若∠BOC=56°，则∠ADB=度．图23 图24 图25 图26 图27 图2823、（2013•黄冈）如图，M是CD的中点，EM⊥CD，若CD=4，EM=8，则所在圆的半径为．24、（2013•绥化）如图，在⊙O中，弦AB垂直平分半径OC，垂足为D，若⊙O的半径为2，则弦AB 的长为．25、（2013哈尔滨）如图，直线AB与⊙O相切于点A，AC、CD是⊙O的两条弦，且CD∥AB，若⊙O的半径为52，CD=4，则弦AC的长为．26、（2013•张家界）如图，⊙O的直径AB与弦CD垂直，且∠BAC=40°，则∠BOD=．27、（2013•遵义）如图，OC是⊙O的半径，AB是弦，且OC⊥AB，点P在⊙O上，∠APC=26°，则∠BOC=度．28、（2013陕西）如图，AB是⊙O的一条弦，点C是⊙O上一动点，且∠ACB=30°，点E、F分别是AC、BC的中点，直线EF与⊙O交于G、H两点，若⊙O的半径为7，则GE+FH的最大值为．29、（2013年广州市）如图7，在平面直角坐标系中，点O为坐标原点，点P在第一象限，PΘ与x轴交于O,A两点，点A的坐标为（6,0），PΘ的半径为13，则点P的坐标为 ____________.30、(2013年深圳市)如图5所示，该小组发现8米高旗杆DE的影子EF落在了包含一圆弧型小桥在内的路上，于是他们开展了测算小桥所在图的半径的活动。

圆的垂径定理习题一. 选择题 1.如图1,00的直径为10,圆心0到弦AB 的距离0M 的长为3,那么弦AB 的长是（ ）2.如图，O 0的半径为5,弦AB 的长为8,M 是弦AB 上的一个动点，则线段0M 长的最小值为（）3.过O 0内一点M 的最长弦为10cm 最短弦长为8cm 则0M 的长为（）A* 9cmE, 5cm4.如图，小明同学设计了一个测量圆直径的工具，标有刻度的尺子 0A 0B 在 0点钉在一起，并使它们保持垂直，在测直径时，把 0点靠在圆周上，读得刻度0E=8个单位，0F=6个单位，则圆的直位 D. 15个单位5.如图，00的直径AB 垂直弦CD 于 P,且P 是半径0B 的中点，6cmCD ，则直径AB 的长是（）6. 下列命题中，正确的是（A .平分一条直径的弦必垂直于这条直径B .平分一条弧的直线垂直于这条弧所对的弦C .弦的垂线必经过这条弦所在圆的圆心D .在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心7. 如图，某公园的一座石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则拱高为A.4B. 6C. 7D. 8 B. 3 C. 4 D. 5B . 10个单位 C. 1个单A . 212个单位E & 5米B, 8米C. 7米D,出米D8.0O 的半径为5cm 弦AB//CD ,且AB=8cm,CD=6cn 则AB 与CD 之间的距离为( ) A . 1 cm B. 7cm C. 3 cm 或 4 cm D. 1cm 或 7cm9•已知等腰△ ABC 的三个顶点都在半径为5的0 0上，如果底边BC 的长为8,那么BC 边上的高为 ( ) A . 2 B. 8 C. 2 或 8 D. 3 二、填空题1. _________________________________________________________________________ 已知AB 是O 0的弦，AB= 8cm, OCL AB 与C, 0C=3cm 则O 0的半径为 __________________________ c m2. ____________________________________________________________________ 在直径为10cm 的圆中，弦 AB 的长为8cm,则它的弦心距为 _______________________________ cm3. 在半径为10的圆中有一条长为16的弦，那么这条弦的弦心距等于 _____________________4. 已知AB 是O 0的弦，AB= 8cm, OC L AB 与C, 0C=3cm 则O O 的半径为 ________________ cm5. ______________________________________________________________________________ 如图，O 0的直径AB 垂直于弦CD ，垂足为E ，若/C0氐120°, 0E= 3厘米，贝U CD= ___________ 厘6. _____________________________________________________________ 半径为6cm 的圆中，垂直平分半径 0A 的弦长为 _______________________________________________ c m7. 过O 0内一点M 的最长的弦长为6cm,最短的弦长为4cm,则0M 勺长等于 cm8. 已知AB 是O 0的直径，弦CDL AB E为垂足，CD=8 0E=1则AB= __________9. 如图，AB 为O 0的弦，O 0的半径为5, OC L AB 于点D,交O 0于点C,且CD= l ，则弦AB 的长11. __________________________ 如图，在直角坐标系中，以点P 为圆心的圆弧与轴交于 A 、B 两点，已知P(4, 2)和A(2, 0), 贝卩点B 的坐标是12. ____________________________________________________________ 如图，AB 是O 0的直径，ODL AC 于点D, BC=6cm 则0D ________________________________ cm10. 某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示，已知 AB= 16m 半径04 10m 则中间柱 CD的高度为13. 如图，矩形ABCDf圆心在AB上的圆0交于点G B、F、E, GB=10 EF=8 那么AD= ______14.___________________________________________________________________________ 如图，O O 的半径是 5cm P 是o o 外一点，PO=8cm / P=3GO,则 AB ______________________ cm是 __________________ Cm16. 已知AB 是圆O 的弦,半径OC 垂直AB 交AB 于D,若AB=8 CD=2则圆的半径为 _______________ 17. 一个圆弧形门拱的拱高为1米，跨度为4米，那么这个门拱的半径为 ___________________ 米 18. 在直径为10厘米的圆中，两条分别为6厘米和8厘米的平行弦之间的距离是厘米19. 如图,是一个隧道的截面,如果路面AB 宽为8米,净高CD 为8米,那么这个 隧道所在圆的20. 如图,AB 为半圆直径,O 为圆心,C 为半圆上一点,E 是弧AC 的中点,OE 交弦AC 于点0 若 AC=8cm DE=2cm 则 OD 的长为 _____________ c m21. 已知等腰△ ABC 的三个顶点都在半径为5的。

初中垂径定理试题及答案一、选择题1. 在圆中，垂直于弦的直径是该弦的（）。

A. 垂线B. 垂径C. 弦心距D. 弦长答案：B2. 垂径定理告诉我们，如果一条线段垂直于弦，并且平分弦，那么它也平分弦所对的（）。

A. 弧B. 圆心角C. 弦心距D. 弦长答案：A3. 在圆中，如果一条直径垂直于弦，那么这条直径将弦分成的两段长度（）。

A. 相等B. 不相等C. 无法确定D. 取决于圆的大小答案：A二、填空题4. 在圆中，如果弦AB的中点为M，且直径CD垂直于弦AB于点M，则弦AB所对的弧ACB的度数为______。

答案：90°5. 垂径定理在圆的几何学中非常重要，它说明了垂直于弦的直径将弦平分，并且平分的弦所对的弧是______。

答案：相等的三、解答题6. 已知圆O的半径为10cm，弦AB垂直于直径CD于点M，求弦AB的长度。

答案：由于直径CD垂直于弦AB，根据垂径定理，弦AB被直径CD平分，因此弦AB的长度为圆的直径，即20cm。

7. 在一个圆中，弦AC的长度为12cm，弦BC的长度为8cm，且AC和BC相交于点O，求圆的半径。

答案：由于AC和BC相交于圆心O，根据垂径定理，OA=OC，OB=OA，因此OA=OC=6cm，OB=OA=6cm。

根据勾股定理，圆的半径r满足r^2 =OA^2 + OB^2 = 6^2 + 6^2 = 72，所以r = √72 = 6√2 cm。

四、证明题8. 证明：在圆中，如果一条直径垂直于弦，那么这条直径将弦平分。

答案：设圆心为O，直径为CD，弦为AB，且CD垂直于AB于点M。

要证明CM=MD。

由于CD是直径，所以∠CMO=∠DMO=90°。

根据垂径定理，CM=MD，因此这条直径将弦平分。

28．在距离某学校的教室A点正东240米的O点处有一货场，经过O点沿北偏西 方向有一条公路OB，假定这条公路上的车辆形成的噪音影响范围在130米以内.
（1）这条公路上的车辆形成的噪音是否会对学校造成影响？
（2）若车辆形成的噪音会对学校造成影响，为消除噪音，计划在公路边修筑一段消音墙，请你计算消音墙的长度.（只考虑声音的直线传播）
37．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，连接AC、BC，若∠BAC＝30º，CD＝6cm．
（1）求∠BCD的度数；
（2）求⊙O的直径．
38．如图，AC为⊙O的直径，CD为⊙O的弦，BE⊥CD于点E， ＝ ．
（1）求证：BE的⊙O切线．Fra bibliotek（2）若AD＝4，EC＝1，求BD的长．
39．如图，A，B，C是⊙O上的点，其中 ，过点B画BD⊥OC于点D．
C．若△BCD是等腰三角形，则△ACD也是等腰三角形
D．若PB=4PA，则CD=PB
3．如图，在 中， ， 为互相垂直且相等的两条弦， ， ，垂足分别为 ， ，若 ，则 的半径是（）
A． B． C． D．
4．如图， 的直径为10，弦 ， 是 上一个动点，则 的最小值为（）
A．2B．3C．4D．5
5．如图是一个圆弧形门拱，拱高 ，跨度 ，那么这个门拱的半径为（）
A． B． C． D．
11．平面直角坐标系中，在以（2，1）为圆心，5为半径的圆上的点的坐标是（）
A．（4，7）B．（－1，－2）C．（5，4）D．（2，－4）
12．如图，⊙O的半径OA＝8，以A为圆心，OA为半径的弧交⊙O于B，C点，则BC＝（ ）
A． B． C． D．
13．如图，AB是⊙O的直径，C是⊙O上一点，OD⊥BC于点D，AC＝4，则OD的长为（ ）

第三节垂径定理一．选择题1．如图，⊙O的半径为3，点P是弦AB延长线上的一点，连接OP，若OP＝4，∠P＝30°，则弦AB的长为（）A．2B．2C ．D．22．如图，⊙O的直径CD＝10cm，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OC＝3：5，则AB的长为（）A ．cm B．8cm C．6cm D．4cm3．往直径为52cm的圆柱形容器内装入一些水以后，截面如图所示，若水面宽AB＝48cm，则水的最大深度为（）A．8cm B．10cm C．16cm D．20cm4．如图，C是以AB为直径的半圆O上一点，连结AC，BC，分别以AC、BC为直径作半圆，其中M，N分别是AC、BC 为直径作半圆弧的中点，，的中点分别是P，Q．若MP+NQ＝7，AC+BC＝26，则AB的长是（）A．17B．18C．19D．205．如图，在圆O中，弦AB＝4，点C在AB上移动，连接OC，过点C做CD⊥OC交圆O于点D，则CD的最大值为（）A．2B．2C ．D ．6．《九章算术》是我国古代著名数学暮作，书中记载：“今有圆材，埋在壁中，不知大小以锯锯之，深一寸，锯道长一尺，问径几何？”用数学语言可表述为：“如图，CD为⊙O的直径，弦AB⊥DC于E，ED＝1寸，AB ＝10寸，求直径CD的长．”则CD＝（）A．13寸B．20寸C．26寸D．28寸7．如图，在⊙O中，弦AB为8mm，圆心O到AB的距离为3mm，则⊙O的半径等于（）A．3mm B．4mm C．5mm D．8mm8．如图，将半径为4cm的圆折叠后，圆弧恰好经过圆心，则折痕的长为（）A ．B ．C ．D ．9．如图，将⊙O沿弦AB折叠，圆弧AB恰好经过圆心O，P 是上一点，则∠APB的度数为（）A．30°B．45°C．60°D．75°10．如图，C、D是以AB为直径的圆O上的两个动点（点C、D不与A、B重合），在运动过程中弦CD始终保持不变，M是弦CD的中点，过点C作CP⊥AB于点P．若CD＝3，AB＝5，PM＝x，则x的最大值是（）A．3B ．C．2.5D．211．如图，⊙O的直径CD＝12cm，AB是⊙O的弦，AB⊥CD，垂足为E，OE：OC＝1：3，则AB的长为（）A．2cm B．4cm C．6cm D．8cm12．如图，AB是⊙O的一条弦，OD⊥AB于点C，交⊙O于点D，连接OA．若AB＝4，CD＝1，则⊙O的半径为（）A．5B ．C．3D ．13．一条排水管的截面如图所示，已知排水管的半径OB＝10，水面宽AB＝16，则截面圆心O到水面的距离OC 是（）A．4B．5C．6D．614．如图，⊙O的半径是2，直线l与⊙O相交于A、B两点，M、N是⊙O上的两个动点，且在直线l的异侧，若∠AMB＝45°，则四边形MANB面积的最大值是（）A．2B．4C．4D．815．如图，AB是半圆O的直径，AC为弦，OD⊥AC于D，过点O作OE∥AC交半圆O于点E，过点E作EF ⊥AB于F．若AC＝2，则OF的长为（）A ．B ．C．1D．216．如图，⊙O的直径CD＝20，AB是⊙O的弦，AB⊥CD，垂足为M，OM：OC＝3：5，则AB的长为（）A．8B．12C．16D．217．⊙O的半径是13，弦AB∥CD，AB＝24，CD＝10，则AB与CD的距离是（）A．7B．17C．7或17D．3418．如图，⊙O的半径OD⊥弦AB于点C，连结AO并延长交⊙O于点E，连结EB．若AB＝4，CD＝1，则EB 的长为（）A．3B．4C．5D．2.5二．填空题19．如图，AB为⊙O的直径，弦CD⊥AB于E，已知CD＝12，BE＝2，则⊙O 半径为．20．如图，AB为⊙O的直径，弦CD⊥AB于点H，若AB＝10，CD＝8，则OH的长度为．21．如图，AC是⊙O的直径，弦BD⊥AO，垂足为点E，连接BC，过点O作OF⊥BC，垂足为F，若BD＝8cm，AE＝2cm，则OF的长度是cm．22．如图，AB为⊙O的直径，弦CD⊥AB于点E，已知CD＝8，OE＝3，则⊙O的半径为．23．如图，AB是⊙O的直径，弦CD交AB于点P，AP＝2，BP＝6，∠APC＝30°，则CD的长为．24．如图，在△ABC中，∠A＝62°，⊙O截△ABC三边所得的弦长相等，则∠BOC的度数是．25．如图，圆心在y轴的负半轴上，半径为5的⊙B与y轴的正半轴交于点A（0，1），过点P（0，﹣7）的直线l与⊙B相交于C，D两点，则弦CD长的所有可能的整数值有个．26．如图，矩形ABCD的边AB过⊙O的圆心，E、F分别为AB、CD与⊙O的交点，若AE＝3cm，AD＝4cm，DF＝5cm，则⊙O的直径等于．27．如图，⊙O的直径为10，弦AB的长为8，M是弦AB上的动点，则OM的长的取值范围是．28．王江泾是著名的水乡，如图，圆拱桥的拱顶到水面的距离CD为9m，水面宽AB为6m，则桥拱半径OC为。

《垂径定理》典型例题例1. 选择题：（1）下列说法中，正确的是（）A. 长度相等的弧是等弧B. 两个半圆是等弧C. 半径相等的弧是等弧D. 直径是圆中最长的弦答案：D（2）下列说法错误的是（）A. 圆上的点到圆心的距离相等B. 过圆心的线段是直径C. 直径是圆中最长的弦D. 半径相等的圆是等圆答案：B例2. 如图，已知AB是⊙O的直径，M、N分别是AO、BO的中点，CM⊥AB，DN⊥AB。

分析：要证弧相等，可证弧所对的弦相等，也可证弧所对的圆心角相等。

证明：连结OC、OD∵M、N分别是OA、OB的中点∵OA＝OB，∴OM＝ON又CM⊥AB，DN⊥AB，OC＝OD∴Rt△OMC≌Rt△OND∴∠AOC＝∠BOD例3. 在⊙O中，弦AB＝12cm，点O到AB的距离等于AB的一半，求∠AOB 的度数和圆的半径。

分析：根据O到AB的距离，可利用垂径定理解决。

解：过O点作OE⊥AB于E∵AB＝12由垂径定理知：∴△ABO为直角三角形，△AOE为等腰直角三角形。

例4. 如图，在Rt△ABC中，∠C＝90°，AC＝3，BC＝4，以点C为圆心，CA 为半径的圆与AB、BC分别交于点D、E。

求AB、AD的长。

分析：求AB较简单，求弦长AD可先求AF。

解：过点C作CF⊥AB于F∵∠C＝90°，AC＝3，BC＝4∵∠A＝∠A，∠AFC＝∠ACB∴△AFC∽△ACB例5. 如图，⊙O中，弦AB＝10cm，P是弦AB上一点，且PA＝4cm，OP＝5cm，求⊙O的半径。

分析：⊙O中已知弦长求半径，通常作弦心距构造直角三角形，利用勾股定理求解。

解：连OA，过点O作OM⊥AB于点M∵点P在AB上，PA＝4cm即⊙O的半径为7cm。

例6. 如图“五段彩虹展翅飞”是某省利用国债资金修建的横跨渡江的琼洲大桥已正式通车，该桥的两边均有五个红色的圆拱，最高的圆拱的跨度为110米，拱高为22米，求这个圆拱所在圆的直径。

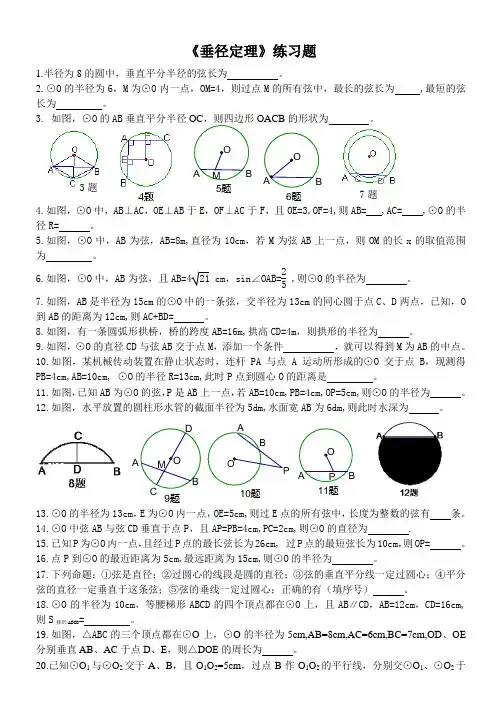
9题10题11题5题6题《垂径定理》练习题1.半径为8的圆中，垂直平分半径的弦长为 。

2.⊙O 的半径为6，M 为⊙O 内一点，OM=4，则过点M 的所有弦中，最长的弦长为 ,最短的弦长为 。

3. 如图，⊙O 的AB 垂直平分半径OACB 的形状为 。

4.如图，⊙O 中，AB ⊥AC ，OE ⊥AB 于E ，OF ⊥AC 于F ，且OE=3,OF=4,则AB= ,AC= ,⊙O 的半径R= 。

5.如图，⊙O 中，AB 为弦，AB=8m,直径为10cm ，若M 为弦AB 上一点，则OM 的长x 的取值范围为 。

6.如图，⊙O 中，AB 为弦，且AB=421 cm ，sin ∠OAB=25,则⊙O 的半径为 。

7.如图，AB 是半径为15cm 的⊙O 中的一条弦，交半径为13cm 的同心圆于点C 、D 两点，已知，O 到AB 的距离为12cm,则AC+BD= 。

8.如图，有一条圆弧形拱桥，桥的跨度AB=16m,拱高CD=4m ，则拱形的半径为 。

9.如图，⊙O 的直径CD 与弦AB 交于点M ，添加一个条件 ，就可以得到M 为AB 的中点。

10.如图，某机械传动装置在静止状态时，连杆PA 与点A 运动所形成的⊙O 交于点B ，现测得PB=4cm,AB=10cm, ⊙O 的半径R=13cm,此时P 点到圆心O 的距离是 。

11.如图，已知AB 为⊙O 的弦，P 是AB 上一点，若AB=10cm,PB=4cm,OP=5cm,则⊙O 的半径为 。

12.如图，水平放置的圆柱形水管的截面半径为5dm,水面宽AB 为6dm,则此时水深为 。

13.⊙O 的半径为13cm ，E 为⊙O 内一点，OE=5cm,则过E 点的所有弦中，长度为整数的弦有 条。

14.⊙O 中弦AB 与弦CD 垂直于点P ，且AP=PB=4cm,PC=2cm,则⊙O 的直径为 .15.已知P 为⊙O 内一点，且经过P 点的最长弦长为26cm, 过P 点的最短弦长为10cm ，则OP= 。

2013中考全国100份试卷分类汇编圆的垂径定理1、（2013年潍坊市）如图，O O 的直径AB=12 CD 是O O 的弦，CD! AB,垂足为P ,且BP AP=1:5, 则CD 的长为（ ）.结论中不一定正确的是（ ） 4、 （2013?泸州）已知OO 的直径CD=10cm AB 是OO 的弦，AB 丄CD 垂足为 M 且AB=8cm 贝U AC 的长为（ ）A.B. 匚-cmC. 上 cm 或D. - :;cm 或匚电V cm5、 （2013?广安）如图，已知半径 OD 与弦AB 互相垂直，垂足为点 C,若AB=8cm CD=3cm 则圆O6 （2013?绍兴）绍兴市著名的桥乡，如图，石拱桥的桥顶到水面的距离CD 为8m ，桥拱半径OC 为 5m 则水面宽AB %（ ）B. 8,2C. 2 5D. 4 590，AC 3，BC 4，以点C 为圆心，CA 为C.18 D. 55 23、（2013A. AG =BGB. AB// BF C.AD // BC D. / ABC= ADCcm B. 5cm C. 4cm D. 19 cmA. 4mB. 5mC. 6mD. 8mA. 2、（2013年黄石）如右图，在Rt ABC 中， ACB 半径的圆与AB 交于点D ，则AD 的长为（） 河南省）如图，CD 是 O 的直径，弦AB CD 于点G,直线EF 与 O 相切与点D,则下列的半径为（A.11、（2013浙江丽水）一条排水管的截面如图所示，已知排水管的半径 OB=10水面宽AB=16面圆心O 到水面的距离OC 是 A. 4 B. 5 C.6 D.812、（2013?宜昌）如图，DC 是OO 直径，弦AB 丄CD 于 F ，连接BQ DB 则下列结论错误的是（A. AD-BD B AF=BF C. OF=CF D. / DBC=90 13、（2013?毕节地区）如图在OO 中，弦AB=8 OCLAB 垂足为C,且OC=3则OO 的半径（7、（2013?温州）如图，在OO 中，OC L 弦AB 于点C, AB=4 OC=1贝U OB 的长是（ ）；B. !■ C. 一， D. IOO 的半径ODL 弦AB 于点C,连结AO 并延长交OO 于点E ,连结EC.若I!， D. . ■9、（2013?莱芜）将半径为3cm 的圆形纸片沿AB 折叠后，圆弧恰好能经过圆心 O,用图中阴影部分 的扇形围成一个圆锥的侧面，贝U 这个圆锥的高为（ ）-:B. 一： C. I" D. 如图，AB 是OO 的直径，弦CDLAB,垂足为 32P.若CD=8 OP=3则OO 的半径为则截A. 5B. 10C. 8D. 6AB=8 CD=2 贝U EC 的长为（ ）A. 2 I!.B. ・C. A. A. 10 B. 8 C. 5D. 314、（2013?南宁）如图，AB 是OO的直径，弦CD交AB于点E,且AE=CD=, / BAC= / BOD则OOA.4 :B. 5C. 4D. 315、（2013年佛山）半径为3的圆中，一条弦长为4,则圆心到这条弦的距离是（16、（2013甘肃兰州4分、12）如图是一圆柱形输水管的横截面，阴影部分为有水部分，如果水2cm则该输水管的半径为（17、（2013?内江）在平面直角坐标系xOy中，以原点O为圆心的圆过点A（ 13,0）,直线y=kx - 3k+4与OO交于B C两点，则弦BC的长的最小值为___________ .18、（13年安徽省4分、10）如图，点P是等边三角形ABC外接圆O O上的点，在以下判断中，不正确的是（）当弦PE■最长时.△馭是等腰三角形。

（苏科版）九年级上册数学《第2章对称图形---圆》
2.2圆的对称性
第二课时 垂径定理
圆的轴对称性
圆是轴对称图形，圆有无数条对称轴，任何一条直径所在直线都是它的对称轴；圆又是中心对称图形，它的对称中心是圆心.
◆1、垂径定理：垂直于弦的直径平分弦，并且平分弦所对的两条弧；垂径定理的依据是圆的轴对称的性质.
A． B． C． D．
【例题5】（2022•甘肃模拟）如图，⊙O的半径为5，弦AB＝8，点M是弦AB上的动点，则（ ）
A．4≤OM≤5B．3≤OM＜5C．3＜OM≤5D．3≤OM≤5
解题技巧提炼
本题考查了垂径定理、勾股定理以及线段的最值问题来求范围，熟练掌握垂径定理和勾股定理是解题的关键．
【变式5-1】（2023•同心县校级二模）如图，⊙O的半径为10，弦AB＝16，M是弦AB上的动点，则OM不可能为（ ）
推导格式：
◆2、垂径定理的用法：
（1）连接圆心与弦的一端，与过圆心且垂直与弦的线段和弦的一半构成直角三角形（即垂径定理三角形），利用勾股定理列式求值.
（2）如图弦长a，弦心距d，弓形高h，半径r之间有以下关系：
（3）r,a，d，h，已知其中任意两个量，即可求出另外两个量.
◆1、垂径定理的推论：平分弦(不是直径)的直径垂巧提炼
作弦的垂线并连接圆心与弦的一个端点，构造“垂径定理三角形”，利用勾股定理求解.
【变式2-1】（2023春•渝中区校级期末）如图，AB是⊙O的直径，弦CD⊥AB于E，若 ，
BE＝2，则AB的长是（ ）
A．12B．16C． D．
【变式2-2】（2023•伊川县一模）如图，在半径为1的扇形AOB中，∠AOB＝90°，点P是 上任意一点（不与点A，B重合），OC⊥AP，OD⊥BP，垂足分别为C，D，则CD的长为（ ）

垂径定理一、单选题A．82．如图，圆弧形桥拱的跨度A．2米B．43．如图，一个圆柱形的玻璃水杯，将其水平放置，截面是个圆，是弧AB的中点，2CD=cm，杯内水面宽A．6cm4．如图，CD是圆O长为（）A．33A ．45︒6．如图，O 的半径是A ．27．如图是一段圆弧 AB 点．若63,AB CD =A ．6πB ．4π8．如图，在O 中，半径23r =，AB 过点C 作CD OC ⊥交O 于点D ，则A ．4B的直径，11．如图，AB是O==，则CD5,3AB BC的弦，半径12．如图，AB是O中，直径13．如图，在O一点，连AE，过点C作14．如图，在圆O中，弦的直径15．如图．O为．的外接圆，16．如图，⊙O是ABC∠的度数为于点D，连接BD，则D三、解答题17．如图，AB为半圆O点D，若4，==AB AC(1)DE的长．(2)阴影部分的面积．18．如图，AB 为O 的直径，CD 为弦，CD AB ⊥于点E ，连接DO 并延长交O 于点F ，连接AF 交CD 于点G ，CG AG =，连接AC ．(1)求证：AC DF ∥；(2)若12AB =，求AC 和GD 的长．19．如图，在以O 为圆心的两个同心圆中，大圆的弦AB 交小圆于C D 、两点，若16cm 6cm AB CD ==，．(1)求AC 的长；(2)若大圆半径为10cm ，求小圆的半径．∠；(1)连接AD，求OAD(2)点F在 BC上，CDF∠=参考答案：∵OA OB =，C 为弦AB 中点，∴OC AB ⊥，4AC =，∴OE 平分 AB ，∵D 为 AB 的中点，∴点,D E 重合，∴,,O C D 三点共线，设圆的半径为r ，则：2OC OD CD r =-=-，由勾股定理，得：222OA AC OC =+，∴()22242r r =+-，解得：=5r ；故选B ．4．C【分析】本题考查了勾股定理的应用，垂径定理，熟练掌握和运用垂径定理是解决本题的关键．连接OC ，首先根据题意可求得63OC OE ==，，根据勾股定理即可求得CE 的长，再根据垂径定理即可求得CD 的长．【详解】解：如图，连接OC ，∵123AB BE ==，，∴63OB OC OE ===，，∵AB CD ⊥，∵50BOC ∠=︒，OC ∴OCB OBC ∠=∠=∵OC AB ⊥，∴AD BD =，故选：B．7．B【分析】本题考查的是垂径定理，勾股定理及弧长的计算公式，先根据垂径定理求出=长，由题意得OD OAOE AB ⊥ ，132AE BE AB ∴===，22OE OA AE ∴=-=在Rt COE △中，∵AB 是O 的直径，∴152OD OB AB ===∵,6CD AB CD ⊥=，∴13,2DE CD DEO ==∠∴22OE OD DE =-=∵5AB =，∴25OE =，∵DE 切O 于点E ，∴OE DE ⊥，∴90OED ∠=︒，∵1OA =，120AOB ∠=︒，∴30A B ==︒∠∠，AC BC =∴1122OC OA ==，AC =∵直径CD 长为4，∴1422OD =⨯=，∵1OG =，∴1DG OD OG =-=，∴AB 垂直平分OD ，OH 经过圆心O ，12AH BH AB ∴===∴2AO AH OH =+故答案为：5．在Rt AOD 中，12OD OA ==，，1cos 2AOD \Ð=，60AOD ∴=︒∠，OE AC ⊥ ，由垂径定理知，点E是CD的中点，也是AB是 的直径，CD⊥AB∴垂直平分CD，M是OA的中点，∴1122OM OA OD==，OA CD于点M，⊥∴点M是CD的中点，∴垂直平分CD，ABNC ND∴=，Q，∠=︒45CDFNCD NDC∴∠=∠=︒，45∴∠=︒，90CND。

九年级圆的垂径定理与圆心角圆周角的大题精选(含答案)九年级圆的垂径定理与圆心角圆周角的大题精选（含答案）圆的性质大题一、解答题（共25小题）1.如图，⊙O中，弦CD与直径AB交于点H。

1）当∠B+∠D=90°时，求证：H是CD的中点。

证明：∠B+∠D=90°，∠B=90°-∠D，又∠ADC=90°（直径所对的角为直角），所以∠___∠B，因此三角形ADC与三角形BDC相似，所以BD/DC=DC/BD，即BD²=DC²，所以BH=HD，即H为CD的中点。

2）若H为CD的中点，且CD=2，BD=√3，求AB的长。

连接OH，由勾股定理得OH=√3，又因为H为CD的中点，所以CH=1，从而CO=√3+1，又AO=CO，所以AB=2AO=2(√3+1)。

2.如图，∠BAC=60°，AD平分∠___于点D，连接OB、OC、BD、CD。

1）求证：四边形OBDC是菱形。

证明：由角平分线定理得∠OAD=∠OBD，又∠OAB=∠OBA=30°，所以∠OBD=30°，又∠OCD=∠OAD=30°，所以∠___∠OCD，所以BD=CD，又∠___∠OCD=30°，所以∠___∠OBC，所以三角形OBD与三角形OBC全等，所以OB=OC，又∠___∠OCD=30°，所以OB=BC，所以四边形OBDC是菱形。

2）当∠BAC为多少度时，四边形OBDC是正方形？当∠BAC=90°时，∠___∠OCD=45°，所以BD=CD，又∠___∠OCD=45°，所以OB=BC，所以四边形OBDC是正方形。

3.如图，CD是⊙O的直径，∠EOD=84°，AE交⊙O于点B，且AB=OB，求∠A的度数。

由圆心角的性质得∠ACB=2∠A，又∠ACB=90°，所以∠A=45°，所以∠EAB=∠OAB-∠OAE=45°-42°=3°，又∠___∠OAB=45°，所以∠DBA=∠OBD-∠OBA=45°-3°=42°，所以∠C=180°-∠A-∠B=180°-45°-42°=93°。

圆的垂径定理习题一.选择题1．如图1，⊙O的直径为10，圆心O到弦AB的距离OM的长为3，那么弦AB的长是（）A．4 B．6 C．7 D．8 2．如图，⊙O的半径为5，弦AB的长为8，M是弦AB上的一个动点，则线段OM长的最小值为（）A．2 B．3 C．4 D．53.过⊙0内一点M的最长弦为10cm，最短弦长为8cm，则OM的长为（）4．如图，小明同学设计了一个测量圆直径的工具，标有刻度的尺子OA、OB在O点钉在一起，并使它们保持垂直，在测直径时，把O点靠在圆周上，读得刻度OE=8个单位，OF=6个单位，则圆的直径为（）A．12个单位B．10个单位C．1个单位D．15个单位5．如图，O⊙的直径AB垂直弦CD于P，且P是半径OB的中点，6cmCD，则直径AB的长是（）6．下列命题中，正确的是（）A．平分一条直径的弦必垂直于这条直径B．平分一条弧的直线垂直于这条弧所对的弦C．弦的垂线必经过这条弦所在圆的圆心D．在一个圆内平分一条弧和它所对的弦的直线必经过这个圆的圆心7．如图，某公园的一座石拱桥是圆弧形（劣弧），其跨度为24米，拱的半径为13米，则拱高为( )8．⊙O的半径为5cm，弦AB//CD，且AB=8cm,CD=6cm,则AB与CD之间的距离为( )A． 1 cm B．7cm C． 3 cm或4 cm D．1cm 或7cm 9．已知等腰△ABC的三个顶点都在半径为5的⊙O上，如果底边BC的长为8，那么BC边上的高为( ) A．2 B．8 C．2或8 D．3二、填空题1．已知AB是⊙O的弦，AB＝8cm，OC⊥AB与C，OC=3cm，则⊙O的半径为cm 2．在直径为10cm的圆中，弦AB的长为8cm，则它的弦心距为cm3．在半径为10的圆中有一条长为16的弦，那么这条弦的弦心距等于4. 已知AB是⊙O的弦，AB＝8cm，OC⊥AB与C，OC=3cm，则⊙O的半径为cm 5．如图，⊙O的直径AB垂直于弦CD，垂足为E，若∠COD＝120°，OE＝3厘米，则CD＝厘米6．半径为6cm的圆中，垂直平分半径OA的弦长为cm7．过⊙O内一点M的最长的弦长为6cm，最短的弦长为4cm，则OM的长等于 cm8．已知AB是⊙O的直径，弦CD⊥AB，E为垂足，CD=8，OE=1，则AB=9．如图，AB为⊙O的弦，⊙O的半径为5，OC⊥AB于点D，交⊙O于点C，且CD＝l，则弦AB的长是10．某蔬菜基地的圆弧形蔬菜大棚的剖面如图所示，已知AB＝16m，半径OA＝10m，则中间柱CD 的高度为m11. 如图，在直角坐标系中，以点P为圆心的圆弧与轴交于A、B两点，已知P(4，2) 和A(2，0)，则点B的坐标是12．如图，AB是⊙O的直径，OD⊥AC于点D，BC=6cm，则OD= cm13．如图，矩形ABCD与圆心在AB上的圆O交于点G、B、F、E，GB=10，EF=8，那么AD=14．如图，⊙O的半径是5cm，P是⊙O外一点,PO=8cm，∠P=30º,则AB= cm15．⊙O的半径为13 cm，弦AB∥CD，AB＝24cm，CD＝10cm，那么AB和CD的距离是Cm16．已知AB是圆O的弦，半径OC垂直AB，交AB于D，若AB=8，CD=2，则圆的半径为17．一个圆弧形门拱的拱高为1米，跨度为4米，那么这个门拱的半径为米18．在直径为10厘米的圆中,两条分别为6厘米和8厘米的平行弦之间的距离是厘米19. 如图，是一个隧道的截面，如果路面AB宽为8米，净高CD为8米，那么这个隧道所在圆的半径OA是___________米20．如图，AB为半圆直径，O 为圆心，C为半圆上一点，E是弧AC的中点，OE交弦AC于点D。

垂径定理专项练习60题（有答案）1．如图，已知⊙O的直径AB=6，且AB⊥弦CD于点E，若CD=2，求BE的长．2．已知：如图，⊙O的直径PQ分别交弦AB，CD于点M，N，AM=BM，AB∥CD．求证：DN=CN．3．如图，AB为⊙O的弦，C、D分别是OA、OB延长线上的点，且CD∥AB，CD交⊙O于点E、F，若OA=3，AC=2．（1）求OD的长；（2）若，求弦EF的长．4．如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交弧BC于D．（1）请写出四个正确的结论；（2）若BC=6，ED=2，求⊙O的半径．5．如图，⊙O的弦AB=8，M是AB的中点，且OM=3，求⊙O的半径．6．已知：如图，AB是⊙O的直径，CD是⊙O的弦，且AB⊥CD，垂足为E，连接OC，OC=5，CD=8，求BE的长．7．如图，过▱ABCD中的三个顶点A、B、D作⊙O，且圆心O在▱ABCD外部，AB=8，OD⊥AB于点E，AB=8的半径为5，求▱ABCD的面积．8．已知：如图，∠PAC=30°，在射线AC上顺次截取AD=2cm，DB=6cm，以DB为直径作⊙O交射线AP于E、F 两点，又OM⊥AP于M．求OM及EF的长．9．如图，已知弦CD⊥直径AB于E，CD=2，BD=，求直径AB的长．10．如图，AB，AC分别是⊙O的直径和弦，OD⊥AC于点D，连接BD、BC，AB=5，AC=4，求：BD的长．11．如图，在⊙O中，=，半径OA交BC于点D．若BC=24，AD=8，求⊙O的半径R．12．如图，已知OE是⊙O的半径，F是OE上任意一点，AB和CD为过点F的弦，且FA=FD．求证：AB=CD．13．已知：如图，AB为半圆的直径，O为圆心，C为半圆上一点，OE⊥弦AC于点D，交⊙O于点E．若AC=8cm，DE=2cm．求OD的长．14．⊙O的两条弦AB，CD相交于点E，（1）若AB=CD，且AB=8，AE=5，求DE的长；（2）若AB是⊙O的直径，AB⊥CD，且AE=2，CD=8，求⊙O的半径．15．如图，⊙O是△ABC的外接圆，AB是⊙O的直径，D为⊙O上一点，OD⊥AC，垂足为E，连接BD．（1）求证：BD平分∠ABC；16．已知：如图，点P是⊙O外的一点，PB与⊙O相交于点A、B，PD与⊙O相交于C、D，AB=CD．求证：（1）PO平分∠BPD；（2）PA=PC．17．如图，在平面直角坐标系xOy中，直径为10的⊙E交x轴于点A、B，交y轴于点C、D，且点A、B的坐标分别为（﹣4，0）、（2，0）．（1）求圆心E的坐标；（2）求点C、D的坐标．18．如图，已知AB为⊙O的直径，CD是弦，且AB⊥CD于点E．若EB=8cm，CD=24cm，求⊙O的直径．19．如图，已知⊙O的半径长为25，弦AB长为48，OC平分AB，交AB于点H，交于点C，求AC的长．20．如图，AB为⊙O的直径，CD为弦，过A、B分别作AE⊥CD、BF⊥CD，分别交直线CD于E、F．（1）求证：CE=DF；（2）若AB=20cm，CD=10cm，求AE+BF的值．21．如图所示，⊙O的直径AB和弦CD交于E，已知AE=6cm，EB=2cm，∠CEA=30°，求圆心O到CD的距离．22．如图，⊙C经过坐标原点，并与坐标轴分别交于A、D两点，点B在⊙C上，∠B=30°，点D的坐标为（0，2），求A、C两点的坐标．23．如图，凸四边形ABCD内接于⊙O，==90°，AB+CD为一偶数．求证：四边形ABCD面积为一完全平方数．24．点A、B、C在⊙O上，且AB=OA，OP⊥BC于P，DB⊥AB交OP于D．（1）找出图中等于30°的角；（2）求证：OA2=AC•．OD．25．如图，AB为⊙O的弦，过点O作OD⊥AB于点E，交⊙O于点D，过点D作CD∥AB，连接OB并延长交CD于点C，已知⊙O的半径为10，OE=6．求：（1）弦AB的长；（2）CD的长．26．如图，⊙O直径CD⊥AB于E，AF⊥BD于F，交CD的延长线于H，连AC．（1）求证：AC=AH；（2）若AB=，OH=5，求⊙O的半径．27．已知：如图⊙O的半径为5，CD为直径，AB为弦，CD⊥AB于M，若AB=6，求DM的长．28．已知：如图，点C在⊙O的弦AB上，且∠BOC=90°，BO=8，CO=6，求线段BC、线段AC的长．29．等腰△ABC中，AB=AC，高AD交对边BC于D，P为AD上任意一点．以P为圆心过B、C两点的圆交直线AB、AC于G、F两点，证明：BG=CF．30．如图所示，已知⊙O的直径为4cm，M是弧的中点，从M作弦MN，且MN=cm，MN交AB于点P，求∠APM的度数．31．已知：⊙O的半径为5cm，CD为直径，AB为弦，CD⊥AB于M，若AB=6cm，求CM的长．32．在⊙O中，弦AB=8cm，P为弦AB上一点，且AP=2cm，则经过点P的最短弦长为多少？33．已知AB是圆O的直径，弦CD垂直AB于E，BE=4cm，CD=16cm，求圆O的半径．34．半径为5cm的⊙O中，两条平行弦的长度分别为6cm和8cm，则这两条弦的距离为多少？35．如图，AB是⊙O的直径，CB是弦，OD⊥CB于E，交于D，连接AC①请写出两个不同类型的正确结论．②若CB=16，ED=4，求⊙O的半径．36．如图，在⊙O中，弦MN=12，半径OA⊥MN，垂足为B，AB=3，求OA的长．37．已知：如图，AB是⊙O的弦，半径OC、OD分别交AB于点E、F，且AE=BF．求证：OE=OF．38．已知：⊙O的直径AB和弦CD，且AB⊥CD于E，F为DC延长线上一点，连接AF交⊙O于M．求证：∠AMD=∠FMC．39．如图，⊙O半径为6厘米，弦AB与半径OA的夹角为30°．求：弦AB的长．40．如图，⊙O中，弦PQ=PR，M、N分别是PQ和PR的中点，求证：∠OMN=∠ONM．41．如图所示，⊙O的直径AB=16cm，P是OB的中点，∠APC=30°，求CD的长．42．⊙O的半径为10厘米，圆内两条平行弦AB、CD的长为12厘米，16厘米，求两弦之间的距离．43．如图，⊙O中，弦AB的长为8厘米，∠AOB的度数是120°，求⊙O的直径．44．如图，⊙O中，AB⊥CD，直径AB的长是12厘米，E是OB的中点，求CD的长．45．如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交于D．请写出五个不同类型的正确结论．46．如图，AB是⊙O的直径，BC=8，E为的中点，OE交BC于D，连接AD，DE=2．（1）求⊙O的半径；（2）求线段AD的长．47．如图，在⊙O中，直径AB⊥弦CD，垂足为P，OB=5，PB=2，求CD的长．48．在三角形ABC中，∠ACB=90°，AC=6，BC=8，以C为圆心，以AC为半径作圆C，交AB于点D，求BD的长．49．如图所示，⊙O的直径AB和弦CD交于E，已知AE=6cm，EB=2cm，∠CEA=30°，求CD．50．如图，AB是⊙O 的一条直径，CD是⊙O的一条弦，交AB与点P，=．若AP=1，CD=4，求⊙O的直径．51．已知，⊙O的半径为1，弦AB=，若点C在⊙O上，且AC=，求∠BAC的度数．（要求画出图形）52．如图所示，在⊙O中，CD是直径，AB是弦，AB⊥CD于M，CD=15cm，OM：OC=3：5，求弦AB的长．53．已知，如图，圆C中，∠ACB=90°，AC=3cm，BC=4cm．（1）求AB长度．（2）求AD长度．54．如图：AB是⊙O的直径，BC是弦，D是弧BC的中点，OD交BC于点E，且BC=8，ED=2．①求⊙O的半径；55．如图，⊙O的弦AB⊥CD于E，OF⊥CD于F，且OF=2，OE=4，OA=．（1）求AB的长；（2）求BE的长．56．如图，AB是⊙O的弦，半径OA=20cm，∠AOB=120°，求（1）弦AB的长；（2）△AOB的面积．57．如图，AD为△ABC外接圆的直径，AD⊥BC，垂足为点F，连接BD，CD．（1）求证：BD=CD；（2）若∠ABC的平分线交AD于点E，求证：CD=DE．58．如图，AB是⊙O的直径，弦CD⊥AB，垂足为E，如果AB=20，CD=16，求线段OE的长．59．如图，梯形ABCD中，AD∥BC，∠C=90°，以AB为直径作⊙O交CD于点E、F，DF=CE，若AB=10，EF=8．求A、B到直线CD的距离之和．60．如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交弧BC于D．（1）请写出四个不同类型的正确结论；（2）若BC=，∠CBD=30°，求⊙O的半径．参考答案：1．连接OC，∵直径AB⊥弦CD于点E，CD=2，∴CE=ED=，∵在Rt△OEC中，∠OEC=90°，CE=，OC=3，∴OE=2，∴BE=1．2．∵PQ是直径，AM=BM，∴PQ⊥AB于M．又∵AB∥CD，∴PQ⊥CD于N．∴DN=CN．3．（1）∵OA=3，AC=2，∴OC=5，∵CD∥AB，∴，∵OB=OA=3，∴，（2）过点O作OG⊥CD于G，连接OE，∴OE=OA=3，∵，∴，∴，在Rt△OEG中，∴，∵OG⊥EF，EF是弦，∴EF=2EG=4．4．（1）正确的结论有：CE=BE；D 为的中点；OE∥AC；OE=AC；（2）∵OD⊥BC，∴E为BC的中点，又BC=6，∴BE=CE=3，设圆的半径为r，由DE=2，得到OE=r﹣2，在Rt△BOE中，OB=r，OE=r﹣2，EB=3，根据勾股定理得：r2=（r﹣2）2+32，解得：r=，则圆的半径为．5．连接OA，∵在圆O中，M为AB的中点，AB=8，∴OM⊥AB，AM=AB=4，在Rt△OAM中，OM=3，AM=4，根据勾股定理得：OA===5．6．∵AB为直径，AB⊥CD，∴CE=DE=CD=4，在Rt△COE中，OE===3，∴BE=OB﹣OE=5﹣3=2，故BE=2．7．连接OA，∴OA=OD=5．∵AB是⊙O的一条弦，OD⊥AB，AB=8∴AE=AB=4，在Rt△OEA中，由勾股定理得，OE2=OA2﹣EA2，∴OE=3，∴DE=2，∴S平行四边形ABCD=AB•DE=8×2=168．连接OF，∵DB=6cm，∴OD=3cm，∴AO=AD+OD=2+3=5cm，∵∠PAC=30°，OM⊥AP，∴在Rt△AOM中，OM=AO=×5=cm∵OM⊥EF，∴EM=MF，∵MF==cm∴EF=cm．9．连接OC，∵CD⊥AB，∴E为CD的中点，即CE=DE=CD=，在Rt△BDE中，BD=，DE=，根据勾股定理得：EB==1，设半径OC=OB=r，则OE=OB﹣EB=r﹣1，在Rt△COE中，OC=r，CE=，OE=r﹣1，根据勾股定理得：r2=（）2+（r﹣1）2，解得：r=，则直径AB为3．10．∵OD过圆心O，OD⊥AC，AC=4，∴CD=AC=2，∵AB是⊙O的直径，∴∠C=90°，∴BC===3，在Rt△BCD中，DB===11．连接OC，∵=，AO过圆心O，∴OA⊥BC，CD=BC，∵BC=24，AD=8，∴CD=BC=12，OD=OA﹣AD=R﹣8，在Rt△ODC中，OC2=OD2+DC2，即R2=122+（R﹣8）2，解得：R=13．则圆O的半径R=13．12．连接OA，OD，作AB、CD的弦心距OM，ON，∵OA=OD，FA=FD，OF=OF，∴△AOF≌△DOF，∴∠AFO=∠DFO，∴OM=ON，∴AB=CD．13．∵OE⊥AC，AC=8cm，∴AD=AC=4．设OA=r，则OD=OA﹣DE=r﹣2，在Rt△AOD中，∴OA2=OD2+AD2，∴r2=（r﹣2）2+16解得，r=5．∴OD=3．14．（1）如图甲，当点C在AB的左侧时，∵AB=CD，∴=，∴=，∴∠B=∠C，∴CE=BE，∴DE=AE=5；如图乙，当点C在AB的右侧时，同理：DE=BE=AB﹣AE=3，（2）如图丙，若点A在CD的下方，连结OC，∵AB是⊙O的直径，AB⊥CD，∴CE=CD=4，设OC=x，则OE=x﹣2，∵AB⊥CD，∴OE2+CE2=OC2，即（x﹣2）2+42=x2，解得：x=5．如图丁，若点A在CD的上方，则AB＜2AE=4，与CD=8产生矛盾（或与上类似地计算得OE为负数）．答：⊙O的半径为5．15．（1）证明：∵OE⊥AC，∴=，∴∠ABD=∠CBD，即BD平分∠ABC；（2）解：∵OD⊥AC，∴AE=AC，∠OEA=90°，∵OE=3，OA=5，∴在Rt△AOE中，AE==4，∴AC=2AE=816．（1）过点O作OE⊥AB，OF⊥CD，垂足分别为E、F，∵AB=CD，∴OE=OF，∴PO平分∠BPD；（2）在Rt△POE与Rt△POF中，∵OP=OP，OE=OF，∴Rt△POE≌Rt△POF，∴PE=PF，∵AB=CD，OE⊥AB，OF⊥CD，E、F分别为垂足，∴AE=，CF=，∴AE=CF，∴PE﹣AE=PF﹣CF，即PA=PC．17．（1）作EF⊥x轴，交x轴于点F，连接EA，∵A、B的坐标分别为（﹣4，0）、（2，0），∴AB=6，OA=4，∴AF=3，∴OF=1，∵⊙E的直径为10，∴半径EA=5，∴EF=4，∴E的坐标是（﹣1，4）．（2）同理，作EG⊥y轴，交y轴于点G，连接EC、ED，由勾股定理CG==2，∴点C的坐标是（0，4+），点D的坐标是（0，4﹣）18．∵AB为⊙O的直径，AB⊥CD，∴CE=DE=CD=×24=12（cm），设⊙O的半径为xcm，则OC=xcm，OE=OB﹣BE=x﹣8（cm），在Rt△OCE中，OC2=OE2+CE2，∴x2=122+（x﹣8）2，解得：x=13，∴⊙O的半径为13cm，∴⊙O的直径为26cm．故答案为：2619．连接OA，∵OC平分AB，即H为AB的中点，∴OH⊥AB，在Rt△OAH中，OA=25，AH=24，根据勾股定理得：OH==7，∴HC=OC﹣OH=25﹣7=18，在Rt△AHC中，根据勾股定理得：AC==30．20．（1）证明：过点O作OG⊥CD于G，∵AE⊥EF，OG⊥EF，BF⊥EF，∴AE∥OG∥BF，（1分）∴=又∵OA=OB，∴==，∴GE=GF，（2分）∵OG过圆心O，OG⊥CD，∴CG=GD，（3分）∴EG﹣CG=GF﹣GD，即CE=DF；（4分）（2）解：连接OC，则OC=AB=10，（5分）∵OG过圆心O，OG⊥CD，∴CG=CD=5，（6分）∴OG=，（7分）∵梯形ABFE中，EG=GF，AO=OB，∴OG=（AE+BF），∴AE+EF=2OG=．（8分）21．过O作OF⊥CD于F，则OF的长是圆心O到CD的距离，∵AE=6cm，EB=2cm，∴OB=4cm，∴OE=4cm﹣2cm=2cm，∵∠OFE=90°，∠CEA=30°，∴OF=OE=1cm，即圆心O到CD的距离是1cm22．连接AC、OC，过点C分别作CM⊥OD于M，CN⊥OA 于N．∵点B在⊙C上，∠B=30°，∴∠ACO=60°．∵CA=CO，∴△CAO是等边三角形．∴CA=CO=OA，∠COA=60°．∴∠COM=30°．∵CM⊥OD，点C为圆心，点D的坐标为（0，2），∴．在Rt△OCM中，，由勾股定理得，．∴．同理可得．∴点A的坐标为．点C的坐标为．23．∵=，∴AB∥DC，ABCD为梯形．过O作MN⊥AB于M交CD于N，易知MN⊥CD于N，由垂径定理知M为AB中点，N为CD中点，连接OA，OD．∵∠AOD=90°，∴∠AOM=90°﹣∠DON=∠ODN，从而有∴∴==∵AB+CD为偶数，∴S ABCD必是完全平方数．24．（1）解：∠OBP=30°；∠ACB=30°，先根据AB=OA得到△ABO是正三角形，所以∠ABO是60°．又DB⊥AB交OP于D，所以∠OBP是30°；∠ACB 是60°圆心角对的弧所对的圆周角，所以∠ACB是30°；（2）证明：∵OP⊥BC于P，∴∠BOD=∠BOC，∴∠BAC=∠BOD，在△ABC和△ODB中，∴△ABC∽△ODB，∴，∴AB•OB=AC•OD，∵AB=OB=OA，∴OA2=AC•OD．25．（1）∵OE2+BE2=OB2∴BE=8．（2分）又∵OE⊥AB，∴AB=2BE=16．（4分）（2）∵CD∥AB，∴∠OBE=∠C．又∠BOE=∠COD，∴△BOE∽△COD．（6分）∴=．∴CD=．26．（1）∵AF⊥BD，CD⊥AB，∴∠H=∠B，又∵∠C=∠B，∴∠C=∠H，∴AC=AH；（2）连接AO，∵AC=AH，CD⊥AB，∴AE=，CE=EH，设ED=x，OE=y，∴OA=OC=OD=x+y，∴EH=CE=x+2y，∴OH=x+3y，∴x+3y=5，又∵OA2=AE2+OE2，∴，∴x=2，y=1，∴⊙O的半径x+y=3．27．连接OA，∵CD为直径，AB为弦，AB⊥CD，AB=6，∴根据垂径定理可知AM=AB=3，在Rt△OAM中，OA=5，OM==4，∴DM=OD+OM=9．28．∵∠BOC=90°，BO=8，CO=6，∴．（2分）作OH⊥AB于H，则OH=，（3分）∴．∵OH⊥AB，∴AB=2BH=12.8，（5分）∴AC=12.8﹣10=2.8．（6分）29．连接GF交AD于H．则∠AGF=∠C，∠AFG=∠B，∵AB=AC，∴∠B=∠C，∴∠AGF=∠AFG，∴AG=AF，∴BG=CF．30．连接OM交AB于点E，∵M是弧的中点，∴OM⊥AB于E．（2分）过点O作OF⊥MN于F，由垂径定理得：，（4分）在Rt△OFM中，OM=2，，∴cos∠OMF=，（6分）∴∠OMF=30°，∴∠APM=60°．（8分）31．连接OB，∵CD⊥AB，AB=6cm，∴由垂径定理得：AM=BM=AB=3cm，∠bmo=90°，在Rt△BOM中，由勾股定理得：OM===4（cm），则CM=OC﹣OM=5cm﹣4cm=1cm．32．如图，设过P点最短的弦为CD，则OP⊥CD，由垂径定理可知CP=PD，∵AB=8，AP=2，∴PB=8﹣2=6，由相交弦定理可知，CP•PD=AP•PB，即CP2=2×6，解得CP=2，∴CD=2CP=4．答：经过点P的最短弦长为4cm．33．∵AB是圆O的直径，弦CD垂直AB于E，CD=16cm，∴CE=CD=×16=8cm，连接OC，设OC=r，则OE=OB﹣BE=r﹣4，在Rt△OCE中，OC2=OE2+CE2，即r2=（r﹣4）2+82，解得r=10cm．答：⊙O的半径是10cm．34．分两种情况讨论：两弦在圆心同侧或两弦在圆心两侧，过点O作OE⊥AB于点E，作OF⊥CD于点F，连接OA，OC，∴AE=AB=4（cm），CF=CD=3（cm），∴OE==3（cm），OF==4cm．当在同侧时，两弦之间距离为1cm，当在两侧时，两弦之间距离为7cm．35．（1）不同类型的正确结论有：①BE=CE，②=，③∠BED=90°，④∠BOD=∠A，⑤AC∥OD，⑥AC⊥BC，⑦OE2+BE2=OB2，⑧S△ABC=AC•CE等．（写出2个即可），（2）设⊙O的半径为x，则OE=x﹣4，∵OD⊥BC，∴CE=EB=BC=8；在Rt△OBE中，∵OE2+EB2=OB2，∴（x﹣4）2+82=x2，解得x=10，所以⊙O的半径是10．36．连接ON∵OA⊥MN于点B∴（2分）设ON=x，则OB=x﹣3在Rt△OBN中∵ON2=OB2+BN2∴x2=（x﹣3）2+62（4分）解得（5分）即37．连接OA，OB，∵OA=OB，∴∠A=∠B．又∵AE=BF，∴△OAE≌△OBF．∴OE=OF．38. 连接AD，∵⊙O的直径AB和弦CD，且AB⊥CD，∴弧AC=弧AD，∴∠AMD=∠ADC，∵A、M、C、D四点共圆，∴∠FMC=∠ADC（圆内接四边形的一个外角等于它的内对角），∴∠AMD=∠FMC39．作OD⊥AB于D，则AD=DB，在Rt△AOD中，∵∠DAO=30°∴OD=OA=3∵AD2=OA2﹣OD2∴AD=∴AB=2AD=．40．M、N分别是PQ和PR的中点，∴OM⊥PQ，ON⊥PR．∴∠OMP=∠ONP．∵PQ=PR，M、N分别是PQ和PR的中点，∴PM=PN．∴∠PMN=∠PNM．∴∠OMN=∠ONM．41．过O作OE⊥CD，垂足为E，连接OC，∵AB=16cm，∴OC=OB=8cm，∵P是OB的中点，∴OP=OB=4cm，∵∠APC=30°，OE⊥CD，∴OE=OP=2cm，在Rt△COE中CE===2cm，∴CD=2CE=4cm．42．过O作EF⊥AB于E点，交CD于F点，连OA、OC，∵AB∥CD，∴EF⊥CD，∴AE=BE=6cm，CF=DF=8cm，在Rt△AEO中，OA=10，OE===8，在Rt△OCF中，OF===6，如图：，当圆心O在AB与CD之间，EF=OE+OF=8+6=14（cm）；，当圆心O不在AB与CD之间，EF=OE﹣OF=8﹣6=2（cm）．所以两弦之间的距离为14cm或2cm43．如图，过O作OC⊥AB于C，∴C为AB的中点，而OA=OB，∴OC平分∠AOB，而弦AB的长为8厘米，∠AOB的度数是120°，∴∠AOC=60°，AC=4，∴在Rt△AOC中，OC=4，∴AO=8，∴⊙O的直径为16．44．如图，连接OC，∵AB⊥CD，且E是OB的中点，∴∠OCE=30°，CE=DE，而AB=12，∴OC=6，OE=3，∴CE=3，∴CD=645．∵AB是⊙O的直径，OD⊥BC于E，∴CE=BE ，=，∠ACB=90°，∴AC⊥BC，∴AC∥OD，∴△BOE∽△BAC，∵OA=OB，∴OE=AC．∴五个不同类型的正确结论为：CE=BE，=，∠ACB=90°，AC∥OD，OE=AC，△BOE∽△BAC等46．（1）∵BC=8，E 为的中点，∴OE⊥BC，BD=CD=BC=×8=4，设⊙O的半径为r，则OB=r，OD=r﹣DE=r﹣2，在Rt△OBD中，OB2=OD2+BD2，即r2=（r﹣2）2+42，解得r=5；答：⊙O的半径为5；（2）连接AC，∵AB是⊙O的直径，BC=8，AB=2OB=2×5=10，∴AC===6，在Rt△ACD中，AD===2．答：线段AD的长为247．连接OC，∵⊙O中，直径AB⊥弦CD，∴CD=2CP．在Rt△OPC中，∵PC2+PO2=OC2，且OP=OB﹣PB=5﹣2=3．∴PC===4，∴CD=2CP=848．∵在三角形ABC中，∠ACB=90°，AC=6，BC=8，∴AB===10，点C作CE⊥AB于点E，则AD=2AE，AC2=AE•AB，即62=AE×10，∴AE=3.6，∴AD=2AE=2×3.6=7.2，∴BD=AB﹣AD=10﹣7.2=2.8．49．∵AE=6cm，EB=2cm，∴OA=（6cm+2cm）÷2=4cm，∴OE=4cm﹣2cm=2cm，过点O作OF⊥CD于F，可得∠OEF=90°，即△OEF为直角三角形，∵∠CEA=30°，∴OF=OE=1cm，连接OC，根据勾股定理可得，在Rt△COF中，CD=2CF=2=2=2cm．50．连接OC，设OC=x，∵=，∴CD⊥AB，∵CD=4，∴CP=2，∵AP=1，∴OP=x﹣1，在Rt△CPO中，x2=22+（x﹣1）2，解得：x=，∴⊙O的直径为2×=5．51．分别作OD⊥AB，OE⊥AC，垂足分别是D、E．根据特殊角的三角函数值可得，∠AOE=60°，∠AOD=45°，∴∠BAO=30°，∠CAO=45°，∴∠BAC=45°+30°=75°，或∠BAC=45°﹣30°=15°．52．如图，连接OA，设OM=3x，OC=5x，则DM=2x，∵CD=15cm，∴3x+5x+2x=15，解得x=1.5cm，∴OM=3×1.5cm=4.5cm，∴AM===6cm，∴AB=12cm．53．（1）在Rt△ACB中，AC=3cm，BC=4cm，由勾股定理得：AB=5cm；（2）过C作CE⊥AD于E ，∵S△ABC=×AC×BC=×AB×CE，∴3cm×4cm=5cm×CE，∴CE=cm，在Rt△ACE中，由勾股定理得：AE==cm，∵CE⊥AD，CE过C，∴AB=2AC=cm．54．①∵OD是半径，D是弧BC的中点，∴OD垂直平分BC，∵BC=8，ED=2设半径为R，则BE=4，OE=R﹣2，∴R2=（R﹣2）2+42∴R=5②∵AB是直径∴∠C=90°，AB=10，BC=8∴AC=6作CF⊥AB于F，则∴55．（1）过点O作OG⊥AB于G，连接OA，则AG=BG=AB，∵OF⊥CD，AB⊥CD，∴∠OGE=∠OFE=∠FEG=90°，∴四边形OFEG是矩形，∴OG=EF，EG=OF，在Rt△OEF中，EF===2∴OG=2，在Rt△OAG中，AG===，∴AB=2．（2）∵由（1）得，四边形OFEG是矩形，∴EG=OF=2，∵由（1）得，BG=AG=AB=×2=，∴BE=BG﹣EG=﹣2．56．（1）过O作OC⊥AB于C，∵∠AOB=120°，OA=OB，∴∠A=∠B=30°，∴OC=OA=10cm，由勾股定理得：AC==10（cm），∴由垂径定理得：AB=2AC=20cm；（2）S△AOB=×AB×OC=×20cm×10cm=100cm257．（1）∵AD为直径，AD⊥BC，∴，∴BD=CD．（2）∵，∴∠BAD=∠CBD，∵∠ABC的平分线交AD于点E，∴∠ABE=∠CBE，∵∠DBE=∠CBE+∠CBD，∠BED=∠ABE+∠BAD，∴∠BAD+∠ABE=∠CBD+∠EBF，即∠BED=∠EBD，∴BD=DE，∴CD=DE．58．连接OD，如图所示：∵弦CD⊥AB，AB为圆O的直径，∴E为CD的中点，又CD=16，∴CE=DE=CD=8，又OD=AB=10，∵CD⊥AB，∴∠OED=90°，在Rt△ODE中，DE=8，OD=10，根据勾股定理得：OE2+DE2=OD2，∴OE==6，则OE的长度为6．59．连接OE，过点O作OG⊥EF于点G，∵点O是⊙O的圆心，EF=8，∴GE=EF=4，∵AB=10，∴OB=OC=5，∴OG===3，∵梯形ABCD中，AD∥BC，∠C=90°，∴点O是梯形ABCD的中位线，∴AD+BC=2OG=2×3=6．答：A、B到直线CD的距离之和是6．60．（1）①根据垂径定理可知，CE=BE；②根据直径所对的圆周角是直角可知，∠C=90°；③根据三角形中位线定理可知，OE=AC；④根据垂径定理可知，=．（2）∵OD⊥BC于E，BC=，∴CE=BE=4，在Rt△BED中，ED=4•tan30°=4，设半径为R，根据勾股定理得，R2=（R﹣4）2+（4）2，解得R=8．答：⊙O的半径为8。