双原子分子电子态振动跃迁F-C因子的计算

双原子分子电子态振动跃迁F-C因子的计算摘要：分子激光冷却作为当前冷分子研究的热点，受到广泛关注。

针对激光冷却分子中如何找到合适的候选分子，最为关键的问题就是要找到这些分子部的结构参数、能量光谱，从而为下一步的能级激发奠定基本依据。

本文结合F-C因子计算原理，给出了F-C因子计算的理论解释；以MgF双原子分子为例，提出一种利用Morse 精确求解薛定谔方程；通过计算，得到MgF不同振动态的F-C 因子。

通过利用这种方法，也为激光冷却实验中的光谱数据测量提供了参考。

关键词：振动跃迁；Franck - Condon 因子；振动结构强度；Morse势能函数Calculation of the F-C factor of the electronic states of the doubleatom moleculeAbstract: molecular laser cooling, as a hot spot in the research of cold molecules, has received extensive attention. In order to find a suitable candidate molecule in laser cooling, the key problem is to find the molecular structure parameters, the internal energy spectrum, which lay a fundamental basis for the next step of the excitation level. This paper combines the F-C factor calculation principle, explain the F-C factor calculation theory; secondly, the MgF diatomic molecule as an example, using a Morse exact solution of Schrodinger equation; finally through calculation, MgF dynamic different vibration factor F-C. By using this method, it also provides a reference for the measurement of spectral data in laser cooling experiments.Key words: vibrational transition; Condon - Franck factor; vibrational structure intensity; Morse potential energy function在分子结构与分子光谱理论中，有关分子光谱带系的跃迁几率、谱线相对强度等光谱参量的计算公式都包含 Franck - Condon 因子(简称 F-C 因子) , 可以说 , F- C 因子与分子光谱问题的研究直接相关. 双原子分子 F- C 因子的计算在化学物理、定量光谱学 、等离子体辐射诊断等领域中都有着极其重要的意义. 计算F- C 因子，常常需要应用各种数值计算方法来求解能量算符的本征值方程。

本文则结合F-C 原理，提出一种通过 Morse 对薛定谔方程进行求解，从而得到其振动波函数。

1、Franck-Condon 原理1925 年 Franck 在分析光解离现象，讨论分子光解离过程时，提出了一套假说。

他认为：在“冷”气体中，分子无振动地处于最低电子态（基态），原子核的运动由势函数)(1r V 决定，如果分子吸收一份量子的能量能够从基态跃迁到激发态，那么在这样的过程中，除分子电子态的能量发生变化外，无其它变化。

光的吸收仅仅使原子核的相互作用势由)(1r V 变为)(2r V （即)(2r V 代替)(1r V ），但由于新的作用势)(2r V 有不同于)(2r V 的平衡位置，分子吸收光能量后，原子将离开平衡位置开始振动。

如果max 2012)(V r V >（其中，max 2V 是)(2r V 在区域 ∞<<r r 01中的最大值），分子趋于无限大振幅振动，分子发生解离。

1926 年 Condon 发展了 Franck 的假说，将上述观点推广到分子的电子跃迁，不管是吸收还是发射过程，以及初始状态有无振动。

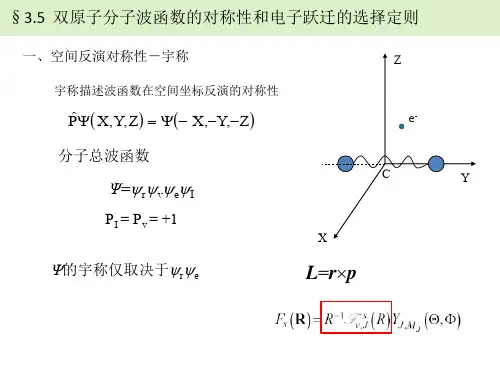
主要观点是：（1）由于原子核的质量远远大于电子的质量，相对于原子核周期性振动而言，电子跃迁被认为是发生在可以忽略的极短时间。

（2）如果跃迁时刻的原子间距是r ，动量是r p ，那么可以假设电子跃迁不改变r 和r p 值，仅仅以一个新的势函数代替原先的势函数。

（3）电子跃迁时刻的r 和r p 值，完全决定末态分子的振动运动。

两年后，Condon 又用全量子理论对上述观点进行了解释。

1.1电子谱带振动结构强度分布的经典解释Franck-Condon 原理可以解释分子电子光谱振动结构的强度分布。

由于分子中的电子跃迁发生得很快(约 10-16秒)，而核运动的周期较大(约 10-13秒)，以至跃迁前后的核间距和核运动速度几乎不变，换句话说，在两个势能曲线之间垂直向上和向下跃迁的几率最大。

也就说是在发生电子跃迁时，分子中各原子核的位置及其环境可视为几乎不变。

即垂直跃迁的几率最大。

这个思想是 J. Franck 在 1925年首先提出来的。

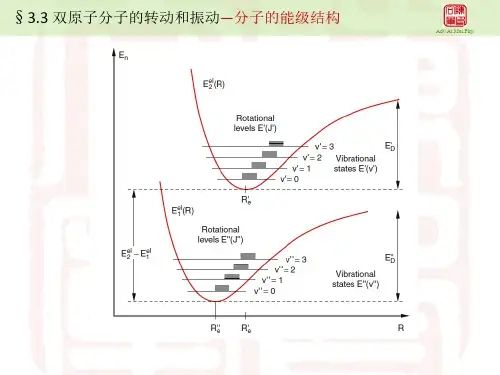
图1 对吸收光谱的解释对于吸收光谱，因为大多数分子原来都处于基态，即如图1中，势能曲线e E 的最低点 A 处（忽略零点振动）。

根据 Franck-Condon 原理，电子跃迁后的一瞬间，分子将处于 A 点正上方上势能曲线'e E 上的 B 点处。

B 点处对应的分子核间距和 A 点处的相同，并且相对速度为零（势能曲线上各点的振动动能为零）。

根据两势能曲线的最低点核间距 R 值的对比，可以解释吸收光谱振动带强度分布的不同情况。

1.2电子谱带振动结构强度分布的量子力学解释1928 年 E.Condon 运用波动力学，进一步解释了 Franck-Condon 原理。

我们知道，发射谱或吸收谱的强度与电偶极跃迁矩平方2mn d 成正比，mn d 是一个积分 ：⎰*==τψψd d n d m d mn ˆ|ˆ|（1）其中*ψ和ψ是相结合的两个态的总波函数，dˆ是电偶极算符。

在考虑振动结构强度时可不涉及转动波函数，所以总波函数近似为电子与振动波函数乘积：v e Eev φφψ==|（2）另一方面分子的电偶极矩d ˆ可以分为核的电偶极矩nd ˆ与电子的电偶极矩ed ˆ： d ˆ=n d ˆ+ed ˆ（3） 因此，根据上述的分析，我们可以将dˆ的矩阵元分为两项： ⎰⎰**==ee e v e e mn dV vdR v E d v E d φφφφ''|ˆ|''（4） 在上述公式中，'v φ和v φ表示不同电子态的振动波函数。

谱带强度与公式（4）右边的重叠积分的平方成正比，有：[]2'dR I v v φφ*∝（5）而公式（5）中的[]2'dR v v φφ*则表示为F-C 因子。

2、F-C 因子计算基于 Franck-Condon 原理，我们将振动谱带的跃迁强度的量子表达公式为：***=∝⎰''22''2')(v v e v v e v v q R dR R I ψψ（6） 式中 *v v I '表示跃迁强度，*''v v ψψ、分别是上下两个电子态的振动波函数，ν′ 和 ν″ 表示上下两个态的振动量子数，用平均值 e R 2替换电子跃迁距e R ， R 表示核间距，*''v v q 表示上下电子态的振动波函数的重叠积分的平方，即为 Franck-Condon 因子。

而根据Franck-Condon 因子的不同理论解释，可以将其对应的跃迁强度表示为：2''''''''')(⎰∝dR I j v j v v v ψψ（7）''''''j v j v ψψ、是振转波函数。

根据求解径向波函数vj vj vj vj E j R U dR d ψψψ=+-),(2122，其中J 为转动量子数， E 为本征能量，由此通过公式（7）可以得出近似波函数。

这样，在这里仅讨论无转动的情况下，要求出波函数vj ψ就得先得到势能函数),(J R U 。

通常可以用 Morse 势 )]}R - ex p[-βx p - {1D = U(R)2e e 代替势能函数，其中 e D 表示解离能，β 为 Morse 势能参数。

相较于Rees -Klein -Rydberg 法(RKR)或者是DPR 方法计算 F-C ，在近平衡状态下，用 Morse 势计算较为方便，而且与实验所测得值也比较吻合。

采用 Morse 可以精确求解薛定谔方程，获得振动波函数和能量。

图 2是 MgF 分子的电子态基态的 Morse 势函数图。

采用 Morse 势近似可得出当e R =R 时势能取得最小值，以及在核间距取值较大时的解离能e D ，这个和实际势能函数较为类似，但是在 R = 0 处，U 趋向于无穷大，这个在物理上是不成立的，而对于核间距值为零的势能函数是没有实际意义的。

图 2 MgF 电子态基态的 Morse 势函数要求解出上述的径向方程，可以将它改写成'ψ'+0=∂Ω∂ψ,其中''ψ表示为ψ的3阶导数，2B(R)ψ21 =ψ)Ω(R,，U)-2(E =B(R)。

若将 R 看成是类似于时间的变量，那么 ψ(R)和 ψ)Ω(R,就可以看成是广义坐标和势函数。

因此，可以将 (R) 'ψ' (R) ψ' 、分别看成是广义速度和广义加速度。

从而我们可以将方程 0 = ψΩ + 'ψ' ∂∂直接理解为某粒子在复空间中运动的牛顿方程。

假定 Lagrange 方程 B(R)ψ21 - ψ'2 1 = Ω - T =R), ψ'L(ψ( 22是关于'ψ的二次函数，函数 Ω、 T 分别等于 B(R)ψ21 ψ'2 122、，这样将R), ψ'L(ψ( 进行 Legendre 变换，从而可以得：),',('),,(R L R H ψψϕψϕψ-=（8）0)],',('['=-∂∂R L ψψϕψψ（9） 同时公式（9）可以得到：'''ψψϕ=∂∂=L (10) 将上述的公式ϕ代入到公式（8）当中，从而可以得到其哈密顿方程：22)(2121),,(ψϕϕψR B R H +=(11) 那么可以得到与(7)式相等价的哈密顿正则方程为：⎪⎩⎪⎨⎧=∂∂=-=ϕϕψψϕH R B ')('(12)根据哈密顿正则方程的空间演化可知，只需（12）式在1R 处的值，就可解得在2R 处的值，它们之间的演化关系为：⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡)()()()(212121R R g R R R R H ψϕψϕ(13)其中，)d 01)(0exp(1221R R B g R R R R H ⎰⎥⎦⎤⎢⎣⎡-= 可以看出（12）式具有 Symplectic 结构，那么可以考虑用 Symplectic 变换 对(13)式薛定谔方程进行求数值解。