虚数物理概念在前沿问题中的神秘作用 老教授的PPT
- 格式:ppt
- 大小:494.00 KB
- 文档页数:50




基础研究的重大突破,虚数(i²=基础研究的重大突破,虚数(i²=-1)不“虚”,而具有现实上的重大意义。
这可是人类的首次发现,该项研究由中科院院士、中科大副校长潘建伟领衔的团队完成。
虚数的定义:在数学里,将偶指数幂(i²)是负数的数定义为纯虚数,即i²=-1。
所有的虚数都是复数。
从虚数的英文名称imaginary number来看,字面意思是想象出来的数字。
关于虚数与复数的一些基本理解,如图所示。
中科大潘建伟、陆朝阳、朱晓波团队此次的研究与西班牙塞维利亚大学Cabello教授合作,利用超高精度超导量子线路实现确定性纠缠交换,以超过43个标准差的实验精度确立了复数的客观实在性,证明了实数无法完整描述标准量子力学。
长久以来,经典物理学中复数往往仅仅作为一个数学工具发挥计算作用,但量子力学的出现使复数逐渐表现出其不可排除性,量子物理是否必须使用复数是一个长期的基础性问题,实验证明复数并非主观产生而是可以用实验检测到的物理实在,因此在量子力学中必须使用复数,且复数有其相关的重大物理学意义。
该研究发表在《物理学评论快报》上,Physics网站和《自然》邀请国际专家为其撰写了相关评论文章。
该项基础研究说明虚数不虚,对基础物理可能有重大启发和意义(未来不知会以此为基础诞生多少诺奖)。
这得从薛定谔方程说起。
薛定谔方程,又称薛定谔波动方程(Schrodinger wave equation),是奥地利物理学家薛定谔提出的量子力学中的一个基本方程,也是量子力学的一个基本假定,是描述量子力学系统的核心方程。
它是将物质波的概念和波动方程相结合建立的二阶偏微分方程,可描述微观粒子的运动,每个微观系统都有一个相应的薛定谔方程式,通过解方程可得到波函数的具体形式以及对应的能量,从而了解微观系统的性质。
这个方程里的函数叫波函数(如图),可以理解为一种概率密度。
方程中的虚数i一般认为是没有物理意义的,但在量子力学中,引入虚数i,是个数学技巧,把它当做工具来用,而在物理测量上实验测得的物理量按照以往的理解,都应该是一个实数,在计算的过程中,只要给出的是个可被实验仪器测到的物理量,比如质量、能量、电荷量、波长等等,都必须是个实数,如果算出来的结果是个虚数,以前认为肯定是算错了。

杨振宁先生普通物理课:虚数在物理学中的应用
最近在看杨振宁先生的普通物理课
其中他就有说到过虚数在物理学中的应用。
他认为在20世纪之前,虚数从来没有真正进入过物理学中(或许是指其是否有不可替代的作用或者物理意义)
纵然说虚数在物理中的应用早就有之也是有一定道理的。
但是我认为杨老说的或许也是有他的道理:在某些地方其实并不是非用复数不可,比如波,其实其实可以不引入复数的概念;再比如留数定理,留数定理的确有利于计算,但左看右看都更像数学工具,在20世纪之前不具备太强的物理意义。
(虽然说我觉得数学应该称之为物理的语言更加妥当,但是这里的诸如留数定理这样的数学的确更加接近于工具,而其中触及的对物理的表达或许较少)当然之后不一样的了,留数定理之后会有实际的物理意义。
而这些在二十世纪之前就已经被用于物理上。
直到二十世纪来临,量子革命,薛定谔的那个著名的薛定谔方程让虚数第一次真正进入了物理学,因为无论薛定谔做什么操作,这个虚数单位是消不掉的,而且它有明确的物理指向——某种波。
在那一刻,物理才有了非复数不可的必要性。
以上杨先生的观点,不可谓不精妙,与我所想,不谋而合。
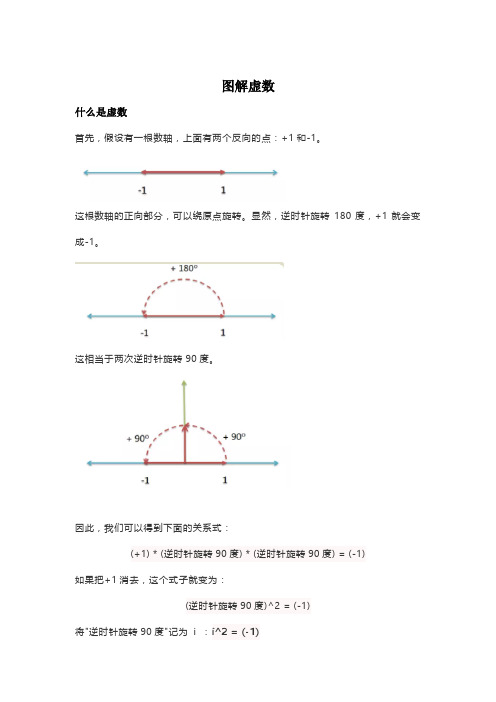
图解虚数什么是虚数首先,假设有一根数轴,上面有两个反向的点:+1和-1。
这根数轴的正向部分,可以绕原点旋转。
显然,逆时针旋转180度,+1就会变成-1。
这相当于两次逆时针旋转90度。
因此,我们可以得到下面的关系式:(+1) * (逆时针旋转90度) * (逆时针旋转90度) = (-1)如果把+1消去,这个式子就变为:(逆时针旋转90度)^2 = (-1)将"逆时针旋转90度"记为i :i^2 = (-1)这个式子很眼熟,它就是虚数的定义公式。
所以,我们可以知道,虚数i 就是逆时针旋转90度,i 不是一个数,而是一个旋转量。
复数的定义既然i 表示旋转量,我们就可以用i ,表示任何实数的旋转状态。
将实数轴看作横轴,虚数轴看作纵轴,就构成了一个二维平面。
旋转到某一个角度的任何正实数,必然唯一对应这个平面中的某个点。
只要确定横坐标和纵坐标,比如( 1 , i ),就可以确定某个实数的旋转量(45度)。
数学家用一种特殊的表示方法,表示这个二维坐标:用+ 号把横坐标和纵坐标连接起来。
比如,把( 1 , i ) 表示成 1 + i 。
这种表示方法就叫做复数(complex number),其中 1 称为实数部,i 称为虚数部。
为什么要把二维坐标表示成这样呢,下一节告诉你原因。
虚数的作用:加法虚数的引入,大大方便了涉及到旋转的计算。
比如,物理学需要计算"力的合成"。
假定一个力是 3 + i ,另一个力是 1 + 3i ,请问它们的合成力是多少?根据"平行四边形法则",你马上得到,合成力就是 ( 3 + i ) + ( 1 + 3i ) = ( 4 + 4i )。
这就是虚数加法的物理意义。
虚数的作用:乘法如果涉及到旋转角度的改变,处理起来更方便。
比如,一条船的航向是 3 + 4i 。
如果该船的航向,逆时针增加45度,请问新航向是多少?45度的航向就是 1 + i 。
虚数知识点课件什么是虚数?在数学中,虚数是指不带有数字部分的数,以字母“i” 来表示。
虚数是一个特殊类型的复数,它的平方值为负数。
与虚数相对的是实数,它们是我们日常生活中常见的数字。
虚数的定义和表示虚数定义为一个实数乘以虚数单位“i”。
虚数单位“i” 定义为满足等式 i^2 = -1的数。
这样的定义使得虚数在数学运算中起到了重要的作用。
虚数可以用 a + bi 的形式表示,其中“a” 为实部,“b” 为虚部。
例如,复数 3 +2i 中,实部为 3,虚部为 2i。
虚数的性质和运算1.虚数单位的平方为 -1,即 i^2 = -1。
2.虚数可以进行加法、减法、乘法和除法运算。
3.虚数的乘法满足交换律和结合律。
4.虚数与实数可以进行运算,结果仍为复数。
虚数的应用虚数在数学和物理中有广泛的应用。
以下是一些常见的应用领域:1.电路分析:虚数常用于描述交流电路中的电压和电流。
2.量子力学:虚数常用于描述量子力学中的波函数。
3.控制系统:虚数在控制系统中用于描述系统的稳定性和频率响应。
4.信号处理:虚数在信号处理中用于频域分析和滤波。
总结虚数是数学中的重要概念,它是复数中的一种特殊形式。
虚数由实数乘以虚数单位“i” 得到,其中“i” 是满足 i^2 = -1 的数。
虚数具有一些特殊的性质,可以进行各种运算。
虚数在电路分析、量子力学、控制系统和信号处理等领域有广泛的应用。
希望这份虚数知识点课件能够帮助大家更深入地理解虚数的概念和应用。
如果有任何问题,欢迎讨论和交流!。
物理里面虚数的应用
虚数,在物理学中扮演着重要的角色。
它们虽然在数学中没有物理意义,但在物理问题的求解中起到了关键作用。
本文将介绍虚数在物理领域的应用,并探讨其背后的原理。
虚数在电路分析中起到了重要作用。
在交流电路中,电流和电压经常呈正弦波形式变化。
而虚数可以方便地描述这种周期性变化。
例如,交流电的电压可以用复数表示,实数部分表示振幅,虚数部分表示相位。
通过对复数进行运算,可以方便地分析电路的特性,如电流、功率和阻抗等。
虚数在波动理论中也得到了广泛应用。
例如,在光学中,光的传播可以用电磁场的波动来描述。
而电磁场的振幅和相位也可以用复数来表示。
通过对复数进行运算,可以方便地分析光的干涉、衍射和偏振等现象。
虚数的引入使得光学问题的求解更加简洁和优雅。
虚数还在量子力学中扮演着重要角色。
量子力学是描述微观粒子行为的理论。
在量子力学中,波函数用来描述粒子的状态。
而波函数也可以用复数来表示,实数部分表示粒子的位置概率分布,虚数部分表示相位。
通过对波函数进行运算,可以求解粒子的能级、波包的传播和粒子的碰撞等问题。
虚数在物理学中的应用十分广泛。
它们为物理学家提供了一种便捷的数学工具,用于描述和分析复杂的物理现象。
尽管虚数在数学中
没有实际意义,但它们在物理学中的应用却是实实在在的。
通过虚数的引入,我们能够更好地理解和解决物理问题,推动科学的发展和进步。