山东建筑大学05-09年概率统计试题及答案
- 格式:doc
- 大小:2.29 MB
- 文档页数:45


山东建筑大学历年概率论试题汇总···········································································································装 订线··································································································山东建筑大学试卷 共 3 页 第 1 页2009至2010第 1 学期 课程名称 概率论与数理统计 试卷 (A ) 专业: 理工科各专业考试性质: 闭卷 考试时间 120 分钟 题号 一 二 三 总分 分数一、 填空题(每题3分,共24分)1、 掷两颗骰子,已知两颗骰子的点数之和为6,则其中有一颗为1点的概率为______.2、 若()0.4P A =,7.0)(=⋃B A P ,A 和B 独立,则()P B = 。
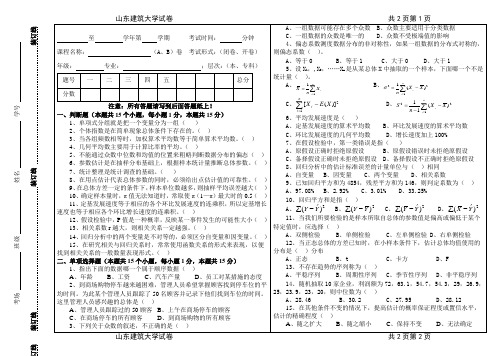



概率统计试题山东建筑大学《概率论与数理统计》近年试题及参考答案xx年1月山东建筑大学《概率论与数理统计》近年试题及参考答案05-06-2《概率论与数理统计》试题A本试题中可能用到的标准正态分布N?0,1?的分布函数??x?的部分值:x ??x? 一、填空题 1、掷两颗骰子,已知两颗骰子的点数之和为6,则其中有一颗为1点的概率为________. 2、已知随机变量X服从参数为2的泊松分布,且随机变量Z?2X?2,则E?Z?? ____________.3、设A、B是随机事件,P?A??,P?A?B??,则P?AB??4、设总体X~B?1,p?,?X1,X2,?,Xn?是从总体X中抽取的一_____________________.个样本,则参数p的矩估计量为p5、设总体X~N(0,5),X1,X2,X3,X4,X5是总体的一个样本,则12222(X12?X2?X3?X4?X5)服从分布。
5二、袋中有4个白球,7个黑球,从中不放回地取球,每次取一个球.求第二次取出白球的概率. 三、对两台仪器进行独立测试,已知第一台仪器发生故障的概率为p1,第二台仪器发生故障的概率为p2.令X表示测试中发生故障的仪器数,求E?X?四、一房间有3扇同样大小的窗户,其中只有一扇是打开的.有一只鸟在房子里飞来飞去,它只能从开着的窗子飞出去.假定这只鸟是没有记忆的,且鸟飞向各个窗子是随机的.若令X表示鸟为了飞出房间试飞的次数.求⑴ X的概率函数.⑵这只鸟最多试飞3次就飞出房间的概率.⑶若有一只鸟飞进该房间5次,求有4次它最多试飞了3次就飞出房间的概率。
五、1山东建筑大学《概率论与数理统计》近年试题及参考答案设随机变量X~N?0,1?,Y?X?1,试求随机变量Y的密度函数.2六、设二维随机变量?X,Y?的联合密度函数为212xyx2y1fx,y4其它?0分别求出求X与Y的边缘密度函数;判断随机变量X与Y是否相互独立?七、在总体X~N52,中随机抽取一个容量为36的样本,求 PX.八、设总体X~N??,?,?x,x,?,x?是从中抽取的一个样本21216的样本观测值,算得x?,求?的置信度为的置信区间。
概率论与数理统计作业(山东建筑大学作业纸)概率论与数理统计作业(山东建筑大学作业纸)概率论与数理统计作业4(§2.1~§2.3)一、填空题b(其中k 1,2,...)可以作为离散型随机变量的概率分布.k(k 1)12. 同时掷3枚质地均匀的硬币,则至多有1枚硬币正面向上的概率为.2-23. X~P(2),则P(X 2) 0.594 1-3e1. 常数b=时,pk二、选择题设随机变量X是离散型的,则可以成为X的分布律0 x2x3x4x5 1 x1(A) (是任意实数)(B) pp1 p0.10.30.30.2 0.2e 33ne 33n(C) P{X n} (n 1,2,.....) (D) P{X n} (n 0,1,2,...)n!n!三、计算题1.一批零件中有9个合格品与3个废品。
安装机器时从中任取1个。
如果每次取出的废品不再放回去,求在取得合格品以前已取出的废品数的概率分布。
解:设X表示取得合格品以前已取出的废品数,P3kP91则X=0,1,2,3;P(X k) k 1P12.2.解:设X表示射击次数,则X=1,2,3;P(X.k) p 1 p1 k3.20个产品中有4个次品,(1)不放回抽样,抽取6个产品,求样品中次品数的概率分布;(2)放回抽样,抽取6个产品,求样品中次品数的概率分布。
解:(1) 不放回抽样,设X表示样品中次品数,则X=0,1,2,3, 4;X~H(6,4,20)k4 kC4C16P(X k) 6C20.(1) 放回抽样,设X表示样品中次品数,则X=0,1,2,3, 4;X~B (6,0.2)k0.2 0.8 P(X k) C6k6 k.概率分布表如下概率论与数理统计作业(山东建筑大学作业纸)4. 一批产品分一,二,三级, 其中一级品是二级品的两倍, 三级品是二级品的一半, 从这批产品中随机地抽取一个检验质量, 设X表示抽出产品的级数,写出它的概率函数. 解:X=1,2,3;一、填空题~§2.7)1.设随机变量X的密度函数0 x 1 xf(x) 2 x1 x 2,则P X 1.50其它0.875 ;PX 1.50 . 2. 设随机变量X的密度函数为1k 1 2 1 x 2f x x其它0则k 2 .二、判断题1可否是连续随机变量X的分布函数,如果X的可能值充满区间:1 x2(1), ;10 1. 解:不可以. 因F limx 1 x2(2),0 .函数解:可以.110;F0 lim 1.x 1 x2x 01 x2且F(x)在,0 上单调非减,F lim1 ,x 0故令F x 1 x2可以是连续随机变量X的分布函数x 0 1三、计算题1.已知随机变量1)确定常数X只能取-1,0,1,2四个值,相应概率依次为c;__解:1, c .2c4c8c16c162)计算P(X 1|X 0);P X 1 X 0 P X 1 解:P X 1X 0PX 0PX 1 PX 1 PX 21357,,,,2c4c8c16c概率论与数理统计作业(山东建筑大学作业纸) 1=8 25.2c 8c 16c3)求X的分布函数并做出其图像x 8137 1 x 0 解:F x 200 x 137 30 1 x 2 37 1x 2 0x 1 1 x 12. 设离散型随机变量X的分布函数为F(x) 0.4 0.71 x 3,求X的分布列。
05-06-2《概率论与数理统计》试题A本试题中可能用到的标准正态分布()10,N 的分布函数()x Φ的部分值:1、掷两颗骰子,已知两颗骰子的点数之和为6,则其中有一颗为1点的概率为________.2、已知随机变量X 服从参数为2的泊松(Poisson )分布,且随机变量22-=X Z ,则()=Z E ____________.3、设A 、B 是随机事件,()7.0=A P ,()3.0=-B A P ,则()=AB P4、设总体()p B X ,1~,()n X X X ,,, 21是从总体X 中抽取的一个样本,则参数p 的矩估计量为=pˆ_____________________. 5、设总体X ~)5,0(N ,1X ,2X ,3X ,4X ,5X 是总体的一个样本,则)(512524232221X X X X X ++++服从 分布。
二、(本题满分6分)袋中有4个白球,7个黑球,从中不放回地取球,每次取一个球.求第二次取出白球的概率. 三、(本题满分8分)对两台仪器进行独立测试,已知第一台仪器发生故障的概率为1p ,第二台仪器发生故障的概率为2p .令X 表示测试中发生故障的仪器数,求()X E四、(本题满分12分)一房间有3扇同样大小的窗户,其中只有一扇是打开的.有一只鸟在房子里飞来飞去,它只能从开着的窗子飞出去.假定这只鸟是没有记忆的,且鸟飞向各个窗子是随机的.若令X 表示鸟为了飞出房间试飞的次数.求⑴ X 的概率函数.⑵ 这只鸟最多试飞3次就飞出房间的概率.⑶ 若有一只鸟飞进该房间5次,求有4次它最多试飞了3次就飞出房间的概率。
五、(本题满分10分)1设随机变量()1,0~N X ,12+=X Y ,试求随机变量Y 的密度函数.六、(本题满分12分) 设二维随机变量()Y X ,的联合密度函数为()⎪⎩⎪⎨⎧≤≤=其它,0142122y x yx y x f分别求出求X 与Y 的边缘密度函数;判断随机变量X 与Y 是否相互独立?七、(本题满分10分)在总体()23.652~,N X 中随机抽取一个容量为36的样本,求{}8.538.50≤≤X P .八、(本题满分8分)设总体()24.0~,μN X ,()1621x x x ,,, 是从中抽取的一个样本的样本观测值,算得12.10=x ,求μ的置信度为0.95的置信区间。
九、(本题满分12分) 设总体()2~σμ,N X ,其中μ是已知参数,02>σ是未知参数.()n X X X ,,, 21是从该总体中抽取的一个样本,⑴. 求未知参数2σ的极大似然估计量2ˆσ; ⑵. 判断2ˆσ是否为未知参数2σ的无偏估计.205-06-2《概率论与数理统计》试题B一、填空题(每题4分,共20分)1、袋中有红球4只,黑球3只,从中任意取出2只,这2只球的颜色不相同的概率为2、设随机变量X 服从区间()20,上的均匀分布,则.()=2XE3、已知P(A)=0.3, P(B)=0.4, P(AB)=0.2, 则=)|(A B P4、设总体X ~)1,0(N ,1X ,2X ,3X ,4X 是总体的一个样本,则24232221X XXX Y +++= 服从 分布。
5、 设21,X X 是正态总体)1,(~μN X 的样本,21^14132X X +=μ ;21^22131X X +=μ;1^3X =μ均为μ的估计量,则这些估计量中是μ的无偏估计量的是二、(本题8分)一道选择题有四个答案,其中只有一个正确,某考生知道正确答案的概率为0.5,不知道答案乱猜而猜对的概率为41,求该考生答对这道题的概率.三、(本题10分)掷2颗均匀的骰子,令:{}第一颗骰子出现4点=A ,{}和为7两颗骰子出现的点数之=B .⑴ 试求()A P ,()B P ,()AB P ;⑵ 判断随机事件A 与B 是否相互独立? 四、(本题10分)袋中有5个球,分别编号1,2,3,4,5, 从其中任取3个球,求取出的3个球中最大号码X 的概率函数、数学期望、方差与标准差. 五、(本题10分)设X 的密度函数为⎩⎨⎧<<=其他10 02)(X x xx f 求 12+=XY 的密度函数六、(本题14分) 设二维随机变量()Y X ,服从平面区域3(){}122≤+=y x y x D :,上的均匀分布.⑴. 试求二维随机变量()Y X ,的联合密度函数;⑵. 求随机变量X 及Y 各自的边缘密度函数; ⑶. 求()X E ,()Y E 及()XY E ;⑷ 判断随机变量X 与Y 是否相互独立?是否不相关? 七、(本题满分8分)设总体X 的分布律为其中10<<θn X X X ,,,21 是从中抽取的一个样本,求参数θ的矩估计量θˆ。
八.(本题满分12分) 设总体X 的密度函数为()()⎩⎨⎧≤>=+-cx c x x c x f 01θθθ.其中0>c 是已知常数,而1>θ是未知参数.()m X X X ,,,21 是从该总体中抽取的一个样本,试求参数θ的最大似然估计量.九、(本题8分)从一批零件,抽取9个零件,算得其直径的样本均值为01.20=x ,设零件直径服从),(2ομN ,且已知15.0=σ,求这批零件的直径的均值μ的置信水平为0.95的置信区间。
(已知96.1025.0=u )406-07-1《概率论与数理统计》试题A一、填空题(每题3分,共15分)1. 设A ,B 相互独立,且2.0)(,8.0)(==A P B A P ,则=)(B P __________. 2. 已知),2(~2σN X ,且3.0}42{=<<X P ,则=<}0{X P __________. 3. 设X 与Y 相互独立,且2)(=X E ,()3E Y =,()()1D X D Y ==,则=-])[(2Y X E ___4.设12,,,n X X X 是取自总体),(2σμN 的样本,则统计量2211()nii Xμσ=-∑服从__________分布.5. 设),3(~),,2(~p B Y p B X ,且95}1{=≥X P ,则=≥}1{Y P __________.二、选择题(每题3分,共15分)1. 一盒产品中有a 只正品,b 只次品,有放回地任取两次,第二次取到正品的概率为 【 】 (A)11a ab -+-;(B)(1)()(1)a a ab a b -++-;(C)a a b+;(D)2a ab ⎛⎫ ⎪+⎝⎭.2. 设随机变量X 的概率密度为()130, 其他c x p x <<⎧=⎨⎩则方差D(X)= 【 】(A) 2; (B)12; (C) 3; (D)13.3. 设A 、B 为两个互不相容的随机事件,且()0>B P ,则下列选项必然正确的是【 】()A ()()B P A P -=1;()B ()0=B A P ;()C ()1=B A P ;()D ()0=AB P .4. 设()x x f sin =是某个连续型随机变量X 的概率密度函数,则X 的取值范围是【 】()A ⎥⎦⎤⎢⎣⎡2,0π; ()B []π,0; ()C ⎥⎦⎤⎢⎣⎡-2,2ππ; ()D ⎥⎦⎤⎢⎣⎡23,ππ. 5. 设()2,~σμN X ,b aX Y-=,其中a 、b 为常数,且0≠a ,则~Y 【 】 ()A ()222,ba b a N +-σμ; ()B ()222,ba b a N -+σμ;()C ()22,σμa b a N +; ()D ()22,σμa b a N -.5三、(本题满分8分) 甲乙两人独立地对同一目标射击一次,其命中率分别为0.5和0.4,现已知目标被命中,求它是乙命中的概率. 四、(本题满分12分)设随机变量X 的密度函数为xxee A xf -+=)(,求:(1)常数A ; (2)}3ln 210{<<X P ; (3)分布函数)(x F .五、(本题满分10分)设随机变量X 的概率密度为()⎩⎨⎧<<-=其他,010),1(6x x x x f求12+=X Y 的概率密度.六、(本题满分10分)将一枚硬币连掷三次,X 表示三次中出现正面的次数,Y 表示三次中出现正面次数与出现反面次数之差的绝对值,求:(1)(X ,Y )的联合概率分布;(2){}X Y P >.七、(本题满分10分)二维随机变量(X ,Y )的概率密度为⎩⎨⎧>>=+-其他,00,0,),()2(y x Aey x f y x求:(1)系数A ;(2)X ,Y 的边缘密度函数;(3)问X ,Y 是否独立。
八、(本题满分10分)设总体X 的密度函数为⎪⎩⎪⎨⎧≤>=+1,01,),(1x x x x f βββ其中未知参数1>β,n X X X ,,,21 为取自总体X 的简单随机样本,求参数β的矩估计量和极大似然估计量. 九、(本题满分10分)设总体()2,~σμN X ,其中且μ与2σ都未知,+∞<<∞-μ,02>σ.现从总体X 中抽取容量16=n 的样本观测值()1621x x x ,,,,算出75.503161161==∑=i ix x ,()2022.61511612=-=∑=i ix x s ,试在置信水平95.01=-α下,求μ的置信区间.(已知:()7531.11505.0=t ,()7459.11605.0=t ,()1315.215025.0=t ,()1199.216025.0=t ).6 06-07-1《概率论与数理统计》试题B一、填空题(每题3分,共15分)1.设A ,B 为两随机事件,6.0)|(,5.0)(==A B P A P ,则=)(AB P ______.2.设随机变量X 的分布律为0),2,1,0(!}{>===λλ, K K a K X P K为常数,则常数a = .3. 设4)(=X D ,9)(=Y D ,5.0),(=Y X R ,则=-)(Y X D _________.4. 设1221,,,X X X 是取自总体)1,0(N 的样本,则统计量)(221221121029282221X X X X X XX Y ++++++=服从__________分布.5. 设),4(~),,2(~p B Y p B X ,且95}1{=≥X P ,则=≥}1{Y P ________.二、选择题(每题3分,共15分) 1. 设随机变量X 有密度⎩⎨⎧<<=其它10,4)(3x x x f则使概率)()(a X P a X P <=>的常数=a 【 】. (A )421(B )42 (C )321(D )4211-2. 设随机变量X 的概率密度函数为)(x f ,分布函数为)(x F ,对于任意实数x 有【 】()0()1A f x ≤≤; (B )0)(==x X P ; ()()()C P X x F x ==;0()()()x D P X x f u du ≤=⎰3. 设A 、B 是事件,且B A ⊂,则下式正确的是【 】.(A )P (AB )=P (B )(B )P (B | A )=P (B )(C ))()(A P A B P =(D ))()(A P B P ≤4. 已知),,(~a a N X 且b aX Y +=服从标准正态分布)1,0(N 则【 】成立.(A )⎩⎨⎧==11b a ;(B )⎩⎨⎧-==11b a ;(C )⎩⎨⎧-=-=11b a ;(D )⎩⎨⎧=-=11b a5. 设X Y 与为任意二个随机变量,若已知cov(,)0,X Y =则必有【 】7()()()()A D XY D X D Y =;相互独立与Y X B )(; ()()()()C E XY E X E Y =;不独立与Y X )D (三、(本题满分9分)设每张体育彩票是一个7位数,求在某次摇奖时,(1)出现7位数全不相同的概率;(2)至少有两位数字相同的概率;(3)恰好三个位置上数字相同,其余位置上数字全都不相同的概率。