高考数学 考前三个月压轴大题突破练 函数与导数二 文 新人教版

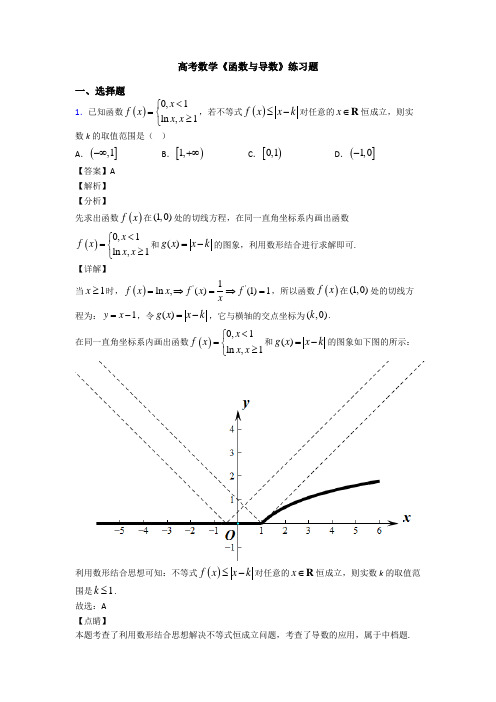
高考数学《函数与导数》练习题一、选择题1．已知函数()0,1ln ,1x f x x x <⎧=⎨≥⎩，若不等式()≤-f x x k 对任意的x ∈R 恒成立，则实数k 的取值范围是（ ） A ．(],1-∞B ．[)1,+∞C ．[)0,1D ．(]1,0-【答案】A【解析】【分析】先求出函数()f x 在(1,0)处的切线方程，在同一直角坐标系内画出函数()0,1ln ,1x f x x x <⎧=⎨≥⎩和()g x x k =-的图象，利用数形结合进行求解即可. 【详解】当1x ≥时，()''1ln ,()(1)1f x x f x f x=⇒=⇒=，所以函数()f x 在(1,0)处的切线方程为：1y x =-，令()g x x k =-，它与横轴的交点坐标为(,0)k .在同一直角坐标系内画出函数()0,1ln ,1x f x x x <⎧=⎨≥⎩和()g x x k =-的图象如下图的所示：利用数形结合思想可知：不等式()≤-f x x k 对任意的x ∈R 恒成立，则实数k 的取值范围是1k ≤.故选：A【点睛】本题考查了利用数形结合思想解决不等式恒成立问题，考查了导数的应用，属于中档题.2．给出下列说法：①“tan 1x =”是“4x π=”的充分不必要条件；②定义在[],a b 上的偶函数2()(5)f x x a x b =+++的最大值为30；③命题“0001,2x x x ∃∈+≥R ”的否定形式是“1,2x x x∀∈+>R ”. 其中错误说法的个数为（ ） A ．0B ．1C ．2D ．3 【答案】C【解析】【分析】利用充分条件与必要条件的定义判断①；利用函数奇偶性的性质以及二次函数的性质判断②；利用特称命题的否定判断③，进而可得结果.【详解】对于①，当4x π=时，一定有tan 1x =，但是当tan 1x =时，,4x k k ππ=+∈Z ，所以“tan 1x =”是“4x π=”的必要不充分条件，所以①不正确；对于②，因为()f x 为偶函数，所以5a =-.因为定义域[],a b 关于原点对称，所以5b =，所以函数2()5,[5,5]f x x x =+∈-的最大值为()()5530f f -==，所以②正确；对于③，命题“0001,2x x x ∃∈+≥R ”的否定形式是“1,2x x x∀∈+<R ”，所以③不正确； 故错误说法的个数为2.故选：C.【点睛】 本题考查了特称命题的否定、充分条件与必要条件，考查了函数奇偶性的性质，同时考查了二次函数的性质，属于中档题..3．已知3215()632f x x ax ax b =-++的两个极值点分别为()1212,x x x x ≠，且2132x x =，则函数12()()f x f x -=（ ）A ．1-B ．16C ．1D ．与b 有关【答案】B【解析】【分析】求出函数的导数，利用韦达定理得到12,,a x x 满足的方程组，解方程组可以得到12,,a x x ，从而可求()()12f x f x -．【详解】()2'56f x x ax a =-+，故125x x a +=，126x x a =，且225240a a ->， 又2132x x =，所以122,3x a x a ==，故266a a =，解得0a =（舎）或者1a =． 此时122,3x x ==， ()3215632f x x x x b =-++， 故()()()()()1215182749623326f x f x -=⨯---+-= 故选B ．【点睛】 如果()f x 在0x 处及附近可导且0x 的左右两侧导数的符号发生变化，则0x x =必为函数的极值点且()00f x =．极大值点、极小值点的判断方法如下：（1）在0x 的左侧附近，有()'0f x >，在0x 的右侧附近，有()'0f x <，则0x x =为函数的极大值点；（2）在0x 的左侧附近，有()'0f x <，在0x 的右侧附近()'0f x >，有，则0x x =为函数的极小值点．4．已知直线2y kx =-与曲线ln y x x =相切，则实数k 的值为（ ）A ．ln 2B ．1C ．1ln2-D ．1ln2+ 【答案】D【解析】由ln y x x =得'ln 1y x =+，设切点为()00,x y ，则0ln 1k x =+，000002ln y kx y x x =-⎧⎨=⎩，0002ln kx x x ∴-=，002ln k x x ∴=+，对比0ln 1k x =+，02x ∴=，ln 21k ∴=+，故选D.5．在二项式26()2a x x+的展开式中，其常数项是15.如下图所示，阴影部分是由曲线2y x =和圆22x y a +=及x 轴围成的封闭图形，则封闭图形的面积为（ ）A ．146π+ B ．146π- C ．4π D ．16【答案】B【解析】【分析】 用二项式定理得到中间项系数，解得a ，然后利用定积分求阴影部分的面积．【详解】（x 2+a 2x ）6展开式中，由通项公式可得122r 162r r r r a T C x x --+⎛⎫= ⎪⎝⎭, 令12﹣3r ＝0，可得r ＝4,即常数项为4462a C ⎛⎫ ⎪⎝⎭，可得4462a C ⎛⎫ ⎪⎝⎭＝15，解得a ＝2． 曲线y ＝x 2和圆x 2+y 2＝2的在第一象限的交点为（1，1） 所以阴影部分的面积为()1223100111-x-x |442346dx x x πππ⎛⎫=--=- ⎪⎝⎭⎰． 故选：B【点睛】本题主要考查二项式定理的应用，二项式展开式的通项公式，属于基础题．6．已知函数()lg f x x =，0a b >>，()()f a f b =，则22a b a b+-的最小值等于（ ）． A 5B ．3C ．23 D ．22【答案】D【解析】 试题分析：因为函数()lg f x x =，0a b >>，()()f a f b =所以lg lg a b =- 所以1a b=，即1ab =，0a b >> 22a b a b+-22()2()22()a b ab a b a b a b a b a b -+-+===-+---2()22a b a b ≥-⨯=-当且仅当2a b a b-=-，即a b -=时等号成立所以22a b a b+-的最下值为故答案选D考点：基本不等式．7．已知定义在R 上的函数()f x 满足(2)(2)f x f x +=-，且当2x >时，()()2()x f x f x f x ''⋅+>，若(1)1f =.则不等式1()2f x x <-的解集是（ ） A ．(2,3)B ．(,1)-∞C ．()(1,2)2,3⋃D ．()(,1)3,-∞⋃+∞ 【答案】C【解析】【分析】 令()|2|()F x x f x =-，当2x >时，则()(2)()F x x f x =-，利用导数可得当2x >时，()F x 单调递增，根据题意可得()F x 的图象关于2x =对称，不等式1()|2|f x x <-等价于|2|()1(2)x f x x -<≠，从而()(1)F x F <，利用对称性可得|2||12|x -<-，解不等式即可.【详解】当2x >时，()()2()x f x f x f x ''⋅+>，∴(2)()()0x f x f x '-+>，令()|2|()F x x f x =-.当2x >时，则()(2)()F x x f x =-，()(2)()()0F x x f x f x ''=-+>，即当2x >时，()F x 单调递增.函数()f x 满足(2)(2)f x f x +=-，所以(2)(2)F x F x +=-，即()F x 的图象关于2x =对称， 不等式1()|2|f x x <-等价于|2|()1(2)x f x x -<≠， (1)|12|(1)(1)1F f f =-==，即()(1)F x F <，所以|2||12|x -<-，解得13x <<且2x ≠，解集为(1,2)(2,3)U .故选：C【点睛】本题考查了导数在解不等式中的应用、函数的对称性的应用以及绝对值不等式的解法，属于中档题.8．已知函数()f x 是定义在R 上的偶函数,当0x ≥时,2()4f x x x =-,则不等式(2)5f x +<的解集为（ ）A ．(3,7)-B ．()4,5-C ．(7,3)-D ．()2,6- 【答案】C【解析】【分析】首先求出当0x ≥时不等式的解集，在根据偶函数的对称性求出当0x <时不等式的解集，从而求出()5f x <的解集，则525x -<+<，即可得解.【详解】当0x ≥时,2()45f x x x =-<的解为05x <≤；当0x <时，根据偶函数图像的对称性知不等式()5f x <的解为5x 0-<<， 所以不等式()5f x <的解集为{}55x x -<<，所以不等式(2)5f x +<的解集为{}{}52573x x x x -<+<=-<<.故选：C【点睛】本题考查偶函数的性质，涉及一元二次不等式，属于基础题.9．函数()xe f x x=的图象大致为（ ） A ． B ．C ．D ．【答案】B【解析】函数()xe f x x=的定义域为(,0)(0,)-∞+∞U ，排除选项A ； 当0x >时，()0f x >，且()2(1)'xx e f x x-= ，故当()0,1x ∈时，函数单调递减，当()1,x ∈+∞时，函数单调递增，排除选项C ；当0x <时，函数()0xe f x x=<，排除选项D ，选项B 正确．选B ． 点睛：函数图象的识别可从以下方面入手：(1)从函数的定义域，判断图象的左右位置；从函数的值域，判断图象的上下位置；(2)从函数的单调性，判断图象的变化趋势；(3)从函数的奇偶性，判断图象的对称性；(4)从函数的周期性，判断图象的循环往复；(5)从函数的特征点，排除不合要求的图象．10．函数()1sin cos 1sin cos 1tan 01sin cos 1sin cos 32x x x x f x x x x x x x π+-++⎛⎫=++<< ⎪+++-⎝⎭的最小值为（ ）A．13+ BCD【答案】B【解析】【分析】利用二倍角公式化简函数()f x ，求导数，利用导数求函数的最小值即可.【详解】22222sin 2sin cos 2cos 2sin cos 1sin cos 1sin cos 2222221sin cos 1sin cos 2cos 2sin cos 2sin 2sin cos 222222x x x x x x x x x x x x x x x xx x x x +++-+++=++++-++ 2sin sin cos 2cos sin cos sin cos 222222222sin cos sin 2cos sin cos 2sin sin cos 22222222x x x x x x x xx x x x x x x x x ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭=+=+=⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭， 则()21tan 0sin 32f x x x x π⎛⎫=+<< ⎪⎝⎭， 32222221sin 2cos 16cos cos 1()sin 3cos sin 3cos 3sin cos x x x x f x x x x x x x '''--+⎛⎫⎛⎫=+=-+= ⎪ ⎪⎝⎭⎝⎭.令()cos 0,1t x =∈，()3261g t t t =--+为减函数，且102g ⎛⎫= ⎪⎝⎭， 所以当03x π<<时，()11,02t g t <<<，从而()'0f x <； 当32x ππ<<时，()10,02t g t <<>，从而()'0f x >.故()min 33f x f π⎛⎫==⎪⎝⎭. 故选：A【点睛】 本题主要考查了三角函数的恒等变换，利用导数求函数的最小值，换元法，属于中档题.11．函数log (3)1a y x =-+（0a >且1a ≠）的图像恒过定点A ，若点A 在直线10mx ny +-=上，其中·0m n >，则41m n +的最小值为（） A ．16B ．24C ．50D ．25【答案】D【解析】【分析】 由题A （4，1），点A 在直线上得4m+n ＝1，用1的变换构造出可以用基本不等式求最值的形式求最值．【详解】令x ﹣3＝1，解得x ＝4，y ＝1，则函数y ＝log a （x ﹣3）+1（a ＞0且a≠1）的图象恒过定点A （4，1），∴4m+n ＝1， ∴41m n +=（41m n +）（4m+n ）＝16+14n 4m m n++=17+8＝25，当且仅当m ＝n 15=时取等号， 故则41m n+的最小值为25， 故选D ．【点睛】本题考查均值不等式，在应用过程中，学生常忽视“等号成立条件”，特别是对“一正、二定、三相等”这一原则应有很好的掌握．12．若函数f （x ）=()x 1222a x 1log x 1x 1⎧++≤⎪⎨+⎪⎩，，＞有最大值，则a 的取值范围为（ ） A ．()5,∞-+B ．[)5,∞-+C ．(),5∞--D ．(],5∞-- 【答案】B【解析】【分析】分析函数每段的单调性确定其最值，列a 的不等式即可求解.【详解】由题()x f x 22a,x 1=++≤,单调递增，故()()f x f 14a,;≤=+ ()()12f x log x 1,x 1,=+>单调递减，故()()f x f 11>=-,因为函数存在最大值，所以4a 1+≥-，解a 5≥-. 故选B.【点睛】本题考查分段函数最值，函数单调性，确定每段函数单调性及最值是关键，是基础题.13．函数()||()a f x x a R x=-∈的图象不可能是( ) A ． B ．C ．D ．【答案】C【解析】【分析】变成分段函数后分段求导，通过对a 分类讨论，得到函数的单调性，根据单调性结合四个选项可得答案.【详解】,0(),0a x x x f x a x x x ⎧->⎪⎪=⎨⎪--<⎪⎩,∴221,0()1,0a x x f x a x x ⎧+>⎪⎪=⎨⎪-+<⎩'⎪.(1)当0a =时,,0(),0x x f x x x >⎧=⎨-<⎩,图象为A; (2)当0a >时,210a x+>,∴()f x 在(0,)+∞上单调递增,令210a x-+=得x =∴当x <,210a x-+<,当0x <<时,210a x-+>,∴()f x 在(,-∞上单调递减,在(上单调递增,图象为D;(3)当0a <时,210a x -+<,∴()f x 在(,0)-∞上单调递减,令210a x+=得x =∴当x >时,210a x+>,当0x <<,210a x +<,∴()f x 在上单调递减,在)+∞上单调递增,图象为B;故选：C.【点睛】本题考查了分段函数的图像的识别，考查了分类讨论思想，考查了利用导数研究函数的单调性，属于中档题.14．三个数0.377,0.3,ln 0.3a b c ===大小的顺序是（ ）A ．a c b >>B ．a b c >>C ．b a c >>D ．c a b >> 【答案】B【解析】试题分析：根据指数函数和对数函数的单调性知：0.30771a =>=，即1a >；7000.30.31b <=<=，即01b <<；ln0.3ln10c =<=，即0c <；所以a b c >>，故正确答案为选项B ．考点：指数函数和对数函数的单调性；间接比较法．15．已知函数2()f x x m =+与函数1()ln 3g x x x =--，1,22x ⎡∈⎤⎢⎥⎣⎦的图象上恰有两对关于x 轴对称的点，则实数m 的取值范围是（ ）A ．5ln )4[2,2+ B ．5[2ln 2,ln 2)4-+ C ．5(ln 2,2ln 2)4+- D ．(]2ln2,2-【答案】A 【解析】 【分析】将问题转化为()()f x g x =-在1,22⎡⎤⎢⎥⎣⎦恰有两个不同的解，令()()()h x f x g x =+，将问题转化为()h x 在1,22⎡⎤⎢⎥⎣⎦上有两个零点的问题，利用导数可求得()h x 的单调性，进而确定区间端点值和最值，由此构造不等式求得结果. 【详解】()f x Q 与()g x 在1,22x ⎡∈⎤⎢⎥⎣⎦的图象上恰有两对关于x 轴对称的点，()()f x g x ∴=-在1,22⎡⎤⎢⎥⎣⎦恰有两个不同的解，即221ln3ln 30x m x x x x m x +--=+-+=在1,22⎡⎤⎢⎥⎣⎦上恰有两个不同的解， 令()2ln 3h x x x x m =+-+，则()()()2211123123x x x x h x x x x x---+'=+-==， ∴当1,12x ⎛⎫∈ ⎪⎝⎭时，()0h x '<；当()1,2x ∈时，()0h x '>，()h x ∴在1,12⎛⎫⎪⎝⎭上单调递减，在()1,2上单调递增，又15ln 224h m ⎛⎫=--+⎪⎝⎭，()12h m =-，()2ln 22h m =-+， 原问题等价于()h x 在1,22⎡⎤⎢⎥⎣⎦上恰有两个零点，则5ln 2024m m --+≥>-，解得：5ln 224m +≤<，即m 的取值范围为5ln 2,24⎡⎫+⎪⎢⎣⎭.故选：A . 【点睛】本题考查根据函数零点个数求解参数范围的问题，关键是能够将两函数图象对称点个数的问题转化为方程根的个数的问题，进一步通过构造函数的方式将问题转化为函数零点个数的问题.16．若函数()()sin xf x e x a =+在区间,22ππ⎛⎫- ⎪⎝⎭上单调递增，则实数a 的取值范围是（）A ．)+∞ B ．[)1,+∞ C ．()1,+∞D ．()+∞【答案】B 【解析】 【分析】将问题转化为()0f x '≥在,22ππ⎛⎫- ⎪⎝⎭上恒成立；根据导函数解析式可知问题可进一步转化04x a π⎛⎫++≥ ⎪⎝⎭在,22ππ⎛⎫-⎪⎝⎭上恒成立；利用正弦型函数值域求法可求得(14x a a a π⎛⎫⎤++∈-+ ⎪⎦⎝⎭，则只需10a -+?即可，解不等式求得结果. 【详解】由题意得：()()sin cos 4x x xf x e x a e x e x a π⎫⎛⎫'=++=++ ⎪⎪⎝⎭⎭()f x Q 在,22ππ⎛⎫- ⎪⎝⎭上单调递增 ()0f x '∴≥在,22ππ⎛⎫- ⎪⎝⎭上恒成立又0x e > 04x a π⎛⎫++≥ ⎪⎝⎭在,22ππ⎛⎫-⎪⎝⎭上恒成立当,22x ππ⎛⎫∈- ⎪⎝⎭时，3,444x πππ⎛⎫+∈- ⎪⎝⎭ sin ,142x π⎛⎤⎛⎫∴+∈- ⎥ ⎪ ⎝⎭⎝⎦(14x a a a π⎛⎫⎤++∈-+ ⎪⎦⎝⎭10a ∴-+≥，解得：[)1,a ∈+∞ 本题正确选项：B 【点睛】本题考查根据函数在一段区间内的单调性求解参数范围问题，涉及到正弦型函数值域的求解问题；本题解题关键是能够将问题转化为导函数在区间内恒大于等于零的问题，从而利用三角函数的最值来求得结果.17．已知函数()2cos f x x x =-，若15log 3a f ⎛⎫= ⎪⎝⎭，31log 5b f ⎛⎫= ⎪⎝⎭，315c f ⎛⎫⎛⎫ ⎪ ⎪ ⎝⎭⎝⎭=⎪，则（ ） A ．a b c >> B ．b a c >> C ．c b a >> D ．c a b >>【答案】B 【解析】【分析】判断()f x 为偶函数，利用导数得出()f x 在()0,π上单调递增，由对数函数的性质，结合函数()f x 的单调性和奇偶性，即可得出答案. 【详解】()()()()22cos cos f x x x x x f x -=---=-=，故()f x 为偶函数故只需考虑()0,x ∈+∞的单调性即可.()'2sin f x x x =+，当()0,x π∈时，易得()'0f x >故()f x 在()0,π上单调递增，()155log 3log 3a f f ⎛⎫== ⎪⎝⎭，()331log log 55b f f ⎛⎫== ⎪⎝⎭，由函数单调性可知()()3531log 3log 55f f f ⎛⎫⎛⎫<< ⎪ ⎪ ⎪⎝⎭⎝⎭，即c a b << 故选：B 【点睛】本题主要考查了利用函数的奇偶性以及单调性比较大小，属于中档题.18．已知定义在R 上的函数()f x 满足()()3221f x f x -=-,且()f x 在[1, )+∞上单调递增,则（ ）A ．()()()0.31.130. 20.54f f log f <<B ．()()()0.31.130. 240.5f f f log <<C ．()()()1.10.3340.20.5f f f log << D ．()()()0.31.130.50.24f log f f << 【答案】A 【解析】 【分析】由已知可得()f x 的图象关于直线1x =对称.因为0.31.130.21log 0.5141-<-<-，又()f x 在[1,)+∞上单调递增,即可得解.【详解】解：依题意可得,()f x 的图象关于直线1x =对称. 因为()()()0.31.1330.20,1,0.5 2 1,,044,8log log ∈=-∈-∈,则0.31.130.21log 0.5141-<-<-，又()f x 在[1,)+∞上单调递增, 所以()()()0.31.130.20.54f f log f <<.故选:A. 【点睛】本题考查了函数的对称性及单调性，重点考查了利用函数的性质判断函数值的大小关系，属中档题.19．函数()()()log 5,0,1a f x ax a a =->≠在()1,3上是减函数，则a 的取值范围是( ) A ．5,3⎛⎫+∞ ⎪⎝⎭B ．1,15⎛⎫ ⎪⎝⎭C ．51,3⎛⎫ ⎪⎝⎭D ．51,3⎛⎤ ⎥⎝⎦【答案】D 【解析】 【分析】根据0a >可知5y ax =-在定义域内单调递减，若使得函数()()()log 5,0,1a f x ax a a =->≠在()1,3上是减函数，则需1530a a >⎧⎨-≥⎩，解不等式即可.【详解】 0a >Q5y ax ∴=-在定义域内单调递减若使得函数()()()log 5,0,1a f x ax a a =->≠在()1,3上是减函数则需1530a a >⎧⎨-≥⎩，解得513a <≤故选：D 【点睛】本题考查对数函数的单调性，属于中档题.20．已知函数()2ln 2xx f x e x =+-的极值点为1x ，函数()2xg x e x =+-的零点为2x ，函数()ln 2xh x x=的最大值为3x ，则（ ） A ．123x x x >> B ．213x x x >>C ．312x x x >>D ．321x x x >>【答案】A 【解析】 【分析】根据()f x '在()0,∞+上单调递增，且11024f f ⎛⎫⎛⎫''⋅<⎪ ⎪⎝⎭⎝⎭，可知导函数零点在区间11,42⎛⎫⎪⎝⎭内，即()f x 的极值点111,42x ⎛⎫∈ ⎪⎝⎭；根据()g x 单调递增且11024g g ⎛⎫⎛⎫⋅< ⎪ ⎪⎝⎭⎝⎭可知211,42x ⎛⎫∈ ⎪⎝⎭；通过判断()()12g x g x >，结合()g x 单调性可得12x x >；利用导数可求得()max 1124h x e =<，即314x <，从而可得三者的大小关系. 【详解】()1x f x e x x'=+-Q 在()0,∞+上单调递增且1213022f e ⎛⎫'=-> ⎪⎝⎭，14115044f e ⎛⎫'=-< ⎪⎝⎭ 111,42x ⎛⎫∴∈ ⎪⎝⎭且11110x e x x +-= Q 函数()2x g x e x =+-在()0,∞+上单调递增且1213022g e ⎛⎫=-> ⎪⎝⎭，14112044g e ⎛⎫=+-< ⎪⎝⎭211,42x ⎛⎫∴∈ ⎪⎝⎭又()()11111211112220xg x e x x x g x x x ⎛⎫=+-=-+-=->=⎪⎝⎭且()g x 单调递增 12x x ∴> 由()21ln 2x h x x -'=可得：()()max12h x h e e ==，即31124x e =< 123x x x ∴>>本题正确选项：A 【点睛】本题考查函数极值点、零点、最值的判断和求解问题，涉及到零点存在定理的应用，易错点是判断12,x x 大小关系时，未结合()g x 单调性判断出()()12g x g x >，造成求解困难.。

压轴大题突破练——函数与导数（二）１．设函数f（x）＝a e x＋错误!＋b（a>0）．（１）求f（x）在[0，＋∞）内的最小值；（２）设曲线y＝f（x）在点（２，f（２））处的切线方程为y＝错误!x，求a，b的值．解（１）f′（x）＝a e x—错误!，当f′（x）>0，即x>—ln a时，f（x）在（—ln a，＋∞）上递增；当f′（x）<0，即x<—ln a时，f（x）在（—∞，—ln a）上递减．１当0<a<１时，—ln a>0，f（x）在[0，—ln a）上递减，在（—ln a，＋∞）上递增，从而f（x）在[0，＋∞）内的最小值为f（—ln a）＝２＋b；２当a≥１时，—ln a≤0，f（x）在[0，＋∞）上递增，从而f（x）在[0，＋∞）内的最小值为f（0）＝a＋错误!＋b.（２）依题意f′（２）＝a e２—错误!＝错误!，解得a e２＝２或a e２＝—错误!（舍去）．所以a＝错误!，代入原函数可得２＋错误!＋b＝３，即b＝错误!.故a＝错误!，b＝错误!.２．已知函数f（x）＝a ln x—bx２.（１）当a＝２，b＝错误!时，求函数f（x）在[错误!，e]上的最大值；（２）当b＝0时，若不等式f（x）≥m＋x对所有的a∈[0，错误!]，x∈（１，e２]都成立，求实数m的取值范围．解（１）由题知，f（x）＝２ln x—错误!x２，f′（x）＝错误!—x＝错误!，当错误!≤x≤e时，令f′（x）>0得错误!≤x<错误!；令f′（x）<0，得错误!<x≤e，∴f（x）在[错误!，错误!）上单调递增，在（错误!，e]上单调递减，∴f（x）max＝f（错误!）＝ln ２—１．（２）当b＝0时，f（x）＝a ln x，若不等式f（x）≥m＋x对所有的a∈[0，错误!]，x∈（１，e２]都成立，则a ln x≥m＋x对所有的a∈[0，错误!]，x∈（１，e２]都成立，即m≤a ln x—x，对所有的a∈[0，错误!]，x∈（１，e２]都成立，令h（a）＝a ln x—x，则h（a）为一次函数，m≤h（a）min.∵x∈（１，e２]，∴ln x>0，∴h（a）在[0，错误!]上单调递增，∴h（a）min＝h（0）＝—x，∴m≤—x对所有的x∈（１，e２]都成立．∵１<x≤e２，∴—e２≤—x<—１，∴m≤（—x）min＝—e２.３．已知函数f（x）＝x３—２x＋１，g（x）＝ln x.（１）求F（x）＝f（x）—g（x）的单调区间和极值；（２）是否存在实常数k和m，使得x>0时，f（x）≥kx＋m且g（x）≤kx＋m？若存在，求出k 和m的值；若不存在，说明理由．解（１）由F（x）＝x３—２x＋１—ln x（x>0），得F′（x）＝错误!（x>0），令F′（x）＝0得x＝１，易知F（x）在（0,１）上单调递减，在（１，＋∞）上单调递增，从而F（x）的极小值为F（１）＝0．（２）易知f（x）与g（x）有一个公共点（１,0），而函数g（x）在点（１,0）处的切线方程为y＝x—１，下面只需验证错误!都成立即可．设h（x）＝x３—２x＋１—（x—１）（x>0），则h′（x）＝３x２—３＝３（x＋１）（x—１）（x>0）．易知h（x）在（0,１）上单调递减，在（１，＋∞）上单调递增，所以h（x）的最小值为h（１）＝0，所以f（x）≥x—１恒成立．设k（x）＝ln x—（x—１），则k′（x）＝错误!（x>0）．易知k（x）在（0,１）上单调递增，在（１，＋∞）上单调递减，所以k（x）的最大值为k（１）＝0，所以g（x）≤x—１恒成立．故存在这样的实常数k＝１和m＝—１，使得x>0时，f（x）≥kx＋m且g（x）≤kx＋m.４．已知定义在正实数集上的函数f（x）＝错误!x２＋２ax，g（x）＝３a２ln x＋b，其中a>0．设两曲线y＝f（x），y＝g（x）有公共点，且在该点处的切线相同．（１）用a表示b，并求b的最大值；（２）求证：f（x）≥g（x）．（１）解f′（x）＝x＋２a，g′（x）＝错误!，由题意知f（x0）＝g（x0），f′（x0）＝g′（x0），即错误!由x0＋２a＝错误!，得x0＝a或x0＝—３a（舍去）．即有b＝错误!a２＋２a２—３a２ln a＝错误!a２—３a２ln a.令h（t）＝错误!t２—３t２ln t（t>0），则h′（t）＝２t（１—３ln t）．于是当t（１—３ln t）>0，即0<t<e错误!时，h′（t）>0；当t（１—３ln t）<0，即t>e错误!时，h′（t）<0．故h（t）在（0，e错误!）上为增函数，在（e错误!，＋∞）上为减函数，于是h（t）在（0，＋∞）上的最大值为h（e错误!）＝错误!e错误!，即b的最大值为错误!e错误!.（２）证明设F（x）＝f（x）—g（x）＝错误!x２＋２ax—３a２ln x—b（x>0），则F′（x）＝x＋２a—错误!＝错误!（x>0）．故F′（x）在（0，a）上为减函数，在（a，＋∞）上为增函数．于是F（x）在（0，＋∞）上的最小值是F（a）＝F（x0）＝f（x0）—g（x0）＝0．故当x>0时，有f（x）—g（x）≥0，即当x>0时，f（x）≥g（x）．。

【步步高】（全国通用）2016版高考数学复习 考前三个月 压轴大题突破练4 函数与导数（二 ）理1.已知函数f (x )＝e x－a (x ＋1)在x ＝ln 2处的切线的斜率为1.(其中e ＝2.718 28…)(1)求a 的值及f (x )的最小值；(2)当x ≥0时，f (x )≥mx 2恒成立，求m 的取值X 围；(3)求证：∑n i ＝2ln i i 4<12e(i ，n ∈N *).(参考数据：ln 2≈0.693 1)2.已知函数f (x )＝ln x －x 2＋x .(1)求函数f (x )的单调递减区间； (2)若关于x 的不等式f (x )≤⎝ ⎛⎭⎪⎫a 2－1x 2＋ax －1恒成立，求整数a 的最小值； (3)若正实数x 1，x 2满足f (x 1)＋f (x 2)＋2(x 21＋x 22)＋x 1x 2＝0，证明：x 1＋x 2>5－12.3.已知f (x )＝x ln x ，g (x )＝－x 2＋ax －3.(1)求函数f (x )在[t ，t ＋2](t >0)上的最小值；(2)对一切x ∈(0，＋∞)，2f (x )≥g (x )恒成立，某某数a 的取值X 围；(3)证明：对一切x ∈(0，＋∞)，都有ln x >1e x －2e x成立.4.已知函数f (x )＝ln(x ＋a )＋2x，g (x )＝ln x . (1)已知f (x )在[e ，＋∞)上是单调函数，求a 的取值X 围；(2)已知m ，n ，ξ满足n >ξ>m >0，且g ′(ξ)＝g n －g m n －m，试比较ξ与mn 的大小； (3)已知a ＝2，是否存在正数k ，使得关于x 的方程f (x )＝kg (x )在[e ，＋∞)上有两个不相等的实数根？如果存在，求k 满足的条件；如果不存在，说明理由.答案精析压轴大题突破练41.(1)解 f ′(x )＝e x －a ，由已知得f ′(ln 2)＝2－a ＝1，∴a ＝1，此时f (x )＝e x －x －1，f ′(x )＝e x －1，∴当0<e x <1，即x <0时，f ′(x )<0，当e x>1，即x >0时，f ′(x )>0，∴当x ＝0时，f (x )取得极小值即为最小值，∴f (x )min ＝f (0)＝0.(2)解 记g (x )＝e x －x －1－mx 2， g ′(x )＝e x －1－2mx ，设h (x )＝g ′(x )＝e x －1－2mx ，则h ′(x )＝e x －2m .①当m ≤12时，h ′(x )≥0(x ≥0)，∴h (x )≥h (0)＝0， ∴g ′(x )≥0，∴g (x )≥g (0)＝0，∴m ≤12时满足题意. ②当m >12时，令h ′(x )＝0，得x ＝ln 2m >0， 当x ∈[0，ln 2m )时，h ′(x )<0，h (x )在此区间上是减函数，g ′(x )＝h (x )≤h (0)＝0， ∴g (x )在此区间上是减函数，∴g (ln 2m )≤g (0)＝0不合题意.综上得m 的取值X 围为⎝⎛⎦⎥⎤－∞，12. (3)证明 记k (x )＝ln x x 2，则k ′(x )＝1－2ln x x 3， 令k ′(x )＝0，得x ＝ e.不难知当x ＝e 时，k (x )有最大值，且最大值为12e. ∴ln x x 2≤12e ，∴ln n n 4≤12e ·1n 2 (n ≥2)，∴∑n i ＝2ln i i 4≤12e ⎝ ⎛⎭⎪⎫122＋132＋142＋…＋1n 2， 又122＋132＋142＋…＋1n 2<11×2＋12×3＋…＋1n －1n＝⎝ ⎛⎭⎪⎫1－12＋⎝ ⎛⎭⎪⎫12－13＋…＋⎝ ⎛⎭⎪⎫1n －1－1n ＝1－1n<1， ∴∑ni ＝2ln i i 4<12e ⎝ ⎛⎭⎪⎫122＋132＋142＋…＋1n 2<12e ， 即∑ni ＝2ln i i 4<12e . 2.(1)解 f ′(x )＝1x－2x ＋1＝－2x 2＋x ＋1x (x >0), 由f ′(x )<0，得2x 2－x －1>0，又x >0，所以x >1.所以f (x )的单调递减区间为(1，＋∞).(2)解 令g (x )＝f (x )－[(a 2－1)x 2＋ax －1] ＝ln x －12ax 2＋(1－a )x ＋1， 所以g ′(x )＝1x －ax ＋(1－a )＝－ax 2＋1－a x ＋1x. 当a ≤0时，因为x >0，所以g ′(x )>0.所以g (x )在(0，＋∞)上是递增函数，又因为g (1)＝ln 1－12a ×12＋(1－a )＋1＝－32a ＋2>0， 所以关于x 的不等式f (x )≤⎝ ⎛⎭⎪⎫a 2－1x 2＋ax －1不能恒成立. 当a >0时，g ′(x )＝－ax 2＋1－a x ＋1x＝－a x －1ax ＋1x ，令g ′(x )＝0，得x ＝1a. 所以当x ∈⎝ ⎛⎭⎪⎫0，1a 时，g ′(x )>0；当x ∈⎝ ⎛⎭⎪⎫1a ，＋∞时，g ′(x )<0， 因此函数g (x )在⎝ ⎛⎭⎪⎫0，1a 是增函数，在⎝ ⎛⎭⎪⎫1a ，＋∞是减函数. 故函数g (x )的最大值为g ⎝ ⎛⎭⎪⎫1a ＝ln 1a －12a ×⎝ ⎛⎭⎪⎫1a 2＋(1－a )×1a ＋1＝12a －ln a . 令h (a )＝12a－ln a ， 因为h (1)＝12>0，h (2)＝14－ln 2<0， 因为h (a )在a ∈(0，＋∞)是减函数.所以当a ≥2时，h (a )<0.所以整数a 的最小值为2.(3)证明 由f (x 1)＋f (x 2)＋2(x 21＋x 22)＋x 1x 2＝0，即ln x 1＋x 21＋x 1＋ln x 2＋x 22＋x 2＋x 1x 2＝0，从而(x 1＋x 2)2＋(x 1＋x 2)＝x 1·x 2－ln(x 1·x 2)，令t ＝x 1·x 2，则由φ(t )＝t －ln t 得，φ′(t )＝t －1t， 可知，φ(t )在区间(0,1)上单调递减，在区间(1，＋∞)上单调递增. 所以φ(t )≥φ(1)＝1，所以(x 1＋x 2)2＋(x 1＋x 2)≥1，又x 1＋x 2>0，因此x 1＋x 2≥5－12成立. 3.(1)解 由f (x )＝x ln x ，x >0，得f ′(x )＝ln x ＋1，令f ′(x )＝0，得x ＝1e. 当x ∈(0，1e)时，f ′(x )<0，f (x )单调递减； 当x ∈(1e，＋∞)时，f ′(x )>0，f (x )单调递增. ①当0<t <1e <t ＋2，即0<t <1e时， f (x )min ＝f (1e )＝－1e；②当1e ≤t <t ＋2，即t ≥1e 时，f (x )在[t ，t ＋2]上单调递增，f (x )min ＝f (t )＝t ln t . 所以f (x )min ＝⎩⎪⎨⎪⎧－1e ，0<t <1e ，t ln t ，t ≥1e. (2)解 2x ln x ≥－x 2＋ax －3 (x >0)， 则a ≤2ln x ＋x ＋3x ，设h (x )＝2ln x ＋x ＋3x (x >0)， 则h ′(x )＝x ＋3x －1x 2， ①当x ∈(0,1)时，h ′(x )<0，h (x )单调递减，②当x ∈(1，＋∞)时，h ′(x )>0，h (x )单调递增，所以h (x )min ＝h (1)＝4，对一切x ∈(0，＋∞)，2f (x )≥g (x )恒成立，所以a ≤h (x )min ＝4.(3)证明 问题等价于证明x ln x >x e x －2e(x ∈(0，＋∞)). 由(1)可知f (x )＝x ln x (x ∈(0，＋∞))的最小值是－1e， 当且仅当x ＝1e 时取到，设m (x )＝x e x －2e (x ∈(0，＋∞))，则m ′(x )＝1－x e x ，易知m (x )max ＝m (1)＝－1e， 当且仅当x ＝1时取到.从而对一切x ∈(0，＋∞)，都有ln x >1e x －2e x成立. 4.解 (1)∵f (x )＝ln(x ＋a )＋2x， ∴f ′(x )＝1x ＋a －2x 2＝x 2－2x －2a x 2x ＋a. ∵f (x )在[e ，＋∞)上单调，∴⎩⎪⎨⎪⎧ x ＋a >0，x 2－2x －2a ≥0或⎩⎪⎨⎪⎧ x ＋a >0，x 2－2x －2a ≤0.∴⎩⎪⎨⎪⎧ a >－e ，a ≤12x 2－x 或⎩⎪⎨⎪⎧ a >－e ，a ≥12x 2－x .∵当x ≥e 时，12x 2－x ≥12e 2－e ， ∴－e<a ≤12e 2－e. (2)∵g ′(ξ)＝g n －g m n －m ，∴1ξ＝ln n －ln m n －m. 设h (x )＝2ln x －x ＋1x (x >1)，则h ′(x )＝2x －1－1x 2＝－x －12x 2<0，∴h (x )<h (1)＝0，∴当x >1时，2ln x <x －1x ，令x ＝n m， 得2ln n m <n m －m n， ∴ln n －ln m <n －m mn ⇒ln n －ln m n －m <1mn. ∴1ξ<1mn，即ξ>mn . (3)假设方程f (x )＝kg (x )存在满足条件的两个实数根x 1，x 2，且x 2>x 1≥e，则 ⎩⎪⎨⎪⎧ lnx 1＋2＋2x 1＝k ln x 1，lnx 2＋2＋2x 2＝k ln x 2 ⇒ln x 1＋2＋2x 1ln x 2＋2＋2x 2＝ln x 1ln x 2， 即ln x 1＋2＋2x 1ln x 1＝ln x 2＋2＋2x 2ln x 2，ln x 1＋2＋2x 1－ln x 1ln x 1＝ln x 2＋2＋2x 2－ln x 2ln x 2.ln ⎝ ⎛⎭⎪⎫1＋2x 1＋2x 1ln x 1＝ln ⎝ ⎛⎭⎪⎫1＋2x 2＋2x 2ln x 2⇒ln ⎝ ⎛⎭⎪⎫1＋2x 1＋2x 1ln ⎝ ⎛⎭⎪⎫1＋2x 2＋2x 2＝ln x1ln x 2.∵x 2>x 1≥e，∴2x 1>2x 2⇒ln ⎝⎛⎭⎪⎫1＋2x 1＋2x 1ln ⎝ ⎛⎭⎪⎫1＋2x 2＋2x 2>1，而ln x 1ln x 2<1，∴ln ⎝ ⎛⎭⎪⎫1＋2x 1＋2x 1ln ⎝ ⎛⎭⎪⎫1＋2x 2＋2x 2>ln x 1ln x 2，∴方程不存在满足条件的两根.。

压轴大题突破练——函数与导数(二)1．已知函数f (x )＝a ln x －bx 2.(1)当a ＝2，b ＝12时，求函数f (x )在[1e，e]上的最大值； (2)当b ＝0时，若不等式f (x )≥m ＋x 对所有的a ∈[0，32]，x ∈(1，e 2]都成立，求实数m 的取值范围．解 (1)由题知，f (x )＝2ln x －12x 2， f ′(x )＝2x －x ＝2－x 2x， 当1e ≤x ≤e 时，令f ′(x )>0得1e≤x <2； 令f ′(x )<0，得2<x ≤e，∴f (x )在[1e ，2)上单调递增，在(2，e]上单调递减， ∴f (x )max ＝f (2)＝ln 2－1.(2)当b ＝0时，f (x )＝a ln x ，若不等式f (x )≥m ＋x 对所有的a ∈[0，32]，x ∈(1，e 2]都成立，则a ln x ≥m ＋x 对所有的a ∈[0，32]，x ∈(1，e 2]都成立，即m ≤a ln x －x ，对所有的a ∈[0，32]，x ∈(1，e 2]都成立， 令h (a )＝a ln x －x ，则h (a )为一次函数，m ≤h (a )min .∵x ∈(1，e 2]，∴ln x >0，∴h (a )在[0，32]上单调递增，∴h (a )min ＝h (0)＝－x ， ∴m ≤－x 对所有的x ∈(1，e 2]都成立．∵1<x ≤e 2，∴－e 2≤－x <－1，∴m ≤(－x )min ＝－e 2.2．函数f (x )＝x ln x －ax 2－x (a ∈R )．(1)若函数f (x )在x ＝1处取得极值，求a 的值；(2)若函数f (x )的图象在直线y ＝－x 图象的下方，求a 的取值范围；(3)求证：2 0132 012<2 0122 013.(1)解 f ′(x )＝ln x －2ax .因为f ′(1)＝0，所以a ＝0.(2)解 由题意，得x ln x －ax 2－x <－x ，所以x ln x －ax 2<0.因为x ∈(0，＋∞)，所以a >ln x x. 设h (x )＝ln x x ，则h ′(x )＝1－ln x x 2. 令h ′(x )>0，得0<x <e ，所以h (x )在(0，e)上单调递增；令h ′(x )<0，得x >e ，所以h (x )在(e ，＋∞)上单调递减．所以h (x )max ＝h (e)＝1e， 所以a >1e. (3)证明 由(2)知h (x )＝ln x x在(e ，＋∞)上单调递减， 所以当x >e 时，h (x )>h (x ＋1)，即ln x x >ln (x ＋1)x ＋1， 所以(x ＋1)ln x >x ln(x ＋1)，所以ln xx ＋1>ln(x ＋1)x ， 所以x x ＋1>(x ＋1)x ，令x ＝2 012，得2 0122 013>2 0132 012.3．已知函数f (x )＝ln x －ax ＋1.(1)若函数f (x )在点A (1，f (1))处的切线l 与直线4x ＋3y －3＝0垂直，求a 的值；(2)若f (x )≤0恒成立，求实数a 的取值范围；(3)证明：ln(n ＋1)>12＋13＋…＋1n ＋1(n ∈N *)． (1)解 函数f (x )的定义域为(0，＋∞)，f ′(x )＝1x－a . 所以f ′(1)＝1－a .所以切线l 的斜率为1－a .因为切线l 与直线4x ＋3y －3＝0垂直，所以1－a ＝34，解得a ＝14.(2)解 若a ≤0，则f ′(x )＝1x－a >0，f (x )在(0，＋∞)上是单调递增函数． 而f (1)＝1－a >0，f (x )≤0不恒成立，故a >0.考虑a >0，则当x ∈(0，1a ]时，f ′(x )＝1x－a >0； 当x ∈[1a ，＋∞)时，f ′(x )＝1x－a <0. 所以f (x )在(0，1a]上是单调递增函数， 在[1a，＋∞)上是单调递减函数． 所以f (x )的最大值为f (1a)＝－ln a . 要使f (x )≤0恒成立，只须－ln a ≤0即可．由－ln a ≤0，解得a ≥1，即a 的取值范围为[1，＋∞)．(3)证明 由(2)，知当a ＝1时，f (x )≤0在(0，＋∞)上恒成立，且f (x )在(0,1)上是增函数，f (1)＝0，所以ln x <x －1在x ∈(0,1)上恒成立．令x ＝kk ＋1(k ∈N *)，则ln k k ＋1<k k ＋1－1＝－1k ＋1， 令k ＝1,2，…，n ，则有ln 12<－12，ln 23<－13，ln 34<－14，…，ln n n ＋1<－1n ＋1， 以上各式两边分别相加，得ln 12＋ln 23＋…＋ln n n ＋1<－(12＋13＋…＋1n ＋1)， 即ln 1n ＋1<－(12＋13＋…＋1n ＋1)， 故ln(n ＋1)>12＋13＋…＋1n ＋1(n ∈N *)． 4．已知函数f (x )＝a ln x ＋x 2－(a ＋2)x .(1)当a ＝1时，求函数f (x )的极小值；(2)当a ＝－1时，过坐标原点O 作曲线y ＝f (x )的切线，设切点为P (m ，n )，求实数m 的值；(3)设定义在D 上的函数y ＝g (x )在点Q (x 0，y 0)处的切线方程为l ：y ＝h (x )，当x ≠x 0时，若g (x )－h (x )x －x 0>0在D 内恒成立，则称点Q 为函数y ＝g (x )的“好点”．当a ＝8时，试问函数y ＝f (x )是否存在“好点”，若存在，请求出“好点”的横坐标；若不存在，请说明理由．解 (1)当a ＝1时，f (x )＝ln x ＋x 2－3x ，f ′(x )＝2x －3＋1x ＝2x 2－3x ＋1x ＝(x －1)(2x －1)x(x >0)，当0<x <12时，f ′(x )>0，f (x )单调递增； 当12<x <1时，f ′(x )<0，f (x )单调递减； 当x >1时，f ′(x )>0，f (x )单调递增．所以当x ＝1时，f (x )取到极小值－2.(2)当a ＝－1时，f (x )＝－ln x ＋x 2－x ， f ′(x )＝2x －1－1x(x >0)， 所以切线的斜率k ＝2m －1－1m ＝n －0m －0 ＝m 2－m －ln m m， 整理得m 2＋ln m －1＝0，显然m ＝1是这个方程的解，又y ＝x 2＋ln x －1在(0，＋∞)上是增函数，所以方程x 2＋ln x －1＝0有唯一实数解，故m ＝1.(3)当a ＝8时，f (x )＝8ln x ＋x 2－10x ， f ′(x )＝2x －10＋8x， 函数y ＝f (x )在其图象上一点Q (x 0，f (x 0))处的切线方程h (x )＝(2x 0＋8x 0－10)(x －x 0)＋x 20－10x 0＋8ln x 0.设F (x )＝f (x )－h (x )，则F (x 0)＝0，F ′(x )＝f ′(x )－h ′(x )＝(2x ＋8x －10)－(2x 0＋8x 0－10) ＝2(x －x 0)(x －4x 0)x， ①若0<x 0<2，F (x )在(x 0，4x 0)上单调递减， 所以当x ∈(x 0，4x 0)时，F (x )<F (x 0)＝0， 此时F (x )x －x 0<0，不合题意， 所以y ＝f (x )在(0，＋∞)上不存在“好点”；②若x 0>2，F (x )在(4x 0，x 0)上单调递减，所以当x ∈(4x 0，x 0)时，F (x )>F (x 0)＝0， 此时F (x )x －x 0<0，不合题意， 所以y ＝f (x )在(0，＋∞)上不存在“好点”；③若x 0＝2，F ′(x )＝2(x －2)2x≥0， 即F (x )在(0，＋∞)上是增函数，当x >x 0时，F (x )>F (x 0)＝0，当x <x 0时，F (x )<F (x 0)＝0，F (x )x －x 0>0恒成立， 所以点(2，－16＋8ln 2)为函数y ＝f (x )的“好点”． 故函数y ＝f (x )存在“好点”，“好点”的横坐标为2.。

压轴大题突破练2对应学生用书P158(满分24分，限时30分钟)解答题：本大题共2小题．解答应写出文字说明、证明过程或演算步骤．20．(本小题12分)如下图，已知椭圆x2 a2＋y2b2＝1(a＞b＞0)经过点(0，3)，离心率为12，左、右焦点分别为F1(－c,0)，F2(c,0)．(1)求椭圆的方程；(2)若直线l：y＝－12x＋m与椭圆交于A，B两点，与以线段F1F2为直径的圆交于C，D两点，且满足|AB||CD|＝534，求直线l的方程．解析(1)由题设知⎩⎪⎨⎪⎧b＝3，ca＝12，b2＝a2－c2，解得⎩⎪⎨⎪⎧a＝2，b＝3，c＝1.∴椭圆的方程为x24＋y23＝1.(4分)(2)由题设知，以线段F1F2为直径的圆的方程为x2＋y2＝1，∴圆心(0,0)到直线l的距离d＝2|m|5.由d ＜1，得|m |＜52，∴|CD |＝21－d 2＝2 1－45m 2＝25·5－4m 2.(6分) 设A (x 1，y 1)，B (x 2，y 2)，由⎩⎪⎨⎪⎧ y ＝－12x ＋m ，x 24＋y 23＝1，得x 2－mx ＋m 2－3＝0， 由根与系数的关系得x 1＋x 2＝m ，x 1x 2＝m 2－3， ∴|AB |＝⎣⎢⎡⎦⎥⎤1＋⎝ ⎛⎭⎪⎫－122[m 2－4(m 2－3)]＝152·4－m 2.(8分) 由|AB ||CD |＝534，得 4－m 25－4m 2＝1， 解得m ＝±33，满足|m |＜52，(10分)∴直线l 的方程为y ＝－12x ＋33或y ＝－12x －33.(12分)21．(本小题12分)已知f (x )＝x 2－2ax ＋ln x .(1)当a ＝1时，判断f (x )的单调性；(2)若f ′(x )为f (x )的导函数，f (x )有两个不相等的极值点x 1，x 2(x 1＜x 2)，求2f (x 1)－f (x 2)的最小值．解析 (1)当a ＝1时，f (x )＝x 2－2x ＋ln x (x ＞0)，f ′(x )＝2x －2＋1x ＝2x 2－2x ＋1x ＝(x －1)2＋x 2x＞0. 所以f (x )在区间(0，＋∞)上单调递增．(3分)(2)f ′(x )＝2x －2a ＋1x ＝2x 2－2ax ＋1x，(4分) 由题意得，x 1和x 2是方程2x 2－2ax ＋1＝0的两个不相等的正实数根，所以⎩⎪⎨⎪⎧ x 1＋x 2＝a ＞0，x 1x 2＝12，Δ＝4a 2－8＞0，得a ＞2，2ax 1＝2x 21＋1,2ax 2＝2x 22＋1，由a 2＞22，所以x 1∈⎝ ⎛⎭⎪⎫0，22，x 2∈⎝ ⎛⎭⎪⎫22，＋∞.(5分) 2f (x 1)－f (x 2)＝2(x 21－2ax 1＋ln x 1)－(x 22－2ax 2＋ln x 2)＝2x 21－x 22－4ax 1＋2ax 2－ln x 2＋2ln x 1＝－2x 21＋x 22－ln x 2x 21－1 ＝－12x 22＋x 22－ln x 32(x 1x 2)2－1 ＝－12x 22＋x 22－32ln x 22－2ln 2－1.(7分) 令t ＝x 22⎝ ⎛⎭⎪⎫t ＞12，g (t )＝－12t ＋t －32ln t －2ln 2－1，(8分) 则g ′(t )＝12t 2＋1－32t ＝2t 2－3t ＋12t 2＝(2t －1)(t －1)2t 2， 当12＜t ＜1时，g ′(t )＜0，当t ＝1时，g ′(t )＝0，当t ＞1时，g ′(t )＞0，所以y ＝g (t )在⎝ ⎛⎭⎪⎫12，1上单调递减，在(1，＋∞)上单调递增， g (t )min ＝g (1)＝－1＋4ln 22，(11分) 所以2f (x 1)－f (x 2)的最小值为－1＋4ln 22.(12分)。

(四)函数与导数(2)1．(2018·成都模拟)已知f (x )＝ln x －ax ＋1(a ∈R )．(1)讨论函数的单调性；(2)证明：当a ＝2，且x ≥1时，f (x )≤e x －1－2恒成立．(1)解 ∵ f (x )＝ln x －ax ＋1，a ∈R ，∴f ′(x )＝1x －a ＝－ax ＋1x， 当a ≤0时，f (x )的增区间为(0，＋∞)，无减区间，当a >0时，增区间为⎝ ⎛⎭⎪⎫0，1a ，减区间为⎝ ⎛⎭⎪⎫1a ，＋∞. (2)证明 当x ∈[1，＋∞)时，由(1)可知当a ＝2时，f (x )在[1，＋∞)上单调递减， f (x )≤f (1)＝－1，再令G (x )＝e x －1－2，在x ∈[1，＋∞)上，G ′(x )＝ex －1>0，G (x )单调递增，所以G (x )≥G (1)＝－1， 所以G (x )≥f (x )恒成立，当x ＝1时取等号，所以原不等式恒成立．2．(2018·合肥模拟)已知函数f (x )＝x ln x ，g (x )＝λ(x 2－1)(λ为常数)．(1)若函数y ＝f (x )与函数y ＝g (x )在x ＝1处有相同的切线，求实数λ的值；(2)当x ≥1时，f (x )≤g (x )，求实数λ的取值范围．解 (1)由题意得f ′(x )＝ln x ＋1，g ′(x )＝2λx ，又f (1)＝g (1)＝0，且函数y ＝f (x )与y ＝g (x )在x ＝1处有相同的切线，∴f ′(1)＝g ′(1)，则2λ＝1，即λ＝12. (2)设h (x )＝x ln x －λ(x 2－1)，则h (x )≤0对∀x ∈[1，＋∞)恒成立．∵h ′(x )＝1＋ln x －2λx ，且h (1)＝0，∴h ′(1)≤0，即1－2λ≤0，∴λ≥12. 另一方面，当λ≥12时，记φ(x )＝h ′(x )，则φ′(x )＝1x －2λ＝1－2λx x. 当x ∈[1，＋∞)时，φ′(x )≤0，∴φ(x )在[1，＋∞)内为减函数，∴当x ∈[1，＋∞)时，φ(x )≤φ(1)＝1－2λ≤0，即h ′(x )≤0，∴h (x )在[1，＋∞)内为减函数，∴当x ∈[1，＋∞)时，h (x )≤h (1)＝0恒成立，符合题意．当λ<12时， ①若λ≤0，则h ′(x )＝1＋ln x －2λx ≥0对∀x ∈[1，＋∞)恒成立，∴h (x )在[1，＋∞)内为增函数，∴当x ∈[1，＋∞)时，h (x )≥h (1)＝0恒成立，不符合题意．②若0<λ<12， 令φ′(x )>0，则1<x <12λ， ∴φ(x )在⎝ ⎛⎭⎪⎫1，12λ内为增函数， ∴当x ∈⎝ ⎛⎭⎪⎫1，12λ时，φ(x )>φ(1)＝1－2λ>0， 即h ′(x )>0，∴h (x )在⎝ ⎛⎭⎪⎫1，12λ内为增函数， ∴当x ∈⎝ ⎛⎭⎪⎫1，12λ时，h (x )>h (1)＝0，不符合题意， 综上所述，λ的取值范围是⎣⎢⎡⎭⎪⎫12，＋∞. 3．(2018·山东省名校联盟模拟)已知f (x )＝x e x ＋a (x ＋1)2＋1e. (1)若函数f (x )在x ＝1处取得极值，求a 的值；(2)当x >－2时，f (x )≥0，求a 的取值范围．解 (1)f ′(x )＝(x ＋1)e x＋2a (x ＋1)＝(x ＋1)(e x ＋2a )，若函数f (x )在x ＝1处取得极值，则f ′(1)＝0，所以a ＝－e 2，经检验，当a ＝－e 2时，函数f (x )在x ＝1处取得极值． (2)f ′(x )＝(x ＋1)e x ＋2a (x ＋1)＝(x ＋1)(e x＋2a )，①a ≥0时，当－2<x <－1时，f ′(x )<0，f (x )为减函数，当x >－1时，f ′(x )>0，f (x )为增函数；又f (－1)＝0，∴当x >－2时，f (x )≥0成立．②a <0时，令e x ＋2a ＝0，得x ＝ln(－2a )，当ln(－2a )>－1，即a <－12e时， 当－2<x <－1或x >ln(－2a )时，f ′(x )>0；当－1<x <ln(－2a )时，f ′(x )<0，则f (x )在(－2，－1)，(ln(－2a )，＋∞)上为增函数，在(－1，ln(－2a ))上为减函数， 又f (－1)＝0，∴f (x )在(－1，ln(－2a ))上小于零，不符合题意，舍去．当ln(－2a )＝－1，即a ＝－12e 时， 当－2<x <－1或x >－1时，f ′(x )>0，∴f (x )在(－2，＋∞)上单调递增，又f (－1)＝0，当x ∈(－2，－1)时，f (x )<0，不符合题意，舍去；当－2<ln(－2a )<－1，即－12e <a <－12e 2时， 当－2<x <ln(－2a )或x >－1时，f ′(x )>0，当ln(－2a )<x <－1时，f ′(x )<0，则f (x )在(－2，ln(－2a ))，(－1，＋∞)上为增函数，在(ln(－2a )，－1)上为减函数，又f (－1)＝0，要使f (x )≥0恒成立，则f (－2)≥0，则a ≥2－e e 2， 又∵－12e <a <－12e 2， ∴2－e e 2≤a <－12e 2. 当ln(－2a )≤－2，即－12e 2≤a <0时， 当x >－1时，f ′(x )>0，当－2<x <－1时，f ′(x )<0，则f (x )在(－2，－1)上为减函数，在(－1，＋∞)上为增函数，又f (－1)＝0，满足题意，综上所述，a 的取值范围为⎣⎢⎡⎭⎪⎫2－e e 2，＋∞. 4．(2018·威海模拟)已知函数f (x )＝12x 2＋ax －a e x ，g (x )为f (x )的导函数． (1)求函数g (x )的单调区间；(2)若函数g (x )在R 上存在最大值0，求函数f (x )在[0，＋∞)上的最大值；(3)求证：当x >0时，x e x －eln x >12x 3＋x 2. (1)解 由题意可知，g (x )＝ f ′(x )＝x ＋a －a e x，则g ′(x )＝1－a e x ，当a ≤0时，g ′(x )>0，∴g (x )在(－∞，＋∞)上单调递增；当a >0时，当x <－ln a 时，g ′(x )>0，当x >－ln a 时，g ′(x )<0，∴g (x )在(－∞，－ln a )上单调递增，在(－ln a ，＋∞)上单调递减，综上，当a ≤0时，g (x )的单调递增区间为(－∞，＋∞)，无递减区间；当a >0时，g (x )的单调递增区间为(－∞，－ln a )，单调递减区间为(－ln a ，＋∞)．(2)解 由(1)可知，a >0，且g (x )在x ＝－ln a 处取得最大值， g (－ln a )＝－ln a ＋a －a ·e1ln a ＝a －ln a －1，即a －ln a －1＝0， 观察可得当a ＝1时，方程成立，令h (a )＝a －ln a －1(a >0)，h ′(a )＝1－1a ＝a －1a， 当a ∈(0,1)时，h ′(a )<0，当a ∈(1，＋∞)时，h ′(a )>0，∴h (a )在(0,1)上单调递减，在(1，＋∞)上单调递增，∴h (a )≥h (1)＝0，∴当且仅当a ＝1时，a －ln a －1＝0，∴f (x )＝12x 2＋x －e x ， 由题意可知f ′(x )＝g (x )≤0，f (x )在[0，＋∞)上单调递减，∴f (x )在x ＝0处取得最大值f (0)＝－1.(3)证明 由(2)知，若a ＝1，当x >0时，f (x )<－1，即12x 2＋x －e x <－1， ∴12x 3＋x 2－x e x <－x ， ∴12x 3＋x 2－x e x ＋eln x <eln x －x ， 令F (x )＝eln x －x ，F ′(x )＝e x －1＝e －x x， 当0<x <e 时，F ′(x )>0；当x >e 时，F ′(x )<0，∴F (x )在(0，e)上单调递增，在(e ，＋∞)上单调递减，∴F (x )≤F (e)＝0，即eln x －x ≤0，∴12x 3＋x 2－x e x ＋eln x <0， ∴当x >0时，x e x －eln x >12x 3＋x 2. 5．(2018·四省名校大联考)已知函数f (x )＝a (x ＋1)2－e x(a ∈R )．(1)当a ＝12时，判断函数f (x )的单调性； (2)若f (x )有两个极值点x 1，x 2(x 1<x 2)．①求实数a 的取值范围；②证明：－12<f (x 1)<－1e. (1)解 当a ＝12时，f (x )＝12(x ＋1)2－e x ， f ′(x )＝x ＋1－e x ，记g (x )＝x ＋1－e x ，则g ′(x )＝1－e x，由g ′(x )＝1－e x >0，得x <0，由g ′(x )＝1－e x <0，得x >0，∴g (x )即f ′(x )在区间(－∞，0)上单调递增，在区间(0，＋∞)上单调递减．∴f ′(x )max ＝f ′(0)＝0.∴对∀x ∈R ，f ′(x )≤0，∴f (x )在R 上单调递减．(2)①解 ∵f (x )有两个极值点，∴关于x 的方程f ′(x )＝2a (x ＋1)－e x＝0有两个根x 1，x 2，设φ(x )＝2a (x ＋1)－e x ，则φ′(x )＝2a －e x ，当a ≤0时，φ′(x )＝2a －e x <0，φ(x )即f ′(x )在R 上单调递减，∴f ′(x )＝0最多有一根，不合题意，当a >0 时，由φ′(x )>0，得x <ln 2a ，由φ′(x )<0，得x >ln 2a ，∴φ(x )即f ′(x )在区间(－∞，ln 2a )上单调递增，在区间(ln 2a ，＋∞)上单调递减． 且当x →－∞时，f ′(x )→－∞，当x →＋∞时，f ′(x )→－∞，要使f ′(x )＝0有两个不同的根，必有f ′(x )max ＝f ′(ln 2a )＝2a (ln 2a ＋1)－2a ＝2a ln 2a >0，解得a >12， ∴实数a 的取值范围是⎝ ⎛⎭⎪⎫12，＋∞. ②证明 ∵f ′(－1)＝－1e<0，f ′(0)＝2a －1>0， ∴－1<x 1<0，又f ′(x 1)＝2a (x 1＋1)－e x 1＝0，∴a ＝e 1x 2(x 1＋1)， ∴f (x 1)＝a (x 1＋1)2－1e x＝12(x 1＋1)11e e x x － ＝12(x 1－1)1e x (－1<x 1<0)， 令h (x )＝12(x －1)e x (－1<x <0)， 则h ′(x )＝12x e x <0， ∴h (x )在区间(－1,0)上单调递减，∴f (0)<f (x 1)<f (－1)．又f (0)＝a －1>－12，f (－1)＝－1e， ∴－12<f (x 1)<－1e.。

考前三个月2022届高考数学（人教通用文科）练透高考必会题型第4练再谈“三个二次”的转化策略[内容精要]函数与不等式是高考的热点和重点，其中“二次”又是各不等式的基础．“三个二次”经常相互转化，相辅相成，可以说是“密不可分”，是一个有机的整体，解决好这部分题目时要学会触类旁通．题型一函数与方程的转化|lg某|，某>0，例1设定义域为R的函数f(某)＝2则关于某的函数y＝2f2(某)－3f(某)＋1的零－某－2某，某≤0，点的个数为________．破题切入点将函数的零点问题转化为对应方程根的问题．答案7解析由y＝2f2(某)－3f(某)＋1＝0得f(某)＝或f(某)＝1，2如图画出f(某)的图象，由f(某)＝知有4个根，由f(某)＝1知有3个根，故函数y＝2f2(某)－3f(某)2＋1共有7个零点．题型二函数与不等式的转化例2已知一元二次不等式f(某)<0的解集为{某|某}，则f(10某)>0的解集为()2A．{某|某lg2}C．{某|某>－lg2}B．{某|－1破题切入点由题意，可得f(10某)>0等价于－1<10某2-1-答案D解析方法一由题意可知f(某)>0的解集为{某|－121故f(10某)>0等价于－1<10某2由指数函数的值域为(0，＋∞)，知一定有10某>－1，11而10某22即10某<10－lg2.由指数函数的单调性可知某当某＝－1时，f()>0，排除B.10题型三方程与不等式的转化例3已知关于某的二次方程某2＋2m某＋2m＋1＝0.(1)若方程有两根，其中一根在区间(－1,0)内，另一根在区间(1,2)内，求m的取值范围；(2)若方程两根均在区间(0,1)内，求m的取值范围．破题切入点将二次函数的特殊点按照题目要求固定到区间内，转化为不等式(组)进行求解．解(1)由条件，抛物线f(某)＝某2＋2m某＋2m＋1与某轴的交点分别在区间(－1,0)和(1,2)内，如右图所示，f－1＝2>0得f1＝4m＋2<0f2＝6m＋5>051即－62f0＝2m＋1<0m∈R，1m5m>－6.1m51故m的取值范围是(－，－)．62(2)抛物线与某轴交点的横坐标均在区间(0,1)内，如右图所示，列不等式组-2-f0>0f1>0Δ≥00m>－1，2m≥1＋2或m≤1－－11m>－，22，即－2故m的取值范围是(－，1－2]．2总结提高“三个二次”是一个整体，不可分割．有关“三个二次”问题的解决办法通常是利用转化与化归思想来将其转化，其中用到的方法主要有数形结合、分类讨论的思想，其最基本的理念可以说是严格按照一元二次不等式的解决步骤来处理．1．若A＝{某|某2＋(p＋2)某＋1＝0，某∈R}，B＝{某|某>0}，且A∩B＝，则实数p的取值范围是()A．p>－4C．p≥0答案A解析当A＝时，Δ＝(p＋2)2－4<0，∴－4当A≠时，方程某2＋(p＋2)某＋1＝0有一个或两个非正根，B．－4Δ≥0，∴∴p≥0.某1＋某2＝－p＋2≤0，综上所述，p>－4.2．已知函数f(某)＝某2－2某＋3在闭区间[0，m]上的最大值为3，最小值为2，则m的取值范围为()A．[1，＋∞)C．(－∞，－2] B．[0,2]D．[1,2]-3-答案D解析∵f(某)＝(某－1)2＋2，其对称轴为某＝1，当某＝1时，f(某)min＝2，故m≥1，又∵f(0)＝3，f(2)＝3，∴m≤2.综上可知1≤m≤2.33．方程某2－某－m＝0在某∈[－1,1]上有实根，则m的取值范围是()29A．m≤－165C．m≥2答案D339某－2－，某∈[－1,1]．解析m＝某2－某＝24165当某＝－1时，m取最大值为，23995当某＝时，m取最小值为－，∴－≤m≤.416162某＋1，某≤0，4．已知函数f(某)＝2若关于某的方程f2(某)－af(某)＝0恰有5个不同的实数解，某－2某＋1，某>0，95B．－162则a的取值范围是()A．(0,1)B．(0,2)C．(1,2)D．(0,3)答案A解析设t＝f(某)，则方程为t2－at＝0，解得t＝0或t＝a，即f(某)＝0或f(某)＝a.如图，作出函数f(某)的图象，由函数图象，可知f(某)＝0的解有两个，故要使方程f2(某)－af(某)＝0恰有5个不同的解，则方程f(某)＝a的解必有三个，此时0 5．(2022·重庆)若a-4-A．(a，b)和(b，c)内C．(b，c)和(c，＋∞)内答案AB．(－∞，a)和(a，b)内D．(－∞，a)和(c，＋∞)内解析由于a0，f(b)＝(b－c)(b－a)<0，f(c)＝(c－a)(c－b)>0.因此有f(a)·f(b)<0，f(b)·f(c)<0，又因f(某)是关于某的二次函数，函数的图象是连续不断的曲线，因此函数f(某)的两零点分别位于区间(a，b)和(b，c)内，故选A.6．已知函数f(某)＝某3＋a某2＋b某＋c有两个极值点某1，某2.若f(某1)＝某1解析因为函数f(某)＝某3＋a某2＋b某＋c有两个极值点某1，某2，可知关于导函数的方程f′(某)＝3某2＋2a某＋b＝0有两个不等的实根某1，某2.则方程3(f(某))2＋2af(某)＋b＝0的根的个数就是方程f(某)＝某1和f(某)＝某2的不等实根的个数之和，再结合图象可看出函数y ＝f(某)的图象与直线y＝某1和直线y＝某2共有3个不同的交点，故所求方程有3个不同的实根．7．若关于某的不等式(2某－1)2解析因为不等式等价于(－a＋4)某2－4某＋1<0，其中(－a＋4)某2－4某＋1＝0中的Δ＝4a>0，且11111有4－a>0，故02＋a2－a42＋a225491，.求的整数解集．所以38．已知函数f(某)＝某2－2a某＋2，当某∈[－1，＋∞)时，f(某)≥a恒成立，则a的取值范围________．答案[－3,1]解析因为f(某)＝(某－a)2＋2－a2，所以此二次函数图象的对称轴为某＝a.①当a∈(－∞，－1)时，f(某)在[－1，＋∞)上单调递增，所以f(某)min＝f(－1)＝2a＋3.-5-要使f(某)≥a恒成立，只需f(某)min≥a，即2a＋3≥a，解得a≥－3，即－3≤a9．已知函数f(某)＝2a某2＋2某－3.如果函数y＝f(某)在区间[－1,1]上有零点，则实数a的取值范围为______________．1答案2，＋∞解析若a＝0，则f(某)＝2某－3，3f(某)＝0某＝[－1,1]，不合题意，故a≠0.2下面就a≠0分两种情况讨论：15①当f(－1)·f(1)≤0时，f(某)在[－1,1]上有一个零点，即(2a－5)(2a －1)≤0，解得≤a≤.22②当f(－1)·f(1)>0时，f(某)在[－1,1]上有零点的条件是－12af－1·f1>0，，＋∞.综上，实数a的取值范围为2－f1≤0，f2a5解得a>.2π10．已知定义在R上的单调递增奇函数f(某)，若当0≤θ≤时，f(co2θ＋2minθ)＋f(－2m－2)<02恒成立，则实数m的取值范围是________．1答案(－，＋∞)2解析方法一f(co2θ＋2minθ)＋f(－2m－2)<0f(co2θ＋2minθ)－1－in2θ.π当θ＝时，2m·0>－2，此时m∈R；2-6-1＋in2θπ当0≤θ－，令t＝1－inθ，221－inθ11＋1－t12则t∈(0,1]，此时m>－某＝－(t＋－2)．2t2t12设φ(t)＝－(t＋－2)，2t而φ(t)在t∈(0,1]上的值域是(－∞，－]，21故m>－.2方法二同方法一，求得2m(1－inθ)>－1－in2θ，设inθ＝t，则t2－2mt＋2m＋1>0对于t∈[0,1]恒成立．设g(t)＝t2－2mt＋2m＋1，其图象的对称轴方程为t＝m.①当m<0时，g(t)在[0,1]上单调递增，1从而g(0)＝2m＋1>0，即m>－，21又m<0，所以－2②当0≤m≤1时，g(t)在[0，m]上单调递减，在[m,1]上单调递增，从而g(m)＝m2－2m2＋2m＋1>0，即m2－2m－1<0，所以1－2③当m>1时，g(t)在[0,1]上单调递减，从而g(1)＝1－2m＋2m＋1＝2>0恒成立，所以m>1.1综合①②③，可知m>－.2π0，，值域是[－5,1]，11．已知函数f(某)＝2ain2某－23ain某co 某＋a＋b(a≠0)的定义域是2求常数a，b的值．解f(某)＝2a·(1－co2某)－3ain2某＋a＋b213＝－2aco2某＋in2某＋2a＋b22-7-2π2某＋＋2a＋b，＝－2ain6πππ7又∵0≤某≤，∴≤2某＋≤π，2666π12某＋≤1.∴－≤in62因此，由f(某)的值域为[－5,1]a>0，可得－2a某－2＋2a＋b＝1，－2a某1＋2a＋b＝－5，a<0，－2a某1＋2a＋b＝1，或1－2a某－＋2a＋b＝－5，2a＝2，a＝－2，解得或b＝－5b＝1.12．已知函数f(某)＝a某2＋a某和g(某)＝某－a，其中a∈R，且a≠0.若函数f(某)与g(某)的图象相交于不同的两点A、B，O为坐标原点，试求△OAB的面积S的最大值．解依题意，f(某)＝g(某)，即a某2＋a某＝某－a，整理得a某2＋(a－1)某＋a＝0，①∵a≠0，函数f(某)与g(某)的图象相交于不同的两点A、B，∴Δ>0，即Δ＝(a－1)2－4a2＝－3a2－2a＋1＝(3a－1)(－a－1)>0，1∴－13设A(某1，y1)，B(某2，y2)，且某1由①得某1某2＝1>0，某1＋某2＝－.a设点O到直线g(某)＝某－a的距离为d，-8-则d＝|－a|2，∴S＝11＋12|某|－a|21－某2|·2＝12－3a2－2a＋1＝12－3a＋132＋43.∵－13且a≠0，∴当a＝－13时，S取得最大值3 3.-9-。

1．函数与导数1．设函数f (x )＝x ln x ＋ax ，a ∈R .(1)当a ＝1时，求曲线y ＝f (x )在点(1，f (1))处的切线方程；(2)求函数y ＝f (x )在⎣⎢⎡⎦⎥⎤1e ，e 上的最小值； (3)若g (x )＝f (x )＋12ax 2－(2a ＋1)x ，求证：a ≥0是函数y ＝g (x )在x ∈(1,2)时单调递增的充分不必要条件．(1)解 由f (x )＝x ln x ＋ax ，得f ′(x )＝ln x ＋a ＋1.当a ＝1时，f ′(x )＝ln x ＋2，f (1)＝1，f ′(1)＝2，求得切线方程为y ＝2x －1.(2)解 令f ′(x )＝0，得x ＝e－(a ＋1)． ∴当e －(a ＋1)≤1e ，即a ≥0时，x ∈⎣⎢⎡⎦⎥⎤1e ，e 时f ′(x )≥0恒成立，f (x )单调递增， 此时f (x )min ＝f ⎝ ⎛⎭⎪⎫1e ＝a －1e . 当e －(a ＋1)≥e ，即a ≤－2时，x ∈⎣⎢⎡⎦⎥⎤1e ，e 时f ′(x )≤0恒成立，f (x )单调递减，此时f (x )min ＝f (e)＝a e ＋e.当1e <e －(a ＋1)<e ，即－2<a <0时，x ∈⎣⎢⎡⎭⎪⎫1e ，e －(a ＋1)时f ′(x )<0，f (x )单调递减；当x ∈(e －(a ＋1)，e)时，f ′(x )>0，f (x )单调递增，此时f (x )min ＝f (e－(a ＋1))＝－e －(a ＋1)．(3)证明 g ′(x )＝f ′(x )＋ax －(2a ＋1)＝ln x ＋ax －a ＝ln x ＋a (x －1)，∴当a ≥0时，x ∈(1,2)时，ln x >0，a (x －1)≥0， g ′(x )>0恒成立，函数y ＝g (x )在x ∈(1,2)时单调递增，充分条件成立；又当a ＝－12时，代入g ′(x )＝ln x ＋a (x －1) ＝ln x －12x ＋12. 设h (x )＝g ′(x )＝ln x －12x ＋12，x ∈(1,2)， 则h ′(x )＝1x －12＝2－x 2x>0恒成立，∴当x ∈(1,2)时，h (x )单调递增．又h (1)＝0，∴当x ∈(1,2)时，h (x )>0恒成立．而h (x )＝g ′(x )，∴当x ∈(1,2)时，g ′(x )>0恒成立，函数y ＝g (x )单调递增，∴必要条件不成立．综上，a ≥0是函数y ＝g (x )在x ∈(1,2)时单调递增的充分不必要条件．2．设函数f (x )＝e x －|x －a |，其中a 是实数．(1)若f (x )在R 上单调递增，求实数a 的取值范围；(2)若函数有极大值点x 2和极小值点x 1，且f (x 2)－f (x 1)≥k (x 2－x 1)恒成立，求实数k 的取值范围．解 (1)因为f (x )＝e x －|x －a |＝⎩⎪⎨⎪⎧ e x －x ＋a ，x ≥a ，e x ＋x －a ，x <a ，则f ′(x )＝⎩⎪⎨⎪⎧ e x －1，x ≥a ，e x ＋1，x <a ，因为f (x )在R 上单调递增，所以f ′(x )≥0恒成立，当x <a 时，f ′(x )＝e x ＋1≥1>0恒成立，当x ≥a 时，f ′(x )＝e x－1≥0恒成立， 故应f ′(a )≥0，即a ≥0.(2)由(1)知当a ≥0时，f (x )在R 上单调递增，不符合题意，所以有a <0.此时，当x <a 时，f ′(x )＝e x ＋1≥1>0，f (x )单调递增，当x ≥a 时，f ′(x )＝e x －1，令f ′(x )＝0，得x ＝0，所以f ′(x )<0在(a,0)上恒成立，f (x )在(a,0)上单调递减，f ′(x )>0在(0，＋∞)上恒成立，f (x )在(0，＋∞)上单调递增，所以f (x )极大＝f (a )＝e a ，f (x )极小＝f (0)＝1＋a ，即a <0符合题意．由f (x 2)－f (x 1)≥k (x 2－x 1)恒成立，可得e a －a －1≥ka 对任意a <0恒成立，设g (a )＝e a －(k ＋1)a －1，求导，得g ′(a )＝e a －(k ＋1)，①当k ≤－1时，g ′(a )>0恒成立，g (a )在(－∞，0)上单调递增，又因为g (－1)＝1e＋k <0，与g (a )>0矛盾；②当k ≥0时，g ′(a )<0在(－∞，0)上恒成立，g (a )在(－∞，0)上单调递减， 又因为g (0)＝0，所以此时g (a )≥0恒成立，符合题意；③当－1<k <0时，g ′(a )>0在(－∞，0)上的解集为(ln(k ＋1)，0)，即g (a )在(ln(k ＋1)，0)上单调递增，又因为g (0)＝0，所以g (ln (k ＋1))<0不符合题意． 综上，实数k 的取值范围为[0，＋∞)．3．(2017·江苏泰兴中学质检)已知函数f (x )＝13x 3－mx 2－x ＋13m ，其中m ∈R . (1)求函数y ＝f (x )的单调区间；(2)若对任意的x 1，x 2∈[－1,1]，都有|f ′(x 1)－f ′(x 2)|≤4，求实数m 的取值范围；(3)求函数f (x )的零点个数．解 (1)f ′(x )＝x 2－2mx －1，由f ′(x )≥0，得x ≤m －m 2＋1或x ≥m ＋m 2＋1；故函数f (x )的单调增区间为(－∞，m －m 2＋1)，(m ＋m 2＋1，＋∞)，由f ′(x )<0，得m －m 2－1<x <m ＋m 2＋1，故函数f (x )的单调减区间为(m －m 2＋1，m ＋m 2＋1)．(2)“对任意的x 1，x 2∈[－1,1]，都有|f ′(x 1)－f ′(x 2)|≤4”等价于“函数y ＝f ′(x )，x ∈[－1,1]的最大值与最小值的差小于等于4”．对于f ′(x )＝x 2－2mx －1，对称轴x ＝m .①当m ＜－1时，f ′(x )的最大值为f ′(1)，最小值为f ′(－1)，由f ′(1)－f ′(－1)≤4，即－4m ≤4，解得m ≥－1，舍去；②当－1≤m ≤1时，f ′(x )的最大值为f ′(1)或f ′(－1)，最小值为f ′(m )，由⎩⎪⎨⎪⎧ f ′(1)－f ′(m )≤4，f ′(－1)－f ′(m )≤4，即⎩⎪⎨⎪⎧ m 2－2m －3≤0，m 2＋2m －3≤0，解得－1≤m ≤1；③当m ＞1时，f ′(x )的最大值为f ′(－1)，最小值为f ′(1)，由f ′(－1)－f ′(1)≤4，即4m ≤4，解得m ≤1，舍去．综上，实数m 的取值范围是[－1,1]．(3)由f ′(x )＝0，得x 2－2mx －1＝0，因为Δ＝4m 2＋4＞0，所以y ＝f (x )既有极大值也有极小值．设f ′(x 0)＝0，即x 20－2mx 0－1＝0，x 20＝2mx 0＋1，则f (x 0)＝13x 30－mx 20－x 0＋13m ＝－13mx 20－23x 0＋13m ＝－23x 0(m 2＋1)， 所以极大值f (m －m 2＋1)＝－23(m －m 2＋1)(m 2＋1)＞0， 极小值f (m ＋m 2＋1)＝－23(m ＋m 2＋1)(m 2＋1)＜0， 故函数f (x )有三个零点．4．已知函数f (x )＝x 3＋ax 2－a 2x ＋2，a ∈R .(1)若a <0，试求函数y ＝f (x )的单调递减区间；(2)若a ＝0，且曲线y ＝f (x )在点A ，B (A ，B 不重合)处切线的交点位于直线x ＝2上，证明：A ，B 两点的横坐标之和小于4；(3)如果对于一切x 1，x 2，x 3∈[0,1]，总存在以f (x 1)，f (x 2)，f (x 3)为三边长的三角形，试求正实数a 的取值范围．(1)解 函数f (x )的导函数f ′(x )＝3x 2＋2ax －a 2＝3(x ＋a )⎝ ⎛⎭⎪⎫x －a 3.因为a <0，由f ′(x )<0，解得a 3<x <－a .所以函数y ＝f (x )的单调递减区间为⎝ ⎛⎭⎪⎫a 3，－a .(2)证明 当a ＝0时，f (x )＝x 3＋2.设在点A (x 1，x 31＋2)，B (x 2，x 32＋2)处的切线交于直线x ＝2上一点P (2，t )． 因为y ′＝3x 2，所以曲线y ＝f (x )在点A 处的切线斜率为k ＝3x 21，所以在点A 处的切线方程为y －(x 31＋2)＝3x 21(x －x 1)．因为切线过点P ，所以t －(x 31＋2)＝3x 21(2－x 1)，即2x 31－6x 21＋(t －2)＝0.同理可得2x 32－6x 22＋(t －2)＝0，两式相减得2(x 31－x 32)－6(x 21－x 22)＝0，即(x 1－x 2)(x 21＋x 1x 2＋x 22)－3(x 1－x 2)(x 1＋x 2)＝0，因为x 1－x 2≠0，所以x 21＋x 1x 2＋x 22－3(x 1＋x 2)＝0，即(x 1＋x 2)2－x 1x 2－3(x 1＋x 2)＝0.因为x 1x 2≤⎝ ⎛⎭⎪⎫x 1＋x 222，且x 1≠x 2，所以x 1x 2<⎝ ⎛⎭⎪⎫x 1＋x 222.从而上式可以化为(x 1＋x 2)2－⎝ ⎛⎭⎪⎫x 1＋x222－3(x 1＋x 2)<0，即(x 1＋x 2)(x 1＋x 2－4)<0.解得0<x 1＋x 2<4，即A ，B 两点的横坐标之和小于4.(3)解 由题设知，f (0)<f (1)＋f (1)，即2<2(－a 2＋a ＋3)，解得－1<a <2.又因为a >0，所以0<a <2.因为f ′(x )＝3(x ＋a )⎝ ⎛⎭⎪⎫x －a 3，所以当x ∈⎝ ⎛⎭⎪⎫0，a 3时，f ′(x )<0，f (x )单调递减，当x ∈⎝ ⎛⎭⎪⎫a 3，1时，f ′(x )>0，f (x )单调递增．所以当x ＝a 3时，f (x )有最小值f ⎝ ⎛⎭⎪⎫a 3＝－527a 3＋2.从而条件转化为⎩⎪⎨⎪⎧ f ⎝ ⎛⎭⎪⎫a 3＝－527a 3＋2>0， ①f (0)<2⎝ ⎛⎭⎪⎫－527a 3＋2， ②f (1)<2⎝ ⎛⎭⎪⎫－527a 3＋2. ③由①得a <33235；由②得a <335，再根据0<a <2，得0<a <335.不等式③化为1027a 3－a 2＋a －1<0.令g (a )＝1027a 3－a 2＋a －1，则g ′(a )＝109a 2－2a ＋1>0，所以g (a )为增函数． 又g (2)＝－127<0，所以当a ∈⎝ ⎛⎭⎪⎪⎫0，335时，g (a )<0恒成立，即③成立．所以a 的取值范围为⎝ ⎛⎭⎪⎪⎫0，335.。

压轴大题突破练——函数与导数(二)1． 设函数f(x)＝ae x＋1aex ＋b(a>0)． (1)求f(x)在[0，＋∞)内的最小值；(2)设曲线y ＝f(x)在点(2，f(2))处的切线方程为y ＝32x ，求a ，b 的值．解 (1)f′(x)＝ae x－1ae x ，当f′(x)>0，即x>－ln a 时，f(x)在(－ln a ，＋∞)上递增； 当f′(x)<0，即x<－ln a 时，f(x)在(－∞，－ln a)上递减．①当0<a<1时，－ln a>0，f(x)在[0，－ln a)上递减，在(－ln a ，＋∞)上递增，从而f(x)在[0，＋∞)内的最小值为f(－ln a)＝2＋b ；②当a≥1时，－ln a≤0，f(x)在[0，＋∞)上递增，从而f(x)在[0，＋∞) 内的最小值为f(0)＝a ＋1a ＋b.(2)依题意f′(2)＝ae 2－1ae 2＝32， 解得ae 2＝2或ae 2＝－12(舍去)．所以a ＝2e 2，代入原函数可得2＋12＋b ＝3，即b ＝12.故a ＝2e 2，b ＝12.2． 已知函数f(x)＝aln x －bx 2.(1)当a ＝2，b ＝12时，求函数f(x)在[1e，e]上的最大值；(2)当b ＝0时，若不等式f(x)≥m＋x 对所有的a∈[0，32]，x∈(1，e 2]都成立，求实数m 的取值范围．解 (1)由题知，f(x)＝2ln x －12x 2，f′(x)＝2x －x ＝2－x2x ，当1e≤x≤e 时， 令f′(x)>0得1e≤x<2；令f′(x)<0，得2<x≤e，∴f(x)在[1e ，2)上单调递增，在(2，e]上单调递减，∴f(x)max ＝f(2)＝ln 2－1.(2)当b ＝0时，f(x)＝aln x ，若不等式f(x)≥m＋x 对所有的a∈[0，32]，x∈(1，e 2]都成立，则aln x≥m＋x 对所有的a∈[0，32]，x∈(1，e 2]都成立，即m≤aln x－x ，对所有的a∈[0，32]，x∈(1，e 2]都成立，令h(a)＝aln x －x ，则h(a)为一次函数，m≤h(a)min . ∵x∈(1，e 2]，∴ln x>0，∴h(a)在[0，32]上单调递增，∴h(a)min ＝h(0)＝－x ，∴m≤－x 对所有的x∈(1，e 2]都成立． ∵1<x≤e 2，∴－e 2≤－x<－1， ∴m≤(－x)min ＝－e 2.3． 已知函数f(x)＝x 3－2x ＋1，g(x)＝ln x.(1)求F(x)＝f(x)－g(x)的单调区间和极值；(2)是否存在实常数k 和m ，使得x>0时，f(x)≥kx＋m 且g(x)≤kx＋m ？若存在，求出k 和m 的值；若不存在，说明理由．解 (1)由F(x)＝x 3－2x ＋1－ln x(x>0)，得F′(x)＝3x 3－2x －1x(x>0)，令F′(x)＝0得x ＝1，易知F(x)在(0,1)上单调递减，在(1，＋∞)上单调递增，从而F(x)的极小值为F(1)＝0.(2)易知f(x)与g(x)有一个公共点(1,0)，而函数g(x)在点(1,0)处的切线方程为y ＝x －1，下面只需验证⎩⎪⎨⎪⎧－1－1都成立即可．设h(x)＝x 3－2x ＋1－(x －1)(x>0)， 则h′(x)＝3x 2－3＝3(x ＋1)(x －1)(x>0)．易知h(x)在(0,1)上单调递减，在(1，＋∞)上单调递增，所以h(x)的最小值为h(1)＝0，所以f(x)≥x－1恒成立．设k(x)＝ln x －(x －1)，则k′(x)＝1－xx(x>0)． 易知k(x)在(0,1)上单调递增，在(1，＋∞)上单调递减，所以k(x)的最大值为k(1)＝0，所以g(x)≤x－1恒成立．故存在这样的实常数k ＝1和m ＝－1，使得x>0时，f(x)≥kx＋m 且g(x)≤kx＋m.4． 已知函数f(x)＝x －aln xx，其中a 为常数．(1)证明：对任意x∈R，函数y ＝f(x)的图象恒过定点；(2)当a ＝1时，不等式f(x)＋2b≤0在x∈(0，＋∞)上有解，求实数b 的取值范围； (3)若对任意a∈[m,0)，函数y ＝f(x)在定义域上单调递增，求m 的最小值．解 (1)令ln x ＝0，得x ＝1，且f(1)＝1，所以函数y ＝f(x)的图象恒过定点(1,1)．(2)当a ＝1时，f(x)＝x －ln x x ，所以f′(x)＝1－1－ln x x 2，即f′(x)＝x 2＋ln x －1x 2. 令f′(x)＝0，得x ＝1所以[f(x)]min ＝f(1)＝1.因为f(x)＋2b≤0在x∈(0，＋∞)上有解，所以－2b≥[f(x)]min ，即b≤－12，所以实数b 的取值范围为⎝⎛⎦⎥⎤－∞，－12. (3)f′(x)＝1－a －aln x x 2，即f′(x)＝x 2＋aln x －ax2.令h(x)＝x 2＋aln x －a.由题意可知，对任意a∈[m,0)，f′(x)≥0在x∈(0，＋∞)上恒成立，即h(x)＝x 2＋aln x －a≥0在x∈(0，＋∞)上恒成立．因为h′(x)＝2x ＋a x ＝2x 2＋a x ，令h′(x)＝0，得x ＝－－a2(舍)或x ＝ －a 2. h′(x)，所以[h(x)]解得a≥－2e 3.所以m 的最小值为－2e 3.。