第十二章 第一节 相似三角形的判定及有关性质

选修4－1几何证明选讲第1讲相似三角形的判定及有关性质对应学生203考点梳理1．平行线等分线段定理及其推论(1)定理：如果一组平行线在一条直线上截得的线段相等，那么在其他直线上截得的线段也相等．(2)推论：①经过三角形一边的中点与另一边平行的直线必平分第三边．②经过梯形一腰的中点，且与底边平行的直线平分另一腰．2．平行线分线段成比例定理及推论(1)定理：三条平行线截两条直线，所得的对应线段成比例．(2)推论：平行于三角形一边的直线截其他两边(或两边的延长线)所得的对应线段成比例．3．相似三角形的判定(1)定义：如果在两个三角形中，对应角相等、对应边成比例，则这两个三角形叫做相似三角形．(2)判定定理1：两角对应相等的两个三角形相似．(3)判定定理2：两边对应成比例，并且夹角相等的两个三角形相似．(4)判定定理3：三边对应成比例的两个三角形相似．4．相似三角形的性质(1)性质定理1：相似三角形对应边上的高、中线和它们周长的比都等于相似比．(2)性质定理2：相似三角形的面积比等于相似比的平方．5．直角三角形的射影定理直角三角形斜边上的高是两直角边在斜边上射影的比例中项；两直角边分别是它们在斜边上射影与斜边的比例中项． 如图，在Rt △ABC 中，CD 是斜边上的高， 则有CD 2＝AD ·BD ， AC 2＝AD ·AB ，BC 2＝BD ·AB .考点自测1.如图，已知a ∥b ∥c ，直线m ，n 分别与a ，b ，c 交于点A ，B ，C 和A ′，B ′，C ′，如果AB ＝BC ＝1，A ′B ′＝32，则B ′C ′＝________.解析 由平行线等分线段定理可直接得到答案． 答案 322.如图，BD ，CE 是△ABC 的高，BD ，CE 交于F ，写出图中所有与△ACE 相似的三角形________．解析 由Rt △ACE 与Rt △FCD 和Rt △ABD 各共一个锐角，因而它们均相似，又易知∠BFE ＝∠A ，故Rt △ACE ∽Rt △FBE . 答案 △FCD 、△FBE 、△ABD3. (2013·西安模拟)如图，在△ABC 中，M ，N 分别是AB ，BC 的中点，AN ，CM 交于点O ，那么△MON 与△AOC 面积的比是________． 解析 ∵M ，N 分别是AB 、BC 中点，故MN 綉12AC ， ∴△MON ∽△COA ，∴S △MON S △AOC ＝⎝ ⎛⎭⎪⎫MN AC 2＝14. 答案 1∶44. (2011·陕西)如图，∠B ＝∠D ，AE ⊥BC ，∠ACD ＝90°，且AB ＝6，AC ＝4，AD ＝12，则AE ＝________.解析 由于∠ACD ＝∠AEB ＝90°，∠B ＝∠D ，∴△ABE ∽△ADC ，∴AB AD ＝AE AC . 又AC ＝4，AD ＝12，AB ＝6，∴AE ＝AB ·AC AD ＝6×412＝2. 答案 25. (2010·广东)如图，在直角梯形ABCD 中，DC ∥AB ，CB ⊥AB ，AB ＝AD ＝a ，CD ＝a2，点E ，F 分别为线段AB ，AD 的中点，则EF ＝________.解析 连接DE 和BD ，依题知，EB ∥DC ，EB ＝DC ＝a2，∴EBCD 为矩形，∴DE ⊥AB ，又E 是AB 的中点，所以△ABD 为等腰三角形．故AD ＝DB ＝a ，∵E ，F 分别是AD ，AB 的中点，∴EF ＝12DB ＝12a . 答案 a 2对应学生204考向一 平行线等分线段成比例定理的应用【例1】►如图，F 为▱ABCD 边AB 上一点，连DF 交AC 于G ，延长DF 交CB 的延长线于E . 求证：DG ·DE ＝DF ·EG .证明 ∵四边形ABCD 是平行四边形， ∴AD ∥BC ，AB ∥DC ，AD ＝BC ， ∵AD ∥BC ，∴DG EG ＝AD EC ，又∵AB ∥DC ，∴DF DE ＝BC EC ＝AD EC ，∴DG EG ＝DFDE ， 即DG ·DE ＝DF ·EG .利用平行截割定理解决问题，特别注意被平行线所截的直线，找准成比例的线段，得到相应的比例式，有时需要进行适当的变形，从而得到最终的结果．【训练1】如图，在△ABC 中，DE ∥BC ，EF ∥CD ，若BC ＝3，DE ＝2，DF ＝1，则AB 的长为________．解析由⎩⎨⎧DE ∥BC ，EF ∥CD ，BC ＝3，DE ＝2⇒AE AC ＝AF AD ＝DE BC ＝23，又DF ＝1，故可解得AF ＝2，∴AD ＝3，又AD AB ＝23，∴AB ＝92. 答案 92考向二 相似三角形的判定【例2】►如图，在△ABC 中，D 、E 分别是BC 、AB 上任意点，△EFM ∽△CDM ，求证：△AEF ∽△ABD .证明 ∵△EFM ∽△CDM ，∴∠1＝∠2，∴EF ∥BC ，∴△AEF ∽△ABD .判定三角形相似的思路大致有以下几条：(1)已知条件，判定思路；(2)一对等角，再找一对等角或找夹边成比例； (3)两边成比例，找夹角相等；(4)含有等腰三角形，找顶角相等或找一对底角相等或找腰对应成比例． 【训练2】 如图，网格中的每个小正方形的边长都是1，每个小正方形的顶点叫做格点．△ACB 和△DCE 的顶点都在格点上，ED 的延长线交AB 于点F .(1)求证：△ACB ∽△DCE ； (2)求证：EF ⊥AB .证明 (1)因为DC AC ＝CE BC ＝DE AB ＝23，所以△ACB ∽△DCE . (2)由△ACB ∽△DCE ，知∠B ＝∠E . 又∠BDF ＝∠CDE ，在Rt △CDE 中，∠E ＋∠CDE ＝90°，所以∠BDF＋∠B＝90°，所以∠EFB＝90°，即EF⊥AB.考向三相似三角形的性质【例3】►如图，在Rt△ABC中，∠ACB＝90°，CD⊥AB，E为AC的中点，ED、CB延长线交于一点F.求证：FD2＝FB·FC.证明∵E是Rt△ACD斜边中点，∴ED＝EA，∴∠A＝∠1，∵∠1＝∠2，∴∠2＝∠A，∵∠FDC＝∠CDB＋∠2＝90°＋∠2，∠FBD＝∠ACB＋∠A＝90°＋∠A，∴∠FBD＝∠FDC，∵∠F是公共角，∴△FBD∽△FDC，∴FBFD＝FDFC，∴FD2＝FB·FC.运用相似三角形的性质解决问题，主要考虑相似三角形的对应边、对应角、周长、面积之间的关系，多用于求某条线段的长度、求证比例式的存在、求证等积式的成立等，在做题时应注意认真观察图形特点，确定好对应边、对应角等．【训练3】如图，△ABC中，AB＝AC，AD是边BC的中线，P为AD上一点，CF∥AB，BP的延长线分别交AC，CF于点E，F，求证：BP2＝PE·PF.证明连接CP，∵△ABC为等腰三角形，AD为中线，∴BP＝CP，∠ABP＝∠ACP，∵AB∥CF，∴∠ABP＝∠F，∴∠F＝∠ACP.∵∠EPC为公共角，∴△PCE∽△PFC，∴PCPF＝PEPC，∴PC2＝PF·PE.又∵BP＝PC，∴BP2＝PF·PE.考向四直角三角形射影定理的应用【例4】►已知圆的直径AB＝13，C为圆上一点，过C作CD⊥AB于D(AD＞BD)，若CD＝6，则AD＝________.解析如图，连接AC，CB，∵AB是⊙O的直径，∴∠ACB＝90°.设AD＝x，∵CD⊥AB于D，∴由射影定理得CD2＝AD·DB，即62＝x(13－x)，∴x2－13x＋36＝0，解得x1＝4，x2＝9.∵AD＞BD，∴AD＝9.答案9利用直角三角形的射影定理解决问题首先确定直角边与其射影，再就是要善于将有关比例式进行适当的变形转化，有时还要将等积式转化为比例式或将比例式转化为等积式，并且注意射影定理的其他变式．【训练4】在△ABC中，∠ACB＝90°，CD⊥AB于D，AD∶BD＝2∶3.则△ACD与△CBD的相似比为________．解析如图所示，在Rt△ACB中，CD⊥AB，由射影定理得：CD 2＝AD ·BD ，又∵AD ∶BD ＝2∶3，令AD ＝2x ， BD ＝3x (x ＞0)，∴CD 2＝6x 2，∴CD ＝6x .又∵∠ADC ＝∠BDC ＝90°，∠A ＝∠BCD . ∴△ACD ∽△CBD .易知△ACD 与△CBD 的相似比为AD CD ＝2x 6x ＝63.即相似比为6∶3. 答案6∶3对应学生355(时间：30分钟 满分：60分)一、填空题(每小题5分，共40分)一、填空题(每小题5分，共40分)1. 如图，在Rt △ABC 中，∠ACB ＝90°，CD ⊥AB 于点D ，AD ＝4，sin ∠ACD ＝45，则CD ＝________，BC ＝________.解析 在Rt △ADC 中，AD ＝4，sin ∠ACD ＝AD AC ＝45，得 AC ＝5，CD ＝AC 2－AD 2＝3，又由射影定理AC 2＝AD ·AB ，得AB ＝AC 2AD ＝254.∴BD ＝AB －AD ＝254－4＝94，由射影定理BC 2＝BD ·AB ＝94×254，∴BC ＝154. 答案 3 1542. (2013·揭阳模拟)如图，BD ⊥AE ，∠C ＝90°，AB ＝4，BC ＝2，AD ＝3，则EC ＝________. 解析 在Rt △ADB 中， DB ＝AB 2－AD 2＝7， 依题意得，△ADB ∽△ACE ， ∴DB EC ＝AD AC ，可得EC ＝DB ·ACAD ＝27. 答案 273. (2013·茂名模拟)如图，已知AB ∥EF ∥CD ，若AB ＝4，CD ＝12，则EF ＝________. 解析 ∵AB ∥CD ∥EF ， ∴AB EF ＝BC CF ，BC BF ＝CD EF ， ∴4EF ＝BC BC －BF，BC BF ＝12EF ，∴4(BC －BF )＝12BF ，∴BC ＝4BF ， ∴BC BF ＝14＝12EF ，∴EF ＝3. 答案 34. (2013·湛江模拟)如图，在△ABC 中，D 是AC 的中点，E 是BD 的中点，AE 交于BC 于F ，则BF FC ＝________.解析 如图，过点D 作DG ∥AF ，交BC 于点G ，易得FG ＝GC ，又在三角形BDG 中，BE ＝DE ，即EF 为三角形BDG 的中位线，故BF ＝FG ，因此BFFC ＝12. 答案 125. 如图，∠C ＝90°，∠A ＝30°，E 是AB 中点，DE ⊥AB于E ，则△ADE 与△ABC 的相似比是________．解析 ∵E 为AB 中点，∴AE AB ＝12，即AE ＝12AB ， 在Rt △ABC 中，∠A ＝30°，AC ＝32AB ， 又∵Rt △AED ∽Rt △ACB ，∴相似比为AE AC ＝13.故△ADE 与△ABC 的相似比为1∶ 3. 答案 1∶ 36.如图，AE ∥BF ∥CG ∥DH ，AB ＝12BC ＝CD ，AE ＝12，DH ＝16，AH 交BF 于M ，则BM ＝________，CG ＝________. 解析 ∵AE ∥BF ∥CG ∥DH ，AB ＝12BC ＝CD ，AE ＝12，DH ＝16，∴AB AD ＝14，BM DH ＝AB AD .∴BM 16＝14，∴BM ＝4. 取BC 的中点P ，作PQ ∥DH 交EH 于Q ，如图，则PQ 是梯形ADHE 的中位线，∴PQ ＝12(AE ＋DH )＝12(12＋16)＝14. 同理：CG ＝12(PQ ＋DH )＝12(14＋16)＝15. 答案 4 157. 在△ABC 中，D 是BC 边上的中点，且AD＝AC ，DE ⊥BC ，DE 与AB 相交于点E ，EC 与AD 相交于点F ，S △FCD ＝5，BC ＝10，则DE ＝________.解析 过点A 作AM ⊥BC 于M ，由于∠B ＝∠ECD ，且∠ADC ＝∠ACD ，得△ABC与△FCD 相似，那么S △ABC S △FCD ＝⎝ ⎛⎭⎪⎫BC CD 2＝4又S △FCD ＝5，那么S △ABC ＝20，由于S △ABC ＝12BC ·AM ，由BC ＝10，得AM ＝4，又因为DE ∥AM ，得DE AM ＝BD BM ，∵DM ＝12DC ＝52，因此DE 4＝55＋52，得DE ＝83. 答案 838. 如图，在梯形ABCD 中，AB ∥CD ，且AB ＝2CD ，E 、F 分别是AB 、BC 的中点，EF 与BD 相交于点M .若DB ＝9，则BM ＝________. 解析 ∵E 是AB 的中点， ∴AB ＝2EB .∵AB ＝2CD ，∴CD ＝EB .又AB ∥CD ，∴四边形CBED 是平行四边形． ∴CB ∥DE ，∴⎩⎨⎧∠DEM ＝∠BFM ，∠EDM ＝∠FBM ，∴△EDM ∽△FBM .∴DM BM ＝DEBF . ∵F 是BC 的中点，∴DE ＝2BF . ∴DM ＝2BM .∴BM ＝13DB ＝3. 答案 3二、解答题(共20分)9．(10分)如图，在等腰梯形ABCD 中，AD ∥BC ，AB ＝DC ，过点D 作AC 的平行线DE ，交BA 的延长线于点E ，求证： (1)△ABC ≌△DCB ； (2)DE ·DC ＝AE ·BD .证明 (1)∵四边形ABCD 是等腰梯形，∴AC ＝BD . ∵AB ＝DC ，BC ＝CB ，∴△ABC ≌△DCB . (2)∵△ABC ≌△DCB .∴∠ACB ＝∠DBC ，∠ABC ＝∠DCB .∵AD ∥BC ，∴∠DAC ＝∠ACB ，∠EAD ＝∠ABC . ∴∠DAC ＝∠DBC ，∠EAD ＝∠DCB.∵ED ∥AC ，∴∠EDA ＝∠DAC . ∴∠EDA ＝∠DBC ，∴△ADE ∽△CBD . ∴DE ∶BD ＝AE ∶CD . ∴DE ·DC ＝AE ·BD .10．(10分)如图，△ABC 中，AB ＝AC ，∠BAC ＝90°，AE ＝13AC ，BD ＝13AB ，点F 在BC 上，且CF ＝13BC .求证： (1)EF ⊥BC ； (2)∠ADE ＝∠EBC .证明 设AB ＝AC ＝3a ，则AE ＝BD ＝a ，CF ＝2a . (1)CE CB ＝2a 32a＝23，CF CA ＝2a 3a ＝23.又∠C 为公共角，故△BAC ∽△EFC ，由∠BAC ＝90°. ∴∠EFC ＝90°，∴EF ⊥BC . (2)由(1)得EF ＝2a ，故AE EF ＝a 2a ＝22，AD BF ＝2a 22a ＝22，∴AE EF ＝ADFB .∵∠DAE ＝∠BFE ＝90°， ∴△ADE ∽△FBE ， ∴∠ADE ＝∠EBC .第2讲直线与圆的位置关系对应学生206考点梳理1．圆周角定理(1)圆周角定理及其推论①定理：圆上一条弧所对的圆周角等于它所对的圆心角的一半．②推论(i)推论1：同弧或等弧所对的圆周角相等；同圆或等圆中，相等的圆周角所对的弧也相等．(ii)推论2：半圆(或直径)所对的圆周角是直角；90°的圆周角所对的弦是直径．(2)圆心角定理：圆心角的度数等于它所对弧的度数．2．圆内接四边形的性质与判定定理(1)圆内接四边形的性质定理①定理1：圆内接四边形的对角互补．②定理2：圆内接四边形的外角等于它的内角的对角．(2)圆内接四边形的判定定理及推论①判定定理：如果一个四边形的对角互补，那么这个四边形的四个顶点共圆．②推论：如果四边形的一个外角等于它的内角的对角，那么这个四边形的四个顶点共圆．3．圆的切线的性质及判定定理切线的性质定理及推论(1)定理：圆的切线垂直于经过切点的半径．(2)推论：①推论1：经过圆心且垂直于切线的直线必经过切点．②推论2：经过切点且垂直于切线的直线必经过圆心．4．弦切角的性质弦切角定理：弦切角等于它所夹的弧所对的圆周角．5．与圆有关的比例线段圆中的比例线段1.如图，AB、AC是⊙O的两条切线，切点分别为B、C，D是优弧BC上的点，已知∠BAC＝80°，那么∠BDC＝________.解析连接OB、OC，则OB⊥AB，OC⊥AC，∴∠BOC＝180°－∠BAC＝100°，∴∠BDC＝12∠BOC＝50°.答案50°2．(2012·湖北)如图，点D在⊙O的弦AB上移动，AB＝4，连接OD，过点D 作OD的垂线交⊙O于点C，则CD的最大值为________．解析当OD的值最小时，DC最大，易知D为AB的中点时，DB＝DC＝2最大．答案 23．(2012·北京)如图，∠ACB＝90°，CD⊥AB于点D，以BD为直径的圆与BC 交于点E，则()．A．CE·CB＝AD·DBB．CE·CB＝AD·ABC．AD·AB＝CD2D．CE·EB＝CD2解析在直角三角形ABC中，根据直角三角形射影定理可得CD2＝AD·DB，再根据切割线定理可得CD2＝CE·CB，所以CE·CB＝AD·DB.答案 A4. (2012·湖南)如图所示，过点P的直线与⊙O相交于A，B两点．若P A＝1，AB＝2，PO＝3，则⊙O的半径等于________．解析设圆的半径为r，则(3－r)(3＋r)＝1×3，即r2＝6，解得r＝ 6.答案 65. (2012·天津)如图，已知AB 和AC 是圆的两条弦，过点B 作圆的切线与AC 的延长线相交于点D .过点C 作BD 的平行线与圆相交于点E ，与AB 相交于点F ，AF ＝3，FB ＝1，EF ＝32，则线段CD 的长为________．解析 因为AF ·BF ＝EF ·CF ，解得CF ＝2，所以34＝2BD ，即BD ＝83.设CD ＝x ，AD ＝4x ，所以4x 2＝649，所以x ＝43. 答案 43对应学生207考向一 圆的切线的性质与判定【例1】►如图，已知AB 是⊙O 的直径，直线CD 与⊙O 相切于点C ，AC 平分∠DAB ，AD ⊥CD . (1)求证：OC ∥AD ；(2)若AD ＝2，AC ＝5，求AB 的长． (1)证明 ∵直线CD 与⊙O 相切于点C ， ∴∠DCO ＝∠DCA ＋∠ACO ＝90°， ∵AO ＝CO ，∴∠OAC ＝∠ACO ， ∵AC 平分∠DAB ，∴∠DAC ＝∠OAC ，∴∠DAC＝∠ACO，∴OC∥AD. (2)解连接BC，∵AB是⊙O的直径，∴∠ACB＝90°，∴∠ADC＝∠ACB，又∵∠DAC＝∠BAC，∴△ADC∽△ACB，∴ADAC＝ACAB，∵AD＝2，AC＝5，∴AB＝5 2.利用圆的切线的性质来证明或进行有关的计算，有时需添加辅助线，其中连接圆心和切点的半径是常用辅助线，从而可以构造直角三角形，利用直角三角形边角关系求解，或利用勾股定理求解，或利用三角形相似求解等．【训练1】如图，⊙O是△ABC的外接圆，AB＝AC，过点A作AP∥BC，交BO的延长线于点P.(1)求证：AP是⊙O的切线；(2)若⊙O的半径R＝5，BC＝8，求线段AP的长．(1)证明过点A作AE⊥BC，交BC于点E，∵AB＝AC，∴AE平分BC，∴点O在AE上．又∵AP∥BC，∴AE⊥AP，∴AP为圆O的切线．(2)解BE＝12BC＝4，∴OE＝OB2－BE2＝3，又∵∠AOP＝∠BOE，∴△OBE∽△OP A，∴BEAP＝OEOA，即4AP＝35，∴AP＝203.考向二弦切角定理及推论的应用【例2】►如图，梯形ABCD内接于⊙O，AD∥BC，过B引⊙O的切线分别交DA、CA的延长线于E、F.已知BC＝8，CD＝5，AF＝6，则EF的长为________．解析∵BE切⊙O于B，∴∠ABE＝∠ACB.又∵AD∥BC，∴∠EAB＝∠ABC，∴△EAB∽△ABC，∴BEAC＝AB BC.又∵AE∥BC，∴EFAF＝BEAC，∴ABBC＝EFAF.又∵AD∥BC，∴AB＝CD，∴AB＝CD，∴CDBC＝EFAF，∴58＝EF6，∴EF＝308＝154.答案15 4(1)圆周角定理及其推论与弦切角定理及其推论多用于推出角的关系，从而证明三角形全等或相似，可求线段或角的大小．(2)涉及圆的切线问题时要注意弦切角的转化；关于圆周上的点，常作直线(或半径)或向弦(弧)两端画圆周角或作弦切角．【训练2】如图，已知圆上的弧AC＝BD，过C点的圆的切线与BA的延长线交于E点，证明：(1)∠ACE＝∠BCD；(2)BC2＝BE·CD.证明(1)因为AC＝BD，所以∠BCD＝∠ABC.又因为EC与圆相切于点C，故∠ACE＝∠ABC，所以∠ACE＝∠BCD.(2)因为∠ECB＝∠BDC，∠EBC＝∠BCD，所以△BDC∽△ECB，故BCBE＝CDBC，即BC2＝BE·CD.考向三圆内接四边形性质的应用【例3】►(2013·辽宁三校联考)已知四边形PQRS是圆内接四边形，∠PSR＝90°，过点Q作PR、PS的垂线，垂足分别为点H、K.(1)求证：Q、H、K、P四点共圆；(2)求证：QT＝TS.证明(1)∵∠PHQ＝∠PKQ＝90°，∴Q、H、K、P四点共圆．(2)∵Q、H、K、P四点共圆，∴∠HKS＝∠HQP，①∵∠PSR＝90°，∴PR为圆的直径，∴∠PQR＝90°，∠QRH＝∠HQP，②而∠QSP＝∠QRH，③由①②③得，∠QSP＝∠HKS，TS＝TK，又∵∠SKQ＝90°，∵∠SQK＝∠TKQ，∴QT＝TK，∴QT＝TS.(1)四边形ABCD的对角线交于点P，若P A·PC＝PB·PD，则它的四个顶点共圆．(2)四边形ABCD的一组对边AB、DC的延长线交于点P，若P A·PB＝PC·PD，则它的四个顶点共圆．以上两个命题的逆命题也成立．该组性质用于处理四边形与圆的关系问题时比较有效．【训练3】如图，AB是⊙O的直径，G为AB延长线上的一点，GCD是⊙O 的割线，过点G作AB的垂线，交AC的延长线于点E，交AD的延长线于点F，过G作⊙O的切线，切点为H.求证：(1)C，D，F，E四点共圆；(2)GH2＝GE·GF.证明(1)如图，连接BC.∵AB是⊙O的直径，∴∠ACB＝90°.∵AG⊥FG，∴∠AGE＝90°.又∵∠EAG＝∠BAC，∴∠ABC＝∠AEG.又∵∠FDC＝∠ABC，∴∠FDC＝∠AEG.∴∠FDC＋∠CEF＝180°.∴C，D，F，E四点共圆．(2)∵GH为⊙O的切线，GCD为割线，∴GH2＝GC·GD.由C，D，F，E四点共圆，得∠GCE＝∠AFE，∠GEC＝∠GDF.∴△GCE∽△GFD.∴GCGF＝GEGD，即GC·GD＝GE·GF.∴GH2＝GE·GF.对应学生356(时间：30分钟 满分：60分)一、填空题(每小题5分，共40分)1. 如图，AB 是⊙O 的直径，MN 与⊙O 切于点C ，AC＝12BC ，则sin ∠MCA ＝________.解析 由弦切角定理得，∠MCA ＝∠ABC ， sin ∠ABC ＝ACAB ＝AC AC 2＋BC2＝AC 5AC ＝55. 答案 552. 如图，AB 为⊙O 的直径，C 为⊙O 上一点．AD 和过C 点的切线互相垂直，垂足为D ，∠DAB ＝80°，则∠ACO ＝________.解析 ∵CD 是⊙O 的切线，∴OC ⊥CD ， 又∵AD ⊥CD ，∴OC ∥AD . 由此得，∠ACO ＝∠CAD ， ∵OC ＝OA ，∴∠CAO ＝∠ACO ，∴∠CAD ＝∠CAO ，故AC 平分∠DAB .∴∠CAO ＝40°， 又∵∠ACO ＝∠CAO ，∴∠ACO ＝40°. 答案 40°3. 如图，在△ABC 中，AB ＝AC ，∠C ＝72°，⊙O 过A 、B 两点且与BC 相切于点B ，与AC 交于点D ，连接BD ，若BC ＝5－1，则AC ＝________.解析 由题易知，∠C ＝∠ABC ＝72°，∠A ＝∠DBC ＝36°，所以△BCD ∽△ACB ，又易知BD ＝AD ＝BC ，所以BC 2＝CD ·AC ＝(AC －BC )·AC ，解得AC ＝2. 答案 24. 如图，已知Rt △ABC 的两条直角边AC ，BC 的长分别为3 cm ，4 cm ，以AC 为直径的圆与AB 交于D ，则BDDA ＝________.解析 ∵∠C ＝90°，AC 为圆的直径， ∴BC 为圆的切线，AB 为圆的割线，∴BC 2＝BD ·AB ，即16＝BD ·5，解得BD ＝165， ∴DA ＝BA －BD ＝5－165＝95，∴BD DA ＝169. 答案 1695. 如图，四边形ABCD 是圆O 的内接四边形，延长AB 和DC 相交于点P ，若PB P A ＝12，PC PD ＝13，则BCAD 的值为________．解析 ∵∠P ＝∠P ，∠PCB ＝∠P AD ， ∴△PCB ∽△P AD ， ∴PB PD ＝PC P A ＝BC DA ，∵PB P A ＝12，PC PD ＝13，∴BC AD ＝66. 答案 666. (2012·陕西)如图，在圆O 中，直径AB 与弦CD 垂直，垂足为E ，EF ⊥DB ，垂足为F ，若AB ＝6，AE ＝1，则DF ·DB ＝________.解析 由题意知，AB ＝6，AE ＝1，∴BE ＝5.∴CE ·DE ＝DE 2＝AE ·BE ＝5.在Rt △DEB 中，∵EF ⊥DB ，∴由射影定理得DF ·DB ＝DE 2＝5. 答案 57．(2012·广东)如图，圆O 的半径为1，A 、B 、C 是圆周上的三点，满足∠ABC ＝30°，过点A 作圆O 的切线与OC 的延长线交于点P ，则P A ＝________.解析 如图，连接OA .由∠ABC ＝30°，得∠AOC ＝60°，在直角三角形AOP 中，OA ＝1，于是P A ＝OA tan 60°＝ 3. 答案38. 如图，⊙O 和⊙O ′相交于A 、B 两点，过A 作两圆的切线分别交两圆于C 、D .若BC ＝2，BD ＝4，则AB 的长为________．解析 ∵AC 、AD 分别是两圆的切线， ∴∠C ＝∠2，∠1＝∠D ，∴△ACB ∽△DAB . ∴BC AB ＝AB BD ，∴AB 2＝BC ·BD ＝2×4＝8. ∴AB ＝8＝22(舍去负值)． 答案 2 2 二、解答题(共20分)9．(10分)(2012·新课标全国)如图，D ，E 分别为△ABC 边AB ，AC 的中点，直线DE 交△ABC 的外接圆于F ，G 两点．若CF ∥AB ，证明：(1)CD ＝BC ； (2)△BCD ∽△GBD .证明 (1)因为D ，E 分别为AB ，AC 的中点，所以DE ∥BC .又已知CF ∥AB ，故四边形BCFD 是平行四边形，所以CF ＝BD ＝AD .而CF ∥AD ，连结AF ，所以四边形ADCF 是平行四边形，故CD ＝AF .因为CF ∥AB ，所以BC ＝AF ，故CD ＝BC . (2)因为FG ∥BC ，故GB ＝CF .由(1)可知BD ＝CF ，所以GB ＝BD .所以∠BGD ＝∠BDG . 由BC ＝CD 知∠CBD ＝∠CDB . 而∠DGB ＝∠EFC ＝∠DBC ， 故△BCD ∽△GBD .10．(10分)(2012·辽宁)如图，⊙O 和⊙O ′相交于A ，B 两点，过A 作两圆的切线分别交两圆于C ，D 两点，连结DB 并延长交⊙O 于点E . 证明：(1)AC ·BD ＝AD ·AB ； (2)AC ＝AE .证明 (1)由AC 与⊙O ′相切于A ， 得∠CAB ＝∠ADB ， 同理∠ACB ＝∠DAB ， 所以△ACB ∽△DAB . 从而AC AD ＝AB BD ， 即AC ·BD ＝AD ·AB .(2)由AD 与⊙O 相切于A ，得∠AED ＝∠BAD ， 又∠ADE ＝∠BDA ，得△EAD ∽△ABD . 从而AE AB ＝AD BD ， 即AE ·BD ＝AD ·AB . 结合(1)的结论知，AC ＝AE .选修4－4坐标系与参数方程第1讲坐标系对应学生209考点梳理1．极坐标系的概念(1)极坐标系如图，在平面内取一个定点O，叫做极点，自极点O引一条射线Ox，叫做极轴；再选定一个长度单位，一个角度单位(通常取弧度)及其正方向(通常取逆时针方向)，这样就建立了一个极坐标系．(2)极坐标设M是平面内一点，极点O与点M的距离|OM|叫做点M的极径，记为ρ；以极轴Ox为始边，射线OM为终边的角xOM叫做点M的极角，记为θ.有序数对(ρ，θ)叫做点M的极坐标，记作M(ρ，θ)．一般地，不作特殊说明时，我们认为ρ≥0，θ可取任意实数．特别地，当点M在极点时，它的极坐标为(0，θ)，θ可以取任意实数．(3)点与极坐标的关系一般地，极坐标(ρ，θ)与(ρ，θ＋2kπ)(k∈Z)表示同一个点．特别地，极点O的坐标为(0，θ)(θ∈R)．和直角坐标不同，平面内一个点的极坐标有无数种表示．如果规定ρ>0，0≤θ<2π，那么除极点外，平面内的点可用唯一的极坐标(ρ，θ)表示；同时，极坐标(ρ，θ)表示的点也是唯一确定的．2．直角坐标与极坐标的互化把直角坐标系的原点作为极点，x 轴正半轴作为极轴，且在两坐标系中取相同的长度单位．如图，设M 是平面内的任意一点，它的直角坐标、极坐标分别为(x ，y )和(ρ，θ)，则⎩⎨⎧x ＝ρcos θ，y ＝ρsin θ或⎩⎪⎨⎪⎧ρ2＝x 2＋y 2，tan θ＝yx (x ≠0).3．直线的极坐标方程若直线过点M (ρ0，θ0)，且极轴到此直线的角为α，则它的方程为：ρsin(θ－α)＝ρ0sin (θ0－α)．几个特殊位置的直线的极坐标方程 (1)直线过极点：θ＝θ0和θ＝π－θ0；(2)直线过点M (a,0)且垂直于极轴：ρcos θ＝a ； (3)直线过M ⎝ ⎛⎭⎪⎫b ，π2且平行于极轴：ρsin θ＝b . 4．圆的极坐标方程若圆心为M (ρ0，θ0)，半径为r 的圆方程为ρ2－2ρ0ρcos(θ－θ0)＋ρ20－r 2＝0.几个特殊位置的圆的极坐标方程 (1)当圆心位于极点，半径为r ：ρ＝r ；(2)当圆心位于M (a,0)，半径为a ：ρ＝2a cos_θ； (3)当圆心位于M ⎝ ⎛⎭⎪⎫a ，π2，半径为a ：ρ＝2a sin_θ.考点自测1．若曲线的极坐标方程为ρ＝2sin θ＋4cos θ，以极点为原点，极轴为x 轴正半轴建立直角坐标系，则该曲线的直角坐标方程为________． 解析 ∵ρ＝2sin θ＋4cos θ，∴ρ2＝2ρsin θ＋4ρcos θ. ∴x 2＋y 2＝2y ＋4x ，即x 2＋y 2－2y －4x ＝0. 答案 x 2＋y 2－2y －4x ＝02．(2013·西安五校一模)在极坐标系(ρ，θ)(0≤θ＜2π)中，曲线ρ＝2sin θ与ρcos θ＝－1的交点的极坐标为________．解析 ρ＝2sin θ的直角坐标方程为x 2＋y 2－2y ＝0，ρcos θ＝－1的直角坐标方程为x ＝－1，联立方程，得⎩⎨⎧ x 2＋y 2－2y ＝0，x ＝－1，解得⎩⎨⎧x ＝－1，y ＝1，即两曲线的交点为(－1,1)，又0≤θ＜2π，因此这两条曲线的交点的极坐标为⎝ ⎛⎭⎪⎫2，3π4.答案 ⎝ ⎛⎭⎪⎫2，3π43．(2012·上海)如图，在极坐标系中，过点M (2,0)的直线l 与极轴的夹角α＝π6.若将l 的极坐标方程写成ρ＝f (θ)的形式，则f (θ)＝________.解析 在直线l 上任取一点，再利用正弦定理求直线的极坐标方程．在直线l 上取点P (ρ，θ)，在△OPM 中，由正弦定理得OM sin ∠OPM ＝OPsin ∠OMP，即2sin ⎝ ⎛⎭⎪⎫π6－θ＝ρsin 5π6，化简得ρ＝1sin ⎝ ⎛⎭⎪⎫π6－θ，故f (θ)＝1sin ⎝ ⎛⎭⎪⎫π6－θ. 答案 1sin ⎝ ⎛⎭⎪⎫π6－θ4．(2012·安徽)在极坐标系中，圆ρ＝4sin θ的圆心到直线θ＝π6(ρ∈R )的距离是________．解析 将ρ＝4sin θ化成直角坐标方程为x 2＋y 2＝4y ，即x 2＋(y －2)2＝4，圆心为(0,2)．将θ＝π6(ρ∈R )化成直角坐标方程为x －3y ＝0，由点到直线的距离公式可知圆心到直线的距离d ＝|0－23|2＝ 3.答案 35．(2012·陕西)直线2ρcos θ＝1与圆ρ＝2cos θ相交的弦长为________． 解析 直线的方程为2x ＝1，圆的方程为x 2＋y 2－2x ＝0，圆心为(1,0)，半径r ＝1，圆心到直线的距离为d ＝|2－1|22＋0＝12，设所求的弦长为l ，则12＝⎝ ⎛⎭⎪⎫122＋⎝ ⎛⎭⎪⎫l 22，解得l ＝ 3.答案3对应学生210考向一 极坐标和直角坐标的互化【例1】►(2013·广州测试)设点A 的极坐标为⎝ ⎛⎭⎪⎫2，π6，直线l 过点A 且与极轴所成的角为π3，则直线l 的极坐标方程为________________．解析 ∵点A 的极坐标为⎝ ⎛⎭⎪⎫2，π6，∴点A 的平面直角坐标为(3，1)，又∵直线l 过点A 且与极轴所成的角为π3，∴直线l 的方程为y －1＝(x －3)tan π3，即3x －y －2＝0，∴直线l 的极坐标方程为3ρcos θ－ρsin θ－2＝0，可整理为ρcos ⎝ ⎛⎭⎪⎫θ＋π6＝1或ρsin ⎝ ⎛⎭⎪⎫π3－θ＝1.答案 ρcos ⎝ ⎛⎭⎪⎫θ＋π6＝1或ρsin ⎝ ⎛⎭⎪⎫π3－θ＝1(1)在由点的直角坐标化为极坐标时，一定要注意点所在的象限和极角的范围，否则点的极坐标将不唯一．(2)在曲线的方程进行互化时，一定要注意变量的范围．要注意转化的等价性． 【训练1】 (2013·佛山检测)在平面直角坐标系xOy 中，点P 的直角坐标为(1，－3)．若以原点O 为极点，x 轴正半轴为极轴建立极坐标系，则点P 的极坐标可以是________．解析 由极坐标与直角坐标的互化公式ρcos θ＝x ，ρsin θ＝y 可得，ρcos θ＝1, ρsin θ＝－3，解得ρ＝2，θ＝2k π－π3(k ∈Z )，故点P 的极坐标为⎝ ⎛⎭⎪⎫2，2k π－π3(k∈Z )．答案 ⎝ ⎛⎭⎪⎫2，2k π－π3(k ∈Z )考向二 圆的极坐标方程的应用【例2】►(2013·广州测试)在极坐标系中，若过点(1,0)且与极轴垂直的直线交曲线ρ＝4cos θ于A 、B 两点，则|AB |＝________.解析 过点(1,0)且与极轴垂直的直线的直角坐标方程是x ＝1，曲线ρ＝4cos θ的直角坐标方程是x 2＋y 2＝4x ，即(x －2)2＋y 2＝4，圆心(2,0)到直线x ＝1的距离等于1，因此|AB |＝24－1＝2 3. 答案 2 3解决此类问题的关键还是将极坐标方程化为直角坐标方程．【训练2】 (2013·深圳调研)在极坐标系中，P ，Q 是曲线C ：ρ＝4sin θ上任意两点，则线段PQ 长度的最大值为________．解析 由曲线C ：ρ＝4sin θ，得ρ2＝4ρsin θ，x 2＋y 2－4y ＝0，x 2＋(y －2)2＝4，即曲线C ：ρ＝4sin θ在直角坐标系下表示的是以点(0,2)为圆心、以2为半径的圆，易知该圆上的任意两点间的距离的最大值即是圆的直径长，因此线段PQ 长度的最大值是4. 答案 4考向三 极坐标方程的综合应用【例3】►如图，在圆心的极坐标为A (4,0)，半径为4的圆中，求过极点O 的弦的中点的轨迹．解 设M (ρ，θ)是所求轨迹上任意一点．连接OM 并延长交圆A 于点P (ρ0，θ0)，则有θ0＝θ，ρ0＝2ρ.由圆心为(4,0)，半径为4的圆的极坐标方程为ρ＝8cos θ，得ρ0＝8cos θ0.所以2ρ＝8cos θ，即ρ＝4cos θ.故所求轨迹方程是ρ＝4cos θ.它表示以(2,0)为圆心，2为半径的圆．求轨迹的方法与普通方程的方法相同，但本部分只要求简单的轨迹求法．【训练3】 从极点O 作直线与另一直线ρcos θ＝4相交于点M ，在OM 上取一点P ，使|OM |·|OP |＝12，求点P 的轨迹方程． 解 设动点P 的坐标为(ρ，θ)，则M (ρ0，θ)． ∵|OM |·|OP |＝12.∵ρ0ρ＝12.ρ0＝12ρ. 又M 在直线ρcos θ＝4上，∴12ρcos θ＝4， ∴ρ＝3cos θ.这就是点P 的轨迹方程．对应学生357(时间：30分钟 满分：60分)一、填空题(每小题5分，共40分)1．在极坐标系中，直线l 的方程为ρsin θ＝3，则点⎝ ⎛⎭⎪⎫2，π6到直线l 的距离为________．解析 ∵直线l 的极坐标方程可化为y ＝3，点⎝ ⎛⎭⎪⎫2，π6化为直角坐标为(3，1)，∴点⎝ ⎛⎭⎪⎫2，π6到直线l 的距离为2.答案 22．(2013·汕头调研)在极坐标系中，ρ＝4sin θ是圆的极坐标方程，则点A ⎝ ⎛⎭⎪⎫4，π6到圆心C 的距离是________．解析 将圆的极坐标方程ρ＝4sin θ化为直角坐标方程为x 2＋y 2－4y ＝0，圆心坐标为(0,2)．又易知点A ⎝ ⎛⎭⎪⎫4，π6的直角坐标为(23，2)，故点A 到圆心的距离为(0－23)2＋(2－2)2＝2 3. 答案 2 33．在极坐标系中，过圆ρ＝6cos θ－22sin θ的圆心且与极轴垂直的直线的极坐标方程为________．解析 由ρ＝6cos θ－22sin θ⇒ρ2＝6ρcos θ－22ρsin θ，所以圆的直角坐标方程为x 2＋y 2－6x ＋22y ＝0，将其化为标准形式为(x －3)2＋(y ＋2)2＝11，故圆心的坐标为(3，－2)，所以过圆心且与x 轴垂直的直线的方程为x ＝3，将其化为极坐标方程为ρcos θ＝3. 答案 ρcos θ＝34．(2013·华南师大模拟)在极坐标系中，点M ⎝ ⎛⎭⎪⎫4，π3到曲线ρcos ⎝ ⎛⎭⎪⎫θ－π3＝2上的点的距离的最小值为________．解析 依题意知，点M 的直角坐标是(2,23)，曲线的直角坐标方程是x ＋3y －4＝0，因此所求的距离的最小值等于点M 到该直线的距离，即为|2＋23×3－4|12＋(3)2＝2.答案 25．在极坐标系中，圆ρ＝4上的点到直线ρ(cos θ＋3sin θ)＝8的距离的最大值是________．解析 把ρ＝4化为直角坐标方程为x 2＋y 2＝16，把ρ(cos θ＋3sin θ)＝8化为直角坐标方程为x ＋3y －8＝0，∴圆心(0,0)到直线的距离为d ＝82＝4.∴直线和圆相切，∴圆上的点到直线的最大距离是8. 答案 86．在极坐标系中，曲线C 1：ρ＝2cos θ，曲线C 2：θ＝π4，若曲线C 1与C 2交于A 、B 两点，则线段AB ＝________.解析 曲线C 1与C 2均经过极点，因此极点是它们的一个公共点．由⎩⎪⎨⎪⎧ρ＝2cos θ，θ＝π4得⎩⎪⎨⎪⎧ρ＝2，θ＝π4，即曲线C 1与C 2的另一个交点与极点的距离为2，因此AB ＝ 2. 答案27．(2013·湛江模拟)在极坐标系中，圆C 的极坐标方程为：ρ2＋2ρcos θ＝0，点P的极坐标为⎝ ⎛⎭⎪⎫2，π2过点P 作圆C 的切线，则两条切线夹角的正切值是________．解析 圆C 的极坐标方程：ρ2＋2ρcos θ＝0化为普通方程：(x ＋1)2＋y 2＝1，点P 的直角坐标为(0,2)，圆C 的圆心为(－1,0)．如图，当切线的斜率存在时，设切线方程为y ＝kx ＋2，则圆心到切线的距离为|－k ＋2|k 2＋1＝1，∴k ＝34，即tan α＝34.易知满足题意的另一条切线的方程为x ＝0.又∵两条切线的夹角为α的余角，∴两条切线夹角的正切值为43. 答案 438．若直线3x ＋4y ＋m ＝0与曲线ρ2－2ρcos θ＋4ρsin θ＋4＝0没有公共点，则实数m 的取值范围是________．解析 注意到曲线ρ2－2ρcos θ＋4ρsin θ＋4＝0的直角坐标方程是x 2＋y 2－2x ＋4y ＋4＝0，即(x －1)2＋(y ＋2)2＝1.要使直线3x ＋4y ＋m ＝0与该曲线没有公共点，只要圆心(1，－2)到直线3x ＋4y ＋m ＝0的距离大于圆的半径即可，即|3×1＋4×(－2)＋m |5＞1，|m －5|＞5，解得，m ＜0或m ＞10.答案 (－∞，0)∪(10，＋∞) 二、解答题(共20分)9．(10分)以直角坐标系的原点O 为极点，x 轴的正半轴为极轴，已知点P 的直角坐标为(1，－5)，点M 的极坐标为⎝ ⎛⎭⎪⎫4，π2，若直线l 过点P ，且倾斜角为π3，圆C 以M 为圆心、4为半径．(1)求直线l 的参数方程和圆C 的极坐标方程； (2)试判定直线l 和圆C 的位置关系．解 (1)由题意，直线l 的普通方程是y ＋5＝(x －1)tan π3，此方程可化为y ＋5sin π3＝x －1cos π3，令y ＋5sin π3＝x －1cos π3＝a (a 为参数)，得直线l 的参数方程为⎩⎪⎨⎪⎧x ＝12a ＋1，y ＝32a －5(a为参数)．如图，设圆上任意一点为Q (ρ，θ)，则在△QOM 中， 由余弦定理，得QM 2＝QO 2＋OM 2－2·QO ·OM cos ∠QOM ， ∴42＝ρ2＋42－2×4ρcos ⎝ ⎛⎭⎪⎫θ－π2.化简得ρ＝8sin θ，即为圆C 的极坐标方程． (2)由(1)可进一步得出圆心M 的直角坐标是(0,4)， 直线l 的普通方程是3x －y －5－3＝0， 圆心M 到直线l 的距离d ＝|0－4－5－3|3＋1＝9＋32＞4，所以直线l 和圆C 相离．10．(10分)(2012·辽宁)在直角坐标系xOy 中，圆C 1：x 2＋y 2＝4，圆C 2：(x －2)2＋y 2＝4.(1)在以O 为极点，x 轴正半轴为极轴的极坐标系中，分别写出圆C 1，C 2的极坐标方程，并求出圆C 1，C 2的交点坐标(用极坐标表示)； (2)求圆C 1与C 2的公共弦的参数方程． 解 (1)圆C 1的极坐标方程为ρ＝2， 圆C 2的极坐标方程为ρ＝4cos θ. 解⎩⎨⎧ρ＝2，ρ＝4cos θ得ρ＝2，θ＝±π3， 故圆C 1与圆C 2交点的坐标为⎝ ⎛⎭⎪⎫2，π3，⎝ ⎛⎭⎪⎫2，－π3.注：极坐标系下点的表示不唯一．(2)法一 由⎩⎨⎧x ＝ρcos θ，y ＝ρsin θ得圆C 1与C 2交点的直角坐标分别为(1，3)，(1，－3)．故圆C 1与C 2的公共弦的参数方程为⎩⎨⎧x ＝1，y ＝t (－3≤t ≤3)．⎝ ⎛⎭⎪⎪⎫或参数方程写成⎩⎨⎧x ＝1，y ＝y (－3≤y ≤3) 法二 将x ＝1代入⎩⎨⎧x ＝ρcos θ，y ＝ρsin θ得ρcos θ＝1， 从而ρ＝1cos θ.于是圆C 1与C 2的公共弦的参数方程为 ⎩⎨⎧x ＝1，y ＝tan θ⎝ ⎛⎭⎪⎫－π3≤θ≤π3.第2讲 参数方程对应学生211考点梳理1．参数方程的概念一般地，在平面直角坐标系中，如果曲线上任意一点的坐标x ，y 都是某个变数t 的函数⎩⎨⎧x ＝f (t )y ＝g (t )①，并且对于t 的每一个允许值，由方程组①所确定的点M (x ，y )都在这条曲线上，那么方程组①就叫做这条曲线的参数方程，联系变数x ，y 的变数t 叫做参变数，简称参数，相对于参数方程而言，直接给出点的坐标间关系的方程叫做普通方程． 2．参数方程和普通方程的互化(1)曲线的参数方程和普通方程是曲线方程的不同形式，一般地可以通过消去参数而从参数方程得到普通方程．(2)如果知道变数x ，y 中的一个与参数t 的关系，例如x ＝f (t )，把它代入普通。

九年级数学科辅导讲义（第讲）学生姓名：授课教师：授课时间：一、相关概念：1. 相似图形：形状相同的图形。

2. 相似多边形的性质：对应角相等，对应边成比例。

3. 相似比：相似多边形对应边的比。

二、平行线分线段成比例定理:三条平行线截两条直线，所得的对应线段的比相等三、相似三角形的判定✓通过定义（三边对应成比例，三角相等）✓平行于三角形一边的直线✓三边对应成比例（SSS）✓两边对应成比例且夹角相等（SAS）✓两角对应相等（AA）✓两直角三角形的斜边和一条直角边对应成比例（HL）四、相似三角形的性质✓对应角相等。

✓对应边成比例。

✓对应高的比等于相似比。

✓对应中线的比等于相似比。

✓对应角平分线的比等于相似比。

✓周长比等于相似比。

✓面积比等于相似比的平方。

五、位似：✓位似图形的概念：如果两个图形不仅相似,而且对应顶点的连线相交于一点,像这样的两个图形叫做位似图形, 这个点叫做位似中心, 这时的相似比又称为位似比.✓在平面直角坐标系中,如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k.考点一一、选择题（每小题3分，共24分）1.下列命题：①所有的等腰三角形都相似，②所有的等边三角形都相似，③所有的等腰直角三角形都相似，④所有的直角三角形都相似.其中，正确的是 ( )A.②③B.②③④C.③④D.②④2.有两个顶角相等的等腰三角形框架，其中一个三角形框架的腰长为6，底边长为4，另一个三角形框架的底边长为2，则这个三角形框架的腰长为 ( ) A.6 B.4 C.3 D.23.如图，点P 是△ABC 的边AB 上的一点，过点P 作直线（不与直线AB 重合）截△ABC ，使截得的三角形与原三角形相似.满足这样条件的直线最多有 ( ) A.2条 B.3条 C.4条 D.5条4.如图，E 是□ABCD 的边BC 延长线上的一点，连结AE 交CD 于F ，则图中共有相似三角形 （ ）A.1对B.2对C.3对D.4对5.两个相似菱形边长的比是1:4，那么它们的面积比是 ( ) A ．1:2 B ．1:4 C ．1:8 D ．1:166.下列条件中，不能判定以A /、B /、C /为顶点的三角形与△ABC 相似的是（ ） A.∠C=∠C /=90°,∠B=∠A /=50° B.AB=AC ，A /B /=A /C /，∠B=∠B /C.∠B=∠B /，////C B BC B A AB =D. ∠A=∠A /，////C B BC B A AB =7.△ABC 的周长等于16，D 是AC 的中点，DE ∥AB ，交BC 于点E ，则△DEC 的周长等于( ) A.2 B.4 C.6 D.88.在□ABCD 中，E 是BC 的中点，F 是BE 的中点，AE 与DF 相交于H ，则△EFH 的面积与△ADH 的面积的比值为 （ ） A ．21 B ． 81 C ．161 D ．41二、填空题（每小题3分，共18分）9．有一张比例尺为1∶4000的地图上，一块多边形地区的周长是60cm ，则这个地区的实际周长________。

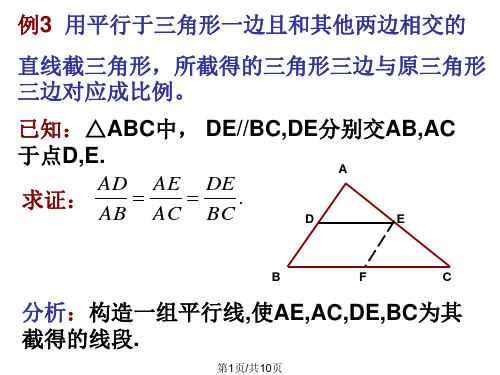
相似三角形的判定及有关性质【学习目标】1. 了解平行线截割定理，会证明并应用直角三角形射影定理．2. 理解并掌握相似三角形的判定及性质。

【要点梳理】要点一、平行截割定理 1。

平行线等分线段定理：如果一组平行线在一条直线上截得的线段相等，那么在其他与这组平行线相交的直线上截得的线段也相等。

推论1：经过三角形一边的中点与另一边平行的直线必平分第三边． 推论2：经过梯形一腰的中点，且与底边平行的直线平分另一腰． 2．平行线分线段成比例定理：三条平行线截两条直线，所得的对应线段成比例． 如右图：l 1∥l 2∥l 3，则，，，…AB BC DE EF AB AC DE DF BC AC EFDF=== 推论：平行于三角形一边的直线截其他两边（或两边的延长线）所得的对应线段成比例．要点诠释：由上述定理可知：在证明有关比例线段时，辅助线往往作平行线,但应遵循的原则是不要破坏条件中的两条线段的比及所求的两条线段的比.要点二、相似三角形 1.定义对应角相等，对应边成比例的两个三角形叫做相似三角形，相似三角形对应边的比值叫做相似比（或相似系数）．相似用符号“∽”表示，读作“相似于”。

要点诠释：关于相似三角形要注意以下几点：① 对应性：即两个三角形相似时，一定要把表示对应顶点的字母写在对应位置上，这样写比较容易找到相似三角形的对应角和对应边．② 顺序性：相似三角形的相似比是有顺序的． ③ 两个三角形形状一样，但大小不一定一样．④ 全等三角形是相似比为1的相似三角形．二者的区别在于全等要求对应边相等，而相似要求对应边成比例．2．相似三角形的判定定理①两角对应相等的两个三角形相似。

②两边对应成比例且夹角相等的两个三角形相似。

③三边对应成比例的两个三角形相似。

④平行于三角形一边的直线和其他两边（或两边的延长线）相交，所构成的三角形与原三角形相似． 3．相似直角三角形的判定定理①如果两个直角三角形有一个锐角对应相等，那么它们相似． ②如果两个直角三角形的两条直角边对应成比例，那么它们相似．③如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边对应成比例，那么这两个直角三角形相似。

第一讲相似三角形的判定及有关性质学习提纲一、“引言”告诉我们要注意四点：1.注重证明.利用数学证明的严谨性，训练我们的逻辑推理技能，提高我们的逻辑思维能力.（思维能力主要体现在：严谨性、深刻性、灵活性、批判性、创新性）2.强调过程.正确的数学结论（包括定义、定理、公理、公式、性质等）既要理解并记住内容，也要领悟背景，经历发现和证明，提高我们提出问题和解决问题的能力.“大胆猜测，小心求证”.3.突出思想.努力领悟数学思想方法，善于反思和总结，这是快速提高解题能力的捷径.4.加强探究.注重书中的“观察”、“思考”、“探究”等地方，我们不仅能做别人出的题，不仅能猜测出别人怎么出题，逐步我们还能自己编题给自己做或出题给别人做.此外，教科书中强调类比、推广、特殊化、化归等思想方法，我们在学习中尽最大可能常用以下的逻辑思考方法：推广类比当前内容类比特殊化二、“学习总结报告”告诉我们应当把握五个方面：1.明确数学证明的地位和作用.2.领会知识的系统性.各专题的知识结构和整体知识结构，知识间的内在联系，更大的知识体系.3.体验知识发展的过程.突出知识的探究与发现4.掌握重要的数学思想方法.主要数学思想方法包括：特殊化思想方法、化归思想方法，分类思想方法、运动变化思想方法，涉及到观察、实验、猜想、归纳等合情推理的方法，也涉及到演绎推理、反证法、同一法等逻辑推理的方法，深入体会，逐步掌握.5.知道数学知识应用的广泛性.三、整体知识结构四、第一讲相似三角形的判断及有关性质（一）.重点：1.理解相似三角形的判定定理，能应用判定定理解决相关的几何问题.2.理解相似三角形的性质，能应用这些性质解决相关的几何问题.3.体验相似三角形判定及性质的探究，感受和体会蕴涵在知识与探究过程中的数学思想方法.（二）难点：1.判定定理2的证明.2.相似三角形拓广性质的探究.3.利用同一法证明几何问题.（三）本讲知识结构五、补充内容：三角形的常用公式及关系 1.三角形面积公式：（1）111222a b c S ah bh ch ∆===（2）111sin sin sin 222S bc A ac B ab C ∆===（3）海伦公式：S ∆=，式中1()2p a b c =++ （4）S pr ∆=，式中1()2p a b c =++，r 是三角形内切圆的半径（5）22sin sin sin 4abcS R A B C R∆==，式中R 是三角形外接圆的半径 （6）三角形三个顶点为112233(,),(,),(,)A x y B x y C x y ，则11223311|1|21x y S x y x y ∆= 2.正弦定理：2s i n s i n s i na bcR A B C ===，式中R 是三角形外接圆的半径 3.余弦定理：2222c o s a b c b c A =+-， 2222c o s b a c a c B =+-， 2222c o s c a b a b C =+-， 4.射影定理：c o s c o s a b C c B =+， c o s c o s b a C c A =+， c o s c o s c a B b A=+ 六、问题选讲试题选讲1. 任作一个四边形ABCD ，再分别作A 、B 、C 、D 关于B 、C 、D 、A 的对称点A '、B '、C '、D '，若A B C D 的面积为S ，则四边形A 'B 'C 'D '的面积是（ C ） A ．3s B ．4s C ．5s D ．6s2.在锐角ABC ∆中，已知,AB c AC b ==()b c >，060BAC ∠=，其垂心为H ，外心为O ，OH 与AB 、AC 分别交于点D 、E ，则DE 的长为（ ）（C ）（A ）2()b c - （Ｂ）3()b c - （Ｃ）3b c + （Ｄ）2b c+3.边长为5的菱形，它的一条对角线的长不大于6，另一条对角线的长不小于6，则这个菱形两条对角线长度之和的最大值是（ ）A ．B ．14C ．D ．12解析：设菱形A B C D 的对角线,A C B D交于点O ，6,6AC BD ≥≤，则2225(1)3(2)AO BO AO BO⎧+=⎨≥≥⎩可令3,3AO a BO b =+=-，其中0,0a b ≥≥，由（1）,a b 不同时为0，且0a >，于是2222(3)(3)25AO BO a b +=++-=，即2()6()9162a b a b ab -+-+=-，3a b -=-0b =时，a b -取得最大值1，故2(3)2(3)122()AC BD a b a b +=++-=+-的最大值为14.BACQ· 4. 如图, Q 为等边ABC ∆内一点, 已知6,8,10QA QB QC ===,则最接近ABC ∆的面积的整数是A ．79B ．80C ．158D ．159解析:把AQC ∆绕点A 顺时针旋转060至ADB ∆位置,则QDB ∆的三边长为6,8,10,所以QDB ∆是直角三角形,090,DQB ∠=可见0009060150AQB ∠=+=.在ABQ ∆中,222068268cos150100AB=+-⨯⨯⨯=+所以2(10079.30ABC S AB ∆==+≈ 故最接近ABC ∆的面积的整数是79.5.在ABC ∆中,045A ∠=,AD BC ⊥于点D ,2CD =,3BD =,则AB AC⋅的值为方法很多，易求得6,AD AB AC ===AB AC ⋅=6. 已知等腰Rt ABC ∆中，90ACB ∠=︒，点D 为Rt ABC ∆内一点，且15DBC DCB ∠=∠=︒.（Ⅰ）求证：AD AC =; （Ⅱ）求CAD ∠的度数.BACQD·7. 如图，把三根长为1㎝的火柴杆和三根长为3㎝的火柴杆顺次相接摆放在圆周上，构成一个六边形ABCDEF ，此六边形的面积是由三根长为1㎝的火柴杆所构成的等边三角形面积的多少倍？任意调整上述六根火柴杆的摆放次序是否改变上述结果？证明你的结论.方法一：每对一大一小的弧的度数之和为0120，0120A ∠=，FAB ∆，线段BF =FOB ∆是顶角为0120的等腰三角形，面积为12， 六边形ABCDEF 的面积等于3个四边形ABOF的面积，为4， 是边长为122倍。

相似三角形的判定与性质一、学习要求1．了解相似多边形的概念，知道相似多边形的性质；2．了解两个三角形相似的概念，会利用相似三角形的性质与判定进行简单的推理和计算；3．会利用相似三角形的知识解决一些实际问题；认识现实生活中物体的相似；会运用相似多边形的性质解决简单的问题；利用图形的相似解决一些简单实际问题.二、知识梳理及例题分析1．相似三角形的概念：在和中，如果，，，，我们就说和相似，记作∽，就是它们的相似比(注意：要把表示对应顶点的字母写在对应的位置上).思考：在中,点是边的中点,，交于点，与有什么关系？猜想：与相似. 证明：在与中，∴，.过点作，交于点在中，，，∴. 又，∴∴，∴∽(对应角相等，对应边的比相等的两三角形相似)，相似比为.改变点在上的位置，可以进一步猜想以上两个三角形依然相似.2．相似三角形的判定定理：平行于三角形一边的直线和其他两边相交，所构成的三角形与原三角形相似.小结：判定三角形相似的方法：(1)相似三角形的定义；(2)由平行线得相似.思考：对比三角形全等判定的简单方法()，看是否也有简便的方法？已知：在和中，.求证：∽.分析：要证明∽，可以先作一个与全等的三角形，证明它与相似，这里所作的三角形是证明的中介，它把与联系起来证明：在线段(或它的延长线)上截取，过点作，交于点，根据前面的结论可得∽. ∴又，∴∴同理：∴≌∴∽相似三角形的判定定理：如果两个三角形的三组对应边的比相等，那么这两个三角形相似.可简单说成：三边对应成比例，两三角形相似.思考：若，，与是否相似呢？相似三角形的判定定理：如果两个三角形的两组对应边的比相等，并且相应的夹角相等，那么这两个三角形相似可简单说成：两边对应成比例且夹角相等，两三角形相似.进一步引申：若，，与是否相似呢？不一定问：全等中的边边角不能用，那么边边角也不能证相似，反例同全等.例1.根据下列条件，判断与是否相似，并说明理由：(1)，，；，，.(2)，，；，，.解：(1)，∴又∴∽问：这两个相似三角形的相似比是多少？(答：是)(2)，，∴与的三组对应边的比不等，它们不相似.问：要使两三角形相似，不改变的长，的长应当改为多少？(答：)例2.要做两个形状相同的三角形框架，其中一个三角形框架的三边的长分别为4、5、6，另一个三角形的一边长为2，怎样选料可使这两个三角形相似？注：此题没说2与哪条边是对应边，所以要进行分类讨论.可以是：，3；或，；或，.注：当两三角形相似而边不确定时，要注意分类讨论.相似三角形的判定定理：如果一个三角形的两个角与另一个三角形的两个角对应相等的，那么这两个三角形相似.简单说成：两角对应相等，两三角形相似.3．三角形相似的判定的应用例3.如图，弦和弦相交于内一点，求证：.分析:题目中求证的是等积式，我们可以转化为比例式，从而找到应证哪两个三角形相似.同时圆当中同弧或等弧所对的圆周角相等要会灵活应用.证明：连接，.在∴∽∴.例4.已知：如图，在中，于点.(1)求证：∽∽；(2)求证：；；(此结论称之为射影定理)(3)若，求.(4)若，求.分析：(1)利用两角相等证相似；(2)把相似三角形的相似比的比例式改为乘积式即可；(3)利用射影定理和勾股定理直接求；(4)利用上面的定理和方程求.进一步引申：在中，于点，这个条件可以放在圆当中，是直径，是圆上任意一点，于点，则可得到双垂直图形.例.已知：∽，分别是两个三角形的角平分线.求证：.分析：先利用相似三角形的性质得到，，再利用角平分线的定义，得到，从而可证得∽，则比例式可证得得到：相似三角形对应角的平分线的比等于相似比.那么对应中线的比，对应高线的比呢？4．相似三角形的性质(1)相似三角形的对应角相等，对应边的比相等，都等于相似比.(2)相似三角形对应高的比，对应角的平分线的比，对应中线的比都等于相似比.(3)相似三角形周长的比等于相似比；相似多边形周长的比等于相似比.证明：如果∽，相似比为，那么.因此，，.从而，.同理可得相似多边形对应周长的比也等于相似比.如图，已知：∽，相似比为.分别作出与的高和和都是直角三角形，并且，∽相似多边形面积的比等于相似比的平方.对于两个相似多边形，可以把他们分成若干个相似三角形证明.例5.如图，在和中，，，，的周长是24，面积是48，求的周长和面积.解：在和中，，又∽，相似比为.的周长为，的面积是.例6.已知点P在线段AB上，点O在线段AB的延长线上.以点O为圆心，OP为半径作圆，点C是圆O上的一点.(1)如图，如果AP=2PB，PB=BO.求证：△CAO∽△B CO；(2)如果AP=m(m 是常数，且)，BP=1，OP是OA、OB的比例中项.当点C在圆O 上运动时，求的值(结果用含m的式子表示)；(3)在(2)的条件下，讨论以BC为半径的圆B和以CA为半径的圆C的位置关系，并写出相应m的取值范围.分析：此题第1问：利用两边的比相等，夹角相等证相似. 即，第2问：设∵是的比例中项，∴是的比例中项即∴解得又∵第3问：∵ ，，即当时，两圆内切；当时，两圆内含；当时，两圆相交.例7.如图，已知中，，，，，点在上，(与点不重合)，点在上.(1)当的面积与四边形的面积相等时，求的长.(2)当的周长与四边形的周长相等时，求的长.(3)在上是否存在点，使得为等腰直角三角形？要不存在，请说明理由；若存在，请求出的长.解：(1)，∽(2)∵的周长与四边形的周长相等∽(3)在线段上存在点，使得为等腰直角三角形.过作于，则，设交于若，则.∵∽若，同理可求. 若，∽∴ 在线段上存在点，使得为等腰直角三角形，此时，或.三、总结归纳：1、相似三角形的判定：(1)相似三角形的定义；(2)平行得相似；(3)三边的比相等；(4)两边的比相等，夹角相等；(5)两角对应相等.三角形相似判定的方法较多，要根据已知条件适当选择.3、相似三角形的常见图形及其变换：4、证明四条线段成比例的常用方法：(1)线段成比例的定义(2)三角形相似的预备定理(3)利用相似三角形的性质(4)利用中间比等量代换(5)利用面积关系证明题常用方法归纳：(1)通过“横找”“竖看”寻找三角形，即横向看或纵向寻找的时候一共各有三个不同的字母，并且这几个字母不在同一条直线上，能够组成三角形，并且有可能是相似的，则可证明这两个三角形相似，然后由相似三角形对应边成比例即可证的所需的结论.(2)若没有三角形(即横向看或纵向寻找的时候一共有四个字母或者三个字母，但这几个字母在同一条直线上)，则需要进行“转移”(或“替换”)，常用的“替换”方法有这样的三种：等线段代换、等比代换、等积代换.(3)若上述方法还不能奏效的话，可以考虑添加辅助线(通常是添加平行线)构成比例.以上步骤可以不断的重复使用，直到被证结论证出为止.。