江苏省2016届高三数学一轮复习专题突破训练:三角函数带答案
- 格式:doc
- 大小:1.68 MB
- 文档页数:13

2016届高三数学理一轮复习专题突破训练——三角函数一、选择、填空题1、在ABC ∆中,6,5,4===c b a 则=CAsin 2sin .2、设函数)sin()(ϕω+=x x f ,0,0>>ωA ,若)(x f 在区间]2,6[ππ上具有单调性,且⎪⎭⎫ ⎝⎛-=⎪⎭⎫ ⎝⎛=⎪⎭⎫ ⎝⎛6322πππf f f ,则)(x f 的最小正周期为________.3、在△ABC 中,若A 3π=,cosB=3,BC = 6,则 AC =A .B . 4C .D 4、23sin()6π-=(A ) (B )12- (C )12 (D 5、将函数1cos()26y x π=-图象向左平移3π个长度单位,再把所得图象上各点的横坐标缩短到原来的一半(纵坐标不变),所得图象的函数解析式是 (A) cos(+)6y x π= (B) 1cos 4y x = (C) cos y x = (D) 1cos()43y x π=- 6、已知函数()cos(2)f x x ϕ=+(ϕ为常数)为奇函数,那么cos ϕ=( )(A )2-(B )0(C )2(D )17、在△ABC 中,角 A , B , C 所对的边分别为a , b , c ,若则a= .8、如图,某地一天中6时至14时的温度变化曲线近似满足函数()b x A y ++=ϕωsin (其中 0ω>,2ϕπ<<π), 则估计中午12时的温度近似为( )A. 30 ℃B. 27 ℃C.25 ℃D.24 ℃9、要得到函数πsin(2)3y x =+的图象,只需将函数sin 2y x =的图象( ) (A )向左平移3π个单位 (B )向左平移6π个单位(C )向右平移3π个单位 (D )向右平移6π个单位10、设函数()sin(2)3f x x π=-的图象为C ,下面结论中正确的是 A .函数()f x 的最小正周期是2π B .图象C 关于点(,0)6π对称C .图象C 可由函数()sin 2g x x =的图象向右平移3π个单位得到D .函数()f x 在区间(,)2ππ-12上是增函数11、在ABC ∆中,a ,b π3B =,则A 等于 (A ) π6 (B ) π4 (C ) 3π4 (D ) π4或3π412、在锐角∆ABC 中,角A ,B ,C 所对的边分别为a ,b ,c . 若2a b =,sin B =,则( )(A )3A π=(B )6A π= (C )sin A =(D )2sin 3A =13、在△ABC 中,3a =,b =60B = ,则c = ;△ABC 的面积为_______ 14、将函数()cos 3f x x π⎛⎫=+ ⎪⎝⎭的图象上各点的纵坐标不变,横坐标伸长到原来的2倍,所得图象的一条对称轴方程可能是A .3x π=B .6x π=-C .3x π=-D .23x π=-15、设sin393,cos55,tan50a b c =︒=︒=︒,则,,a b c 的大小关系为( )A. a b c << B .c b a << C .b a c << D .a c b <<二、解答题1、已知函数22sin 22cos 2sin 2)(x x x x f -=.(Ⅰ) 求)(x f 的最小正周期;(Ⅱ) 求)(x f 在区间[]0,π-上的最小值.2、如图,在ABC ∆中,8,3==∠AB B π,点D 在BC 边上,且71cos ,2=∠=ADC CD (1)求BAD ∠sin (2)求AC BD ,的长3、在△ABC 中,a =3,b =,∠B =2∠A ,(1)求cos A 的值; (2)求c 的值.4、已知函数 f (x ) = cos 2x x cos x ,x ∈R .(1)求 f (x )的最小正周期和单调递减区间;(2)设 x = m (m ∈R )是函数 y = f (x )图象的对称轴,求sin 4m 的值.5、已知函数2sin 22sin ()sin x xf x x-=.(Ⅰ)求()f x 的定义域及其最大值; (Ⅱ)求()f x 在(0,π)上的单调递增区间.6、已知函数2()sin(2)2cos 1()6f x x x x π=--∈+R .(Ⅰ)求()f x 的单调递增区间;(Ⅱ)在△ABC 中,三个内角,,A B C 的对边分别为,,a b c ,已知()12f A =,且△ABC 外接a 的值.7、已知函数21()coscos2222xxx f x ωωω=+-(0)ω>的最小正周期为π.(Ⅰ)求ω的值及函数()f x 的最大值和最小值; (Ⅱ)求函数()f x 的单调递增区间.8、在ABC ∆中,5c =,b =a A =. (Ⅰ)求a 的值;(Ⅱ)求证:2B A ∠=∠.9、在平面直角坐标系xOy 中,设锐角α的始边与x 轴的非负半轴重合,终边与单位圆交于点11(,)P x y ,将射线OP 绕坐标原点O 按逆时针方向旋转2π后与单位圆交于点22(,)Q x y . 记12()f y y α=+.(Ⅰ)求函数()f α的值域;(Ⅱ)设ABC ∆的角,,A B C 所对的边分别为,,a b c ,若()f Ca =1c =,求b .10、设函数(Ⅰ)当, 时,求函数 f (x )的值域;(Ⅱ)已知函数 y = f (x )的图象与直线 y =1有交点,求相邻两个交点间的最短距离.11、已知函数()cos cos 442x x xf x =+, x ∈R 的部分图象如图所示. (Ⅰ)求函数()f x 的最小正周期和单调递增区间;(Ⅱ) 设点B 是图象上的最高点,点A 是图象与x 轴的交点,求BAO ∠tan 的值.12、已知函数()sin )sin f x x x x =-,x ∈R . (Ⅰ)求函数()f x 的最小正周期与单调增区间; (Ⅱ)求函数()f x 在0,4π⎡⎤⎢⎥⎣⎦上的最大值与最小值.13、已知函数()cos f x x a x =-(x ∈R )的图象经过点(,1)3π. (Ⅰ)求函数()f x 的解析式;(Ⅱ)求函数()f x 的最小正周期和单调递减区间.14、在△ABC 中,角A ,B ,C 所对的边分别为c b a ,,,满足1=c ,且()()0cos sin sin cos =+-+B A B a C B 。

高考数学一轮复习提高题专题复习三角函数与解三角形多选题练习题含答案一、三角函数与解三角形多选题1.已知函数()2sin (0)6f x x πωω⎛⎫=+> ⎪⎝⎭且对于R x ∀∈都有144f x f x ππ⎛⎫-=- ⎪⎛⎫⎝⎭+ ⎪⎝⎭成立.现将函数()2sin 6f x x πω⎛⎫=+ ⎪⎝⎭的图象向右平移6π个单位长度,再把所有点的横坐标伸长到原来的2倍(纵坐标不变)得到函数()g x 的图象,则下列说法正确的是( ) A .函数066g x g x ππ⎛⎫⎛⎫-++=⎪ ⎪⎝⎭⎝⎭B .函数()g x 相邻的对称轴距离为πC .函数23g x π⎛⎫+ ⎪⎝⎭是偶函数 D .函数()g x 在区间,63ππ⎡⎤⎢⎥⎣⎦上单调递增 【答案】ABCD 【分析】先利用已知条件求出()f x 的周期T π=,即可得2ω=,再利三角函数图象的平移伸缩变换得()g x 的解析式,在逐一判断四个选项的正误即可得正确选项. 【详解】因为对于R x ∀∈都有144f x f x ππ⎛⎫-=-⎪⎛⎫⎝⎭+ ⎪⎝⎭成立 所以()12f x f x π=-⎛⎫+ ⎪⎝⎭,()12f x f x ππ⎛⎫+=- ⎪+⎝⎭, 所以()()()11f x f x f x ππ=-=+-+对于R x ∀∈都成立, 可得()f x 的周期T π=,所以22Tπω==, 所以()2sin 26f x x π⎛⎫=+⎪⎝⎭, 将函数()2sin 26f x x π⎛⎫=+⎪⎝⎭的图象向右平移6π个单位长度,可得 2sin 22sin 2666y x x πππ⎡⎤⎛⎫⎛⎫=-+=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦再把所有点的横坐标伸长到原来的2倍可得()2sin 6g x x π⎛⎫=- ⎪⎝⎭,对于选项A:()2sin 2sin 2sin 2sin 0666666g x g x x x x x ππππππ⎛⎫⎛⎫⎛⎫⎛⎫-++=--++-=-+= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,故选项A 正确;对于选项B :函数()g x 周期为221T ππ==,所以相邻的对称轴距离为2Tπ=,故选项B正确;对于选项C :222sin 2sin 2cos 3362g x x x x ππππ⎛⎫⎛⎫⎛⎫+=+-=+=⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭是偶函数,故选项C 正确; 对于选项D :当63x ππ≤≤,066x ππ≤-≤,所以函数()g x 在区间,63ππ⎡⎤⎢⎥⎣⎦上单调递增,故选项D 正确, 故选:ABCD 【点睛】关键点点睛:本题解题的关键点是由144f x f x ππ⎛⎫-=-⎪⎛⎫⎝⎭+ ⎪⎝⎭恒成立得出 ()()f x f x π=+可得ω的值,求出()f x 的解析式.2.在单位圆O :221x y +=上任取一点()P x y ,,圆O 与x 轴正向的交点是A ,将OA 绕原点O 旋转到OP 所成的角记为θ,若x ,y 关于θ的表达式分别为()x fθ=,()y g θ=,则下列说法正确的是( )A .()x f θ=是偶函数,()y g θ=是奇函数;B .()x f θ=在()0,π上为减函数,()y g θ=在()0,π上为增函数;C .()()1fg θθ+≥在02πθ⎛⎤∈ ⎥⎝⎦,上恒成立;D .函数()()22t f g θθ=+.【答案】ACD 【分析】依据三角函数的基本概念可知cos x θ=,sin y θ=,根据三角函数的奇偶性和单调性可判断A 、B;根据辅助角公式知()()4f g πθθθ⎛⎫+=+ ⎪⎝⎭,再利用三角函数求值域可判断C ;对于D ,2cos sin2t θθ=+,先对函数t 求导,从而可知函数t 的单调性,进而可得当1sin 2θ=,cos θ=时,函数t 取得最大值,结合正弦的二倍角公式,代入进行运算即可得解. 【详解】由题意,根据三角函数的定义可知,x cos θ=,y sin θ=, 对于A ,函数()cos fθθ=是偶函数,()sin g θθ=是奇函数,故A 正确;对于B ,由正弦,余弦函数的基本性质可知,函数()cos f θθ=在()0,π上为减函数,函数()sin g θθ=在0,2π⎛⎫⎪⎝⎭为增函数,在,2ππ⎛⎫⎪⎝⎭为减函数,故B 错误; 对于C ,当0θπ⎛⎤∈ ⎥2⎝⎦,时,3,444πππθ⎛⎤+∈ ⎥⎝⎦()()cos sin 4f g πθθθθθ⎛⎫+=+=+∈ ⎪⎝⎭,故C 正确;对于D ,函数()()222cos sin2t fg θθθθ=+=+,求导22sin 2cos22sin 2(12sin )2(2sin 1)(sin 1)t θθθθθθ'=-+=-+-=--+, 令0t '>,则11sin 2θ-<<;令0t '<,则1sin 12θ<<, ∴函数t 在06,π⎡⎤⎢⎥⎣⎦和5,26ππ⎡⎤⎢⎥⎣⎦上单调递增,在5,66ππ⎛⎫⎪⎝⎭上单调递减,当6πθ=即1sin 2θ=,cos 2θ=时,函数取得极大值1222t =⨯=又当2θπ=即sin 0θ=,cos 1θ=时,212012t =⨯+⨯⨯=,所以函数()()22t f g θθ=+,故D 正确.故选:ACD. 【点睛】方法点睛:考查三角函数的值域时,常用的方法:(1)将函数化简整理为()()sin f x A x ωϕ=+,再利用三角函数性质求值域; (2)利用导数研究三角函数的单调区间,从而求出函数的最值.3.设函数()2sin 1xf x x x π=-+,则( ) A .()43f x ≤B .()5f x x ≤C .曲线()y f x =存在对称轴D .曲线()y f x =存在对称中心【答案】ABC【分析】通过()22sin sin11324x xf xx xxππ==-+⎛⎫-+⎪⎝⎭可发现函数()y f x=具有对称轴及最大值,再利用函数对称中心的特点去分析()y f x=是否具有对称中心,再将()5f x x≤化为32sin555x x x xπ≤-+,通过数形结合判断是否成立.【详解】函数解析式可化为:()22sin sin11324x xf xx xxππ==-+⎛⎫-+⎪⎝⎭,因为函数siny x=π的图象关于直线12x=对称,且函数21324y x⎛⎫=-+⎪⎝⎭的图象也关于直线12x=对称,故曲线()y f x=也关于直线12x=对称,选项C正确;当12x=时,函数siny x=π取得最大值1,此时21324y x⎛⎫=-+⎪⎝⎭取得最小值34,故()14334f x≤=,选项A正确;若()5f x x≤,则32sin555x x x xπ≤-+,令()32555g x x x x=-+,则()()221510553210g x x x x x'=-+=-+>恒成立,则()g x在R上递增,又()00g=,所以当0x<时,()00g<;当0x>时,()0g x>;作出sin xπ和32555x x x-+的图象如图所示:由图象可知32sin555x x x xπ≤-+成立,即()5f x x≤,选项B正确;对于D选项,若存在一点(),a b使得()f x关于点(),a b对称,则()()2f a x f a x b-++=,通过分析发现()()f a x f a x -++不可能为常数,故选项D 错误. 故选:ABC. 【点睛】本题考查函数的综合应用,涉及函数的单调性与最值、对称轴于对称中心、函数与不等式等知识点,难度较大. 对于复杂函数问题一定要化繁为简,利用熟悉的函数模型去分析,再综合考虑,注意数形结合、合理变形转化.4.将函数()2πsin 23f x x ⎛⎫=- ⎪⎝⎭的图象向左平移π6个单位长度后得到函数()g x 的图象,则下列说法正确的是( )A .π4g ⎛⎫= ⎪⎝⎭B .π,06⎛⎫⎪⎝⎭是函数()g x 图象的一个对称中心 C .函数()g x 在π0,4⎡⎤⎢⎥⎣⎦上单调递增D .函数()g x 在ππ,63⎡⎤-⎢⎥⎣⎦上的值域是⎡⎢⎣⎦【答案】BC 【分析】首先求得函数()sin 23g x x π=-⎛⎫ ⎪⎝⎭,再根据选项,整体代入,判断函数的性质.【详解】()2sin 2sin 2633g x x x πππ⎡⎤⎛⎫⎛⎫=+-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,1sin 462g ππ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,故A 错误;sin 0633g πππ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,故B 正确;0,4x π⎡⎤∈⎢⎥⎣⎦时,2,,33622x πππππ⎡⎤⎡⎤-∈-⊆-⎢⎥⎢⎥⎣⎦⎣⎦,所以函数()g x 在0,4⎡⎤⎢⎥⎣⎦π上单调递增,故C 正确;,63x ππ⎡⎤∈-⎢⎥⎣⎦时,22,333x πππ⎡⎤-∈-⎢⎥⎣⎦,当232x ππ-=-时,函数取得最小值-1,当233x ππ-=时,函数取得最大值2,所以函数的值域是1,2⎡-⎢⎣⎦.故选:BC 【点睛】思路点睛:本题考查()sin y A ωx φ=+的解析式和性质的判断,可以整体代入验证的方法判断函数性质:(1)对于函数()sin y A ωx φ=+,其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此判断直线0x x =或点()0,0x 是否是函数的对称轴和对称中心时,可通过验证()0f x 的值进行判断;(2)判断某区间是否是函数的单调区间时,也可以求x ωϕ+的范围,验证此区间是否是函数sin y x =的增或减区间.5.设M 、N 是函数()()()2sin 0,0f x x ωϕωϕπ=+><<的图象与直线2y =的交点,若M 、N 两点距离的最小值为6,1,22P ⎛⎫- ⎪⎝⎭是该函数图象上的一个点,则下列说法正确的是( )A .该函数图象的一个对称中心是()7,0B .该函数图象的对称轴方程是132x k =-+,Z k ∈ C .()f x 在71,23⎡⎤--⎢⎥⎣⎦上单调递增 D .()2cos 36x f x ππ⎛⎫=+ ⎪⎝⎭ 【答案】ABD 【分析】根据函数()f x 的基本性质求出函数()f x 的解析式,可判断D 选项的正误,利用余弦型函数的对称性可判断AB 选项的正误,利用余弦型函数的单调性可判断C 选项的正误. 【详解】因为M 、N 是函数()()()2sin 0,0f x x ωϕωϕπ=+><<的图象与直线2y =的交点,若M 、N 两点距离的最小值为6,则函数()f x 的最小正周期为6T =,23T ππω∴==, 所以,()2sin 3x f x πϕ⎛⎫=+⎪⎝⎭, 将点P 的坐标代入函数()f x 的解析式,可得12sin 226f πϕ⎛⎫⎛⎫-=-= ⎪ ⎪⎝⎭⎝⎭,则sin 16πϕ⎛⎫-= ⎪⎝⎭.0ϕπ<<,5666πππϕ∴-<-<,则62ππϕ-=,23πϕ∴=,()22sin 2sin 2cos 3336236f x x x x πππππππ⎛⎫⎛⎫⎛⎫∴=+=++=+ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,D 选项正确;对于A 选项,()7572cos 2cos 0362f πππ⎛⎫=+== ⎪⎝⎭,A 选项正确; 对于B 选项,由()36x k k Z πππ+=∈,解得()132x k k Z =-+∈, 所以,函数()f x 的图象的对称轴方程是132x k =-+,k Z ∈,B 选项正确;对于C 选项,当71,23x ⎡⎤∈--⎢⎥⎣⎦时,3618x ππππ-≤+≤,所以,函数()f x 在区间71,23⎡⎤--⎢⎥⎣⎦上不单调,C 选项错误.故选:ABD. 【点睛】方法点睛:求较为复杂的三角函数的单调区间时,首先化简成()sin y A ωx φ=+或()cos y A x ωϕ=+形式,再求()sin y A ωx φ=+或()cos y A x ωϕ=+的单调区间,只需把x ωϕ+看作一个整体代入sin y x =或cos y x =的相应单调区间内即可,注意要先把ω化为正数.6.如图,已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的图象与x 轴交于点A ,B ,若7OB OA =,图象的一个最高点42,33D ⎛⎫⎪⎝⎭,则下列说法正确的是( )A .4πϕ=-B .()f x 的最小正周期为4C .()f x 一个单调增区间为24,33⎛⎫-⎪⎝⎭D .()f x 图象的一个对称中心为5,03⎛⎫- ⎪⎝⎭【答案】BCD 【分析】先利用7OB OA =设0OA x =,得到点A 处坐标,结合周期公式解得选项A 错误,再利用最高点42,33D ⎛⎫⎪⎝⎭解出0x 得到周期,求得解析式,并利用代入验证法判断单调区间和对称中心,即判断选项BCD 正确. 【详解】由7OB OA =,设0OA x =,则07OB x =,06AB x =,选项A 中,点A ()0,0x 处,()0sin 0x ωϕ+=,则00x ωϕ+=,即0x ϕω=-,0612262T x AB ϕπωω-==⋅==,解得6πϕ=-,A 错误; 选项B 中,依题意0004343D x x x x =+==,得013x =,故1,03A ⎛⎫⎪⎝⎭, 最小正周期414433T ⎛⎫=-= ⎪⎝⎭,B 正确; 选项C 中,由24T πω==,得2πω=,结合最高点42,33D ⎛⎫⎪⎝⎭,知43A =,即()4sin 326f x x ππ⎛⎫=- ⎪⎝⎭,当24,33x ⎛⎫∈- ⎪⎝⎭时,,2622x ππππ⎛⎫-∈- ⎪⎝⎭,故24,33⎛⎫- ⎪⎝⎭是()f x 的一个单调增区间,C 正确;选项D 中,53x =-时()5454sin sin 0332363f πππ⎡⎤⎛⎫⎛⎫-=⨯--=-= ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,故5,03⎛⎫- ⎪⎝⎭是()f x 图象的一个对称中心,D 正确.故选:BCD. 【点睛】 思路点睛:解决三角函数()sin y A ωx φ=+的图象性质,通常利用正弦函数的图象性质,采用整体代入法进行求解,或者带入验证.7.已知函数)()lg1( 2.7)x x f x x e e e -=+-+≈⋯,若不等式(sin cos )2(sin 2)f f t θθθ+<--对任意R θ∈恒成立,则实数t 的可能取值为( )A .1B C .3D .4【答案】CD 【分析】令)()lgx x g x x e e -=+-,则()()1f x g x =+,可判断()g x 是奇函数且单调递增,不等式可变形可得(sin cos )(sin 2)g g t θθθ+<-,所以sin cos sin 2t θθθ>++,令()sin cos sin 2h θθθθ=++,换元法求出()h θ的最大值,()max t h θ>即可. 【详解】令)()lgx x g x x e e -=+-,则()()1f x g x =+,()g x 的定义域为R ,))()()lglgx x x x g x g x x e e x e e ---+=+-++-0=,所以()()g x g x -=-,所以()g x 是奇函数, 不等式(sin cos )2(sin 2)f f t θθθ+<--等价于[](sin cos )1(sin 2)1f f t θθθ+-<---,即(sin cos )(sin 2)(sin 2)g g t g t θθθθ+<--=-,当0x >时y x =单调递增,可得)lgy x =单调递增,x y e =单调递增,x y e -=单调递减,所以)()lgx x g x x e e -=+-在()0,∞+单调递增,又因为)()lg x x g x x e e -=+-为奇函数,所以)()lgx x g x x e e -=+-在R 上单调递增,所以sin cos sin 2t θθθ+<-,即sin cos sin 2t θθθ>++, 令()sin cos sin 2h θθθθ=++,只需()max t h θ>,令sin cos m θθ⎡+=∈⎣,则21sin 2m θ=+,2sin 21m θ=-,所以()21h m m m =+-,对称轴为12m =-,所以m =()max 211h m ==,所以1t >可得实数t 的可能取值为3或4,故选:CD 【点睛】关键点点睛:本题解题的关键点是构造函数()g x 奇函数且是增函数,将原不等式脱掉f 转化为函数恒成立问题.8.在ABC 中,下列说法正确的是( ) A .若A B >,则sin sin A B > B .若2C π>,则222sin sin sin C A B >+C .若sin cos A B <,则ABC 为钝角三角形D .存在ABC 满足cos cos 0A B +≤ 【答案】ABC 【分析】根据大角对大边,以及正弦定理,判断选项A ;利用余弦定理和正弦定理边角互化,判断选项B ;结合诱导公式,以及三角函数的单调性判断CD. 【详解】 A.A B >,a b ∴>,根据正弦定理sin sin a bA B=,可知sin sin A B >,故A 正确; B.2C π>,222cos 02a b c C ab +-∴=<,即222a b c +<,由正弦定理边角互化可知222sin sin sin C A B >+,故B 正确;C.当02A π<<时,sin cos cos cos 2A B A B π⎛⎫<⇔-<⎪⎝⎭,即22A B A B ππ->⇒+<,即2C π>,则ABC 为钝角三角形,若2A π>,sin cos cos cos 2A B A B π⎛⎫<⇔-< ⎪⎝⎭,即22A B A B ππ->⇒>+成立,A 是钝角,当2A π=是,sin cos A B >,所以综上可知:若sin cos A B <,则ABC 为钝角三角形,故C 正确;D.A B A B ππ+<⇒<-,0,0A B πππ<<<-<,()cos cos cos A B B π∴>-=-,即cos cos 0A B +>,故D 不正确. 故选:ABC 【点睛】关键点点睛:本题考查判断三角形的形状,关键知识点是正弦定理和余弦定理,判断三角形形状,以及诱导公式和三角函数的单调性.二、数列多选题9.已知数列{}n a 的前n 项和为2n 33S n n =-,则下列说法正确的是( )A .342n a n =-B .16S 为n S 的最小值C .1216272a a a +++=D .1230450a a a +++=【答案】AC【分析】 利用和与项的关系,分1n =和2n ≥分别求得数列的通项公式,检验合并即可判定A; 根据数列的项的正负情况可以否定B;根据前16项都是正值可计算判定C;注意到121617193300()a a a S a a a +++=+----16302S S =-可计算后否定D.【详解】 1133132a S ==-=,()()()2213333113422n n n a S S n n n n n n -=-=---+-=-≥,对于1n =也成立,所以342n a n =-,故A 正确;当17n <时,0n a >,当n=17时n a 0=,当17n >时,n a 0<, n S ∴只有最大值,没有最小值,故B 错误;因为当17n <时,0n a >,∴21216163316161716272a a a S +++==⨯-=⨯=,故C 正确; 121617193300()a a a S a a a +++=+---- 2163022272(333030S S =-=⨯-⨯-)54490454=-=,故D 错误.故选:AC.【点睛】本题考查数列的和与项的关系,数列的和的最值性质,绝对值数列的求和问题,属小综合题.和与项的关系()()1112n nn S n a S S n -⎧=⎪=⎨-≥⎪⎩,若数列{}n a 的前 k 项为正值,往后都是小于等于零,则当n k ≥时有122n k n a a a S S ++⋯+=-,若数列{}n a 的前 k 项为负值,往后都是大于或等于零,则当n k ≥时有122n k n a a a S S ++⋯+=-+.若数列的前面一些项是非负,后面的项为负值,则前n 项和只有最大值,没有最小值,若数列的前面一些项是非正,后面的项为正值,则前n 项和只有最小值,没有最大值.10.(多选)设数列{}n a 是等差数列,公差为d ,n S 是其前n 项和,10a >且69S S =,则( )A .0d >B .80a =C .7S 或8S 为n S 的最大值D .56S S >【答案】BC【分析】 根据69S S =得到80a =,再根据10a >得到0d <,可得数列{}n a 是单调递减的等差数列,所以7S 或8S 为n S 的最大值,根据6560S S a -=>得65S S >,故BC 正确.【详解】由69S S =得,960S S -=, 即7890a a a ++=,又7982a a a +=, 830a ∴=,80a ∴=,∴B 正确; 由8170a a d =+=,得17a d =-,又10a >,0d ∴<, ∴数列{}n a 是单调递减的等差数列, ()()0,70,9n n a n N n a n N n **⎧>∈≤⎪∴⎨<∈≥⎪⎩, 7S ∴或8S 为n S 的最大值,∴A 错误,C 正确; 6560S S a -=>,65S S ∴>,所以D 错误. 故选:BC .【点睛】关键点点睛:根据等差中项推出80a =,进而推出0d <是解题关键.。

专题4.4 三角函数图像与性质【考纲解读】【直击考点】题组一 常识题1. 函数y =2sin 12x -3的最小正周期是________.【解析】最小正周期T =2π12=4π.2. 函数y =A sin x +1(A >0)的最大值是5,则它的最小值是________.【解析】依题意得A +1=5,所以A =4,所以函数y =4sin x +1的最小值为-4+1=-3. 3.判断函数y =2cos x 在[-π,0]上的单调性:____________.(填“增函数”或“减函数”) 【解析】由余弦函数的单调性,得函数y =2cos x 在[-π,0]上是增函数. 4.不等式2sin x >3的解集为______________________________. 【解析】不等式2sin x >3,即sin x >32,由函数y =sin x 的图像得所求解集为⎩⎨⎧⎭⎬⎫x π3+2k π<x <2π3+2k π,k ∈Z .题组二 常错题5.函数y =1-2cos x 的单调递减区间是___________________________.【解析】函数y =1-2cos x 的单调递减区间即函数y =-cos x 的单调递减区间,也即函数y =cos x 的单调递增区间,即[2k π-π,2k π](k ∈Z ).6.若动直线x =a 与函数f (x )=sin x 和g (x )=cos x 的图像分别交于M ,N 两点,则|MN |的最大值为________.【解析】设直线x =a 与函数f (x )=sin x 的图像的交点为M (a ,y 1),直线x =a 与函数g (x )=cos x的图像的交点为N (a ,y 2),则|MN |=|y 1-y 2|=|sin a -cos a |=2⎪⎪⎪⎪⎪⎪sin ⎝⎛⎭⎪⎫a -π4≤2,7.函数f (x )=2sin x4对任意的x ∈R ,都有f (x 1)≤f (x )≤f (x 2),则|x 1-x 2|的最小值为________.题组三 常考题8.定义在区间[0,2π]上的函数y =sin 2x 的图像与y =sin x 的图像的交点个数是________. 【解析】由sin 2x =sin x 得sin x =0或cos x =12,因为x ∈[0,2π],所以x =0,π3,π,5π3,2π,交点个数是5.9. 在函数①y =cos|2x |,②y =|sin x |,③y =sin ⎝ ⎛⎭⎪⎫2x -π3,④y =tan ⎝ ⎛⎭⎪⎫2x +π5中,最小正周期为π的所有函数是________.(填序号)【解析】函数y =cos|2x |=cos 2x ,其最小正周期为π,①正确;将函数y =sin x 的图像中位于x 轴上方的图像不变,位于x 轴下方的图像对称地翻折至x 轴上方,即可得到y =|sin x |的图像,所以其最小正周期为π,②正确;函数y =sin ⎝ ⎛⎭⎪⎫2x -π3的最小正周期为π,③正确;函数y =tan ⎝ ⎛⎭⎪⎫2x +π5的最小正周期为π2,④不正确.【知识清单】1.正弦、余弦、正切函数的图像与性质 1.三角函数线三角函数线是通过有向线段直观地表示出角的各种三角函数值的一种图示方法。

弘知教育内部资料中小学课外辅导专家三角函数典型习题1 .设锐角ABC 的内角 A, B, C 的对边分别为a,b, c , a 2bsin A .(Ⅰ)求B的大小 ;(Ⅱ )求cos A sin C的取值范围 .A B C在中 ,角A, B,C所对的边分别为,, 2 .ABC c , sin sin2 . 2 2(I)试判断△ABC的形状 ;(I I)若△ABC的周长为 16,求面积的最大值 .3 .已知在ABC 中, A且与tan B是方程 x2 5 x 6 0 的两个根.B , tan A(Ⅰ )求tan( A B) 的值;(Ⅱ )若 AB 5 ,求BC的长.4.在ABC 中,角A.B.C所对的边分别是a,b,c,且a2 c 2 b 2 1 ac.A C 2(1)求sin2 cos 2B 的值;2(2)若 b=2,求△ABC面积的最大值 .5.已知函数f ( x) 2sin 2 π3 cos2x , xπ π.x4,4 2(1)求f ( x)的最大值和最小值;(2)f ( x) m 2 在 x π π上恒成立,求实数m 的取值范围.,4 26.在锐角△ABC 中,角..的对边分别为a、b、已知(b2 c 2 a 2) tanA bcA B C c, 3 .(I)求角 A;(II)若 a=2,求△ ABC面积 S 的最大值 ?7.已知函数f ( x) (sin x cos x)2 +cos2 x .(Ⅰ )求函数f x 的最小正周期 ;(Ⅱ )当x 0,2时 ,求函数f x 的最大值 ,并写出 x 相应的取值 .8 .在ABC中,已知内角 A . B . C 所对的边分别为 a 、 b 、 c, 向量r2sin B, rcos2B, 2cos2 B1r rm 3 , n 2 ,且m / / n ?(I)求锐角 B 的大小 ;(II)如果b 2 ,求ABC 的面积S ABC的最大值?答案解析11【解析】 :(Ⅰ )由 a2b sin A ,根据正弦定理得 sin A2sin B sin A ,所以 sin B ,2π由ABC 为锐角三角形得B.6(Ⅱ ) cos A sin C cos A sinAcos A sin6Acos A13 sin Acos A223 sin A .32【解析】 :I. sinC sin C cos C sin C 2 sin( C)C2 22 2 2 4即 C ,所以此三角形为直角三角形 .2422II. 16 a b22ab2ab , ab64(22) 2a b 时取等ab2 当且仅当 号,此时面积的最大值为326 4 2 .3【解析】 :(Ⅰ )由所给条件 ,方程 x 2 5 x 6 0 的两根 tan A 3, tan B2 .∴ tan( A B)tan A tan B2 311 tan A tan B 12 3(Ⅱ)∵ A B C 180 ,∴ C180 (A B) .由(Ⅰ )知 , tanCtan( A B)1,∵ C 为三角形的内角 ,∴ sin C22∵ tan A3 , A 为三角形的内角 ,∴ sin A3 ,10由正弦定理得 :AB BC5 3 ∴ BC 3 5 .21028【解析】 :(1)r r2sinB(2cos 2 B m / / n-1)=- 3cos2B22sinBcosB=- 3cos2Btan2B=- 32ππ ∵ 0<2B< π,∴ 2B= 3 ,∴ 锐角 B=3(2)由 tan2B=- 3π 5πB= 或63π① 当B= 时 ,已知 b=2,由余弦定理 ,得 :34=a 2+c 2 -ac ≥ 2ac-ac=ac(当且仅当 a=c=2 时等号成立 )1 3∵△ ABC 的面积 S △ABC =2 acsinB= 4 ac ≤ 3∴△ ABC 的面积最大值为 35π ② 当 B= 6 时 ,已知 b=2,由余弦定理 ,得 :4=a 2+c 2 + 3ac ≥2ac+ 3ac=(2+ 3)ac(当且仅当 a=c= 6- 2时等号成立 )∴ac ≤ 4(2-3)1 1∵△ ABC 的面积 S △ABC =2 acsinB=4ac ≤2- 3 ∴△ ABC 的面积最大值为 2- 314【解析】 :(1) 由余弦定理 :cosB=4sin 2A C+cos2B=124(2)由 cos B1,得 sin B15. ∵ b=2,44a218 115 2+ c =2ac+4≥2ac,得 ac ≤ ,S △ABC =2acsinB ≤(a=c 时取等号 )33故 S △ABC 的最大值为 1535 【解析】∵f ( x) 1 π3 cos2 x 1 sin 2x 3cos2 x( Ⅰ )cos2x21 2sin 2xπ.3又∵ xπ ππ 2xπ 2π, , ∴≤≤,4 2633即2≤12sin 2xπ≤ 3,3∴ f ( x) max 3, f ( x) min 2 .(Ⅱ ) ∵ f ( x)m 2f (x) 2 mf (x) 2 , xπ π ,4,2∴ mf ( x)max 2 且 m f ( x) min 2 ,∴1 m 4 ,即 m 的取值范围是 (14), .6【解析】 :(I)由已知得b 2c 2a 2 sin A3 32bccos A sin A22又在锐角 △ABC 中,所以 A=60°,[不说明是锐角 △ABC 中,扣 1 分 ](II)因为 a=2,A=60 所°以 b2c2bc 4, S1bc sin A3bc24而b 2c 22bc4 2bcbc4bc又 S1bc sin A3bc3 4 3244所以 △ ABC 面积 S 的最大值等于37【解析】 :(Ⅰ )因为 f ( x) (sin xcos x)2 +cos2 xsin 2 x 2sin x cos x cos 2 x cos2 x1 sin2 x cos2x ( ) =1+ 2 sin(2 x)4所以 2,即函数 f (x) 的最小正周期为, T2(Ⅱ )因为 0 x,得4 2x45,所以有2 sin(2 x) 1242 4 12 sin(2 x) 2,即0 12 sin(2 x)1244所以 ,函数 f x的最大值为 1 2此时 ,因为2 x5,所以 , 2 x,即 x844442。

高考数学一轮复习提高题专题复习三角函数与解三角形多选题练习题及答案一、三角函数与解三角形多选题 1.(多选题)如图,设ABC 的内角、、A B C 所对的边分别为a b c 、、,若a b c 、、成等比数列,、、A B C 成等差数列,D 是ABC 外一点,1,3DC DA ==,下列说法中,正确的是( )A .3B π=B .ABC 是等边三角形C .若A B CD 、、、四点共圆,则13AC =D .四边形ABCD 面积无最大值 【答案】ABC 【分析】根据等差数列的性质和三角形内角和可得3B π=,根据等比中项和余弦定理可得a c =,即ABC 是等边三角形,若A B C D 、、、四点共圆,根据圆内接四边形的性质可得23D π=,再利用余弦定理可求13AC =211sin sin 223ACD ABC S S S AD CD D AC π∆∆=+=⋅+和2222cos AC AD CD AD CD D 可得3335353sin 3sin()23S D D D π=-+=-+. 【详解】由、、A B C 成等差数列可得,2A+C =B ,又A B C π++=, 则3B π=,故A 正确;由a b c 、、成等比数列可得,2b ac =,根据余弦定理,2222cos b a c ac B =+-,两式相减整理得,2()0a c -=,即a c =,又3B π=,所以,ABC 是等边三角形,故B 正确;若A B C D 、、、四点共圆,则B D π+=,所以,23D π=, ADC 中,根据余弦定理,2222cos AC AD CD AD CD D ,解得13AC =C 正确;四边形ABCD 面积为:211sin sin 223ACD ABC S S S AD CD D AC π∆∆=+=⋅+23sin 2D AC = 又2222cos 106cos AC AD CD AD CD D D =+-⋅=-,所以,3sin 3sin()22232S D D D π=-+=-+, 因为(0,)D π∈,当四边形面积最大时,sin()13D π-=,此时max 3S =,故D 错误. 故选:ABC 【点睛】本题考查解三角形和平面几何的一些性质,同时考查了等差等比数列的基本知识,综合性强,尤其是求面积的最大值需要一定的运算,属难题.2.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且::4:5:6a b c =,则下列结论正确的是( )A .sin :sin :sin 4:5:6ABC = B .ABC 是钝角三角形C .ABC 的最大内角是最小内角的2倍D .若6c =,则ABC 【答案】ACD 【分析】由正弦定理可判断A ;由余弦定理可判断B ;由余弦定理和二倍角公式可判断C ;由正弦定理可判断D. 【详解】解:由::4:5:6a b c =,可设4a x =,5b x =,6c x =,()0x >, 根据正弦定理可知sin :sin :sin 4:5:6A B C =,选项A 描述准确;由c 为最大边,可得2222221625361cos 022458a b c x x x C ab x x +-+-===>⋅⋅,即C 为锐角,选项B 描述不准确;2222222536163cos 22564b c a x x x A bc x x +-+-===⋅⋅,291cos 22cos 121cos 168A A C =-=⨯-==, 由2A ,C ()0,π∈,可得2A C =,选项C 描述准确;若6c =,可得1672sin1164cR C===-,ABC 外接圆半径为87,选项D 描述准确. 故选:ACD. 【点睛】本题考查三角形的正弦定理和余弦定理,二倍角公式,考查化简运算能力,属于中档题.3.已知函数()()cos 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图像如图所示,则下列关于函数()f x 的说法中正确的是( )A .函数()f x 最靠近原点的零点为3π-B .函数()f x 的图像在y 3C .函数56f x π⎛⎫-⎪⎝⎭是偶函数 D .函数()f x 在72,3ππ⎛⎫⎪⎝⎭上单调递增 【答案】ABC 【分析】首先根据图象求函数的解析式,利用零点,以及函数的性质,整体代入的方法判断选项. 【详解】根据函数()()cos f x A x ωϕ=+的部分图像知,2A =, 设()f x 的最小正周期为T ,则24362T πππ=-=,∴2T π=,21T πω==. ∵2cos 266f ππϕ⎛⎫⎛⎫=+=⎪ ⎪⎝⎭⎝⎭,且2πϕ<,∴6πϕ=-, 故()2cos 6f x x π⎛⎫=-⎪⎝⎭.令()2cos 06f x x π⎛⎫=-= ⎪⎝⎭,得62x k πππ-=+,k Z ∈, 即23x k ππ=+,k Z ∈,因此函数()f x 最靠近原点的零点为3π-,故A 正确;由()02cos 6f π⎛⎫=-= ⎪⎝⎭()f x 的图像在y B 正确;由()52cos 2cos 6f x x x ππ⎛⎫-=-=- ⎪⎝⎭,因此函数56f x π⎛⎫-⎪⎝⎭是偶函数,故C 正确; 令226k x k ππππ-≤-≤,k Z ∈,得52266k x k ππππ-≤≤+,k Z ∈,此时函数()f x 单调递增,于是函数()f x 在132,6ππ⎛⎫ ⎪⎝⎭上单调递增,在137,63ππ⎛⎫⎪⎝⎭上单调递减,故D 不正确. 故选:ABC . 【点睛】思路点睛:本题考查()sin y A ωx φ=+的解析式和性质的判断,可以整体代入验证的方法判断函数性质:(1)对于函数()sin y A ωx φ=+,其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此判断直线0x x =或点()0,0x 是否是函数的对称轴和对称中心时,可通过验证()0f x 的值进行判断;(2)判断某区间是否是函数的单调区间时,也可以求x ωϕ+的范围,验证此区间是否是函数sin y x =的增或减区间.4.将函数()2πsin 23f x x ⎛⎫=- ⎪⎝⎭的图象向左平移π6个单位长度后得到函数()g x 的图象,则下列说法正确的是( )A .π4g ⎛⎫= ⎪⎝⎭B .π,06⎛⎫⎪⎝⎭是函数()g x 图象的一个对称中心 C .函数()g x 在π0,4⎡⎤⎢⎥⎣⎦上单调递增D .函数()g x 在ππ,63⎡⎤-⎢⎥⎣⎦上的值域是⎡⎢⎣⎦【答案】BC 【分析】首先求得函数()sin 23g x x π=-⎛⎫⎪⎝⎭,再根据选项,整体代入,判断函数的性质.【详解】()2sin 2sin 2633g x x x πππ⎡⎤⎛⎫⎛⎫=+-=- ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦,1sin 462g ππ⎛⎫⎛⎫== ⎪ ⎪⎝⎭⎝⎭,故A 错误;sin 0633g πππ⎛⎫⎛⎫=-= ⎪ ⎪⎝⎭⎝⎭,故B 正确;0,4x π⎡⎤∈⎢⎥⎣⎦时,2,,33622x πππππ⎡⎤⎡⎤-∈-⊆-⎢⎥⎢⎥⎣⎦⎣⎦,所以函数()g x 在0,4⎡⎤⎢⎥⎣⎦π上单调递增,故C 正确;,63x ππ⎡⎤∈-⎢⎥⎣⎦时,22,333x πππ⎡⎤-∈-⎢⎥⎣⎦,当232x ππ-=-时,函数取得最小值-1,当233x ππ-=时,函数取得最大值32,所以函数的值域是31,2⎡⎤-⎢⎥⎣⎦.故选:BC 【点睛】思路点睛:本题考查()sin y A ωx φ=+的解析式和性质的判断,可以整体代入验证的方法判断函数性质:(1)对于函数()sin y A ωx φ=+,其对称轴一定经过图象的最高点或最低点,对称中心的横坐标一定是函数的零点,因此判断直线0x x =或点()0,0x 是否是函数的对称轴和对称中心时,可通过验证()0f x 的值进行判断;(2)判断某区间是否是函数的单调区间时,也可以求x ωϕ+的范围,验证此区间是否是函数sin y x =的增或减区间.5.已知函数()()sin 0,0,2f x A x A πωϕωϕ⎛⎫=+>>< ⎪⎝⎭的部分图象如图所示,下列说法正确的是( )A .函数()y f x =的周期为πB .函数()y f x =在2,36ππ⎡⎤--⎢⎥⎣⎦单调递减 C .函数()y f x =的图象关于直线512x π=-对称D .该图象向右平移6π个单位可得2sin 2y x =的图象 【答案】ACD 【分析】先根据图像求出()y f x =的解析式,再分别验证A 、B 、C 、D 是否正确. 对于A :利用周期公式求周期;对于B :利用复合函数“同增异减”求单调区间; 对于C :计算512f π⎛-⎫⎪⎝⎭,看512x π=-是否经过顶点; 对于D :利用“左加右减”判断. 【详解】由图像可知:A =2,周期24,2312T T ππππω⎛⎫=-=∴==⎪⎝⎭; 由=2sin 2212122f ππϕπϕ⎧⎛⎫⎛⎫⨯+= ⎪ ⎪⎪⎪⎝⎭⎝⎭⎨⎪<⎪⎩解得:3πϕ=故函数()2sin 23f x x π⎛⎫=+ ⎪⎝⎭对于A :4312T πππ⎛⎫=-= ⎪⎝⎭,故A 正确; 对于B :当236x ππ-≤≤- 时203x ππ-≤+≤,所以()y f x =在2,36ππ⎡⎤--⎢⎥⎣⎦上不单调.故B 错误; 对于C :当512x π=-时255s 2121232in f πππ⎛⎫⎛⎫=-=- ⎪ ⎭⎝-⎪⎭+⎝⨯,即直线512x π=-是()y f x =的一条对称轴.故C 正确;对于D :()y f x =向右平移6π个单位得到2sin 222sin 263y x x ππ⎛⎫=-⨯+= ⎪⎝⎭,故D 正确. 故选:ACD 【点睛】求三角函数解析式的方法: (1)求A 通常用最大值或最小值; (2)求ω通常用周期;()求φ通常利用函数上的点带入即可求解.6.已知函数()1cos cos 632f x x x ππ⎛⎫⎛⎫=+-+⎪ ⎪⎝⎭⎝⎭,则以下说法中正确的是( ) A .()f x 的最小正周期为π B .()f x 在7,1212ππ⎡⎤⎢⎥⎣⎦上单调递减 C .51,62π⎛⎫⎪⎝⎭是()f x 的一个对称中心 D .()f x 的最大值为12【答案】ABC 【分析】利用三角恒等变换思想化简()11sin 2232f x x π⎛⎫=++ ⎪⎝⎭,利用正弦型函数的周期公式可判断A 选项的正误,利用正弦型函数的单调性可判断B 选项的正误,利用正弦型函数的对称性可判断C 选项的正误,利用正弦型函数的有界性可判断D 选项的正误. 【详解】cos cos sin 3266x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫-=-+=+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦, 所以,()1111cos cos cos sin sin 2632662232f x x x x x x πππππ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=+-+=+++=++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭.对于A 选项,函数()f x 的最小正周期为22T ππ==,A 选项正确; 对于B 选项,当7,1212x ππ⎡⎤∈⎢⎥⎣⎦时,32232x πππ≤+≤,此时,函数()f x 在7,1212ππ⎡⎤⎢⎥⎣⎦上单调递减,B 选项正确; 对于C 选项,5151111sin 2sin 262632222f ππππ⎛⎫⎛⎫=⨯++=+= ⎪ ⎪⎝⎭⎝⎭, 所以,51,62π⎛⎫⎪⎝⎭是()f x 的一个对称中心,C 选项正确; 对于D 选项,()max 111122f x =⨯+=,D 选项错误. 故选:ABC. 【点睛】方法点睛:求较为复杂的三角函数的单调区间时,首先化简成()sin y A ωx φ=+形式,再求()sin y A ωx φ=+的单调区间,只需把x ωϕ+看作一个整体代入sin y x =的相应单调区间内即可,注意要先把ω化为正数.7.已知函数)()lg1( 2.7)x x f x x e e e -=+-+≈⋯,若不等式(sin cos )2(sin 2)f f t θθθ+<--对任意R θ∈恒成立,则实数t 的可能取值为( )A .1BC .3D .4【答案】CD 【分析】令)()lgx x g x x e e -=+-,则()()1f x g x =+,可判断()g x 是奇函数且单调递增,不等式可变形可得(sin cos )(sin 2)g g t θθθ+<-,所以sin cos sin 2t θθθ>++,令()sin cos sin 2h θθθθ=++,换元法求出()h θ的最大值,()max t h θ>即可. 【详解】令)()lgx x g x x e e -=+-,则()()1f x g x =+,()g x 的定义域为R ,))()()lglgx x x x g x g x x e e x e e ---+=+-++-0=,所以()()g x g x -=-,所以()g x 是奇函数, 不等式(sin cos )2(sin 2)f f t θθθ+<--等价于[](sin cos )1(sin 2)1f f t θθθ+-<---,即(sin cos )(sin 2)(sin 2)g g t g t θθθθ+<--=-,当0x >时y x =单调递增,可得)lgy x =单调递增,x y e =单调递增,x y e -=单调递减,所以)()lgx x g x x e e -=+-在()0,∞+单调递增,又因为)()lg x x g x x e e -=+-为奇函数,所以)()lgx x g x x e e -=+-在R 上单调递增,所以sin cos sin 2t θθθ+<-,即sin cos sin 2t θθθ>++, 令()sin cos sin 2h θθθθ=++,只需()max t h θ>,令sin cos m θθ⎡+=∈⎣,则21sin 2m θ=+,2sin 21m θ=-,所以()21h m m m =+-,对称轴为12m =-,所以m =()max 211h m ==,所以1t >可得实数t 的可能取值为3或4, 故选:CD 【点睛】关键点点睛:本题解题的关键点是构造函数()g x 奇函数且是增函数,将原不等式脱掉f 转化为函数恒成立问题.8.设函数()()sin f x A x =+ωϕ,x ∈R (其中0A >,0>ω,2πϕ<),在,62ππ⎛⎫ ⎪⎝⎭上既无最大值,也无最小值,且()026f f f ππ⎛⎫⎛⎫-== ⎪ ⎪⎝⎭⎝⎭,则下列结论错误的是( )A .若()()()12f x f x f x ≤≤对任意x ∈R ,则21min x x π-=B .()y f x =的图象关于点,03π⎛-⎫⎪⎝⎭中心对称 C .函数()f x 的单调减区间为()7,1212k k k Z ππππ⎡⎤++∈⎢⎥⎣⎦D .函数()()y f x x R =∈的图象相邻两条对称轴之间的距离是2π【答案】ABD 【分析】根据条件先求函数的解析式,对于A:判断出()1f x 为最小值,()2f x 为最大值,即可; 对于B:根据函数的对称性进行判断;对于C:求出角的范围,结合三角函数的单调性进行判断; 对于D:根据函数的对称性即对称轴之间的关系进行判断. 【详解】 因为函数()f x 在,62ππ⎛⎫⎪⎝⎭上既无最大值,也无最小值, 所以,62ππ⎛⎫⎪⎝⎭是函数的一个单调区间,区间长度为263πππ-=,即函数的周期2233T ππ≥⨯=,即223ππω≥,则03ω<≤因为()06f f π⎛⎫= ⎪⎝⎭,所以06212ππ+=为函数的一条对称轴;则1223πππωϕωϕπ+=+=①②由①②解得:=2=3πωϕ,,即()sin 23f x A x π⎛⎫=+⎪⎝⎭,函数的周期=T π. 对于A: 若()()()12f x f x f x ≤≤对任意x ∈R 恒成立,则()1f x 为最小值,()2f x 为最大值,所以12||22T k x x k π-==,则21x x -必为2π的整数倍,故A 错误,可选A; 对于B:3x π=-时,()sin 03f x A π⎛⎫=-≠ ⎪⎝⎭,故,03π⎛-⎫⎪⎝⎭不是()y f x =的对称中心,B错误,可选B; 对于C:当7,1212x k k ππππ⎡⎤∈++⎢⎥⎣⎦时,322,2322x k k πππππ⎡⎤+∈++⎢⎥⎣⎦,此时()y f x =单调递减,C 正确,不选C;对于D: 函数()()y f x x R =∈的图象相邻两条对称轴之间的距离是44T π=,故D 错误,可选D 故选:ABD 【点睛】(1)求三角函数解析式的方法:①求A 通常用最大值或最小值;②(2)求ω通常用周期;③求φ通常利用函数上的点带入即可求解;(2)三角函数问题通常需要把它化为“一角一名一次”的结构,借助于sin y x =或cos y x =的性质解题.9.已知函数()26f x x π⎛⎫=- ⎪⎝⎭,则下列结论正确的是( )A .函数()f x 的最小正周期为πB .函数()f xC .函数()f x 的图象关于点,012π⎛⎫⎪⎝⎭对称 D .函数()f x 的图象关于直线712x π=对称 【答案】BD 【分析】首先要熟悉()26g x x π⎛⎫=- ⎪⎝⎭的图象和性质,将()26g x x π⎛⎫=- ⎪⎝⎭在x 轴下方的图象沿x 轴翻折(x 轴上方的图象不变),可以得到函数()f x 的图象,并判断选项. 【详解】由题意,将()26g x x π⎛⎫=- ⎪⎝⎭在x 轴下方的图象沿x 轴翻折(x 轴上方的图象不变),可以得到函数()f x 的图象,故函数()f x 的最小正周期为2π,故A 错误;函数()f x B 正确;函数()f x 的图象是由()26g x x π⎛⎫=- ⎪⎝⎭在x 轴下方的图象沿x 轴翻折(x 轴上方的图象不变),所以不是中心对称图形,故C 错误; 由7012f π⎛⎫= ⎪⎝⎭知D 正确, 故选:BD .【点睛】思路点睛:要判断函数()f x 的性质,需先了解函数()26g x x π⎛⎫=- ⎪⎝⎭的性质,并且知道函数()26g x x π⎛⎫=- ⎪⎝⎭在x 轴下方的图象沿x 轴翻折(x 轴上方的图象不变),可以得到函数()f x 的图象,函数的周期变为原来的一半,()g x 的对称轴和对称中心都是函数()f x 的对称轴.10.设函数()()1sin 022f x x x πωωω⎛⎫=++> ⎪⎝⎭,已知()f x 在[]0,π有且仅有3个零点,则( )A .在()0,π上存在1x 、2x ,满足()()122f x f x -=B .()f x 在()0,π有且仅有1个最小值点C .()f x 在0,2π⎛⎫ ⎪⎝⎭上单调递增 D .ω的取值范围是1723,66⎡⎫⎪⎢⎣⎭【答案】AD【分析】 化简函数()f x 的解析式为()sin 6f x x πω⎛⎫=+ ⎪⎝⎭,令6t x πω=+,由[]0,x π∈可求得,66t ππωπ⎡⎤∈+⎢⎥⎣⎦,作出函数sin ,066y t t ππωπω⎛⎫=≤≤+> ⎪⎝⎭的图象,可判断AB 选项的正误;由图象得出346ππωππ≤+<可判断D 选项的正误;取3ω=,利用正弦型函数的单调性可判断C 选项的正误.【详解】()3131sin sin sin cos sin 2226f x x x x x x ππωωωωω⎛⎫⎛⎫=++=+=+ ⎪ ⎪⎝⎭⎝⎭, 当[]0,x π∈时,,666x πππωωπ⎡⎤+∈+⎢⎥⎣⎦,令6t x πω=+,则,66t ππωπ⎡⎤∈+⎢⎥⎣⎦, 作出函数sin ,066y t t ππωπω⎛⎫=≤≤+> ⎪⎝⎭的图象如下图所示:对于A 选项,由图象可知,max 1y =,min 1y =-,所以,在()0,π上存在1x 、2x ,满足()()122f x f x -=,A 选项正确;对于B 选项,()f x 在()0,π上有1个或2个最小值点,B 选项错误;对于D 选项,由于函数()f x 在[]0,π有且仅有3个零点,则346ππωππ≤+<,解得172366ω≤<,D 选项正确; 对于C 选项,由于172366ω≤<,取3ω=,当0,2x π⎛⎫∈ ⎪⎝⎭时,53663x πππ<+<, 此时,函数()f x 在区间0,2π⎛⎫ ⎪⎝⎭上不单调,C 选项错误. 故选:AD.【点睛】 关键点点睛:本题考查利用正弦型函数在区间上的零点个数判断正弦型函数的基本性质,解本题的关键在于换元6t x πω=+,将问题转化为函数sin y t =在区间,66ππωπ⎡⎤+⎢⎥⎣⎦上的零点个数问题,数形结合来求解.。
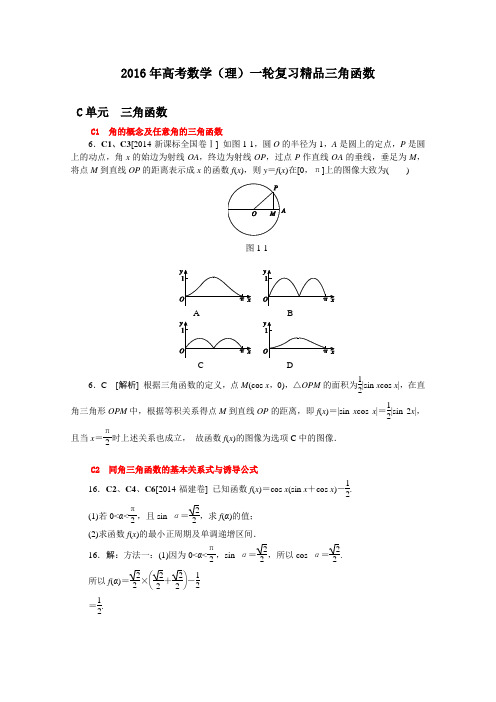
2016年高考数学(理)一轮复习精品三角函数C 单元 三角函数C1 角的概念及任意角的三角函数 6.C1、C3[2014·新课标全国卷Ⅰ] 如图1-1,圆O 的半径为1,A 是圆上的定点,P 是圆上的动点,角x 的始边为射线OA ,终边为射线OP ,过点P 作直线OA 的垂线,垂足为M ,将点M 到直线OP 的距离表示成x 的函数f (x ),则y =f (x )在[0,π]上的图像大致为( )图1-1A BC D6.C [解析] 根据三角函数的定义,点M (cos x ,0),△OPM 的面积为12|sin x cos x |,在直角三角形OPM 中,根据等积关系得点M 到直线OP 的距离,即f (x )=|sin x cos x |=12|sin 2x |,且当x =π2时上述关系也成立, 故函数f (x )的图像为选项C 中的图像.C2 同角三角函数的基本关系式与诱导公式16.C2、C4、C6[2014·福建卷] 已知函数f (x )=cos x (sin x +cos x )-12.(1)若0<α<π2,且sin α=22,求f (α)的值;(2)求函数f (x )的最小正周期及单调递增区间.16.解:方法一:(1)因为0<α<π2,sin α=22,所以cos α=22.所以f (α)=22×⎝⎛⎭⎫22+22-12=12.(2)因为f (x )=sin x cos x +cos 2x -12=12sin 2x +1+cos 2x 2-12 =12sin 2x +12cos 2x =22sin ⎝⎛⎭⎫2x +π4, 所以T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,得k π-3π8≤x ≤k π+π8,k ∈Z .所以f (x )的单调递增区间为⎣⎡⎦⎤k π-3π8,k π+π8,k ∈Z .方法二:f (x )=sin x cos x +cos 2x -12=12sin 2x +1+cos 2x 2-12 =12sin 2x +12cos 2x =22sin ⎝⎛⎭⎫2x +π4. (1)因为0<α<π2,sin α=22,所以α=π4,从而f (α)=22sin ⎝⎛⎭⎫2α+π4=22sin 3π4=12. (2)T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,得k π-3π8≤x ≤k π+π8,k ∈Z .所以f (x )的单调递增区间为⎣⎡⎦⎤k π-3π8,k π+π8,k ∈Z .17.C2,C3,C4[2014·重庆卷] 已知函数f (x )=3sin(ωx +φ)⎝⎛⎭⎫ω>0,-π2≤φ<π2的图像关于直线x =π3对称,且图像上相邻两个最高点的距离为π.(1)求ω和φ的值;(2)若f ⎝⎛⎭⎫α2=34⎝⎛⎭⎫π6<α<2π3,求cos ⎝⎛⎭⎫α+3π2的值.17.解:(1)因为f (x )的图像上相邻两个最高点的距离为π,所以ƒ(x )的最小正周期T =π,从而ω=2πT=2.又因为f (x )的图像关于直线x =π3对称,所以2×π3+φ=k π+π2,k =0,±1,±2,….因为-π2≤φ<π2,所以φ=-π6.(2)由(1)得ƒ⎝⎛⎭⎫α2=3sin(2×α2-π6)=34, 所以sin ⎝⎛⎭⎫α-π6=14.由π6<α<2π3得0<α-π6<π2, 所以cos ⎝⎛⎭⎫α-π6=1-sin 2⎝⎛⎭⎫α-π6=1-⎝⎛⎭⎫142=154.因此cos ⎝⎛⎭⎫α+3π2=sin α=sin ⎣⎡⎦⎤(α-π6)+π6=sin ⎝⎛⎭⎫α-π6cos π6+cos ⎝⎛⎭⎫α-π6sin π6=14×32+154×12 =3+158.C3 三角函数的图象与性质9.C3[2014·辽宁卷] 将函数y =3sin ⎝⎛⎭⎫2x +π3的图像向右平移π2个单位长度,所得图像对应的函数( )A .在区间⎣⎡⎦⎤π12,7π12上单调递减B .在区间⎣⎡⎦⎤π12,7π12上单调递增C .在区间⎣⎡⎦⎤-π6,π3上单调递减D .在区间⎣⎡⎦⎤-π6,π3上单调递增9.B [解析] 由题可知,将函数y =3sin ⎝⎛⎭⎫2x +π3的图像向右平移π2个单位长度得到函数y=3sin ⎝⎛⎭⎫2x -23π的图像,令-π2+2k π≤2x -23π≤π2+2k π,k ∈Z ,即π12+k π≤x ≤7π12+k π,k ∈Z 时,函数单调递增,即函数y =3sin ⎝⎛⎭⎫2x -23π的单调递增区间为⎣⎡⎦⎤π12+k π,7π12+k π,k ∈Z ,可知当k =0时,函数在区间⎣⎡⎦⎤π12,7π12上单调递增.3.C3[2014·全国卷] 设a =sin 33°,b =cos 55°,c =tan 35°,则( ) A .a >b >c B .b >c >a C .c >b >a D .c >a >b3.C [解析] 因为b =cos 55°=sin 35°>sin 33°,所以b >a .因为cos 35°<1,所以1cos 35°>1,所以sin 35°cos 35°>sin 35°.又c =tan 35°=sin 35°cos 35°>sin 35°,所以c >b ,所以c >b >a .6.C1、C3[2014·新课标全国卷Ⅰ] 如图1-1,圆O 的半径为1,A 是圆上的定点,P 是圆上的动点,角x 的始边为射线OA ,终边为射线OP ,过点P 作直线OA 的垂线,垂足为M ,将点M 到直线OP 的距离表示成x 的函数f (x ),则y =f (x )在[0,π]上的图像大致为( )图1-1A BC D6.C [解析] 根据三角函数的定义,点M (cos x ,0),△OPM 的面积为12|sin x cos x |,在直角三角形OPM 中,根据等积关系得点M 到直线OP 的距离,即f (x )=|sin x cos x |=12|sin 2x |,且当x =π2时上述关系也成立, 故函数f (x )的图像为选项C 中的图像.14.C3、C5[2014·新课标全国卷Ⅱ] 函数f (x )=sin(x +2φ)-2sin φcos(x +φ)的最大值为________.14.1 [解析] 函数f (x )=sin(x +2φ)-2sin φcos(x +φ)=sin[(x +φ)+φ]-2sin φcos(x +φ)=sin(x +φ)cos φ-cos(x +φ)sin φ=sin x ,故其最大值为1.17.C2,C3,C4[2014·重庆卷] 已知函数f (x )=3sin(ωx +φ)⎝⎛⎭⎫ω>0,-π2≤φ<π2的图像关于直线x =π3对称,且图像上相邻两个最高点的距离为π.(1)求ω和φ的值;(2)若f ⎝⎛⎭⎫α2=34⎝⎛⎭⎫π6<α<2π3,求cos ⎝⎛⎭⎫α+3π2的值.17.解:(1)因为f (x )的图像上相邻两个最高点的距离为π,所以ƒ(x )的最小正周期T =π,从而ω=2πT=2.又因为f (x )的图像关于直线x =π3对称,所以2×π3+φ=k π+π2,k =0,±1,±2,….因为-π2≤φ<π2,所以φ=-π6.(2)由(1)得ƒ⎝⎛⎭⎫α2=3sin(2×α2-π6)=34, 所以sin ⎝⎛⎭⎫α-π6=14.由π6<α<2π3得0<α-π6<π2, 所以cos ⎝⎛⎭⎫α-π6=1-sin 2⎝⎛⎭⎫α-π6=1-⎝⎛⎭⎫142=154.因此cos ⎝⎛⎭⎫α+3π2=sin α=sin ⎣⎡⎦⎤(α-π6)+π6=sin ⎝⎛⎭⎫α-π6cos π6+cos ⎝⎛⎭⎫α-π6sin π6=14×32+154×12 =3+158.C4 函数sin()y A x ωϕ=+的图象与性质3.C4[2014·四川卷] 为了得到函数y =sin (2x +1)的图像,只需把函数y =sin 2x 的图像上所有的点( )A .向左平行移动12个单位长度B .向右平行移动12个单位长度C .向左平行移动1个单位长度D .向右平行移动1个单位长度3.A [解析] 因为y =sin(2x +1)=sin2⎝⎛⎭⎫x +12,所以为得到函数y =sin(2x +1)的图像,只需要将y =sin 2x 的图像向左平行移动12个单位长度.11.C4[2014·安徽卷] 若将函数f (x )=sin ⎝⎛⎭⎫2x +π4的图像向右平移φ个单位,所得图像关于y 轴对称,则φ的最小正值是________.11.3π8 [解析] 方法一:将f (x )=sin ⎝⎛⎭⎫2x +π4的图像向右平移φ个单位,得到y =sin ⎝⎛⎭⎫2x +π4-2φ的图像,由该函数的图像关于y 轴对称,可知sin ⎝⎛⎭⎫π4-2φ=±1,即sin ⎝⎛⎭⎫2φ-π4=±1,故2φ-π4=k π+π2,k ∈Z ,即φ=k π2+3π8,k ∈Z ,所以当φ>0时,φmin =3π8.方法二:由f (x )=sin ⎝⎛⎭⎫2x +π4的图像向右平移φ个单位后所得的图像关于y 轴对称可知,π4-2φ=π2+k π,k ∈Z ,又φ>0,所以φmin =3π8. 14.C4[2014·北京卷] 设函数f (x )=A sin(ωx +φ)(A ,ω,φ是常数,A >0,ω>0).若f (x )在区间⎣⎡⎦⎤π6,π2上具有单调性,且f ⎝⎛⎭⎫π2=f ⎝⎛⎭⎫2π3=-f ⎝⎛⎭⎫π6,则f (x )的最小正周期为________.14.π [解析] 结合图像得T 4=π2+2π32-π2+π62,即T =π.16.C2、C4、C6[2014·福建卷] 已知函数f (x )=cos x (sin x +cos x )-12.(1)若0<α<π2,且sin α=22,求f (α)的值;(2)求函数f (x )的最小正周期及单调递增区间.16.解:方法一:(1)因为0<α<π2,sin α=22,所以cos α=22.所以f (α)=22×⎝⎛⎭⎫22+22-12=12. (2)因为f (x )=sin x cos x +cos 2x -12=12sin 2x +1+cos 2x 2-12 =12sin 2x +12cos 2x =22sin ⎝⎛⎭⎫2x +π4, 所以T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,得k π-3π8≤x ≤k π+π8,k ∈Z .所以f (x )的单调递增区间为⎣⎡⎦⎤k π-3π8,k π+π8,k ∈Z .方法二:f (x )=sin x cos x +cos 2x -12=12sin 2x +1+cos 2x 2-12 =12sin 2x +12cos 2x =22sin ⎝⎛⎭⎫2x +π4. (1)因为0<α<π2,sin α=22,所以α=π4,从而f (α)=22sin ⎝⎛⎭⎫2α+π4=22sin 3π4=12. (2)T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,得k π-3π8≤x ≤k π+π8,k ∈Z .所以f (x )的单调递增区间为⎣⎡⎦⎤k π-3π8,k π+π8,k ∈Z .7.C4、C5[2014·广东卷] 若空间中四条两两不同的直线l 1,l 2,l 3,l 4满足l 1⊥l 2,l 2⊥l 3,l 3⊥l 4,则下列结论一定正确的是( )A .l 1⊥l 4B .l 1∥l 4C .l 1与l 4既不垂直也不平行D .l 1与l 4的位置关系不确定7.D [解析] 本题考查空间中直线的位置关系,构造正方体进行判断即可. 如图所示,在正方体ABCD - A 1B 1C 1D 1中,设BB 1是直线l 1,BC 是直线l 2,AB 是直线l 3,则DD 1是直线l 4,l 1∥l 4;设BB 1是直线l 1,BC 是直线l 2,CC 1是直线l 3,CD 是直线l 4,则l 1⊥l 4.故l 1与l 4的位置关系不确定.17.C4、C5、C7、C9[2014·湖北卷] 某实验室一天的温度(单位:℃)随时间t (单位:h)的变化近似满足函数关系:f (t )=10-3cos π12t -sin π12t ,t ∈[0,24).(1)求实验室这一天的最大温差.(2)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?17.解:(1)因为f (t )=10-2⎝⎛⎭⎫32cos π12t +12sin π12t =10-2sin ⎝⎛⎭⎫π12t +π3,又0≤t <24,所以π3≤π12t +π3<7π3,-1≤sin ⎝⎛⎭⎫π12t +π3≤1.当t =2时,sin ⎝⎛⎭⎫π12t +π3=1;当t =14时,sin ⎝⎛⎭⎫π12t +π3=-1. 于是f (t )在[0,24)上取得的最大值是12,最小值是8.故实验室这一天的最高温度为12 ℃,最低温度为8 ℃,最大温差为4 ℃. (2)依题意,当f (t )>11时,实验室需要降温.由(1)得f (t )=10-2sin ⎝⎛⎭⎫π12t +π3,故有10-2sin ⎝⎛⎭⎫π12t +π3>11,即sin ⎝⎛⎭⎫π12t +π3<-12.又0≤t <24,因此7π6<π12t +π3<11π6,即10<t <18.故在10时至18时实验室需要降温. 16.C4、C7[2014·江西卷] 已知函数f (x )=sin(x +θ)+a cos(x +2θ),其中a ∈R ,θ∈⎝⎛⎭⎫-π2,π2. (1)当a =2,θ=π4时,求f (x )在区间[0,π]上的最大值与最小值;(2)若f ⎝⎛⎭⎫π2=0,f (π)=1,求a ,θ的值.16.解:(1)f (x )=sin ⎝⎛⎭⎫x +π4+2cos ⎝⎛⎭⎫x +π2=22(sin x +cos x )-2sin x =22cos x -22sin x =sin ⎝⎛⎭⎫π4-x . 因为x ∈[0,π],所以π4-x ∈⎣⎡⎦⎤-3π4,π4,故f (x )在区间[0,π]上的最大值为22,最小值为-1. (2)由⎩⎪⎨⎪⎧f ⎝⎛⎭⎫π2=0,f (π)=1,得⎩⎪⎨⎪⎧cos θ(1-2a sin θ)=0,2a sin 2θ-sin θ-a =1. 又θ∈⎝⎛⎭⎫-π2,π2,知cos θ≠0,所以⎩⎪⎨⎪⎧1-2a sin θ=0,(2a sin θ-1)sin θ-a =1,解得⎩⎪⎨⎪⎧a =-1,θ=-π6.12.E3、C4[2014·新课标全国卷Ⅱ] 设函数f (x )=3sinπxm,若存在f (x )的极值点x 0满足x 20+[f (x 0)]2<m 2,则m 的取值范围是( )A .(-∞,-6)∪(6,+∞)B .(-∞,-4)∪(4,+∞)C .(-∞,-2)∪(2,+∞)D .(-∞,-1)∪(1,+∞)12.C [解析] 函数f (x )的极值点满足πx m =π2+k π,即x =m ⎝⎛⎭⎫k +12,k ∈Z ,且极值为±3,问题等价于存在k 0使之满足不等式m 2⎝⎛⎭⎫k 0+122+3<m 2.因为⎝⎛⎭⎫k +122的最小值为14,所以只要14m 2+3<m 2成立即可,即m 2>4,解得m >2或m <-2,故m 的取值范围是(-∞,-2)∪(2,+∞).16.F2,C4[2014·山东卷] 已知向量a =(m ,cos 2x ),b =(sin 2x ,n ),函数f (x )=a ·b ,且y =f (x )的图像过点⎝⎛⎭⎫π12,3和点⎝⎛⎭⎫2π3,-2.(1)求m ,n 的值;(2)将y =f (x )的图像向左平移φ(0<φ<π)个单位后得到函数y =g (x )的图像,若y =g (x )图像上各最高点到点(0,3)的距离的最小值为1,求y =g (x )的单调递增区间.16.解:(1)由题意知,f (x )=a·b =m sin 2x +n cos 2x .因为y =f (x )的图像过点⎝⎛⎭⎫π12,3和点⎝⎛⎭⎫2π3,-2,所以⎩⎨⎧3=m sin π6+n cos π6,-2=m sin 4π3+n cos 4π3,即⎩⎨⎧3=12m +32n ,-2=-32m -12n ,解得m =3,n =1.(2)由(1)知f (x )=3sin 2x +cos 2x =2sin ⎝⎛⎭⎫2x +π6.由题意知,g (x )=f (x +φ)=2sin ⎝⎛⎭⎫2x +2φ+π6.设y =g (x )的图像上符合题意的最高点为(x 0,2).由题意知,x 20+1=1,所以x 0=0,即到点(0,3)的距离为1的最高点为(0,2). 将其代入y =g (x )得,sin ⎝⎛⎭⎫2φ+π6=1.因为0<φ<π,所以φ=π6.因此,g (x )=2sin ⎝⎛⎭⎫2x +π2=2cos 2x .由2k π-π≤2x ≤2k π,k ∈Z 得k π-π2≤x ≤k π,k ∈Z ,所以函数y =g (x )的单调递增区间为⎣⎡⎦⎤k π-π2,k π,k ∈Z .2.C4[2014·陕西卷] 函数f (x )=cos ⎝⎛⎭⎫2x -π6的最小正周期是( )A.π2B .πC .2πD .4π2.B [解析] 已知函数y =A cos(ωx +φ)(A >0,ω>0)的周期为T =2πω,故函数f (x )的最小正周期T =2π2=π.16.C4,C5,C6,C7[2014·四川卷] 已知函数f (x )=sin ⎝⎛⎭⎫3x +π4.(1)求f (x )的单调递增区间;(2)若α是第二象限角,f ⎝⎛⎭⎫α3=45cos ⎝⎛⎭⎫α+π4cos 2α,求cos α-sin α的值.16.解:(1)因为函数y =sin x 的单调递增区间为⎣⎡⎦⎤-π2+2k π,π2+2k π,k ∈Z ,由-π2+2k π≤3x +π4≤π2+2k π,k ∈Z ,得-π4+2k π3≤x ≤π12+2k π3,k ∈Z .所以,函数f (x )的单调递增区间为⎣⎡⎦⎤-π4+2k π3,π12+2k π3,k ∈Z . (2)由已知,得sin ⎝⎛⎭⎫α+π4=45cos ⎝⎛⎭⎫α+π4(cos 2α-sin 2α),所以sin αcos π4+cos αsin π4=45⎝⎛⎭⎫cos α cos π4-sin αsin π4(cos 2 α-sin 2 α),即sin α+cos α=45(cos α-sin α)2(sin α+cos α).当sin α+cos α=0时,由α是第二象限角, 得α=3π4+2k π,k ∈Z ,此时,cos α-sin α=- 2.当sin α+cos α≠0时,(cos α-sin α)2=54.由α是第二象限角,得cos α-sin α<0,此时cos α-sin α=-52. 综上所述,cos α-sin α=-2或-52. 15.C4、C5、C6[2014·天津卷] 已知函数f (x )=cos x ·sin ⎝⎛⎭⎫x +π3-3cos 2x +34,x ∈R .(1)求f (x )的最小正周期;(2)求f (x )在闭区间⎣⎡⎦⎤-π4,π4上的最大值和最小值.15.解:(1)由已知,有f (x )=cos x ·⎝⎛⎭⎫12sin x +32cos x -3cos 2x +34=12sin x ·cos x -32cos 2x +34=14sin 2x -34(1+cos 2x )+34 =14sin 2x -34cos 2x =12sin ⎝⎛⎭⎫2x -π3, 所以f (x )的最小正周期T =2π2=π.(2)因为f (x )在区间⎣⎡⎦⎤-π4,-π12上是减函数,在区间⎣⎡⎦⎤-π12,π4上是增函数,f ⎝⎛⎭⎫-π4=-14,f ⎝⎛⎭⎫-π12=-12,f ⎝⎛⎭⎫π4=14, 所以函数f (x )在区间⎣⎡⎦⎤-π4,π4上的最大值为14,最小值为-12.4.C4[2014·浙江卷] 为了得到函数y =sin 3x +cos 3x 的图像,可以将函数y =2cos 3x 的图像( )A .向右平移π4个单位B .向左平移π4个单位C .向右平移π12个单位D .向左平移π12个单位4.C [解析] y =sin 3x +cos 3x =2cos ⎝⎛⎭⎫3x -π4=2cos ⎣⎡⎦⎤3⎝⎛⎭⎫x -π12,所以将函数y =2cos3x 的图像向右平移π12个单位可以得到函数y =sin 3x +cos 3x 的图像,故选C.17.C2,C3,C4[2014·重庆卷] 已知函数f (x )=3sin(ωx +φ)⎝⎛⎭⎫ω>0,-π2≤φ<π2的图像关于直线x =π3对称,且图像上相邻两个最高点的距离为π.(1)求ω和φ的值;(2)若f ⎝⎛⎭⎫α2=34⎝⎛⎭⎫π6<α<2π3,求cos ⎝⎛⎭⎫α+3π2的值.17.解:(1)因为f (x )的图像上相邻两个最高点的距离为π,所以ƒ(x )的最小正周期T =π,从而ω=2πT=2.又因为f (x )的图像关于直线x =π3对称,所以2×π3+φ=k π+π2,k =0,±1,±2,….因为-π2≤φ<π2,所以φ=-π6.(2)由(1)得ƒ⎝⎛⎭⎫α2=3sin(2×α2-π6)=34, 所以sin ⎝⎛⎭⎫α-π6=14.由π6<α<2π3得0<α-π6<π2,所以cos ⎝⎛⎭⎫α-π6=1-sin 2⎝⎛⎭⎫α-π6=1-⎝⎛⎭⎫142=154.因此cos ⎝⎛⎭⎫α+3π2=sin α=sin ⎣⎡⎦⎤(α-π6)+π6=sin ⎝⎛⎭⎫α-π6cos π6+cos ⎝⎛⎭⎫α-π6sin π6=14×32+154×12 =3+158.C5 两角和与差的正弦、余弦、正切 14.C3、C5[2014·新课标全国卷Ⅱ] 函数f (x )=sin(x +2φ)-2sin φcos(x +φ)的最大值为________.14.1 [解析] 函数f (x )=sin(x +2φ)-2sin φcos(x +φ)=sin[(x +φ)+φ]-2sin φcos(x +φ)=sin(x +φ)cos φ-cos(x +φ)sin φ=sin x ,故其最大值为1.16.C5、C8[2014·安徽卷] 设△ABC 的内角A ,B ,C 所对边的长分别是a ,b ,c ,且b =3,c =1,A =2B .(1)求a 的值;(2)求sin ⎝⎛⎭⎫A +π4的值.16.解: (1)因为A =2B ,所以sin A =sin 2B =2sin B cos B ,由余弦定理得cos B =a 2+c 2-b 22ac =sin A2sin B ,所以由正弦定理可得a =2b ·a 2+c 2-b 22ac. 因为b =3,c =1,所以a 2=12,即a =2 3. (2)由余弦定理得cos A =b 2+c 2-a 22bc =9+1-126=-13.因为0<A <π,所以sin A =1-cos 2A =1-19=2 23. 故sin ⎝⎛⎭⎫A +π4=sin A cos π4+cos A sin π4=2 23×22+⎝⎛⎭⎫-13×22=4-26.7.C4、C5[2014·广东卷] 若空间中四条两两不同的直线l 1,l 2,l 3,l 4满足l 1⊥l 2,l 2⊥l 3,l 3⊥l 4,则下列结论一定正确的是( )A .l 1⊥l 4B .l 1∥l 4C .l 1与l 4既不垂直也不平行D .l 1与l 4的位置关系不确定7.D [解析] 本题考查空间中直线的位置关系,构造正方体进行判断即可. 如图所示,在正方体ABCD - A 1B 1C 1D 1中,设BB 1是直线l 1,BC 是直线l 2,AB 是直线l 3,则DD 1是直线l 4,l 1∥l 4;设BB 1是直线l 1,BC 是直线l 2,CC 1是直线l 3,CD 是直线l 4,则l 1⊥l 4.故l 1与l 4的位置关系不确定.16.C5、C7[2014·广东卷] 已知函数f (x )=A sin ⎝⎛⎭⎫x +π4,x ∈R ,且f ⎝⎛⎭⎫5π12=32.(1)求A 的值;(2)若f (θ)+f (-θ)=32,θ∈⎝⎛⎭⎫0,π2,求f ⎝⎛⎭⎫3π4-θ.17.C4、C5、C7、C9[2014·湖北卷] 某实验室一天的温度(单位:℃)随时间t (单位:h)的变化近似满足函数关系:f (t )=10-3cos π12t -sin π12t ,t ∈[0,24).(1)求实验室这一天的最大温差.(2)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?17.解:(1)因为f (t )=10-2⎝⎛⎭⎫32cos π12t +12sin π12t =10-2sin ⎝⎛⎭⎫π12t +π3,又0≤t <24,所以π3≤π12t +π3<7π3,-1≤sin ⎝⎛⎭⎫π12t +π3≤1.当t =2时,sin ⎝⎛⎭⎫π12t +π3=1;当t =14时,sin ⎝⎛⎭⎫π12t +π3=-1.于是f (t )在[0,24)上取得的最大值是12,最小值是8.故实验室这一天的最高温度为12 ℃,最低温度为8 ℃,最大温差为4 ℃. (2)依题意,当f (t )>11时,实验室需要降温.由(1)得f (t )=10-2sin ⎝⎛⎭⎫π12t +π3,故有10-2sin ⎝⎛⎭⎫π12t +π3>11,即sin ⎝⎛⎭⎫π12t +π3<-12.又0≤t <24,因此7π6<π12t +π3<11π6,即10<t <18.故在10时至18时实验室需要降温. 17.C5、C8[2014·辽宁卷] 在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a >c .已知BA →·BC →=2,cos B =13,b =3.求:(1)a 和c 的值; (2)cos(B -C )的值.17.解:(1)由BA →·BC →=2得c ·a ·cos B =2,又cos B =13,所以ac =6.由余弦定理,得a 2+c 2=b 2+2ac cos B , 又b =3,所以a 2+c 2=9+2×2=13.解⎩⎪⎨⎪⎧ac =6,a 2+c 2=13,得⎩⎪⎨⎪⎧a =2,c =3或⎩⎪⎨⎪⎧a =3,c =2. 因为a >c ,所以a =3,c =2. (2)在△ABC 中,sin B =1-cos 2B =1-⎝⎛⎭⎫132=223.由正弦定理,得sin C =c b sin B =23·2 23= 4 29.因为a =b >c ,所以C 为锐角,因此cos C =1-sin 2C =1-⎝⎛⎭⎫4 292=79.所以cos(B -C )=cos B cos C +sin B sin C =13×79+2 23×4 29=2327.17.C8,C5 [2014·全国卷] △ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知3a cos C =2c cos A ,tan A =13,求B .17.解:由题设和正弦定理得 3sin A cos C =2sin C cos A , 故3tan A cos C =2sin C .因为tan A =13,所以cos C =2sin C ,所以tan C =12.所以tan B =tan[180°-(A +C )] =-tan(A +C ) =tan A +tan Ctan A tan C -1=-1,所以B =135°.8.C5[2014·新课标全国卷Ⅰ] 设α∈⎝⎛⎭⎫0,π2,β∈⎝⎛⎭⎫0,π2,且tan α=1+sin βcos β,则( )A .3α-β=π2B .3α+β=π2C .2α-β=π2D .2α+β=π28.C [解析] tan α=1+sin βcos β=⎝⎛⎭⎫cos β2+sin β2cos 2β2-sin 2β2=cos β2+sin β2cos β2-sin β2=1+tanβ21-tanβ2=tan ⎝⎛⎭⎫π4+β2,因为β∈⎝⎛⎭⎫0,π2,所以π4+β2∈⎝⎛⎭⎫π4,π2,又α∈⎝⎛⎭⎫0,π2且tan α=tan ⎝⎛⎭⎫π4+β2,所以α=π4+β2,即2α-β=π2.13.C5,C8[2014·四川卷] 如图1-3所示,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为67°,30°,此时气球的高度是46 m ,则河流的宽度BC 约等于________m .(用四舍五入法将结果精确到个位.参考数据:sin 67°≈0.92,cos 67°≈0.39,sin 37°≈0.60,cos 37°≈0.80,3≈1.73)图1-313.60 [解析] 过A 点向地面作垂线,记垂足为D ,则在Rt △ADB 中,∠ABD =67°,AD =46 m ,∴AB =AD sin 67°=460.92=50(m),在△ABC 中,∠ACB =30°,∠BAC =67°-30°=37°,AB =50 m , 由正弦定理得,BC =AB sin 37°sin 30°=60 (m),故河流的宽度BC 约为60 m.16.C4,C5,C6,C7[2014·四川卷] 已知函数f (x )=sin ⎝⎛⎭⎫3x +π4.(1)求f (x )的单调递增区间;(2)若α是第二象限角,f ⎝⎛⎭⎫α3=45cos ⎝⎛⎭⎫α+π4cos 2α,求cos α-sin α的值.16.解:(1)因为函数y =sin x 的单调递增区间为⎣⎡⎦⎤-π2+2k π,π2+2k π,k ∈Z ,由-π2+2k π≤3x +π4≤π2+2k π,k ∈Z ,得-π4+2k π3≤x ≤π12+2k π3,k ∈Z .所以,函数f (x )的单调递增区间为⎣⎡⎦⎤-π4+2k π3,π12+2k π3,k ∈Z . (2)由已知,得sin ⎝⎛⎭⎫α+π4=45cos ⎝⎛⎭⎫α+π4(cos 2α-sin 2α),所以sin αcos π4+cos αsin π4=45⎝⎛⎭⎫cos α cos π4-sin αsin π4(cos 2 α-sin 2 α),即sin α+cos α=45(cos α-sin α)2(sin α+cos α).当sin α+cos α=0时,由α是第二象限角, 得α=3π4+2k π,k ∈Z ,此时,cos α-sin α=- 2.当sin α+cos α≠0时,(cos α-sin α)2=54.由α是第二象限角,得cos α-sin α<0,此时cos α-sin α=-52.综上所述,cos α-sin α=-2或-52. 15.C4、C5、C6[2014·天津卷] 已知函数f (x )=cos x ·sin ⎝⎛⎭⎫x +π3-3cos 2x +34,x ∈R .(1)求f (x )的最小正周期;(2)求f (x )在闭区间⎣⎡⎦⎤-π4,π4上的最大值和最小值.15.解:(1)由已知,有f (x )=cos x ·⎝⎛⎭⎫12sin x +32cos x -3cos 2x +34=12sin x ·cos x -32cos 2x +34 =14sin 2x -34(1+cos 2x )+34 =14sin 2x -34cos 2x =12sin ⎝⎛⎭⎫2x -π3, 所以f (x )的最小正周期T =2π2=π.(2)因为f (x )在区间⎣⎡⎦⎤-π4,-π12上是减函数,在区间⎣⎡⎦⎤-π12,π4上是增函数,f ⎝⎛⎭⎫-π4=-14,f ⎝⎛⎭⎫-π12=-12,f ⎝⎛⎭⎫π4=14, 所以函数f (x )在区间⎣⎡⎦⎤-π4,π4上的最大值为14,最小值为-12.10.C8,C5[2014·重庆卷] 已知△ABC 的内角A ,B ,C 满足sin 2A +sin(A -B +C )=sin(C-A -B )+12,面积S 满足1≤S ≤2,记a ,b ,c 分别为A ,B ,C 所对的边,则下列不等式一定成立的是( )A .bc (b +c )>8B .ab (a +b )>16 2C .6≤abc ≤12D .12≤abc ≤2410.A [解析] 因为A +B +C =π,所以A +C =π-B ,C =π-(A +B ),所以由已知等式可得sin 2A +sin(π-2B )=sin[π-2(A +B )]+12,即sin 2A +sin 2B =sin 2(A +B )+12,所以sin[(A +B )+(A -B )]+sin[(A +B )-(A -B )]=sin 2(A +B )+12,所以2 sin(A +B )cos(A -B )=2sin(A +B )cos(A +B )+12,所以2sin(A +B )[cos(A -B )-cos(A +B )]=12,所以sin A sin B sin C =18.由1≤S ≤2,得1≤12bc sin A ≤2.由正弦定理得a =2R sin A ,b =2R sin B ,c =2R sin C ,所以1≤2R 2·sin A sin B sin C ≤2,所以1≤R 24≤2,即2≤R ≤2 2,所以bc (b +c )>abc =8R 3sin A sinB sinC =R 3≥8.C6 二倍角公式15.H4、C6[2014·全国卷] 直线l 1和l 2是圆x 2+y 2=2的两条切线.若l 1与l 2的交点为(1,3),则l 1与l 2的夹角的正切值等于________.15.43 [解析] 如图所示,根据题意,OA ⊥P A ,OA =2,OP =10,所以P A =OP 2-OA 2=2 2,所以tan ∠OP A =OA P A =22 2=12,故tan ∠APB =2tan ∠OP A 1-tan 2∠OP A =43, 即l 1与l 2的夹角的正切值等于43.16.B5、C6[2014·全国卷] 若函数f (x )=cos 2x +a sin x 在区间⎝⎛⎭⎫π6,π2是减函数,则a 的取值范围是________.16.(-∞,2] [解析] f (x )=cos 2x +a sin x =-2sin 2x +a sin x +1,令sin x =t ,则f (x )=-2t 2+at +1.因为x ∈⎝⎛⎭⎫π6,π2,所以t ∈⎝⎛⎭⎫12,1,所以f (x )=-2t 2+at +1,t ∈⎝⎛⎭⎫12,1.因为f (x )=cos 2x +a sin x 在区间⎝⎛⎭⎫π6,π2是减函数,所以f (x )=-2t 2+at +1在区间⎝⎛⎭⎫12,1上是减函数,又对称轴为x =a 4,∴a 4≤12,所以a ∈(-∞,2].16.C2、C4、C6[2014·福建卷] 已知函数f (x )=cos x (sin x +cos x )-12.(1)若0<α<π2,且sin α=22,求f (α)的值;(2)求函数f (x )的最小正周期及单调递增区间.16.解:方法一:(1)因为0<α<π2,sin α=22,所以cos α=22.所以f (α)=22×⎝⎛⎭⎫22+22-12=12. (2)因为f (x )=sin x cos x +cos 2x -12=12sin 2x +1+cos 2x 2-12=12sin 2x +12cos 2x =22sin ⎝⎛⎭⎫2x +π4, 所以T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,得k π-3π8≤x ≤k π+π8,k ∈Z .所以f (x )的单调递增区间为⎣⎡⎦⎤k π-3π8,k π+π8,k ∈Z .方法二:f (x )=sin x cos x +cos 2x -12=12sin 2x +1+cos 2x 2-12 =12sin 2x +12cos 2x =22sin ⎝⎛⎭⎫2x +π4. (1)因为0<α<π2,sin α=22,所以α=π4,从而f (α)=22sin ⎝⎛⎭⎫2α+π4=22sin 3π4=12. (2)T =2π2=π.由2k π-π2≤2x +π4≤2k π+π2,k ∈Z ,得k π-3π8≤x ≤k π+π8,k ∈Z .所以f (x )的单调递增区间为⎣⎡⎦⎤k π-3π8,k π+π8,k ∈Z .16.C4,C5,C6,C7[2014·四川卷] 已知函数f (x )=sin ⎝⎛⎭⎫3x +π4.(1)求f (x )的单调递增区间;(2)若α是第二象限角,f ⎝⎛⎭⎫α3=45cos ⎝⎛⎭⎫α+π4cos 2α,求cos α-sin α的值.16.解:(1)因为函数y =sin x 的单调递增区间为⎣⎡⎦⎤-π2+2k π,π2+2k π,k ∈Z ,由-π2+2k π≤3x +π4≤π2+2k π,k ∈Z ,得-π4+2k π3≤x ≤π12+2k π3,k ∈Z .所以,函数f (x )的单调递增区间为⎣⎡⎦⎤-π4+2k π3,π12+2k π3,k ∈Z .(2)由已知,得sin ⎝⎛⎭⎫α+π4=45cos ⎝⎛⎭⎫α+π4(cos 2α-sin 2α),所以sin αcos π4+cos αsin π4=45⎝⎛⎭⎫cos α cos π4-sin αsin π4(cos 2 α-sin 2 α),即sin α+cos α=45(cos α-sin α)2(sin α+cos α).当sin α+cos α=0时,由α是第二象限角, 得α=3π4+2k π,k ∈Z ,此时,cos α-sin α=- 2.当sin α+cos α≠0时,(cos α-sin α)2=54.由α是第二象限角,得cos α-sin α<0,此时cos α-sin α=-52. 综上所述,cos α-sin α=-2或-52. 15.C4、C5、C6[2014·天津卷] 已知函数f (x )=cos x ·sin ⎝⎛⎭⎫x +π3-3cos 2x +34,x ∈R .(1)求f (x )的最小正周期;(2)求f (x )在闭区间⎣⎡⎦⎤-π4,π4上的最大值和最小值.15.解:(1)由已知,有f (x )=cos x ·⎝⎛⎭⎫12sin x +32cos x -3cos 2x +34=12sin x ·cos x -32cos 2x +34 =14sin 2x -34(1+cos 2x )+34 =14sin 2x -34cos 2x =12sin ⎝⎛⎭⎫2x -π3, 所以f (x )的最小正周期T =2π2=π.(2)因为f (x )在区间⎣⎡⎦⎤-π4,-π12上是减函数,在区间⎣⎡⎦⎤-π12,π4上是增函数,f ⎝⎛⎭⎫-π4=-14,f ⎝⎛⎭⎫-π12=-12,f ⎝⎛⎭⎫π4=14, 所以函数f (x )在区间⎣⎡⎦⎤-π4,π4上的最大值为14,最小值为-12.C7 三角函数的求值、化简与证明16.C5、C7[2014·广东卷] 已知函数f (x )=A sin ⎝⎛⎭⎫x +π4,x ∈R ,且f ⎝⎛⎭⎫5π12=32.(1)求A 的值;(2)若f (θ)+f (-θ)=32,θ∈⎝⎛⎭⎫0,π2,求f ⎝⎛⎭⎫3π4-θ.17.C4、C5、C7、C9[2014·湖北卷] 某实验室一天的温度(单位:℃)随时间t (单位:h)的变化近似满足函数关系:f (t )=10-3cos π12t -sin π12t ,t ∈[0,24).(1)求实验室这一天的最大温差.(2)若要求实验室温度不高于11℃,则在哪段时间实验室需要降温?17.解:(1)因为f (t )=10-2⎝⎛⎭⎫32cos π12t +12sin π12t =10-2sin ⎝⎛⎭⎫π12t +π3,又0≤t <24,所以π3≤π12t +π3<7π3,-1≤sin ⎝⎛⎭⎫π12t +π3≤1.当t =2时,sin ⎝⎛⎭⎫π12t +π3=1;当t =14时,sin ⎝⎛⎭⎫π12t +π3=-1.于是f (t )在[0,24)上取得的最大值是12,最小值是8.故实验室这一天的最高温度为12 ℃,最低温度为8 ℃,最大温差为4 ℃. (2)依题意,当f (t )>11时,实验室需要降温.由(1)得f (t )=10-2sin ⎝⎛⎭⎫π12t +π3,故有10-2sin ⎝⎛⎭⎫π12t +π3>11,即sin ⎝⎛⎭⎫π12t +π3<-12.又0≤t <24,因此7π6<π12t +π3<11π6,即10<t <18.故在10时至18时实验室需要降温. 16.C4、C7[2014·江西卷] 已知函数f (x )=sin(x +θ)+a cos(x +2θ),其中a ∈R ,θ∈⎝⎛⎭⎫-π2,π2. (1)当a =2,θ=π4时,求f (x )在区间[0,π]上的最大值与最小值;(2)若f ⎝⎛⎭⎫π2=0,f (π)=1,求a ,θ的值.16.解:(1)f (x )=sin ⎝⎛⎭⎫x +π4+2cos ⎝⎛⎭⎫x +π2=22(sin x +cos x )-2sin x =22cos x -22sin x =sin ⎝⎛⎭⎫π4-x . 因为x ∈[0,π],所以π4-x ∈⎣⎡⎦⎤-3π4,π4,故f (x )在区间[0,π]上的最大值为22,最小值为-1. (2)由⎩⎪⎨⎪⎧f ⎝⎛⎭⎫π2=0,f (π)=1,得⎩⎪⎨⎪⎧cos θ(1-2a sin θ)=0,2a sin 2θ-sin θ-a =1.又θ∈⎝⎛⎭⎫-π2,π2,知cos θ≠0,所以⎩⎪⎨⎪⎧1-2a sin θ=0,(2a sin θ-1)sin θ-a =1,解得⎩⎪⎨⎪⎧a =-1,θ=-π6.16.C4,C5,C6,C7[2014·四川卷] 已知函数f (x )=sin ⎝⎛⎭⎫3x +π4.(1)求f (x )的单调递增区间;(2)若α是第二象限角,f ⎝⎛⎭⎫α3=45cos ⎝⎛⎭⎫α+π4cos 2α,求cos α-sin α的值.16.解:(1)因为函数y =sin x 的单调递增区间为⎣⎡⎦⎤-π2+2k π,π2+2k π,k ∈Z ,由-π2+2k π≤3x +π4≤π2+2k π,k ∈Z ,得-π4+2k π3≤x ≤π12+2k π3,k ∈Z .所以,函数f (x )的单调递增区间为⎣⎡⎦⎤-π4+2k π3,π12+2k π3,k ∈Z . (2)由已知,得sin ⎝⎛⎭⎫α+π4=45cos ⎝⎛⎭⎫α+π4(cos 2α-sin 2α),所以sin αcos π4+cos αsin π4=45⎝⎛⎭⎫cos α cos π4-sin αsin π4(cos 2 α-sin 2 α),即sin α+cos α=45(cos α-sin α)2(sin α+cos α).当sin α+cos α=0时,由α是第二象限角, 得α=3π4+2k π,k ∈Z ,此时,cos α-sin α=- 2.当sin α+cos α≠0时,(cos α-sin α)2=54.由α是第二象限角,得cos α-sin α<0,此时cos α-sin α=-52. 综上所述,cos α-sin α=-2或-52.C8 解三角形12.C8[2014·天津卷] 在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .已知b -c =14a ,2sin B =3sin C ,则cos A 的值为________.12.-14[解析] ∵2sin B =3sin C ,∴2b =3c .又∵b -c =a 4,∴a =2c ,b =32c ,∴cos A =b 2+c 2-a 22bc =94c 2+c 2-4c 22×32c ×c=-14.16.C8、C9[2014·新课标全国卷Ⅱ] 设点M (x 0,1),若在圆O :x 2+y 2=1上存在点N ,使得∠OMN =45°,则x 0的取值范围是________.16.[-1,1] [解析] 在△OMN 中,OM =1+x 20≥1=ON ,所以设∠ONM =α,则45°≤α<135°.根据正弦定理得1+x 20sin α=1sin 45°,所以1+x 20=2sin α∈[1,2],所以0≤x 2≤1,即-1≤x 0≤1,故符合条件的x 0的取值范围为[-1,1].12.C8[2014·广东卷] 在△ABC 中,角A ,B ,C 所对应的边分别为a ,b ,c .已知b cos C +c cos B =2b ,则ab=________.12.2 [解析] 本题考查了正弦定理以及两角和与差的正弦函数公式,熟练掌握正弦定理是解本题的关键.利用正弦定理,将b cos C +c cos B =2b 化简得sin B cos C +sin C cos B =2sin B ,即sin(B +C )=2sin B .∵sin(B +C )=sin A ,∴sin A =2sin B ,利用正弦定理化简得a =2b ,故a b =2.16.C5、C8[2014·安徽卷] 设△ABC 的内角A ,B ,C 所对边的长分别是a ,b ,c ,且b =3,c =1,A =2B .(1)求a 的值;(2)求sin ⎝⎛⎭⎫A +π4的值.16.解: (1)因为A =2B ,所以sin A =sin 2B =2sin B cos B ,由余弦定理得cos B =a 2+c 2-b 22ac =sin A2sin B ,所以由正弦定理可得a =2b ·a 2+c 2-b 22ac. 因为b =3,c =1,所以a 2=12,即a =2 3. (2)由余弦定理得cos A =b 2+c 2-a 22bc =9+1-126=-13.因为0<A <π,所以sin A =1-cos 2A =1-19=2 23. 故sin ⎝⎛⎭⎫A +π4=sin A cos π4+cos A sin π4=2 23×22+⎝⎛⎭⎫-13×22=4-26.15.C8[2014·北京卷] 如图1-2,在△ABC 中,∠B =π3,AB =8,点D 在BC 边上,且CD =2,cos ∠ADC =17.(1)求sin ∠BAD ; (2)求BD ,AC 的长.图1-215.解:(1) 在△ADC 中,因为cos ∠ADC =17,所以sin ∠ADC =4 37.所以sin ∠BAD =sin(∠ADC -∠B )=sin ∠ADC cos B -cos ∠ADC sin B =4 37×12-17×32=3 314. (2)在△ABD 中,由正弦定理得 BD =AB ·sin ∠BADsin ∠ADB =8×33144 37=3.在△ABC 中,由余弦定理得 AC 2=AB 2+BC 2-2AB ·BC ·cos B =82+52-2×8×5×12=49,所以AC =7.12.C8[2014·福建卷] 在△ABC 中,A =60°,AC =4,BC =2 3,则△ABC 的面积等于________.12.2 3 [解析] 由BC sin A =ACsin B ,得sin B =4sin 60°23=1,∴B =90°,C =180°-(A +B )=30°,则S △ABC =12·AC ·BC sin C =12×4×23sin 30°=23,即△ABC 的面积等于2 3.18.C8、C9[2014·湖南卷] 如图1-5所示,在平面四边形ABCD 中,AD =1,CD =2,AC=7.图1-5(1)求cos ∠CAD 的值;(2)若cos ∠BAD =-714,sin ∠CBA =216,求BC 的长.18.解:(1)在△ADC 中,由余弦定理,得cos ∠CAD =AC 2+AD 2-CD 22AC ·AD,故由题设知,cos ∠CAD =7+1-427=277.(2)设∠BAC =α,则α=∠BAD -∠CAD .因为cos ∠CAD =277,cos ∠BAD =-714,所以sin ∠CAD =1-cos 2∠CAD = 1-⎝⎛⎭⎫2772=217, sin ∠BAD =1-cos 2∠BAD =1-⎝⎛⎭⎫-7142=32114.于是sin α=sin (∠BAD -∠CAD )=sin ∠BAD cos ∠CAD -cos ∠BAD sin ∠CAD=32114×277-⎝⎛⎭⎫-714×217=32.在△ABC 中,由正弦定理,得BC sin α=ACsin ∠CBA .故BC =AC ·sin αsin ∠CBA =7×32216=3.4.C8[2014·江西卷] 在△ABC 中,内角A ,B ,C 所对的边分别是a ,b ,c .若c 2=(a -b )2+6,C =π3,则△ABC 的面积是( )A .3 B.9 32 C.3 32D .3 34.C [解析] 由余弦定理得,cos C =a 2+b 2-c 22ab =2ab -62ab =12,所以ab =6,所以S △ABC=12ab sin C =3 32. 17.C5、C8[2014·辽宁卷] 在△ABC 中,内角A ,B ,C 的对边分别为a ,b ,c ,且a >c .已知BA →·BC →=2,cos B =13,b =3.求:(1)a 和c 的值; (2)cos(B -C )的值.17.解:(1)由BA →·BC →=2得c ·a ·cos B =2,又cos B =13,所以ac =6.由余弦定理,得a 2+c 2=b 2+2ac cos B , 又b =3,所以a 2+c 2=9+2×2=13. 解⎩⎪⎨⎪⎧ac =6,a 2+c 2=13,得⎩⎪⎨⎪⎧a =2,c =3或⎩⎪⎨⎪⎧a =3,c =2. 因为a >c ,所以a =3,c =2.(2)在△ABC 中,sin B =1-cos 2B =1-⎝⎛⎭⎫132=223.由正弦定理,得sin C =c b sin B =23·2 23= 4 29.因为a =b >c ,所以C 为锐角,因此cos C =1-sin 2C =1-⎝⎛⎭⎫4 292=79.所以cos(B -C )=cos B cos C +sin B sin C =13×79+2 23×4 29=2327.17.C8,C5 [2014·全国卷] △ABC 的内角A ,B ,C 的对边分别为a ,b ,c .已知3a cos C =2c cos A ,tan A =13,求B .17.解:由题设和正弦定理得 3sin A cos C =2sin C cos A , 故3tan A cos C =2sin C .因为tan A =13,所以cos C =2sin C ,所以tan C =12.所以tan B =tan[180°-(A +C )] =-tan(A +C ) =tan A +tan Ctan A tan C -1=-1,所以B =135°. 16.C8[2014·新课标全国卷Ⅰ] 已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,a =2,且(2+b )·(sin A -sin B )=(c -b )sin C ,则△ABC 面积的最大值为________.16.3 [解析] 根据正弦定理和a =2可得(a +b )(a -b )=(c -b )c ,故得b 2+c 2-a 2=bc ,根据余弦定理得cos A =b 2+c 2-a 22bc =12,所以A =π3.根据b 2+c 2-a 2=bc 及基本不等式得bc ≥2bc -a 2,即bc ≤4,所以△ABC 面积的最大值为12×4×32= 3.4.C8[2014·新课标全国卷Ⅱ] 钝角三角形ABC 的面积是12,AB =1,BC =2,则AC =( )A .5 B. 5 C .2 D .14.B [解析] 根据三角形面积公式,得12BA ·BC ·sin B =12,即12×1×2×sin B =12,得sin B =22,其中C <A .若B 为锐角,则B =π4,所以AC =1+2-2×1×2×22=1=AB ,易知A 为直角,此时△ABC 为直角三角形,所以B 为钝角,即B =3π4,所以AC =1+2-2×1×2×⎝⎛⎭⎫-22= 5. 12.F3,C8[2014·山东卷] 在△ABC 中,已知AB →·AC →=tan A ,当A =π6时,△ABC 的面积为______.12.16 [解析] 因为AB ·AC =|AB →|·|AC →|cos A =tan A ,且A =π6,所以|AB →|·|AC →|=23,所以△ABC 的面积S =12|AB →|·|AC →|sin A =12×23×sin π6=16.16.D2,D3,C8[2014·陕西卷] △ABC 的内角A ,B ,C 所对的边分别为a ,b ,c .(1)若a ,b ,c 成等差数列,证明:sin A +sin C =2sin(A +C ); (2)若a ,b ,c 成等比数列,求cos B 的最小值. 16.解:(1)∵a ,b ,c 成等差数列,∴a +c =2b . 由正弦定理得sin A +sin C =2sin B . ∵sin B =sin[π-(A +C )]=sin(A +C ), ∴sin A +sin C =2sin(A +C ).(2)∵a ,b ,c 成等比数列,∴b 2=ac . 由余弦定理得cos B =a 2+c 2-b 22ac =a 2+c 2-ac 2ac ≥2ac -ac 2ac =12,当且仅当a =c 时等号成立, ∴cos B 的最小值为12.13.C5,C8[2014·四川卷] 如图1-3所示,从气球A 上测得正前方的河流的两岸B ,C 的俯角分别为67°,30°,此时气球的高度是46 m ,则河流的宽度BC 约等于________m .(用四舍五入法将结果精确到个位.参考数据:sin 67°≈0.92,cos 67°≈0.39,sin 37°≈0.60,cos 37°≈0.80,3≈1.73)图1-313.60 [解析] 过A 点向地面作垂线,记垂足为D ,则在Rt △ADB 中,∠ABD =67°,AD =46 m ,∴AB =AD sin 67°=460.92=50(m),在△ABC 中,∠ACB =30°,∠BAC =67°-30°=37°,AB =50 m , 由正弦定理得,BC =AB sin 37°sin 30°=60 (m),故河流的宽度BC 约为60 m. 18.C8 [2014·浙江卷] 在△ABC 中,内角A ,B ,C 所对的边分别为a ,b ,c .已知a ≠b ,c =3,cos 2A -cos 2B =3sin A cos A -3sin B cos B .(1)求角C 的大小;(2)若sin A =45,求△ABC 的面积.18.解:(1)由题意得1+cos 2A 2-1+cos 2B 2=32sin 2A -32sin 2B ,即32sin 2A -12cos 2A=32sin 2B -12cos 2B ,sin ⎝⎛⎭⎫2A -π6=sin ⎝⎛⎭⎫2B -π6.。
第三节 两角和与差及二倍角三角函数公式 题号1 2 3 4 5 6 答案1.计算1-2sin 222.5°的结果等于( )A.12B.22C.33D.32解析:原式=cos 45°=22.故选B. 答案:B2.设tan(α+β)=25,tan ⎝ ⎛⎭⎪⎫β-π4=14,则tan ⎝⎛⎭⎪⎫α+π4的值是( ) A.318 B.322 C.1318 D .-1322解析:tan ⎝ ⎛⎭⎪⎫α+π4=tan ⎣⎢⎡⎦⎥⎤(α+β)-⎝⎛⎭⎪⎫β-π4=322. 答案:B3.求值:⎝ ⎛⎭⎪⎫cos π12-sin π12⎝ ⎛⎭⎪⎫cos π12+sin π12=( ) A .-32 B .-12C.12D.32答案:D4.若tan θ+1tan θ=4,则sin 2θ=( ) A.15 B.14C.13D.12解析:由tan θ+1tan θ=4得,sin θcos θ+cos θsin θ=sin 2θ+cos 2θsin θcos θ=4,即112sin 2θ=4,∴si n 2θ=12.故选D.答案:D5.sin 47°-sin 17°cos 30°cos 17°=( ) A .-32 B .-12 C.12 D.32解析:sin 47°-sin 17°cos 30°cos 17°=sin (17°+30°)-sin 17°cos 30°cos 17° =sin 17°cos 30°+cos 17°sin 30°-sin 17°cos 30°cos 17°=sin 30°=12.故选C. 答案:C6.已知α,β都是锐角,cos 2α=-725,cos(α+β)=513,则sin β=( ) A.1665 B.1365 C.5665 D.3365解析:∵cos 2α=2cos 2α-1,cos 2α=-725,又α为锐角, ∴cos α=35, sin α=45. ∵cos(α+β)=513,∴(α+β)为锐角,sin(α+β)=1213. ∴sin β=sin [](α+β)-α=sin(α+β)cos α-cos(α+β)sin α=1213×35-513×45=1665.故选A. 答案:A7.(2013·上海卷)若cos xcos y +sin xsin y =13,则cos(2x -2y)=________. 解析:cos x cos y +sin x sin y =cos(x -y )=13, 所以cos 2(x -y )=2cos 2(x -y )-1=-79. 答案:-798.sin α=35,cos β=35,其中α,β∈⎝ ⎛⎭⎪⎫0,π2,则α+β=______.解析:∵α,β∈⎝⎛⎭⎪⎫0,π2,sin α=35,cos β=35, ∴cos α=45,sin β=45. ∴cos(α+β)=cos αcos β-sin αsin β=0.∵α,β∈⎝⎛⎭⎪⎫0,π2,∴0<α+β<π,故α+β=π2. 答案:π29.已知tan α=2,则2sin 2α+1sin 2α=________. 解析:2sin 2α+1sin 2α=3sin 2α+cos 2α2sin αcos α=3tan 2α+12tan α=3×22+12×2=134. 答案:13410.已知α为锐角,且cos ⎝⎛⎭⎪⎫α+π4=35,则sin α=__________. 解析:因为α为锐角,所以α+π4∈⎝ ⎛⎭⎪⎫π4,3π4, 因为cos ⎝⎛⎭⎪⎫α+π4=35, 所以sin ⎝ ⎛⎭⎪⎫α+π4= 1-cos 2⎝ ⎛⎭⎪⎫α+π4=45, 则sin α=sin ⎣⎢⎡⎦⎥⎤⎝⎛⎭⎪⎫α+π4-π4=sin ⎝ ⎛⎭⎪⎫α+π4cos π4-cos ⎝ ⎛⎭⎪⎫α+π4sin π4=45×22-35×22=210. 答案:21011.已知函数f(x)=cos 2x +sin xcos x ,x ∈R.(1)求f ⎝ ⎛⎭⎪⎫π6的值; (2)若sin α=35,且α∈⎝ ⎛⎭⎪⎫π2,π,求f ⎝ ⎛⎭⎪⎫α2+π24. 解析:(1)f ⎝ ⎛⎭⎪⎫π6=cos 2π6+sin π6cos π6=⎝ ⎛⎭⎪⎫322+12×32=3+34. (2)f (x )=cos 2x +sin x cos x=1+cos 2x 2+12sin 2x =12+12(sin 2x +cos 2x ) =12+22sin ⎝⎛⎭⎪⎫2x +π4,f ⎝ ⎛⎭⎪⎫α2+π24=12+22sin ⎝ ⎛⎭⎪⎫α+π12+π4 =12+22sin ⎝⎛⎭⎪⎫α+π3 =12+22⎝ ⎛⎭⎪⎫sin α·12+cos α·32. 因为sin α=35,且α∈⎝ ⎛⎭⎪⎫π2,π,所以cos α=-45, 所以f ⎝ ⎛⎭⎪⎫α2+π24=12+22⎝ ⎛⎭⎪⎫35×12-45×32=10+32-4620. 12.已知函数f(x)=sin ⎝⎛⎭⎪⎫ωx +π6(ω>0)的最小正周期为π. (1)求ω的值;(2)设α∈⎝ ⎛⎭⎪⎫0,π2,β∈⎝ ⎛⎭⎪⎫π2,π,f ⎝ ⎛⎭⎪⎫-12α+π6=35,f ⎝ ⎛⎭⎪⎫12β+5π12=-1213,求sin(α+β)的值. 解析:(1)∵函数f (x )=sin ⎝⎛⎭⎪⎫ωx +π6的最小正周期为π,且ω>0,∴2πω=π, ∴ω=2.(2)由(1)得f (x )=sin ⎝⎛⎭⎪⎫2x +π6, ∴f ⎝ ⎛⎭⎪⎫-12α+π6=sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫-12α+π6+π6 =sin ⎝ ⎛⎭⎪⎫π2-α=cos α=35. ∵α∈⎝⎛⎭⎪⎫0,π2, ∴sin α=1-cos 2α=45. 又f ⎝ ⎛⎭⎪⎫12β+5π12=sin ⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫12β+5π12+π6=sin(π+β)=-sin β=-1213, ∴sin β=1213. ∵β∈⎝ ⎛⎭⎪⎫π2,π, ∴cos β=-1-sin 2β=-513, ∴sin(α+β)=sin αcos β+cos αsin β=45×⎝ ⎛⎭⎪⎫-513+35×1213=1665.。
§3.5两角和与差的正弦、余弦、正切公式1.两角和与差的余弦、正弦、正切公式cos(α-β)=cos αcos β+sin αsin β(C(α-β))cos(α+β)=cos_αcos_β-sin_αsin_β(C(α+β))sin(α-β)=sin_αcos_β-cos_αsin_β(S(α-β))sin(α+β)=sin_αcos_β+cos_αsin_β(S(α+β))tan(α-β)=错误!(T(α-β))tan(α+β)=错误!(T(α+β))2.二倍角公式sin 2α=2sin_αcos_α;cos 2α=cos2α-sin2α=2cos2α-1=1-2sin2α;tan 2α=错误!。
3.在准确熟练地记住公式的基础上,要灵活运用公式解决问题:如公式的正用、逆用和变形用等.如T(α±β)可变形为tan α±tanβ=tan(α±β)(1∓tan_αtan_β),tan αtan β=1-错误!=错误!-1.【思考辨析】判断下面结论是否正确(请在括号中打“√"或“×")(1)存在实数α,β,使等式sin(α+β)=sin α+sin β成立.( √)(2)在锐角△ABC中,sin A sin B和cos A cos B大小不确定.( ×)(3)公式tan(α+β)=tan α+tan β1-tan αtan β可以变形为tanα+tan β=tan(α+β)(1-tan αtan β),且对任意角α,β都成立.(×)(4)存在实数α,使tan 2α=2tan α。
(√)(5)设sin 2α=-sin α,α∈(错误!,π),则tan 2α=错误!.( √)1.(2013·浙江)已知α∈R,sin α+2cos α=错误!,则tan 2α等于( )A。
错误!B。
错误!C.-错误!D.-错误!答案C解析∵sinα+2cos α=错误!,∴sin2α+4sin αcos α+4cos2α=错误!.化简得:4sin 2α=-3cos 2α,∴tan 2α=sin 2αcos 2α=-错误!.故选C.2.若错误!=错误!,则tan 2α等于( )A.-错误! B.错误!C.-错误! D.错误!答案B解析由错误!=错误!,等式左边分子、分母同除cos α得,错误!=错误!,解得tan α=-3,则tan 2α=错误!=错误!.3.(2013·课标全国Ⅱ)设θ为第二象限角,若tan错误!=错误!,则sin θ+cos θ=________。
江苏省13市县2016届高三上学期期末考试数学试题分类汇编三角函数一、填空题1、(淮安、宿迁、连云港、徐州苏北四市2016届高三上期末)函数)sin(2)(ϕω+=x x f )0(>ω的部分图像如图所示,若5=AB ,则ω的值为 .2、(南京、盐城市2016届高三上期末)在ABC ∆中,设,,a b c 分别为角,,A B C 的对边,若5a =,4A π=,3cos 5B =,则边c = ▲ 3、(南通市海安县2016届高三上期末)若函数)4cos(3)4sin()(ππ-++=x x a x f 是偶函数,则实数a 的值为4、(南通市海安县2016届高三上期末)将函数)0)(2sin()(πϕϕ<<+=x x f 的图像向右平移2个单位后得到的函数图像关于原点对称,则实数ϕ的值为 ;5、(苏州市2016届高三上期末)已知θ是第三象限角,且2sin 2cos 5θθ-=-,则sin cos θθ+= ▲ .6、(泰州市2016届高三第一次模拟)已知函数π()sin()cos cos()262x x f x A x θ=+--(其中A 为常数,(π,0)θ∈-),若实数123,,x x x 满足:①123x x x <<,②31x x -<2π,③123()()()f x f x f x ==,则θ的值为 ▲ .7、(无锡市2016届高三上期末)将函数()2sin 2f x x =的图象上没一点向右平移6π个单位,得到函数()y g x =的图象,则()g x = 8、(扬州市2016届高三上期末)已知函数)32sin()(π+=x x f (π<x ≤0),且21)()(==βαf f (βα≠),则=+βα ▲9、(镇江市2016届高三第一次模拟) 函数y =a sin(ax +θ)(a >0,θ≠0)图象上的一个最高点和其相邻最低点的距离的最小值为________.10、(无锡市2016届高三上期末)已知sin(45)α-= 且090α<< ,则cos 2α的值为11、(镇江市2016届高三第一次模拟)由sin 36°=cos 54°,可求得cos 2 016°的值为________.填空题答案1、3π 2、7 3 4、4π- 5、3125- 6、23π-7、 8、76π9、2π. 10、72511、【答案】. 【命题立意】本题旨在考查三角函数值,诱导公式.考查概念的理解和运算能力,难度中等. 【解析】由sin 36°=cos 54°得()00000sin 362sin18cos18cos 3618==+即24sin 182sin1810+-=,解得0sin18==()()0000020cos 2016cos 5360144cos 144cos362sin 181=⨯-==-=-=,二、解答题1、(常州市2016届高三上期末)在△ABC 中,角A ,B ,C 的对边分别为,,a b c ,已知cos()1cos B C A -=-,且,,b a c 成等比数列,求:(1)sin sin B C 的值; (2)A ;(3)tan tan B C +的值。
第1讲弧度制与任意角的三角函数考试要求 1.任意角的概念,弧度制的概念,弧度与角度的互化,A级要求;2.任意角的三角函数(正弦、余弦、正切)的定义,B级要求.知识梳理1.角的概念的推广(1)正角、负角和零角:一条射线绕顶点按逆时针方向旋转所形成的角叫作正角,按顺时针方向旋转所形成的角叫作负角;如果射线没有作任何旋转,那么也把它看成一个角,叫作零角.(2)象限角:以角的顶点为坐标原点,角的始边为x轴的正半轴,建立平面直角坐标系,这样,角的终边在第几象限,我们就说这个角是第几象限的角.终边落在坐标轴上的角(轴线角)不属于任何象限.(3)终边相同的角:与角α的终边相同的角的集合为{β|β=k·360°+α,k∈Z}.2.弧度制的定义和公式(1)定义:把长度等于半径长的弧所对的圆心角叫做1弧度的角,弧度记作rad.(2)公式3.续表1.判断正误(在括号内打“√”或“×”)(1)小于90°的角是锐角.( )(2)锐角是第一象限角,反之亦然.( )(3)将表的分针拨快5分钟,则分针转过的角度是30°.()(4)若α∈,则tanα>α>sinα.( )(5)相等的角终边一定相同,终边相同的角也一定相等.( )解析(1)锐角的取值范围是.(2)第一象限角不一定是锐角.(3)顺时针旋转得到的角是负角.(5)终边相同的角不一定相等.答案(1)×(2)×(3)×(4)√(5)×2.若角α与角的终边相同,则在[0,2π]内终边与角终边相同的角是________.解析由题意知,α=2kπ+,k∈Z,∴=+,k∈Z,又∈[0,2π],∴k=0,α=;k=1,α=;k=2,α=;k=3,α=.答案,,,3.(必修4P15习题6改编)若tanα>0,sinα<0,则α在第________象限.解析由tanα>0,得α在第一或第三象限,又sinα<0,得α在第三或第四象限或终边在y轴的负半轴上,故α在第三象限.答案三4.已知角α的终边经过点(-4,3),则cosα=________.解析∵角α的终边经过点(-4,3),∴x=-4,y=3,r=5.∴cosα==-.答案-5.(必修4P10习题8改编)一条弦的长等于半径,这条弦所对的圆心角大小为________弧度.答案考点一角的概念及其集合表示【例1】(1)若角α是第二象限角,则是第________象限角.(2)终边在直线y=x上,且在[-2π,2π)内的角α的集合为________.解析(1)∵α是第二象限角,∴+2kπ<α<π+2kπ,k∈Z,∴+kπ<<+kπ,k∈Z.当k为偶数时,是第一象限角;当k为奇数时,是第三象限角.(2)如图,在坐标系中画出直线y=x,可以发现它与x轴的夹角是,在[0,2π)内,终边在直线y=x 上的角有两个:,π;在[-2π,0)内满足条件的角有两个:-π,-π,故满足条件的角α构成的集合为.答案(1)一或三(2)规律方法(1)利用终边相同的角的集合可以求适合某些条件的角,方法是先写出与这个角的终边相同的所有角的集合,然后通过对集合中的参数k赋值来求得所需的角.(2)确定kα,(k∈N*)的终边位置的方法先用终边相同角的形式表示出角α的范围,再写出kα或的范围,然后根据k的可能取值讨论确定kα或的终边所在位置.【训练1】(1)设集合M=,N=,则下列结论:①M=N;②M?N;③N?M;④M∩N=?.其中正确的是________(填序号).(2)集合中的角所表示的范围(阴影部分)是________(填序号).解析(1)法一由于M=={…,-45°,45°,135°,225°,…},N=={…,-45°,0°,45°,90°,135°,180°,225°,…},显然有M?N.法二由于M中,x=·180°+45°=k·90°+45°=(2k+1)·45°,2k+1是奇数;而N中,x=·180°+45°=k·45°+45°=(k+1)·45°,k+1是整数,因此必有M?N.(2)当k=2n(n∈Z)时,2nπ+≤α≤2nπ+,此时α表示的范围与≤α≤表示的范围一样;当k=2n+1(n∈Z)时,2nπ+≤α≤2nπ+,此时α表示的范围与≤α≤表示的范围一样.答案(1)②(2)③考点二弧度制及其应用【例2】已知一扇形的圆心角为α,半径为R,弧长为l.(1)若α=60°,R=10cm,求扇形的弧长l;(2)已知扇形的周长为10cm,面积是4cm2,求扇形的圆心角;(3)若扇形周长为20cm,当扇形的圆心角α为多少弧度时,这个扇形的面积最大?解(1)α=60°=rad,∴l=α·R=×10=(cm).(2)由题意得解得(舍去),故扇形圆心角为.(3)由已知得,l+2R=20.所以S=lR=(20-2R)R=10R-R2=-(R-5)2+25,所以当R=5时,S取得最大值25,此时l=10,α=2.规律方法应用弧度制解决问题的方法(1)利用扇形的弧长和面积公式解题时,要注意角的单位必须是弧度.(2)求扇形面积最大值的问题时,常转化为二次函数的最值问题,利用配方法使问题得到解决.(3)在解决弧长问题和扇形面积问题时,要合理地利用圆心角所在的三角形.【训练2】已知一扇形的圆心角为α(α>0),所在圆的半径为R.(1)若α=90°,R=10cm,求扇形的弧长及该弧所在的弓形的面积;(2)若扇形的周长是一定值C(C>0),当α为多少弧度时,该扇形有最大面积?解(1)设弧长为l,弓形面积为S弓,则α=90°=,R=10,l=×10=5π(cm),S=S扇-S△=×5π×10-×102=25π-50(cm2).弓(2)扇形周长C=2R+l=2R+αR,∴R=,∴S扇=α·R2=α·2=·=·≤.当且仅当α2=4,即α=2时,扇形面积有最大值.考点三三角函数的概念【例3】(1)(2017·扬州一中月考)已知角α的终边与单位圆x2+y2=1交于点P,则cos2α=________.(2)(2017·泰州模拟)已知角α的终边过点P(-8m,-6sin30°),且cosα=-,则m的值为________.(3)若sinα·tanα<0,且<0,则角α是第________象限角.解析(1)根据题意可知,cosα=,∴cos2α=2cos2α-1=2×-1=-.(2)∵r=,∴cosα==-,∴m>0,∴=,即m=.(3)由sinα·tanα<0可知sinα,tanα异号,从而α为第二或第三象限的角,由<0,可知cosα,tanα异号,从而α为第三或第四象限角.综上,α为第三象限角.答案(1)-(2) (3)三规律方法(1)利用三角函数的定义,求一个角的三角函数值,需确定三个量:角的终边上任意一个异于原点的点的横坐标x,纵坐标y,该点到原点的距离r.(2)根据三角函数定义中x,y的符号来确定各象限内三角函数的符号,理解并记忆:“一全正、二正弦、三正切、四余弦”.(3)利用三角函数线解三角不等式时要注意边界角的取舍,结合三角函数的周期性正确写出角的范围.【训练3】(1)(2017·无锡期末)已知角α的终边与单位圆的交点P,则sinα·tanα=________.(2)满足cosα≤-的角α的集合为________.解析(1)由|OP|2=+y2=1,得y2=,y=±.当y=时,sinα=,tanα=-,此时,sinα·tanα=-.当y=-时,sinα=-,tanα=,此时,sinα·tanα=-.(2)作直线x=-交单位圆于C,D两点,连接OC,OD,则OC与OD围成的区域(图中阴影部分)即为角α终边的范围,故满足条件的角α的集合为.答案(1)-(2)[思想方法]1.在利用三角函数定义时,点P可取终边上任一点,如有可能则取终边与单位圆的交点.|OP|=r一定是正值.2.三角函数符号是重点,也是难点,在理解的基础上可借助口诀:一全正,二正弦,三正切,四余弦.3.在解决简单的三角不等式时,利用单位圆及三角函数线是一个小技巧.[易错防范]1.注意易混概念的区别:象限角、锐角、小于90°的角是概念不同的三类角.第一类是象限角,第二、第三类是区间角.2.角度制与弧度制可利用180°=πrad进行互化,在同一个式子中,采用的度量制度必须一致,不可混用.3.已知三角函数值的符号确定角的终边位置不要遗漏终边在坐标轴上的情况.基础巩固题组(建议用时:30分钟)1.给出下列四个命题:①-是第二象限角;②是第三象限角;③-400°是第四象限角;④-315°是第一象限角.其中正确的命题的个数为________.解析-是第三象限角,故①错误.=π+,从而是第三象限角,②正确.-400°=-360°-40°,从而③正确.-315°=-360°+45°,从而④正确.答案32.已知点P(tanα,cosα)在第三象限,则角α的终边在第________象限.解析由题意知tanα<0,cosα<0,∴α是第二象限角.答案二3.(2017·苏州期末)已知角θ的终边经过点P(4,m),且sinθ=,则m=________.解析sinθ==,解得m=3.答案34.已知角α的终边在如图所示阴影表示的范围内(不包括边界),则角α用集合可表示为________.解析在[0,2π)内,终边落在阴影部分角的集合为,所以,所求角的集合为(k∈Z).答案(k∈Z)5.设P是角α终边上一点,且|OP|=1,若点P关于原点的对称点为Q,则Q点的坐标是________.解析由已知P(cosα,sinα),则Q(-cosα,-sinα).答案(-cosα,-sinα)6.已知扇形的圆心角为,面积为,则扇形的弧长等于________.解析设扇形半径为r,弧长为l,则解得答案7.点P从(1,0)出发,沿单位圆逆时针方向运动弧长到达Q点,则Q点的坐标为________.解析由三角函数定义可知Q点的坐标(x,y)满足x=cos=-,y=sin=.答案8.设θ是第三象限角,且=-cos,则是第________象限角.解析由θ是第三象限角,知为第二或第四象限角,∵=-cos,∴cos≤0,综上知为第二象限角.答案二9.若一圆弧长等于其所在圆的内接正三角形的边长,则其圆心角α∈(0,π)的弧度数为________.解析设圆半径为r,则其内接正三角形的边长为r,所以r=α·r,∴α=.答案10.已知角θ的顶点与原点重合,始边与x轴的正半轴重合,终边在直线y=2x上,则cos2θ=________.解析由题意知,tanθ=2,即sinθ=2cosθ,将其代入sin2θ+cos2θ=1中可得cos2θ=,故cos2θ=2cos2θ-1=-.答案-11.给出下列命题:①第二象限角大于第一象限角;②三角形的内角是第一象限角或第二象限角;③不论是用角度制还是用弧度制度量一个角,它们与扇形的半径的大小无关;④若sinα=sinβ,则α与β的终边相同;⑤若cosθ<0,则θ是第二或第三象限的角.其中正确命题的个数是________.解析举反例:第一象限角370°不小于第二象限角100°,故①错;当三角形的内角为90°时,其既不是第一象限角,也不是第二象限角,故②错;③正确;由于sin=sin,但与的终边不相同,故④错;当cosθ=-1,θ=π时既不是第二象限角,也不是第三象限角,故⑤错.综上可知只有③正确.答案112.(2017·苏北四市期末)已知角α的终边经过点(3a-9,a+2),且cosα≤0,sinα>0,则实数a的取值范围是________.解析∵cosα≤0,sinα>0,∴角α的终边落在第二象限或y轴的正半轴上.∴∴-2<a≤3.答案(-2,3]能力提升题组(建议用时:15分钟)13.已知圆O:x2+y2=4与y轴正半轴的交点为M,点M沿圆O顺时针运动弧长到达点N,以ON为终边的角记为α,则tanα=________.解析圆的半径为2,的弧长对应的圆心角为,故以ON为终边的角为,故tanα=1.答案114.(2017·泰州模拟)设α是第二象限角,P(x,4)为其终边上的一点,且cosα=x,则tanα=________.解析因为α是第二象限角,所以cosα=x<0,即x<0.又cosα=x=,解得x=-3,所以tanα==-.答案-15.函数y=的定义域为________.解析∵2sin x-1≥0,∴sin x≥.由三角函数线画出x满足条件的终边范围(如图阴影所示).∴x∈(k∈Z).答案(k∈Z)16.如图,在平面直角坐标系xOy中,一单位圆的圆心的初始位置在(0,1),此时圆上一点P 的位置在(0,0),圆在x轴上沿正向滚动,当圆滚动到圆心位于(2,1)时,的坐标为________.解析如图,作CQ∥x轴,PQ⊥CQ,Q为垂足.根据题意得劣弧=2,故∠DCP=2,则在△PCQ中,∠PCQ=2-,|CQ|=cos=sin2,|PQ|=sin=-cos2,所以P点的横坐标为2-|CQ|=2-sin2,P点的纵坐标为1+|PQ|=1-cos2,所以P点的坐标为(2-sin2,1-cos2),故=(2-sin2,1-cos2).答案(2-sin2,1-cos2)第2讲同角三角函数基本关系式及诱导公式考试要求 1.同角三角函数的基本关系式:sin2α+cos2α=1,=tanα,B级要求;±α,π±α,-α的正弦、余弦的诱导公式,B级要求.知识梳理1.同角三角函数的基本关系(1)平方关系:sin2α+cos2α=1.(2)商数关系:=tanα.2.三角函数的诱导公式公式一二三四五六角2kπ+α(k∈Z)π+α-απ-α-α+α正弦sinα-sin_α-sin_αsin_αcos_αcos_α余弦cosα-cos_αcos_α-cos_αsin_α-sin_α正切tanαtan_α-tan_α-tan_α口诀函数名不变,符号看象限函数名改变,符号看象限1.判断正误(在括号内打“√”或“×”)(1)sin(π+α)=-sinα成立的条件是α为锐角.( )(2)六组诱导公式中的角α可以是任意角.( )(3)诱导公式的记忆口诀中“奇变偶不变,符号看象限”,其中的奇、偶是指的奇数倍和偶数倍,变与不变指函数名称的变化.( )(4)若sin(kπ-α)=(k∈Z),则sinα=.( )解析(1)对于α∈R,sin(π+α)=-sinα都成立.(4)当k为奇数时,sinα=,当k为偶数时,sinα=-.答案(1)×(2)√(3)√(4)×2.sin600°的值为________.解析sin600°=sin(360°+240°)=sin240°=sin(180°+60°)=-sin60°=-.答案-3.(2017·苏北四市摸底)已知sin=,那么cosα=________.解析∵sin=sin=cosα,∴cosα=.答案4.(2017·南通调研)已知sinθ+cosθ=,θ∈,则sinθ-cosθ=________.解析∵sinθ+cosθ=,∴sinθcosθ=.又∵(sinθ-cosθ)2=1-2sinθcosθ=,∴sinθ-cosθ=或-.又∵θ∈,∴sinθ-cosθ=-.答案-5.(必修4P23习题11改编)已知tanα=2,则的值为________.解析原式===3.答案3考点一同角三角函数基本关系式及其应用【例1】(1)(2015·福建卷改编)若sinα=-,且α为第四象限角,则tanα的值等于________.(2)(2017·盐城模拟)已知sinαcosα=,且<α<,则cosα-sinα的值为________.(3)(2016·全国Ⅲ卷改编)若tanα=,则cos2α+2sin2α=________.解析(1)∵sinα=-,且α为第四象限角,∴cosα==,∴tanα==-.(2)∵<α<,∴cosα<0,sinα<0且cosα>sinα,∴cosα-sinα>0.又(cosα-sinα)2=1-2sinαcosα=1-2×=,∴cosα-sinα=.(3)tanα=,则cos2α+2sin2α===.答案(1)-(2) (3)规律方法(1)利用sin2α+cos2α=1可以实现角α的正弦、余弦的互化,利用=tanα可以实现角α的弦切互化.(2)应用公式时注意方程思想的应用:对于sinα+cosα,sinαcosα,sinα-cosα这三个式子,利用(sinα±cosα)2=1±2sinαcosα,可以知一求二.(3)注意公式逆用及变形应用:1=sin2α+cos2α,sin2α=1-cos2α,cos2α=1-sin2α.【训练1】(1)已知sinα-cosα=,α∈(0,π),则tanα=________.(2)(2017·盐城调研)若3sinα+cosα=0,则=________.解析(1)由得:2cos2α+2cosα+1=0,即2=0,∴cosα=-.又α∈(0,π),∴α=,∴tanα=tan=-1.(2)3sinα+cosα=0?cosα≠0?tanα=-,====.答案(1)-1 (2)考点二诱导公式的应用【例2】(1)化简:sin(-1200°)cos1290°+cos(-1020°)·sin(-1050°);(2)求值:设f(α)=(1+2sinα≠0),求f的值.解(1)原式=-sin1200°cos1290°-cos1020°sin1050°=-sin(3×360°+120°)cos(3×360°+210°)-cos(2×360°+300°)sin(2×360°+330°)=-sin120°cos210°-cos300°sin330°=-sin(180°-60°)cos(180°+30°)-cos(360°-60°)·sin(360°-30°)=sin60°cos30°+cos60°sin30°=×+×=1.(2)∵f(α)====,∴f====.规律方法(1)诱导公式的两个应用①求值:负化正,大化小,化到锐角为终了.②化简:统一角,统一名,同角名少为终了.(2)含2π整数倍的诱导公式的应用由终边相同的角的关系可知,在计算含有2π的整数倍的三角函数式中可直接将2π的整数倍去掉后再进行运算,如cos(5π-α)=cos(π-α)=-cosα.【训练2】(1)已知A=+(k∈Z),则A的值构成的集合是________.(2)化简:=______.解析(1)当k为偶数时,A=+=2;k为奇数时,A=-=-2.(2)原式====-1.答案(1){2,-2} (2)-1考点三诱导公式、同角三角函数关系式的综合应用【例3】(1)已知tan=,则tan=________.(2)(2017·南京、盐城模拟)已知cos=,且-π<α<-,则cos=________.解析(1)∵+=π,∴tan=tan=-tan=-.(2)因为+=,所以cos=sin=sin.因为-π<α<-,所以-<α+<-.又cos=>0,所以-<α+<-,所以sin=-=-=-.规律方法(1)常见的互余的角:-α与+α;+α与-α;+α与-α等.(2)常见的互补的角:+θ与-θ;+θ与-θ等.【训练3】(1)已知sin=,则cos=________.(2)设函数f(x)(x∈R)满足f(x+π)=f(x)+sin x,当0≤x<π时,f(x)=0,则f=________.解析(1)∵+=,∴cos=cos=sin=.(2)由f(x+π)=f(x)+sin x,得f(x+2π)=f(x+π)+sin(x+π)=f(x)+sin x-sin x=f(x),所以f=f=f=f=f+sinπ.因为当0≤x<π时,f(x)=0.所以f=0+=.答案(1) (2)[思想方法]1.同角三角函数基本关系可用于统一函数;诱导公式主要用于统一角,其主要作用是进行三角函数的求值、化简和证明,已知一个角的某一三角函数值,求这个角的其它三角函数值时,要特别注意平方关系的使用.2.三角求值、化简是三角函数的基础,在求值与化简时,常用方法有:(1)弦切互化法:主要利用公式tan x=进行切化弦或弦化切,如,a sin2x+b sin x cos x+c cos2x等类型可进行弦化切.(2)和积转换法:如利用(sinθ±cosθ)2=1±2sinθcosθ的关系进行变形、转化.(3)巧用“1”的变换:1=sin2θ+cos2θ=cos2θ(1+tan2θ)=sin2θ=tan=…. [易错防范]1.利用诱导公式进行化简求值时,可利用公式化任意角的三角函数为锐角三角函数,其步骤:去负—脱周—化锐.特别注意函数名称和符号的确定.2.在利用同角三角函数的平方关系时,若开方,要特别注意判断符号.3.注意求值与化简后的结果一般要尽可能有理化、整式化.基础巩固题组(建议用时:30分钟)解析sin750°=sin(720°+30°)=sin30°=.答案2.(2017·镇江期末)已知α是第四象限角,sinα=-,则tanα=________.解析因为α是第四象限角,sinα=-,所以cosα==,故tanα==-.答案-3.已知tanα=,且α∈,则sinα=________.解析∵tanα=>0,且α∈,∴sinα<0,∴sin2α====,∴sinα=-.答案-=________.解析===|sin2-cos2|=sin2-cos2.答案sin2-cos25.(2016·全国Ⅰ卷)已知θ是第四象限角,且sin=,则tan=________.解析由题意,得cos=,∴tan=.∴tan=tan=-=-.答案-6.(2017·扬州中学质检)向量a=,b=(cosα,1),且a∥b,则cos=________.解析∵a=,b=(cosα,1),且a∥b,∴×1-tanαcosα=0,∴sinα=,∴cos=-sinα=-.答案-7.(2017·广州二测改编)cos=,则sin=________.解析sin=sin=cos=.答案8.(2017·泰州模拟)已知tanα=3,则的值是________.解析原式======2.9.已知α为钝角,sin=,则sin=________.解析因为α为钝角,所以cos=-,所以sin=cos=cos=-.答案-10.已知sinα=,则sin4α-cos4α的值为________.解析sin4α-cos4α=sin2α-cos2α=2sin2α-1=-1=-.答案-11.化简:=________.解析原式===1.答案112.(2017·西安模拟)已知函数f(x)=a sin(πx+α)+b cos(πx+β),且f(4)=3,则f(2017)的值为________.解析∵f(4)=a sin(4π+α)+b cos(4π+β)=a sinα+b cosβ=3,∴f(2017)=a sin(2017π+α)+b cos(2017π+β)=a sin(π+α)+b cos(π+β)=-a sinα-b cosβ=-3.答案-3能力提升题组(建议用时:15分钟)13.已知sin(π+θ)=-cos(2π-θ),|θ|<,则θ=________.解析∵sin(π+θ)=-cos(2π-θ),∴-sinθ=-cosθ,∴tanθ=,∵|θ|<,∴θ=.答案14.若sinθ,cosθ是方程4x2+2mx+m=0的两根,则m的值为________.解析由题意知sinθ+cosθ=-,sinθ·cosθ=.又2=1+2sinθcosθ,∴=1+,解得m=1±.又Δ=4m2-16m≥0,∴m≤0或m≥4,∴m=1-.15.(2017·苏州调研)已知sin=,则sin+sin2的值为________.解析sin+sin2=sin+sin2=-sin+cos2=-sin+1-sin2=.答案16.已知cos=a,则cos+sin=________.解析∵cos=cos=-cos=-a.sin=sin=cos=a,∴cos+sin=0.答案0第3讲三角函数的图象和性质考试要求=sin x,y=cos x,y=tan x的图象及周期性,A级要求;2正弦函数、余弦函数在区间[0,2π]上的性质(如单调性、最值及与x轴的交点等),B级要求;3.正切函数在区间内的单调性,B级要求.知识梳理1.用五点法作正弦函数和余弦函数的简图(1)正弦函数y=sin x,x∈[0,2π]的图象中,五个关键点是:(0,0),,(π,0),,(2π,0).(2)余弦函数y=cos x,x∈[0,2π]的图象中,五个关键点是:(0,1),,(π,-1),,(2π,1).2.正弦、余弦、正切函数的图象与性质(下表中k∈Z)1.判断正误(在括号内打“√”或“×”)(1)由sin=sin知,是正弦函数y=sin x(x∈R)的一个周期.( )(2)余弦函数y=cos x的对称轴是y轴.( )(3)正切函数y=tan x在定义域内是增函数.( )(4)已知y=k sin x+1,x∈R,则y的最大值为k+1.( )(5)y=sin|x|是偶函数.( )解析(1)函数y=sin x的周期是2kπ(k∈Z).(2)余弦函数y=cos x的对称轴有无穷多条,y轴只是其中的一条.(3)正切函数y=tan x在每一个区间(k∈Z)上都是增函数,但在定义域内不是单调函数,故不是增函数.(4)当k>0时,y max=k+1;当k<0时,y max=-k+1.答案(1)×(2)×(3)×(4)×(5)√2.(必修4P33例4改编)函数y=2tan的定义域为________.解析∵x-≠kπ+,k∈Z,∴x≠kπ+,k∈Z,即函数的定义域为.答案3.(2017·苏州一模)若函数f(x)=sin(φ∈[0,2π])是偶函数,则φ=________.解析由已知f(x)=sin是偶函数,可得=kπ+,即φ=3kπ+(k∈Z),又φ∈[0,2π],所以φ=.答案4.函数f(x)=sin在区间上的最小值为________.解析由已知x∈,得2x-∈,所以sin∈,故函数f(x)=sin在区间上的最小值为-.答案-5.(2017·南通调研)若函数y=2cosωx在区间上单调递减,且有最小值1,则ω的值为________.解析因为y=cos x在上单调递增,在上单调递减,所以必有ω>0,且·ω≤.所以0<ω≤.当x=时,2cosπ=1,cosπ=.所以ω=.答案考点一三角函数的定义域及简单的三角不等式【例1】(1)函数f(x)=-2tan的定义域是________.(2)不等式+2cos x≥0的解集是________.(3)函数f(x)=+log2(2sin x-1)的定义域是________.解析(1)由正切函数的定义域,得2x+≠kπ+,即x≠+(k∈Z).(2)由+2cos x≥0,得cos x≥-,由余弦函数的图象,得在一个周期[-π,π]上,不等式cos x≥-的解集为,故原不等式的解集为.(3)由题意,得由①得-8≤x≤8,由②得sin x>,由正弦曲线得+2kπ<x<π+2kπ(k∈Z).所以不等式组的解集为∪∪.答案(1)(2)(3)∪∪规律方法(1)三角函数定义域的求法①以正切函数为例,应用正切函数y=tan x的定义域求函数y=A tan(ωx+φ)的定义域.②转化为求解简单的三角不等式求复杂函数的定义域.(2)简单三角不等式的解法①利用三角函数线求解.②利用三角函数的图象求解.【训练1】(1)函数y=tan2x的定义域为________.(2)函数y=的定义域为________.解析(1)由2x≠kπ+,k∈Z,得x≠+,k∈Z,∴y=tan2x的定义域为.(2)法一要使函数有意义,必须使sin x-cos x≥0.利用图象,在同一坐标系中画出[0,2π]上y=sin x和y=cos x的图象,如图所示.在[0,2π]内,满足sin x=cos x的x为,,再结合正弦、余弦函数的周期是2π,所以原函数的定义域为.法二利用三角函数线,画出满足条件的终边范围(如图阴影部分所示).所以定义域为.法三sin x-cos x=sin≥0,将x-视为一个整体,由正弦函数y=sin x的图象和性质可知2kπ≤x-≤π+2kπ(k∈Z),解得2kπ+≤x≤2kπ+(k∈Z).所以定义域为.答案(1)(2)考点二三角函数的值域【例2】(1)函数y=-2sin x-1,x∈的值域是________.(2)(2016·全国Ⅱ卷改编)函数f(x)=cos2x+6cos的最大值为________.(3)函数y=sin x-cos x+sin x cos x的值域为________.解析(1)由正弦曲线知y=sin x在上,-1≤sin x<,所以函数y=-2sin x-1,x∈的值域是(-2,1].(2)由f(x)=cos2x+6cos=1-2sin2x+6sin x=-22+,所以当sin x=1时函数的最大值为5.则t2=sin2x+cos2x-2sin x cos x,sin x cos x=,且-≤t≤.∴y=-+t+=-(t-1)2+1.当t=1时,y max=1;当t=-时,y min=--.∴函数的值域为.答案(1)(-2,1] (2)5 (3)规律方法求解三角函数的值域(最值)常见到以下几种类型:(1)形如y=a sin x+b cos x+c的三角函数化为y=A sin(ωx+φ)+c的形式,再求值域(最值);(2)形如y=a sin2x+b sin x+c的三角函数,可先设sin x=t,化为关于t的二次函数求值域(最值);(3)形如y=a sin x cos x+b(sin x±cos x)+c的三角函数,可先设t=sin x±cos x,化为关于t的二次函数求值域(最值).【训练2】(1)(2017·泰州模拟)函数y=2sin(0≤x≤9)的最大值与最小值之和为________.(2)函数y=-2cos+1的最大值是________,此时x的取值集合为________.解析(1)因为0≤x≤9,所以-≤x-≤,所以sin∈.所以y∈[-,2],所以y max+y min=2-.(2)y max=-2×(-1)+1=3,此时,x-=2kπ+π,即x=4kπ+(k∈Z).答案(1)2-(2)3考点三三角函数的性质(多维探究)命题角度一三角函数的奇偶性与周期性【例3-1】(1)(2017·常州期末)函数y=2cos2-1的最小正周期为________的________函数(填“奇”或“偶”).(2)(2017·衡水中学金卷)设函数f(x)=sin-cos的图象关于y轴对称,则θ=________.解析(1)y=2cos2-1=cos2=cos则函数为最小正周期为π的奇函数.(2)f(x)=sin-cos=2sin,由题意可得f(0)=2sin=±2,即sin=±1,∴θ-=+kπ(k∈Z),∴θ=+kπ(k∈Z),∵|θ|<,∴k=-1时,θ=-.答案(1)π奇(2)-规律方法(1)若f(x)=A sin(ωx+φ)(A,ω≠0),则①f(x)为偶函数的充要条件是φ=+kπ(k∈Z);②f(x)为奇函数的充要条件是φ=kπ(k∈Z).(2)函数y=A sin(ωx+φ)与y=A cos(ωx+φ)的最小正周期T=,y=A tan(ωx+φ)的最小正周期T=.命题角度二三角函数的单调性【例3-2】(1)函数f(x)=sin的单调递减区间为________.(2)若f(x)=2sinωx+1(ω>0)在区间上是增函数,则ω的取值范围是________.解析(1)由已知可得函数为y=-sin,欲求函数的单调减区间,只需求y=sin的单调增区间.由2kπ-≤2x-≤2kπ+,k∈Z,得kπ-≤x≤kπ+,k∈Z.故所求函数的单调递减区间为(k∈Z).(2)法一由2kπ-≤ωx≤2kπ+,k∈Z,得f(x)的增区间是(k∈Z).因为f(x)在上是增函数,所以?.所以-≥-且≤,所以ω∈.法二因为x∈,ω>0.所以ωx∈,又f(x)在区间上是增函数,所以?,则又ω>0,得0<ω≤.法三因为f(x)在区间上是增函数,故原点到-,的距离不超过,即得T≥,即≥,又ω>0,得0<ω≤.答案(1)(k∈Z) (2)规律方法(1)求较为复杂的三角函数的单调区间时,首先化简成y=A sin(ωx+φ)形式,再求y=A sin(ωx+φ)的单调区间,只需把ωx+φ看作一个整体代入y=sin x的相应单调区间内即可,注意要先把ω化为正数.(2)对于已知函数的单调区间的某一部分确定参数ω的范围的问题,首先,明确已知的单调区间应为函数的单调区间的子集,其次,要确定已知函数的单调区间,从而利用它们之间的关系可求解.命题角度三三角函数的对称轴或对称中心【例3-3】(1)(2017·苏、锡、常、镇四市调研)若函数f(x)=2sin(4x+φ)(φ<0)的图象关于直线x=对称,则φ的最大值为________.(2)(2016·全国Ⅰ卷改编)已知函数f(x)=sin(ωx+φ),x=-为f(x)的零点,x=为y=f(x)图象的对称轴,且f(x)在上单调,则ω的最大值为________.解析(1)由题可得,4×+φ=+kπ,k∈Z,∴φ=+kπ,k∈Z,∵φ<0,∴φmax=-. (2)因为x=-为f(x)的零点,x=为f(x)的图象的对称轴,所以-=+kT,即=T=·,所以ω=4k+1(k∈N*),又因为f(x)在上单调,所以-=≤=,即ω≤12,由此得ω的最大值为9.答案(1)-(2)9规律方法(1)对于可化为f(x)=A sin(ωx+φ)形式的函数,如果求f(x)的对称轴,只需令ωx+φ=+kπ(k∈Z),求x即可;如果求f(x)的对称中心的横坐标,只需令ωx+φ=kπ(k∈Z),求x即可.(2)对于可化为f(x)=A cos(ωx+φ)形式的函数,如果求f(x)的对称轴,只需令ωx+φ=kπ(k∈Z),求x即可;如果求f(x)的对称中心的横坐标,只需令ωx+φ=+kπ(k∈Z),求x即可.【训练3】(1)(2017·无锡期末)若函数f(x)=cos的图象关于点(x0,0)成中心对称,x0∈,则x0=______.(2)已知ω>0,函数f(x)=cos在上单调递增,则ω的取值范围是________.解析(1)因为f(x)=cos=cos=-sin2x,f(-x)=-sin(-2x)=sin2x=-f(x),所以f(x)=-sin2x是奇函数,所以f(x)的图象关于原点对称.(2)函数y=cos x的单调递增区间为[-π+2kπ,2kπ],k∈Z,则(k∈Z),解得4k-≤ω≤2k-,k∈Z,又由4k--≤0,k∈Z且2k->0,k∈Z,得k=1,所以ω∈.答案(1)0 (2)[思想方法]1.讨论三角函数性质,应先把函数式化成y=A sin(ωx+φ)(ω>0)的形式.2.对于函数的性质(定义域、值域、单调性、对称性、最值等)可以通过换元的方法令t=ωx+φ,将其转化为研究y=sin t的性质.3.数形结合是本讲的重要数学思想.[易错防范]1.闭区间上最值或值域问题,首先要在定义域基础上分析单调性;含参数的最值问题,要讨论参数对最值的影响.2.要注意求函数y=A sin(ωx+φ)的单调区间时A和ω的符号,尽量化成ω>0时情况,避免出现增减区间的混淆.基础巩固题组(建议用时:40分钟)一、填空题1.在函数①y=cos|2x|,②y=|cos x|,③y=cos,④y=tan中,最小正周期为π的函数有________(填序号).解析①y=cos|2x|=cos2x,最小正周期为π;②由图象知y=|cos x|的最小正周期为π;③y=cos的最小正周期T==π;④y=tan的最小正周期T=.答案①②③2.(2017·南京模拟)函数f(x)=tan的单调递增区间是________.解析当kπ-<2x-<kπ+(k∈Z)时,函数y=tan单调递增,解得-<x<+(k∈Z),所以函数y=tan的单调递增区间是(k∈Z).答案(k∈Z)3.(2017·南通、扬州、泰州、淮安调研)设函数y=sin(0<x<π),当且仅当x=时,y取得最大值,则正数ω的值为________.解析由题意可得ω+=+2kπ,k∈Z且π≤,解得ω=2.答案24.(2017·徐州检测)函数y=cos2x-2sin x的最大值与最小值分别为________.解析y=cos2x-2sin x=1-sin2x-2sin x=-sin2x-2sin x+1,令t=sin x,则t∈[-1,1],y=-t2-2t+1=-(t+1)2+2,所以y max=2,y min=-2.答案2,-25.(2017·苏北四市联考)函数y=sin x+cos x的单调递增区间是________.解析∵y=sin x+cos x=sin,由2kπ-≤x+≤2kπ+(k∈Z),解得2kπ-≤x≤2kπ+(k∈Z).∴函数的单调递增区间为(k∈Z),又x∈,∴单调递增区间为.答案6.(2017·盐城调研)若函数f(x)=cos(0<φ<π)是奇函数,则φ=________.解析因为f(x)为奇函数,所以φ-=+kπ,φ=+kπ,k∈Z.又因为0<φ<π,故φ=.答案7.(2017·银川模拟)已知函数f(x)=sin(x∈R),给出以下结论:①函数f(x)的最小正周期为π;②函数f(x)是偶函数;③函数f(x)的图象关于直线x=对称;④函数f(x)在区间上是增函数.其中正确的是________(填序号).解析f(x)=sin=-cos2x,故其最小正周期为π,故①正确;易知函数f(x)是偶函数,②正确;由函数f(x)=-cos2x的图象可知,函数f(x)的图象不关于直线x=对称,③错误;由函数f(x)的图象易知,函数f(x)在上是增函数,④正确.答案①②④8.(2017·承德模拟)若函数f(x)=sinωx(ω>0)在上单调递增,在区间上单调递减,则ω=________.解析法一由于函数f(x)=sinωx(ω>0)的图象经过坐标原点,由已知并结合正弦函数的图象可知,为函数f(x)的周期,故=,解得ω=.法二由题意,得f(x)max=f=sinω=1.由已知并结合正弦函数图象可知,ω=,解得ω=.答案二、解答题9.(2015·安徽卷)已知函数f(x)=(sin x+cos x)2+cos2x.(1)求f(x)的最小正周期;(2)求f(x)在区间上的最大值和最小值.解(1)因为f(x)=sin2x+cos2x+2sin x cos x+cos2x=1+sin2x+cos2x=sin+1,所以函数f(x)的最小正周期为T==π.(2)由(1)的计算结果知,f(x)=sin+1.当x∈时,2x+∈,由正弦函数y=sin x在上的图象知,当2x+=,即x=时,f(x)取最大值+1;当2x+=,即x=时,f(x)取最小值0.综上,f(x)在上的最大值为+1,最小值为0.10.(2016·天津卷)已知函数f(x)=4tan x sin·cos-.(1)求f(x)的定义域与最小正周期;(2)讨论f(x)在区间上的单调性.解(1)f(x)的定义域为.f(x)=4tan x cos x cos-=4sin x cos-=4sin x-=2sin x cos x+2sin2x-=sin2x+(1-cos2x)-=sin2x-cos2x=2sin.所以f(x)的最小正周期T==π.(2)由-+2kπ≤2x-≤+2kπ,得-+kπ≤x≤+kπ,k∈Z.由+2kπ≤2x-≤+2kπ,得+kπ≤x≤+kπ,k∈Z.所以当x∈时,f(x)在区间上单调递增,在区间上单调递减.能力提升题组(建议用时:20分钟)11.(2016·江苏卷)定义在区间[0,3π]上的函数y=sin2x的图象与y=cos x的图象的交点个数是________.解析在区间[0,3π]上分别作出y=sin2x和y=cos x的简图如下:由图象可得两图象有7个交点.答案712.若函数f(x)=4sin5ax-4cos5ax的图象的相邻两条对称轴之间的距离为,则实数a的值为________.解析因为f(x)=8sin,依题意有,=,所以T=.又因为T=,所以=,解得a=±.答案±13.已知函数f(x)=sin(ω>0),若f=f,且f(x)在区间上有最小值,无最大值.则ω的值为________.解析f(x)在区间上有最小值,无最大值,则:①说明中有最低点.∵f=f,∴最低点必为x==.代入+=-+2kπ,得ω=+8k,k为整数.②说明中无最高点,故>-=,∴T=>,∴0<ω<6.由①和②得ω=.答案14.(2017·南通调研)已知函数f(x)=a+b.(1)若a=-1,求函数f(x)的单调增区间;(2)若x∈[0,π]时,函数f(x)的值域是[5,8],求a,b的值.解f(x)=a(1+cos x+sin x)+b=a sin+a+b.(1)当a=-1时,f(x)=-sin+b-1,由2kπ+≤x+≤2kπ+(k∈Z),得2kπ+≤x≤2kπ+(k∈Z),∴f(x)的单调增区间为(k∈Z).(2)∵0≤x≤π,∴≤x+≤,∴-≤sin≤1,依题意知a≠0.(ⅰ)当a>0时,∴a=3-3,b=5.(ⅱ)当a<0时,∴a=3-3,b=8.综上所述,a=3-3,b=5或a=3-3,b=8.第4讲函数y=A sin(ωx+φ)的图象及应用考试要求 1.函数y=A sin(ωx+φ)的物理意义,图象的画法,参数A,ω,φ对函数图象变化的影响,A级要求;2.利用三角函数解决一些简单实际问题,A级要求.知识梳理1.“五点法”作函数y=A sin(ωx+φ)(A>0,ω>0)的简图“五点法”作图的五点是在一个周期内的最高点、最低点及与x轴相交的三个点,作图时的一般步骤为:(1)定点:如下表所示.(2)ωx+φ)在一个周期内的图象.(3)扩展:将所得图象,按周期向两侧扩展可得y=A sin(ωx+φ)在R上的图象.2.函数y=A sin(ωx+φ)中各量的物理意义当函数y=A sin(ωx+φ)(A>0,ω>0),x∈[0,+∞)表示简谐振动时,几个相关的概念如下表:3.诊断自测1.判断正误(在括号内打“√”或“×”)(1)将函数y=3sin2x的图象左移个单位长度后所得图象的解析式是y=3sin.( )(2)利用图象变换作图时“先平移,后伸缩”与“先伸缩,后平移”中平移的长度一致.( )(3)函数y=A cos(ωx+φ)的最小正周期为T,那么函数图象的两个相邻对称中心之间的距离为.( )。
江苏省2016年高考一轮复习专题突破训练三角函数一、填空题1、(2015年江苏高考)已知tan 2α=-,1tan()7αβ+=,则tan β的值为_________3_________。
2、(2014年江苏高考)已知函数x y cos =与)0)(2sin(πϕϕ≤≤+=x y ,它们的图象有一个横坐标为3π的交点,则ϕ的值是 ▲ . 3、(2013年江苏高考)函数)42sin(3π+=x y 的最小正周期为 。
4、(2015届南京、盐城市高三二模)已知βα,均为锐角,且βαβαsin sin )cos(=+,则αtan 的最大值是5、(南通、扬州、连云港2015届高三第二次调研(淮安三模))若函数()π()2sin 3f x x ω=+(0)ω>的图象与x 轴相邻两个交点间的距离为2,则实数ω的值为 ▲6、(苏锡常镇四市2015届高三教学情况调研(二))函数3sin(2)4y x π=+的图象向左平移(0)2πϕϕ<<个单位后,所得函数图象关于原点成中心对称,则ϕ= ▲7、(泰州市2015届高三第二次模拟考试)设函数π()3sin(π)3f x x =+和π()sin(π)6g x x =-的图象在y 轴左、右两侧靠近y 轴的交点分别为M 、N ,已知O 为原点,则OM ON ⋅=▲8、(盐城市2015届高三第三次模拟考试)若角+4πα的顶点为坐标原点,始边与x 轴的非负半轴重合,终边在直线12y x =上,则tan α的值为 ▲ . 9、(苏州市2015届高三上期末)已知函数()sin()5f x kx π=+的最小正周期是3π,则正数k 的值为10、(泰州市2015届高三上期末)函数()sin(3)6f x x π=+的最小正周期为 ▲11、(无锡市2015届高三上期末)已知角a 的终边经过点(),6P x -,且3tan 5a =-, 则x 的值为12、(扬州市2015届高三上期末)已知4(0,),cos 5απα∈=-,则tan()4πα+=____13、(泰州市2015届高三上期末)在ABC ∆中,角,,A B C 所对的边分别为,,a b c ,若B C ∠=∠且222743a b c ++=,则ABC ∆面积的最大值为 ▲14、(2015届江苏南京高三9月调研)在△ABC 中,角A ,B ,C 所对边的长分别为a ,b ,c .已知a +2c =2b ,sin B =2sin C ,则cos A = ▲ .15、(2015届江苏苏州高三9月调研)已知函数()sin 0,0,2y A x A πωϕωϕ⎛⎫=+>><⎪⎝⎭的图象上有一个最高点的坐标为()2,2,由这个最高点到其右侧相邻最低点间的图像与x 轴交于点()6,0,则此解析式为 ▲二、解答题1、(2015年江苏高考)在ABC V 中,已知2AB =,3AC =,60A =︒。
(1)求BC 的长; (2)求sin 2C 的值。
2、(2014年江苏高考)已知5sin 25παπα⎛⎫∈= ⎪⎝⎭,,。
(1)求sin()4πα+的值;(2)求5cos(2)6πα-的值。
3、(2013年江苏高考)如图,游客从某旅游景区的景点A 处下山至C 处有两种路径。
一种是从A 沿直线步行到C ,另一种是先从A 沿索道乘缆车到B ,然后从B 沿直线步行到C 。
现有甲.乙两位游客从A 处下山,甲沿AC 匀速步行,速度为min /50m 。
在甲出发min 2后,乙从A 乘缆车到B ,在B 处停留min 1后,再从匀速步行到C 。
假设缆车匀速直线运动的速度为min /130m ,山路AC 长为m 1260,经测量,1312cos =A ,53cos =C 。
(1)求索道AB 的长;(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?(3)为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?C BA4、(苏锡常镇四市2015届高三教学情况调研(二))已知函数()sin()cos 6f x x x π=++(1)求函数()f x 的最大值,并写出当()f x 取得最大值时x 的取值集合;(2)若33(0,),()265f ππαα∈+=,求()2f α的值5、(苏锡常镇四市2015届高三教学情况调研(一))如图,有一段河流,河的一侧是以O 为圆心,半径为103米的扇形区域OCD ,河的另一侧是一段笔直的河岸l ,岸边有一烟囱AB (不计B 离河岸的距离),且OB 的连线恰好与河岸l 垂直,设OB 与圆弧 CD的交点为E .经测量,扇形区域和河岸处于同一水平面,在点C ,点O 和点E 处测得烟囱AB 的仰角分别为45︒,30︒和60︒. (1)求烟囱AB 的高度;(2)如果要在CE 间修一条直路,求CE 的长.6、(2015届江苏南京高三9月调研)已知函数f (x )=2sin(2x +φ)(0<φ<2π)的图象过点(π2,-2).(1)求φ的值;(2)若f (α2)=65,-π2<α<0,求sin(2α-π6)的值.7、(2015届江苏南通市直中学高三9月调研)已知在△ABC 中,sin()2sin()A B A B +=-. (1)若π6B =,求A ; (2)若tan 2A =,求tan B 的值.(第17题)l8、(扬州市2015届高三上期末)已知函数()sin()(0,0,0)2f x A x A πωϕωϕ=+>><<部分图象如图所示。
(1)求函数f (x )的解析式;(2)当15[,]22x ∈时,求函数(1)()y f x f x =-+的值域。
9、(南通市2015届高三)在长为20m ,宽为16m 的长方形展厅正中央有一圆盘形展台(圆心为点)C ,展厅入口位于长方形的长边的中间,在展厅一角B 点处安装监控摄像头,使点B 与圆C 在同一水平面上,且展台与入口都在摄像头水平监控范围内(如图阴影所示).()1若圆盘半径为25m ,求监控摄像头最小水平视角的正切值;()2过监控摄像头最大水平视角为60 ,求圆盘半径的最大值.(注:水平摄像视角指镜头中心点水平观察物体边缘的实现的夹角.)10、(扬州市2015届高三上期末)如图,某商业中心O 有通往正东方向和北偏东30º方向的两条街道,某公园P 位于商业中心北偏东θ角(0t a n 332πθθ=<<,),且与商业中心O 的距离为21公里处,现要经过公园P 修一条直路分别与两条街道交汇于A ,B 两处。
(1)当AB 沿正北方向时,试求商业中心到A ,B 两处的距离和;(2)若要使商业中心O 到A ,B 两处的距离和最短,请确定A ,B 的最佳位置。
参考答案一、填空题1、 12t a n ()t a n 7t a n 311t a n ()t a n 1(2)7αβαβαββ++-===+++⨯- 2、6π3、π4、24 5、π2 6、38π 7、89- 8、13- 9、6 10、23π 11、10 12、17 13、5514、2415、2sin 84y x ππ⎛⎫=+ ⎪⎝⎭二、解答题1、解:(1)2,3,60AB c AC b A =====︒,所以222cos a BC b c bc A ==+- 1941272=+-⨯=. (2)根据正弦定理,32sin 212sin 77c AC a⨯===,又因为c a <,所以C A <,故C 为锐角,所以27cos 7C =。
所以:212743sin 22sin cos 2777C C C ==⨯⨯=2.(1)∵α∈(错误!未找到引用源。
,π),错误!未找到引用源。
=错误!未找到引用源。
∴错误!未找到引用源。
=错误!未找到引用源。
∴错误!未找到引用源。
=错误!未找到引用源。
+错误!未找到引用源。
=错误!未找到引用源。
(2)错误!未找到引用源。
=1错误!未找到引用源。
2错误!未找到引用源。
=错误!未找到引用源。
,错误!未找到引用源。
=2错误!未找到引用源。
=错误!未找到引用源。
错误!未找到引用源。
=错误!未找到引用源。
+错误!未找到引用源。
=错误!未找到引用源。
+错误!未找到引用源。
(错误!未找到引用源。
)=错误!未找到引用源。
3、解:(1)∵1312cos =A ,53cos =C ∴),(、20π∈C A ∴135sin =A ,54sin =C∴[]6563sin cos cos sin sin sin sin =+=+=+-=C A C A C A C A B )()(π 根据sinB sinC AC AB =得m C ACAB 1040sin sinB== (2)设乙出发t 分钟后,甲.乙距离为d ,则1312)50100(1302)50100()130(222⨯+⨯⨯-++=t t t t d ∴)507037(20022+-=t t d∵13010400≤≤t 即80≤≤t ∴3735=t 时,即乙出发3735分钟后,乙在缆车上与甲的距离最短。
(3)由正弦定理sinBsinA ACBC =得50013565631260sin sinB ===A AC BC (m )乙从B 出发时,甲已经走了50(2+8+1)=550(m ),还需走710 m 才能到达C 设乙的步行速度为V min /m ,则350710500≤-v ∴3507105003≤-≤-v ∴14625431250≤≤v ∴为使两位游客在C 处互相等待的时间不超过3分钟,乙步行的速度应控制在⎥⎦⎤⎢⎣⎡14625,431250范围内 法二:解:(1)如图作BD ⊥CA 于点D ,设BD =20k ,则DC =25k ,AD =48k ,AB =52k ,由AC =63k =1260m , 知:AB =52k =1040m .(2)设乙出发x 分钟后到达点M ,此时甲到达N 点,如图所示. 则:AM =130x ,AN =50(x +2),由余弦定理得:MN 2=AM 2+AN 2-2 AM ·AN cos A =7400 x 2-14000 x +10000,其中0≤x ≤8,当x =3537(min)时,MN 最小,此时乙在缆车上与甲的距离最短. (3)由(1)知:BC =500m ,甲到C 用时:126050 =1265(min). 若甲等乙3分钟,则乙到C 用时:1265 +3=1415 (min),在BC 上用时:865(min) . 此时乙的速度最小,且为:500÷865 =125043 m/min .若乙等甲3分钟,则乙到C 用时:1265 -3=1115 (min),在BC 上用时:565(min) . 此时乙的速度最大,且为:500÷565 =62514 m/min .故乙步行的速度应控制在[125043 ,62514]范围内.4、C BADMN5、解:(1)设AB 的高度为h ,在△CAB 中,因为45ACB ∠=︒,所以CB h =, ………………………………1分 在△OAB 中,因为30AOB ∠=︒,60AEB ∠=︒, ………………………………2分所以3OB h =,33EB h =, ………………………………………………………4分 由题意得331033hh -=,解得15h =. ………………………………………6分 答:烟囱的高度为15米. ……………………………………………………………7分(2)在△OBC 中,222cos 2OC OB BC COB OC OB+-∠=⋅3002253225562103153+⨯-==⨯⨯, …………………10分所以在△OCE 中,2222cos CE OC OE OC OE COE =+-⋅∠ 53003006001006=+-⨯=. …………………13分答:CE 的长为10米. ……………………………………………………………14分6、解:(1)因为函数f (x )=2sin(2x +φ)(0<φ<2π)的图象过点(π2,-2),所以f (π2)=2sin(π+φ)=-2,即sin φ=1. …………………………………………… 4分 因为0<φ<2π,所以φ=π2. …………………………………………… 6分(2)由(1)得,f (x )=2cos2x . ………………………………………… 8分因为f (α2)=65,所以cos α=35.又因为-π2<α<0,所以sin α=-45. …………………………………… 10分所以sin2α=2sin αcos α=-2425,cos2α=2cos 2α-1=-725.…………………… 12分从而sin(2α-π6)=sin2αcos π6-cos2αsin π6=7-24350. …………………… 14分7.解:(1)由条件,得 ππsin()2sin()66A A +=-.3131sin cos 2(sin cos )2222A A A A ∴+=-. …………………………………………3分化简,得 s i n 3c o s A A =.tan 3A ∴=.……………………………………………………………………………6分 又(0,π)A ∈, π3A ∴=. ………………………………………………………………7分 (2)sin()2sin()A B A B +=- ,sin cos cos sin 2(sin cos cos sin )A B A B A B A B ∴+=-. 化简,得 3c o s s i n s i n c o AB A B =.…………………………………………………11分又 c o s c o s 0A B ≠,tan 3tan A B ∴=.又tan 2A =,2tan 3B ∴=.……………………………………………………………………………14分 8、⑴由图,212,()1433T A ==--=,得4T =,2πω=,则()2sin()26f x x ππ=+,…3分由22()2sin()2323f πϕ=⋅+=,得sin()13πϕ+=,所以2()32k k Z ππϕπ+=+∈,又02πϕ<<,得6πϕ=,所以()2sin()26f x x ππ=+; ……7分⑵(1)()2sin()2cos()22sin()2626212y f x f x x x x ππππππ=-+=+-+=-, ……10分因为15[,]22x ∈,故762126x ππππ≤-≤,则1sin()12212x ππ-≤-≤,即2()22f x -≤≤,所以函数(1)()y f x f x =-+的值域为[2,22]-. ……14分 9.P m n,10、⑴以O为原点,OA所在直线为x轴建立坐标系.设(,)∵02πθ<<,tan 33θ=∴7cos 14θ=,321sin 14θ=, 则9sin 2m OP θ=⋅=,3cos 2n OP θ=⋅=, ……4分 依题意,AB ⊥OA ,则OA =92,OB =2OA =9,商业中心到A 、B 两处的距离和为13.5km .⑵方法1:当AB 与x 轴不垂直时,设AB :39()22y k x -=-,① 令0y =,得3922A x k =-+;由题意,直线OB 的方程为3y x =,② 解①②联立的方程组,得932(3)B k x k -=-,∴229323B B B k OB x y x k -=+==-, ∴3993223k y OA OB k k -=+=-++-,由0A x >,0B x >,得3k >,或0k <. ……11分 22228333(33)(53)'2(3)2(3)k k y k k k k --+-=+=--,令'0y =,得33k =-, 当33k <-时,'0y <,y 是减函数;当303k -<<时,'0y >,y 是增函数, ∴当33k =-时,y 有极小值为9km ;当3k >时,'0y <,y 是减函数,结合⑴知13.5y >km . 综上所述,商业中心到A 、B 两处的距离和最短为9km ,此时OA =6km ,OB =3km ,方法2:如图,过P 作PM //OA 交OB 于M ,PN //OB 交OA 于N ,设∠BAO =α,△OPN 中sin(90)sin(30)sin120PN ON OP θθ︒==-- ,得PN =1,ON =4=PM , △PNA 中∠NPA =120°-α∴sin sin(120)PN NA αα︒=-得sin(120)sin NA αα︒-= 同理在△PMB 中,sin sin(120)BM PM αα︒=-,得4sin sin(120)MB αα︒=-, s i n (120)4s i n 142459s i n s i n (120)y O A O B αααα︒︒-=+=+++≥+=-, ……13分 当且仅当sin(120)4sin sin sin(120)αααα︒︒-=-即sin(120)2sin αα︒-=即3tan 3α=时取等号. N M P 北BO A方法3:若设点(,3)B m m ,则AB :392293322y x m m --=--,得4(4,0)21A m +-, ∴4424211492121OA OB m m m m +=++=-+++≥--, ……13分 当且仅当42121m m -=-即32m =时取等号. 方法4:设(,0)A n ,AB :093022y x n n --=--,得2142B x n =+-, 442441(4)5944B OA OB n x n n n n +=+=-+++=-++≥--, ……13分 当且仅当444n n -=-即6n =时取等号. 答:A 选地址离商业中心6km ,B离商业中心3km 为最佳位置. ……15分。