初二下数学《第11周周练》答案

八年级数学第二学期第11周周练试卷班级姓名一、选择题（共8小题，每小题2分，满分16分）1．下列图形中既是轴对称图形又是中心对称图形的是（）A．B．C．D．2．完成以下任务，适合用抽样调查的是（）A．调查你班同学的年龄情况B．为订购校服，了解学生衣服的尺寸C．考察一批炮弹的杀伤半径D．对航天飞机上的零部件进行检查3．要使分式有意义，那么x的取值范围是（）A．x＞2 B．x＞3 C．x≠2 D．x≠34．一个黑色不透明的袋子里装有除颜色外其余都相同的7个红球和3个白球，那么从这个袋子中摸出一个红球的可能性和摸出一个白球的可能性相比（）A．摸出一个红球的可能性大B．摸出一个白球的可能性大C．两种可能性一样大D．无法确定5．分式，﹣，的最简公分母是（）A．x2y B．2x3y C．4x2y D．4x3y6．▱ABCD中，∠A=4∠B，则∠D的度数是（）A．18°B．36°C．72°D．144°7．一件工作甲单独做a小时完成，乙单独做b小时完成，甲、乙两人一起完成这项工作需要的小时数是（）A． B． C． +D．8．如图，将矩形ABCD绕点C顺时针旋转90°得到矩形FGCE，点M、N分别是BD、GE的中点，若BC=14，CE=2，则MN的长（）A．7 B．8 C．9 D．10二、填空题（共10小题，每小题2分，满分20分）9．若分式的值为0，则x的值是______．10．在06006000600006的各个数位中，数字“6”出现的频率是______．11．计算：（）=______．12．“平行四边形的对角线互相垂直”是______事件．（填“必然”、“随机”、“不可能”）13．已知，则分式的值为______．14．如图，四边形ABCD的两条对角线AC、BD的长分别为5cm、4cm，点A1，B1，C1，D1是四边形ABCD各边上的中点，则四边形A1B1C1D1的周长为______cm．15．如图，△COD是由△AOB绕点O按顺时针方向旋转40°后得到的图形，点C恰好在边AB上．若∠AOD=100°，则∠D的度数是______°．16．如图，在平行四边形ABCD中，AB=4cm，AD=7cm，∠ABC的角平分线交AD于点E，交CD的延长线于点F，则DE=______cm．17．如图，在平面直角坐标系xOy中，A（2，0），B（2，4），C（0，4）．若直线y=kx﹣2k+1（k是常数）将四边形OABC分成面积相等的两部分，则k的值为______．18．如图，在菱形ABCD中，AB=6，∠B=60°，点G是边CD边的中点，点E、F分别是AG、AD上的两个动点，则EF+ED的最小值是______．三、解答题（共8小题，满分64分）19．（16分）（2016春•常州期中）化简：（1）（2）（3）先化简，再求值：（），其中a=5．20．设中学生体质健康综合评定成绩为x 分，满分为100分，规定：85≤x ≤100为A 级，75≤x ≤85为B 级，60≤x ≤75为C 级，x ＜60为D 级．现随机抽取福海中学部分学生的综合评定成绩，整理绘制成如下两幅不完整的统计图，请根据图中的信息，解答下列问题：（1）在这次调查中，一共抽取了______名学生，α=______%；（2）补全条形统计图；（3）扇形统计图中C 级对应的圆心角为______度；（4）若该校共有2000名学生，请你估计该校D 级学生有多少名？21．用直尺和圆规作图：作出四边形ABCD 关于O 点成中心对称的四边形A ′B ′C ′D ′．（保留作图痕迹）22．如图，正方形ABCD 的对角线AC 与BD 交于点O ，分别过点C 、点D 作CE ∥BD ，DE ∥AC ．求证：四边形OCED 是正方形．23．如图，在▱ABCD中，DE⊥AC，BF⊥AC，垂足分别为点E、F．（1）求证：四边形BEDF是平行四边形．（2）若AB=13，AD=20，DE=12，求▱BEDF的面积．25．如图，平面直角坐标系xOy中，点O为坐标原点，四边形OABC为矩形，A（10，0），C（0，4），点D是OA的中点，点P在边BC上以每秒1个单位长的速度由点C向点B运动．（1）当四边形PODB是平行四边形时，求t的值；（2）在线段PB上是否存在一点Q，使得四边形ODQP为菱形？若存在，求处当四边形ODQP为菱形时t 的值，并求出Q点的坐标；若不存在，请说明理由；（3）△OPD为等腰三角形时，写出点P的坐标（请直接写出答案，不必写过程）．。

初二（下）数学周末作业十一（B ）2013.5.10班级__________学号____________姓名__________成绩__________1．若一个梯形的中位线长是6，面积是30，则这个梯形的高是（）．【1】（A ）2．5（B ）5（C ）10（D ）202．若等腰梯形的腰长等于中位线为6cm ，则周长为（）cm ．【1】（A ）6（B ）12（C ）24（D ）483．将一张直角梯形纸片沿中位线剪开，拼成一个新的图形，这个新的图形不可能是下列图形中的（）．【1】（A ）三角形（B ）平行四边形（C ）矩形（D ）正方形4．若等腰梯形的对角线互相垂直，且它的中位线等于m ，则此梯形的高等于（）．【2】（A ）2m（B ）2m （C ）2m （D ）m5．一个梯形的上底和中位线长分别为6和8，这个梯形的下底长为____________．【1】6．梯形的中位线长为3，上底长为x ，下底长为y()y x >，则y 与x 的函数关系式是____________，定义域是____________．【1】7．如果等腰梯形底角为45°，高等于上底，那么梯形的中位线和高的比为____________．【1】8．直角梯形的一条对角线把梯形分成两个三角形，其中有一个是边长为8的等边三角形，则梯形中位线长是____________．【2】9．在梯形ABCD 中，AD BC ∥，对角线AC BD ⊥，且5AC =cm ，12BD =cm ，则梯形中位线的长等于____________．【2】10．梯形的上底AB 与下底CD 的比是4:9，中位线EF 将梯形分成的两部分，:=ABFE FECD S S 梯形梯形____________．【2】11．如图22-34-2，直角梯形ABCD 中，==90A B ∠∠︒，M 是AB 的中点，且=90DMC ∠︒．求证：DC AD BC =+．【8】12．如图22-34-3，在梯形ABCD 中，AD BC ∥，H 、G 分别是两条对角线BD 、AC 的中点。

1 / 6仪征市三中八下数学周末练十一一、选择题（每小题3分，共24分）1、如果a ＞b ，下列各式中不正确．．．的是 A ．a －3＞b －3 B ．-2a ＜-2b C ．2a ＞2b D ． a 1＜b12、若分式242x x -+的值为0，则x 的值为A ．±2 B ．2 C ．－2 D ．03、如果不等式组⎩⎨⎧≥<mx x 5有解，那么m 的取值范围是 （ ）A ．m >5B ．m <5C ．m ≥5D ．m ≤54、不等式2（x －2）≤x －2的非负整数解的个数为A ．1个 B ．2个 C ．3个 D ．4个5、在同一坐标系中，函数x ky =和3+=kx y 的图像大致是（ ）A ．B ．C ．D ．6、反比例函数y=xk(k>0)在第一象限内的图象如图，点M 是图象上一点，MP 垂直x 轴于点P ，如果△MOP 的面积为1，那么k 的值是( )(A) 1 (B) 2 (C) 47、已知()111,P x y 、()222,P x y 、()333,P x y 是反比例函数2y x=的图象上的三点，且 1230x x x <<<，则1y 、2y 、3y 的大小关系是A ．321y y y <<B ．123y y y <<C ．213y y y <<D ．231y y y << 8、如果关于x 的分式方程xmx x -=--552无解，则m 的值为A ．B ．3 C ．－5 D ．－3二、填空题（每小题3分，共27分）9、若反比例函数ky x=的图象经过点()1,2-，则k = 。

10、已知反比例函数32m y x-=，当______m 时，其图象的两个分支在第一、三象限内；当______m 时，其图象在每个象限内y 随x 的增大而增大；x2 / 611、若分式方程12552x ax x+=--的解为0x =，则a 的值为12、分式23544-2m m-与的最简公分母是___________________________。

南昌一中 2007-2008 学年度第二学期初二周练数学（^一） 命题：谢莉一、选择题（每题3分，共30分）1. 在口ABCD 中，/ A ：Z B ：Z C ：Z D 的值可以是（）:2 : 3 : 4 : 2 : 2 : 1:1 : 2 : 2 : 1 : 2 : 12. 平行四边行的两条对角线把它分成全等三角形的对数是（）3. 在口 ABCD 中，/ A 、/ B 的度数之比为5 : 4,则/ C 等于（）O O O O4、 一个四边形的三个内角度数依次如下，那么其中是平行四边形的是（）A 、88 °， 108°， 88°B 、88 °，104 °， 108 °C 、88°、92°、92°D 、88° ,92 °，88°5、 下列哪组条件能判别四边形 ABCD 是平行四边形（ ）A 、AB // CD ，AD = BC B 、AB = CD ，AD = BCC 、/ A = / B ，/ C = /D D 、AB = AD ，CB = CD6、 平行四边形的一边长为 10,那么它的两条对角线的长度可以是（）A 、8 和 12B 、4 和 16C 、20 和 30D 、8 和 6 ㈡的周长为40cm,A ABC 的周长为25cm ,则对角线AC 长为5的周长为36cm , AB=-BC ，则较长边的长为（）如图，□ ABCD 中，EF 过对角线的交点O , AB=4, AD=3，OF=，则四边形BCEF 的周长为（）D 的坐标分别是（0, 0）,（ 5, 0）（2, 3）,贝师点C 的坐标是（）A.（3, 7）B. （5, 3） C . （7, 3） D . （8, 2）二、填空题（本大题8个小题，每小题3分，共24 分）11、 在平行四边形中，若一个角为其邻角的 2倍，则这个平行四边形中两邻角的度数分别是。

八年级第11周周末练习1.231a a +有意义，则a 应满足（）A.1a ≤且13a ≠- B.1a ≤ C.13a ≠- D.1a ≤且13a ≠2.若y＜x＜0，则222y xy x +-＋222y xy x ++=（）A.2x B.2y C.-2x D.-2y3、直线y=2x+m 和直线y=3x+3的交点在第二象限，求m 的取值范围（）A.m＞3 B.m＜2 C.2＜m ＜3 D.m＜2或m＞34、如图，直线y=kx+b 与x 轴交于点A（-4，0），则当y＞0时，x 的取值范围是（）A.x＞-4B.x＞0C.x＜-4D.x＜05、某农场租用收割机收割小麦，甲收割机单独收割2天后，又调来乙收割机参与收割，直至完成800亩的收割任务，收割亩数与天数之间的函数关系如图所示，那么乙参与收割的天数是（）A.6天 B.5天 C.4天 D.3天6、函数y=ax +b 与y=bx+a 的图象在同一坐标系内的大致位置正确的是（）（A）.（B）.（C）.（D）.7.已知四边形ABCD,有以下四个条件:①AB∥CD;②AB=CD;③BC//AD;④BC=AD.从这四个条件中任选两个,能使四边形ABCD 成为平行四边形的选法种数共有（）A.6种 B.5种 C.4种D.3种8.若等腰三角形的两边长分别为4和6,则底边上的高为（）．A.7 B.724或 C.24 D.417或9.如图,已知矩形纸片ABCD,点E 是AB 的中点,点G 是BC 上的一点,︒>∠60BEG ，现沿直线EG 将纸片折叠,使点B 落在约片上的点H 处,连接AH,则与BEG ∠相等的角的个数为()A.4B.3C.2D.110.如图,已知121=A A , 9021=∠A OA , 3021=∠OA A 以斜边2OA 为直角边作直角三角形,使得 3032=∠OA A ，依次以前一个直角三角形的斜边为直角边一直作含300角的直角三角形,则20152016Rt A OA ∆的最小边长为（）A.22015 B.22016 C.20143 ⎪⎝⎭ D.20153 ⎪⎝⎭11．如图1，在Rt △ABC 中，∠B =90°，AC =10cm ，BC =6cm ，现有两个动点P ，Q 分别从A ，B 两点同时出发沿规定路径匀速运动．其中点P 运动路径：A B C A →→→，点Q 运动路径：B C A →→．点P 的运动速度为2cm /s ，点Q 的运动速度为1cm /s ．若用y 表示P ，Q 两点在运动路径上的距离，用t 表示运动时间，且y 与t 的关系如图2所示．根据图中的信息，下列说法错误的是（）A ．AB =8cmB ．当t =8s 时，P ，Q 两点第一次相遇C ．当y =3cm 时，t =5s 或11sD ．图2中m =412、|1－2|+（3．14-π）0-91)21(-+=13．函数b kx y +=的图象平行于直线12--=x y ，且与y 轴交于点（0,3），则k=______，b=_______．14．在平面直角坐标系中，点O 是坐标原点，过点A （1，2）的直线y=kx+b 与x 轴交于点B，且S △AOB =4，则k 的值是_________．15．如图，点C 的坐标为（2，0），四边形ABCO 是菱形，∠AOC=60o，点M 是BC 的中点，则直线AM 的解析式为___________.16．已知A 、B 两地相距4千米，上午8:00，甲从A 地出发步行到B 的，8:20乙从B 地出发骑自行车到A 地，甲乙两人离A 地的距离（千米）与甲所用的时间（分）之间的关系如图所示．由图中的信息可知，乙到达A 地的时间为．17.如图,在四边形ABCD 中,AB//DC,AD=BC=5,DC=7,AB=11,点P 从点A 出发,以3个单位/s 的速度沿AD→DC 向终点C 运动,同时点Q 从点B 出发,以1个单位/s 的速度沿BA 向终点A 运动,在运动期间,当四边形PQBC 为平行四边形时,运动时间为秒．18.如图,E 是边长为1的正方形ABCD 的对角线BD 上的一点,且BE=BA,P 是CE 上任意一点,PQ⊥BC 于点Q,PR⊥BE 于点R.则（1）DE=；（2）PQ＋PR=．19．化简下列各式（1）（a+b ）2+（2a ﹣b ）（a+2b ）（2）20、如图，直线L：221+-=x y 与x 轴、y 轴分别交于A、B 两点，在y 轴上有一点C（0，4）,动点M 从A 点以每秒1个单位的速度沿x 轴向左移动。

2020-2021学年度八年级（下）数学周练（十一）一、选择题（每小题3分，共30分）1．使√x+1有意义的x的取值范围是（B）A．x＞﹣1B．x≥﹣1C．x≠﹣1D．x≤﹣12．下列计算正确的是（ D ）A．√2+√3=√5B．3√2−2√2=3C．√6÷2=√3D．√8=2√23．如果一组数据3，x，7，8，11的平均数为7，那么x为（B）A．5B．6C．7D．84．以下列各组数据中的三个数作为三角形的边长，其中能构成直角三角形的是（C）A．2，3，4B．√3，√4，√5C．1，√3，2D．7，8，95．若实数a、b、c满足a+b+c＝0，且a＞b＞c，则函数y＝ax+c的图象可能是（C）A．B．C．D．6．对于函数y＝﹣3x+1，下列结论正确的是（C）A．它的图象必经过点（﹣1，3）B．它的图象经过第一、二、三象限C．当x＞1时，y＜0D．y随x的增大而增大7．小兰和小琳约好在公共汽车站一起乘车去博物馆，小兰从家出发步行到车站，等小琳到了以后两人一起乘公共汽车到博物馆．图中的折线表示小兰距离博物馆的路程y（km）与所用时间x（min）之间的函数关系，下列说法错误的是（D）A．小兰从家到公共汽车站步行了1kmB．小兰在公共汽车站等汽车用了15minC．公共汽车的平均速度为30km/hD．小兰和小琳乘公共汽车用了55min8. 直线y=kx+b经过点（3，-2），且当−1≤x≤2时，y的最大值为5，则k的值为（B）A. -2B. −74C. −74或−7 D. -1或29．在平面直角坐标系中，横、纵坐标都是整数的点叫作整点，直线y ＝kx ﹣3（k ＞0）与坐标轴围成的三角形内部（不包含边界）有且只有三个整点，则k 的取值范围是（ C ） A ．23≤k ≤34B. 34≤k ＜1C ．23≤k ＜1D ．12≤k ＜110. 如图，直角三角形EAB 中，∠EAB =90°，AB =6，AE =8，分别以AB 和AE 为边作正方形HFBA 和正方形AEDC ，连接BD 和EF ，相交于点O ，则△BOF 的面积是（ C ） A. 3237 B. 1324 C. 37837D. 15527HOFEDCBA11. 化简：√45＝2√55．12. 已知直线y =x −3与y =2x +2的交点为（-5， -8），则方程组{x −y −3=0，2x −y =−2的解是__{x =−5y =−8_________. 13. 甲、乙两人进行射击比赛，在相同条件下各射击10次．已知他们的平均成绩相同，方差分别是S 甲2=2.6，S 乙2=3，那么甲、乙两人成绩较为稳定的是 甲 ．14. 在平面直角坐标系xOy 中，一次函数y ＝kx 和y ＝mx +n 的图象如图所示，则关于x 的一元一次不等式kx ﹣n ＞mx 的解集是 x >1 ．15. 如图，在正方形中，点P 是边CD 上一点，PE ⊥BD 于点E ，O 为BP 的中点，则AEOE的值为_________√2___________.16. 在矩形ABCD 中，AB =2，BC =4，点E 、F 分别在BC 、CD 上，若AE =√5，∠EAF =45°，则AF 的长为_____4√103___________.21y=mx+ny=kxO y xFEDCBA OPED CBA17．（8分）计算（1）（4√6−6√2）÷2√2； （2）7a √8a −4a 2√18a +7a √2a . 2√3−3 20a √a18. （8分）直线a ：y =x +2和直线b ：y =-x +4相交于点A ，分别交x 轴于点B 和点C ，与y 轴相交于点D 和点E . （1）求△ABC 的面积； 9 （2）求四边形ADOC 的面积. 719. （8分）如图，在Rt △ABC 中，∠ACB =90°，点D 是斜边AB 的中点，DE ⊥AC ，垂足为点E . 若DE =2，CD =2√5，求BE 的长. 4√2EDCBA20．（8分）如图是由边长为1的小正方形构成的网格，每个小正方形的顶点叫做格点．△ABC 的顶点在格点上，仅用无刻度尺的直尺在给定网格中画图，画图过程用虚线表示，画图结果用实线表示，按步骤完成下列问题：(1)直接写出△ABC 的形状____等腰三角形_________.(2)如图1，在△ABC 内画出点O ，使得点O 到△ABC 三个顶点的距离相等. (3)如图2，在BC 的右侧作∠PBC =∠ABC .图1 图221. （8分）武汉市第十一届运动会于2021年10月在东西湖区举行. 某中学开展了主题为“你对我市第十一届运动会了解多少”的知识问答比赛，校学生会随机抽取了部分学生的成绩（比赛成绩为整数），并绘制了如下尚不完整的统计图表.51 83 67 73 86 95 100 88 77 80 65 74 70 85 79 96 90 81 73 83 72 85 100 72 84 99 87 58 75 63C BA C BA82 98 91 89 87 79 94 78 90 73（1）表格中的a =___12________，b =____14________； （2）本次抽取的学生成绩的中位数为_____82.5_________；（3）求扇形统计图中，扇形C 的圆心角度数； 4÷10%=40（人），360°×1240=108°（4）该校参加知识问答比赛的学生共有400人，请估计比赛成绩在80.5≤x ＜100.5范围的人数. 400×14+840=220人答：估计比赛成绩在80.5≤x ＜100.5范围的人数为220人.10%20%E DCB A22.（10分）某商场计划购进A、B两种商品进行销售. A每件进价30元，原定售价48元，B每件进价40元，原定售价60元，设购进A商品x件，商场总利润为y元．（1）一月份计划购进A、B两种商品共20件，A商品的数量不低于B商品的数量，且按预售价全部卖完后总利润不低于376元，有几种进货方案？（2）若按（1）中方案进货，实际销售中由于某原因，决定降价销售，A每件降价a元，B 每件降价2a元（a＞0），全部售完，可获得最大利润350元，求a的值；（3）二月份商场购进A、B两种商品共100件，均按原定售价卖完，商场拿出部分资金奖励销售人员，每卖一件A奖励m元，每卖一件B奖励n元，结果发现无论购进A商品多少件，商场利润恒为1500元，直接写出m、n的值.23．（10分）在矩形ABCD 中，AB =6，AD =8，E 是边BC 上一点，以E 为直角顶点，在AE 的右侧作等腰直角△AEF .（1）如图1，当点F 在CD 边上时，求BE 的长； （2）如图2，若EF ⊥DF ，求BE 的长；（3）如图3，若动点E 从点B 出发，沿边BC 向右运动，运动到点C 停止，直接写出线段AF 的中点Q 的运动路径长.图1 图2 图3FEDCBA A BCD EFFEDCBA24．（12分）如图，点O 为平面直角坐标系的原点，在矩形OABC 中，两边OC 、OA 分别在x 轴和y 轴上，且点B （a ，b ）满足：√a −4√3+（b +4）2=0． （1）求点B 的坐标（ 4√3 ， −4 ）；（2）若过点B 的直线BP 与矩形OABC 的OC 边交于点P ，且将矩形OABC 的面积分为1：3两部分，①求直线BP 的解析式；②在直线BP 确定一点Q ，使得△ACQ 的面积等于矩形OABC 的面积，求点Q 的坐标； （3）D 在线段AB 上，AD ＝14AB ，M 点是x 轴上一点，N 为（2）中直线BP 上一动点，若四点O 、D 、M 、N 构成平行四边形，直接写出M 的坐标．C OBAyx C O BAyx。

重庆市巴川中学校2018~2019学年度八（下）第11周数学周周清试卷（满分120分，时间90分钟）班级___________ 姓名____________ 总分____________（A 卷100分）一、选择题（每小题4分，共40分）1．下列一次函数中，y 随x 值的增大而减小的是……………………………………………（ ） A ．y =2x +1 B ．y =3－4x C ．y =2x +2 D ．y =0.3x2．不在32+-=x y 的图象上的是（ ）A .（-5，13）B ．（0.5，2）C ．（3，0）D ．（1，1）3．一次函数y =kx +b 的图象经过点（2，-1）和（0，3），•那么这个一次函数的解析式为（ ） A ．y =-2x +3 B ．y =-3x +2 C ．y =3x -2 D ．y =12x -3 4．已知一次函数的图象与直线y =-2x +1平行，且过点（2，-7），那么此一次函数的解析式为（ ）A ．y =2x -11B ．y =-2x -3C ．y =-2x -4D ．y =-2x -55．如图，一次函数图象经过点A ，且与正比例函数y x =-的图象交于点B ，则该一次函数的表达式为（ ）A ．2y x =-+B ．2y x =+C ．2y x =-D ．2y x =--6．已知一次函数y kx b =+的图象如图所示，当x <1时，y 的取值范围是…………………（ ）Ａ．20y -<<Ｂ．40y -<<Ｃ．4y <-Ｄ．2y <-O x y A B2第5题xy O3第7题第6题2－4 xy7．一次函数1y kx b =+与2y x a =+的图象如图，则下列结论①0<k ；②0a >；③当3x <时，21y y <；④关于x 的方程b a x kx -=-的解为x =3中，正确的个数是……………（ ）A ．1B ．2C ．3D ．48．已知在一次函数y =－1.5x +3的图象上,有三点(－3,y 1),(－1,y 2),(2,y 3),则y 1,y 2,y 3的大小关系为( ) A .y 1>y 2>y 3 B .y 1>y 3>y 2 C .y 2>y 1>y 3 D .无法确定9．两个一次函数b ax y -=1与a bx y -=2在同一坐标系下的图象只可能是……………（ ）10.直线y =－2x ＋m 与直线y =2x －1的交点在第四象限，则m 的取值范围是（ ） A .1->m B .1<m C .11<<-mD .11≤≤-m二、填空题（每小题4分，共20分）11．如果一次函数y =(m －3)x +m 2－9是正比例函数，则m 的值为_________．12．如图，已知函数y ax b =+和y kx =的图象交于点P , 则根据图象可得，关于y ax by kx =+⎧⎨=⎩的二元一次方程组的解是 ．13．如图，函数y =2x 和y =ax +5的图象相交于A （m ，3），则不等式2x ＜ax +5的解集为_________． 14．在平面直角坐标系中，点O 是坐标原点，过点A （0，2）的直线y =kx +b 与x 轴交于点B ，且x y o A y 1 y 2x y o B y 1 y 2x y o C y 1y 2 x y o D y 1y 2 15题－4－2 y =ax +by =kx x y 0 P 第12题图13题S△AO B=4，则k的值是_________．15．如图，点C的坐标为（2，0），四边形ABCO是菱形，∠AOC=60o，点M是BC的中点，则直线AM的解析式为___________.三、解答题（每小题10分，共40分）16．如图所示，直线y=2x+3与x轴交于点A，与y轴交于点B.（1）求A、B两点的坐标；（2）点P在x轴上，且OP=2OA，求△ABP的面积. 17.已知一个正比例函数与一个一次函数的图象交于点A（3,4），且OA=OB. （1）求两个函数的解析式；（2）求△AOB的面积；18．如图，在△ABC中，△ABC=90°，点D为AC的中点，过点C作CE△BD于点E，过点A作BD 的平行线，交CE的延长线于点F，在AF的延长线上截取FG=BD，连接BG、DF．（1）证明：四边形BDFG是菱形；（2）若AC=10，CF=6，求线段AG的长度．19.某个体小服装准备在夏季来临前，购进甲、乙两种T恤，在夏季到来时进行销售．两种T恤的相关信息如下表：根据上述信息，该店决定用不少于6195元，但不超过6299元的资金购进这两种T恤共100件．设购进甲种T恤x件. 请解答下列问题：(1)该店有哪几种进货方案?(2)写出所获得利润w（元）与x（件）之间的函数关系式，并求出该店按哪种方案进货所获利润最大，最大利润是多少?B 卷（20分）20.（4分）一次函数b kx y +=，当20≤≤x 对应的函数值y 的取值范围为42≤≤-y ,则kb 的值为（ ） A .12 B .6- C .6或12 D .6- 或 12-21.（4分）甲、乙两车分别从A 、B 两地同时出发，相向行驶，已知甲车的速度大于乙车的速度，甲车到达B 地后马上以另一速度原路返回A 地(掉头的时间忽略不 计)，乙车到达A 地以后即停在A 地等待甲车．如图所示为甲乙 两车间的距离y (千米)与甲车的行驶时间x (小时)之间的函数图象，则当乙车到达A 地的时候，甲车与B 地的距离为 千米．22.（12分）已知，如图在锐角△ABC 中，∠ABC =45o ，AD ⊥BC 于点D ，BE ⊥AC 于点E ，BE 于AD 交于点F .（1）若BF =5，DC =3，求AB 的长;（2）过点F 作BE 的垂线，过点A 作AB 的垂线，两条垂线交于点G ，连接BG . ①求证：∠BGF =45o ； ②求证：第21题图2020届八下数学第11周周周清参考答案一、选择题：BCABB DBABC二、填空题：11．3-； 12．⎩⎨⎧-=-=24y x ； 13．23<x ； 14．21±； 15．33433+-=x y 三、解答题：16.解：（1）A 点坐标为（﹣1.5，0），B 点坐标为（0，3）； （2）设P 点坐标为（x ，0），∵OP ＝2OA ，A （﹣1.5，0），∴x ＝±3， ∴P 点坐标分别为P 1（3，0）或P 2（﹣3，0）． ∴S △ABP 1＝×（1.5+3）×3＝6.75，S △ABP 2＝×（3﹣1.5）×3＝2.25， ∴△ABP 的面积为6.75或2.25．17.解：（1）正比例函数的解析式为y ＝x ；一次函数的解析式为y ＝x，（2）∵A（3，4），B（-5，0），∴三角形AOB的面积为5×4×＝10．18.解：（1）证明：∵AG∥BD，BD＝FG，∴四边形BGFD是平行四边形，∵CE⊥BD∴CE⊥AG，又∵BD为AC的中线，∴BD＝DF＝AC，∵四边形BGFD是平行四边形，BD＝DF∴四边形BDFG是菱形；（2）解：∵四边形BDFG是菱形，∠ABC＝90°，点D为AC的中点，∴GF＝DF＝AC＝5，∵CF⊥AG，∴AF＝＝＝8，∴AG＝AF+GF＝8+5＝13．19解：（1）设购进甲种T恤x件，则购进乙种T恤（100﹣x）件．可得，6195≤35x+70（100一x）≤6299．解得，20≤x≤23．∵x为解集内的正整数，∴x＝21，22，23．∴有三种进货方案：方案一：购进甲种T恤21件，购进乙种T恤79件；方案二：购进甲种T恤22件，购进乙种T 恤78件；方案三：购进甲种T恤23件，购进乙种T恤77件．（2）设所获得利润为W元．W＝30x+40（100一x）＝﹣10x+4000．∵k＝﹣10＜0，∴W随x的增大而减小．∴当x＝21时，W＝3790．该店购进甲种T恤21件，购进乙种T恤79件时获利最大，最大利润为3790元．20解：（1）当k＞0时，y随x的增大而增大，即一次函数为增函数，∴当x＝0时，y＝﹣2，当x＝2时，y＝4，代入一次函数解析式y＝kx+b得：，解得，∴kb＝3×（﹣2）＝﹣6；（2）当k＜0时，y随x的增大而减小，即一次函数为减函数，∴当x＝0时，y＝4，当x＝2时，y＝﹣2，代入一次函数解析式y＝kx+b得：，解得，∴kb＝﹣3×4＝﹣12．所以kb的值为﹣6或﹣12．故选：D．21.解：设甲车从A 地到B 地的速度为x 千米/时，乙车从B 地到A 地的速度是y 千米/时，，解得，，∴甲车从A 地到B 地用的时间为：900÷100＝9小时，甲车从B 地到A 地的速度为：900÷（16.5﹣9）＝120千米/时，乙车从B 地到甲地的时间为：900÷80＝11.25小时，∴当乙车到达A 地的时候，甲车与B 地的距离为：120×（11.25﹣9）＝270（千米），22．（1）解：（2）法一：证明：①如图2，在BD 上取一点M,使BM=AF.)4......(.......... (2)4,4353.5..,45220分，，，，又，，为等腰三角形，，=∴=-=∴===∴∆≅∆∴∠=∠∠=∠∴∠=∠∠=∠∴⊥=∴∆∴⊥=∠AB AD DC AC BF ADC BDF ADC BDF DAC BDF AFE BFD BDF AEF AC BE AD BD ABD BC AD ABC ΘΘΘΘΘ②作FN//BD交AB于N，则为等腰直角三角形，法二：过点F作FH FA交AB于点N.（此法更优越！）。

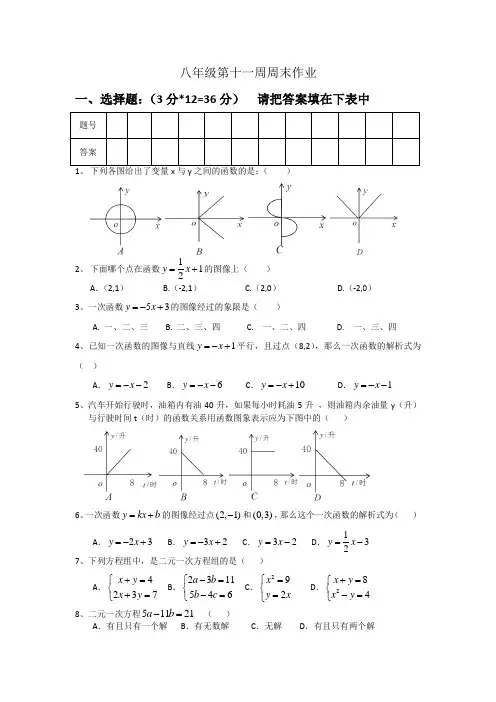
八年级第十一周周末作业一、选择题：（3分*12=36分） 请把答案填在下表中1、 下列各图给出了变量x 与y 之间的函数的是：（ ）2、 下面哪个点在函数112y x =+的图像上（ ） A ．（2,1） B.（-2,1） C.（2,0） D.（-2,0） 3、一次函数53y x =-+的图像经过的象限是（ ）A. 一、二、三B. 二、三、四C. 一、二、四D. 一、三、四4、已知一次函数的图像与直线1y x =-+平行，且过点（8,2），那么一次函数的解析式为（ ）A ．2y x =--B ．6y x =--C ．10y x =-+D ．1y x =--5、汽车开始行驶时，油箱内有油40升，如果每小时耗油5升 ，则油箱内余油量y （升）与行驶时间t （时）的函数关系用函数图象表示应为下图中的（ ）6、一次函数y kx b =+的图像经过点(2,1)-和(0,3)，那么这个一次函数的解析式为（ ）A ．23y x =-+B ．32y x =-+C ．32y x =-D ．132y x =- 7、下列方程组中，是二元一次方程组的是（ ）A ．4237x y x y +=⎧⎨+=⎩B ．2311546a b b c -=⎧⎨-=⎩C ．292x y x ⎧=⎨=⎩D ．284x y x y +=⎧⎨-=⎩8、二元一次方程51121a b -= （ ）A ．有且只有一个解B ．有无数解C ．无解D ．有且只有两个解9、下列各式，属于二元一次方程的个数有（ ） ① 27xy x y +-= ② 41x x y +=- ③15y x+= ④x y =⑤222x y -= ⑥ 62x y - ⑦1x y z ++= ⑧22(y 1)2y y y x -=-=A ．1B ．2C ．3D ．410、某年级共有246人，其中男生人数y 比女生人数x 的2倍少2人，则下面所列的方程组符合题意的有（ ） A ．24622x y y x +=⎧⎨=-⎩ B ． 24622x y x y +=⎧⎨=+⎩ C ．21622x y y x +=⎧⎨=+⎩ D ．24622x y y x +=⎧⎨=+⎩11、对方程组47194517x y x y +=⎧⎨-=⎩，用加减法消去x ，得到的方程为（ ）A ．22y =-B ．236y =-C ．122y =-D ．1236y =- 12、一次函数y ax b =+，若1a b +=，则它的函数图像必定经过点（ ） A ．(1,1)-- B ．(1,1)- C ．(1,1)- D ．(1,1)二、填空题（每题3分，共12分）13、已知自变量为x 的函数2y mc m =+-是正比例函数则m= 。

第11周每周一练 相似图形复习 班级： 姓名： 学号：一、选择1、如图1，DE ∥BC ，则下列不成立的是（ ）A ECAE BD AD = B AE AC AD AB = C BC DE BD AD = D DB EC AB AC =2、如图2， 平行四边形ABCD 中，E 是BC 上一点，BE ∶EC=2∶3，AE 交BD 于F ，则BF ∶FD 等于（ ）A ．2∶5B ．3∶5C ．2∶3D ．5∶73、如图3，△ABC 中∠ACB ＝90o ，CD ⊥AB 于D 。

则图中能够相似的三角形共有（ ）A ．1对B ．2对C ．3对D ．4对4、如图4，ABCD 中，F 是BC 延长线上一点，AF 交BD 于O ，与DC 交于点E ，则图中相似三角形共有（ ）对（全等除外）．A ．3B ．4C ．5D ．6二、填空5．在某天的同一时刻，高为1.5m 的小明的影长为1m ，烟囱的影长为20m ，则这座烟囱的高为_______m ．6、如图，已知矩形ABCD 中，AB=10，BC=12，E 为DC 中点，AF ⊥BE 于点F ，则AF=_____．7、如图所示，已知AB ∥EF ∥CD ，AC 、BD 相交于点E ，AB=6cm ，CD=12cm ，则EF=__ __．E D A （第1题图） （第2题图） （第3题图） （第4题图）（第5题图） （第6题图）三、解答题8、如图，CD是RtΔABC的斜边AB上的高，∠BAC的平分线分别交BC、CD于点E、F.AC•AE=AF•AB吗？说明理由.9、如图，路灯（P点）距地面8米，身高1.6米的小明从距路灯的底部（O点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？10、如图，四边形ABCD、CDEF、EFGH都是正方形.(1) ΔACF与ΔACG相似吗？说说你的理由.(2)求∠1+∠2的度数.【若缺失公式、图片现象属于系统读取不成功，文档内容齐全完整，请放心下载。

八年级数学(下)周周练11（10.4-10.5）一、选择题1．下列命题：①三边对应成比例的两个三角形相似；②两边对应成比例且一个角对应相等的两个三角形相似；③一个锐角对应相等的两个直角三角形相似；④有一个角对应相等的两个等腰三角形相似，其中正确的是( ) A．①③B．①④C．①②④D．①③④2．下列命题错误的是( ) A．两角对应相等的两个三角形相似B．两边对应成比例的两个三角形相似C．两边对应成比例且夹角相等的两个三角形相似D．三边对应成比例的两个三角形相似3．如图，E是□ABCD的边BC延长线上的一点，连接AE交CD于点F，则图中共有相似三角形( )A．1对B．2 对C．3对D．4对4．如果一个直角三角形的两条边长分别是6和8，另一个与它相似的直角三角形边长分别是3、4和x，那么x的值( ) A．只有1个B．可以有2个C．有2个以上但有限D．有无数个5．已知四边形ABCD∽四边形A′B′C′D′．四边形ABCD与四边形A′B′C′D′的周长分别为24、36，则它们的对角线AC与A′C′的比为( )A．2：3 B．3：2 C．4：9 D．9：46．如图，大正方形是由边长为1的小正方形组成的，则下列图形中的三角形(阴影部分) 与△ABC相似的是( )7．如图，在钝角△ABC中，AB=6 cm，AC=12 cm，动点D从点A出发到点B止．动点E从点C出发到点A止．点D运动的速度为1 cm／s，点E运动的速度为2 cm／s．如果两点同时运动，那么当以点A、D、E为顶点的三角形与△ABC相似时．运动的时间是( )A．3 s或4．8 s B．3 s C．4．5 s D．4．5 s或4．8 s8．如图，在Rt△ABC内有边长分别为a、b、c的三个正方形，则a、b、c满足的关系式是( )A．b=a+c B．b=ac C．b2=a2+c2 D．b=2a=2c二、填空题9．下列命题：①有一对锐角相等的两个直角三角形相似；②所有的等腰三角形都相似； ③全等的三角形一定相似；④所有的等边三角形都相似，其中是真命题的有______(写 出正确答案的序号)．10．如图，在△ABC 中，若∠AEB=∠ADC ，则图中共有相似三角形_________对．11．两个相似多边形的面积之比为9：25，且这两个多边形的周长之和为160 cm ，则其中较大多边形的周长为_________cm ．12．如图，D 、E 分别是△ABC 的边AB 、AC 上的点，DE ∥BC ，2AD DB =，若S △ABC 的面积为9，则四边形DBCE 的面积为_________．13．如图，在□ABCD 中，E 是边BC 上的点，AE 交BD 于点F ，如果23BE BC =，那么BF FD=__________． 14．如图，D 、E 两点分别在△ABC 的边AB 、AC 上，DE 与BC 不平行，当_________(写出一个即可)时，△AD E ∽△ACB ．15．如图，A B ⊥BD ，ED ⊥BD ，C 是线段BD 的中点，且AC ⊥CE ，ED=1，BD=4，那么 AB=_________．16．在△ABC 中，AB=16，AC=12，点D 在AB 上，且AD=4，若要在AC 上找一点E ，使△ADE 与原三角形相似，那么AE=__________．17．在Rt △ABC 中，∠C=90°，CD ⊥AB 于点D ，BC=3，AB=5，则其中的一对相似三角形是___________和__________．它们的面积比为___________．18．如图，电影胶片上每一个图片的规格为3．5 cm ×3．5 cm ，放映屏幕的规格为2 m × 2 m ，如果放映机的光源S 距胶片20 cm ．那么光源S 距屏幕_________米时，放映的图像刚好不满整个屏幕．三、解答题19．如图，E是矩形ABCD的边CD上的一点，BF⊥AE于点F．试说明：△ABF∽△EAD．20．如图，在△ABC中，∠C=90°，在AB边上取一点D，使BD=BC，过点D作DE⊥AB交AC于点E，AC=8，BC=6．求DE的长．21．如图，在等边△CDE中，A、B分别是ED、DF延长线上的两个动点，线段DE、AD与EB之间满足关系：DE2=AD·EB．试求∠ACB的度数．22．(9分)如图，在□ABCD中，E是CD延长线上的一点，BE与AD交于点F，1 2DE CD．(1)△ABF与△CEB相似吗?为什么?(2)若△DEF的面积为2，求□ABCD的面积．23．如图，在△ABC和△DEF中，∠A=∠D=90°，AB=DE=3，AC=2DF=4．(1)这两个三角形是否相似?请说明理由．(2)能否分别过点A、D在这两个三角形中各作一条辅助线，使△ABC分割成的两个三角形与△DEF分割成的两个三角形分别对应相似?证明你的结论．24．在等腰△ABC中，AB=AC，∠BAC=120°，P为BC的中点，小慧拿着含30°角的透明三角板，使30°角的顶点落在点P，三角板绕点P旋转．(1)如图(1)，当三角板的两边分别交AB、AC于点E、F时，△BPE与△CFP相似吗?为什么?(2)将三角板绕点P旋转到图(2)的情形时，三角板的两边分别交BA的延长线、边AC于点E、F．①△BPE与△CFP还相似吗(只需写出结论)?②连接EF，△BPE与△PFE是否相似?请说明理由．参考答案一、1．A 2．B 3．C 4．B 5．A 6．A 7．A 8．A二、9．①③④ 10．2 11．100 12．5 13．23 14．∠ADE=∠ACB(或∠AED=∠ABC 或AD AE AC AB =) 15．4 16．3或16317．△BCD △CAD 9：16(或△BCD △BAC 9：25或△CAD △BAC 16：25) 18．807三、19．因为四边形ABCD 是矩形，AB ∥CD ，∠D=90°，所以∠BAF=∠AED ．因为BF ⊥AE ，所以∠AFB=90°．所以∠AFB=∠D ．所以△AB F ～△EAD 20．因为在△ABC 中，∠C=90°，AC=8，BC=6，所以2210AB AC BC =+=．又因为BD=BC=6，所以AD=AB －BD=4．因为DE ⊥A B ，所以∠ADE=∠C=90°．又因为∠A=∠A ，所以△AE D ～△ABC ．所以DE AD BC AC =．所以4638AD DE BC AC ==⨯= 21．因为△CDE 为等边三角形，所以∠CDE=∠CED=∠DCE=60°．CD=CE=DE ．所以∠ADC=∠BEC=120°．因为DE 2=AD ·EB ，所以DE EB AD ED =，即DC EB AD EC =．所以△ACD ∽△CBE ．所以∠ACD=∠B ．又因为∠ACB=∠ECD+∠ACD+∠ECB ，所以∠ACB=∠B+∠ECB+∠ECD=∠CED+∠ECD=60°+60°=120°．即∠ACB 的度数为120° 22．(1)因为四边形ABCD 是平行四边形，所以∠A=∠C ，AB ∥CD ．所以∠ABF=∠CEB ．所以△AB F ∽△CEB (2)因为四边形ABCD 是平行四边形，所以AD ∥BC ，ABCD ．所以△DEF ∽△CEB ，△DEF ∽△ABF ．因为12DE CD =，所以219DEF CEB S DE S EC ∆∆⎛⎫== ⎪⎝⎭，214DEF ABF S DE S AB ∆∆⎛⎫== ⎪⎝⎭．因为S △DEF =2，所以S △CEB =18，S △ABF =8．所以S 四边形BCDF =S △CEB －S △DEF =16．所以S 四边形ABCD =S 四边形BCDF +S △ABF =16+8=24 23．(1)不相似．因为在Rt △BAC 中，∠A=90°，AB=3，AC=4；在Rt △EDF 中，∠D=90°，DE=3，DF=2．所以1AB DE =，2AC DF =．所以AB AC DE DF ≠．同理AB AC DF DE≠．所以Rt △BAC 与Rt △EDF 不相似 (2)能作如图所示的辅助线进行分割．具体作法；作∠BAM=∠E ，交BC 于点M ；作∠ND E=∠B ，交EF 于点N ．由作法和已知条件可知△BAM ≌△DEN ．因为∠BAM=∠E ，∠NDE=∠B ，∠AMC=∠BAM+∠B ，∠FND=∠E+∠NDE ，所以∠AMC =∠FND ．因为∠FDN=90°－∠NDE ，∠C=90°－∠B ，所以∠FDN=∠C ．所以△AM C ∽△FND24．(1)在△ABC中，∠BAC=120°，AB=AC，所以∠B=∠C=30°．因为∠B+∠BPE+∠BEP=180°，所以∠BPE+∠BEF=150°．因为∠EPF=30°．∠BPE+∠EPF+∠CPF=180°，所以∠BPE+∠CPF=150°．所以∠BEP=∠CPF．所以△BP E∽△CFP(两角对应相等的两个三角形相似) (2)①△BPE∽△CFP ②△BPE与△PFE相似．同(1)可证△BP E∽△CFP，得CP PFBE PE=．而CP=BP，因此BP PFBE PE=．又因为∠EBP=∠EPF．所以△BP E∽△PFE(两边对应成比例且夹角相等的两个三角形相似)。

江都区宜陵镇中学2021-2021学年八年级数学下学期第十一周周练试题1．函数y ＝(m －2)25m x -是反比例函数，那么m 的值是 ( )A ．2B ．－2C ．2或者－2D ．任意实数2．关于反比例函数y ＝4x的图像，以下说法正确的选项是 ( ) A ．必经过点(1，1)B ．两个分支分布在第二、四象限C ．两个分支关于x 轴成轴对称D ．两个分支关于原点成中心对称 3．〔2021．〕假设反比例函数y ＝kx的图像过点〔－2，1〕，那么一次函数y ＝kx －k 的图像过( ) A ．第一、二、四象限 B ．第一、三、四象限 C ．第二、三、四象限D ．第一、二、三象限4．假设反比例函数y ＝1x的图像上有两点P 1(1，y 1)和P 2(2，y 2)，那么 ( )A ．y 2<y 1<0B ．y 1<y 2<0C ．y 2>y 1>0D ．y 1>y 2>0 5．在同一直角坐标系中，正比例函数y ＝2x 的图像与反比例函数y ＝42k x-的图像没有交点，那么实数k 的取值范围在数轴上表示为 ( )OyxDCB A6．假如函数y ＝〔k －1〕2k x -是反比例函数，那么k ＝_______，此函数的解析式是_______．7．变量y 与x 成反比例，当x ＝1时，y ＝－6，那么当y ＝3时，x ＝_______． 8．反比例函数y ＝kx的图像经过点〔－2，3〕，那么k 的值是_______，图像在_______象限，当x<0时，y 随x 的减小而_______．9．反比例函数的图像经过点(m ，2)和〔－2，3〕，那么m 的值是_______． 10．点A 为双曲线y ＝kx图像上的点，点O 为坐标原点，过点－A 作AB ⊥x 轴子点B ，连接OA ．假设△ABO 的面积为5，那么是的值是_______． 11．假设关于x 1011m xx x --=--有增根，那么m 的值是 12. (2021．)当x>0时，函数y ＝－5x的图像在 ( ) A ．第四象限 B ．第三象限 C ．第二象限 D ．第一象限13.如图，△ABO 的顶点A 和AB 边的中点C 都在双曲线y ＝xk 〔x ＞o 〕的一个分支上，点B 在x 轴上，CD ⊥OB 于D ，假设△AOC 的面积为3，那么k 的值是A.2B.3C.4D.23 14．〔2021．〕A 〔－1y 1〕，B(2，y 2)两点在双曲线y ＝上，且y 1>y 2，那么m 的取值范围是 ( )A ．m>0 B ．m<0C ．m>－32D ．m<－3 215．如图，反比例函数y＝kx的图像经过点P，那么k＝_______．16．如图，点A在双曲线y＝1x上，点B在双曲线y＝3x上，且AB∥x轴，C、D在x轴上，假设四边形ABCD为矩形，那么它的面积为_______17．y－1与x＋2成反比例函数关系，且当x＝－1时，y＝3．求：(1)y与x的函数关系式；(2)当x＝0时，y的值．18．A(-4，2)、B(n，-4)是一次函数y=kx+b的图像与反比例函数myx的图像的两个交点.〔1〕求此反比例函数和一次函数的解析式；〔2〕根据图像写出使一次函数的值小于反比例函数的值的x的取值范围.19．y ＝y 1－y 2，y 1与x 2成正比例，y 2与x ＋3成反比例，当x ＝0时，y ＝2；当x ＝2时，y ＝0，求y 与x 的函数关系式，并指出自变量的取值范围．20．(2021．)如图，直线y ＝k 1x ＋b(k 1≠0)与双曲线y ＝2k x(k 2≠0)相交于A(1，m)、B(－2，－1)两点．， (1)求直线和双曲线的解析式；(2)假设A 1(x 1，y 1)，A 2(x 2，y 2)，A 3(x 3，y 3)为双曲线上的三点，且x 1<x 2<0<x 3，请直接写出y 1、y 2、y 3的大小关系式．21．反比例函数y=xk1 的图像经过A 〔2，－4〕. ① 求k 的值。

苏教版初中数学八年级下册第二学期第11周周练试卷一、选择题(每小题3分，共24分)1．下列各式：51（1 – x ），34-πx ，222y x -，x x 25，其中分式有（ ） A ．1个B ．2个C ．3个D ．4个 2．如果分式13-x 有意义，则x 的取值范围是（ ） A ．全体实数 B ．x ≠1 C ．x=1 D ．x ＞13．下列约分正确的是（ ）A ．313m m m +=+B ．212y x y x -=-+C ．123369+=+a b a bD ．yx a b y b a x =--)()( 4．若x ，y 的值均扩大为原来的2倍，则下列分式的值保持不变的是（ ）A ．yx 23 B ． 223y x C ．y x 232 D ．2323y x 5．计算xx -++1111的正确结果是（ ） A ．0 B ．212x x - C ．212x - D ．122-x 6．在一段坡路，小明骑自行车上坡时的速度为v 1千米/时，下坡时的速度为v 2千米/时，则他在这段坡路上、下坡的平均速度是（ ）A ．221v v +千米/时B ．2121v v v v +千米/时C ．21212v v v v +千米/时 D ．无法确定 7．若关于x 的方程xm x m x -+-+333=3的解为正数，则m 的取值范围是（ ） A ．m ＜29 B ．m ＜29且m ≠23 C ．m ＞49- D ．m ＞49-且m ≠43- 8．某厂接到加工720件衣服的订单，预计每天做48件，正好按时完成，后因客户要求提前5天交货，每天多做x 件才能按时交货，则x 满足的方程为（ ）A ．54872048720=-+x B ．x+=+48720548720 C ．572048720=-x D ．54872048720=+-x 二、填空题（每小题3分，共24分）9．分式x 21，221y ，xy51-的最简公分母为____________．10．约分：①b a ab 2205=____________，②96922+--x x x =____________． 11．代数式11x -有意义时，x 应满足的条件为x_______． 12．计算：2422x x x+=--_______．13．要使15-x 与24-x 的值相等，则x=____________． 14．计算：若1171m n m +=+，则n m m n+的值为_______． 15．化简（1+）÷的结果为 _________ ． 16．若关于x 的方程12123++=+-x m x x 无解，则m 的值为____________．三、解答题（共52分）17．（每小题5分，共10分）计算：（1）224816x x x x --+； （2）2m n m n n m m n n m -++---．18．（每小题5分，共10分）解下列方程：（1）1123x x =-； （2）2124111x x x +=+--．19．（10分）先化简，再求值：2222a a a b a ab b ⎛⎫- ⎪--+⎝⎭÷222a a a b a b ⎛⎫- ⎪+-⎝⎭+1，其中a=23，b = –3．20．（10分）已知关于x 的方程233x m x x=---的解是一个正数，求m 的取值范围．21．（12分）甲、乙两同学的家与学校的距离均为3000米．甲同学先步行600米，然后乘公交车去学校，乙同学骑自行车去学校．已知甲步行的速度是乙骑自行车速度的21，公交车的速度是乙骑自行车速度的2倍．甲、乙两同学同时从家出发去学校，结果甲同学比乙同学早到2分钟．（1）求乙骑自行车的速度；（2）当甲到达学校时，乙同学离学校还有多远？附加题（20分）22．一列按一定顺序和规律排列的数：第1个数是112⨯； 第2个数是123⨯； 第3个数是134⨯； ……对任何正整数n ，第n 个数与第（n+1）个数的和等于2(2)n n +． （1）经过探究，我们发现：112⨯=1112-，123⨯=1123-，134⨯=1134-， 设这列数的第5个数为a ，那么a >1156-，a =1156-，a <1156-，哪个正确？ 请你直接写出正确的结论；（2）请你观察第1个数、第2个数、第3个数，猜想这列数的第n 个数（即用正整数n 表示第n 个数），并且证明你的猜想满足“第n 个数与第（n+1）个数的和等于2(2)n n +”； （3）设M 表示211，212，213，…，212016这2016个数的和，即M =211+212+213+…+212016， 求证：2016403120172016M <<．。

外国语2021-2021学年八年级数学下学期第11周周测试题1.以下说法正确的选项是〔 〕 A ． 0.25是0.5 的一个平方根B ．.正数有两个平方根，且这两个平方根之和等于0C ． 7 2的平方根是7 D ． 负数有一个平方根2.x 的取值范围是〔 〕A ．2x ≥-B ．2x >-C ．2x <D ．2x ≤y kx =的图像经过()3,2，那么k 的值是〔 〕A ．32-B ．32C ．23-D ．234. 以下二次根式是最简二次根式的是〔 〕A.a 32B.28x C.3y D.4b5. 假如a>b,a+b<0，那么下面各式：①bab a =，②1=⋅a b b a ，③b b a ab -=÷，其中正确的选项是〔 〕 A. ①② B.②③ C.①③ D.①②③4(0)y xn n n =+>的图像与x 轴的交点的坐标〔 〕A ．()0,4B ．()0,4-C ．()4,0D ．()4-0， 一次函数y=－2x+5图象性质错误的选项是 〔 〕A 、 y 随x 的增大而减小B 、直线经过第一、二、四象限图1DCBAEC 、直线从左到右是下降的D 、直线与x 轴交点坐标是〔0，5〕 8. 如图1，点E 在正方形ABCD 内，满足∠AEB ＝90° AE ＝6，BE ＝8，那么阴影局部的面积是( )A ． 48B ．60C ．76D ． 809.如图，在平行四边形ABCD 中，AB =4， ∠BAD 的平分线与BC 的延长线相交于点E ， 与DC 交于点F ，且点F 为边DC 的中点，DG ⊥AE ，垂足为G ，假设DG =1，那么AE 的长为〔 〕A ．23B ．43C ．4D ．83是无理数，而无理数是无限不循环小数，因此3的小数局部我们不可能全部写出来，但是因为1<3<2，因此我们可以用1来表示它的整数局部，用3-1表示它的小数局部。

A CDB 新北师大版 八年级下数学第11周周末作业姓名 学号 完成情况 家长签名1、在式子：a 1、πx 2015、2015y x -、m +20151、20152015y x -、yx 20152014-中，其中是分式的个数为( )A 、2个B 、3个C 、4个D 、5个2、下列电视台图标中，属于中心对称图形的是( )3、对于分式32-x 有意义，则x 应满足的条件是（ ） A 、3≥x B 、3>x C 、3≠x D 、3<x4、下列多项式的分解因式，正确的是（ ）A 、)34(391222xyz xyz y x xyz -=-B 、)2(363322+-=+-a a y y ay y aC 、)(22z y x x xz xy x -+-=-+-D 、)5(522a a b b ab b a +=-+ 5、不等式⎩⎨⎧≤-<-9321x x 的解集在数轴上表示出来是（ ）6、下列多项式中，不能运用公式进行分解因式的是（ ）A 、412+-x x B 、2242b b a a +- C 、254-m D 、222y xy x -+ 7、(南通中考)设a 、b 、c 满足0≠abc ，且c b a =+，则abcb aca ba c bc a cb 222222222222-++-++-+的值为（ ）A 、－1 B 、1 C 、2 D 、3 8、要使分式22--x x 为零，那么x 的值是（ ）A 、－2 B 、2 C 、±2 D 、0A 、B 、C 、D 、第10题9、m 、n 是常数，若0>+n mx 的解是21<x ，则0<+m nx 的解集是（ ） A 、2>x B 、2<x C 、2->x D 、2-<x 10、直线b x k y l +=11:与直线x k y l 22:=在同一平面直角坐标系中的 图象如图所示，关于x 的不等式b x k x k +>12的解集为（ ） A 、1->x B 、1-<x C 、2-<x D 、无法确定二、填空题：（每小题3分，共15分）11、若2294b kxy a ++可以因式分解为2)32(b a -，则k 的值为 。

仪征市三中八下数学周末练十一一、选择题（每小题3分，共24分）1、如果a ＞b ，下列各式中不正确．．．的是 A ．a －3＞b －3 B ．-2a ＜-2b C ．2a ＞2b D ． a 1＜b12、若分式242x x -+的值为0，则x 的值为A ．±2 B ．2 C ．－2 D ．03、如果不等式组⎩⎨⎧≥<mx x 5有解，那么m 的取值范围是 （ ） A ．m >5 B ．m <5 C ．m ≥5 D ．m ≤54、不等式2（x －2）≤x －2的非负整数解的个数为A ．1个 B ．2个 C ．3个 D ．4个5、在同一坐标系中，函数x ky =和3+=kx y 的图像大致是（ ）A ．B ．C ．D ．6、反比例函数y=xk(k>0)在第一象限内的图象如图，点M 是图象上一点，MP 垂直x 轴于点P ，如果△MOP 的面积为1，那么k 的值是( )(A) 1 (B) 2 (C) 47、已知()111,P x y 、()222,Px y 、()333,P x y 是反比例函数2y x=的图象上的三点，且 1230x x x <<<，则1y 、2y 、3y 的大小关系是A ．321y y y << B ．123y y y << C ．213y y y << D ．231y y y <<8、如果关于x 的分式方程xmx x -=--552无解，则m 的值为A ．B ．3 C ．－5 D ．－3二、填空题（每小题3分，共27分）9、若反比例函数ky x=的图象经过点()1,2-，则k = 。

10、已知反比例函数32m y x-=，当______m 时，其图象的两个分支在第一、三象限内；当______m 时，其图象在每个象限内y 随x 的增大而增大；x11、若分式方程12552x ax x+=--的解为0x =，则a 的值为12、分式23544-2m m-与的最简公分母是___________________________。

初二（下）数学周末作业十一（A ）2013.5.10——四边形班级____________学号______________姓名____________成绩____________一、填空题（每题3分）1、三角形三边长分别为6、7、10，顺次连结这个三角形三边中点所得三形的周长为____________。

2、菱形的周长为32cm ，较短一条对角线长是8cm ，则这个菱形的面积为____________cm 2。

3、平行四边形ABCD 中，10BC =cm ，12CD =cm ．若A 到BC 的距离与它到CD 的距离之和为22cm ，则平行四边形ABCD 的面积为____________cm 2。

4、若梯形的面积为6cm 2，高为2cm ，则此梯形的中位线长为____________cm 。

5、顺次联结一个等腰梯形的四边的中点，所得的四边形是____________。

6、如果一个四边形的两条对角线____________，那么顺次连接其各边中点所得的四边形是矩形．7、梯形的中位线长为10，一条对角线将中位线分成长度比为2:3的两段，则梯形的两底长为____________8、梯形的上底边长为5，下底边长为9，中位线把梯形会成上、下两部分，则这两部分的面积的比为____________。

9、在梯形ABCD 中，//AB CD ，:2:3CD AB =，E 、F 分别是两腰BC 、AD 的中点，则:EF AB =____________。

10、如图，等腰形ABCD 中，对角线AC BC AD =+则DBC ∠的度数为____________。

11、如图，梯形ABCD 中，AD BC ∥，EF 为中位线，G 为BC 上任一点，如果GEF S ∆=2，那么梯形的面积是____________cm 2．12、如图，在平行四边形ABCD 中，2AD AB =，点M 是AD 的中点，CE AB ⊥与点E ，若38CEM ∠=︒，则DME ∠=____________。