下载文档原格式
![二重积分的计算法[精编文档]](https://img.taocdn.com/s1/m/eded425011661ed9ad51f01dc281e53a59025178.png)
二重积分的计算教案教案标题：二重积分的计算教学目标：1. 理解二重积分的概念和意义；2. 学会利用直角坐标系下的二重积分及其性质计算二重积分；3. 掌握变量替换法计算二重积分。
教学准备：1. 幻灯片及投影仪；2. 教学板及白板笔；3. 直角坐标纸；4. 计算器。
教学过程：一、导入（5分钟）1. 讲师介绍二重积分的概念和意义：二重积分是对二元函数在一个有界区域上的积分运算，可以用来计算平面区域的面积、质量等物理量。
2. 引导学生思考：如何计算函数在某个区域的面积？二、直角坐标系下的二重积分（20分钟）1. 讲解二重积分的概念和符号表示；2. 利用直角坐标系下的二重积分性质，分别介绍极坐标系和直角坐标系下的二重积分计算方法；3. 通过示例，详细讲解直角坐标系下二重积分的计算步骤。
三、变量替换法计算二重积分（25分钟）1. 介绍变量替换法的基本思想和要点；2. 通过示例，引导学生掌握变量替换法计算二重积分的步骤和技巧；3. 鼓励学生积极思考、探索新的变量替换方法，提升解题能力。
四、练习与巩固（15分钟）1. 提供一些典型的计算二重积分的练习题，让学生自主完成并讨论解法；2. 教师逐个讲解练习题的解题思路和方法。
五、拓展应用（10分钟）1. 引导学生思考并讨论：二重积分在实际问题中的应用；2. 讲解几个具体实例，让学生理解二重积分在不同领域中的应用。
六、总结与反思（5分钟）1. 客观回顾本节课所学内容；2. 鼓励学生提出问题、分享心得；3. 解答学生提出的问题，澄清疑惑。
教学延伸：1. 建议学生参考相关教材，复习和巩固本节课所学内容；2. 鼓励学生应用二重积分解决实际问题，提升实际运用能力；3. 教师可布置相关的作业，以检查学生对本节课内容的掌握情况。
教学评价：1. 通过课堂教学中的互动讨论，观察学生的参与度和理解程度；2. 教师根据学生作业的完成情况和答案的正确性评价学生对知识点的掌握程度；3. 反馈学生的问题和困惑，及时给予指导和解答。
二重积分的计算法教案一、教材分析本节课的内容是二重积分的计算法。
在高中阶段的数学教学中，二重积分的计算是重要的内容之一、根据高中数学课程标准要求，学生需要掌握二重积分定义、二重积分的计算法以及应用等内容。
本节课的教学目标是使学生能够掌握二重积分的计算方法，提高学生的综合运算能力和解题能力。
二、教学目标1.知识与能力目标(1)掌握二重积分的计算方法；(2)熟练掌握二重积分的定义；(3)能够运用二重积分的计算方法解决实际问题。
2.过程与方法目标(1)通过示例引入，让学生理解二重积分的概念；(2)结合图形进行讲解，培养学生的几何直观；(3)通过分析具体题目，培养学生的计算能力与解题思路。
3.情感、态度与价值观目标(1)培养学生的数学兴趣，提高学生对数学的认知和理解；(2)培养学生解决问题的能力，让学生能够将数学知识应用到实际中。
三、教学重难点1.教学重点(1)二重积分的计算方法；(2)几何图形与二重积分的关系。
2.教学难点(1)解决实际问题时的二重积分的计算；(2)综合运用二重积分的知识与解题能力。
四、教学过程与方法1.模块一：复习导入（10分钟）复习上节课的内容，引入本节课的主题。
2.模块二：二重积分的定义（20分钟）(1)通过几何图形解释二重积分的含义；(2)介绍二重积分的定义，并进行示例讲解；(3)引导学生进行练习题。
3.模块三：二重积分的计算方法（40分钟）(1)对可分离变量的函数进行计算；(2)对相对简单的函数进行计算；(3)利用换元法进行计算；(4)利用极坐标进行计算；(5)引导学生进行练习题。
4.模块四：实际问题的应用（20分钟）(1)提供一些实际问题，并引导学生用二重积分来求解；(2)引导学生进行练习题。
5.模块五：课堂小结（10分钟）总结本节课的重点内容，强调二重积分的计算方法和应用。
五、教学手段与学具设备1.教学手段：讲授、示范、练习、提问等；2.学具设备：黑板、多媒体设备、教材、练习册等。
二重积分优秀教学设计二重积分优秀教学设计教学目标1.理解二重积分的概念和意义；2.学会计算可积函数的二重积分；3.掌握二重积分的性质和计算方法；4.能够应用二重积分解决实际问题。
教学内容1.二重积分的概念和意义–了解累次积分和二重积分的概念；–探究二重积分的物理意义和几何意义；–通过例题理解二重积分的计算过程。
2.可积函数的二重积分计算–学习二重积分的计算方法；–掌握使用定积分计算二重积分；–理解可积函数的二重积分和累次积分的关系。
3.二重积分的性质–掌握二重积分的线性性质、可加性和保号性质等；–了解二重积分对交换次序的影响。
4.二重积分的计算方法–学习使用极坐标、换元法等方法计算二重积分；–通过例题巩固计算方法。
5.应用二重积分解决实际问题–学习如何应用二重积分计算面积、质量、重心等物理量；–通过实际问题的讲解和解答，培养应用二重积分解决问题的能力。
教学步骤1.导入知识，介绍二重积分的概念和意义；2.通过具体的例题引入可积函数的二重积分计算；3.讲解二重积分的性质和计算方法，并进行例题演示；4.分组讨论、合作解题，巩固所学的二重积分计算方法；5.引入实际问题，讲解如何应用二重积分解决问题；6.完成课堂练习和作业，检验学生的掌握情况；7.总结课程内容，梳理知识点，解答学生提出的问题。
教学资源1.教科书《高等数学》或相关参考书籍；2.教学投影仪、电脑等多媒体设备；3.课堂练习题和作业。
教学评价1.课堂参与度：学生在课堂中的积极参与程度；2.反馈问题：学生提出的问题和疑惑；3.课堂练习和作业：学生对所学知识的掌握和运用能力；4.学习成果：学生对二重积分相关概念和计算方法的理解和应用。
参考书目1.严蔚敏，李冬梅. 高等数学[M]. 清华大学出版社, 2018.2.斯图尔特. 单变量微积分学：早期变量函数的概念[M]. 科学出版社, 2008.3.Anton Howard, Bivens Irl，Davis Stephen. 微积分[M]. 高等教育出版社, 2006.教学方法1.探究式教学：通过引导学生进行探究，从而加深对二重积分概念和意义的理解；2.演示教学：通过解题演示，让学生掌握二重积分计算方法；3.合作学习：组织学生进行小组讨论和合作解题，培养团队合作能力；4.实际问题解决：引入实际问题讲解，帮助学生应用二重积分解决实际问题；5.提问和讨论：通过提问和讨论，激发学生的思考和参与度。
二重积分教案设计三个导入方式二重积分教案设计导入方式一：图形引入目标：通过观察图形引入二重积分的概念和应用。
步骤：1. 准备一个简单的图形，如一个矩形或三角形。
2. 引导学生观察图形，并提问相关问题，如图形的面积如何计算？3. 引导学生思考如何将图形划分为更小的部分，并估计每个小部分的面积。
4. 引导学生思考如何计算整个图形的面积，进而引出二重积分的概念。
导入方式二：实际问题引入目标：通过实际问题引入二重积分的概念和应用。
步骤：1. 提供一个实际问题，如某地区一天内的降雨量分布情况。
2. 引导学生思考如何描述和计算这种降雨量分布。
3. 引导学生思考如何将地区划分为更小的部分，并估计每个小部分的降雨量。
4. 引导学生思考如何计算整个地区的总降雨量，进而引出二重积分的概念。
导入方式三：数学公式引入目标：通过数学公式引入二重积分的概念和应用。
步骤：1. 提供一个简单的数学公式，如函数f(x, y) = x^2 + y^2。
2. 引导学生思考如何计算该函数在某个区域上的积分。
3. 引导学生思考如何将该区域划分为更小的部分，并估计每个小部分的贡献值。
4. 引导学生思考如何计算整个区域上的积分，进而引出二重积分的概念。
教学目标：1. 理解二重积分的概念和应用；2. 掌握二重积分的计算方法；3. 能够将实际问题转化为二重积分并求解。
教学内容：1. 二重积分的定义和性质；2. 二重积分的计算方法，包括直角坐标系下的面积法和极坐标系下的面积法；3. 二重积分在实际问题中的应用。
教学步骤：第一步：引入二重积分概念1. 导入方式一：图形引入- 学生观察图形，并讨论图形面积如何计算。
- 引导学生思考如何将图形划分为更小的部分，并估计每个小部分的面积。
- 引导学生思考如何计算整个图形的面积，进而引出二重积分的概念。
第二步：二重积分的定义和性质1. 定义：介绍二重积分的定义，即将函数在一个有限区域上的值乘以该区域的面积，并求和。
教
案
参赛教师:
职称: 助教
所在院系: 数学与统计学院
所授课程: 高等数学
20XX年5月
第十章重积分
第二节二重积分的计算法
（第1课时）
教学目的：理解二重积分计算公式导出的方法，理解公式中符号的意义；熟练掌握X-型区域与Y-型区域上的积分公式，并能根据条件选择恰当的积分次序计算二重积分.重点：X-型区域上二重积分的积分公式；根据条件选择恰当的积分次序计算二重积分.
难点：选择合适的方法计算二重积分.
教学方法：直观教学，启发式讲授.
教学过程：
一、利用直角坐标系计算二重积分
1．积分区域D的分类
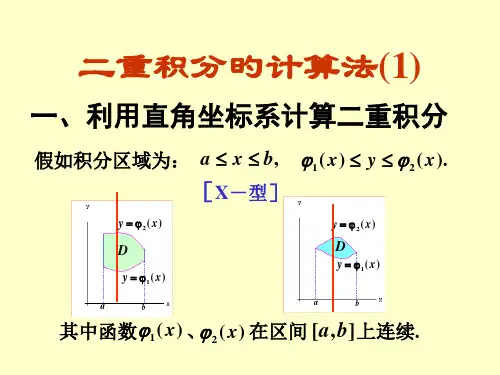
（1）积分区域D 为X-型区域
图1 图2 图1，图2表示的区域都是X-型区域.
X-型区域的特点：穿过D 的内部平行于y 轴的直线与D 的边界的交点个数不超过两个. 用不等式组表示为
).()(21x y x b x a D ϕϕ≤≤≤≤，： （2）积分区域D 为Y-型区域
图3 图3，图4表示的都是Y-型区域.
Y-型区域的特点：穿过D 的内部平行于y 轴的直线与D 边界交点的个数不多于两个. 当积分区域为Y-型区域时，即
12:,()()
D c y d y x y ψψ≤≤≤≤
2．二重积分计算公式
（1）积分区域D 为X-型区域时
(,)D
f x y d σ
⎰⎰的计算公式.
当0),(≥y x f 时，由二重积分的几何意义
(,)D
f x y d σ
⎰⎰的值等于以D 为底，以(,)z f x y =为顶的
曲顶柱体（图5）的体积V .
即
⎰⎰=D
d y x f V σ
),(.
过x 轴上
x 点作平行于yOz 的平面
x π, 0a x b ≤≤ . 图5
x π截V 得一以1020[(),()]x x ϕϕ长为底,0(,)z f x y =为曲边的曲边梯形, 其面积为
2010()
00()
()(,)x x A x f x y dy
ϕϕ=⎰
.
y x O )
(2y d c
[]21()
()
,,()(,)x x x a b A x f x y dy
ϕϕ∀∈=⎰
对.
根据平行截面面积已知的立体求体积的方法，可得
21()
()()(,)b
b
x a a x V A x dx f x y dy dx
ϕϕ⎡⎤==⎢⎥⎣⎦⎰⎰⎰ EMBED Equation.DSMT4 21()
()
(,)b
x a x dx f x y dy
ϕϕ=⎰⎰
.
于是21()
()
(,)(,)b
x a
x D
f x y d dx f x y dy
ϕϕσ=⎰⎰⎰⎰
.
（2）积分区域D 为Y-型区域时
(,)D
f x y d σ
⎰⎰的计算公式
2121()
()
()
()
(,)[(,)](,)d
y c y D
d y c
y f x y d f x y dx dy dy f x y dx
ψψ
ψψσ==⎰⎰⎰⎰⎰⎰
说明：这是在(,)0f x y ≥的条件下得到的计算公式, 但是对于一般的情况这个公式依然成立.
当(,)f x y 在D 上变号时，由于
(,)(,)(,)-(,)
(,)22f x y f x y f x y f x y f x y +=
-
，
记1(,)(,)(,)2f x y f x y f x y +=
EMBED Equation.DSMT4
2(,)(,)
(,)2f x y f x y f x y -=
， 则
12(,),(,)f x y f x y 在D 上非负，12(,),(,)f x y f x y 在D 上可以应用上面的公式计算.
于是1
2
(,)(,)(,)D D D f x y dxdy f x y dxdy f x y dxdy
=-⎰⎰⎰⎰⎰⎰
. 3．例题应用
例1. 计算
D
yd σ
⎰⎰，其中D 是抛物线
2
y x =及直线2y x =-所围成的闭区域. 解：把D 看成Y-型区域（图6），则
2
2:12y x y D y ⎧≤≤+⎨
-≤≤⎩
222
12
21
342
21
(2)[]3494
y y
D
yd dy ydx
y y y dy
y y y σ+---∴==+-=+-=⎰⎰⎰⎰⎰ 图6
另解：把D 看成X-型区域（图7），则
122::0114y x y D D x x ⎧⎧≤≤-≤≤⎪⎪⎨⎨
≤≤≤≤⎪⎪⎩⎩
1
2
140
1
2
24
4
21110[](54)2294D
D D x yd yd yd dx ydy dx ydy
y dx x x dx
σσσ
-∴=+=+=+=-+-=⎰⎰⎰⎰⎰⎰⎰⎰⎰⎰ 图7
例2.计算二次积分
11
22
sin (sin )
x
D dx y dy y d σ=⎰⎰⎰⎰
解：将所给的积分区域D 用不等式组表示
:01,1D x x y ≤≤≤≤
画出草图（图8），改写D 为：
01,0y x y ≤≤≤≤ 图8
1
112220001sin sin sin (1cos1)2y x D dx y dy y d dy y dx σ∴
===-⎰⎰⎰⎰⎰⎰. 二次积分交换积分次序的步骤： （1）写出积分区域D ； （2）画出草图；
（3）将D 改写为另一类型的不等式组，交换积分次序。
例题反思：化二重积分为二次积分时，为了计算简便，需要选择恰当的二次积分次序。
这时，既要考虑积分区域D 的形状，又要考虑被积函数(,)f x y 的特性。
y
o x
y
小结
直角坐标系下计算二重积分的步骤： 一、画出积分区域D
二、选择积分次序（依据：容易积分；分块少）
三、⎧⎨
⎩定外限——域边两线夹（是常数）
定积分限定内限——域中一线穿
若D 为X-型区域： 若D 为Y-型区域：
左右夹，从下向上穿 上下夹，从左向右穿
12()():x y x D a x b ϕϕ≤≤⎧⎨≤≤⎩ 1
2()():y x y D c y d ψψ≤≤⎧⎨≤≤⎩
四、计算两个定积分
X-型按下公式计算： 21()
()
(,)(,)b
x a x D
f x y d dx f x y dy
ϕϕσ=⎰⎰⎰⎰
.
Y-型按下公式计算： 21()
()
(,)(,)d
y c
y D
f x y d dy f x y dx
ψψσ=⎰⎰
⎰⎰
.。
