二重积分的计算方法

二重积分的计算一、利用直角坐标计算二重积分1.X 型区域1) 定义：先把x 看做常数，f(x,y)只看做y 的函数，对f(x,y)计算从1ϕ(x)到2ϕ(x)的定积分，然后把所得结果（为x 的函数）再对x 从a 到b 计算定积分，称其为X 型积分。

2) 积分区域D={(x,y)|21,ϕϕ≤≤≤≤y b x a },称为X 型区域。

3) 记作：⎰⎰⎰⎰⎰⎰⎰==⎥⎦⎤⎢⎣⎡=)(2)(1)(2)(1),(),(),(),(x x Db a Db a x x dy y x f dx d y x f dx dy y x f d y x f ϕϕϕϕσσ4) 例题1注意：积分限：由下向上作平行为y 轴的直线，先经过的为积分下限，后经过的为积分上限。

.2,1,所围闭区域及：由其中计算xy x y D xyd D===⎰⎰σ⎩⎨⎧≤≤≤≤xy x D X 121:2211[]2xy x dx =⋅⎰89)22(213=-=⎰dx x x 211xDxyd dx xydyσ=⎰⎰⎰⎰解： 12 oxyy=xy=1Dx2.Y 型区域1）定义：先对x ，后对y 的二次积分，称之为Y 型积分。

2）积分区域D={})()(,),(21y x y d x c y x ϕϕ≤≤≤≤，称之为Y 型区域。

3）记作：⎰⎰⎰⎰⎰⎰⎰==⎥⎦⎤⎢⎣⎡=)(2)(1)(2)(1),(),(),(),(y y Dd c Dd c y y dx y x f dy d y x f dy dx y x f d y x f ϕϕϕϕσσ4）例题2注意：积分限：由左向右做平行于x 轴的直线，先经过的为积分下限，后经过的为积分上限。

.2,1,所围闭区域及：由其中计算xy x y D xyd D===⎰⎰σ⎩⎨⎧≤≤≤≤221:x y y D Y 2221[]2y x y dy =⋅⎰89)22(213=-=⎰dy y y 221yDxyd dy xydxσ=⎰⎰⎰⎰解：12 o xy x = y x=2D y1 2例题3所围闭区域及：由其中计算2,2-==⎰⎰x y x y D xyd Dσ［法1］⎩⎨⎧+≤≤≤≤-221:2y x y y D Y 232511(44)2y y y y dy -=++-⎰46322114[2]2436y yy y -=++-13[12]24=-=2221y y D xyd dy xydx σ+-=⎰⎰⎰⎰22221[]2y y x y dy +-=⎰458［法2］⎩⎨⎧≤≤-≤≤x y x x D 10:1⎩⎨⎧≤≤-≤≤xy x x D 241:2⎰⎰⎰⎰⎰⎰+=21DD D xyd σ=+=⎰⎰⎰⎰--xx x x xydydx xydy dx 24110845例题四 计算()22Dxy dxdy +⎰⎰其中D 是以y x y x a y a ==+=，，和()30y a a =>为边的平行四边形区域。

二重积分计算方法
二重积分是指同时计算两个复杂变量，如空间或一维时间尺度上均有复杂变量，即进行双重多元积分运算。

二重积分法是科学研究和工程分析的β解析最常用的
计算方法。

由于经常需要解决复杂的数学问题，因此二重积分的计算在现代科学和工程领域有着广泛的应用。

二重积分计算方法是以一维自变量再组合成双维自变量，它首先将单重积分划
分为两个子题，即沿着一个方向进行单重积分，其次再沿着另一个方向进行单重积分。

例如，有一个变量专为u，如果将u偏导后的复杂函数用二维变量X和y来表示，则：
du=f(x,y)dxdy
二重积分可以通过两个步骤来完成:在第一步中，x先作为自变量，上下限的
特定的h, k ,f (x, y) 求定积分，第二步中，y作为自变量，对每一个固定的x，求解特定h, k 等积分。

二重积分法在微分方程、概率理论、拟静力学，拉格朗日
方法以及费马多元法等领域得到了广泛应用。

此外，二重积分法可以进行在线计算，在互联网领域有着重要应用。

现代技术
在二重积分法方面取得了新的进展，特别是机器学习等技术对二重积分法的计算和应用有着深远的影响。

现有的技术可以更加聪明的理解和处理信息，这也大大提高了利用二重积分法研究互联网数据的效率。

综上所述，二重积分计算方法是一种数学运算的技术，在现代科学和工程领域，它被广泛应用于多种多样的领域，特别是在互联网领域，二重积分法为研究者提供了更大的可能性，研究互联网数据更快更有效地获取信息。

二重积分的概念与计算二重积分是微积分中的重要概念，在数学和物理学等领域有广泛应用。

本文将介绍二重积分的基本概念和计算方法，帮助读者更好地理解和应用该概念。

一、二重积分的基本概念二重积分是对二元函数在给定区域上的积分运算。

通常表示为∬_Df(x,y)dxdy，其中D为积分区域。

二重积分的结果是一个实数。

二、二重积分的计算方法1. 通过迭代积分计算如果积分区域D可以表示为两个范围有限的连续函数g(x)和h(x)之间的交集，即D={(x,y)|a≤x≤b,g(x)≤y≤h(x)}，则二重积分可以通过先计算内层积分再计算外层积分的方式进行计算。

具体计算步骤如下：步骤1：计算内层积分将变量y看作常数，将二元函数f(x,y)带入到内层积分中，进行y 的积分运算。

得到一个关于x的函数。

步骤2：计算外层积分将步骤1得到的关于x的函数带入到外层积分中，进行x的积分运算。

得到最终的结果。

2. 通过坐标变换计算在某些情况下，二重积分的计算可以通过坐标变换来简化。

常见的坐标变换包括极坐标变换和直角坐标变换。

以极坐标变换为例，如果积分区域D可以用极坐标表示，则可以通过将二元函数f(x,y)转化为二元函数g(r,θ)来计算二重积分。

具体计算步骤如下：步骤1：进行坐标变换将二元函数f(x,y)用极坐标变换的公式来表示，并计算坐标变换的Jacobi行列式。

步骤2：计算新函数的二重积分将坐标变换后得到的二元函数g(r,θ)进行二重积分计算，得到最终结果。

三、二重积分的应用二重积分在数学和物理学中有广泛的应用。

以下是一些常见的应用场景：1. 几何体的面积二重积分可以用来计算平面上有界区域的面积。

对于给定区域D和一个常数函数f(x,y)=1，在D上进行二重积分即可得到该区域的面积。

2. 质量和质心的计算已知二元函数f(x,y)表示平面上的质量密度分布，二重积分∬_Df(x,y)dxdy可以用来计算平面上有界区域D的质量。

质心的坐标可以通过以下公式计算：x_0=1/m∬_Dxf(x,y)dxdyy_0=1/m∬_Dyf(x,y)dxdy其中m为区域D的总质量。

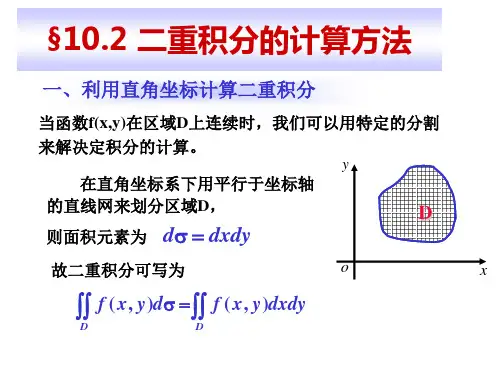
二重积分的计算方法二重积分是微积分中的重要内容，用于计算平面上的曲线与坐标轴所围成的面积或求平面上的散布点的平均性质等。

在实际运用中，可以通过直接计算、换元法、极坐标法等多种方法来进行二重积分的计算。

一、直接计算法直接计算法是最常用也是最基础的计算二重积分的方法。

其基本步骤是将所给的二重积分转化为累次积分，先对一个变量进行积分，再对另一个变量进行积分。

1.内部积分内部积分即对于每个固定的y值，对x进行积分。

可以根据具体的题目决定如何进行内部积分，常用的有定积分、不定积分和积分换元等方法。

2.外部积分外部积分即对内部积分的结果再进行一次积分，这一步是对y进行积分。

同样的，可以根据具体题目决定如何进行外部积分，可以选择定积分、不定积分和积分换元等方法。

需要注意的是，直接计算法在面对比较复杂的函数或曲线时计算量较大，需要进行复杂的代数计算，常常需要对整个积分范围进行划分，或者使用边界定理简化计算。

二、换元法换元法是将二重积分变换到坐标系上的简单区域。

换元法分为直角坐标系的变换和极坐标系的变换两种情况。

1.直角坐标系的变换直角坐标系的变换是指将原先的积分变为关于新的变量的积分，使得积分计算更加简化。

常见的直角坐标系变换有平移变换、旋转变换和放缩变换等。

例如，当变量的变化范围较大或边界不规则时，使用平移变换可以将积分范围变为一个更加简单的区域，从而简化计算。

2.极坐标系的变换极坐标系的变换是将原先的直角坐标系变为极坐标系，使得计算过程更加简单明了。

极坐标系变换常用于对称图形或圆形区域进行积分计算。

极坐标系变换需要通过变量替换来实现，通常需要将原函数和积分上下限由直角坐标形式转换为极坐标形式，再进行计算。

换元法可以大大简化积分计算过程，但需要选择合适的坐标变换，有时会引入更多的计算量。

需要根据具体问题的特点来决定选择哪种变换。

三、几何意义根据题目所给的条件，可以确定积分范围和被积函数形式，将二重积分转化为面积或长度的几何问题。

二重积分的计算方法2. 二重积分的计算法目前所能接触到的方法是：将二重积分化为两次单积分将二重积分化为两次单积分_接下来介绍：①直角坐标系②极坐标③二重积分的换元法（至于二重积分的换元法，仅作简单介绍）2.1 利用直角坐标计算二重积分本质思想是通过画图来判断是先对x还是先对y积分。

（先对哪一个积分不绝对，需要具体问题具体分析，但仍需考虑图形，这里不过多解释为什么，仅给出相关题型的做法）下面的介绍中，默认f(x,y)≥0①有如下闭区域D：∬Df(x,y) dσ=∫abdx∫ϕ1(x)ϕ2(x)f(x,y) dy（先对y后对x）②∬Df(x,y) dσ=∫cddy∫ψ1(y)ψ2(y)f(x,y) dx（先对x后对y）（注：这里未考虑在立体空间中的形状，但只研究物体在xOy面上的投影即可解决问题）我们称①、②中的区域分别为X型区域、Y型区域。

（按先对、x、y中的哪个积分来命名）若闭区域D既是X型区域，又是Y型区域，则选择哪一种都可以（尽量找简单的）不管先对还是进行积分，要找准积分限不管先对x还是y进行积分，要找准积分限“每个人都有每个人的理解方式，这里我有些解释不出来，大家自行领会吧”注：在解题时，注意使用可加性"可加性"，区间可以分为X型、Y型，既是X型又是Y型的，此时我们对其分别求二重积分即可。

这里给出一个例子来让大家认识到选择正确的积分次序的重要性：计算∬Dy1+x2−y2 dσ，其中区域D是由、、y=x、x=−1、y=1围成的闭区域。

显然D既是X型，又是Y型积分区域，现在我们用两种方法来看一下：①先对y后对x：∫−11dx∫x1y1+x2−y2 dσ（偶函数，想想为什么这里是）=−13∫−11[(1+x2−y2)32|x1] dx=−13∫−11(|x|3−1) dx_（偶函数，想想为什么这里是|x|3）=−23∫01(x3−1)dx=−23(x44−x)|01 =−23⋅(14−1)=12②先对x后对y：∫−11dy∫y1y1+x2−y2dx=∫−11[xy(1+x2−y2)12|1y−∫1yx d[y(1+x2−y2)12]]=∫−11[y2−y2−y2−∫1yx2y1+x2−y2 dx]dy此时还需求∫1yx2y1+x2−y2 dx，难免比较麻烦。

二重积分的计算法直角坐标二重积分是微积分中的重要概念，用来计算平面区域上的其中一种性质，比如面积、质心等。

在直角坐标系中，二重积分的计算需要将被积函数表示成两个变量的函数，并确定积分区域的边界。

下面将介绍二重积分的计算方法及其应用。

一、二重积分的定义二重积分是对一个平面区域上的函数进行积分，其定义如下：设函数$f(x,y)$在有界闭区域$D$上有定义，且$D$为$x$轴上$[a,b]$的一个闭区间，$y$轴上$[c,d]$的一个闭区间，将$D$划分为有限个小区域，每个小区域用$(\Delta x_i,\Delta y_j)$表示，其中$i=1,2,...,m$，$j=1,2,...,n$，则二重积分$\iint_D f(x,y)dxdy$定义为：$$\iint_D f(x,y)dxdy=\lim_{\lambda\rightarrow0}\sum_{i=1}^{m}\sum_{j=1}^{n}f(x_{ij}^*,y{j}^*)\Delta A_{ij}$$其中$x_{ij}^*,y_{ij}^*$为$(x,y)$在第$i$行第$j$列小区域内的任意一点，$\Delta A_{ij}=\Delta x_i\Delta y_j$为第$i$行第$j$列小区域的面积，$\lambda$为小区域的最大直径，$\lambda=\max\{\Deltax_1,\Delta x_2,...,\Delta x_m,\Delta y_1,\Delta y_2,...,\Delta y_n\}$。

二、二重积分的计算在直角坐标系中，二重积分的计算分为三种情况：换序积分、累次积分和极坐标积分。

下面将依次介绍这三种情况的计算方法。

1.换序积分当被积函数是可分离变量的函数时，可以进行换序积分。

换序积分可以简化计算过程。

设函数$f(x,y)=g(x)h(y)$，则有：$$\iint_D f(x,y)dxdy=\int_a^bg(x)dx\int_c^dh(y)dy$$也可以先对$y$积分再对$x$积分，即：$$\iint_D f(x,y)dxdy=\int_c^dh(y)dy\int_a^bg(x)dx$$2.累次积分对于一般的被积函数，可以通过累次积分的方法进行计算。

二重积分的概念和计算方法二重积分是在二维平面上对一些区域上的函数进行求和的操作。

它可以用于求解平面区域上的面积、质量、重心等物理量，也可以用于解决求解二元函数的平均值、概率密度等问题。

在本文中，我们将讨论二重积分的概念以及几种常见的计算方法。

一、二重积分的概念二重积分是对二维平面上的一个闭区域D上的函数f(x,y)进行求和的操作，可以表示为：∬Df(x,y)dA其中D表示区域D上的面积，f(x,y)表示在点(x,y)上的函数值，dA 表示在D上的一个微小面积元素。

对于二重积分的计算，可以分为定积分和区域积分两种方法。

定积分的计算是将区域D划分成许多小的矩形面积，并将这些小矩形的面积乘以对应的函数值求和。

区域积分的计算是将区域D分成许多小的曲面元素，并将这些小曲面的面积乘以对应的函数值求和。

二、二重积分的计算方法1.直角坐标系下的二重积分计算在直角坐标系下，我们可以通过在区域D上设置两个变量x和y，将原来的二重积分转化为两个一重积分的问题。

将区域D分成许多小的矩形面积，每个小矩形的面积为ΔA，左下角的坐标为(x,y)，则我们可以得到二重积分的计算公式为：∬D f(x,y) dA = lim ΔA→0 Σ f(x,y)ΔA其中Σ表示对所有小矩形面积求和。

对于简单的区域D，我们可以直接通过计算极限来求解二重积分。

但对于较为复杂的区域D，可以使用变量替换、拆分区域等方法来简化计算过程。

2.极坐标系下的二重积分计算在极坐标系下，我们可以通过引入极角θ和极径ρ，将二重积分转化为极坐标下的一重积分问题。

区域D可以用极坐标表示为：D={(ρ,θ)，α≤θ≤β，g(θ)≤ρ≤h(θ)}。

对于极坐标下的二重积分公式，我们有：∬D f(x,y) dA = ∫βα ∫h(θ)g(θ) f(ρcosθ,ρsinθ)ρdρdθ。

通过将二重积分转化为极坐标系下的一重积分问题，可以简化复杂区域的计算过程。

3.坐标变换方法对于一些特殊的区域D，我们可以通过坐标变换来简化二重积分的计算过程。

二重积分的计算方法在数学的广袤领域中，二重积分是一个重要的概念，它在许多实际问题和理论研究中都有着广泛的应用。

理解和掌握二重积分的计算方法，对于我们解决诸如计算平面区域的面积、物体的质量、重心等问题具有关键意义。

首先，让我们来明确一下二重积分的定义。

二重积分是用来计算在一个平面区域上的函数的累积量。

简单来说，就是把这个区域划分成无数个小的部分，对每个小部分上的函数值乘以小部分的面积，然后把这些乘积加起来。

接下来，我们探讨几种常见的二重积分计算方法。

直角坐标系下的计算方法是基础且重要的。

当积分区域是一个矩形时，计算相对简单。

假设积分区域为＄D ＝＼｛（x,y) ｜ a ＼leq x ＼leq b, c ＼leq y ＼leq d\｝＄，被积函数为＄f(x,y)＄，则二重积分可以表示为：＼＼iint_D f(x,y) ＼，dx\，dy ＝＼int_a^b ＼left(＼int_c^d f(x,y) ＼，dy ＼right)dx＼这意味着我们先对＄y$ 进行积分，把＄x$ 看作常数，得到一个关于＄x$ 的函数，然后再对＄x$ 进行积分。

如果积分区域不是矩形，而是由直线围成的一般区域，比如＄D ＝＼｛（x,y) ｜＼varphi_1(x) ＼leq y ＼leq ＼varphi_2(x)， a ＼leq x ＼leq b\｝＄，那么二重积分可以表示为：＼＼iint_D f(x,y) ＼，dx\，dy ＝＼int_a^b ＼left(＼int_{＼varphi_1(x)｝＾｛＼varphi_2(x)｝ f(x,y) ＼，dy ＼right)dx＼这种情况下，我们先对＄y$ 积分，然后对＄x$ 积分。

极坐标系下的计算方法在处理具有圆形或扇形特征的积分区域时非常有用。

在极坐标系中，点的坐标表示为＄（r,＼theta)＄，其中＄r$ 表示点到原点的距离，＄＼theta$ 表示极角。

如果积分区域可以用极坐标表示为＄D ＝＼｛（r,＼theta) ｜＼alpha ＼leq ＼theta ＼leq ＼beta, ＼varphi(＼theta) ＼leq r ＼leq ＼psi(＼theta)＼｝＄，被积函数为＄f(x,y) ＝ f(r\cos\theta, r\sin\theta)＄，那么二重积分可以表示为：＼＼iint_D f(x,y) ＼，dx\，dy ＝＼int_{＼alpha}＾｛＼beta} ＼left(＼int_{＼varphi(＼theta)｝＾｛＼psi(＼theta)｝ f(r\cos\theta, r\sin\theta) r ＼，dr ＼right)d\theta＼这里需要注意的是，多了一个＄r$ ，这是因为在极坐标下，面积元素＄dx\，dy$ 要换成＄r\，dr\，d\theta$ 。

二重积分简便计算方法
二重积分是微积分中的一种重要概念，用于计算平面图形内某一量的值。

但是，对于一些简单的图形，可以使用一些简便的方法来计算二重积分，大大缩短计算时间。

下面介绍几种二重积分简便计算方法。

1. 极坐标变换法
当被积函数在极坐标下具有简单的形式时，可以使用极坐标变换法来简化计算。

具体步骤如下：
（1）将直角坐标系下的积分区域用极坐标方程表示出来；
（2）求出相应的极坐标变换的雅可比行列式；
（3）将被积函数用极坐标表示；
（4）代入二重积分公式进行计算。

2. 对称性法
当积分区域具有对称性时，可以使用对称性法来简化计算。

具体步骤
如下：
（1）利用对称性将积分区域分成若干个部分；
（2）计算其中一部分的积分，然后将结果乘以对称部分的个数。

3. 矩形分割法
当积分区域为矩形形状时，可以使用矩形分割法来简化计算。

具体步骤如下：
（1）将积分区域分成若干个矩形；
（2）对每个矩形进行二重积分的计算，然后将结果相加。

以上三种方法是二重积分常用的简便计算方法，掌握这些方法可以在解决问题时事半功倍。

二重积分四则运算公式二重积分的定义是求某一域内的函数的积分，概念是由一重积分到二重积分扩展而来的，而二重积分的计算一般是采用一些公式进行运算。

这里，我们介绍一下二重积分中四则运算的公式，以便读者能够更准确、更方便地积分并得到想要的计算结果。

1.法二重积分加法的公式是：∫∫f(x,y)dxdy+∫∫g(x,y)dxdy=∫∫[f(x,y)+g(x,y)]dxdy其中，f(x,y)代表积分中的函数一，g(x,y)代表函数二，dxdy 代表积分求和，也就是把函数同时积分在一个面积域内，[f(x,y)+g(x,y)]不过是把两个函数相加而已。

2.法二重积分减法的公式是：∫∫f(x,y)dxdy-∫∫g(x,y)dxdy=∫∫[f(x,y)-g(x,y)]dxdy 其中，f(x,y)代表函数一，g(x,y)代表函数二，dxdy代表积分求和，也就是把函数同时积分在一个面积域内，[f(x,y)-g(x,y)]不过是把两个函数相减而已。

3. 乘法二重积分乘法的公式是：∫∫f(x,y)dxdy×∫∫g(x,y)dxdy=∫∫[f(x,y)g(x,y)]dxdy其中，f(x,y)代表函数一，g(x,y)代表函数二，dxdy代表积分求和，也就是把函数同时积分在一个面积域内，[f(x,y)g(x,y)]不过是把两个函数相乘而已。

4.法二重积分除法的公式是：∫∫f(x,y)dxdy÷∫∫g(x,y)dxdy=∫∫[f(x,y)÷g(x,y)]dxdy 其中，f(x,y)代表函数一，g(x,y)代表函数二，dxdy代表积分求和，也就是把函数同时积分在一个面积域内，[f(x,y)÷g(x,y)]不过是把两个函数相除而已。

以上就是二重积分四则运算的公式，它们都能够帮助人们快速、准确地算出二重积分。

在现实应用中，这些公式是实现计算机自动求积分的重要基础，对于域内的函数积分及数值求解有极大的帮助，值得大家反复研习、积极运用。