最优风险资产风险组合
- 格式:docx
- 大小:175.62 KB
- 文档页数:10
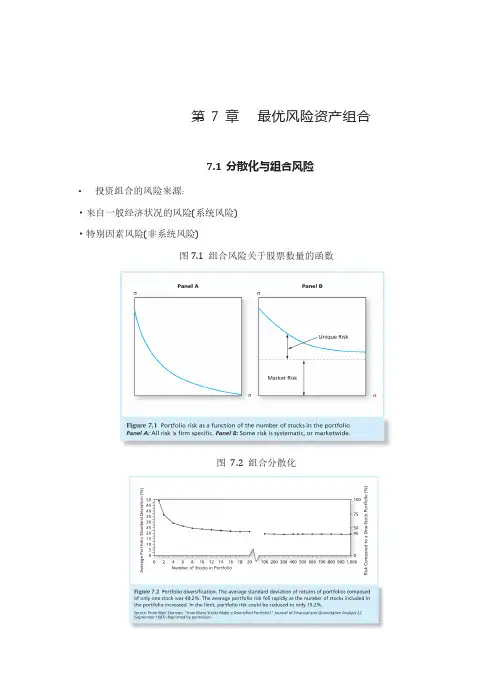
第7章最优风险资产组合7.1分散化与组合风险•投资组合的风险来源:·来自一般经济状况的风险(系统风险)·特别因素风险(非系统风险) 图7.1 组合风险关于股票数量的函数图7.2 组合分散化7.2 两个风险资产的组合设某一风险资产组合P 由长期债券组合D 和股票基金E 组成2222222222()()() 2(,)(,)211P D D E E P D D E E D E D E D E DE D E P D D E E D E D E DEDE E r w E r w E r w w w w Cov r r Cov r r w w w w σσσρσσσσσσσρρ=+=++=⇒=++-≤≤Q 则有:又:∴ρ越大,组合P 的方差越大 三个风险资产的组合112233()()()()p E r w E r w E r w E r =++2222222112233121,2131,3232,3222p w w w w w w w w w σσσσσσσ=+++++分散化的效果:如果协方差为负,组合的方差会降低,即使协方差为正,组合的标准差依然低于两个证券标准差的加权平均,除非两个证券是完全正相关221() DE P D D E E P D D E Ew w w w ρσσσσσσ==+=+若,则有:即:结论:ρ=1时组合P 的风险就是两个收益完全正相关资产标准差的加权平均。
221() -0,1DE P D D E E P D D E E D D E E E DD E D D E D Ew w w w w w w w w ρσσσσσσσσσσσσσσ=-=-=-=⇒==-=++若,则有:即:令结论:ρ=-1组合P 的风险可降至零11 1DE P D D E Ew w P ρσσσρ-<<<+<若,则有:结论:时组合的风险可有一定程度降低表7-1两个共同基金的描述性统计表7.2 不同相关系数下的期望收益与标准差图7.3组合期望收益关于投资比例的函数图7.4 组合标准差关于投资比例的函数最小方差组合由具有最小标准差的风险资产组成,这一组合的风险最低。



实验四:无风险资产与多种风险型资产最优投资组合的模型分析 一、实验目的通过上机实验,使学生充分理解Excel 软件系统管理和基本原理,掌握多资产投资组合优化的Excel 应用。
二、预备知识(一)相关的计算机知识: Windows 操作系统的常用操作;数据库的基础知识;Excel 软件的基本操作。
(二)实验理论预备知识现代资产组合理论发端于Markowitz(1952)提出的关于投资组合的理论。
该理论假设投资者只关心金融资产(组合)收益的均值(期望收益)和方差,在一定方差下追求尽可能高的期望收益,或者在一定的期望水平上尽可能降低投资收益的方差。
投资者的效用是关于投资组合的期望回报率和方差的函数,理性的投资者通过选择有效地投资组合以实现期望效用最大。
该理论第一次将统计学中期望与方差的概念引入投资组合的研究,提出用资产收益率的期望来衡量预期收益,用资产预期收益的标准差来度量风险的思想。
1、理论假设(Ⅰ)市场上存在n ≥2种风险资产,资产的收益率服从多元正态分布,允许卖空行为的存在。
{}12(,,,)T n ωωωωω=,代表投资到这n 种资产上的财富(投资资金)相对份额,它是n 维列向量,有11=∑=ni i ω,允许0<i ω,即卖空不受限制。
(Ⅱ) 用e 表示所有由n 种风险资产的期望收益率组成的列向量。
12(,,,)T n e R R R R == (1)p r 表示资产组合的收益率,)(p r E 和)(p r σ分别为资产组合p 的期望收益率和收益率标准差。
∑=⋅=⋅=ni ii Tp e r E 1)(μωω (2)(Ⅲ)假设n 种资产的收益是非共线性的(其经济意义为:没有任何一种资产的期望收益率可以通过其他资产的线性组合来得到,它们的期望收益是线性独立的。
)。
这样它们的方差-协方差矩阵可以表示为:⎪⎪⎭⎪⎪⎬⎫⎪⎪⎩⎪⎪⎨⎧=nn n n n n Q σσσσσσσσσ212222111211 (3)由于总是假定非负的总体方差,它还必须是一个正定矩阵,即对于任何非0的n 维列向量a ,都有0T a Qa >。

第7章最优风险资产组合一、习题1.以下哪些因素反映了单纯市场风险?a.短期利率上升b.公司仓库失火c.保险成本增加d.首席执行官死亡e.劳动力成本上升答:ae。
2.当增加房地产到一个股票、债券和货币的资产组合中,房地产收益的哪些因素影响组合风险?a.标准差b.期望收益c.和其他资产的相关性答:ac。
房地产被添加到组合中后,在投资组合中有四个资产类别:股票、债券、现金和房地产。
现在投资组合的方差包括房地产收益的方差项和房地产收益与其他三个资产类别之间的协方差项。
因此,房地产收益的方差(或标准差)和房地产收益与其他资产类别收益之间的相关性影响着投资组合的风险。
(注意房地产收益和现金收益之间的相关性很有可能为零。
)3.以下关于最小方差组合的陈述哪些是正确的? a .它的方差小于其他证券或组合 b .它的期望收益比无风险利率低 c .它可能是最优风险组合 d .它包含所有证券 答:a 。
4.用以下数据回答习题4~10:一个养老金经理考虑3个共同基金。
第一个是股票基金,第二个是长期政府和公司债基金,第三个是短期国债货币基金,收益率为8%。
风险组合的概率分布如表7-1所示。
表7-1基金的收益率之间的相关系数为0.1。
两种风险基金的最小方差投资组合的投资比例是多少?这种投资组合收益率的期望值与标准差各是多少?答:机会集的参数为:E (r S )=20%,E (r B )=12%,σS =30%,σB =15%,ρ=0.10。
根据标准差和相关系数,可以推出协方差矩阵(注意()ov ,S B S B C r r ρσσ=⨯⨯):债券 股票 债券 225 45 股票45900最小方差组合可由下列公式推出:w Min(S)=()()()222,225459002252452,B S BS B S BCov r rCov r rσσσ−−=+−⨯+−=0.1739w Min(B)=1-0.1739=0.8261最小方差组合的均值和标准差为:E(r Min)=(0.1739×0.20)+(0.8261×0.12)=0.1339=13.39%σMin=()122222w w2w w ov,S S B B S B S BC r rσσ/⎡⎤++⎣⎦=[(0.17392×900)+(0.82612×225)+(2×0.1739×0.8261×45)]1/2=13.92%5.制表并画出这两种风险基金的投资可行集,股票基金的投资比率从0~100%按照20%的幅度增长。



![单指数模型的最优风险投资组合研究[权威精品]](https://uimg.taocdn.com/0079ae32cdbff121dd36a32d7375a417866fc1a4.webp)
单指数模型的最优风险投资组合研究-权威精品本文档格式为WORD,感谢你的阅读。
最新最全的学术论文期刊文献年终总结年终报告工作总结个人总结述职报告实习报告单位总结摘要:本文根据威廉·夏普的单指数模型建立最优风险投资组合,选取2008年1月至2012年12月间的沪深300指数月收益率和来自IT产业、零售产业和能源产业的6只股票月收益率进行回归分析,同时预测股票的α和β值,根据回归和预测数据进行最优风险组合的构建。
关键词:单指数模型;回归分析;最优风险投资组合1.单指数模型和最优风险投资组合的构建1.1单指数模型与马科维茨资产组合选择模型相比,单指数模型克服了马克维茨模型必须使用大量数据的缺点,能更好地解决GIGO 问题。
使得单指数模型具有可操作性的合理方法是将某个有代表性的大盘综合指数的收益率视为共同宏观经济因素,也就是使用市场指数来代表共同经济因素,这样任何单一证券的超额收益率就只与这一共同的宏观经济因素有关。
其回归方程为:Ri(t)=αi+βiRM(t)+ei(t)(1)式中:Ri(t)代表t时期内某只证券的超额收益RM(t)代表t时期内市场指数的超额收益αi代表市场超额收益为零时证券的期望超额收益βi是证券对市场的敏感程度系数ei(t)代表t时期内实际收益率与估计值之间的残差,均值为零所以证券的期望超额收益为:E(RI)=αI+βiE(RM)在单指数模型中某只证券的风险分为系统性风险和非系统性风险,即σ2i=β2iσ2M+σ2(ei)(2)因此,对于单指数模型的计算,我们只需要以下数据:1) n个αi、βi、σ2(ei)的估计值2)一个E(RM)和一个σ2M的估计值1.2单指数模型的最优风险投资组合的构建根据市场指数的风险溢价和积极组合的α值,可以得出最优风险投资组合的风险溢价:以上是运用单指数模型计算最优风险投资组合的完整流程,一共需要(3n+2)估计值,与马科维茨资产组合选择模型相比大大简化了需要估计的参数。
最优风险资产的风险组合8.1 分散化与资产组合风险分散化(diversification):投资者如果不是进行单一证券的投资,而是投资于由两种以上证券构成的投资组合。
如果构成投资组合的证券不是完全正相关,那么投资组合就会降低风险,在最充分分散条件下还保存的风险是市场风险(market risk),它源于与市场有关的因素,这种风险亦称为系统风险(systematic risk),或不可分散风险(nondiversifiable risk)。
相反,那些可被分散化消除的风险被称为独特风险(unique risk)、特定公司风险(firm-specific risk)、非系统风险(nonsystematic risk)或可分散风险(diversifiable risk)资产组合中股票的个数8.2 两种风险资产的资产组合两种资产的资产组合较易于分析,它们体现的原则与思考可以适用于多种资产的资产组合,我们将考察包括的资产组合,一个为只投资于长期债券的资产组合D,另一个专门投资于股权证券的股票基金E,两个共同基金的数据列表(8-1)如下:债券股权期望收益率E(r)(%)8 13 标准差为σ(%) 12 20 协方差Cov(r D, r E) 72相关系数ρDE 0.3投资于债券基金的份额为w D,剩下的部分为w E=1- w D投资于股票基金,这一资产组合的投资收益r p 为:r p=w D r D,+ w E r E r D为债券基金收益率r E为股权基金的收益率。
资产组合的期望收益:E(r p)=w D E(r D)+ w E E(r E)两资产的资产组合的方差:σ2P =W D2σ2D+ W E2σE2+2W D W E Cov(r D,r E)根据第六章式[6-5]得:ρDE=[Cov(r r D, r E)]/[ σD*σE]Cov(r r D, r E)= ρDE*σD*σE所以:σ2P =W D2σ2D+ W E2σE2+2W D W EρDE*σD*σE 当完全正相关时:ρDE=1σ2P =W D2σ2D+ W E2σE2+2W D W E*σD*σE=(W DσD+ W E σE)2资产组合的标准差σP =W DσD+ W EσE当完全负相关时:ρDE=-1σ2P =W D2σ2D- W E2σE2+2W D W E*σD*σE=(W DσD- W E σE)2资产组合的标准差σP =︱W DσD- W EσE︱当完全负相关时:ρDE=-1 则W DσD- W EσE=0 因为w E=1- w D 两式建立联立方程得运用表(8-1)中的债券与股票数据得:E(r p)=w D E(r D)+ w E E(r E)= 8w D+ 13w Eσ2P =W D2σ2D+ W E2σE2+2W D W EρDE*σD*σE=122 W D2+ 202W E2+2*12*20*0.3*W D W E=144 W D2+400 W E2+144 W D W E表8-3 不同相关系数下的期望收益与标准差给定相关性下的资产组合的标准差W D We E(rp) ρ=-1ρ=0ρ=0.3ρ=1 0113202020200.10.912.516.818.0399618.3956519.20.20.81213.616.17916.8760218.40.30.711.510.414.4554515.4660917.60.40.6117.212.924414.1985916.80.50.510.5411.661913.11488160.60.4100.810.762912.2637715.20.70.39.5 2.410.3227911.6961514.40.80.29 5.610.411.4542613.60.90.18.58.810.9836211.5585512.810812121212图8-3中,当债券的投资比例从0-1(股权投资从1-0)时,资产组合的期望收益率从13%(股票的收益率)下降到8%(债券的收益率)1.0 0 -1.0 债券如果w D〉1,w E〈0时,此时的资产组合策略是做一股权基金空头,并把所得到的资金投入到债券基金。

第5章最优风险资产组合一、单项选择题1.最充分分散化投资也不能消除的风险称为()A、市场风险B、非系统性风险C、公司特有风险D、独特风险2.如果两种证券不是完全正相关,那么投资组合的标准差和该组合这两种证券的标准差的加权平均相比()A、更大B、无变化C、更小D、不确定3.其它条件不变,人们更愿意在投资组合中增加与现有资产()的资产A、正相关B、不相关C、负相关D、完全正相关4.下面两种资产构成的组合中,资产组合标准差可能降到最低的是()A、ρ=-1B、ρ=0C、ρ=0.3D、ρ=15.资本配置线与投资可行集处于什么位置时可得到最高且可行的报酬与波动性比率()A、相交B、相切C、相离D、任意位置6.资本配置线与风险资产组合可行集相切的点是()A、最优完全投资组合B、最优风险投资组合C、次优完全投资组合D、次优风险投资组合7.有风险资产组合的方差是( )。
a. 组合中各个证券方差的加权和b. 组合中各个证券方差的和c. 组合中各个证券方差和协方差的加权和d. 组合中各个证券协方差的加权和8.当其他条件相同,分散化投资在那种情况下最有效?( )a. 组成证券的收益不相关b. 组成证券的收益正相关c. 组成证券的收益很高d. 组成证券的收益负相关9.假设有两种收益完全负相关的证券组成的资产组合,那么最小方差资产组合的标准差为一个_____的常数。
( )a. 大于零b. 等于零c. 等于两种证券标准差的和d. 等于110.考虑两种有风险证券组成资产组合的方差,下列哪种说法是正确的?( )a. 证券的相关系数越高,资产组合的方差减小得越多b. 证券的相关系数与资产组合的方差直接相关c. 资产组合方差减小的程度依赖于证券的相关性11、如果投资组合中包含有50只股票,证券分析师需要得到的协方差估计值的个数为()。
A、50B、100C、1225D、251012.由两只证券组合成的所有可能的资产组合,它们的期望收益率和标准差组成的直线是_____。
第8章最优风险资产组合下面的数据可用于第1至第8题:一位养老基金经理正在考虑三种共同基金。
第一种是股票基金,第二种是长期政府债券与公司债券基金,第三种是回报率为8% 的以短期国库券为内容的货币市场基金。
这些风险基金的概率分布如下:名称期望收益率(% )标准差(% )股票基金(S)20 30债券基金(B)12 15基金回报率之间的相关系数为0.10。
1. 两种风险基金的最小方差资产组合的投资比例是多少?这种资产组合回报率的期望值与标准差各是多少?2. 制表并画出这两种风险基金的投资机会集合,股票基金的投资比率从0%到100%,按照20%的幅度增长。
3. 从无风险回报率到机会集合曲线画一条切线,你的图表表现出来的最优资产组合的期望收益与标准差各是多少?4. 计算出最优风险资产组合下每种资产的比率以及期望收益与标准差。
5. 最优资本配置线下的最优酬报与波动性比率是多少?6. 投资者对他的资产组合的期望收益率要求为14%,并且在最佳可行方案上是有效率的。
a. 投资者资产组合的标准差是多少?b. 投资在短期国库券上的比率以及在其他两种风险基金上的投资比率是多少?7. 如果投资者只用两种风险基金进行投资并且要求14%的收益率,那么投资者资产组合中的投资比率是怎样安排的?把现在的标准差与第6题中的相比,投资者会得出什么结论?8. 假设投资者面对同样的机会集合,但是不能够借款。
投资者希望只由股票与债券构成期望收益率为24%的资产组合。
合适的投资比率是多少?由此的标准差是多少?如果投资者被允许以无风险收益率借款,那么投资者的标准差可以降低多少?9. 股票提供的预期收益率为18%,其标准差为22%。
黄金提供的预期收益率为10%,标准差为30%。
a. 根据黄金在平均收益率和波动性上的明显劣势,有人会愿意持有它吗?如果有,请用图形表示这样做的理由。
b. 由上面的数据,再假设黄金与股票的相关系数为1,重新回答a问题。
画图表示为什么有人会或不会在他的资产组合中持有黄金。
最优风险资产的风险组合分散化与资产组合风险分散化(diversification):投资者如果不是进行单一证券的投资,而是投资于由两种以上证券构成的投资组合。
如果构成投资组合的证券不是完全正相关,那么投资组合就会降低风险,在最充分分散条件下还保存的风险是市场风险(market risk),它源于与市场有关的因素,这种风险亦称为系统风险(systematic risk),或不可分散风险(nondiversifiable risk)。
相反,那些可被分散化消除的风险被称为独特风险(unique risk)、特定公司风险(firm-specific risk)、非系统风险(nonsystematic risk)或可分散风险(diversifiable risk)资产组合中股票的个数两种风险资产的资产组合两种资产的资产组合较易于分析,它们体现的原则与思考可以适用于多种资产的资产组合,我们将考察包括的资产组合,一个为只投资于长期债券的资产组合D,另一个专门投资于股权证券的股票基金E,两个共同基金的数据列表(8-1)如下:债券 股权 期望收益率E(r)(%) 8 13 标准差为σ(%) 12 20 协方差Cov(r D, r E ) 72 相关系数ρDE投资于债券基金的份额为w D ,剩下的部分为w E =1- w D 投资于股票基金,这一资产组合的投资收益r p 为: r p =w D r D,+ w E r Er D 为债券基金收益率 r E 为股权基金的收益率。
资产组合的期望收益:E(r p )=w D E(r D )+ w E E(r E )两资产的资产组合的方差: σ2P =W D 2σ2D + W E 2σE 2+2W D W E Cov(r D ,r E ) 根据第六章式[6-5]得:ρDE =[Cov(r r D, r E )]/[ σD *σE ] Cov(r r D, r E )= ρDE *σD *σE所以:σ2P =W D 2σ2D + W E 2σE 2+2W D W E ρDE *σD *σE当完全正相关时:ρDE =1σ2P =W D 2σ2D + W E 2σE 2+2W D W E *σD *σE =(W D σD + W E σE )2资产组合的标准差 σP =W D σD + W E σE 当完全负相关时:ρDE =-1σ2P =W D 2σ2D - W E 2σE 2+2W D W E *σD *σE =(W D σD - W E σE )2资产组合的标准差σP =︱W D σD - W E σE ︱当完全负相关时:ρDE =-1 则W D σD - W E σE =0 因为 w E =1- w D 两式建立联立方程得运用表(8-1)中的债券与股票数据得:E(r p )=w D E(r D )+ w E E(r E )= 8w D + 13w Eσ2P =W D 2σ2D + W E 2σE 2+2W D W E ρDE *σD *σE=122 W D 2+ 202W E 2+2*12*20**W D W E =144 W D 2+400 W E 2+144 W D W E表8-3 不同相关系数下的期望收益与标准差给定相关性下的资产组合的标准差 WDWe E(rp) ρ=-1 ρ=0 ρ= ρ=1 01132020202012114161091 08 12 12 12 12图8-3中,当债券的投资比例从0-1(股权投资从1-0)时,资产组合的期望收益率从13%(股票的收益率)下降到8%(债券的收益率)1.0 0 -1.0 债券如果wD 〉1, wE〈0时,此时的资产组合策略是做一股权基金空头,并把所得到的资金投入到债券基金。
这将降低资产组合的期望收益率。
如w D =2和wE=-1时,资产组合的期望收益率为 2*8+(-1)*13=3%如果wD〈0, wE〉1时,此时的资产组合策略是做一债券基金空头,并把所得到的资金投入到股权基金。
如wD =-1和wE=2时,资产组合的期望收益率为 -1*8+2*13=16%改变投资比例会影响资产组合的标准差。
根据表(8-3),及公式(8-5)和资产组合的相关系数分别假定为及其它ρ计算出的不同权重下的标准差。
下图显示了标准差和资产组合权重的关系。
当ρDE=的实线,当股权投资比例从0增加到1时,资产组合的标准差首先因分散投资而下降,但随后上升,因为资产组合中股权先是增加,然后全部投资于股权。
那种资产组合的标准差的最小水平时可接受的通过计算机电子表格求得准确解W MIN (D)= W MIN (E)= σMIN =%投资比例的函数,这条线经过w D =1和w E =1两个(两点)非分散化的资产组合。
当ρ=1时,标准差是组合中各资产标准差的简单加权平均值,直线连接非分散化下的全部是债券或全部是股票的资产组合,即w D =1或w E =1,表示资产组合中的资产完全正相关。
时,相关系数越低,分散化就越有效,资产组合风险就越低,最小的标准差为%,低于组合中各个资产的标准差(见表8-1)。
W D =σE /(σD + σE ) = w E =σD /(σD + σE )= σMIN =0图8-5。
对于任一对投资比例为w D ,w E 的资产,我们可以从图8-3得到期望收益率;从图8-4中得到标准差。
股票基金权重 资产组合标准差是投资比例的函数图8-5中的曲线;当ρ=时的资产组合机会集合(Portfolio opportunity set ).我们称它为资产组合机会集合是因为它显示了有两种有关资产构造的所有资产组合的期望收益与标准差。
其他线段显示的是在其他相关系数值下资产组合的机会集合当ρ=1时 为黑色实线连接的两种基金。
对分散化没有益处当ρ=0时 为虚线抛物线,可以从分散化中获得最大利益当ρ=-1时 资产组合机会集合是线性的,它提供了一个完全对冲的机会,此时从分散化中可以获得最大的利益。
并构造了一个零方差的资产组合资产在股票、债券与国库券之间的配置上节内容主要讨论了如何在股票、债券市场进行资金配置,在此基础上,我们引入第三种选择—无风险的资产组合。
对股票、债券与无风险货 14131110 8 58-5 资产组合的期望收益是标准差的函数币市场证券之间的配置。
最优风险资产组合:两种风险资产和一种无风险资产根据表8-1 第一条可能的资本配置线通过最小方差的资产组合A,(债券与股票)即由W MIN (D)= W MIN (E)= 组成 σMIN =%。
资产组合A 期望收益率为:*8+*13=% 由于国库券利率为5%,报酬与波动性比率(REWARD-TO-VARIABILITY RATIO ), 资本配置线(CAL),表示投资者的所有可行的风险收益组合。
它的斜率S ,等于选择资产组合每增加一单位标准差上升的期望收益,即资本配置线的斜率为: S A =[E(r A )-r f ]/ σA =/=第二条可能的资本配置线通过最小方差的资产组合B,即由W MIN (D)= W MIN (E)= 组成σMIN =%。
资产组合B 期望收益率为:*8+*13=% 由于国库券利率为5%,报酬与波动性比例(REWARD-TO-VARIABILITY RATIO ),即资本配置线的斜率为: S A =[E(r B )-r f ]/ σB =/=对图8-6 可理解为,由两条资本配置线,求得的望收益率与最小方差,在其相关系数值下资产组合的机会集合中,在图中找到A,B 两点;我们让资本配置线变动,最终使它的斜率与投资机会集合的斜率一致,从而,获得具有最高的、可行的报酬与波动性比率的资本配置线。
相切的资产组合P (见图8-7)就是加入国库券的最优风险资产组合。
E(r p )=11%,σP =%14 131110 81811 84 08-7 最优资本配置线的债务与股权基金的机会集合与最优风险资产组合如何解决两种风险资产和一种无风险资产的组合问题的通用方法: 在这种情况下,关键是推导出关于最优组合各项资产权重,从而使确定最优化资产组合思路:找出权重w D 和w E ,以使资本配置线的斜率最大即S p =[E(r P )-r f ]/σp对于包含两种风险资产的资产组合P ,它的期望收益和标准差为E(r p )=w D E(r D )+ w E E(r E )σ2P =W D 2σ2D + W E 2σE 2+2W D W E ρDE *σD *σE σ2P = W D 2σ2D + W E 2σE 2+2 w D w E Cov(r D , r E ) =122 W D 2+ 202W E 2+2*12*20**W D W E=144 W D 2+400 W E 2+2*72 W D W Ew D +w E =1在共有两种风险资产的条件下,最优风险资产组合(optimal risky portfolio )P 的权重可表示如下:(对以上方程联立求得) Max S p =[E(r p )-r f ]/ σp因为∑=1Wi ,则有,212222)()],()1(2)1([)1()(E D D D E D D D fD D D r rE p r r Cov w w w w r w r E w MaxS pfp -+-+--+==-σσσ用w D 对S p 求导 w E ,令导数位零:,解w D),(]2)()([])([])([),()]([])([222E D f E D D f E E f D E D f E E f D D r r Cov r r E r E r r E r r E r r Cov r r E r r E w -++-+----=σσσw E =1-w D把数带进去得:w D = w E =从而,求得: E(r p )=w D E(r D )+ w E E(r E )=11%σP =(W D 2σ2D + W E 2σE 2+2W D W E ρDE *σD *σE )1/2=%这个最优风险资产组合的资本配置线的斜率为:S p =该斜率大于任一可能的其它资产组合的斜率。
因此它是最优风险资产组合的资本配置线的斜率。
在第七章中,在给定最优风险资产组合和有这个资产组合与国库券产生的资产配置线下,我们找到了一个最优的完整资产组合。
我们以构造了一个最优风险资产组合P ,如果我们用一个个人的投资风险厌恶程度A 来计算投资于完整资产组合的风险部分的最优比例。
一个风险厌恶相关系数A=4的投资者,他在资产组合P 中的投资头寸为7439.02.14401.051101.0)(22=⨯⨯-=⨯-=Pfp A r r E y σ因此,投资者将74。