同坡屋面交线
- 格式:ppt
- 大小:1.91 MB
- 文档页数:16








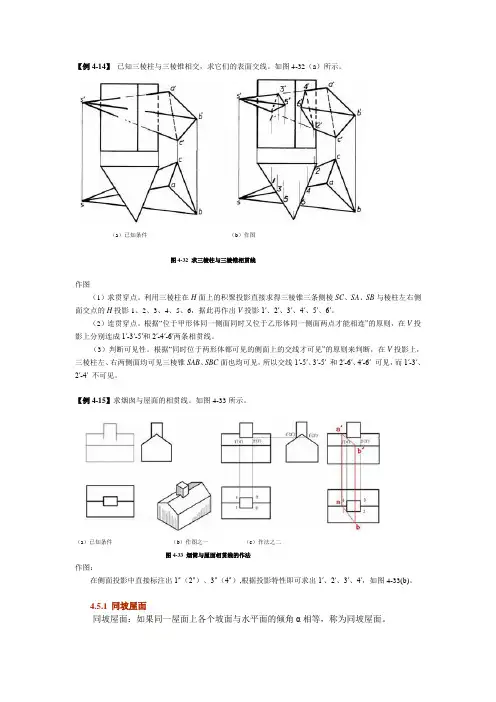
【例4-14】已知三棱柱与三棱锥相交,求它们的表面交线。
如图4-32(a)所示。
(a)已知条件(b)作图图4-32 求三棱柱与三棱锥相贯线作图(1)求贯穿点。
利用三棱柱在H面上的积聚投影直接求得三棱锥三条侧棱SC、SA、SB与棱柱左右侧面交点的H投影1、2、3、4、5、6,据此再作出V投影1′、2′、3′、4′、5′、6′。
(2)连贯穿点。
根据“位于甲形体同一侧面同时又位于乙形体同一侧面两点才能相连”的原则,在V投影上分别连成1′-3′-5′和2′-4′-6′两条相贯线。
(3)判断可见性。
根据“同时位于两形体都可见的侧面上的交线才可见”的原则来判断,在V投影上,三棱柱左、右两侧面均可见三棱锥SAB、SBC面也均可见,所以交线1′-5′、3′-5′ 和2′-6′、4′-6′ 可见,而1′-3′、2′-4′ 不可见。
【例4-15】求烟囱与屋面的相贯线。
如图4-33所示。
(a)已知条件(b)作图之一(c)作法之二图4-33 烟筒与屋面相贯线的作法作图:在侧面投影中直接标注出1″(2″)、3″(4″),根据投影特性即可求出1′、2′、3′、4′,如图4-33(b)。
4.5.1同坡屋面同坡屋面:如果同一屋面上各个坡面与水平面的倾角α相等,称为同坡屋面。
(a)立体图(b)投影图图4-34 同坡屋面同坡屋面有如下特点:1.坡屋面如前后檐口线平行且等高时,前后坡面必相交成水平的屋脊线,屋脊线的H 投影,必平行于檐口线的H 投影,且与檐口线等距。
2.檐口线相交的相邻两个坡面,必相交于倾斜的斜脊线或天沟线。
3.在屋面上如果有两斜脊、两天沟、或一斜脊一天沟相交于一点,则必有第三条屋脊线通过该点。
作同坡屋面的投影图,可根据同坡屋面的投影特点,直接求得水平投影,再根据各坡面与水平面的倾角求得V 面投影以及W 面投影。
【例4-16】已知屋面倾角α和屋面的平面形状,如图4-35(a)所示,求屋面的V、W投影和屋面交线。
作图:(1)在屋面平面图形上经每一屋角作45o分角线。

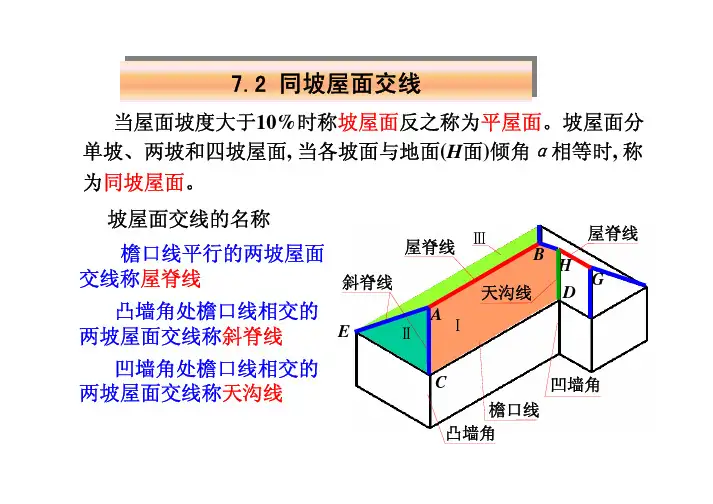
7.2 同坡屋面交线7.2 同坡屋面交线凸墙角檐口线凹墙角斜脊线CE 屋脊线AB 屋脊线GH天沟线D同坡屋面交线特点:(1) 两坡屋面的檐口线平行且等高时, 交成的水平屋脊线的H 投影与该两檐口线的H 投影平行且等距; (2) 檐口线相交的相邻两个坡面交成的斜脊线或天沟线, 它们的H 投影为两檐口线H 投影夹角的平分线。
(3) 在屋面上如果有两斜脊、两天沟、或一斜脊一天沟相交于一点, 则该点上必然有第三条线即屋脊线通过。
(1)作屋面交线的H 投影(2)作屋面的例7-10已知四坡屋面的倾角α=30°及檐口线的投影, 求屋面交线的H 投影和屋面的V 、W 投影。
例7-10已知四坡屋面的倾角α=30°及檐口线的投影, 求屋面交线的H 投影和屋面的V 、W 投影。
投影分析:同一周界不同尺寸的四种典型的屋面①ab<ef②ab=ef二、平面立体与平面立体相贯二、平面立体与平面立体相贯三、平面立体与曲面立体相贯三、平面立体与曲面立体相贯四、曲面立体与曲面立体相贯四、曲面立体与曲面立体相贯一、基本概念一、基本概念7-3 相贯线7-3相贯线一、基本概念一、基本概念二、平面立体与平面立体相贯二、平面立体与平面立体相贯2.相贯线可见性判别原则只有位于两形体都可见的棱面上的交线,才是可见的。
只要有一个棱面不可见,棱面上的交线就不可见。
3.求相贯线的一般步骤(1)投影分析:两形体投影特性,全贯,互贯,有几个贯穿点?(2)求交点:(3)依次连接各点:(4)判别可见性:相贯线可见性、两形体重影部分可见性。
三、平面立体与曲面立体相贯三、平面立体与曲面立体相贯[例7-5 ] 求两坡屋顶屋面与半圆拱屋面的交线。
解题步骤c' b' a' d' e'c" b"(d") a"(e")1.分析 实质是平面截割半圆 柱的截交线。
截交线的空间形 状是半个椭圆。