位移与时间关系全解

匀变速直线运动中位移与时间的关系一、匀速直线运动的位移时间关系1、匀速直线运动的速度始终保持不变，所以 vt x =2、从v-t 图像看位移匀变速直线运动的速度时间图像是一条平行于时间轴的直线即 v观察v-t 图像发现面积刚好就是 0v 位移，其中0v 是高，t 是底。

o t t 面积 位移二、匀变速直线运动的位移时间关系问题：匀速直线运动中位移大小可以用v-t 图像与坐标轴位的面积表示。

这个结论能否用于匀变速直线运动呢？1、我们知道对于变速运动的描述，最初使用的是平均速度即tx v ∆∆= ① 我们由①式出发稍微做一个变形就可以得到t v x ∆=∆ ② 2、我们来看一下匀变速直线运动的v-t 图像v0vo t我们观察图形会发现是一个梯形，所以我们不能用底乘以高即0v t 表示示其面积，那为什么就不行呢？因为这个图像中我们可以看出来从0到t 时刻存在一个很大的速度变化量即v ∆。

若从梯形中间做一条线，将其一分为二，我们在观察，还是不想矩形，但是会发现看其中一半是v ∆变小了，如果我们一直这样分下去会发现对一个细长的小梯形来说v ∆ 0，也就是说这个细长的梯形就可以看做一个矩形了，那么我们就可以用他的面积来表示位移的大小了。

于是我们就将梯形划分成许多细长的小梯形，所有小梯形的面积之和就是这段时间内物体的位移大小，也是整个梯形的面积。

故我们可以用梯形的面积来代表晕变速直线运动的位移大小。

所以我们求位移就可以通过求解梯形的面积。

解梯形的面积高下底上底⨯+==2s x t v v x t ⨯+=20––––––③高中位线⨯==s xt v x t ⨯=2––––––④ 因为at v v t +=0，所以我们将③式做一个简单的变形会得到2021at t v x += 这就是匀变速直线运动中位移与时间的关系，即位移公式3.对比将 ④三式进行对比会发现202t tv v v v +== 即中间时刻的速度等于平均速度等于初末速度之和的一半例：汽车刹车前的速度0v =5m/s ，a=-0.42s m ,求（1）开始刹车后20s 内滑行的距离？（2）汽车从刹车开始，位移x=30m 所用的时间？（3）在静止前2.5s 内滑行的距离？解：（1）错解：由2021at t v x +=可知x =5⨯202204.021⨯⨯-=20m 正解：法1：由a v at v v t 0t 0-v t =+=可知刹车制停的时间 又已知s m v /50= 2/4.0s m a -= 0=t v故t=12.5s 由于12.5<20，所以在t=12.5s 以后车就静止不动了。

第六讲位移与时间的关系知识点一、位移时间公式[提出问题]1.在匀变速直线运动中，虽然速度时刻变化，但只要时间足够小，速度的变化就非常小，如果把每一小段△t 内的运动看做匀速运动，则矩形面积之和等于各段匀速直线运动的位移。

如果把整个运动过程划分得非常非常细，当△t→0时，各矩形面积之和趋近于v-t 图线下面的面积，如图所示。

设初速度为v 0，加速度为a ，试通过V-t 图像推导其位移公式。

答案：方法一：用图形推导由前面的讨论可知，当时间间隔分割得足够小时，折线趋近于直线AP ，由此可以求出匀变速运动在时间t 内的位移，它在数值上等于直线AP 下方的梯形OAPQ 的面积(如图丙)．这个面积等于21201122S S S OA OQ AR RP v t at =+=⨯+⨯=+，即位移2012x v t at =+这就是匀变速直线运动的位移公式．方法二：用公式推导由于位移x vt =，而02t v v v +=，又0t v v at =+，故002v v at x t ++=⨯，即2012x v t at =+．[要点提炼]1.匀变速直线运动的位移与时间的关系：x＝v0t＋12at22.当v0＝0时，x＝12at2(由静止开始的匀加速直线运动)3.当a＝0时，x＝v0t(匀速直线运动)4.公式中x、v0、a都是矢量，应用时必须选取统一的正方向．若选v0方向为正方向，则：物体加速，a取正值；物体减速，a取负值．若位移为正值，位移的方向与正方向相同；若位移为负值，位移的方向与正方向相反．5.公式x＝v0t＋12at2只适用于匀变速直线运动[经典例题]1.做匀加速直线运动的物体初速度是0.50m/s，加速度是20.10m/s，那么第4s末的瞬时速度4v=____，头4秒内的平均速度4v=____，4秒内通过的位移4s=___，第4秒内通过的位移IVs=____。

【答案】0.90m/s0.70m/s 2. 80 m0.85m【详解】[1]第4s末的瞬时速度为4040.90m/sv v at =+=[3][2]头4s 内的位移为240441 2.80m 2s v t at =+=则头4s 内的平均速度为4440.70m /s s v t ==[4]头3s 内的位移为230331 1.95m 2s v t at =+=则第4s 内通过的位移为2.一物体做初速度为零的匀加速直线运动，加速度为a ＝2m/s 2，求：(1)第5s 末物体的速度多大？(2)前4s 的位移多大？(3)第4s 内的位移多大？解析(1)第5s 末物体的速度由v t ＝v 0＋at 1得v 1＝0＋2×5m/s ＝10m/s(2)前4s 的位移由x 1＝v 0t ＋12at 2得x 1＝0＋12×2×42m ＝16m (3)物体第3s 末的速度v 2＝v 0＋at 2＝0＋2×3m/s ＝6m/s则第4s 内的位移x 2＝v 2t 3＋12at 23＝6×1m ＋12×2×12m ＝7m 答案(1)10m/s (2)16m (3)7m3.做匀变速直线运动的物体，在一段时间t 内的平均速度等于这段时间内_____的瞬时速度，还等于这段时间初、末速度矢量和的一半。

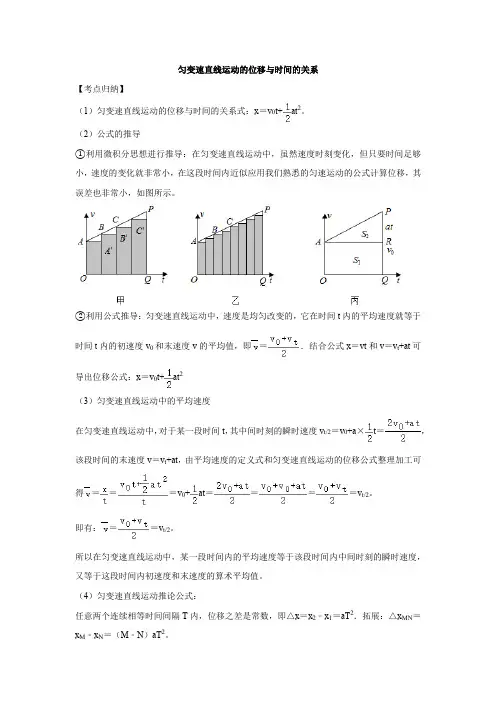
匀变速直线运动的位移与时间的关系【考点归纳】（1）匀变速直线运动的位移与时间的关系式：x＝v0t+at2。

（2）公式的推导①利用微积分思想进行推导：在匀变速直线运动中，虽然速度时刻变化，但只要时间足够小，速度的变化就非常小，在这段时间内近似应用我们熟悉的匀速运动的公式计算位移，其误差也非常小，如图所示。

②利用公式推导：匀变速直线运动中，速度是均匀改变的，它在时间t内的平均速度就等于时间t内的初速度v0和末速度v的平均值，即＝．结合公式x＝vt和v＝v t+at可导出位移公式：x＝v0t+at2（3）匀变速直线运动中的平均速度在匀变速直线运动中，对于某一段时间t，其中间时刻的瞬时速度v t/2＝v0+a×t＝，该段时间的末速度v＝v t+at，由平均速度的定义式和匀变速直线运动的位移公式整理加工可得＝＝＝v0+at＝＝＝＝v t/2。

即有：＝＝v t/2。

所以在匀变速直线运动中，某一段时间内的平均速度等于该段时间内中间时刻的瞬时速度，又等于这段时间内初速度和末速度的算术平均值。

（4）匀变速直线运动推论公式：任意两个连续相等时间间隔T内，位移之差是常数，即△x＝x2﹣x1＝aT2．拓展：△x MN＝x M﹣x N＝（M﹣N）aT2。

推导：如图所示，x1、x2为连续相等的时间T内的位移，加速度为a。

【命题方向】例1：对基本公式的理解汽车在平直的公路上以30m/s的速度行驶，当汽车遇到交通事故时就以7.5m/s2的加速度刹车，刹车2s内和6s内的位移之比（）A.1：1B.5：9C.5：8D.3：4分析：求出汽车刹车到停止所需的时间，汽车刹车停止后不再运动，然后根据位移时间公式求出2s内和6s内的位移。

解：汽车刹车到停止所需的时间＞2s所以刹车2s内的位移＝45m。

t0＜6s，所以刹车在6s内的位移等于在4s内的位移。

＝60m。

所以刹车2s内和6s内的位移之比为3：4．故D正确，A、B、C错误。

第二章匀变速直线运动的研究匀变速直线运动位移与时间的关系情境导入舰载机在航空母舰的甲板上起飞是，在弹射系统的作用下获得一定的速度，然后在甲板上继续加速一段距离便可达到起飞的速度。

知识点一：匀速直线运动的位移1.做匀速直线运动的物体在时间t内的位移：x＝vt 。

2．做匀速直线运动的物体，其v-t图象是一条平行于时间轴的直线，其位移在数值上等于v-t图线与对应的时间轴所包围的矩形的面积，如图所示：（1）当“面积”在t轴上方时，位移取正值，这表示物体的位移与规定的正方向相同；（2）当“面积”在t轴下方时，位移取负值，这表示物体的位移与规定的正方向相反。

知识点二：匀变速直线运动的位移1．微元法与极限思想的应用在匀变速直线运动中，由加速度的定义易得速度的变化量Δv＝a·Δt，只要时间足够短，速度的变化量就非常小，在非常短的时间内，我们就可以用熟悉的匀速直线运动的位移公式近似计算匀变速直线运动的位移。

如图所示，甲图中与Δt对应的每个小矩形的面积就可以看做Δt时间内的位移。

如果把每一小段Δt内的运动看做匀速直线运动，则各小矩形面积之和等于各段Δt时间内做匀速直线运动的位移之和。

时间Δt越短，速度变化量Δv 就越小，我们这样计算的误差也就越小。

当Δt →0时，各矩形面积之和趋近于v -t 图象与时间轴所围成的面积。

由梯形面积公式得x ＝(v 0＋v )·t2在任何运动中都有x ＝·t因此＝v 0＋v 2(适用匀变速直线运动)把v ＝v 0＋at 代入x ＝(v 0＋v )·t2得x ＝v 0t ＋12at 22．x ＝v 0t ＋12at 2的理解公式的意义 反应了位移随时间的变化规律，不是路程随时间的变化规律 适用条件 仅适用于匀变速直线运动矢量性公式中x 、v 0、a 都是矢量，应用时必须选取统一的正方向，一般选v 0方向为正方向 特殊形式(1)当a ＝0时，x ＝v 0t (匀速直线运动)。

1 匀变速直线运动位移与时间的关系一、匀速直线运动的位移 1．位移公式：x ＝v t .2.位移在v －t 图像中的表示：对于匀速直线运动，物体的位移在数值上等于v －t 图线与对应的时间轴所包围的矩形的面积．如图1所示阴影图形的面积就等于物体在t 1时间内的位移．图1二、匀变速直线运动的位移某物体做匀变速直线运动，初速度为v 0，加速度为a ，其v －t 图像如图4所示．请计算物体在t 时间内的位移．答案 v －t 图线下面梯形的面积表示位移x ＝12(OC ＋AB )·OA把面积及各条线段换成其所代表的物理量，上式变成 x ＝12(v 0＋v t )t ① 又因为v t ＝v 0＋at ② 由①②式可得 x ＝v 0t ＋12at 2总结：匀变速直线运动的位移公式 (1)公式：x ＝v 0t ＋12at 2.(2)适用范围：匀变速直线运动(包括匀加速和匀减速直线运动)．公式的矢量性：公式x ＝v 0t ＋12at 2中x 是位移，而不是路程，v 0、a 也是矢量，有方向，一般以初速度v 0的方向为正方向，如果是匀加速直线运动，a 为正值；如果是匀减线运速直动，a 为负值． 算出的位移如果为正，说明与规定的方向相同，位移为负说明与规定的方向相反。

1.5匀变速直线运动位移和时间的关系公式的应用 (就是套一个或者两个公式)1 (多选)某质点的位移随时间变化的关系是x ＝4t ＋4t 2，x 与t 的单位分别为m 和s ，设质点的初速度为v 0，加速度为a ，下列说法正确的是.. ...A ．v 0＝4 m /s ，a ＝4 m/s 2B ．v 0＝4 m /s ，a ＝8 m/s 2C ．2 s 内的位移为24 mD ．2 s 末的速度为24 m/s2．(多选)一质点以一定的初速度向东做匀变速直线运动，其位移与时间的关系为x ＝10t －t 2 (m)，则... ... . A ．质点初速度为10 m/s B ．质点的加速度大小是1 m/s 2 C ．2 s 末的速度为6 m/sD ．在2 s 末，质点在出发点西边，距出发点24 m3．(位移公式)一辆汽车以2 m/s 2的加速度做匀减速直线运动，经过2 s(汽车未停下)，汽车行驶了36 m ．汽车开始减速时的速度是... ... A ．9 m /s B ．18 m/s C ．20 m /sD ．12 m/s4．飞机起飞的过程是由静止开始在平直跑道上做匀加速直线运动的过程．已知飞机在跑道上加速前进的距离为1 600 m 时离开地面，所用时间为40 s ，则飞机的加速度a 和离地速度v 分别为. A ．2 m /s 2 ,80 m/s B ．2 m /s 2, 40m/s C ．1 m /s 2, 40 m/sD ．1 m /s 2 ,80 m/s5．(多选)由静止开始做匀加速直线运动的火车，在第10 s 末的速度为2 m/s ，下列叙述中正确的是.... .... A ．前10 s 内通过的位移为10 m B ．每秒速度变化0.2 m/s C ．10 s 内平均速度为1 m/s D ．第10 s 内的位移为2 m6.一个物体从静止开始做匀加速直线运动，第1秒内的位移为2 m，则下列说法正确的是(D)A．物体运动的加速度为2 m/s2B．物体第2秒内的位移为4 mC．物体在第3秒内的平均速度为8 m/sD．物体从静止开始通过32 m的位移需要4 s的时间-7．一个物体由静止开始做匀加速直线运动，第1 s末的速度达到4 m/s，物体在第2 s内的位移是. A．6 m B．8 mC．4 m D．1.6 m---8．一列火车从静止开始做匀加速直线运动，一人站在第一节车厢前端的旁边观测，第一节车厢通过他历时2 s，整列车厢通过他历时6 s，则这列火车的车厢有... ...A．3节B．6节C．9节D．12节-9．（多种方法）一质点由静止开始做匀加速直线运动，它在第10 s内的位移为19 m，则其加速度大小为.. .. .. A．1.9 m/s2B．2.0 m/s2C．9.5 m/s2D．3.0 m/s2位移公式解决实际问题（练习公式）10一物体做初速度为零的匀加速直线运动，加速度为a＝2 m/s2，求：(1)第5 s末物体的速度多大？(2)前4 s的位移多大？(3)第4 s内的位移多大？11．一滑块自静止开始，从斜面顶端匀加速下滑(斜面足够长)，第5 s末的速度是10 m/s，试求：(1)第4 s末的速度大小；(2)运动后7 s内的位移大小；(3)第3 s内的位移大小．某物体从静止开始做匀加速直线运动，加速度为1 m/s2，求：(1)物体在2 s内的位移大小；(2)物体在第2 s内的位移大小；(3)物体在第二个2 s内的位移大小．2．(位移公式的应用，上题的逆运算)一个做匀加速直线运动的物体，初速度v0＝2.0 m/s，它在第3 s内通过的位移是4.5 m，则它的加速度为(B)A．0.5 m/s2B．1.0 m/s2C．1.5 m/s2D．2.0 m/s212、某飞机起飞的速度是60m/s，在跑道上加速时产生的最大加速度为3m/s2，该飞机从静止到起飞成功需要跑道的长度为多少?13（难，杨镇18年考过）矿井里的升降机由静止开始匀加速上升，经过5s速度达到v=4 m/s后，又以这个速度匀速上升20s，然后匀减速上升，再经4s停在井口．求矿井的深度．刹车问题14．一滑块在水平面上以20 m/s的初速度做匀减速直线运动，加速度大小为4 m/s2.求：滑块10 s时的速度及位移．15 一木块以5m/s的初速度，－2m/s2的加速度在粗糙水平面上滑行，4s内物体通过的位移为...A．4m B．36mC．6.25m D．以上答案都不对16、（2016 惠州模拟）汽车以36km/h的速度行驶，刹车后得到的加速度大小为4m/s2，从刹车开始，经5s，汽车通过的位移是... ...A．0m B．100m C．12.5m D．37.5m23 17．(刹车问题及逆向思维法)一辆卡车紧急刹车过程加速度的大小是5 m /s 2，如果在刚刹车时卡车的速度为10 m/s ，求：(1)刹车开始后1 s 内的位移大小；(2)刹车开始后3 s 内的位移大小和3 s 内的平均速度大小．18 一辆汽车正在平直的公路上以72 km /h 的速度行驶，司机看见红色信号灯便立即踩下制动器，此后，汽车开始做匀减速直线运动．设汽车减速过程的加速度大小为5 m/s 2，求： (1)开始制动后，前2 s 内汽车行驶的距离；(2)开始制动后，前5 s 内汽车行驶的距离．（前2s 或者前5s 的平均速度为多少呢？）（这个刹车问题不错，舍去一个时间）汽车以20 m/s 的速度做匀速直线运动，某时刻关闭发动机而做匀减速直线运动，加速度大小为5 m/s 2，则它关闭发动机后通过37.5 m 所需时间为( ) A ．3 s B ．4 s C ．5 s D ．6 s答案 A解析 根据x ＝v 0t ＋12at 2，将v 0＝20 m/s ，a ＝－5 m/s 2，x ＝37.5 m ，代入得：t 1＝3 s ，t 2＝5 s但因刹车时间t 0＝0－v 0a＝4 s ，所以t 2＝5 s 应舍去．故只有选项A 正确．19．一辆汽车以20 m /s 的速度沿平直公路匀速行驶，突然发现前方有障碍物，立即刹车，汽车以大小为5 m/s 2的加速度做匀减速直线运动，那么刹车后2 s 内与刹车后6 s 内汽车通过的位移大小之比为.. .. ..A ．1∶1B ．3∶4C ．3∶1D ．4∶320 汽车以20 m /s 的速度做匀速直线运动，某时刻关闭发动机而做匀减速直线运动，加速度大小为5 m/s 2，则它关闭发动机后通过37.5 m 所需时间为. A ．3 s B ．4 s C ．5 s D ．6 s21．汽车以v 0＝10 m /s 的速度在水平路面上匀速直线运动，刹车后经过2 s 速度变为6 m/s ，若将刹车过程视为匀减速直线运动，求：(1)从开始刹车起，汽车在6 s 内发生的位移大小； (2)汽车静止前2 s 内通过的位移大小． 答案 (1)25 m (2)4 m解析 (1)汽车刹车时的加速度：a ＝v －v 0t ＝6－102 m /s 2＝－2 m/s 2，则汽车速度减为零所需的时间：t 0＝0－v 0a ＝－10－2s ＝5 s ＜6 s.则6 s 内的位移等于5 s 内的位移：x ＝v 0t 0＋12at 02＝10×5 m －12×2×52 m ＝25 m.(2)采用逆向思维，汽车在静止前2 s 内的位移：x ′＝12a ′t ′2＝12×2×22 m ＝4 m.22．(刹车问题)一辆卡车紧急刹车过程加速度的大小是5 m /s 2，如果在刚刹车时卡车的速度为10 m/s ，求：(1)刹车开始后1 s 内的位移大小；(2)刹车开始后3 s 内的位移大小和3 s 内的平均速度大小． 答案 (1)7.5 m (2)10 m103m/s 解析 (1)v 0＝10 m /s ，a ＝－5 m/s 2，设经时间t 0停下 t 0＝0－v 0a ＝0－10－5s ＝2 s t 1＝1 s ，x 1＝v 0t 1＋12at 12解得x 1＝7.5 m.(2)t 2＝3 s 时的位移大小等于前2 s 内的位移大小 x 2＝v 0t 0＋12at 02＝10 m3 s 内的平均速度v ＝x 2t 2＝103m/s.5．(刹车问题)(2019·豫南九校高一上学期期末联考)汽车在平直公路上以10 m/s 的速度做匀速直线运动，发现前面有情况而刹车，获得的加速度大小是2 m/s 2，求： (1)汽车经3 s 时速度的大小； (2)汽车经6 s 时速度的大小；(3)从刹车开始经过8 s ，汽车通过的距离． 答案 见解析4解析 设汽车经时间t 0速度减为0，有： t 0＝0－v 0a ＝0－10－2s ＝5 s(1)根据速度－时间公式有：v 3＝v 0＋at ＝4 m/s (2)经过6 s 时速度为：v 6＝0 (3)刹车8 s 汽车的位移为： x 8＝x 5＝v 0t 0＋12at 02＝25 m.逆向思维法解题在处理末速度为零的匀减速直线运动时，为了方便解题，可以采用逆向思维法，将该运动对称地看成逆向的加速度大小相等的初速度为零的匀加速直线运动．23 物体做匀减速直线运动，初速度为10 m /s ，加速度大小为1 m/s 2，则物体在停止运动前1 s 内的位移为.... .... A ．5.5 m B ．5 m C ．1 mD ．0.5 m24．(逆向思维法的应用)(多选)用相同材料做成的A 、B 两木块的初速度之比为2∶3，它们以相同的加速度在同一粗糙程度相同的水平面上沿直线滑行直至停止，则它们滑行的( ) A ．时间之比为1∶1 B ．时间之比为2∶3 C ．距离之比为4∶9 D ．距离之比为2∶3答案 BC解析 由匀变速直线运动的速度公式v ＝v 0＋at ，得t ＝v －v 0a ＝－v 0a ，因为加速度相同，因此运动时间之比就等于初速度之比，选项A 错误，B 正确；将其看成逆向的初速度为零的匀加速直线运动，根据位移公式x ＝12at 2，知位移之比等于运动时间的平方之比，选项C 正确，D 错误．能力提高25．一物体由静止开始做匀变速直线运动，在时间t 内通过的位移为x ，则它从出发开始经过4x 的位移所用的时间为... ... A.t 4 B.t2C ．2tD ．4t 26．一物体由静止开始做匀变速直线运动，在时间t 内通过的位移为x ，则它从出发开始经过x4的位移所用的时间为.. .. .. A.t 4 B.t 2 C.t 16D.22t ---多27一质点做匀变速直线运动，某时刻速度大小为4m /s ，1 s 后速度的大小变为10 m /s ，在这1 s 内该质点...A 、位移的大小可能小于4 mB 、位移的大小可能小于10 mC 、加速度的大小可能小于4 m /s 2D 、加速度的大小可能大于10 m /s 2-28. 北京莲花岭高速公路最大限速为30m/s ，一辆小车以25m/s 的速度在该路段紧急刹车，滑行距离为62.5m ．（汽车刹车过程可认为做匀减速直线运动） （1）求该小车刹车时加速度大小； （2）若该小车以最大限速在该路段行驶，驾驶员的反应时间为0.4s ，求该车的安全距离为多少？（安全距离即驾驶员从发现障碍物至停止，车运动的距离）【解析】（1）根据速度时间公式得，0250t v v at at =+=-=及位移时间公式220112562.522x v t at t at m =-=-=联立两式解得：25/a m s =（2）小车在反应时间内做匀速运动10300.412s v t m ==⨯= 刹车后小车做匀减速直线运动所需时间为：0'3065v t s s a ===，222011306569022s v t at m =-=⨯-⨯⨯=小车安全距离为：12102s s s m =+=29．在高速公路上，有时会发生“追尾”事故——后面的汽车撞上前面的汽车．某段高速公路的最高车速限制为108 km /h.设某人驾车正以最高时速沿该高速公路匀速行驶，该车刹车时产生的加速度大小为5 m/s 2，该人的反应时间(从意识到应该停车到操作刹车的时间)为 0.5 s ．计算行驶时的安全车距至少为多少？5 30、（模拟题考过类似题）在高速公路上，有时会发生“追尾”事故——后面的汽车撞上前面的汽车．请分析一下，造成“追尾”事故的原因有哪些?我国高速公路的最高车速限制为120 km/h ．设某人驾车正以最高时速沿平直高速公路行驶，该车刹车时产生的加速度大小为5m/s 2，司机的反应时间(从意识到应该刹车至操作刹车的时间)为0.6～0.7s ．请分析一下，应该如何计算行驶时的安全车距?14．在高速公路上，有时会发生“追尾”事故——后面的汽车撞上前面的汽车．某段平直高速公路的最高车速限制为108 km/h.设某人驾车正以最高时速沿该高速公路匀速行驶，该车刹车时产生的加速度大小为5 m/s 2，该人的反应时间(从意识到应该停车到操作刹车的时间)为0.5 s ．计算行驶时的安全车距至少为多少？ 答案 105 m解析 汽车原来的速度v 0＝108 km/h ＝30 m/s ，运动过程如图所示在反应时间t 1＝0.5 s 内，汽车做匀速直线运动的位移为x 1＝v 0t 1＝30×0.5 m ＝15 m 刹车后，汽车做匀减速直线运动，滑行时间为t 2＝0－30－5s ＝6 s汽车刹车后滑行的位移为x 2＝v 0t 2＋12at 22＝30×6 m ＋12×(－5)×62 m ＝90 m所以行驶时的安全车距至少应为 x ＝x 1＋x 2＝15 m ＋90 m ＝105 m.-31、（2016 山西模拟）某地出现雾霾天气，能见度只有200m ，即看不到200m 以外的情况，A 、B 两辆汽车沿同一公路同向行驶，A 车在前，速度v A =10m/s ，B 车在后，速度v B =30m/s ．B 车在距A 车200m处才发现前方的A 车，这时B 车立即以最大加速度a=0.8m/s 2刹车．问：（1）如果B 车以最大加速度减速，能见度至少达到多少米才能保证两车不相撞？（2）如果B 车以最大加速度减速，同时开始按喇叭，10s 后，A 车发现后，立即加速前进．则A 车的加速度至少多大时才能避免与B 车相撞？【解析】（1）设经过t 时间两车速度相等，根据v A =v B ﹣at ，解得：3010250.8B A v v t s s a --=== 则两车相距的最近距离为：212B A s v t at v t ∆=--代入数据解得：△s =250m ．（2）10s 后，B 车的速度为：v B1=（30﹣0.8×10）m/s=22m/s ，此时两车的距离为：211111200()1010200(30100.810)40m 22A B x v t v t at ∆=+--=⨯+-⨯-⨯⨯=设A 车的加速度大小至少为a ′，10s 后速度相等需经历的时间t ′，有：v B1﹣at ′=v A +a ′t ′，又：2211'''('')22A B v t a t x v t at ++∆=- 两式联立即可解得A 车的加速度：a ′=1m/s 2611．一辆汽车做匀速运动，某时刻遇到紧急情况需刹车，刹车后的第1秒内运动了8 m ，第2秒内运动了4 m ，关于汽车的运动和刹车过程，下列说法正确的是( ) A ．汽车匀速运动时的速度是8 m/s B ．汽车刹车时的加速度大小是2 m/s 2 C ．汽车刹车后3秒末的加速度为0 D ．汽车刹车后运动的距离是16 m 答案 C解析 由位移时间公式可知， v 0×1 s ＋12a ×(1 s)2＝8 m ①v 0×2 s ＋12a ×(2 s)2－8 m ＝4 m ②由①②联立得v 0＝10 m/s ，a ＝－4 m/s 2，A 、B 错误．刹车减速到零所需时间t ＝0－v 0a ＝0－10－4 s ＝2.5 s ，故刹车后3 s 末的速度为零，故C 正确．刹车后的运动距离为x ＝v 0t ＋12at 2＝10×2.5 m －12×4×2.52 m ＝12.5 m ，故D 错误．---针对训练1 一质点做匀变速直线运动，第3 s 内的位移为12 m ，第5 s 内的位移为20 m ，则该质点运动过程中( ) A ．初速度大小为零 B ．加速度大小为4 m/s 2C ．5 s 内的位移为50 mD ．第4 s 内的平均速度为8 m/s 答案 B解析 第3 s 内的位移等于前3 s 内位移与前2 s 内位移之差，即Δx 3＝x 3－x 2＝12 m ，代入数据得v 0×3＋12a ×32－(v 0×2＋12a ×22)＝12①同理可得：v 0×5＋12a ×52－(v 0×4＋12a ×42)＝20②联立①②解得v 0＝2 m /s ，a ＝4 m/s 2，故A 错误，B 正确；5 s 内的位移为x ＝v 0t 5＋12at 52＝60 m ，C 错误；第4 s 内的位移为Δx 4＝x 4－x 3＝v 0t 4＋12at 42－(v 0t 3＋12at 32)＝16 m ，则第4 s 内的平均速度v ＝Δx 4t ＝161 m /s＝16 m/s ，D 错误．8．一辆汽车做匀速直线运动，某时刻遇到紧急情况需刹车，刹车后的第1秒内运动了8 m ，第2秒内运动了4 m ，关于汽车的运动和刹车过程，下列说法正确的是( ) A ．汽车匀速运动时的速度是8 m/s B ．汽车刹车时的加速度大小是2 m/s 2 C ．汽车刹车后3秒末的加速度为0 D ．汽车刹车后运动的距离是16 m 答案 C解析 由位移时间公式可知， v 0×1＋12a ×12＝8①v 0×2＋12a ×22－8＝4②由①②联立得v 0＝10 m /s ，a ＝－4 m/s 2，A 、B 错误．刹车减速到零所需时间t ＝0－v 0a ＝0－10－4 s ＝2.5 s ，故刹车后3 s 末的速度为零，加速度也为零，故C 正确．刹车后的运动距离为x ＝v 0t ＋12at 2＝10×2.5 m －12×4×2.52 m ＝12.5 m ，故D 错误．3．(2018·宁阳一中月考)一个质点以初速度v 0做匀加速直线运动，加速度大小为a ，经过时间t ，位移大小为2at 2，末速度为v ，则初、末速度之比为( ) A ．3∶4 B ．1∶3 C ．3∶5 D ．2∶5答案 C解析 根据匀变速直线运动的位移公式和速度公式有： x ＝v 0t ＋12at 2v ＝v 0＋at7 将x ＝2at 2代入，解得v 0＝32atv ＝52at 所以v 0v ＝35.。

匀变速直线运动的位移与时间的关系【高中】一、匀变速直线运动的位移1.思维过程：可以把甲所表示的运动过程划分为很多的小段，如图乙、丙所示，用所有这些小段的位移之和，近似代表物体在整个过程中的位移。

从v-t 图上看，就是用更多的但是更窄的小矩形的面积之和代表物体的位移。

如果把整个运动过程划分得非常非常细，很多很多小矩形的面积之和就能非常准确地代表物体的位移了。

这时，“很多很多”小矩形顶端的“锯齿形”就看不出来了，这些小矩形合在一起成了一个梯形OABC 。

梯形OABC 的面积就代表做匀变速直线运动的物体从0（此时速度是v 0）到t （此时速度是v ）这段时间间隔的位移。

如图丁所示。

2.位移在v －t 图像中的表示：做匀变速直线运动的物体的位移对应着v －t 图像中的图线和时间轴包围的面积。

如图所示，在0～t 时间内的位移大小等于梯形的面积。

3.位移公式2210at t v x +=4.对位移公式x ＝v 0t ＋12at 2的进一步理解 (1)因为v 0、a 、x 均为矢量，使用公式时应先规定正方向，一般以v 0的方向为正方向。

若a 与v 0同向，则a 取正值；若a 与v 0反向，则a 取负值；若位移计算结果为正值，说明这段时间内位移的方向为正；若位移计算结果为负值，说明这段时间内位移的方向为负。

(2)因为位移公式是关于t 的一元二次函数，故x －t 图像是一条抛物线(一部分)。

但它不表明质点运动的轨迹为曲线。

(3)对于初速度为零(v 0＝0)的匀变速直线运动，位移公式为x ＝12vt ＝12at 2，即位移x 与时间t 的二次方成正比。

(4)x ＝v 0t ＋12at 2是矢量式，应用时x 、v 0、a 都要根据选定的正方向带上“＋”“－”号。

【初中】一、匀速直线运动的路程做匀速直线运动的物体在时间t 内的路程s ＝vt 。

其v －t 图像是一条平行于时间轴的直线，如图所示。

路程在数值上等于v －t 图线与对应的时间轴所包围的矩形的面积。

第9讲 匀变速直线运动的位移与时间的关系匀速直线运动的v ­t 图像如图所示，v ­t 图像与对应的时间轴所包围的矩形的(阴影部分)“面积”有什么意义？提示：表示物体在0～t 1时间内的位移。

一、速度与时间的关系1． v ­t 图像中“面积”的意义：v ­t 图像中的图线和时间轴包围的“面积”等于相应时间内的位移。

如图所示，在0～t 1时间内的位移大小等于梯形的“面积”。

2．位移公式：x ＝v 0t ＋12at 2。

式中v 0表示初速度，x 表示物体在时间t 内运动的位移。

二、速度与位移的关系 1．公式：v 2－v 02＝2ax .2．推导：由速度时间关系式v ＝v 0＋at ，位移时间关系式x ＝v 0t ＋12at 2，得v 2－v 02＝2ax .例题1. 一物体做匀变速直线运动,下列说法中正确的是 ( ) A.物体的末速度一定与时间成正比 B.物体的位移一定与时间的平方成正比C.物体的速度在一定时间内发生的变化与这段时间成正比D.若为匀加速直线运动,速度和位移都随时间增加;若为匀减速直线运动,速度和位移都随时间减小 【答案】Cat2可知,若物体的初速度v0不为零,A、B选项不正确;由【解析】根据v=v0+at和x=v0t+12a=Δv可知,Δv=a·Δt,a不变,Δv与Δt成正比,C正确;当物体做匀减速直线运动时,速度减小但位Δt移可以增大,D不正确。

对点训练1.一质点做匀加速直线运动,初速度v0=2 m/s,4 s内位移为20 m,求6 s末质点的速度大小。

【答案】11 m/sat2【解析】根据匀变速直线运动规律:x=v0t+12代入数据解得:a=1.5 m/s2根据v=v0+at得质点6 s末的速度大小:v=11 m/s。

例题2.如图所示,甲图为某质点的位移­时间图像,乙图为某质点的速度­时间图像,下列关于两质点的运动情况说法正确的是()甲乙A.0～2 s内:甲图质点做匀加速直线运动,乙图质点做匀速直线运动B.2～3 s内:甲图质点和乙图质点均静止不动C.3～5 s内:甲图质点和乙图质点均做匀减速运动,加速度为­15 m/s2D.0～5 s内:甲图质点的位移为­10 m,乙图质点的位移为100 m【答案】D【解析】位移­时间图像的斜率表示物体运动的速度,速度­时间图像的斜率表示物体的加速度,则0～2 s内甲图质点做匀速直线运动,乙图质点做匀加速直线运动,故A错误;2～3 s内甲图图线的斜率为零,即质点速度为零,乙图质点速度恒定不变,做匀速直线运动,故B 错误;3～5 s 内甲图图线的斜率恒定,质点做匀速直线运动,而乙图质点速度均匀减小,做匀减速直线运动,故C 错误;位移­时间图像表示质点的位移随时间的变化,则甲图质点位移为0­10 m=­10 m,速度­时间图像中图线与时间轴围成的面积表示位移,则x =[12×(10+30)×2+30×1+12×30×2] m=100 m,故D 正确。

第2.3课 匀变速直线运动的位移与时间的关系一、匀速直线运动的位移 1.位移公式：x ＝ .2.位移在v －t 图象中的表示：对于匀速直线运动，物体的位移在数值上等于v －t 图线与对应的时间轴所包围的矩形的_____.如图1所示，阴影图形的面积就等于物体在t1时间内的_____.二、匀变速直线运动的位移1.位移在v －t 图象中的表示：做匀变速直线运动的物体的位移对应着v －t 图线与时间轴所包围的_________.如图所示，阴影图形的面积等于物体在t1时间内的_____.2.公式：x ＝_________.三、位移—时间图象（x －t 图象）1.x －t 图象：以______为横坐标，以______为纵坐标，描述位移随时间的变化规律.2.常见的x －t 图象：（1）静止：一条______________的直线. （2）匀速直线运动：一条_____的直线. 3.x －t 图象的斜率等于物体的 .答案：vt 面积 位移 梯形面积 位移 2021at t v 时间t 位移x 平行于时间轴 倾斜 速度考点一 对位移公式2012x v t at =+的进一步理解（1）反映了位移随时间的变化规律。

（2）因为0v 、a 、x 均为矢量，使用公式时应先规定正方向。

一般以0v 的方向为正方向。

若a 与0v 同向，则a 取正值；若a 与0v 反向，则a 取负值； 若位移计算结果为正值，说明这段时间内位移的方向为正；若位移计算结果为负值，说明这段时间内位移的方向为负。

（3）因为位移公式是关于t 的一元二次函数，故x t -图象是一条抛物线（一部分）。

但它不表明质点运动的轨迹为曲线。

（4）对于初速度为零（00v =）的匀变速直线运动，位移公式为21122x vt at ==，即位移x 与时间t 的二次方成正比。

【注意】（1）2012x v t at =+是矢量式，应用时x 、0v 、a 都要根据选定的正方向带上“+”、“—”号。