将前式代入,两端除以z,并令z→0,可得一般传 输线方程(电报方程):抖 ( z, t ) 骣 v i( z, t )
抖 z = - çRl i ( z , t ) + Ll ç ç 桫 t 骣 抖( z , t ) i = - çGl v( z , t ) + Cl ç ç 桫 抖 z
÷ ÷ ÷
m b ln 2p a b 2pe ¢ ln a RS 骣 ç1 + 1 ÷ ÷ ç 桫 2p ç a b÷ b 2pwe ⅱln a
双导线 D:线间距离 d:导线直径
m D+ ln p pe ¢ ln 2 Rs pd pwe ⅱ ln D+
12
D2 - d 2 d D2 - d 2 d
D+
平行板传输线 W:平板宽度 d:板间距离 m,:填充介质 md W e¢ W d 2 RS
电流的解为:
电压电流是 位置的函数
dV ( z ) 1 1 I ( z) = = A1e- g z - A2 eg z ) ( R + jwL dz Z0
式中
Z0 =
Rl + jwLl Gl + jwCl
为传输线的特性阻抗
电压和电流解为:
V ( z ) = V + ( z ) + V - ( z ) = A1e+ -
一维分布参数电路理论
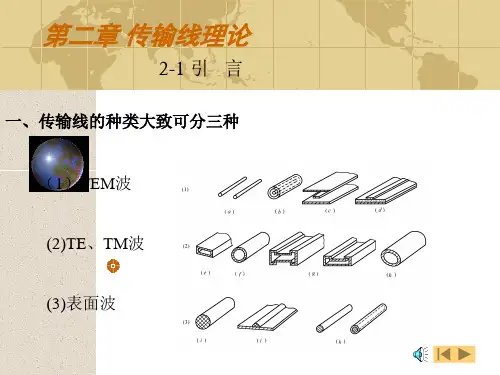
第二章 传输线理论
1)长线理论
传输线的电长度:传输线的几何长度 l 与其上 工作波长l的比值(l/l)。
长线 Long line
当线的长度与波长 可以比拟
l/l > 0.05
短线 Short line
当线的长度远小于线 上电磁波的波长