- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
非线性方程求根
很多工程和科学计算问题常常归结为求解方程:
f (x) 0
例如:非线性有限元问题、非线性断裂问题、及其它
非线性力学问题、电路问题、电力系统计算、医学、 生命学、天气预报、非线性规划、经济问题等。
描述工程和科学技术实际问题的数学模型,通常都难以
获得根的简单易用的显式表达式,因此,要研究求近似 根的方法,并讨论这些方法的收敛性和收敛速度
若f ( x1 ) f (a0 ) 0, 取a1=a0 , b1=x1,即[a1, b1] [a0 , x1];
否则取a1=x1, b1=b0 ,即[a1, b1] [ x1, b0 ].
3. 继续运算, 由区间[ak-1,bk-1]构造区间[ak ,bk]
并得到xk:xk
ak-1
2
bk-1
二分法的基本思想
用对分区间的方法,通过判别函数f (x)在每个
对分区间中点的符号,逐步将有根区间缩小,最 终求得一个具有相当精确程度的近似根
二分法详细步骤
1.记有根区间[a0,b0]=[a,b],取
2. 判断f ( x1 )的值 :
x1
a0
ቤተ መጻሕፍቲ ባይዱ b0 2
(中点),并计算f ( x1).
若f ( x1 ) 0,则x1为根;
Matlab program
function y=erfen(fun,a,b,esp)
if feval(fun, a)*feval(fun, b)< 0 n = 1 ; c = (a+ b) / 2 ; while(b-a)>esp if feval(fun,a)*feval(fun,c)<0 b = c ; c = ( a+b) / 2 ; elseif feval(fun,c)*feval(fun,b)<0 a = c ; c = ( a+b) / 2 ; else y = c ; end n= n+1 ; end
点的横坐标位于区间[2,3]内
画图法
y
y1 x
y log x
0
2 3
x
逐步搜索法
逐步搜索法
对于给定的f (x),设有根区间为[A,B],从x0=A 出发,以步长h=(B-A)/n(n是正整数),在[A,B] 内取定节点:xi=x0+ih (i=0,1,2,…,n), 从左至右检查f (xi)的符号,如发现xi与端点x0
的函数值异号,则得到一个缩小的有根子区间
[xi-1,xi]。 用逐步搜索法进行实根隔离的关键是选取步长h 要选择适当h ,使之既能把根隔离开来,工作量又
不太大。
二分法 Bisection
在方程求根的方法中,最直观、最简单的方法就 是二分法。
给定方程f(x)=0,设f(x)在区间[a,b]连续,且f(a)f(b)<0, 则方程f(x)在(a,b)内至少有一根,为便于讨论,不妨设方 程f(x)=0在(a,b)内只有一个(重根视为一个)实根。
k
bk
x*
,
lim
k
xk
x*
二分法终止的条件
如下条件终止,可否 ?
f (xk )
这不能保证精确值的精度!
x*
x
二分法终止的条件
有如下估计
x* xk
1 2
(bk
ak
)
bk 1
ak 1
因此终止的条件为
bk ak or xk xk 1
对于给定的精度 ,可估计二分法所需的步数 k :
预备知识
满足函数方程 f(x)=0 的x称为方程(1)的根,或称 为函数f(x)的零点。如果函数(x)可分解为 (x)=(xs)mg(x) 且g(s )0,则称s是(x)的m重零点或(x)=0的m重根 。当m=1时,称s是(x)的单根或单零点。
定理 假设函数y=f(x)在x=s的某一邻域内充分可 微,则s是方程f(x )=0的m重根的充分必要条件是
ba 2k
k
log
2
(
b
a)
二分法的优缺点
优点 计算简单,方法可靠,并保证收敛 对函数 要求不高,只要连续即可。
缺点 无法求复根和偶重根 收敛慢 调用一次求解一个[a, b]间的多个根无法求得 一般求方程的近似根,不大单独使用,常用
来为其它方法求方程近似根提供好的初值。方程 求根最常用的方法是迭代法。
,
若f ( xk ) 0,则xk为所求的根;
若f ( xk ) f (ak-1 ) 0,则取[ak ,bk ]=[ak-1,xk ];
否则, 可取[ak ,bk ]=[xk ,bk-1].
这样就得到一系列闭区间:
[a0,b0 ],[a1,b1],...[ak ,bk ],...,k= 0,1,2,...., 并满足:
f (s) f (s) f (m1) (s) 0, f (m) (s) 0
求解非线性方程的根的问题可分为下面几个方面:
根的存在性 根的隔离 根的精确化
非线性方程根的存在性非常复杂。
对于代数方程即多项式方程,其根的个数与代数方程 的次数相同。而且理论上已证明,对于次数n<=4的多项 式方程,它的根可以用公式表示,而次数大于5的多项式方 程,它的根一般不能用解析表达式表达。示.
(a) f (ak ) f (bk ) 0
(b)
bk
ak
1 2k
(b
a)
(c) a0 a1 ...ak ..., b0 b1 ...bk ...;即满足[ak , bk ] [ak1, bk1]
并且
x*, f ( x* ) 0, x* (ak , bk ),
lim
k
ak
x*
,
lim
根的隔离
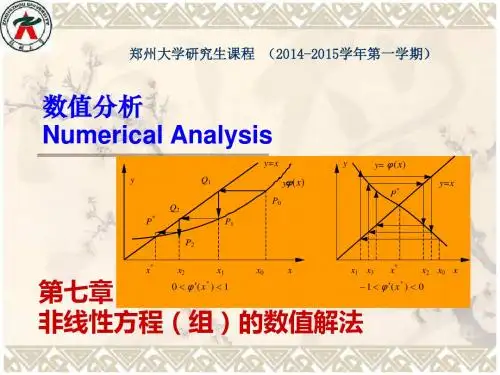
求根的隔离区间的两种方法 画图法
画出y = f (x)的略图,从而看出曲线与x轴交
点的大致位置。
也可将f (x) = 0分解为1(x)= 2(x)的形式, 1(x)与 2(x)两曲线交点的横坐标所在的子
区间即为含根区间。
例如xlgx –1 = 0 可以改写为lgx=1/x 画出对数曲线y=lgx,与双曲线y= 1/x,它们交
对于超越方程或其他非线性方程,可能没有零点,也
可能有一个或若干个零点,甚至无穷多个零点。
根的存在性定理
定理1.(根的存在定理) 假设函数y=f(x)Ca,b,且f(a)·f(b)<0, 则至 少存在一点x (a,b)使得f(x )=0. (并称区间(a,b)为有根区间).
定理2.(根的唯一性) 假设函数y=f(x)在a,b上单调连续,且 f(a)·f(b)<0, 则恰好只存在一点x (a,b)使得 f(x )=0