双曲线的几何性质PPT教学课件
- 格式：ppt
- 大小：2.10 MB
- 文档页数：67
下载文档原格式
合集下载
《双曲线几何性质》课件
双曲线的焦点与准线
要点一
焦点
双曲线的两个顶点，位于双曲线的对称轴上，距离原点的 距离为$c$，其中$c^2 = a^2 + b^2$。
要点二
准线
与双曲线相切的直线，与双曲线的对称轴垂直，距离原点 的距离为$a^2/c$。
02
双曲线的几何性质
双曲线的对称性
水平对称性
双曲线关于x轴对称，即对于任意点P(x, y)在双曲线上，存在 另一点P'(-x, -y)也在双曲线上。
04
双曲线在实际生活中的应用
天文观测中的双曲线
总结词
天文观测中，双曲线有着重要的应用，特别 是在星体的位置确定和轨迹计算中。
详细描述
天文学家利用双曲线的性质来研究星体的运 动轨迹。由于星体运动受到引力的影响，其 轨迹呈现出双曲线的特征。通过观测和计算 ，可以推导出星体的位置、速度和加速度等 参数。
详细描述
双曲线的面积计算公式为 (S = pi ab)， 其中 (a) 和 (b) 分别是双曲线的实半轴和 虚半轴长度。这个公式基于双曲线的参数 方程和定义域，通过积分运算得出。
双曲线的周长
总结词
双曲线的周长可以通过其基本性质和参数方程进行计算，结果是一个与双曲线形状有关的数值。
详细描述
双曲线的周长计算公式为 (C = 2a + 2b)，其中 (a) 和 (b) 分别是双曲线的实半轴和虚半轴长度。这个公式基于 双曲线的参数方程和几何性质，通过求和运算得出。
物理实验中的双曲线
总结词
在物理实验中，双曲线常用于描述某些物理现象或规律，如声波传播、波动等。
详细描述
在声波传播实验中，双曲线可以用来描述声波的传播路径和强度衰减。在波动理规律具有重要意义。
《双曲线的简单几何性质》ppt课件
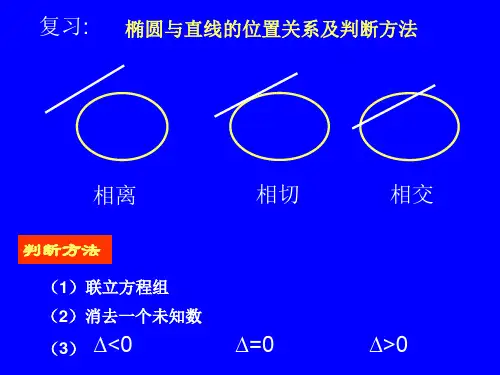
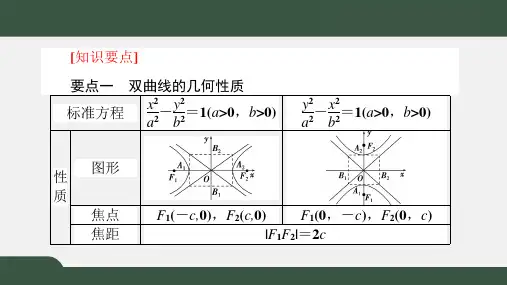
对称性 关于x轴、y轴、原点对称
顶点 离心率 渐进线
A1（- a，0），A2（a，0） B1（0，-b），B2（0，b）
e c (0 e 1) a
无
关于x轴、y轴、原点对称
A1（- a，0），A2（a，0）
e c (e 1) a
y b x a
用“类比学习法”和“数形结合法”
导出双曲线 y2 a2
焦点坐标,离心率.渐近线方程。并画出它的草图。
解：把方程化为标准方程
y2 42
x2 32
1
y
可得:实半轴长a=4
虚半轴长b=3
4
半焦距c= 42 32 5
焦点坐标是(0,-5),(0,5)
-3 o 3 x
离心率: e c 5
-4
渐近线方程:
y
a
4
4
x
(或
y
x
0)
3
43
小结： 一、双曲线的简单几何性质
x2 b2
1(a 0,b 0)
y
的简单几何性质
a
（1）范围: y a, y a
（2）对称性: 关于x轴、y轴、原点都对称 -b （3）顶点: (0,-a)、(0,a)
o bx -a
（4）渐近线:
yax b
或y x 0 ab
（5）离心率:
e
c a
练一练： 求双曲线 9y2 16x2 144的实半轴长,虚半轴长,
2 2
y2 b2
1
k
b a
B2
k
y
(a,b)
b a
b
yb x a
b
A1
a
o
A2
x
xy
双曲线-完整版PPT课件可编辑全文
∴x－32a2＋y2＝a22.
①
又 P 点在双曲线上，得ax22－by22＝1.
②
由①，②消去 y，得
(a2＋b2)x2－3a3x＋2a4－a2b2＝0，
即[(a2＋b2)x－(2a3－ab2)](x－a)＝0.
当 x＝a 时，P 与 A 重合，不符合题意，舍去．
当 x＝2aa32－＋abb2 2时，满足题意的 P 点存在， 需 x＝2aa32－＋abb2 2＞a， 化简得 a2＞2b2， 即 3a2＞2c2，ac＜ 26. 又 e＞1，∴离心率 e＝ac∈1， 26.
考向三 [149] 双曲线的几何性质
(1)(2014·天津高考)已知双曲线ax22－by22＝1(a>0，
b>0)的一条渐近线平行于直线 l：y＝2x＋10，双曲线的一个
焦点在直线 l 上，则双曲线的方程为( )
A.x52－2y02 ＝1
B.2x02 －y52＝1
C.32x52－130y02 ＝1
二、双曲线的标准方程和几何性质
标准方程 ax22－by22＝1(a>0，b>0)
ay22－bx22＝1(a>0， b>0)
图形
范围
x≥a或x≤－a
对称轴： 坐标轴
对称性
对称中心： 原点
y≤－a或y≥a 对称轴： 坐标轴 对称中心： 原点
性 顶点 顶点坐标：
顶点坐标：
质
A1 (－a,0)，A2 (a,0) A1 (0，－a，) A2 (0，a)
————————— [1 个对点练] ——————— 过点2，12能作几条与双曲线x42－y2＝1 有一个公共点的 直线．
【解】 (1)当斜率不存在时，直线方程为 x＝2，显然符 合题意．
3.2.2双曲线的简单几何性质 课件(共24张PPT)
2
2
=λ(λ≠0).
(5)渐近线为y=±kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
(6)渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).
跟踪训练 求适合下列条件的双曲线的标准方程：
5
（1）焦点在x轴上，虚轴长为8，离心率为3 ；ห้องสมุดไป่ตู้
跟踪训练
A.
1
4
双曲线x2-my2＝1的实轴长是虚轴长的2倍，则m等于
B.
1
2
C.2
D.4
（D）
二、求双曲线方程
例2
根据下列条件，求双曲线方程:
（1）双曲线 x
2
9
y2
1 有共同渐近线，且过点 ( 3, 2 3) ；
16
（2）与双曲线 x
2
16
解
y2
1 有公共焦点，且过点 (3 2 , 2) .
第三章
3.2
双曲线
3.2.2 双曲线的简单几何性质
学习目标
1.理解双曲线的简单几何性质（范围、对称性、顶点、渐近线、离心率）.
2.能用双曲线的简单性质解决一些简单的问题
核心素养：数学运算、数学建模
新知学习
复习引入
定义
| |MF1|-|MF2| | =2a（０ < 2a<|F1F2|）
y
y
M
M
F2
(2)焦点在 y 轴上的双曲线的标准方程可设为
2
(3)与双曲线
2
2 +
2
−
2
2
2
−
=1(a>0,b>0).
2
2
=1 共焦点的双曲线方程可设为
2
=λ(λ≠0).
(5)渐近线为y=±kx的双曲线方程可设为k2x2-y2=λ(λ≠0).
(6)渐近线为ax±by=0的双曲线方程可设为a2x2-b2y2=λ(λ≠0).
跟踪训练 求适合下列条件的双曲线的标准方程：
5
（1）焦点在x轴上，虚轴长为8，离心率为3 ；ห้องสมุดไป่ตู้
跟踪训练
A.
1
4
双曲线x2-my2＝1的实轴长是虚轴长的2倍，则m等于
B.
1
2
C.2
D.4
（D）
二、求双曲线方程
例2
根据下列条件，求双曲线方程:
（1）双曲线 x
2
9
y2
1 有共同渐近线，且过点 ( 3, 2 3) ；
16
（2）与双曲线 x
2
16
解
y2
1 有公共焦点，且过点 (3 2 , 2) .
第三章
3.2
双曲线
3.2.2 双曲线的简单几何性质
学习目标
1.理解双曲线的简单几何性质（范围、对称性、顶点、渐近线、离心率）.
2.能用双曲线的简单性质解决一些简单的问题
核心素养：数学运算、数学建模
新知学习
复习引入
定义
| |MF1|-|MF2| | =2a（０ < 2a<|F1F2|）
y
y
M
M
F2
(2)焦点在 y 轴上的双曲线的标准方程可设为
2
(3)与双曲线
2
2 +
2
−
2
2
2
−
=1(a>0,b>0).
2
2
=1 共焦点的双曲线方程可设为
双曲线的简单性质课件ppt课件
04 双曲线的标准方程的推导
推导过程
设双曲线上任意一点为$P(x,y)$， 根据双曲线的定义，点$P$到两 个焦点的距离之差为常数，即 $2a$。
利用距离公式和双曲线的定义， 可以得到点$P$到两个焦点的距 离分别为$sqrt{(x+a)^2+y^2}$ 和$sqrt{(x-a)^2+y^2}$。
对称性
01
02
03
对称性
双曲线关于其对称轴对称， 即关于x轴和y轴都对称。
总结词
双曲线关于其对称轴对称， 即关于x轴和y轴都对称。
详细描述
双曲线上的任意一点关于 x轴和y轴的对称点都在双 曲线上。
顶点
顶点
双曲线与对称轴的交点称 为顶点。
总结词
双曲线与对称轴的交点称 为顶点。
详细描述
顶点是双曲线与对称轴的 交点，也是双曲线离准线 最远的点。
比例常数。
性质
双曲线的焦点到任意一点的距离之 差等于常数2a，即|PF1| - |PF2| = 2a。
应用
通过焦点可以计算出双曲线的离心 率和准线方程。
焦距
定义
双曲线的两个焦点之间的距离称 为焦距，记作2c。
性质
焦距与半主轴长a和半次轴长b有 关，关系为c^2 = a^2 + b^2。
应用
通过焦距可以计算出双曲线的离 心率和准线方程。
双曲线的简单性质课件ppt课件
目录
• 双曲线的定义与标准方程 • 双曲线的几何性质 • 双曲线的焦点与焦距 • 双曲线的标准方程的推导 • 双曲线的应用
01 双曲线的定义与标准方程
定义
总结词
双曲线是由两个无限延伸的分支组成的，其形状类似于开口 的抛物线。
双曲线的性质PPT优秀课件
97.有三个人是我的朋友爱我的人.恨我的人.以及对我冷漠的人。 爱我的人教我温柔；恨我的人教我谨慎；对我冷漠的人教我自立。――[J·E·丁格] 98.过去的事已经一去不复返。聪明的人是考虑现在和未来，根本无暇去想过去的事。――[英国哲学家培根] 99.真正的发现之旅不只是为了寻找全新的景色，也为了拥有全新的眼光。――[马塞尔·普劳斯特] 100.这个世界总是充满美好的事物，然而能看到这些美好事物的人，事实上是少之又少。――[罗丹] 101.称赞不但对人的感情，而且对人的理智也发生巨大的作用，在这种令人愉快的影响之下，我觉得更加聪明了，各种想法，以异常的速度接连涌入我的脑际。――[托尔斯泰] 102.人生过程的景观一直在变化，向前跨进，就看到与初始不同的景观，再上前去，又是另一番新的气候――。[叔本华] 103.为何我们如此汲汲于名利，如果一个人和他的同伴保持不一样的速度，或许他耳中听到的是不同的旋律，让他随他所听到的旋律走，无论快慢或远近。――[梭罗] 104.我们最容易不吝惜的是时间，而我们应该最担心的也是时间；因为没有时间的话，我们在世界上什么也不能做。――[威廉·彭] 105.人类的悲剧，就是想延长自己的寿命。我们往往只憧憬地平线那端的神奇【违禁词，被屏蔽】，而忘了去欣赏今天窗外正在盛开的玫瑰花。――[戴尔·卡内基] 106.休息并非无所事事，夏日炎炎时躺在树底下的草地，听着潺潺的水声，看着飘过的白云，亦非浪费时间。――[约翰·罗伯克] 107.没有人会只因年龄而衰老，我们是因放弃我们的理想而衰老。年龄会使皮肤老化，而放弃热情却会使灵魂老化。――[撒母耳·厄尔曼] 108.快乐和智能的区别在于：自认最快乐的人实际上就是最快乐的，但自认为最明智的人一般而言却是最愚蠢的。――[卡雷贝·C·科尔顿] 109.每个人皆有连自己都不清楚的潜在能力。无论是谁，在千钧一发之际，往往能轻易解决从前认为极不可能解决的事。――[戴尔·卡内基] 110.每天安静地坐十五分钟·倾听你的气息，感觉它，感觉你自己，并且试着什么都不想。――[艾瑞克·佛洛姆] 111.你知道何谓沮丧---就是你用一辈子工夫，在公司或任何领域里往上攀爬，却在抵达最高处的同时，发现自己爬错了墙头。－－[坎伯] 112.「伟大」这个名词未必非出现在规模很大的事情不可；生活中微小之处，照样可以伟大。――[布鲁克斯] 113.人生的目的有二：先是获得你想要的；然后是享受你所获得的。只有最明智的人类做到第二点。――[罗根·皮沙尔·史密斯] 114.要经常听.时常想.时时学习，才是真正的生活方式。对任何事既不抱希望，也不肯学习的人，没有生存的资格。
双曲线的性质课件(PPT 15页)
y
B2
A1 F1 O
F2 A2
x
B1
y C3C2 C1
O
x
焦点在x轴上的双曲线图像
y 渐进线方程： b x a
Y x2 y2 1 a2 b2
B2
F1
A1
A2 F2 X B1
离心率对双曲线形状的影响
焦点在y轴上的双曲线图
像
Y
y2 a2
x2 b2
1
F2
A2
B1
O
B2
X
A1
F1
焦点在y轴上的双曲线的几何性质
2、对称性：关于x轴，y轴，
原点对称。 3、顶点 A1(-a,0),A2(a,0)
F1 A1 O
A2 F2
x
4、轴：实轴 A1A2 虚轴 B1B2
B1
|A1A2|=2ca,|B1B2|=2b 5、离心率：e= a
根据以上几何性质能够
根据以上几何性质能否
较准确地画出椭圆的图形？ 较准确地画出双曲线的图形呢？
双曲线标准方程：y 2 x 2 1 双曲线性质： a 2 b2
Y
1、范围：y≥a或y≤-a
F2
2、对称性：关于x轴，y轴，原点对称。
A2
3、顶点 A1（0，-a），A2（0，a）
4、轴：实轴 A1A2 ; 虚轴 B1B2 B1
5、渐近线方程： y a x
o
b
6、离心率：e=c/a
A1
F2
B2 X
Y
F1
B2
F’1 A1 o
B1
X
A2 F’2
F2
证明:(1)设已知双曲线的方程是:
x2 a2
y2 b2
1
双曲线的性质ppt课件
双曲线的渐近线方程为 y 3 x
b3， 而 c2a2b 2， 3a2b 28 a3
解出 a26， b22
双 曲 线 方 程 为x2
y2
1
6 2 完整版ppt课件
18
小结
x2 a2
y2 b2
1（ a＞ b ＞0）
x2 a2
y2 b2
1
(
a＞
0
b＞0)
c 2 a 2 b 2 (a＞ b＞0) c 2 a 2 b 2 (a＞ 0 b＞0)
完整版ppt课件
7
二、导出 y2双 x2曲 1(a线 0,b0) a2 b2
的简单几何性质 y
（1）范围: ya,ya
（2）对称性: 关于x轴、y轴、原点都对称
a
（3）顶点: (0,-a)、(0,a)
（4）渐近线: y a x
b
（5）离心率: e c a
-b o b x -a
完整版ppt课件
A1
A2
o a
x
它与yybx的x位置的变化:趋势
a
B1
（3）利画用出慢渐双慢近曲靠线线近可的草以图较准确的
ybx
a
完整版ppt课件
y b x a
5
5、离心率
（1）定义：双曲线的焦距与 的实 比 e轴c,长 叫做 a
双曲线离的 心率。
（2）e的范围： c>a>0 e >1
（3）e的含义：
b c2a2 (c)21 e21
20
备选练习:
1. 过点（1，2），且渐近线为 y 3 x 4
的双曲线方程是__1_6_y__2__.9x2 55
2.求中心在原点，对称轴为坐标轴，经过点
双曲线的几何性质课件
双曲线的渐近线方程为y=±b/a*x，其中a和b是双曲线的半焦距。
双曲线的
标准方程
为
：
x^2/a^2 -
y^2/b^2 =
1
a和b是双 曲线的半 轴长， a>b
双曲线的
标准方程
可以表示
为
：
x^2/a^2 -
y^2/b^2 =
1
双曲线的
标准方程
可以表示
为
：
x^2/a^2 -
y^2/b^2 =
1
双曲线的
双曲线关于x轴对称
双曲线关于原点对称
添加标题
添加标题
双曲线关于y轴对称
添加标题
添加标题
双曲线关于直线y=x对称
顶点：双曲线有两个顶点，分 别位于x轴和y轴上
中心：双曲线的中心位于顶点 连线的中点
顶点坐标：顶点的坐标可以通 过双曲线的方程求解得到
中心坐标：中心的坐标可以通 过顶点的坐标和双曲线的方程 求解得到
双曲线的离心率与焦点距离成反比 离心率越大，焦点距离越短 离心率越小，焦点距离越长 双曲线的离心率决定了焦点距离的大小
离心率：双曲线 的离心率是双曲 线的性质之一， 决定了双曲线的 形状和位置
开口大小：双曲 线的开口大小是 指双曲线的两个 焦点之间的距离， 与离心率有关
关系：双曲线的 离心率越大，开 口越小；离心率 越小，开口越大
双曲线的渐近 线与直线的交 点称为渐近线 与直线的交点
渐近线与直线 的交点性质是 双曲线的几何
性质之一
渐近线与直线 的交点性质决 定了双曲线的
形状和位置
渐近线与直线 的交点性质是 双曲线的重要
特征之一
确定双曲线的渐近线方程 计算渐近线与直线的交点坐标 判断交点是否在双曲线上 应用交点坐标求解双曲线的参数
双曲线的
标准方程
为
：
x^2/a^2 -
y^2/b^2 =
1
a和b是双 曲线的半 轴长， a>b
双曲线的
标准方程
可以表示
为
：
x^2/a^2 -
y^2/b^2 =
1
双曲线的
标准方程
可以表示
为
：
x^2/a^2 -
y^2/b^2 =
1
双曲线的
双曲线关于x轴对称
双曲线关于原点对称
添加标题
添加标题
双曲线关于y轴对称
添加标题
添加标题
双曲线关于直线y=x对称
顶点：双曲线有两个顶点，分 别位于x轴和y轴上
中心：双曲线的中心位于顶点 连线的中点
顶点坐标：顶点的坐标可以通 过双曲线的方程求解得到
中心坐标：中心的坐标可以通 过顶点的坐标和双曲线的方程 求解得到
双曲线的离心率与焦点距离成反比 离心率越大，焦点距离越短 离心率越小，焦点距离越长 双曲线的离心率决定了焦点距离的大小
离心率：双曲线 的离心率是双曲 线的性质之一， 决定了双曲线的 形状和位置
开口大小：双曲 线的开口大小是 指双曲线的两个 焦点之间的距离， 与离心率有关
关系：双曲线的 离心率越大，开 口越小；离心率 越小，开口越大
双曲线的渐近 线与直线的交 点称为渐近线 与直线的交点
渐近线与直线 的交点性质是 双曲线的几何
性质之一
渐近线与直线 的交点性质决 定了双曲线的
形状和位置
渐近线与直线 的交点性质是 双曲线的重要
特征之一
确定双曲线的渐近线方程 计算渐近线与直线的交点坐标 判断交点是否在双曲线上 应用交点坐标求解双曲线的参数
高二数学双曲线的几何性质PPT课件
问:有相同渐近线的双曲线方程一定是共轭双曲线吗？
第21页/共22页
感谢您的观看！
第22页/共22页
到炮弹爆炸比在B地晚2 s，且声速为340
m/s，求炮弹爆炸点的轨迹方程。 y
解：如图，建立直角
坐标系xoy，使A、B两
P
点在x轴上，并且坐标
原点o与线段AB的中点 重合。
A oBx
设爆炸点P的坐标为(x,y)，则
第18页/共22页
|PA|-|PB|=340×2=680 ，
即 2a=680，a=340 . 又 |AB|=800
y
A1 O
x
B1
第14页/共22页
1、中心在原点，一个顶点为A（ 3，0），
离心率为4 的双曲线方程是（） 3
A. x2 y2 1 B.7y2 x2 1
97
81 9
C y2 x2 1 D x2 y2 1或 7y2 x2 1
97
97
81 9
第15页/共22页
2.以椭圆x2 y2 1的焦点为顶点， 16 9
顶点为焦点的双曲线的方程是（）
A x2 y2 1 16 9
C y2 x2 1 79
B x2 y2 1 9 16
D x2 y2 1 79
第16页/共22页
双曲线 焦点在x轴
焦点在y轴
标准方程 图形
x2 y2 a2 b2 1(a 0, b 0)
y2 x2 a2 b2 1(a 0, b 0)
所以 2c=800, c=400 b2=c2-a2=44 400 .
因为|PA|-|PB|=340×2=680 ，所以x>0. 因此炮弹爆炸点的轨迹的方程为
x2 y2 1(x 0) 115600 44400
3.2.2双曲线的简单几何性质课件可编辑图片版共54张PPT
x2 a2
＋
y2 b2
＝1(a>b>0)共焦点的双曲线系方程可设为
a2x－2 λ－λ－y2b2＝1(b2<λ<a2)．
题型二 由双曲线方程研究其几何性质
探究 1 利用方程求解几何性质
例 1 (多选)已知双曲线 C：ax22－by22＝1(a>0，b>0)的左、右焦点
分别为
F1(－5,0)，F2(5,0)，则能使双曲线
y2 64
－
x2 16
＝
λ(λ>0)，将点(2,0)的坐标代入方程得λ＝－14<0(舍去)． 综上可知，所求双曲线的标准方程为x42－y2＝1. 答案：x42－y2＝1
4．与椭圆
x2 25
＋
y2 16
＝1有公共焦点，离心率为32
的双曲线方程为
________.
解析：方法一 由椭圆方程可得焦点坐标为(－3,0)，(3,0)，
2．常见双曲线方程的设法
(1)渐近线为y＝±
n m
x的双曲线方程可设为
x2 m2
－
y2 n2
＝λ(λ≠0，
m>0，n>0)；如果两条渐近线的方程为Ax±By＝0，那么双曲线的
方程可设为A2x2－B2y2＝m(m≠0，A>0，B>0)．
(2)与双曲线
x2 a2
－ by22
＝1或
y2 a2
－
x2 b2
系，并想办法转化为关于a，b，c的不等关系，结合c2＝a2＋b2和
c a
＝e得到关于e的不等式，然后求解．在建立不等式求e时，经常用
到结论：双曲线上一点到相应焦点距离的最小值为c－a.
双曲线的离心率常以渐近线为载体进行命题，注意二者参数
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
λλ 0
练习
：
求
以y
3 4
x
为渐近线且
过点A 2 3,3 的双曲线方程。
变
：求以y
3 4
x为渐近
线且
焦距为5的双曲线方程。
特殊的双曲线：
1、定义：实轴和虚轴等长的双曲线 叫做等轴双曲线。
2、等轴双曲线的标准方程：
1x2 y2 a2 2x2 y2 a2
3x2 y2 0
3、性质： 离心率e 2 渐近线方程为y x
7. 咱们去踢球吧。
Let’s play soccer.
4. 他有英英字典吗？ 不，他没有。他有一 本英汉字典。
Does he have an English English dictionary? No,he doesn’t. He has an English Chinese dictionary?
A.4x2 9y2 1 B.9y2 4x2 1
C.4x2 9y2 λ(λR,且λ 0) D.9x2 4y2 1
说明：
1与双
曲
线
x2 m2
y2 n2
1m
0,n 0
共渐近线的双曲线方程可设为:
x2 m2
y2 n2
λλ 0
2以直线
y
n m
x渐近
线的双
曲线
方程可设为:
x2 m2
y2 n2
1、中心在原点，一个顶点为A（ 3，0），
离心率为4 的双曲线方程是（） 3
A. x2 y2 1 B.7y2 x2 1
97
81 9
C y2 x2 1 D x2 y2 1或 7y2 x2 1
97
97
81 9
2.以椭圆x2 y2 1的焦点为顶点， 16 9
顶点为焦点的双曲线的方程是（）
A x2 y2 1 16 9
双曲线的几何性质（2）
双曲线 焦点在x轴
焦点在y轴
标准方程 图形
x2 a2
y2 b2
1(a
0, b
0)
y2 a2
x2 b2
1(a
0, b
0)
范围 对称性 顶点 焦点 渐近线
离心率
x a或x a
x轴：实轴,y轴：虚轴
(± a,0）
(c,0), c a2 b2
yb x a
e>1
y a或y a y轴：实轴,x轴：虚轴
A : x2 y2 1 3
B x2 y2 1 39
Байду номын сангаас
C. x2
y2
1或 x2
y2
1
12 36
12 4
D.x2 y2 1或 x2 y2 1
3
39
初一英语第二学期同步串讲 第七讲
Do you have an eraser?
Do you have a soccer ball?
ball games soccer
C y2 x2 1 79
B x2 y2 1 9 16
D x2 y2 1 79
3.以
y
2 3
x为渐
近线的双曲线
不可能
是()
A.4x2 9y2 1 B.9y2 4x2 1
C.4x2 9y2 λ(λR,且λ 0) D.9x2 4y2 1
4.中心在原点,实轴在x轴上,实轴长为2 3,
且两条渐近线夹角为600的双曲线方程是
42
5双曲线 x2 y2 1的渐近线方程为：
16 8
？？上述求渐近线的过程中你 能发现什么规律？
与 x2
m2
y2 n2
1
x2 m2
y2 n2
λλ
0
具有相同的渐近线。
重新解答： （2）过点（-1，3）和双曲线
x2 4
y2 9
1 有共同的渐近线。
(3)以y 2 x为渐近线的双曲线不可能是() 3
1. 你有一个排球吗？ 是的，我有。
Do you have a volleyball? Yes, I do.
2. 你有表兄妹吗? 不, 我没有。
Do you have any cousins? No,I don’t.
3. 她有网球拍吗？ 是的，她有。
Does she have a tennis racket? Yes, she does.
例2：
1求实轴在x轴上，一个
焦点在直线3x 4y 12 0 上的等轴双曲线的标准方程。
2 求 经 过 点3 ， 1的 等 轴 双 曲
线方程。
例3：已知双曲线与椭圆 25x2 9y2 225有公共焦点， 且它们的离心率之和为2， 求双曲线方程。
小结：
希望大家能掌握与渐 近线有关的双曲线方程 的求法，掌握等轴双曲 线的有关知识。
(0,±a)
(0,c), c a2 b2
xb y a
e>1
填空：龙门教案P136
例1：求适合下列条件的双曲线的 标准方程。
（1）过点(3,4)且虚轴长为实轴长的 2倍
（2）过点（-1，3）和双曲线 x2 y2 1 有共同的渐近线。
49
1
x2 a2
y2 b2
1(焦点在x轴上)
渐近线方程 y
Does he have a basketball?
Yes, he does.
basketball
badminton
baseball
tennis (racket)
volleyball
Ping pong (ball)
table tennis
golf
Do you have an American football / rugby?
Yes, I do. / No, I don’t.
5. 他们有笔记本吗？ 是的，他们有。
Do they have any note books? Yes, they do.
6. 让我看一看。
Let’s have a look.
Does he have a tennis racket?
Yes, he does. /No, he doesn't.
Does she have a soccer ball? Yes, she does. / No, she doesn't.
Golf club
Do you have a golf ball? Yes, I do. / No, I don’t.
Group work
Names
Lucy
Do you have a…?
Yes, I do.
Balls you have
basketball
What balls do you have? I have ….
b x，x2 a a2
y2 b2
0
2
y2 a2
x2 b2
1(
渐近线方程 y
焦
点
在y轴上)
a x， b
y a
2 2
x2 b2
0
练习：
1双曲线 x2
y2
y
2x 2
1 的 渐 近 线 方 程 为：
42
2双曲线 x2 y2 1的渐近线方程为：
84
3双曲线x2 2y2 1的渐近线方程为：
4双曲线 x2 y2 1的渐近线方程为：