通信原理第5章5-6(电子工业出版社张祖凡)[16页]

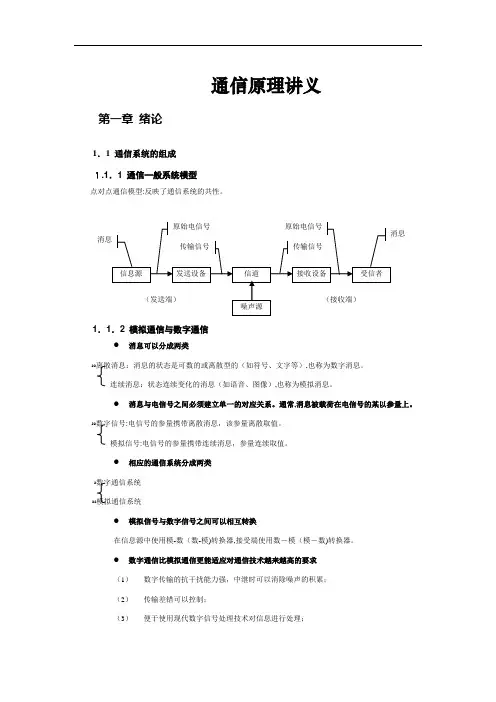
通信原理讲义第一章绪论1．1 通信系统的组成１.1．1 通信一般系统模型点对点通信模型:反映了通信系统的共性。

1．1．2 模拟通信与数字通信●消息可以分成两类ﻩﻩ离散消息：消息的状态是可数的或离散型的（如符号、文字等）,也称为数字消息。

连续消息：状态连续变化的消息（如语音、图像）,也称为模拟消息。

●消息与电信号之间必须建立单一的对应关系。

通常,消息被载荷在电信号的某以参量上。

ﻩﻩ数字信号:电信号的参量携带离散消息，该参量离散取值。

模拟信号:电信号的参量携带连续消息，参量连续取值。

●相应的通信系统分成两类ﻩ数字通信系统ﻩﻩ模拟通信系统●模拟信号与数字信号之间可以相互转换在信息源中使用模-数（数-模)转换器,接受端使用数－模（模－数)转换器。

●数字通信比模拟通信更能适应对通信技术越来越高的要求（1）数字传输的抗干扰能力强，中继时可以消除噪声的积累；（2）传输差错可以控制；（3）便于使用现代数字信号处理技术对信息进行处理；（4） 易于加密处理;（5） 可以综合传递各种消息,增强系统功能。

● 模拟通信系统模型（点对点）基带信号：携带信息，但具有频率很低的频谱分量,不适宜传输的原始电信号。

已调信号：基带信号经过调之后转换成其频带适合信道传输的信号，也称频带信号。

调制器:将基带信号转变为频带信号的设备。

解调器：将频带信号转变为基带信号的设备。

模拟通信强调变换的线性特性,既已调参量与基带信号成比例。

● 数字通信系统模型（点对点） 强调已调参量与基带信号之间的一一对应。

数字通信需要解决的问题:（2） 编码与解码：通过差错控制编码消除噪声或干扰造成的差错; （3） 加密和解密：对基带信号进行人为“搅乱”；（4） 同步:发送和接收节拍一致,包括：位同步（码元同步)和群同步、帧同步、句同步或码组同步。

数字通信模型:同步环节的位置不固定,图中没有出现。

消息消息数字基带传输模型：● 数字通信的缺点 比模拟通信占据更宽的频带。

《通信原理》习题参考答案第一章1-1. 设英文字母E 出现的概率为0.105，x 出现的概率为0.002。

试求E 及x 的信息量。

解： )(25.3105.01)(log 2bit E I ==)(97.8002.01)(log 2bit X I == 题解：这里用的是信息量的定义公式)(1log x P I a =注：1、a 的取值：a ＝2时，信息量的单位为bita ＝e 时，信息量的单位为nita ＝10时，信息量的单位为哈特莱2、在一般的情况下，信息量都用bit 为单位，所以a ＝21-2. 某信息源的符号集由A ，B ，C ，D 和E 组成，设每一符号独立出现，其出现概率分别为1/4，1/8，1/8，3/16和5/16。

试求该信息源符号的平均信息量。

解：方法一：直接代入信源熵公式：)()()()()(E H D H C H B H A H H ++++=516165316163881881441log log log log log 22222++++=524.0453.083835.0++++= 符号）/(227.2bit =方法二：先求总的信息量I)()()()()(E I D I C I B I A I I ++++= 516316884log log log log log 22222++++= 678.1415.2332++++= )(093.12bit =所以平均信息量为：I/5＝12.093/5＝2.419 bit/符号题解：1、方法一中直接采用信源熵的形式求出，这种方法属于数理统计的方法求得平均值，得出结果的精度比较高，建议采用这种方法去计算2、方法二种采用先求总的信息量，在取平均值的方法求得，属于算术平均法求平均值，得出结果比较粗糙，精度不高，所以尽量不采取这种方法计算注：做题时请注意区分平均信息量和信息量的单位：平均信息量单位是bit/符号，表示平均每个符号所含的信息量，而信息量的单位是bit ，表示整个信息所含的信息量。

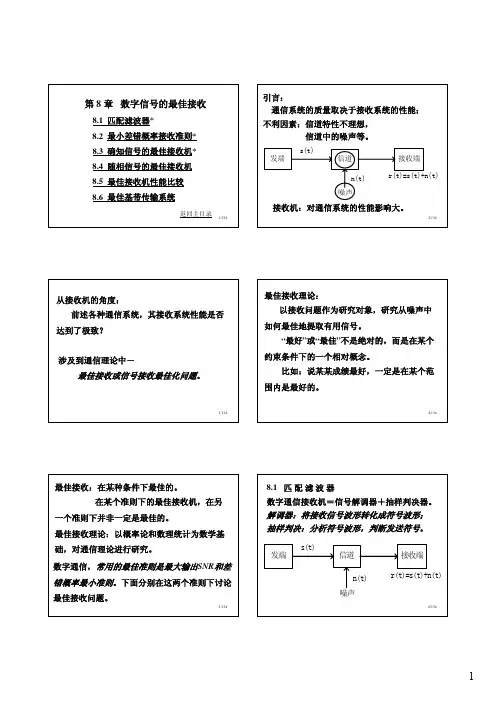
匹配滤波器的单位冲激响应为h(t)=s(t =T ，则有H ω−1(1h(t)=s(T-t)匹配滤波器的单位冲激响应如图8 -3(b)因此，匹配滤波器的传输函数为1((j j j S ωωω【例2】已知匹配滤波器的单位冲激响应h(t)如图所示。

试求：1）输入信号波形；）匹配滤波器的输出波形；）最大输出信噪比时刻和最大输出信噪比；　)t 00.5-A最大输出信噪比出现时刻应在信号结束之；　最大输出信噪比为：哪一个信号是不确定的；即使知道发送哪一个信号，但是信号在传输过程中可能发生）确定匹配滤波器的冲击响应。

）两个匹配滤波器的输出信号。

bs 123/13421112()()s s t T s t ϖϖ≤⎩且，和。

1、画出相关器构成的最佳接收机结构；2、设信息代码为110，画出各点可能波形；3、若接收机输入高斯白噪声功率普密度为n 0/2,试求系统的误码率。

)bE n =解：1、画出最佳相干接收机结构；解：2、设信息代码为110，画出各点可能波形；(t (解：3、若接收机输入高斯白噪声功率普密度为n 试求系统的误码率。

由题可知：信号是等能量的，即2202()2TsTsE t dt s T ==∫∫(2E A erfc画出匹配滤波器的最佳接收机结构确定或画出匹配滤波器的冲击响应。

E E p ∴∵）T s(41)2cos 0)(20)(00200f f j e f f te f dt e s T f f j T f f Tft j +−−+−=+−−−−∫πππππT s][(4)(41)(*)()(202)22000f j e f f j e e f S e f f s s ssT f f j fT j T f f fT j ft j +−+−−=+−−−−ππππππs t T f t −=−),(2cos )0π0/f 0cos 2,0f t π≤因此，其匹配滤波器的传输函数为：t 0(b ) 冲激响应T s∫∞∞−−=τττd t h s t s o )()()(s s s T t T T t ,2,≤≤<≤匹配滤波器输出波形可以由卷积公式求出：)和h (t )在区间(0, Ts )外都等于零，故上式中的积分可以分为如下几段进行计算(a ) 信号波形(b ) 冲激响应(c ) 输出波形T sT sT s2T s积分积分s 1(t )s 0(t )抽样比较判决抽样t = T s t = T s输入用相关器代替上图中的匹配滤波器得到:匹配滤波器输出。

第五章〔正弦载波数字调制系统〕习题及其答案【题5－1】设发送数字信息为，试分别画出 2ASK 、2FSK 、2PSK 及2DPSK 信号的波形示意图。

【答案5－1】2ASK 、2FSK 、2PSK 及2DPSK 信号的波形如下列图所示。

【题5－2】确定某2ASK 系统的码元传输速率为103Band ，所用的载波信号为()6cos 410A π⨯。

1〕设所传送的数字信息为011001，试画出相应的2ASK 信号波形示意图； 2〕求2ASK 信号的带宽。

【答案5－2】1〕由题中的确定条件可知310B R Baud =因此一个码元周期为3110s B T s R -==载波频率为664102102s f Hz ππ⨯==⨯载波周期为61102T s -=⨯所以一个码元周期内有2000个载波周期。

如下列图所示我们画出2ASK 信号的波形图，为简便，我们用两个载波周期代替2000个载波周期。

2〕依据2ASK 的频谱特点，可知其带宽为 222000B B R Hz T ===【题5－3】设某2FSK 调制系统的码元传输速率为1000Baud ，已调信号的载频为1000Hz 或 2000 HZ 。

1〕假设发送数字信息为011010，试画出相应的ZFSK 信号波形；2〕摸索讨这时的2FSK 信号应选择怎样的解调器解调？3〕假设发送数字信息是等可能的，试画出它的功率谱密度草图。

【答案5－3】1〕由题意可画出ZFSK 信号波形如下列图所示。

2〕由于ZFSK 信号载波频差较小，频谱有较大重叠，接受非相干解调时上下两个支路有较大串扰，使解调性能降低。

由于两个载频人与人构成正交信号，接受相干解调可减小相互串扰，所以应接受相干解调。

3〕该2FSK 信号功率谱密度草图如下列图所示。

【题5－4】假设在某2DPSK 系统中，载波频率为 2400 Hz ，码元速率为 1200 Band ，确定相对码序列为11000101ll 。

1〕试画出2DPSK 信号波形〔注：相对偏移ϕ∆，可自行假设〕；2〕假设接受差分相干解调法接收该信号时，试画出解调系统的各点波形；3〕假设发送信息符号0和1的概率分别为0.6和0.4，试求2DPSK 信号的功率谱密度。

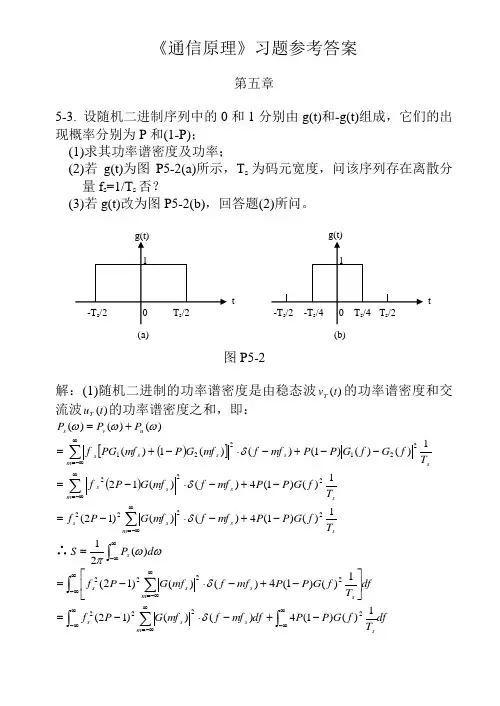
《通信原理》习题参考答案第五章5-3. 设随机二进制序列中的0和1分别由g(t)和-g(t)组成，它们的出现概率分别为P 和(1-P)；(1)求其功率谱密度及功率；(2)若g(t)为图P5-2(a)所示，T s 为码元宽度，问该序列存在离散分量f s =1/T s 否？(3)若g(t)改为图P5-2(b)，回答题(2)所问。

解：(1)随机二进制的功率谱密度是由稳态波)(t v T 的功率谱密度和交流波)(t u T 的功率谱密度之和，即： )()()(ωωωu v s P P P +=()[]sm s s s s T f G f G P P mf f mf G P mf PG f 1)()()1()()(1)(221221--+-⋅-+=∑∞-∞=δ ()sm s s s T f G P P mf fmf G P f1)()1(4)()(12222-+-⋅-=∑∞-∞=δ s m s s s T f G P P mf f mf G P f 1)()1(4)()()12(2222-+-⋅-=∑∞-∞=δ∴⎰∞∞-=ωωπd P S s )(21df T f G P P mf f mf G P f s m s s s ⎰∑∞∞-∞-∞=⎥⎦⎤⎢⎣⎡-+-⋅-=1)()1(4)()()12(2222δ df T f G P P df mf f mf G P f s m s s s ⎰⎰∑∞∞-∞∞-∞-∞=-+-⋅-=1)()1(4)()()12(2222δtt(a) (b) 图P5-2df f G P P T df mf f mf G P f s s m s s⎰⎰∑∞∞-∞∞-∞-∞=-+--=2222)()1(41)()()12(δ (2) 若g(t)为图P5-2(a)，则g(t)经过傅立叶变化可得到它的频谱，即：)2()(ss T Sa T G ωω=将ω换为f 得： ffT f T f T T f T Sa T f G s s s ss s πππππsin sin )()(=== 判断频域中是否存在s T f 1=，就是将sT f 1=代入)(f G 中，得：0sin sin )(===ππππss T f f T f G说明sT f 1=时g(t)的功率为0，所以不存在该分量。