考点24 点线面的判定与性质-2019年高考数学江苏专版五年真题与三年模拟试题考点分类汇编含答案

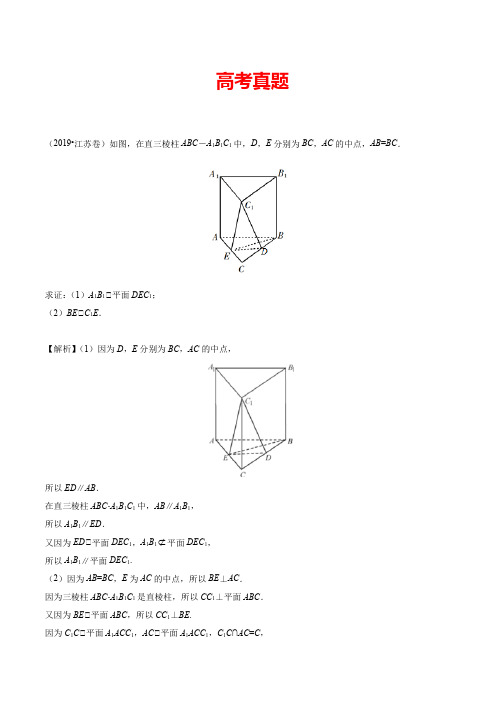
高考真题（2019•江苏卷）如图，在直三棱柱ABC －A 1B 1C 1中，D ，E 分别为BC ，AC 的中点，AB =BC ．求证：（1）A 1B 1∥平面DEC 1； （2）BE ∥C 1E ．【解析】（1）因为D ，E 分别为BC ，AC 的中点，所以ED ∥AB ．在直三棱柱ABC -A 1B 1C 1中，AB ∥A 1B 1， 所以A 1B 1∥ED ．又因为ED ∥平面DEC 1，A 1B 1平面DEC 1， 所以A 1B 1∥平面DEC 1.（2）因为AB =BC ，E 为AC 的中点，所以BE ⊥AC ． 因为三棱柱ABC -A 1B 1C 1是直棱柱，所以CC 1⊥平面ABC ． 又因为BE ∥平面ABC ，所以CC 1⊥BE .因为C 1C ∥平面A 1ACC 1，AC ∥平面A 1ACC 1，C 1C ∩AC =C ，所以BE ⊥平面A 1ACC 1.因为C 1E ∥平面A 1ACC 1，所以BE ⊥C 1E . 【答案】（1）见解析；（2）见解析.（2019•天津卷（理））如图，平面，，.（Ⅰ）求证：平面；（Ⅱ）求直线与平面所成角的正弦值； （Ⅲ）若二面角的余弦值为，求线段的长.【解析】依题意，可以建立以A 为原点，分别以的方向为x 轴，y 轴，z 轴正方向的空间直角坐标系（如图），可得. 设，则.AE ⊥ABCD ,CF AE AD BC ∥∥,1,2AD AB AB AD AE BC ⊥====BF ∥ADE CE BDE E BD F --13CF ,,AB ADAE ()()()()()0,0,0,1,0,0,1,2,0,0,1,0,0,0,2A B C D E ()0CF h h =>()1,2,F h（Ⅰ）依题意，是平面ADE 的法向量， 又，可得，又因为直线平面，所以平面. （Ⅱ）依题意，，设为平面BDE 的法向量，则，即，不妨令z =1，可得， 因此有.所以，直线与平面所成角的正弦值为. （Ⅲ）设为平面BDF 的法向量，则，即. 不妨令y =1，可得. 由题意，有，解得. 经检验，符合题意｡ 所以，线段的长为. 【答案】（Ⅰ）见证明；（Ⅱ）（Ⅲ）（2019•全国I 卷（理））如图，直四棱柱ABCD–A 1B 1C 1D 1的底面是菱形，AA 1=4，AB =2，∠BAD =60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点．()1,0,0AB =()0,2,BF h =0BF AB ⋅=BF ⊄ADE BF ∥ADE (1,1,0),(1,0,2),(1,2,2)BD BE CE =-=-=--(),,n x y z =00n BD n BE ⎧⋅=⎨⋅=⎩020x y x z -+=⎧⎨-+=⎩()2,2,1n =4cos ,9||||CE n CE n CE n ⋅〈〉==-CE BDE 49(),,m x y z =00m BD m BF ⎧⋅=⎨⋅=⎩020x y y hz -+=⎧⎨+=⎩21,1,m h ⎛⎫=-⎪⎝⎭41cos ,332m n m n m n-⋅===⨯87h =CF 874987（1）证明：MN ∥平面C 1DE ； （2）求二面角A -MA 1-N 的正弦值．【解析】（1）连接，，分别为，中点 为的中位线且 又为中点，且 且 四边形为平行四边形，又平面，平面 平面（2）设，由直四棱柱性质可知：平面 四边形为菱形则以为原点，可建立如下图所示的空间直角坐标系：ME 1BC M E 1BB BC ME ∴1B BC ∆1//ME B C ∴112ME B C =N 1A D 11//A D B C 1//ND B C ∴112ND B C =//ME ND ∴∴MNDE //MN DE ∴MN ⊄1C DE DE 1C DE //MN ∴1C DE ACBD O =11111AC B D O =1OO ⊥ABCD ABCD AC BD ∴⊥O则：，，，D （0，-1,0） 取中点，连接，则 四边形为菱形且 为等边三角形又平面，平面平面，即平面为平面的一个法向量，且 设平面的法向量，又， ，令，二面角【答案】（1）见解析；（2 )A()0,1,2M )14A 1,222N ⎛⎫-⎪ ⎪⎝⎭AB F DF 01,,22F ⎛⎫⎪ ⎪⎝⎭ABCD 60BAD ∠=BAD ∴∆DF AB ∴⊥1AA ⊥ABCD DF ⊂ABCD 1DFAA ∴⊥DF ⊥∴11ABB A DF ⊥1AMA DF ∴1AMA 33,022DF ⎛⎫= ⎪⎪⎝⎭1MA N (),,n x y z =()13,1,2MA =-33,022MN ⎛⎫=-⎪ ⎪⎝⎭132033022n MA x y z n MN x y ⎧⋅=-+=⎪∴⎨⋅=-=⎪⎩x 1y =1z =-()3,1,1n ∴=-cos ,515DF n DF n DF n⋅∴<>===⋅10sin ,5DF n ∴<>=∴1A MA N --。

2019年全国普通高等学校招生统一考前模拟数学试题（江苏卷）一、填空题1．已知集合{1,2,3,6},{|23},A B x x =-=-<<则=A B ________________.【答案】{}1,2- 【解析】试题分析：{}{}{}1,2,3,6231,2AB x x =--<<=-．故答案应填：{}1,2- ，【考点】集合运算2．复数(12i)(3i),z =+-其中i 为虚数单位，则z 的实部是________________. 【答案】5【解析】试题分析：(12)(3)55z i i i =+-=+．故答案应填：5 【考点】复数概念3．在平面直角坐标系xOy 中，双曲线22173x y -=的焦距是________________.【答案】【解析】试题分析：222227,3,7310,2a b c a b c c ==∴=+=+=∴=，焦距为2c【考点】双曲线性质4．已知一组数据4.7,4.8,5.1,5.4,5.5，则该组数据的方差是________________. 【答案】0.1【解析】试题分析：这组数据的平均数为1(4.7 4.8 5.1 5.4 5.5) 5.15++++=，2222221(4.7 5.1)(4.8 5.1)(5.1 5.1)(5.4 5.1)(5.5 5.1)0.15S ⎡⎤∴=-+-+-+-+-=⎣⎦．故答案应填：0.1， 【考点】方差5．函数的定义域是 . 【答案】[]3,1-【解析】试题分析：要使函数有意义，必须2320x x --≥，即2230x x +-≤，31x ∴-≤≤．故答案应填：[]3,1-，【考点】函数定义域6．如图是一个算法的流程图，则输出的a 的值是 .【答案】9【解析】试题分析：第一次循环：5,7a b ==，第二次循环：9,5a b ==，此时a b >循环结束9a =，故答案应填：9【考点】循环结构流程图7．将一颗质地均匀的骰子（一种各个面上分别标有1，2，3，4，5，6个点的正方体玩具）先后抛掷2次，则出现向上的点数之和小于10的概率是 . 【答案】5.6【解析】点数小于10的基本事件共有30种，所以所求概率为305.366= 【考点】古典概型概率8．已知{a n }是等差数列，S n 是其前n 项和.若a 1+a 22=-3，S 5=10，则a 9的值是 . 【答案】20.【解析】由510S =得32a =，因此2922(2d)33,23620.d d a -+-=-⇒==+⨯= 【考点】等差数列性质9．定义在区间[0,3π]上的函数y=sin2x 的图象与y=cosx 的图象的交点个数是 . 【答案】7【解析】由1sin 2cos cos 0sin 2x x x x =⇒==或，因为[0,3]x π∈，所以3551317,,,,,,,2226666x πππππππ=共7个【考点】三角函数图像10．如图，在平面直角坐标系xOy 中，F 是椭圆22221()x y a b a b+=＞＞0 的右焦点，直线2by = 与椭圆交于B ，C 两点，且90BFC ∠= ,则该椭圆的离心率是 .【解析】由题意得),C(),22b b B，因此22222()0322b c c a e -+=⇒=⇒= 【考点】椭圆离心率11．设f （x ）是定义在R 上且周期为2的函数，在区间[ −1,1）上，,10,()2,01,5x a x f x x x +-≤<⎧⎪=⎨-≤<⎪⎩其中.a ∈R若59()()22f f -= ，则(5)f a 的值是 . 【答案】25-【解析】51911123()()()()22222255f f f f a a -=-==⇒-+=-⇒=， 因此32(5)(3)(1)(1)155f a f f f ===-=-+=-【考点】分段函数，周期性质12． 已知实数x ，y 满足240220330x y x y x y -+≥⎧⎪+-≥⎨⎪--≤⎩，则x 2+y 2的取值范围是 .【答案】4[,13]5【解析】由图知原点到直线220x y +-=距离平方为22x y +最小值，为245=，原点到点(2,3)距离平方为22x y +最大值，为13，因此22x y +取值范围为4[,13]5【考点】线性规划13．如图，在△ABC 中，D 是BC 的中点，E ，F 是AD 上的两个三等分点，4BC CA ⋅=，1BF CF ⋅=- ，则BE CE ⋅ 的值是 .【答案】78【解析】因为2222436444AO BC FO BC BA CA --⋅===,22414FO BCBF CF -⋅==-,因此22513,BC 82FO ==，22224167448EO BC FO BC BE CE --⋅===【考点】向量数量积14．在锐角三角形ABC 中，若sinA=2sinBsinC ，则tanAtanBtanC 的最小值是 . 【答案】8.【解析】sin sin(B C)2sin sin tan tan 2tan tan A B C B C B C =+=⇒+=，因此tan tan tan tan tan tan tan 2tan tan tan tan tan 8A B C A B C A B C A B C =++=+≥≥，即最小值为8.【考点】三角恒等变换，切的性质应用二、解答题15．在ABC △中，AC=6，4πcos .54B C ==， （1）求AB 的长； （2）求πcos(6A -)的值. 【答案】（1）（2【解析】试题分析：（1）利用同角三角函数关系求3sin 5B ，= 再利用正弦定理求值，（2）利用诱导公式及两角和与差正余弦公式分别求sin sin()cos()A B C A B C =+==-+=，cos(A )6π-试题解析：解（1）因为4cos ,0,5B B π=<<所以3sin ,5B ==由正弦定理知sin sin AC ABB C=，所以6sin 23sin 5AC C AB B ⋅===（2）在三角形ABC 中A B C π++=，所以().A B C π=-+于是cosA cos(B C)cos()cos cossin sin ,444B B B πππ=-+=-+=-+又43cos ,sin ,55B B ==，故43cos 55A =-+=因为0A π<<，所以sin A因此1cos()cos cossin sin6662A A A πππ-=+==【考点】同角三角函数关系，正余弦定理，两角和与差公式16．如图，在直三棱柱ABC-A 1B 1C 1中，D ，E 分别为AB ，BC 的中点，点F 在侧棱B 1B 上，且11B D A F ⊥ ，1111AC A B ⊥.求证：（1）直线DE ∥平面A 1C 1F ； （2）平面B 1DE ⊥平面A 1C1F. 【答案】（1）详见解析（2）详见解析 【解析】试题分析：（1）利用线面平行判定定理证明线面平行，而线线平行的寻找往往结合平几知识，如中位线性质（2）利用面面垂直判定定理证明，即从线面垂直出发给予证明，而线面垂直的证明，往往需要多次利用线面垂直性质与判定定理试题解析：证明：（1）在直三棱柱111ABC A B C -中，11//AC AC 在三角形ABC 中，因为D,E 分别为AB,BC 的中点. 所以//DE AC ，于是11//DE AC又因为DE ⊄平面1111,AC F AC ⊂平面11AC F 所以直线DE//平面11AC F（2）在直三棱柱111ABC A B C -中，1111AA ⊥平面A B C 因为11A C ⊂平面111A B C ，所以111AA ⊥A C又因为111111*********,,AC A B AA ABB A A B ABB A A B AA A ⊥⊂⊂=，平面平面所以11AC ⊥平面11ABB A因为1B D ⊂平面11ABB A ，所以111A C B D ⊥又因为1111111111111C F,C F,B D A AC A A F A AC A F A ⊥⊂⊂=F ，平面平面所以111C F B D A ⊥平面因为直线11B D B DE ⊂平面，所以1B DE 平面11.A C F ⊥平面【考点】直线与直线、平面与平面位置关系17．现需要设计一个仓库，它由上下两部分组成，上部分的形状是正四棱锥1111P A BC D -，下部分的形状是正四棱柱1111ABCD A BC D -（如图所示），并要求正四棱柱的高1PO 的四倍.（1）若16,PO 2,AB m m ==则仓库的容积是多少？（2）若正四棱柱的侧棱长为6m,则当1PO 为多少时，仓库的容积最大？【答案】（1）312（2）1PO =【解析】试题分析：（1）明确柱与锥体积公式区别，分别代入对应公式求解（2）根据体积关系建立函数解析式，()()32636,063V V V h h h =+=-<<锥柱再利用导数求其最值 试题解析：解：（1）由PO 1=2知OO 1=4PO 1=8.因为A 1B 1=AB=6，所以正四棱锥P-A 1B 1C 1D 1的体积()22311111=6224;33V A B PO m ⋅⋅=⨯⨯=柱 正四棱柱ABCD-A 1B 1C 1D 1的体积()2231=68288.V AB OO m ⋅=⨯=柱所以仓库的容积V=V 锥+V 柱=24+288=312（m 3）. （2）设A 1B 1=a （m ）,PO 1=h （m ），则0<h<6,OO 1=4h.连结O 1B 1. 因为在11RT PO B ∆中，222111OB PO PB +=，所以22362h ⎛⎫+=⎪ ⎪⎝⎭，即()22236.a h =- 于是仓库的容积()()222311326436,06333V V V a h a h a h h h h =+=⋅+⋅==-<<锥柱， 从而()()2226'36326123V h h =-=-.令'0V =，得h =或h =-.当0h <<'0V > ，V 是单调增函数；当6h <<时，'0V <，V 是单调减函数.故h =V 取得极大值，也是最大值.因此，当1PO = 时，仓库的容积最大.【考点】函数的概念、导数的应用、棱柱和棱锥的体积18．如图，在平面直角坐标系xOy 中，已知以M 为圆心的圆M:221214600x y x y +--+=及其上一点A（2，4）（1）设圆N 与x 轴相切，与圆M 外切，且圆心N 在直线x=6上，求圆N 的标准方程；（2）设平行于OA 的直线l 与圆M 相交于B 、C 两点，且BC=OA,求直线l 的方程；（3）设点T （t,o ）满足：存在圆M 上的两点P 和Q,使得TA TP TQ +=,求实数t 的取值范围。

13.3 直线、平面平行的判定与性质挖命题【考情探究】分析解读空间的平行问题是江苏高考的热点内容,几乎每年都考,主要考查线面平行的判定,偶尔涉及面面平行的判定与性质,一般与垂直关系综合在一起考查,在解答题的前两题中出现,属于简单题,一般是第一问.在复习中,要注重表述的规范,逻辑的严谨以及定理、公理、定义使用的完备性,这是最近几年高考阅卷的重点.破考点【考点集训】考点一线面平行的判定与性质1.(2018江苏南师大附中检测)空间四边形ABCD的两条对棱AC、BD的长分别为5和4,则平行于两条对棱的截面四边形EFGH在平移过程中,周长的取值范围是.2.(2018江苏启东中学月考)如图,在四棱锥P-ABCD中,AD∥BC,AB=BC=AD,E,F,H分别为AD,PC,CD的中点,AC与BE交于O点,G是OF上一点.(1)求证:AP∥平面BEF;(2)求证:GH∥平面PAD.证明(1)如图,连接EC,∵AD∥BC,AE=AD,BC=AD,∴BC AE.∴四边形ABCE是平行四边形,∴O为AC的中点.又∵F是PC的中点,∴FO∥AP,又FO⊂平面BEF,AP⊄平面BEF,∴AP∥平面BEF.(2)如图,连接FH,OH,∵F,H分别是PC,CD的中点,∴FH∥PD,又PD⊂平面PAD,FH⊄平面PAD,又∵O是AC的中点,H是CD的中点,∴OH∥AD,又AD⊂平面PAD,OH⊄平面PAD,∴OH∥平面PAD.又FH∩OH=H,FH,OH⊂平面OHF,∴平面OHF∥平面PAD.又∵GH⊂平面OHF,∴GH∥平面PAD.考点二面面平行的判定与性质(2019届江苏泰州中学检测)如图,E、F、G、H分别是正方体ABCD-A1B1C1D1的棱BC、CC1、C1D1、AA1的中点.求证:(1)EG∥平面BB1D1D;(2)平面BDF∥平面B1D1H.证明(1)取B1D1的中点O,连接GO,OB,∵O,G分别是B1D1,D1C1的中点,∴OG∥B1C1,且OG=B1C1,又BE∥B1C1,且BE=B1C1,∴OG∥BE,且OG=BE,∴四边形BEGO为平行四边形,故OB∥EG,又EG⊄平面BB1D1D,OB⊂平面BB1D1D,∴EG∥平面BB1D1D.(2)由题意可知BD∥B1D1.如图,连接HB、D1F,易证四边形HBFD1是平行四边形,故HD1∥BF.又B1D1∩HD1=D1,BD∩BF=B,B1D1,HD1⊂平面B1D1H,BD,BF⊂平面BDF,所以平面BDF∥平面B1D1H.炼技法【方法集训】方法一证明直线与平面平行的方法1.(2019届江苏南通一中检测)下列命题(其中a,b表示直线,α表示平面)中正确的个数是.①若a∥b,b⊂α,则a∥α;②若a∥α,b∥α,则a∥b;③若a∥b,b∥α,则a∥α;④若a∥α,b⊂α,则a∥b.答案02.(2019届江苏栟茶中学检测)下列命题中正确的个数是.①若直线l上有无数个点不在平面α内,则l∥α;②若直线l与平面α平行,则l与平面α内的任意一条直线都平行;③如果两条平行直线中的一条与一个平面平行,那么另一条也与这个平面平行;④若直线l与平面α平行,则l与平面α内的任意一条直线都没有公共点.答案 13.(2018江苏邗江中学检测)如图,已知在三棱柱ABC-A1B1C1中,M、N、P、Q分别是AA1、BB1、AB、B1C1的中点.求证:PC1∥平面MNQ.证明连接PB1,与MN相交于K,连接KQ.∵MN∥PB,N为BB1的中点,∴K为PB1的中点.又∵Q是C1B1的中点,∴PC1∥KQ.又KQ⊂平面MNQ,PC1⊄平面MNQ,∴PC1∥平面MNQ.方法二证明平面与平面平行的方法(2018江苏扬中高级中学检测)如图,在四棱锥E-ABCD中,△ABD为正三角形,EB=ED,CB=CD.(1)求证:EC⊥BD;(2)若AB⊥BC,M、N分别为线段AE、AB的中点,求证:平面DMN∥平面BEC.证明(1)取BD的中点O,连接EO、CO,∵CD=CB,EB=ED,∴CO⊥BD,EO⊥BD.又CO∩EO=O,∴BD⊥平面EOC.∵EC⊂平面EOC,∴BD⊥EC.(2)∵N是AB的中点,△ABD为正三角形,∴DN⊥AB.∵BC⊥AB,∴DN∥BC.∵BC⊂平面BCE,DN⊄平面BCE,∴DN∥平面BCE.∵M为AE的中点,N为AB的中点,∴MN∥BE.∵MN⊄平面BCE,BE⊂平面BCE,∴MN∥平面BCE.∵MN∩DN=N,MN,DN⊂平面MND,∴平面MND∥平面BCE.过专题【五年高考】A组自主命题·江苏卷题组1.(2018江苏,15,14分)在平行六面体ABCD-A1B1C1D1中,AA1=AB,AB1⊥B1C1.求证:(1)AB∥平面A1B1C;(2)平面ABB1A1⊥平面A1BC.证明本小题主要考查直线与直线、直线与平面以及平面与平面的位置关系,考查空间想象能力和推理论证能力.(1)在平行六面体ABCD-A1B1C1D1中,AB∥A1B1.因为AB⊄平面A1B1C,A1B1⊂平面A1B1C,所以AB∥平面A1B1C.(2)在平行六面体ABCD-A1B1C1D1中,四边形ABB1A1为平行四边形.又因为AA1=AB,所以四边形ABB1A1为菱形,所以AB1⊥A1B.因为AB1⊥B1C1,BC∥B1C1,所以AB1⊥BC.又因为A1B∩BC=B,A1B⊂平面A1BC,BC⊂平面A1BC,所以AB1⊥平面A1BC,又因为AB1⊂平面ABB1A1,所以平面ABB1A1⊥平面A1BC.2.(2015江苏,16,14分)如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.求证:(1)DE∥平面AA1C1C;(2)BC1⊥AB1.证明(1)由题意知,E为B1C的中点,又D为AB1的中点,因此DE∥AC.又因为DE⊄平面AA1C1C,AC⊂平面AA1C1C,所以DE∥平面AA1C1C.(2)因为棱柱ABC-A1B1C1是直三棱柱,所以CC1⊥平面ABC.因为AC⊂平面ABC,所以AC⊥CC1.又因为AC⊥BC,CC1⊂平面BCC1B1,BC⊂平面BCC1B1,BC∩CC1=C,所以AC⊥平面BCC1B1.又因为BC1⊂平面BCC1B1,所以BC1⊥AC.因为BC=CC1,所以矩形BCC1B1是正方形,因此BC1⊥B1C.因为AC,B1C⊂平面B1AC,AC∩B1C=C,所以BC1⊥平面B1AC.又因为AB1⊂平面B1AC,所以BC1⊥AB1.3.(2017江苏,15,14分)如图,在三棱锥A-BCD中,AB⊥AD,BC⊥BD,平面ABD⊥平面BCD,点E,F(E与A,D不重合)分别在棱AD,BD上,且EF⊥AD.求证:(1)EF∥平面ABC;(2)AD⊥AC.证明(1)在平面ABD内,因为AB⊥AD,EF⊥AD,所以EF∥AB.又因为EF⊄平面ABC,AB⊂平面ABC,所以EF∥平面ABC.(2)因为平面ABD⊥平面BCD,平面ABD∩平面BCD=BD,BC⊂平面BCD,BC⊥BD,所以BC⊥平面ABD.因为AD⊂平面ABD,所以BC⊥AD.又AB⊥AD,BC∩AB=B,AB⊂平面ABC,BC⊂平面ABC,所以AD⊥平面ABC.又因为AC⊂平面ABC,所以AD⊥AC.方法总结立体几何中证明线线垂直的一般思路:(1)利用两平行直线垂直于同一条直线(a∥b,a⊥c⇒b⊥c);(2)线面垂直的性质(a⊥α,b⊂α⇒a⊥b).B组统一命题、省(区、市)卷题组考点直线、平面平行的判定与性质1.(2018浙江改编,6,4分)已知平面α,直线m,n满足m⊄α,n⊂α,则“m∥n”是“m∥α”的.(填“充分不必要条件”“必要不充分条件”“充要条件”或“既不充分又不必要条件”)答案充分不必要条件2.(2016课标全国Ⅱ,14,5分)α,β是两个平面,m,n是两条直线,有下列四个命题:①如果m⊥n,m⊥α,n∥β,那么α⊥β.②如果m⊥α,n∥α,那么m⊥n.③如果α∥β,m⊂α,那么m∥β.④如果m∥n,α∥β,那么m与α所成的角和n与β所成的角相等.其中正确的命题有.(填写所有正确命题的编号)答案②③④3.(2014辽宁改编,4,5分)已知m,n表示两条不同直线,α表示平面.下列说法正确的是.①若m∥α,n∥α,则m∥n ②若m⊥α,n⊂α,则m⊥n③若m⊥α,m⊥n,则n∥α④若m∥α,m⊥n,则n⊥α答案②4.(2015安徽改编,5,5分)已知m,n是两条不同直线,α,β是两个不同平面,则下列命题正确的是.(1)若α,β垂直于同一平面,则α与β平行;(2)若m,n平行于同一平面,则m与n平行;(3)若α,β不平行···,则在α内不存在···与β平行的直线;(4)若m,n不平行···,则m与n不可能···垂直于同一平面.答案(4)5.(2017北京文,18,14分)如图,在三棱锥P-ABC中,PA⊥AB,PA⊥BC,AB⊥BC,PA=AB=BC=2,D为线段AC的中点,E为线段PC上一点.(1)求证:PA⊥BD;(2)求证:平面BDE⊥平面PAC;(3)当PA∥平面BDE时,求三棱锥E-BCD的体积.解析本题考查线面垂直的判定和性质,面面垂直的判定及线面平行的性质,三棱锥的体积.考查空间想象能力.(1)证明:因为PA⊥AB,PA⊥BC,所以PA⊥平面ABC.又因为BD⊂平面ABC,所以PA⊥BD.(2)证明:因为AB=BC,D为AC中点,所以BD⊥AC.由(1)知,PA⊥BD,所以BD⊥平面PAC.所以平面BDE⊥平面PAC.(3)因为PA∥平面BDE,平面PAC∩平面BDE=DE,所以PA∥DE.因为D为AC的中点,所以DE=PA=1,BD=DC=.由(1)知,PA⊥平面ABC,所以DE⊥平面ABC.所以三棱锥E-BCD的体积V=BD·DC·DE=.直击高考立体几何是高考的必考题型,对立体几何的考查主要有两个方面:一是空间位置关系的证明;二是体积或表面积的求解.6.(2016课标全国Ⅲ文,19,12分)如图,四棱锥P-ABCD中,PA⊥底面ABCD,AD∥BC,AB=AD=AC=3,PA=BC=4,M为线段AD上一点,AM=2MD,N为PC的中点.(1)证明MN∥平面PAB;(2)求四面体NBCM的体积.解析(1)证明:由已知得AM=AD=2,取BP的中点T,连接AT,TN,由N为PC中点知TN∥BC,TN=BC=2.(3分)又AD∥BC,故TN AM,故四边形AMNT为平行四边形,于是MN∥AT.因为AT⊂平面PAB,MN⊄平面PAB,所以MN∥平面PAB.(6分)(2)因为PA⊥平面ABCD,N为PC的中点,所以N到平面ABCD的距离为PA.(9分)取BC的中点E,连接AE.由AB=AC=3得AE⊥BC,AE=-=.由AM∥BC得M到BC的距离为,故S△BCM=×4×=2.所以四面体N-BCM的体积V N-BCM=·S△BCM·=.(12分)评析本题考查了线面平行的位置关系,考查了三棱锥的体积,考查了空间想象能力.线段的中点问题一般应用三角形的中位线求解.7.(2016山东,18,12分)在如图所示的几何体中,D是AC的中点,EF∥DB.(1)已知AB=BC,AE=EC,求证:AC⊥FB;(2)已知G,H分别是EC和FB的中点.求证:GH∥平面ABC.证明(1)因为EF∥DB,所以EF与DB确定平面BDEF.连接DE.因为AE=EC,D为AC的中点,所以DE⊥AC. 同理可得BD⊥AC.又BD∩DE=D,所以AC⊥平面BDEF,因为FB⊂平面BDEF,所以AC⊥FB.(2)设FC的中点为I.连接GI,HI.在△CEF中,因为G是CE的中点,所以GI∥EF.又EF∥DB,所以GI∥DB.在△CFB中,因为H是FB的中点,所以HI∥BC. 又HI∩GI=I,所以平面GHI∥平面ABC.因为GH⊂平面GHI,所以GH∥平面ABC.评析本题主要考查线面垂直的判定与性质以及线面平行的判定与性质,考查学生的空间想象能力和逻辑思维能力,同时考查转化与化归思想的应用.8.(2015山东,18,12分)如图,三棱台DEF-ABC中,AB=2DE,G,H分别为AC,BC的中点.(1)求证:BD∥平面FGH;(2)若CF⊥BC,AB⊥BC,求证:平面BCD⊥平面EGH.证明(1)证法一:连接DG,CD,设CD∩GF=M,连接MH.在三棱台DEF-ABC中,AB=2DE,G为AC的中点,可得DF∥GC,DF=GC,所以四边形DFCG为平行四边形.则M为CD的中点,又H为BC的中点,所以HM∥BD,又HM⊂平面FGH,BD⊄平面FGH,所以BD∥平面FGH.证法二:在三棱台DEF-ABC中,由BC=2EF,H为BC的中点,可得BH∥EF,BH=EF,所以四边形HBEF为平行四边形,可得BE∥HF.在△ABC中,G为AC的中点,H为BC的中点, 所以GH∥AB.又GH∩HF=H,所以平面FGH∥平面ABED.因为BD⊂平面ABED,所以BD∥平面FGH.(2)连接HE.因为G,H分别为AC,BC的中点,所以GH∥AB.由AB⊥BC,得GH⊥BC.又H为BC的中点,所以EF∥HC,EF=HC,因此四边形EFCH是平行四边形.所以CF∥HE,又CF⊥BC,所以HE⊥BC.又HE,GH⊂平面EGH,HE∩GH=H,所以BC⊥平面EGH.又BC⊂平面BCD,所以平面BCD⊥平面EGH.评析本题考查空间线面平行、面面垂直的判定等知识;考查推理论证能力及空间想象能力.C组教师专用题组(2014北京,17,14分)如图,在三棱柱ABC-A1B1C1中,侧棱垂直于底面,AB⊥BC,AA1=AC=2,BC=1,E,F分别是A1C1,BC的中点.(1)求证:平面ABE⊥平面B1BCC1;(2)求证:C1F∥平面ABE;(3)求三棱锥E-ABC的体积.解析(1)证明:在三棱柱ABC-A1B1C1中,BB1⊥底面ABC.所以BB1⊥AB,又因为AB⊥BC,所以AB⊥平面B1BCC1.所以平面ABE⊥平面B1BCC1.(2)证明:取AB中点G,连接EG,FG.因为G,E,F分别是AB,A1C1,BC的中点,所以EC1=A1C1,FG∥AC,且FG=AC.因为AC∥A1C1,且AC=A1C1,所以FG∥EC1,且FG=EC1.所以四边形FGEC1为平行四边形.所以C1F∥EG.又因为EG⊂平面ABE,C1F⊄平面ABE,所以C1F∥平面ABE.(3)因为AA1=AC=2,BC=1,AB⊥BC,所以AB=-=.所以三棱锥E-ABC的体积V=S△ABC·AA1=×××1×2=.评析本题考查直线与平面、平面与平面的位置关系及其判定定理与性质定理的应用,考查空间几何体的体积的计算,考查考生的空间想象能力,推理论证能力和运算求解能力.判定线面平行的关键是构造线线平行或面面平行.【三年模拟】一、填空题(每小题5分,共25分)1.(2019届江苏前黄高级中学期初)a、b、c为三条不重合的直线,α、β、γ为三个不重合的平面,现给出四个命题:①⇒α∥β;②⇒α∥β;③⇒a∥α;④⇒a∥α.其中正确的命题是.答案②2.(2018江苏常州第一中学期初)下列命题中,正确的序号为.①平面内一个三角形各边所在的直线都与另一个平面平行,则这两个平面平行;②平行于同一个平面的两个平面平行;③若两个平面平行,则位于这两个平面内的直线也互相平行;④若两个平面平行,则其中一个平面内的直线平行于另一个平面.答案①②④3.(2019届江苏锡山高级中学月考)在正方体ABCD-A1B1C1D1中,E是DD1的中点,则BD1与平面ACE的位置关系为.答案平行4.(2018江苏南京中华中学期初)设α,β是两个不同的平面,m是直线且m⊂α,则“m∥β”是“α∥β”的条件.答案必要而不充分5.(2019届江苏徐州第一中学周考)如图所示,在四面体ABCD中,M,N分别是△ACD,△BCD的重心,则四面体的四个面所在平面中与MN平行的是.答案平面ABC、平面ABD二、解答题(共40分)6.(2019届江苏天一中学周考)如图,ABCD与ADEF均为平行四边形,M,N,G分别是AB,AD,EF的中点.求证:(1)BE∥平面DMF;(2)平面BDE∥平面MNG.证明(1)设GN与DF的交点为O.连接AE,则AE必过DF与GN的交点O,连接MO,则MO为△ABE的中位线,所以BE∥MO,又BE⊄平面DMF,MO⊂平面DMF,所以BE∥平面DMF.(2)因为N,G分别为平行四边形ADEF的边AD,EF的中点,所以DE∥GN,又DE⊄平面MNG,GN⊂平面MNG,所以DE∥平面MNG.因为M为AB的中点,N为AD的中点,所以MN为△ABD的中位线,所以BD∥MN,又MN⊂平面MNG,BD⊄平面MNG,所以BD∥平面MNG,又DE,BD⊂平面BDE,DE∩BD=D,所以平面BDE∥平面MNG.7.(2018江苏南京、盐城、连云港二模)如图,已知矩形ABCD所在平面与△ABE所在平面互相垂直,AE=AB,M,N,H分别为DE,AB,BE的中点.(1)求证:MN∥平面BEC;(2)求证:AH⊥CE.证明(1)证法一:取CE的中点F,连接FB,MF.因为M为DE的中点,F为CE的中点,所以MF∥CD且MF=CD.又因为在矩形ABCD中,N为AB的中点,所以BN∥CD且BN=CD,所以MF∥BN且MF=BN,所以四边形BNMF为平行四边形,所以MN∥BF.又MN⊄平面BEC,BF⊂平面BEC,所以MN∥平面BEC.证法二:取AE的中点G,连接MG,GN.因为G为AE的中点,M为DE的中点,所以MG∥AD.又因为在矩形ABCD中,BC∥AD,所以MG∥BC.又因为MG⊄平面BEC,BC⊂平面BEC,所以MG∥平面BEC.因为G为AE的中点,N为AB的中点,所以GN∥BE.又因为GN⊄平面BEC,BE⊂平面BEC,所以GN∥平面BEC.又因为MG∩GN=G,MG,GN⊂平面GMN,所以平面GMN∥平面BEC.又因为MN⊂平面GMN,所以MN∥平面BEC.(2)因为四边形ABCD为矩形,所以BC⊥AB.因为平面ABCD⊥平面ABE,平面ABCD∩平面ABE=AB,BC⊂平面ABCD,且BC⊥AB, 所以BC⊥平面ABE.因为AH⊂平面ABE,所以BC⊥AH.因为AB=AE,H为BE的中点,所以BE⊥AH.因为BC∩BE=B,BC⊂平面BEC,BE⊂平面BEC,所以AH⊥平面BEC.又因为CE⊂平面BEC,所以AH⊥CE.8.(2018江苏无锡高三期末,15)如图,四边形ABCD是菱形,DE⊥平面ABCD,AF∥DE,DE=2AF.(1)求证:AC⊥平面BDE;(2)求证:AC∥平面BEF.证明(1)因为DE⊥平面ABCD,所以DE⊥AC.因为ABCD是菱形,所以AC⊥BD,因为DE∩BD=D,所以AC⊥平面BDE.(2)设AC∩BD=O,取BE的中点G,连接FG,OG,则OG∥DE且OG=DE.因为AF∥DE,DE=2AF,所以AF∥OG且AF=OG,从而四边形AFGO是平行四边形,所以FG∥AO.因为FG⊂平面BEF,AO⊄平面BEF,所以AO∥平面BEF,即AC∥平面BEF.思路分析(1)由线面垂直的判定定理容易得到,难度不大;(2)要证线面平行,有两个思路:一是证线线平行,二是证面面平行,本题显然是第一个思路,由DE=2AF,容易想到取BE,BD的中点G,O,连接GO,则GO是三角形BDE的中位线,构造平行四边形AFGO得到线线平行,进而证明线面平行.。

绝密★启用前2019年普通高等学校招生全国统一考试江苏卷数学试题卷本试卷共5页，23题(含选考题)。

全卷满分150分。

考试用时120 分钟。

★祝考试顺利★注意事项:1.答题前，先将白己的姓名、准考证号填写在试卷和答题卡上，并将准考证号条形码粘贴在答题卡上的指定位置。

2. 选择题的作答:每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

写在试卷、草稿纸和答题卡上的非答题区域均无效。

3. 非选择题的作答:用黑色签字笔直接答在答题卡.上对应的答题区域内。

写在试卷、草稿纸和答题卡，上的非答题区域均无效。

4.选考题的作答: 先把所选题目的题号在答题卡上指定的位置用2B铅笔涂黑。

答案写在答题卡.上对应的答题区域内，写在试卷、草稿纸和答题卡.上的非答题区域均无效。

.5.考试结束后，请将本试卷和答题卡-并上交。

一、填空题：本大题共14小题，每小题5分，共计70分．（共14题；共70分）1.已知集合A={−1,0,1,6}，B={x|x>0,x∈R}，则A∩B=________.2.已知复数(a+2i)(1+i)的实部为0，其中i为虚数单位，则实数a的值是________.3.下图是一个算法流程图，则输出的S的值是________.4.函数y=√7+6x−x2的定义域是________.5.已知一组数据6，7，8，8，9，10，则该组数据的方差是________.6.从3名男同学和2名女同学中任选2名同学参加志愿者服务，则选出的2名同学中至少有1名女同学的概率是________.=1(b>0)经过点（3，4)，7.在平面直角坐标系xOy中，若双曲线x2−y2b2则该双曲线的渐近线方程是________.8.已知数列{a n}(n∈N∗)是等差数列，S n是其前n项和.若a2a5+a8= 0,S9=27，则S8的值是________.9.如图，长方体ABCD−A1B1C1D1的体积是120，E为CC1的中点，则三棱锥E-BCD的体积是________.10.在平面直角坐标系 xOy 中，P 是曲线 y =x +4x (x >0) 上的一个动点，则点P 到直线x +y =0的距离的最小值是________.11.在平面直角坐标系 xOy 中，点A 在曲线y =ln x 上，且该曲线在点A 处的切线经过点（-e ，-1)(e 为自然对数的底数），则点A 的坐标是________. 12.如图，在 △ABC 中，D 是BC 的中点，E 在边AB 上，BE =2EA ， AD 与CE 交于点 O .若 AB ⃗⃗⃗⃗⃗ ⋅AC ⃗⃗⃗⃗⃗ =6AO ⃗⃗⃗⃗⃗ ⋅EC ⃗⃗⃗⃗⃗ ，则 ABAC的值是________.13.已知 tanαtan(α+π4)=−23 ，则 sin(2α+π4) 的值是________.14.设 f(x),g(x) 是定义在R 上的两个周期函数， f(x) 的周期为4， g(x) 的周期为2，且 f(x) 是奇函数.当 x ∈(0,2] 时， f(x)=√1−(x −1)2 ， g(x)={k(x +2),0<x ≤1−12,1<x ≤2，其中k >0.若在区间(0，9]上，关于x 的方程 f(x)=g(x) 有8个不同的实数根，则k 的取值范围是________. 二、解答题：本大题共6小题，共计90分．（共6题；共90分） 15.在△ABC 中，角A ， B ， C 的对边分别为a ， b ， c ． （1）若a =3c ， b = √2 ，cos B = 23 ，求c 的值；（2）若sinAa =cosB2b，求sin(B+π2)的值．16.如图，在直三棱柱ABC－A1B1C1中，D，E分别为BC，AC的中点，AB=BC．求证：（1）A1B1∥平面DEC1；（2）BE⊥C1E．17.如图，在平面直角坐标系xOy中，椭圆C: x2a +y2b=1(a>b>0)的焦点为F1（–1、0），F2（1，0）．过F2作x轴的垂线l，在x轴的上方，l与圆F2: (x−1)2+y2=4a2交于点A，与椭圆C交于点D.连结AF1并延长交圆F2于点B，连结BF2交椭圆C于点E，连结DF1．已知DF1= 52．（1）求椭圆C的标准方程；（2）求点E的坐标．18.如图，一个湖的边界是圆心为O的圆，湖的一侧有一条直线型公路l，湖上有桥AB（AB是圆O的直径）．规划在公路l上选两个点P、Q，并修建两段直线型道路PB、QA．规划要求:线段PB、QA上的所有点到点O的距离均不小于圆O的半径．已知点A、B到直线l的距离分别为AC和BD（C、D为垂足），测得AB=10，AC=6，BD=12（单位:百米）．（1）若道路PB与桥AB垂直，求道路PB的长；（2）在规划要求下，P和Q中能否有一个点选在D处？并说明理由；（3）对规划要求下，若道路PB和QA的长度均为d（单位：百米）.求当d最小时，P、Q两点间的距离．19.设函数f(x)=(x−a)(x−b)(x−c),a,b,c∈R、f ′(x)为f（x）的导函数．（1）若a=b=c，f（4）=8，求a的值；（2）若a≠b，b=c，且f（x）和f ′(x)的零点均在集合{−3,1,3}中，求f（x）的极小值；（3）若a=0,0<b⩽1,c=1，且f（x）的极大值为M，求证:M≤ 427．20.定义首项为1且公比为正数的等比数列为“M－数列”.（1）已知等比数列{a n} (n∈N∗)满足：a2a4=a5,a3−4a2+4a4=0，求证:数列{a n}为“M－数列”；（2）已知数列{b n}满足: b1=1,1Sn =2b n−2b n+1，其中S n为数列{b n}的前n项和．①求数列{b n}的通项公式；②设m为正整数，若存在“M－数列”{c n} (n∈N∗)，对任意正整数k，当k≤m时，都有c k⩽b k⩽c k+1成立，求m的最大值．三、数学Ⅱ(附加题)（每题10分）【选做题】本题包括21、22、23三题，请选定其中两小题，并在相应的答题区域内作答．若多做，则按作答的前两小题评分．解答时应写出文字说明、证明过程或演算步骤．（共3题；共30分）21.A.[选修4-2：矩阵与变换]已知矩阵A=[31 22]（1）求A2；（2）求矩阵A的特征值.22.在极坐标系中，已知两点A(3,π4),B(√2,π2)，直线l的方程为ρsin(θ+π4)=3.（1）求A，B两点间的距离；（2）求点B到直线l的距离.23.设x∈R，解不等式|x|+|2x−1|>2.四、【必做题】第24题、第25题，每题10分，共计20分．（共2题；共20分）24.设(1+x)n=a0+a1x+a2x2+⋯+a n x n,n⩾4,n∈N∗.已知a32=2a2a4.（1）求n的值；（2）设(1+√3)n=a+b√3，其中a,b∈N∗，求a2−3b2的值.25.在平面直角坐标系xOy中，设点集A n={(0,0),(1,0),(2,0),…,(n,0)}，B n={(0,1),(n,1)},C n={(0,2),(1,2),(2,2),⋯,(n,2)},n∈N∗.令M n=A n∪B n∪C n.从集合M n中任取两个不同的点，用随机变量X表示它们之间的距离.（1）当n=1时，求X的概率分布；（2）对给定的正整数n（n≥3），求概率P（X≤n）（用n表示）.答案解析部分一、填空题：本大题共14小题，每小题5分，共计70分．1.【答案】{1,6}【考点】交集及其运算【解析】【解答】∵集合A={−1,0,1,6}，B={x|x>0,x∈R}，借助数轴得：A∩B={1,6}【分析】根据已知条件借助数轴，用交集的运算法则求出集合A∩B。