大学物理仿真实验凯特摆测量重力加速度

实验题目:用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧，掌握一种比较精确的测量重力加速度的方法。

实验原理:设一质量为m 的刚体，其重心G 到转轴O 的距离为h ，绕O 轴的转动惯量为I ，当摆幅很小时，刚体绕O 轴摆动的周期T 为：mgh I T π2=(1)式中g 为当地的重力加速度.设复摆绕通过重心G 的轴的转动惯量为I G ，当G 轴与O 轴平行时，有I=I G +mh 2 (2)代入式（1）得：mgh mh I T G 22+=π (3)对比单摆周期的公式gl T π2= 可得 mhmh I l G 2+=(4)，称为复摆的等效摆长。

因此只要测出周期和等效摆长便可求得重力加速度。

左图是凯特摆摆杆的示意图。

对凯特摆而言，两刀口间的距离就是该摆的等效摆长l 。

在实验中当两刀口位置确定后，通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期T 1和T 2基本相等。

由公式（3）可得12112mgh mh I T G +=π (5) 22222mgh mh I T G +=π (6)其中T 1和h 1为摆绕O 轴的摆动周期和O 轴到重心G 的距离。

当T 1≈T 2时，h 1+h 2=l即为等效摆长。

由式(5)和(6)消去I G ，可得：()22222121214222T T T T a b g l h l π+-=+=+- (7)此式中，l 、T 1、T 2都是可以精确测定的量，而h 1则不易测准。

由此可知，a 项可以精确求得，而b 项则不易精确求得。

但当T 1=T 2以及 |2h 1-l | 的值较大时，b 项的值相对a 项是非常小的，这样b 项的不精确对测量结果产生的影响就微乎其微了。

实验仪器：凯特摆、光电探头、米尺、数字测试仪。

实验内容：1、仪器调节选定两刀口间得距离即该摆得等效摆长l ，使两刀口相对摆杆基本对称，并相互平行，用米尺测出l 的值，粗略估算T 值。

实验题目：用凯特摆测量重力加速度实验目的：学习凯特摆的实验设计思想和技巧，掌握一种比较精确的测量重力加速度的方法。

实验仪器：凯特摆、光电探头、米尺和VAFN多用数字测试仪。

实验原理：1，复摆。

质量为m的刚体，其重心G到转轴O的距离为h，绕O轴的转动惯量为I。

当摆幅很小时，刚体绕O转动的周期为(1)设复摆绕通过重心G的转动惯量为，当G轴与O轴平行时有：(2)代入(1)得：(3)对比单摆周期公式，可得：(4)l称为复摆的等效摆长，因此只要测出周期和等效摆长便可球的重力加速度。

2，凯特摆。

如左图对凯特摆而言，两刀口间距就是该摆的等效摆长l。

在实验种当两刀口位置确定后，通过调节A、B、C、D四摆锤的位置可以使正、倒悬挂时的摆动周期和基本相等，即。

由公式(3)：(5)(6)当时，即为等效摆长。

由公式(5)和(6)可得：(7)此式中，l、T1、T2都是可以精确测定的量，而h1则不易测准。

由此可知，a项可以精确求得，而b项则不易精确求得。

但当T1=T2以及|2h1-l| 的值较大时，b项的值相对a项是非常小的，这样b项的不精确对测量结果产生的影响就微乎其微了。

实验步骤：1，仪器调节调节摆锤A、B、C、D到合适位置，是正，倒悬的摆动周期相等。

2，测量摆动周期测量凯特摆正，倒悬摆动10个周期的时间，等效摆长和转轴O到G的距离，记录如下：的A类不确定度：的B类不确定度：所以的展伸不确定度：同理，的展伸不确定度：同上，同上，将具体的数值代入一步写清楚3，计算重力加速度及其不确定度根据公式(7)：所以：g=以下求的合成不确定度。

已知：(8)对(8)式等号两边取对数：等号两边求导并合并同类项：所以的合成不确定度公式为：(9)将上述数据代入(9)：所以：注意单位由于，很小可以忽略，所以只合成g和的不确定度。

类似(8)到(9)的过程：所以：最后可得：不确定度取一到两位有效数字思考题：1，凯特摆测重力加速度，在实验设计上有什么特点？避免了什么量的测量？降低了哪个量的测量精度？实验上如何来实现？答：凯特摆测重力加速度设计特点是：减少一些量的测量，提高实验精度。

用凯特摆测量重力加速度化学物理系04级龚晓李PB042060022005-12-5实验目的：学习凯特摆的实验设计思想和技巧，掌握一种比较精确的测量重力加速度的方法。

实验原理：1、当摆幅很小时，刚体绕O轴摆动的周期：刚体质量m，重心G到转轴O的距离h，绕O轴的转动惯量I，复摆绕通过重心G的转轴的转动惯量为I G 。

当G轴与O轴平行时，有I=I G+mh2∴∴复摆的等效摆长l=( I G+mh2 )/mh2、利用复摆的共轭性：在复摆重心G旁，存在两点O和O´，可使该摆以O为悬点的摆动周期T₁与以O´为悬点的摆动周期T₂相同，可证得|OO´|=l，可精确求得l。

3、对于凯特摆，两刀口间距就是l，可通过调节A、B、C、D四摆锤得位置使正、倒悬挂时得摆动周期T₁≈T₂。

∴4π²/g=(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l) = a + b实验仪器：凯特摆、光电探头、米尺、数字测试仪。

实验内容：1、仪器调节选定两刀口间得距离即该摆得等效摆长l，使两刀口相对摆杆基本对称，并相互平行，用米尺测出l的值，粗略估算T值。

将摆杆悬挂到支架上水平的V形刀承上，调节底座上的螺丝，借助于铅垂线，使摆杆能在铅垂面内自由摆动，倒挂也如此。

将光电探头放在摆杆下方，让摆针在摆动时经过光电探测器。

让摆杆作小角度摆动，待稳定后，按下reset钮，则测试仪开始自动记录一个周期的时间。

2、测量摆动周期T₁和T₂调整四个摆锤的位置，使T₁和T₂逐渐靠近，差值小于0.001s，测量正、倒摆动10个周期的时间10T₁和10T₂各测5次取平均值。

3、计算重力加速度g及其标准误差σg 。

将摆杆从刀承上取下，平放在刀口上，使其平衡，平衡点即重心G。

测出|GO|即h₁，代入公式计算g。

推导误差传递公式计算σg 。

实验数据处理：1、l的值l=⅓(l₁+l₂+l₃)=74.17cmσ＝0.03055cm，u A =σ/=0.01764cm，∴ΔA ＝t P·u A =1.32*0.01764=0.02328cmu B=ΔB /C=0.1/3=0.03333cm∴u L ==0.04066cmT e ==1.729s2、T₁和T₂的值T₁＝1.72746sσ＝2.525*10¯⁴s，u A =σ/=1.129*10¯⁴s∴ΔA ＝t P·u A =1.14*0.0001129=1.287*10¯⁴su B=ΔB /C=0.0001/3=0.3333*10¯⁴s∴u T1 ==1.329*10¯⁴sT₂=1.72751sσ＝1.469*10¯⁴s，u A =σ/=0.6570*10¯⁴s∴ΔA ＝t P·u A =1.14*0.00006570=0.7489*10¯⁴su B=ΔB /C=0.0001/3=0.3333*10¯⁴s∴u T2 ==0.8197*10¯⁴s3、重力加速度gh₁=44.46cm∴g=4π²/[(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l)]=4π²/{(1.72746²+1.72751²)/(2*74.17*10¯²)+(1.72746²-1.72751²)/[2*(2*44.46*10¯²-74.17*10¯²)]}=9.813m/s²∴u g0.68 =g·{l¯²* u L²+[2 T₁/(T₁²+T₂²)]²·u T1²+[2 T₂/(T₁²+T₂²)]²·u T2²}=9.813*{(74.17*10¯²)¯²*(0.04066*10¯²)²+[2*1.72746/(1.72746²+1.72751²)]²*(1.329*10¯⁴)²+[2*1.72751/(1.72746²+1.72751²)]²*(0.8197*10¯⁴)²}=0.00545m/s²∴u g0.95 =2* u g0.68 =0.011 m/s²∴g=(9.813±0.011) m/s² P=0.95思考题：1、凯特摆测重力加速度，在实验设计上有什么特点？避免了什么量的测量？降低了哪个量的测量精度？实验上如何来实现?答：凯特摆测重力加速度在实验设计上把不可测的量转换成可测的量，利用复摆上两点的共轭性，对难以精确测定的量，有些避免了对其的测量，不能避免的则降低了其测量精度。

实验报告 87姓名:竺贵强 学号:PB07210017 系别：0706 实验题目:用凯特摆测量重力加速度实验目的:1．学习凯特摆的实验设计思想和技巧2．掌握一种比较精确的测量重力加速度的方法实验内容:1. 仪器调节调平支架:让摆杆做小角度摆动，记录一个周期的时间，反复测量，并调节支架的底座，直到多次测量的一个周期误差在0.001秒之内。

2. 测量摆动周期1T 和2T求出平均值为 mm l 5.7443== 根据gl T π2=粗略估算出 s T 7318.18.97445.02=⨯⨯=π 调节四个摆锤的位置，使正挂的摆动周期1T 和倒挂的摆动周期2T 逐渐靠近，一般粗调用大摆锤，微调用小摆锤，当1T 和2T 接近估计值时，最好移动小摆锤，使1T 和2T 的差值小于0.001s.当周期的调节达到要求后,分别测量5次的101T 和10g (Ⅰ)计算l, 1h ,1T 和2T 的平均值和不确定度 (1)已求出l 的平均值 mm l 5.744=l 的A 类不确定度为 mm l l l u i i A 17.0)13(3)()(312=-⨯-=∑= 查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得mm l U 3.0)3/8.01()17.032.1()(22683.0=⨯+⨯=所以 mm l )3.05.744(±= P=0.683(2)求出1h 的平均值 mm h 5.45933.4598.4595.4591=++=1h 的A 类不确定度为 mm h h h u i i A 15.0)13(3)()(312111=-⨯-=∑=查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得 mm h U 3.0)3/8.01()15.032.1()(221683.0=⨯+⨯=所以 mm h )3.05.459(1±= P=0.683(3)求出1T 的平均值 s T T i 74055.11010515111==∑=1T 的A 类不确定度为 s T T T u i i A 00014.0)15(5)()(512111=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00016.000014.014.1)(1683.0=⨯=所以 s T )00016.074055.1(1±= P=0.683(4)求出2T 的平均值 s T T i 73990.11010515122==∑=2T 的A 类不确定度为 s T T T u i i A 00011.0)15(5)()(512222=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00012.000011.014.1)(2683.0=⨯=所以 s T )00012.073990.1(2±= P=0.683(Ⅱ)计算g 及其不确定度已知b a l h T T l T T g +=--++=)2(2241222122212π(1)由l T T a 22221+=得 21220677.47445.0273990.174055.1s m a -=⨯+=下面求a 的不确定度传递公式：两边取对数 2ln ln )ln(ln 2221--+=l T T a求微分 dl l dT T T T dT T T T da a 1221222212122211-+++= 系数去绝对值并改成不确定度符号，最后写成不确定度传递公式为 2222212222211)1()2()2(21l T T a U l U T T T U T T T a U ++++= 带入数值可求求得a 的不确定度为2222222683.0)0003.07445.01()00012.073990.174055.173990.12()00016.073990.174055.174055.12(0677.4)(⨯+⨯+⨯+⨯+⨯⨯=a U 2-10.0017m s =所以 2-10.0017)m 0677.4(s a ±= P=0.683(2)由)2(212221l h T T b --=得 21220065.0)7445.04595.02(273990.174055.1s m b -=-⨯-= (3)比较a 和b 的大小,%15.0%100=⨯ab ,可见b 与a 相比,b 项可以忽略不计,从而可由a lT T g =+=2422212π求得a g 24π= 229.708m/s 0677.44==πg 再求g 的不确定度传递公式两边取对数 a g ln 4ln ln 2-=π求微分 da adg g 11-= 系数去绝对值并改成不确定度符号，最后写成不确定度传递公式为 a g U ag U = 带入数值可求的g 的不确定度为 2683.0/004.00017.00677.4708.9)(s m g U =⨯= 所以 20.004)m /s 9.708(±=g P=0.683误差分析：1. 使用米尺测量长度,误差太大;2. 在实验过程中支架底座很难调平,从而造成每个周期之间会有偏差;3. 实验中的偶然因素(比如振动)会造成周期的变化;4. 实验中发现凯特摆的周期与振幅有一定关系,从而每次的振幅不同也会造成周期的不同5. 在实验过程中，可能会形成不易察觉的锥面摆6. 从数据果看出，测得的十个周期数据并不理想，在调节时，两个周期分别为1.74005和1.74003，但在测量十个周期时周期的偏差比较大，可能是由于等待稳定的时间选的不好，导致周期有偏差改进方法：先测量一个周期，当稳定后，再迅速调到十个周期的档测量（这样能保证摆动已经稳定）。

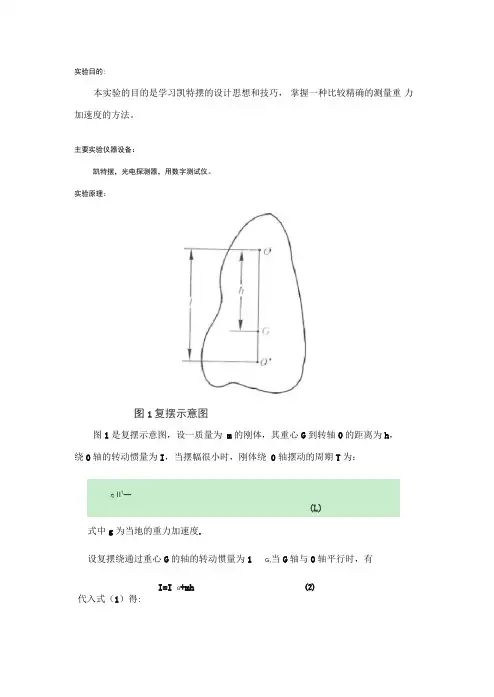
实验目的:本实验的目的是学习凯特摆的设计思想和技巧，掌握一种比较精确的测量重力加速度的方法。

主要实验仪器设备：凯特摆，光电探测器，用数字测试仪。

实验原理：图1复摆示意图图1是复摆示意图，设一质量为m的刚体，其重心G到转轴0的距离为h，绕0轴的转动惯量为I，当摆幅很小时，刚体绕0轴摆动的周期T为：丸II1—(L)式中g为当地的重力加速度.设复摆绕通过重心G的轴的转动惯量为1G,当G轴与0轴平行时，有I=I G+mh⑵代入式（1）得:对比单摆周期的公式称为复摆的等效摆长。

因此只要测出周期和等效摆长便可求得重力加速度。

上图是凯特摆摆杆的示意图。

对凯特摆而言，两刀口间的距离就是该摆的等效摆长I。

在实验中当两刀口位置确定后，通过调节A、B、C、D四摆锤的位置可使正、倒悬挂时的摆动周期T i和T2基本相等。

由公式（3）可得丿G ■+(5)為-21初直妇潜、其中T i和h i为摆绕0轴的摆动周期和O轴到重心G的距离。

当T i〜T2时，h i+h2=l即为等效摆长。

由式(5)和(6)消去I G,可得：I 4，曽十好T^-T^ t I——= ---- + ------ - =宀+0 』、g 21盘绚-。

(?)此式中，l、T i、T2都是可以精确测定的量，而h i则不易测准。

由此可知，a 项可以精确求得，而b项则不易精确求得。

但当T i=T2以及|2h i-l |的值较大时，b项的值相对a项是非常小的，这样b项的不精确对测量结果产生的影响就微乎其微了。

实验内容：i •正确调节仪器，测量凯特摆的等效摆长l，并利用估算摆动周期T值，以作为调节T i: T2的参考。

2•调节四个摆锤的位置，使T i与T2逐渐靠近，当| T i-T2|三时，测量T i和T2的值。

3•根据上述测量值计算重力加速度g及不确定度目数据记录与处理: 分析讨论:。

实验简介实验原理实验仪器实验内容实验指导实验重点、难点1.学习一种比较精确的测量重力加速度的方法。

2.学习凯特摆的实验设计思想和技巧。

3.选定两刀口间的距离，通过调节A、B、C、D四摆锤的位置，使得该摆以两个刀口为悬点的摆动周期基本相等。

操作指导一、主窗口在系统主界面上选择“用凯特摆测量重力加速度”并单击，即可进入本仿真实验平台，显示平台主窗口——实验室场景。

场景里有实验台和实验仪器，如图1。

用鼠标在实验室场景上四处移动，当鼠标指向实验仪器时，鼠标指针处会显示相应的提示信息。

实验室场景里共有三件仪器：凯特摆、多用数字测试仪、光电检测探头。

按住鼠标左键可以拖动仪器在实验室场景里移动。

当拖动到不合理的位置（例如，仪器超出实验台、两件仪器位置重叠）放开鼠标时，仪器会自动返回原位置。

在实验仪器上单击鼠标右键，弹出仪器菜单，选择“调节”项（或双击实验仪器、或在主菜单里选择相应菜单项），弹出放大的仪器窗口，仪器的具体操作就在此窗口内进行。

用鼠标左键拖动仪器窗口顶部的细条，可以移动仪器窗口。

用鼠标右键单击仪器窗口顶部的细条，会弹出仪器菜单。

二、主菜单在主窗口上单击鼠标右键，弹出主菜单。

主菜单共有9项，分别为：实验原理、实验步骤、思考题、实验报告、凯特摆、多用数字测试仪、光电检测探头、最小化、退出。

1．选择“实验原理”菜单项，显示介绍凯特摆的有关文档，请认真阅读。

2．选择“实验步骤”菜单项，显示介绍本仿真实验的内容和步骤的有关文档，请认真阅读。

实验操作中如有不清楚之处，可以反复打开本文档阅读。

3．选择“思考题”菜单项，显示思考题。

4．选择“实验报告”菜单项，将调用“实验报告处理系统”，用户可以建立、查看实验报告，将实验结果存档，以备教师评阅（具体使用方法请参看本手册中“实验报告处理系统”的有关内容）。

5．选择“凯特摆”菜单项，显示凯特摆调节窗口（图2）。

凯特摆由金属摆杆、四个摆锤、两个刀口7部分组成。

凯特摆调节窗口的左方是一个凯特摆，单击摆锤或刀口选定待调节部件，窗口右上方将显示该部件的放大图象。

用凯特摆测量重力加速度实验目的：学习凯特摆的实验设计思想和技巧，掌握一种比较精确的测量重力加速度的方法。

实验原理：1、当摆幅很小时，刚体绕O轴摆动的周期：刚体质量m，重心G到转轴O的距离h，绕O轴的转动惯量I，复。

摆绕通过重心G的转轴的转动惯量为IG当G轴与O轴平行时，有I=I+mh2G∴+mh2 )/mh∴复摆的等效摆长l=( IG2、利用复摆的共轭性：在复摆重心G旁，存在两点O和O´，可使该摆以O为悬点的摆动周期T₁与以O´为悬点的摆动周期T₂相同，可证得|OO´|=l，可精确求得l。

3、对于凯特摆，两刀口间距就是l，可通过调节A、B、C、D四摆锤得位置使正、倒悬挂时得摆动周期T₁≈T₂。

∴4π²/g=(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l) = a + b实验仪器：凯特摆、光电探头、米尺、数字测试仪。

实验内容：1、仪器调节选定两刀口间得距离即该摆得等效摆长l，使两刀口相对摆杆基本对称，并相互平行，用米尺测出l的值，粗略估算T值。

将摆杆悬挂到支架上水平的V形刀承上，调节底座上的螺丝，借助于铅垂线，使摆杆能在铅垂面内自由摆动，倒挂也如此。

将光电探头放在摆杆下方，让摆针在摆动时经过光电探测器。

让摆杆作小角度摆动，待稳定后，按下reset钮，则测试仪开始自动记录一个周期的时间。

2、测量摆动周期T₁和T₂调整四个摆锤的位置，使T₁和T₂逐渐靠近，差值小于0.001s，测量正、倒摆动10个周期的时间10T₁和10T₂各测5次取平均值。

3、计算重力加速度g及其标准误差σg。

将摆杆从刀承上取下，平放在刀口上，使其平衡，平衡点即重心G。

测出|GO|即h₁，代入公式计算g。

推导误差传递公式计算σg。

实验数据处理：1、l的值l=⅓(l₁+l₂+l₃)=74.17cmσ＝0.03055cm，uA=σ/=0.01764cm，∴ΔA ＝tP·uA=1.32*0.01764=0.02328cmu B=ΔB/C=0.1/3=0.03333cm∴uL==0.04066cmTe==1.729s2、T₁和T₂的值T₁＝1.72746sσ＝2.525*10¯⁴s，uA=σ/=1.129*10¯⁴s∴ΔA ＝tP·uA=1.14*0.0001129=1.287*10¯⁴su B=ΔB/C=0.0001/3=0.3333*10¯⁴s∴uT1==1.329*10¯⁴sT₂=1.72751sσ＝1.469*10¯⁴s，uA=σ/=0.6570*10¯⁴s∴ΔA ＝tP·uA=1.14*0.00006570=0.7489*10¯⁴su B=ΔB/C=0.0001/3=0.3333*10¯⁴s∴uT2==0.8197*10¯⁴s3、重力加速度gh₁=44.46cm∴g=4π²/[(T₁²+T₂²)/2l + (T₁²-T₂²)/2(2h₁-l)]=4π²/{(1.72746²+1.72751²)/(2*74.17*10¯²)+(1.72746²-1.72751²)/[2*(2*44.46*10¯²-74.17*10¯²)]} =9.813m/s²∴ug0.68 =g·{l¯²* uL²+[2 T₁/(T₁²+T₂²)]²·uT1²+[2 T₂/(T₁²+T₂²)]²·uT2²}=9.813*{(74.17*10¯²)¯²*(0.04066*10¯²)²+[2*1.72746/(1.72746²+1.72751²)]²*(1.329*10¯⁴)²+[2*1.72751/(1.72746²+1.72751²)]²*(0.8197*10¯⁴)²}=0.00545m/s²∴ug0.95 =2* ug0.68=0.011 m/s²∴g=(9.813±0.011) m/s² P=0.95思考题：1、凯特摆测重力加速度，在实验设计上有什么特点？避免了什么量的测量？降低了哪个量的测量精度？实验上如何来实现?答：凯特摆测重力加速度在实验设计上把不可测的量转换成可测的量，利用复摆上两点的共轭性，对难以精确测定的量，有些避免了对其的测量，不能避免的则降低了其测量精度。

实验目的：本实验的目的是学习凯特摆的设计思想和技巧，掌握一种比较精确的测量重力加速度的方法。

主要实验仪器设备：凯特摆，光电探测器，用数字测试仪。

实验原理：图1是复摆示意图，设一质量为m的刚体，其重心G到转轴O的距离为h，绕O轴的转动惯量为I，当摆幅很小时，刚体绕O轴摆动的周期T为：式中g为当地的重力加速度.，当G轴与O轴平行时，有设复摆绕通过重心G的轴的转动惯量为IG+mh2(2)I=IG代入式（1）得：对比单摆周期的公式可得称为复摆的等效摆长。

因此只要测出周期和等效摆长便可求得重力加速度。

上图是凯特摆摆杆的示意图。

对凯特摆而言，两刀口间的距离就是该摆的等效摆长l。

在实验中当两刀口位置确定后，通过调节A、B、C、D四摆锤的位置可使正、倒悬挂时的摆动周期T1和T2基本相等。

由公式（3）可得其中T1和h1为摆绕O轴的摆动周期和O轴到重心G的距离。

当T1≈T2时，h 1+h2=l即为等效摆长。

由式(5)和(6)消去IG，可得：此式中，l、T1、T2都是可以精确测定的量，而h1则不易测准。

由此可知，a项可以精确求得，而b项则不易精确求得。

但当T1=T2以及|2h1-l| 的值较大时，b项的值相对a项是非常小的，这样b项的不精确对测量结果产生的影响就微乎其微了。

实验内容：1．正确调节仪器，测量凯特摆的等效摆长l，并利用，粗略估算摆动周期T值，以作为调节T1：T2的参考。

2．调节四个摆锤的位置，使T1与T2逐渐靠近，当| T1-T2|≦时，测量T1和T2的值。

3．根据上述测量值计算重力加速度g及不确定度。

数据记录与处理：分析讨论：。

⽤凯特摆测量重⼒加速度（4）实验报告 87姓名:竺贵强学号:PB07210017 系别：0706 实验题⽬:⽤凯特摆测量重⼒加速度实验⽬的:1．学习凯特摆的实验设计思想和技巧2．掌握⼀种⽐较精确的测量重⼒加速度的⽅法实验内容:1. 仪器调节调平⽀架:让摆杆做⼩⾓度摆动，记录⼀个周期的时间，反复测量，并调节⽀架的底座，直到多次测量的⼀个周期误差在0.001秒之内。

2. 测量摆动周期1T 和2T求出平均值为 mm l 5.7443== 根据gl T π2=粗略估算出 s T 7318.18.97445.02=??=π调节四个摆锤的位置，使正挂的摆动周期1T 和倒挂的摆动周期2T 逐渐靠近，⼀般粗调⽤⼤摆锤，微调⽤⼩摆锤，当1T 和2T 接近估计值时，最好移动⼩摆锤，使1T 和2T 的差值⼩于0.001s.当周期的调节达到要求后,分别测量5次的101T 和10g (Ⅰ)计算l, 1h ,1T 和2T 的平均值和不确定度 (1)已求出l 的平均值 mm l 5.744=l 的A 类不确定度为 mm l l l u i i A 17.0)13(3)()(312=-?-=∑= 查表得卷尺的仪?=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪?+=得mm l U 3.0)3/8.01()17.032.1()(22683.0=?+?=所以 mm l )3.05.744(±= P=0.683(2)求出1h 的平均值 mm h 5.45933.4598.4595.4591=++=1h 的A 类不确定度为 mm h h h u i i A 15.0)13(3)()(312111=-?-=∑=查表得卷尺的仪?=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪?+=得 mm h U 3.0)3/8.01()15.032.1()(221683.0=?+?=所以 mm h )3.05.459(1±= P=0.683(3)求出1T 的平均值 s T T i 74055.11010515111==∑=1T 的A 类不确定度为 s T T T u i i A 00014.0)15(5) ()(512111=-?-=∑=取仪?=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00016.000014.014.1)(1683.0=?=所以 s T )00016.074055.1(1±= P=0.683(4)求出2T 的平均值 s T T i 73990.11010515122==∑=2T 的A 类不确定度为 s T T T u i i A 00011.0)15(5)()(51 2222=-?-=∑=取仪?=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00012.000011.014.1)(2683.0=?=所以 s T )00012.073990.1(2±= P=0.683(Ⅱ)计算g 及其不确定度已知b a l h T T l T T g +=--++=)2(2241222122212π(1)由l T T a 22221+=得 21220677.47445.0273990.174055.1s m a -=?+=下⾯求a 的不确定度传递公式：两边取对数 2ln ln )ln(ln 2221--+=l T T a求微分 dl l dT T T T dT T T T da a 1221222212122211-+++= 系数去绝对值并改成不确定度符号，最后写成不确定度传递公式为 2222212222211)1()2()2(21l T T a U l U T T T U T T T a U ++++= 带⼊数值可求求得a 的不确定度为2222222683.0)0003.07445.01()00012.073990.174055.173990.12()00016.073990.174055.174055.12(0677.4)(?+?+?+?+??=a U 2-10.0017m s =所以 2-10.0017)m 0677.4(s a ±= P=0.683(2)由)2(212221l h T T b --=得 21220065.0)7445.04595.02(273990.174055.1s m b -=-?-= (3)⽐较a 和b 的⼤⼩,%15.0%100=?ab ,可见b 与a 相⽐,b 项可以忽略不计,从⽽可由a lT T g =+=2422212π求得a g 24π= 229.708m/s 0677.44==πg 再求g 的不确定度传递公式两边取对数 a g ln 4ln ln 2-=π求微分 da adg g 11-= 系数去绝对值并改成不确定度符号，最后写成不确定度传递公式为 a g U ag U = 带⼊数值可求的g 的不确定度为 2683.0/004.00017.00677.4708.9)(s m g U =?= 所以 20.004)m /s 9.708(±=g P=0.683误差分析：1. 使⽤⽶尺测量长度,误差太⼤;2. 在实验过程中⽀架底座很难调平,从⽽造成每个周期之间会有偏差;3. 实验中的偶然因素(⽐如振动)会造成周期的变化;4. 实验中发现凯特摆的周期与振幅有⼀定关系,从⽽每次的振幅不同也会造成周期的不同5. 在实验过程中，可能会形成不易察觉的锥⾯摆6. 从数据果看出，测得的⼗个周期数据并不理想，在调节时，两个周期分别为1.74005和1.74003，但在测量⼗个周期时周期的偏差⽐较⼤，可能是由于等待稳定的时间选的不好，导致周期有偏差改进⽅法：先测量⼀个周期，当稳定后，再迅速调到⼗个周期的档测量（这样能保证摆动已经稳定）。

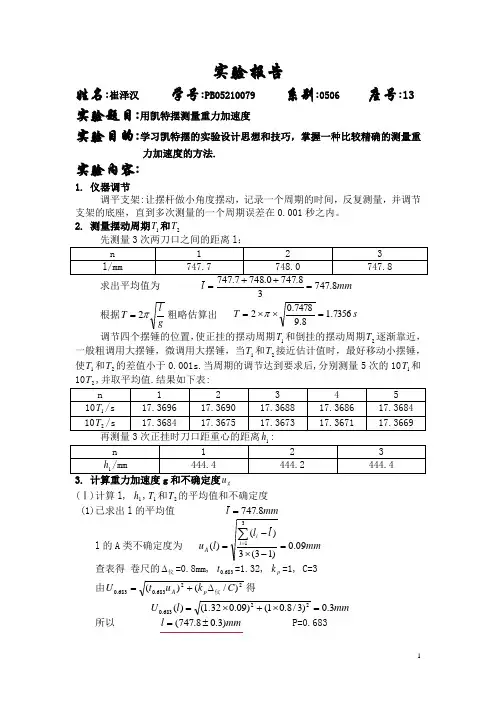
实验报告姓名:崔泽汉 学号:PB05210079 系别:0506 座号:13 实验题目:用凯特摆测量重力加速度实验目的:学习凯特摆的实验设计思想和技巧，掌握一种比较精确的测量重力加速度的方法.实验内容:1. 仪器调节调平支架:让摆杆做小角度摆动，记录一个周期的时间，反复测量，并调节支架的底座，直到多次测量的一个周期误差在0.001秒之内。

2. 测量摆动周期1T 和2T求出平均值为 mm l 8.7473== 根据gl T π2=粗略估算出 s T 7356.18.97478.02=⨯⨯=π 调节四个摆锤的位置，使正挂的摆动周期1T 和倒挂的摆动周期2T 逐渐靠近，一般粗调用大摆锤，微调用大摆锤，当1T 和2T 接近估计值时，最好移动小摆锤，使1T 和2T 的差值小于0.001s.当周期的调节达到要求后,分别测量5次的101T 和10g (Ⅰ)计算l, 1h ,1T 和2T 的平均值和不确定度(1)已求出l 的平均值 mm l 8.747=l 的A 类不确定度为 mm l l l u i i A 09.0)13(3)()(31=-⨯-=∑= 查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得mm l U 3.0)3/8.01()09.032.1()(22683.0=⨯+⨯= 所以 mm l )3.08.747(±= P=0.683(2)求出1h 的平均值 mm h 3.44434.4442.4444.4441=++=1h 的A 类不确定度为 mm h h h u i i A 07.0)13(3)()(31111=-⨯-=∑=查表得 卷尺的仪∆=0.8mm, 683.0t =1.32, p k =1, C=3由22683.0683.0)/()(C k u t U p A 仪∆+=得 mm h U 3.0)3/8.01()07.032.1()(221683.0=⨯+⨯=所以 mm h )3.03.444(1±= P=0.683(3)求出1T 的平均值 s T T i 73689.11010515111==∑=1T 的A 类不确定度为 s T T T u i i A 00002.0)15(5)()(51111=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00002.000002.014.1)(1683.0=⨯=所以 s T )00002.073689.1(1±= P=0.683(4)求出2T 的平均值 s T T i 73674.11010515122==∑=2T 的A 类不确定度为 s T T T u i i A 00003.0)15(5)()(51222=-⨯-=∑=取仪∆=0, 查表得 683.0t =1.14,由A u t U 683.0683.0=得s T U 00003.000003.014.1)(2683.0=⨯=所以 s T )00003.073674.1(2±= P=0.683(Ⅱ)计算g 及其不确定度已知b a l h T T l T T g +=--++=)2(2241222122212π(1)由l T T a 22221+=得 21220339.47478.0273674.173689.1s m a -=⨯+=下面求a 的不确定度传递公式：两边取对数 2ln ln )ln(ln 2221--+=l T T a求微分 dl ldT T T T dT T T Tda a 1221222212122211-+++=系数去绝对值并改成不确定度符号，最后写成不确定度传递公式为 2222212222211)1()2()2(21l T T a U l U T T T U T T T a U ++++= 带入数值可求求得a 的不确定度为2222222683.0)0003.07478.01()00003.073674.173689.173674.12()00002.073674.173689.173689.12(0339.4)(⨯+⨯+⨯+⨯+⨯⨯=a U 2-10.0016m s =所以 2-10.0016)m 0339.4(s a ±= P=0.683(2)由)2(212221l h T T b --=得 21220018.0)7478.04443.02(273674.173689.1s m b -=-⨯-= (3)比较a 和b 的大小,%04.0%100=⨯ab,可见b 与a 相比,b 项可以忽略不计,从而可由a lT T g =+=2422212π求得a g 24π= 229.787m /s 0339.44==πg 再求g 的不确定度传递公式两边取对数 a g ln 4ln ln 2-=π求微分 da adg g 11-= 系数去绝对值并改成不确定度符号，最后写成不确定度传递公式为 a g U ag U = 带入数值可求的g 的不确定度为 2683.0/004.00016.00339.4787.9)(s m g U =⨯= 所以 20.004)m /s 9.787(±=g P=0.683误差分析：1. 使用米尺测量长度,误差太大;2. 在实验过程中支架底座很难调平,从而造成每个周期之间会有偏差;3. 实验中的偶然因素(比如振动)会造成周期的变化;4. 实验中发现凯特摆的周期与振幅有一定关系,从而每次的振幅不同也会造成周期的不同.思考题：1.凯特摆测重力加速度，在实验设计上有什么特点？避免了什么量的测量？降低了哪个量的测量精度？实验上如何来实现？该实验在设计中避免了一些不易直接或精确测量的量的测量,并在计算过程中利用数学技巧把这些量消去.避免了重心到悬点距离h和复摆转动惯量I的测量.G降低了周期T的测量精度.I;利用复摆的两点共轭性可以精确求得等效摆长l,而不必去测量h和G利用数字测试仪精确测10T,可精确求得周期T.2.结合误差计算，你认为影响凯特摆测g精度的主要因素是什么？将所得到的实验结果与当地的重力加速度的公认值相比较，你能得到什么结论？若有偏差是分析之。

西安交通大学实验报告课程物理实验实验名称凯特摆测重力加速度第 1 页 共 4页系 别电气工程与自动化 实 验 日 期 2010年 11月 14日 专业班级电气92组别_________实 验 报 告 日 期 2010年 11月 14日 姓 名万佳东学号09041045报 告 退 发 ( 订正 、 重做 ) 同 组 人_________________________________ 教 师 审 批 签 字一．实验目的学习凯特摆设计的技巧与结构；掌握一种测量重力加速度比较准确的方法。

二．原理简述图1是复摆示意图，设一质量为m 的刚体，其重心G 到转轴O 的距离为h ，绕O 轴的转动惯量为I ，当摆幅很小时，刚体绕O 轴摆动的周期T 为：mghIT π2= (1) 式中g 为当地的重力加速度.设复摆绕通过重心G 的轴的转动惯量为G I ，当G 轴与O 轴平行时，有2mh I I G += (2)代入（1）得：mghmh I T G 22+=π(3) 对比单摆周期公式glT π2= 可得 mh mh I l G 2+= （4）l 称为复摆的等效摆长。

因此只要测出周期和等效摆长便可求得重力加速度。

下图是凯特摆摆杆的示意图。

对凯特摆而言，两刀口间的距离就是该摆的等效摆长l 。

在实验中当两刀口位置确定后，通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期1T 和2T 基本相等。

由公式（3）可得12112mh mh I T G +=π (5)22222mh mh I T G +=π (6)其中1T 和1h 为摆绕O 轴的摆动周期和O 轴到重心G 的距离。

当21T T ≈时，l h h =+21即为等效摆长。

由式(5)和(6)消去G I ，可得：b a l h T T l T T g +=--++=)2(2241222122212π （7） 此式中，l 、1T 、2T 都是可以精确测定的量，而1h 则不易测准。

凯特摆测量重力加速度1818年凯特提出的倒摆，经雷普索里德作了改进后，成为当时测量重力加速度g 最精确的方法。

波斯坦大地测量研究所曾用五个凯特摆用了8年时间（1896-1904），测得当地的重力加速度g=(981.274±0.003)cm/s 2，许多地区的g 值都曾以此为根据。

凯特摆测量重力加速度的方法不仅在科学史上有着重要的价值，而且在实验设计上亦有值得学习的技巧。

教学目的：1. 学习凯特摆的实验设计思想和技巧。

2. 掌握一种比较精确的测量重力加速度的方法。

教学重点及难点：1. 复摆的原理2. 凯特摆的结构及原理3. 利用凯特摆测量重力加速度的方法教学内容：一．实验原理图一是复摆的示意图，设一质量为m 的刚体，其重心G 到转轴Ｏ的距离为h ，绕O 轴的转动惯量为I ，当摆幅很小时，刚体绕O 轴摆动的周期T 为mghI T π2= （1） 式中g 为当地的重力加速度。

设复摆绕通过重心G 的轴的转动惯量为I G ，当G 轴与O 轴平行时，有2mh I I G += （2）代入式（1）得 mgh mh I T G 22+=π （3） 对比单摆周期的公式gl T π2=，可得mh mh Il G2+= （4）l 称为复摆的等效摆长。

因此只要测出周期和等效摆长便可求得重力加速度。

复摆的周期我们能测得非常精确，但利用mhmh I l G 2+=来确定l 是很困难的。

因为重心G 的位置不易测定，因而重心G 到悬点O 的距离h 也是难以精确测定的。

同时由于复摆不可能做成理想的、规则的形状，其密度也难绝对均匀，想精确计算I G 也是不可能的。

我们利用复摆上两点的共轭性可以精确求得l 。

在复摆重心G 的两旁，总可找到两点O 和O ’，使得该摆以O 悬点的摆动周期T 1与以O ’为悬点的摆动周期T 2相同，那么可以证明'OO 就是我们要求的等效摆长l 。

图一 复摆示意图 图二 凯特摆摆杆示意图 图二是凯特摆摆杆的示意图，对凯特摆而言，两刀口间的距离就是该摆的等效摆长l 。

一实验报告906系07级 姓名:刘贝 实验日期:2008-10-14 No.PB07210063 一.实验题目：用凯特摆测量重力加速度．二.实验目的：学习凯特摆的实验设计思想与技巧．掌握一种比较精确地测量重力加速度的 方法．三.实验原理:设一质量为m 的刚体,其重心G 到转轴O 的距离为h,绕O 轴的转动惯量为I,当摆幅很小时,刚体绕O 轴摆的周期T 为mghI T π2= (1)式中g 为当地的重力加速度.设复摆通过重心G 的转动惯量为I G ,当G 轴与O 轴平行时有2mhI I G +=.mghmh I G T 22+=π(2)对比单摆周期的公式gl T π2= (3).可得:mhmh I G l 2+= (4) 复摆示意图l 称为复摆的等效摆长.对于凯特摆而言,两刀口间的距离就是该摆的等效摆长l.在实验中当两刀口位置确定后,通过调节A,B,C,D 四摆锤的位置可使正,倒悬挂时的摆动周期T 1和T 2基本相等,即T 1≈T 2.由公式可得:12121mgh mh I G T +=π(5).22222mgh mh I G T +=π(6).ba l h T T lT T g+=+=--+)2(2241222122212π (7).凯特摆摆杆结构示意图 此式中,l,T 1,T 2都是可以精确测定的量,而h 1则不易测准,由此可知,a 项可以精确求得,而b 项则不易精确测得.但当T 1=T 2以及|2h 1-l|的值较大时,b 项的值相对a 项是非常小的,这样b 项的不精确度对测量结果产生的影响就微乎其微了.四.实验数据处理:(1)实验中用米尺测得等效摆长l 的值分别如下:3次测量等效摆长所得到的数据表等效摆长l次数 1 2 3 l(cm)75.4575.4375.42取参考g 值(g ≈9.80m/s 2),利用公式(3)粗略估算T 值.而等效摆长的平均值二l=(l 1+l 2+l 3)/3=(75.42+75.43+75.45)/3=226.3/3=75.433cm. 所以参考值T=2π√(75.433)/9.80=1.7432 s.cmx i i l x 2210)*69.109.089.2(31210*528.1)13/()(4-++=-==--=-∑σ∴μl =σl /√2=1.0807*10-2cm.(2)在满足实验条件的情况下(即T 1与T 2的差值小于0.001s)分别测量5次10T 1和5次10T 2得到的数据如下:由以上数据可得到10T 1的平均值为10T 1=(17.4296+17.4287+17.4326+17.4315+17.4290)/5=17.43032 s.sx i i T x 3410)*7424.13924.11984.56244.25184.0(5121010*6938.1)15/()(61-++++=-==--=-∑σ所以取T 1=17.43032/10=1.74303 s.σT1=σ10T1/10=1.6938*10-4 s. ∴μT1=σT1/√5=0.7575*10-4 s.在同样情况下测量5次10T 2得到的数据如下:由以上数据可得到10T 1的平均值为10T 2=(17.4300+17.4267+17.4317+17.4318+17.4305)/5=17.43014 s.sx i i T x 3410)*96.1256.27536.24336.118396.1(5121010*7196.2)15/()(82-++++=-==--=-∑σ所以取T 2=17.43014/10=1.74301 s.σT2=σ10T2/10=2.7196*10-4s.∴μT2=σT2/√5=1.2163*10-4 s.(3)实验中所测得的相应的h 1得到的数据如下:由以上数据可得到h 1的平均值为cmh i i h477.293/)50.2948.2945.29(3/311=++==∑=-.三cmx i i h x 2210)*29.509.029.7(31210*5169.22/)(41-++=-==-=-∑σ.∴μh1=σh1/√3=1.4532*10-2cm.将以上相关数据代入公式(7),则有:.02727.432958.010*97208.650866.1076098.6)75433.029477.0*2*(274301.174303.175433.0*27430.17430.1)2(224522221222122212=-=+=+=+=---+--+ba l h T T lT T gπ所以有:./80277.9202727.44422s m g ba ===+ππ由于在测量周期中n 的值为5,所以若取P=0.68,t=1.14,T 1的不确定度为μT1=1.14*0.7575*10-4=0.86355*10-4. P=0.95,t=2.78,T 1的不确定度为μT1=2.78*0.7575*10-4=2.10585*10-4. P=0.99,t=4.60,T 1的不确定度为μT1=4.60*0.7575*10-4=3.4845*10-4. 由于在测量周期中n 的值为5,所以若取P=0.68,t=1.14,T 2的不确定度为μT2=1.14*1.2163*10-4=1.3866*10-4. P=0.95,t=2.78,T 2的不确定度为μT2=2.78*1.2163*10-4=3.3813*10-4. P=0.99,t=4.60,T 2的不确定度为μT2=4.60*1.2163*10-4=5.5949*10-4. 在测量h 1中n 的值为3,所以若取P=0.68,t=1.32,h 1的不确定度为μh1=1.32*1.4532*10-2=1.9182*10-2. P=0.95,t=4.30,h 1的不确定度为μh1=4.30*1.4532*10-2=6.2488*10-2. P=0.99,t=9.93,h 1的不确定度为μh1=9.93*1.4532*10-2=14.4303*10-2. 在测量l 中n 的值为3,所以若取P=0.68,t=1.32,l 的不确定度为μl =1.32*1.0807*10-2=1.4265*10-2. P=0.95,t=4.30,l 的不确定度为μl =4.30*1.0807*10-2=4.6470*10-2. P=0.99,t=9.93,l 的不确定度为μl =9.93*1.0807*10-2=10.7313*10-2.由不确定度的传递公式有(P=0.68):T 12的不确定度为2*μT1*T 1=2*0.86355*10-4*1.74303=3.0104*10-4. T 22的不确定度为2*μT2*T 2=2*3.3813*10-4*1.74301=11.7872*10-4.T 12+T 22的不确定度为3.0104*10-4+11.7872*10-4=14.7978*10-4.T 12-T 22的不确定度为3.0104*10-4-11.7872*10-4=8.7769*10-4.(2h1-l)的不确定度为2*μh1-μl=2*1.9182*10-2-1.4265*10-2=2.4099*10-4.a的不确定度为(yΔx+xΔy)/2y2=(14.7978*10-4*0.75433+1.4265*10-4*6.0761)/(2*0.5690)=1.7425*10-3. b的不确定度为(yΔx+xΔy)/2y2=(0.16479*8.7769*10-4+1.8257*10-4*6.97208*10-5)/(2*0.02716)=2.6626*10-3.所以a+b的不确定度为(1.7425+2.6626)*10-3=4.4051*10-3.由公式(7)有g=4π2/(a+b).所以g的不确定度σg=4π2*(4.4051*10-3)/16.2206=1.0721*10-2.所以,综上数据可得实验所得的当地重力加速度为:g=(9.80277±0.01072)m/s2.而σg/g=0.01072*10-2/9.80277=1.0938*10-3<0.2%.所以认为这个数据是理想的.由不确定度的传递公式有(P=0.95):T12的不确定度为2*μT1*T1=2*2.10585*10-4*1.74303=7.3411*10-4.T22的不确定度为2*μT2*T2=2*3.3813*10-4*1.74301=11.7872*10-4.T12+T22的不确定度为7.3411*10-4+11.7872*10-4=19.1284*10-4.T12-T22的不确定度为7.3411*10-4-11.7872*10-4=4.4461*10-4.(2h1-l)的不确定度为2*μh1-μl=2*6.2488*10-4-4.6470*10-4=7.8506*10-4.a的不确定度为(yΔx+xΔy)/2y2=(19.1284*10-4*0.75433+4.6470*10-4*6.0761)/(2*0.5690)=3.7491*10-3. b的不确定度为(yΔx+xΔy)/2y2=(0.16479*4.4461*10-4+1.8257*10-4*6.97208*10-5)/(2*0.02716)=2.4782*10-3.所以a+b的不确定度为(3.7491+2.4782)*10-3=6.2273*10-3.由公式(7)有g=4π2/(a+b).所以g的不确定度σg=4π2*(6.2273*10-3)/16.2206=1.5156*10-2.所以,综上数据可得实验所得的当地重力加速度为:g=(9.80277±0.01516)m/s2.而σg/g=0.01516*10-2/9.80277=1.5461*10-3<0.2%.所以认为这个数据是理想的.由不确定度的传递公式有(P=0.99):T12的不确定度为2*μT1*T1=2*3.4845*10-4*1.74303=12.1472*10-4.T22的不确定度为2*μT2*T2=2*5.5949*10-4*1.74301=19.5039*10-4.T12+T22的不确定度为12.1472*10-4+19.5039*10-4=31.6511*10-4.T12-T22的不确定度为12.1472*10-4-19.5039*10-4=7.3567*10-4.(2h1-l)的不确定度为2*μh1-μl=2*14.4303*10-4-10.7313*10-4=18.1293*10-4.a的不确定度为(yΔx+xΔy)/2y2=(31.6511*10-4*0.75433+10.7313*10-4*6.0761)/(2*0.5690)=7.8278*10-3. b的不确定度为(yΔx+xΔy)/2y2=(0.16479*7.3567*10-4+18.1293*10-4*6.97208*10-5)/(2*0.02716)=1.2123*10-3.所以a+b的不确定度为(7.8278+1.2123)*10-3=9.0401*10-3.由公式(7)有g=4π2/(a+b).四所以g的不确定度σg=4π2*(9.0401*10-3)/16.2206=2.2002*10-2.所以,综上数据可得实验所得的当地重力加速度为:g=(9.80277±0.02200)m/s2.而σg/g=0.02200*10-2/9.80277=2.244*10-3<0.3%.所以认为这个数据是理想的.综上数据分析可得,当地的重力加速度的实验值为:(1)P=0.68时, g=(9.80277±0.01072)m/s2.(2)P=0.95时, g=(9.80277±0.01516)m/s2.(3)P=0.99时, g=(9.80277±0.02200)m/s2.五.实验分析及总结:本实验学到了一种可以比较精确测量当地重力加速度的方法--用凯特摆测量重力加速度.由以上实验数据得到了当地的重力加速度的实验值.由实验数据分析所得到的结果分析来看,认为这次实验是成功的,得到的实验数据值也是较为理想的.另外,实验中仍存在着一些细节需要注意和一些可以再进一步改进的地方.T1和T2的值应当尽量接近.当然,让它们相等是很难的.这其中有仪器自身的原因,也有实验者人为的原因影响.另外,在测量等效摆长l和h1时由于使用的是米尺,所以精确度还不是太高.加之人为的读取数据和数据的取舍影响了实验数据的精确度.所以,若用较为精确的测量仪器并保证在读取数据时能尽可能的精确和在实验数据计算处理过程中也尽可能的精确,则得到的实验数据将会更加精确,更加接近其真实值.六.思考题:1.用凯特摆测重力加速度,在实验设计上有什么特点?避免了什么量的测量?降低了哪个量的测量精度?实验上如何来实现?答:凯特摆测重力加速度在实验设计上成功避免和减少了一些不易测量量对实验结果的影响,减少了单摆测重力加速度中一些非理想情况对实验结果的影响(如摆线的质量和摆的体积等),避免了测重力加速度中对摆长的测量,同时降低了悬挂点与重心距离的测量精度.避免测量摆长,采用测量等效摆长的方法来实现,降低悬挂点与重心距离的测量精度.在实验上使用正悬和倒悬分别测量周期的方法来实现.2.结合误差计算,你认为影响凯特摆测重力加速度精度的主要因素是什么?将所得的实验结果与当地的重力加速度的公认值相比较,你能得到什么结论?若有偏差,试分析之.答:影响重力加速度的主要因素有T1和T2的测量精度和等效摆长以及悬挂点与重心距离的测量精度.与当地的重力加速度公认值比较,有偏差.这偏差主要来自实验中T1和T2的测量偏差以及等效摆长和悬挂点与重心距离的测量偏差以及实验数据处理中对实验数据的取舍偏差有关.五。

凯特摆测重力加速度简介凯特摆是一种通过摆动的周期和长度来测量地球重力加速度的装置。

通过测量凯特摆的周期和长度之间的关系，可以计算出重力加速度的数值。

本文将介绍凯特摆的原理、实验步骤以及数据处理方法。

原理凯特摆是由一个线形摆线和一个重力体组成。

当重力体被拉向一侧释放后，由于重力的作用，重力体将开始摆动。

摆动的周期和长度的关系可以通过重力加速度公式来求得：T = 2π * √(L / g)其中，T为周期，L为摆长，g为重力加速度。

实验步骤以下是测量重力加速度的凯特摆的实验步骤：1.准备工作：确定实验场地，将凯特摆悬挂在一个固定的支撑物上。

2.在凯特摆上设置一个固定的摆长，例如 1 米。

3.将重力体拉至一侧，并释放。

4.记录重力体摆动的周期，可以使用计时器或计时器应用程序来记录摆动时间。

5.根据测得的周期和已知的摆长，使用重力加速度公式计算重力加速度的数值。

6.重复步骤 2-5，至少进行三次实验以获得可靠的结果。

7.取多次实验的平均值，计算重力加速度的最终数值。

数据处理在进行实验的过程中，我们得到了多次实验的周期和摆长数据。

为了计算重力加速度的数值，我们需要处理这些数据。

以下是数据处理的步骤：1.将周期数据转换为秒，并计算平均周期。

2.将摆长数据转换为米，并计算平均摆长。

3.使用平均摆长和平均周期，使用重力加速度公式计算重力加速度的数值。

4.使用所有实验的重力加速度数值，计算平均值并计算标准偏差，以评估实验结果的可靠性。

5.根据标准偏差的大小，判断实验结果的可靠性。

如果标准偏差较小，则实验结果较为可靠。

结论通过使用凯特摆来测量重力加速度，我们可以获得重力加速度的数值。

通过多次实验取平均值，并计算标准偏差，可以评估实验结果的可靠性。

凯特摆测重力加速度是一种简单而有效的方法，可以在物理实验中广泛应用。

实验题目：凯特摆测重力加速度实验目的：学习凯特摆的实验设计思想和技巧,掌握一种比较精确的测量重力加速度的方实验原理:设一质量为m 的刚体，其重心G 到转轴O 的距离为h ，绕O 轴的转动惯量为I ，当摆幅很小时，刚体绕O 轴摆动的周期T 为：mghI T π2= 设复摆绕通过重心G 的轴的转动惯量为I G ，当G 轴与O 轴平行时，有2GI=I +mh 得到 mgh mh I T G 22+=π复摆的等效摆长 mhmh I l G 2+=实验仪器:凯特摆右图是凯特摆摆杆的示意图。

对凯特摆而言，两刀口间的距离就是该摆的等效摆长l 。

在实验中当两刀口位置确定后，通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期T 1和T 2基本相等。

12112mgh mh I T G +=π22222mgh mh I T G +=π当12T T ≈时 h 1+h 2=l得到 ()l h T T l T T g --++=12221222122224π 此式中，l 、T 1、T 2都是可以精确测定的量，而h 1则不易测准。

由此可知，a项可以精确求得，而b 项则不易精确求得。

但当T 1=T 2以及 |2h 1-l | 的值较大时，b 项的值相对a 项是非常小的，这样b 项的不精确对测量结果产生的影响就微乎其微了。

实验仪器：凯特摆、光电探头、米尺和VAFN 多用数字测试仪等 实验步骤：1、仪器调节选定两刀口间得距离（实验中不用调了）即该摆得等效摆长l ，使两刀口相对摆杆基本对称，并相互平行，用米尺测出l 的值，取参考的g=9.8m/2s 粗略估算T 值,作为调节T ₁和T ₂参考值。

将摆杆悬挂到支架上水平的V 形刀承上，调节底座上的螺丝，借助于铅垂线，使摆杆能在铅垂面内自由摆动，倒挂也如此。

将光电探头放在摆杆下方，让摆针在摆动时经过光电探测器。

让摆杆作小角度摆动，摆幅取4cm,待稳定后，按下reset 钮，则测试仪开始自动记录一个周期的时间。

用凯特摆测量重力加速度1818年Kater 设计出一种物理摆，他巧妙地利用物理摆的共轭点避免和减少了某些不易测准的物理量对实验结果的影响，提高了测量重力加速度的精度。

19世纪60年代雷普索里德对此作了改进，成为当时测重力加速度的最精确方法。

波斯坦大地测量所曾同时以五个Kater 摆花了八年时间（1896-1904）测得当地重力加速度的值g= ( 981.274 ± 0.003 ) cm / s 2 。

凯特摆测量重力加速度的方法不仅在科学史上有重要价值，而且在实验设计思想上亦有值得学习的地方。

实验原理设一质量为m 的刚体，其重心G 到转轴O 的距离为h ，绕O 轴的转动惯量为I ，当摆幅很小时，刚体绕O 轴摆动的周期T 为：mghIT π2= (1)式中g 为当地的重力加速度.设复摆绕通过重心G 的轴的转动惯量为I G ，当G 轴与O 轴平行时，有I=I G +mh 2(2)代入式（1）得：mghmh I T G 22+=π(3)对比单摆周期的公式gl T π2=可得mhmh I l G 2+=(4)称为复摆的等效摆长。

因此只要测出周期和等效摆长便可求得重力加速度。

上图是凯特摆摆杆的示意图。

对凯特摆而言，两刀口间的距离就是该摆的等效摆长l 。

在实验中当两刀口位置确定后，通过调节A 、B 、C 、D 四摆锤的位置可使正、倒悬挂时的摆动周期T 1和T 2基本相等。

由公式（3）可得12112mgh mh I T G +=π(5)22222mgh mh I T G +=π(6)其中T 1和h 1为摆绕O 轴的摆动周期和O 轴到重心G 的距离。

当T 1≈T 2时，h 1+h 2=l 即为等效摆长。

由式(5)和(6)消去I G ，可得：()l h T T l T T g --++=12221222122224π (7)此式中，l 、T 1、T 2都是可以精确测定的量，而h 1则不易测准。

由此可知，a 项可以精确求得，而b 项则不易精确求得。