贝塞尔公式(建议收藏)

计量贝塞尔公式范文贝塞尔公式是在数学和物理学中常用的一个计量公式，它用于计算贝塞尔函数，这是一类重要的特殊函数。

贝塞尔函数广泛应用于波动理论、信号处理、电磁学、量子力学及其他领域。

贝塞尔公式是一个复杂的公式，它可以用不同的方式表示，下面我们将详细介绍贝塞尔公式及其应用。

贝塞尔函数是由弗里德里希·贝塞尔研究并命名的，它出现在解决柱坐标系中的波动方程时。

贝塞尔函数具有无穷多个解，而贝塞尔函数的具体形式和性质取决于输入参数。

贝塞尔公式实际上是一类特殊函数的定义和计算规则。

贝塞尔公式具有不同的形式，其中最常见的形式是第一类贝塞尔函数和第二类贝塞尔函数。

第一类贝塞尔函数（Jn）由以下公式给出：Jn(x)=Σ(−1)^k*(x/2)^(2k+n)/(k!*(k+n)!)，k从0到无穷大其中x是实数，k是非负整数，n是非负整数。

该公式表示了贝塞尔函数在数轴上的取值。

贝塞尔函数的图像通常由周期性的振荡和指数衰减形成。

第一类贝塞尔函数在物理学中常常用来表示波的柱坐标调制。

第二类贝塞尔函数（Yn）由以下公式给出：Yn(x) = (Jn(x) * cos(nπ) - J−n(x)) / sin(nπ)，当cos(nπ)≠0Yn(x) = lim (Jn(x) * cos(nπ) - J−n(x)) / sin(nπ)，当cos(nπ)=0其中n是非负整数。

第二类贝塞尔函数是第一个贝塞尔函数的补函数，它是贝塞尔函数的幂记录版本。

当x接近0时，第二类贝塞尔函数会出现无穷大的奇点。

第二类贝塞尔函数也用于波的柱坐标调制。

贝塞尔公式有许多重要的应用，其中之一是在声学中的应用。

贝塞尔函数被广泛应用于描述声波的振动模式和传播。

例如，在管道中的声波传播可以用贝塞尔函数来描述。

贝塞尔函数也被用于解决波动方程和边界值问题。

另一个重要的应用是电磁学中的应用。

贝塞尔函数被用来描述电磁波的振动模式和传播，在电磁学中，贝塞尔函数通常用于解决透射线和辐射模式的问题。

贝塞尔函数的有关公式C.贝塞尔函数的有关公式贝塞尔方程的持解B(z)为(柱)贝塞尔函数。

有 p第一类柱贝塞尔函数J(z) pnp为整数n时，J=(,1)J; ,n np不为整数时，J与J线性无关。

p,p第二类柱贝塞尔函数N(z)(柱诺依曼函数) pnn为整数时N=(,1)N。

,n n第三类柱贝塞尔函数H(z) (柱汉开尔函数): p(1) 第一类柱汉开尔函数 H(z)= J(z)+j N(z) pp p(2)第二类柱汉开尔函数 H(z)= J(z),j N(z) pp p大宗量z小宗量z 0，为欧拉常数见微波与光电子学中的电磁理论 p668J(z)的母函数和有关公式 nz(t/2-1/2t)函数e称为第一类贝塞尔函数的母函数，或称生成函数，若将此函数在t=0附近展开成罗朗级数，可得到j j 在上式中作代换，令t=e，t= je等，可得又可得如z=x为实数贝塞尔函数的加法公式J(z)的零点,nniJ’(z)的零点,nni半整数阶贝塞尔函数J(z)的零点,n+1/2npJ'(z)的零点,'n+1/2npD(朗斯基行列式及其它关系式E(修正贝塞尔函数有关公式贝塞尔方程中用(jz)代换z，得到修正的贝塞尔方程方程的两个线性无关的解为,p I(z)=jJ(jz)(称为第一类修正的柱贝塞尔函数。

ppp+1(1)K(z)=(,/2)jH(jz)(称为第二类修正的柱贝塞尔函数。

pp大宗量z小宗量z 0(0210)《古代散文》复习思考题一、填空题1(甲骨卜辞、和《易经》中的卦、爻辞是我国古代散文的萌芽。

2(深于比兴、，是先秦散文的突出特点。

3(《》长于描写外交辞令。

4(《国语》的突出特点是长于。

5(“兼爱”、“非攻”是思想的核心。

6(先秦诸子中，善养“浩然之气”。

7(先秦诸子中，提出了“言不尽意”、“得意忘言” 的观点。

8(荀子的《》是我国最早以“赋”名篇的作品。

9(《鵩鸟赋》是的骚体赋。

10(枚乘的《》标志着散体赋的正式形成。

三阶贝塞尔曲线公式三阶贝塞尔曲线作为一种应用广泛、精度较高的数学曲线，被用于各种复杂的几何形状建模，例如自然界中的山、河、瀑布等，同时也广泛应用于微分平面、立体几何图形的建模中。

因此，贝塞尔曲线的公式被称为是数学中的一个“神奇”。

三阶贝塞尔曲线是一种特殊的曲线，它由给定的四个控制点（两个端点和两个控制点）确定，并可以用曲线上每一点的坐标来表示。

最常见的贝塞尔曲线公式为：B（t）＝（1-t）^3p1+3（1-t）^2tP2+3（1-t）t^2p3+t^3p4，其中t是一个变量，取值范围为[0,1]，p1,p2,p3,p4分别表示四个控制点。

三阶贝塞尔曲线有多种计算方法，其中一种计算方法为采用矩阵的运算，矩阵乘法是由一组数字组成的平面表进行乘法运算的方法，即将贝塞尔曲线的坐标转换成矩阵，利用矩阵乘法求得对应的点坐标，在确定t值后可以求出任意一点的坐标。

另外，三阶贝塞尔曲线还有一种特殊的运算方法贝塞尔基函数，即将曲线上的每一点表达成一个基函数的线性组合，其定义如下：B （t）＝a0+a1t+a2t^2+a3t^3，其中a0,a1,a2,a3分别是四个控制点的坐标，t是一个变量，取值范围为[0,1]。

可以利用基函数的方法更加方便地求得三阶贝塞尔曲线的控制点和任意点的坐标。

三阶贝塞尔曲线由于其灵活性和较高的精度，在实际工程中应用广泛。

例如，在计算机图形学中，三阶贝塞尔曲线可以用来建模更加美观的圆弧和复杂的曲线；在机器人控制领域，三阶贝塞尔曲线可以用来控制机器人的运动轨迹；在几何建模领域，三阶贝塞尔曲线可以用来建模复杂的四边形。

此外，三阶贝塞尔曲线还可以应用于计算机动画、游戏制作和仿真等领域。

从上面可以看出，三阶贝塞尔曲线拥有丰富的功能和广泛的应用。

它是一种有趣且实用的数学曲线，在几何建模、动画和实时控制等方面都有着重要的应用价值。

因此，掌握三阶贝塞尔曲线的公式及其计算方法，对于更加有效地利用它具有重要的意义。

三阶贝塞尔曲线公式
贝塞尔曲线是计算机图形学中被广泛使用的一种曲线，它是一个灵活多样的几何表达方式。

三阶贝塞尔曲线，即指的是三次贝塞尔曲线，是最常用的曲线。

它的最常用的公式如下：
P(t) = (1-t)P0 + 3(1-t)tP1 + 3(1-t)tP2 + tP3，其中P(t)表示t时刻的点的坐标，P0、P1、P2、P3分别表示贝塞尔曲线上的四个基准点的坐标，t的定义域为[0,1]。

三阶贝塞尔曲线的特点在于它可以准确反映出一系列点连续变
化状态，它可以做到在四个基准点之间“平滑”地过渡，使图形看起来更加圆润。

此外，三阶贝塞尔曲线也有很多控制工具，可以通过改变基准点的位置和改变起始点和结束点的位置，从而轻松调整三阶贝塞尔曲线，以达到画出不同曲线的目的。

三阶贝塞尔曲线在计算机图形学中有着重要的作用。

它可以用来表示图形变化的状态，如：可以用来表示离散的几何图形，如多边形、四边形等，也可以用来表示精细的曲线，如云状曲线、抛物线等。

此外，三阶贝塞尔曲线可以用在更多的应用场景中，如：绘制复杂的三维模型；制作动画；用于计算机视觉等。

例如，在计算机视觉中，三阶贝塞尔曲线可以用来检测和识别图形特征，如轮廓和凸包，以及对对象进行分类，恢复和重建，而且这些操作也可以运用在图像处理过程中。

因此可以看出，三阶贝塞尔曲线具有广泛的应用，它不仅可以用来形成复杂的几何图形，也可以用来检测和识别图形特征，从而为计
算机图形学所做出重要的贡献。

C.贝塞尔函数的有关公式贝塞尔方程的持解B p(z)为(柱)贝塞尔函数。

有第一类柱贝塞尔函数J p(z)p为整数n时，J-n=(-1)n J n；p不为整数时，J p与J-p线性无关。

第二类柱贝塞尔函数N p(z)(柱诺依曼函数)n为整数时N-n=(-1)n N n。

第三类柱贝塞尔函数H p(z) (柱汉开尔函数)：第一类柱汉开尔函数H p(1)(z)= J p(z)+j N p(z)第二类柱汉开尔函数H p(2)(z)= J p(z)-j N p(z)大宗量z小宗量z 0，为欧拉常数见微波与光电子学中的电磁理论p668J n(z)的母函数和有关公式函数e z(t/2-1/2t)称为第一类贝塞尔函数的母函数，或称生成函数，若将此函数在t=0附近展开成罗朗级数，可得到在上式中作代换，令t=e j ，t= je j 等，可得又可得如z=x为实数贝塞尔函数的加法公式J n(z)的零点 niJ’n(z)的零点γni半整数阶贝塞尔函数J n+1/2(z)的零点χnpJ'n+1/2(z)的零点χ'npD．朗斯基行列式及其它关系式E．修正贝塞尔函数有关公式贝塞尔方程中用(j z)代换z，得到修正的贝塞尔方程方程的两个线性无关的解为I p(z)=j-p J p(j z)．称为第一类修正的柱贝塞尔函数。

K p(z)=(π/2)j p+1H p(1)(j z)．称为第二类修正的柱贝塞尔函数。

大宗量z小宗量z 0（0210）《古代散文》复习思考题一、填空题1．甲骨卜辞、和《易经》中的卦、爻辞是我国古代散文的萌芽。

2．深于比兴、，是先秦散文的突出特点。

3．《》长于描写外交辞令。

4．《国语》的突出特点是长于。

5．“兼爱”、“非攻”是思想的核心。

6．先秦诸子中，善养“浩然之气”。

7．先秦诸子中，提出了“言不尽意”、“得意忘言”的观点。

8．荀子的《》是我国最早以“赋”名篇的作品。

9．《鵩鸟赋》是的骚体赋。

10．枚乘的《》标志着散体赋的正式形成。

贝塞尔公式详细推导过程《贝塞尔公式的详细推导过程》引言：贝塞尔公式是数学中一种重要且广泛应用的公式，它的推导过程相对较复杂、细致，但却十分精彩。

在本文中，我们将详细介绍贝塞尔公式的推导过程，让读者对这一公式有更深入的理解。

一、贝塞尔公式的定义：贝塞尔公式是一种用连分数表示的数学公式，其一般形式为：J_n(x) = \frac{1}{\pi}\int_{0}^{\pi} \cos(n\theta - x\sin\theta)d\theta其中，J_n(x) 表示第n阶贝塞尔函数，x 是实数，\theta 表示角度，\pi 表示圆周率。

二、推导过程：1. 首先，我们从欧拉公式 e^ix = \cos(x) + i\sin(x) 出发，将其展开得到：e^{ix} = \cos(x) + i\sin(x)2. 接下来，我们将展开中的i\sin(x) 转化为两个实数的乘积。

我们知道，正弦函数的定义式为：\sin(x) = \frac{e^{ix} - e^{-ix}}{2i}代入之前的展开式，得到：i\sin(x) = \frac{e^{ix} - e^{-ix}}{2}3. 现在，我们用这个展开式来推导贝塞尔公式。

我们首先将贝塞尔函数展开成幂级数形式：J_n(x) = \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k}4. 接下来，我们将展开式中的 e^{ix} 替换为 \cos(x) + i\sin(x)：J_n(x) = \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k} \left(\cos(x) + i\sin(x)\right)5. 然后，我们将正弦函数用欧拉公式展开为两个指数函数的乘积：J_n(x) = \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k} \left(\cos(x) + i\frac{e^{ix} - e^{-ix}}{2}\right)6. 继续推导，我们可以将指数函数的乘积展开为两项之差：J_n(x) = \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k} \left(\cos(x) + \frac{i e^{ix}}{2} - \frac{i e^{-ix}}{2}\right)7. 现在，我们可以将展开式中的 i 消去：J_n(x) = \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k} \left(\cos(x) + \frac{e^{ix} - e^{-ix}}{2}\right)8. 之后，我们可以将展开式进行拆分，分别对两项进行求和，并利用复数的性质对其中的复数部分进行化简：J_n(x) = \left(\frac{x}{2}\right)^n \left(\sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k}\cos(x) + \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k}\frac{e^{ix} - e^{-ix}}{2}\right)9. 最后，我们可以将两个求和式进行整理，将其中的复数部分转化为积分形式：J_n(x) = \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k}\cos(x) + \left(\frac{x}{2}\right)^n \sum_{k=0}^{\infty} \frac{(-1)^k}{k!(n+k)!}\left(\frac{x}{2}\right)^{2k}\frac{1}{\pi}\int_{0}^{\pi} \cos(n\theta -x\sin\theta)d\theta10. 将整理后的展开式中的求和式转化为连分数形式，即可得到贝塞尔公式：J_n(x) = \frac{1}{\pi}\int_{0}^{\pi} \cos(n\theta - x\sin\theta)d\theta结论：通过上述推导过程，我们可以将贝塞尔公式从指数函数的展开式推导得到，将其转化为连分数形式。

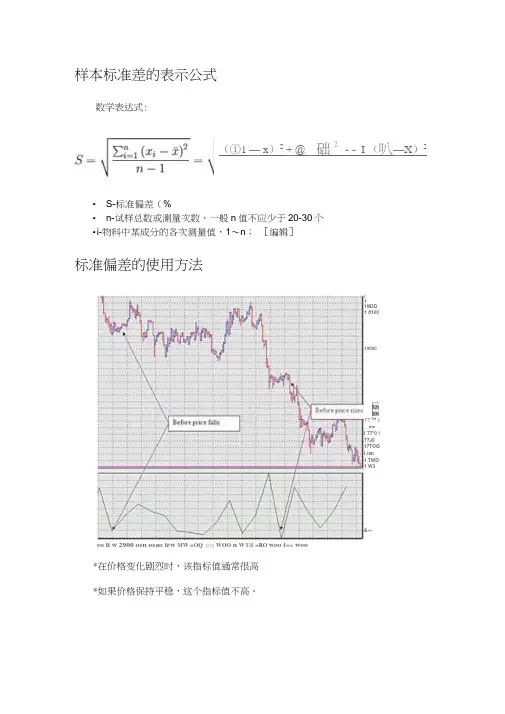
样本标准差的表示公式数学表达式:•S-标准偏差（%•n-试样总数或测量次数，一般n值不应少于20-30个•i-物料中某成分的各次测量值，1〜n；［编辑］标准偏差的使用方法*在价格变化剧烈时，该指标值通常很高*如果价格保持平稳，这个指标值不高。

i11M3D1 810019000TT™ImeI 77*0 I77J017TOQi ran1 TWO1 W3&»«co ii w 2900 oen oeao irw MW «OQ总如WOO n W US »RO woo t«« woo（①1 —x）2+ @ _ 础2 -- I （叭—X）2(1)•在价格发生剧烈的上涨/下降之前，该指标值总是很低。

［编辑］标准偏差的计算步骤标准偏差的计算步骤是：步骤一、（每个样本数据-样本全部数据之平均值） 步骤二、把步骤一所得的各个数值相加。

步骤四、从步骤三所得的数值之平方根就是抽样的标准偏差［编辑］六个计算标准偏差的公式⑴［编辑］标准偏差的理论计算公式设对真值为X 的某量进行一组等精度测量，其测得值为11、丨2、 测得值I 与该量真值X 之差为真差占CT ,则有 （T 1 = 1 i - X（T 2 = I 2 - X(T n= |n - X我们定义标准偏差（也称标准差）C 为步骤三、把步骤二的结果除以（n - 1）（“ n ”指样本数目）a =1 n朽(Hi=l=lun由于真值X都是不可知的，因此真差C占也就无法求得，故式只有理论意义而无实用价值。

［编辑］标准偏差b的常用估计一贝塞尔公式由于真值是不可知的，在实际应用中，我们常用n次测量的算术平均值随着测量次数的增多，算术平均值最接近真值，当时，算术平均值就是真值。

于是我们用测得值li与算术平均值…之差一一剩余误差（也叫残差）V来代替真差（T , 即Vi = Li-L设一组等精度测量值为丨1、丨2、，， In贝U —- .1 - L14 = b - EJ JV n= l n~ L通过数学推导可得真差c与剩余误差v的关系为(1)将上式代入式（1）有式(2)就是著名的贝塞尔公式(Bessel)。

正确认识贝塞尔公式贝塞尔公式是一种数学工具，它可以用来求解傅里叶变换以及计算机图形学中的很多问题。

一、定义贝塞尔公式（Bezier formula）是由法国工程师贝塞尔（P. Bezier）在20世纪60年代提出的一种数学工具，可以用来求解傅里叶变换以及计算机图形学中的很多问题。

它将函数表达式限制为形如：f (x) = P 0 + P 1 x + P 2 x2 + P 3 x3 ... + P n xn其中，P 0 为常量，P i 为贝塞尔控制点，n 为参数的阶数。

P的乘法可以换成加法表示，从而便于计算：f (x) = P 0 + ∑(P i xi)从而得出以下控制点串行函数：f (x) = ∑(C i B i (x))其中，C i 是系数，即曲线上某一点的坐标值，B i (x) 是基函数,i=1,2,3…n+1 。

二、应用贝塞尔公式能够用来求解傅里叶变换，它可以用来分析曲线的频率谱，取得控制频率谱的性质，并可以根据频率谱的变化来确定曲线的形状，当控制频率谱的比率变动的时候，曲线的形状也会相应的发生变化。

贝塞尔公式也在计算机图形学中被广泛应用，它可以实现很多复杂的图形，比如花瓣、树叶等等，此外，贝塞尔公式还可以用来分析坐标空间中任意物体的三维模型，还可以应用于计算机游戏中各种立体物体的建模。

三、优点贝塞尔公式有许多优点：（1）贝塞尔公式可以用非常少的控制点来表示各种复杂的曲线。

（2）它可以极大的精确度来定义曲线，即使要表示的曲线很复杂，它也能保持高精度。

（3）它可以用来分析曲线的频率谱，并利用控制点控制曲线的形状。

（4）贝塞尔公式的计算过程简单，不会耗费太多的时间，可以帮助我们更快的实现图形学中的复杂形状。

四、缺点（1）贝塞尔曲线并不是自发性的，严格来讲，除了它所依赖的控制点之外，它不能体现任何其他信息。

（2）它并不是容易理解的，因为许多情况下，它的参数的计算是很困难的。

（3）它的精度是受限的，比起多边形，它所能表示的精度可能还算低。

两个点生成贝塞尔曲线公式
贝塞尔曲线是由若干个控制点生成的曲线，其中包括两个端点和若干个中间控制点。

这些控制点决定了曲线的形状。

在二维空间中，如果给定两个端点P0和P2以及一个中间控制点P1，可以使用二次贝塞尔曲线的公式来生成曲线上的点。

公式如下：
\[ B(t) = (1-t)^2 * P0 + 2 * (1-t) * t * P1 + t^2 * P2 \]
其中，t的取值范围通常是\[0, 1\]，表示曲线上的位置。

当t取值0时，得到的是曲线的起始点P0，当t取值1时，得到的是曲线的终点P2。

如果有更多的中间控制点，可以使用更高阶的贝塞尔曲线公式来生成曲线。

例如，三次贝塞尔曲线的公式如下：
\[ B(t) = (1-t)^3 * P0 + 3 * (1-t)^2 * t * P1 + 3 * (1-t) * t^2 * P2 + t^3 * P3 \]
这样，通过给定端点和若干个中间控制点，可以生成相应阶数的贝塞尔曲线。

贝塞尔函数的有关公式部门： xxx时间： xxx整理范文，仅供参考，可下载自行编辑C.贝塞尔函数的有关公式贝塞尔方程的持解Bp(z>为(柱>贝塞尔函数。

有第一类柱贝塞尔函数Jp(z>p为整数n时，J-n=(-1>nJn；p不为整数时，Jp与J-p线性无关。

第二类柱贝塞尔函数N p(z>(柱诺依曼函数>n为整数时N-n=(-1>nNn。

第三类柱贝塞尔函数Hp(z> (柱汉开尔函数>：第一类柱汉开尔函数 Hp(1>(z>=Jp(z>+jN p(z>第二类柱汉开尔函数 Hp(2>(z>=Jp(z>-jN p(z>大宗量z→∞小宗量z→0，为欧拉常数见微波与光电子学中的电磁理论 p668Jn(z>的母函数和有关公式函数ez(t/2-1/2t>称为第一类贝塞尔函数的母函数，或称生成函数，若将此函数在t=0附近展开成罗朗级数，可得到b5E2RGbCAP在上式中作代换，令t=ejϕ，t=±jejϕ等，可得又可得如z=x为实数贝塞尔函数的加法公式Jn(z>的零点μniJ’n(z>的零点γni半整数阶贝塞尔函数Jn+1/2(z>的零点χnpJ'n+1/2(z>的零点χ'npD．朗斯基行列式及其它关系式E．修正贝塞尔函数有关公式贝塞尔方程中用(jz>代换z，得到修正的贝塞尔方程方程的两个线性无关的解为Ip(z>=j-pJp(jz>．称为第一类修正的柱贝塞尔函数。

Kp(z>=(π/2>jp+1Hp(1>(jz>．称为第二类修正的柱贝塞尔函数。

大宗量z→∞小宗量z→0申明：所有资料为本人收集整理，仅限个人学习使用，勿做商业用途。

x n2m 2n2m m!(n
, m 1)
(18)
J n (x)
(1) m
m0
x n2m 2n2m m!(n
, m 1)
(19)
情形 2
如果 n 为整数(包括0)，
J n (x) (1)n J n (x).
这就说明了J n (x) 与 J n (x) 当 n(n 0)为整数时是
线性相关的。 为了求出贝塞尔方程的通解，我们
(26)
事实上，在(18)式的两边乘上 x n ,然后对 x
求导，得
d
dx
xn J n (x)
d dx
m0
(1)
m
x2m
2
n2m
m!(n
m
1)
令
m
1
k,
(k
(1)m
m1
0,1, 2,),
2n2m1 (m
得
x 2m1 1)!(n
m
1)
k 0
(1) k 1
x 2k 1 2n2k1 k!(n 1
x n J n (x) nxn1J n (x) x n J n1 (x),
x n J n (x) nxn1 J n (x) x n J n1 (x),
11
d
dx
xn J n (x)
x n J n1 (x),
(25)
d
dx
xn J n (x)
x n J n1 (x).
(26)
如果将以上两式左端的导数表出，化简后则得
x
(27) (30)
同样可得
J1 2
2 cos x.
x
(31)
应用公式(27)得
1

贝塞尔函数的性质贝塞尔函数的性质ν+∞∑n nx 21ν+∞∑n nx 21()(()1)n n n ννν+Γ=++Γ+d J x J x()()()()J x J x d'诺伊曼函数也有与第一类贝塞尔函数相同的递推关系式，只不过将上述(1)—(6)中的换成() vJ x()vN x二. 半整数阶贝塞尔函数一般地有三、贝塞尔方程的固有值问题考虑贝塞尔方程的固有值问题固有值为2λω=(1)求固有函数、固有值(2)证明固有函数正交性(3)求固有函数的模作变换,r x ω=2220 ()()()()0(13)()0|(0)|r R r rR r r R r R R R λν'''⎧++-=⎨=<∞⎩ ，222()()()()0x y x xy x x v y x '''++-=(1)求固有函数、固有值2 d dν所以22n()()()0.Rmm n J r J r rdr ννωωωω-=⎰但，因此,,m n m n ωω≠≠0()()0()Rm n J r J r rdr m n ννωω=≠⎰22 R Rν21四、贝塞尔函数的零点由于正弦函数和余弦函数在0到∞之间振动无限多次，因此从上列渐近公式可以看出，与应该有无穷多个实零点。

)(x J ν)(x N ν性质一: 与有无穷多个实零点，)(x J ν)(x N ν且当时，其相邻两个零点之间距离接近于+∞→x π按照罗尔定理，可得如下推论:推论：与有无穷多个实零点。

)(x J ν''()N x ν由的级数表示形式可得，)(x J ν()(1)()J x J x ννν-=-因此可知当v 为实数时，若x 是的零点–x 也是的零点.)(x J ν)(x J ν性质二: 的无穷多个实零点是在x 轴上关于原)(x Jd第四章-贝塞尔函数的性质3131则该方程必有两个线性无关的解, 假设通解为1122()()().J x C y x C y x ν=+由边界条件可得11221122()()()0,()()()0,J a C y a C y a J a C y a C y a νν=+='''=+=因为1221()()()()0,y a y a y a y a ''-≠120,0.C C ∴==所以()0.J x ν≡这个矛盾说明了的零点都是单零点。

四阶贝塞尔曲线公式
四阶贝塞尔曲线公式是用于描述二维平面上点的轨迹的数学公式。

它可以通过
控制点来实现平滑的曲线绘制。

四阶贝塞尔曲线由四个控制点A、B、C和D组成，其中A和D是曲线的起始点和终点，而B和C是曲线的控制点。

四阶贝塞尔曲线的公式可以表示为：
B(t) = (1-t)^3 * P0 + 3(1-t)^2 * t * P1 + 3(1-t) * t^2 * P2 + t^3 * P3
其中，B(t)是曲线上的点，t是一个介于0和1之间的参数，P0、P1、P2和P3
是控制点的坐标。

通过不同的控制点坐标，可以创建出各种形状和曲线。

四阶贝塞尔曲线的特点是平滑且具有可控性。

通过调整控制点的位置，可以改
变曲线的形状。

例如，将控制点P1和P2拉近或推远可以改变曲线的曲率，从而
实现不同的线型效果。

对于计算机图形学和动画设计来说，四阶贝塞尔曲线是一个重要的工具。

它可
以用来创建平滑的路径、绘制曲线和形状，以及实现各种动画效果。

总结起来，四阶贝塞尔曲线公式是描述二维平面上点轨迹的数学公式。

通过调
整控制点的位置，可以实现不同的线型效果，这在计算机图形学和动画设计中具有重要的应用价值。

贝塞尔函数积分公式
贝塞尔函数积分公式是数学中非常重要的一个公式，广泛应用于物理学、工程学等领域。

它的形式简洁而优美，具有很高的实用价值。

在物理学中，贝塞尔函数积分公式常常用于描述波动现象。

比如在光学中，光的衍射和干涉现象可以通过贝塞尔函数积分公式进行描述和计算。

在声学中，声波的传播和衍射现象也可以用贝塞尔函数积分公式来解释。

贝塞尔函数积分公式的应用使得我们能够更好地理解和预测各种波动现象的规律。

在工程学领域，贝塞尔函数积分公式也有着广泛的应用。

比如在电磁学中，电磁场的分布和传播可以通过贝塞尔函数积分公式进行描述。

在信号处理领域，信号的频谱分析和滤波等问题也可以用贝塞尔函数积分公式来解决。

贝塞尔函数积分公式的应用为工程师们提供了强大的工具，帮助他们解决各种实际问题。

除此之外，在数学研究中，贝塞尔函数积分公式也有着深远的影响。

贝塞尔函数是一类特殊的函数，具有很多独特的性质和规律。

贝塞尔函数积分公式的推导和性质研究对于拓展数学领域的边界和深化数学理论都具有重要意义。

总的来说，贝塞尔函数积分公式是一个非常重要且广泛应用的数学工具。

它的出现和发展丰富了数学理论，拓展了物理学和工程学的应用领域，为科学研究和工程实践提供了有力支持。

贝塞尔函数积
分公式的深入研究和应用将会为人类的科技发展和文明进步注入新的活力和动力。

贝塞尔函数积分公式
贝塞尔函数积分公式是一种重要的数学工具,用于求解复杂微分方程以及求解特定的函数积分。

贝塞尔函数积分公式基于贝塞尔级数的思想,它将一个复杂的函数表示为一系列的有限项之和,这些项拥有不同的贝塞尔函数,如果参数选择得当,它就可以求得函数值或积分值。

贝塞尔函数积分公式包括贝塞尔反变换,贝塞尔级数求积方法以及贝塞尔变分法。

贝塞尔反变换是利用函数的傅里叶级数表示来求解函数积分的方法。

它将一个复杂的多项积分转换为一系列的反变化的函数,即将积分转换为统一的傅里叶级数表示,然后反变换求出函数的值,以实现对复杂函数积分的计算。

贝塞尔级数求积方法也称诺伊曼·瑙波定理,它是非常常用的数值计算方法,用于求解复杂的积分问题。

它利用多项式拟合的方法,将复杂的积分依据贝塞尔函数表示式表示,比如二维空间积分就可以表示为一系列贝塞尔函数的组合。

贝塞尔变分法是将一个复杂函数表示成一系列有限项和的方法,可以用变分法近似求得函数的最值和积分值。

它根据特定随机变量的变分原理,以多项式的方式表示函数,然后叠加多项式的积分,实现求出函数的积分。

贝塞尔函数积分公式也可以用于解决抛物方程的问题,抛物方程是一类有关物理的重要问题,它可以被看做在初速度和加速度下的运
动,可以用贝塞尔函数积分公式求出它的解。

总之,贝塞尔函数积分公式是一种非常有效的数学工具,可以用来求解复杂微分方程以及求解特定的函数积分,也可以用来解决抛物方程的问题。

贝塞尔公式计算范文在二维空间中，贝塞尔曲线的坐标计算可以通过以下贝塞尔公式实现：B(t)=ΣC(n,k)*(1-t)^(n-k)*t^k*P(k)其中，B(t)表示曲线上的点坐标，C(n,k)是组合数公式，为从n个元素中取k个元素的组合数，(1-t)和t是自变量，P(k)是控制点。

使用贝塞尔公式计算曲线上的点坐标时，需要预先确定控制点的坐标和数量，并将其代入公式中进行计算。

控制点的数量决定了曲线的阶数，一般而言，曲线阶数越高，曲线的灵活性越大。

下面以三阶贝塞尔曲线为例来详细说明贝塞尔公式的计算方法：假设有四个控制点P0(x0,y0)，P1(x1,y1)，P2(x2,y2)和P3(x3,y3)。

我们需要计算位于参数t（0≤t≤1）处的曲线点坐标B(t)。

根据贝塞尔公式，我们可以计算三条辅助曲线B0(t)，B1(t)和B2(t)，它们分别连接P0和P1，P1和P2，以及P2和P3、这三条辅助曲线的坐标计算公式为：B0(t)=(1-t)^2*P0+2*(1-t)*t*P1+t^2*P2B1(t)=(1-t)^2*P1+2*(1-t)*t*P2+t^2*P3最终的贝塞尔曲线上的点坐标B(t)可以通过连接B0(t)和B1(t)的一条辅助曲线B01(t)来表示：B(t)=(1-t)*B0(t)+t*B1(t)将B0(t)和B1(t)的计算公式代入上述等式中，可以得到最终的贝塞尔公式：B(t)=(1-t)^3*P0+3*(1-t)^2*t*P1+3*(1-t)*t^2*P2+t^3*P3使用这个贝塞尔公式，我们可以根据给定的控制点和参数t计算曲线上的点坐标。

需要注意的是，贝塞尔公式只能计算三阶贝塞尔曲线的坐标，如果曲线阶数更高，公式会更加复杂。

此外，贝塞尔曲线的截距点也可以使用公式计算得到。

总结而言，贝塞尔公式是计算贝塞尔曲线上的点坐标的数学表达式。

通过确定控制点的坐标和数量，我们可以使用贝塞尔公式计算曲线上的点坐标。