下载文档原格式
MATLABSIMULINK永磁同步电机矢量控制系统仿真一、本文概述随着电机控制技术的快速发展，永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）在工业、交通和能源等领域的应用越来越广泛。
矢量控制作为PMSM的一种高效控制策略，能够实现对电机转矩和磁链的精确控制，从而提高电机的动态性能和稳态性能。
然而，在实际应用中，矢量控制系统的设计和调试过程往往复杂且耗时。
因此，利用MATLAB/Simulink进行永磁同步电机矢量控制系统的仿真研究，对于深入理解矢量控制原理、优化控制策略以及提高系统性能具有重要意义。
本文旨在通过MATLAB/Simulink平台，建立永磁同步电机矢量控制系统的仿真模型，并对其进行仿真分析。
本文将对永磁同步电机的基本结构和数学模型进行介绍，为后续仿真模型的建立提供理论基础。
本文将详细阐述矢量控制策略的基本原理和实现方法，包括坐标变换、空间矢量脉宽调制（SVPWM）等关键技术。
在此基础上，本文将利用MATLAB/Simulink中的电机控制库和自定义模块，搭建永磁同步电机矢量控制系统的仿真模型，并对其进行仿真实验。
本文将根据仿真结果，对矢量控制系统的性能进行分析和评价，并提出优化建议。
通过本文的研究，读者可以全面了解永磁同步电机矢量控制系统的基本原理和仿真实现方法，为后续的实际应用提供有益的参考和指导。
本文的研究结果也为永磁同步电机控制技术的发展和应用提供了有益的探索和启示。
二、永磁同步电机数学模型永磁同步电机（Permanent Magnet Synchronous Motor, PMSM）是一种高性能的电机，广泛应用于各种工业领域。
为了有效地对其进行控制，我们需要建立其精确的数学模型。
PMSM的数学模型主要包括电气方程、机械方程和磁链方程。
PMSM的电气方程描述了电机的电压、电流和磁链之间的关系。
在dq旋转坐标系下，电气方程可以表示为：V_d &= R_i I_d + \frac{d\Phi_d}{dt} - \omega_e \Phi_q \ V_q &= R_i I_q + \frac{d\Phi_q}{dt} + \omega_e \Phi_d其中，(V_d) 和 (V_q) 分别是d轴和q轴的电压；(I_d) 和 (I_q) 分别是d轴和q轴的电流；(\Phi_d) 和 (\Phi_q) 分别是d轴和q轴的磁链；(R_i) 是定子电阻；(\omega_e) 是电角速度。
目录1 异步电动机矢量控制原理 (2)2 坐标变换 (3)2.1 坐标变换基本思路 (3)2.2 三相——两相坐标系变换（3/2变换） (4)2.3 旋转变换 (5)3 转子磁链计算 (6)4 矢量控制系统设计 (7)4.1 矢量控制系统的电流闭环控制方式思想 (7)4.2 MATLAB系统仿真系统设计 (8)4.3 PI调节器设计 (9)5 仿真结果 (10)5.1 电机定子侧的电流仿真结果 (10)5.2 电机输出转矩仿真结果 (11)心得体会 (13)参考文献 (14)异步电机矢量控制Matlab 仿真实验1 异步电动机矢量控制原理矢量控制系统的基本思路是以产生相同的旋转磁动势为准则,将异步电动机在静止三相坐标系上的定子交流电流通过坐标变换等效成同步旋转坐标系上的直流电流,并分别加以控制,从而实现磁通和转矩的解耦控制,以达到直流电机的控制效果。
所谓矢量控制，就是通过矢量变换和按转子磁链定向，得到等效直流电动机模型，在按转子磁链定向坐标系中，用直流电动机的方法控制电磁转矩与磁链,然后将转子磁链定向坐标系中的控制量经变换得到三相坐标系的对应量，以实施控制。
其中等效的直流电动机模型如图1-1所示，在三相坐标系上的定子交流电流i A 、i B 、i C ，通过3/2变换可以等效成两相静止正交坐标系上的交流i sα和i sβ，再通过与转子磁链同步的旋转变换，可以等效成同步旋转正交坐标系上的直流电流i sm 和i st 。
图1-1 异步电动机矢量变换及等效直流电动机模型在三相坐标系上的定子交流电流,,A B C i i i ,通过3/2变换可以等效成两相静止正交坐标系上的交流s i α和s i β再通过与转子磁链同步的旋转变换，可以等效成同步旋转正交坐标系上的直流电流sm i 和st i 。
m 绕组相当于直流电动机的励磁绕组，sm i 相当于励磁电流，t 绕组相当于电枢绕组，st i 相当于与转矩成正比的电枢电流。
异步电动机矢量控制系统的设计与仿真.异步电动机矢量控制系统的设计与仿真在矢量控制技术出现之前，现代交流调速系统采用了恒压频比控制策略。
这种控制策略的缺点是，当电机低速旋转或在加减速、负载加减等动态条件下，系统性能显著降低，导致交流调速系统在低速、启动时转矩的动态响应和整个系统的稳定性方面不如DC调速系统，无法满足人们对高精度的要求。
后来，交流异步电动机控制开始从标量控制向矢量控制迈进。
以下是矢量控制理论的简要介绍。
矢量控制发展的基础和核心理论支撑是电机的一些概念，如坐标转换原理、机电能量转换理论等。
这种控制的基本思想和方法是将异步电机模拟成DC电机来控制。
只要建立等效于三相交流绕组组的两相绕组，就可以建立等效于异步电机的DC电机模型，并增加相应的比例积分调节环节，从而可以按照DC 电机的控制策略来控制异步电机。
因此，矢量控制可以实现对电机电磁转矩的动态实时控制，从而优化和提高调速性能。
根据这一思想，我在本项目中成功地进行了MATLAB仿真。
关键词:交流电机；矢量控制调速系统；矢量控制系统的设计与仿真交流调速系统的仿真采用常V/f比控制方法，通常称为标量控制。
采用这种方法的系统在电机低速运行时或在加速、减速、增加负载、减少负载等情况下会出现重大缺陷。
采用矢量控制的交流电机可以达到与恒流电机相同的控制性能，从此交流异步电机控制从标量控制向矢量控制迈进了一大步。
以下是矢量控制理论的简要介绍。
矢量控制发展的基础和核心理论支撑是电机的一些概念，如坐标转换原理、机电能量转换理论等。
这种控制的基本思想和方法是将异步电机模拟成DC电机来控制。
只要建立等效于三相交流绕组组的两相绕组，就可以建立等效于异步电机的DC电机模型，并增加相应的比例积分调节环节，从而可以按照DC电机的控制策略来控制异步电机。
因此，矢量控制可以实现对电机电磁转矩的动态实时控制，从而优化和提高调速性能。
根据这一思想，我在本项目中成功地进行了MATLAB仿真。
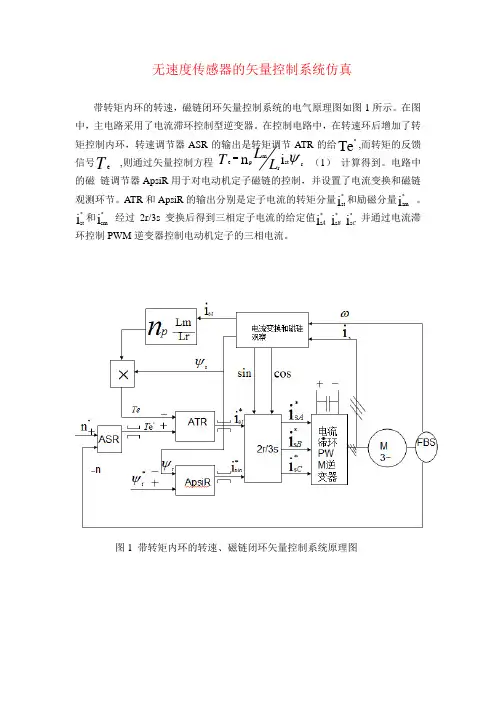
无速度传感器的矢量控制系统仿真带转矩内环的转速，磁链闭环矢量控制系统的电气原理图如图1所示。
在图中，主电路采用了电流滞环控制型逆变器。
在控制电路中，在转速环后增加了转矩控制内环，转速调节器ASR的输出是转矩调节ATR 的给Te *,而转矩的反馈信号Te ,则通过矢量控制方程 （1） 计算得到。
电路中的磁 链调节器ApsiR 用于对电动机定子磁链的控制，并设置了电流变换和磁链观测环节。
ATR 和ApsiR 的输出分别是定子电流的转矩分量i st *和励磁分量i sm *。
i st *和i sm *经过2r/3s 变换后得到三相定子电流的给定值 并通过电流滞环控制PWM 逆变器控制电动机定子的三相电流。
图1 带转矩内环的转速、磁链闭环矢量控制系统原理图ψr st r m p e i n L L T =i s *C i s *B i s *A带磁链和转矩闭环的矢量控制系统仿真如图2所示。
其中直流电源DC，逆变器inverter,电动机motor和电动机测量模块组成了模型的主电路，逆变器的驱动信号由滞环脉冲发生器模块产生。
三个调节器ASR,ATR和AspiR均是带输出限幅的PI调剂器。
转子磁链观测使用二相同步旋转坐标系上的磁链模型(图3)，函数模块Fcn用于计算转矩，dq0-to-abc模块用于2r/3s的坐标变换。
图2 带转矩内环的转速、磁链闭环矢量控制系统仿真模型图3 三相电压的变换模型仿真图带转矩内环的转速，磁链闭环矢量控制系统，调节器参数见表1.模型的仿真算法为ode23tb 。
在矢量控制系统中，为了实现转速的闭环控制和磁场定向，电动机的转速检测是必不可少的，并且转速检测的精度直接影响磁场定向的准确性。
从电动机数学模型可以看出，电动机转速实际上也可以通过推算得到，因此无速度传感器的矢量控制系统成为了交流调速的重要研究内容。
无速度传感器的交流调速一方面减少了设备，另一方面也避免了速度传感器检测本身可能带来的误差。
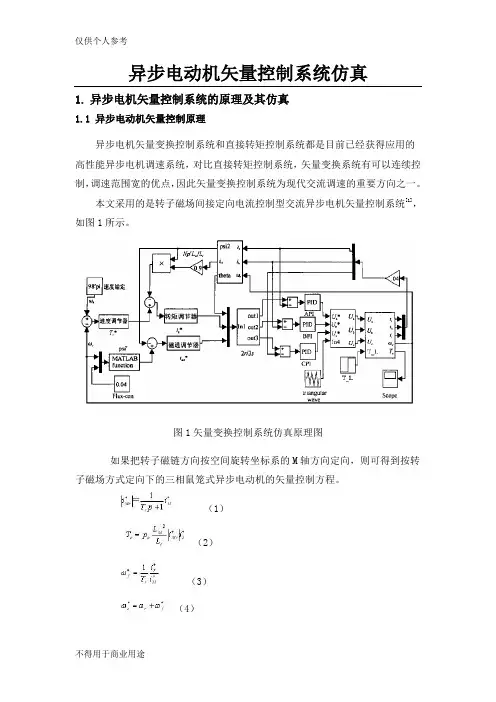
异步电动机矢量控制系统仿真1.异步电机矢量控制系统的原理及其仿真1.1 异步电动机矢量控制原理异步电机矢量变换控制系统和直接转矩控制系统都是目前已经获得应用的高性能异步电机调速系统，对比直接转矩控制系统，矢量变换系统有可以连续控制，调速范围宽的优点，因此矢量变换控制系统为现代交流调速的重要方向之一。
本文采用的是转子磁场间接定向电流控制型交流异步电机矢量控制系统[1]，如图1所示。
图1矢量变换控制系统仿真原理图如果把转子磁链方向按空间旋转坐标系的M轴方向定向，则可得到按转子磁场方式定向下的三相鼠笼式异步电动机的矢量控制方程。
（1）（2）（3）（4）（5）上列各式中，是转子励磁电流参考值；是转差角频率给定值；是定子电流的励磁分量；是定子电流的转矩分量；是定子频率输入角频率；是转子速度；是转子磁场定向角度；是转子时间常数；和分别是电机互感和转子自感。
图4所示控制系统中给定转速与实际电机转速相比较，误差信号送入转速调节器，经转速调节器作用产生给定转矩信号，电机的激磁电流给定信号根据电机实际转速由弱磁控制单元产生，再利用式（1）产生定子电流激磁分量给定信号，定子电流转矩分量给定信号则根据式（2）所示的电机电磁转矩表达式生成。
、和转子时间常数Lr一起产生转差频率信号，与ωr相加生成转子磁场频率给定信号，对积分则得到转子磁场空间角度给定信号。
和经坐标旋转和2/3相变换产生定子三相电流给定信号、和，与定子三相电流实测信号、和相比较，由滞环控制器产生逆变器所需的三相PWM信号。
1.2 异步电机转差型矢量控制系统建模在MATLAB/SIMULINK环境下利用电气系统模块库中的元件搭建交流异步电机转差型矢量控制系统[2]，电流控制变频模型如图2所示。
图2 电流控制变频模型图整个仿真图由电气系统模块库中的元件搭建组成，元件的直观连接与实际的主电路相像似，其中主要包括：速度给定环节，PI速度调节器、坐标变换模块、磁场定向模块、滞环电流调节器、IGBT逆变器元件、异步电动机元件以及测量和显示模块。
基于MatlabSimulink的异步电机矢量控制系统仿真一、本文概述随着电力电子技术和控制理论的不断发展，异步电机矢量控制系统已成为现代电机控制领域的重要分支。
该系统通过精确控制异步电机的磁通和转矩，实现了对电机的高效、稳定和动态性能的优化。
Matlab/Simulink作为一种强大的仿真工具，为异步电机矢量控制系统的研究和设计提供了便捷的平台。
本文旨在探讨基于Matlab/Simulink的异步电机矢量控制系统仿真方法。
文章将简要介绍异步电机矢量控制的基本原理和关键技术，包括空间矢量脉宽调制（SVPWM）技术、转子磁链观测技术以及矢量控制策略等。
详细阐述如何利用Matlab/Simulink搭建异步电机矢量控制系统的仿真模型，包括电机模型、控制器模型以及系统仿真模型的构建过程。
文章还将探讨仿真模型的参数设置、仿真过程以及仿真结果的分析方法。
通过本文的研究，读者可以深入了解异步电机矢量控制系统的基本原理和仿真方法，掌握基于Matlab/Simulink的仿真技术，为异步电机矢量控制系统的实际设计和应用提供有益的参考和借鉴。
本文的研究也有助于推动异步电机矢量控制技术的发展和应用领域的拓展。
二、异步电机基本原理异步电机，又称感应电机，是一种广泛应用于工业领域的电动机。
其基本原理基于电磁感应和电磁力作用。
异步电机主要包括定子（静止部分）和转子（旋转部分）。
定子通常由铁芯和三相绕组构成，而转子则可能由实心铁芯、鼠笼型或绕线型结构组成。
当异步电机通电时，定子绕组中的三相电流会产生旋转磁场。
这个旋转磁场与转子中的导体相互作用，根据法拉第电磁感应定律，会在转子导体中产生感应电动势和感应电流。
这些感应电流在旋转磁场的作用下，受到电磁力的作用，从而使转子产生旋转力矩，驱动转子旋转。
异步电机的旋转速度与定子旋转磁场的旋转速度并不完全同步，这也是其被称为“异步”电机的原因。
异步电机的旋转速度通常略低于旋转磁场的同步速度，这是由于转子导体的电感和电阻导致的电磁延迟效应。
基于交流电动机动态模型的直接矢量控制系统的仿真与设计姓名：班级：电气三班学号：专业：电气工程及其自动化1.引言异步电机的动态数学模型是一个高阶、非线性、强耦合的多变量系统，通过坐标变换，可以使之降阶并化简，但并没有改变其非线性、多变量的本质。
需要高动态性能的异步电机调速系统必须在其动态模型的基础上进行分析和设计，但要完成这一任务并非易事。
经过人们的多年的潜心研究和实践，有几种控制方案已经获得了成功的应用，目前应用最广的就是矢量控制系统。
直接矢量控制就是一种优越的交流电机控制方式，它模拟直流电机的控制方式使得交流电机也能取得与直流电机相媲美的控制效果。
本文研究了交流电动机动态模型的直接矢量控制系统的设计方法。
并用MATLAB 最终得到出仿真结果。
2. 矢量控制系统结构异步电动机经过坐标变换可以等效成直流电动机，那么，模仿直流电动机的控制策略，得到直流电动机的控制量，再经过相应的坐标反变换，就能够控制异步电动机了。
由于进行坐标变换的是电流(代表磁动势)的空间矢量，所以这样通过坐标变换实现的控制系统就称为矢量控制系统(VectorControlSystem)，简称VC 系统。
VC 系统的原理结构如图1所示。
图中的给定和反馈信号经过类似于直流调速系统所用的控制器，产生励磁电流的给定信号*m i 和电枢电流的给定信号*t i ，经过反旋转变换1-VR 一得到*αi 和*βi ，再经过2／3变换得到*A i 、*B i 和*C i 。
把这三个电流控制信号和由控制器得到的频率信号1ω加到电流控制的变频器上，所输出的是异步电动机调速所需的三相变频电流。
图1 矢量控制系统原理结构图在设计VC 系统时，如果忽略变频器可能产生的滞后，并认为在控制器后面的反旋转变换器1-VR 与电机内部的旋转变换环节VR 相抵消，2／3变换器与电机内部的3／2变换环节相抵消，则图1中虚线框内的部分可以删去，剩下的就是直流调速系统了。
可以想象，这样的矢量控制交流变压变频调速系统在静、动态性能上完全能够与直流调速系统相媲美。
摘要近年来，随着电力半导体器件及微电子器件特别是微型计算机及大规模集成电路的发展，再加上现代控制理论，特别是矢量控制技术向电气传动领域的渗透和应用，使得交流电机调速技术日臻成熟。
以矢量控制为代表的交流调速技术通过坐标变换重建电机模型，从而可以像直流电机那样对转矩和磁通进行控制，交流调速系统的调速性能已经可以和直流调速系统相媲美。
因此，研究由矢量控制构成的交流调速系统已成为当今交流变频调速系统中研究的主要发展方向。
最后，综合矩阵变换的控制策略及异步电动机转子磁场定向理论，采用计算机仿真方法分别建立了矩阵变换仿真模型以及基于矩阵变换的异步电动机矢量控制系统仿真模型，对矩阵变换的控制原理、输入、输出性能以及矢量控制系统的优质的抗扰能力及四象限运行特性进行分析验证，展现了该新型交流调速系统的广阔发展前景，并针对基于矩阵变换的异步电动机矢量控制系统的特点，着重对矢量控制单元进行了软件设计。
本设计研究的是矢量控制的异步电动机的调速系统，采用MATLAB软件在其simulink中进行仿真。
关键词：坐标变换矢量控制异步电动机MATLAB simulink仿真ABSTRACTIn recent years, with the development of the power semiconductor device，the microelectronics component, the microcomputer and large-scale integrated circuit and modern control theory, especially the penetration from vector control technology to electric drive field and application, the feasible AC motor speed regulation technology has become more mature day by day.Depend on the control principle of the MC and the rotor-flux orientation theory, and using the computer simulation technology, the simulation model of the MC and the matrix converter fed induction motor vector control drive system has been build. The input-output characteristic and the ability of four-quadrantoperation have been testified, which has proved that the system has wide application field. The software of the vector control unit was designed at the end.This design is the study of vector control of the induction motor speed control system,using MATLAB software in its simulink simulation.Key words: matrix converter vector control induction motor MATLABsimulink simulation.目录1摘要......................................................................................... ABSTRACT .. (I)一.绪论 (4)1.1引言41.2 交流调速技术概况71.3仿真软件的发展状况及应用81.4 MATLAB 概述81.5 Simulink 概述11二.矢量控制理论 (12)2.1 异步电机的动态数学模型122.2 坐标变换162.2.1变换矩阵的确定原则162.2.2功率不变原则162.3矢量控制182.3.1 问题分析182.3.2直流电机的转矩控制182.3.3异步电机的转矩分析192.3.4 矢量控制原理19三. 总体模块设计 (22)3.1矢量控制结构框图223.2各子系统模块233.2.1求解磁链模块233.2.2 求解转子磁链角模块243.2.3 ids*求解模块243.2.4 iqs*求解模块253.2.5 ABC到DQ坐标变换模块253.2.6 DQ到ABC坐标变换模块263.3 电机参数设置263.4矢量控制环节模块283.5矢量控制的异步电动机调速系统模块28四. Simulink 仿真 (30)五. 结论 (36)致谢 (37)参考文献 (38)附录1 3s/2r 坐标变换 (41)附录2 ω*=100和ω*=150时的比较 (43)一.绪论1.1引言交流电机特别是鼠笼异步电机，由于结构简单、制造方便、价格低廉，而且坚固耐用、惯量小、运行可靠、很少需要维护、可用于恶劣环境等优点，在工农业生产中得到了广泛的应用。
矢量控制系统仿真
按矢量控制系统结构建立仿真模型，见图1。
其中，异步电动机仿真模型见异步电动机仿真，SVPWM用惯性环节等效代替，若采用实际的SVPWM方法仿真，会产生电流脉动。
转速、转子磁链和两个电流调节器均采用带有积分和输出限幅的PI调节器，两相磁链
rα
ψ和rβ
ψ由电动机模型直接得到，通过直角坐标到极坐标变换（K/P变换）得到转子磁链的幅值和角度，
r
r
jarctg
j
r r r r
j e
β
α
ψ
ψϕ
αβ
ψψψ
=+==
ψ
图2为空载起动和t=3s突加额定负载的定子电流励磁分量
sm
i（上）和转矩分量
st
i（下）仿真结果，图3a是对应的转速ω（上）与转子磁链r
ψ（下）仿真结果，图3b为转速ω
（上）
图1 矢量控制系统仿真模型
与转子磁链r （下）局部放大图。
图2 空载起动和加载的定子电流励磁分量sm i （上）和转矩分量st i （下）仿真结果
ψ（下）仿真结果图3a 空载起动和加载过程ω（上）和r
图3b ω（上）和ψ（下）局部放大。
矢量控制系统仿真课程设计初始条件：根据转差频率矢量控制系统原理图设计对应的simulink 仿真模型，电机参数为：额定功率power=2.2KW,线电压L U =,额定频率50f Hz =；定子电阻0.435s R =Ω,漏感0.002ls H L =;转子电阻,0.816r R =Ω,漏感,0.002lr H L =;互感0.069m H L =,转动惯量0.089.^2J kg m =,极对数2P =,其余参数为0。
要求完成的主要任务:（1）用MATLAB 建立矢量控制系统仿真模型；（2）根据仿真结果分析起动时定子电流励磁分量和转矩分量； （3）根据仿真结果分析起动时转速与转子磁链。
摘 要因为异步电动机的物理模型是一个高阶、非线性、强耦合的多变量系统，需要用一组非线性方程组来描述，所以控制起来极为不便。
异步电机的物理模型之所以复杂，关键在于各个磁通间的耦合。
如果把异步电动机模型解耦成有磁链和转速分别控制的简单模型，就可以模拟直流电动机的控制模型来控制交流电动机。
直接矢量控制就是一种优越的交流电机控制方式，它模拟直流电机的控制方式使得交流电机也能取得与直流电机相媲美的控制效果。
本文研究了矢量控制系统中磁链调节器的设计方法。
并用MATLAB 最终得到了仿真结果。
关键词：矢量控制 非线性 MATLAB 仿真矢量控制系统仿真1设计条件及任务1.1设计条件根据转差频率矢量控制系统原理图设计对应的simulink 仿真模型，电机参数为：额定功率power=2.2KW,线电压2203L V U =,额定频率50f Hz =；定子电阻0.435s R =Ω,漏感0.002ls H L =;转子电阻,0.816r R =Ω,漏感,0.002lr H L =;互感0.069m H L =,转动惯量0.089.^2J kg m =,极对数2P =,其余参数为0。
1.2设计任务（1）用MATLAB 建立矢量控制系统仿真模型；（2）根据仿真结果分析起动时定子电流励磁分量和转矩分量； （3）根据仿真结果分析起动时转速与转子磁链。
2 异步电动机矢量控制原理及基本方程式2.1矢量控制基本原理矢量控制系统的基本思路是以产生相同的旋转磁动势为准则,将异步电动机在静止三相坐标系上的定子交流电流通过坐标变换等效成同步旋转坐标系上的直流电流,并分别加以控制,从而实现磁通和转矩的解耦控制,以达到直流电机的控制效果。
所谓矢量控制，就是通过矢量变换和按转子磁链定向，得到等效直流电动机模型，在按转子磁链定向坐标系中，用直流电动机的方法控制电磁转矩与磁链,然后将转子磁链定向坐标系中的控制量经变换得到三相坐标系的对应量，以实施控制。
其中等效的直流电动机模型如图2-1所示，在三相坐标系上的定子交流电流,,A B C i i i ,通过3/2变换可以等效成两相静止正交坐标系上的交流s i α和s i β再通过与转子磁链同步的旋转变换，可以等效成同步旋转正交坐标系上的直流电流sm i 和st i 。
m 绕组相当于直流电动机的励磁绕组，sm i 相当于励磁电流，t 绕组相当于电枢绕组，st i 相当于与转矩成正比的电枢电流。
其中矢量控制系统原理结构图如图2-2所示。
图2-1 异步电动机矢量变换及等效直流电动机模型图2-2矢量控制系统原理结构图通过转子磁链定向，将定子电流分量分解为励磁分量sm i 和转矩分量st i ，转子磁链r ψ仅由定子电流分量sm i 产生，而电磁转矩e T 正比与转子磁链和定子电流转矩分量的乘积，实现了定子电流的两个分量的解耦。
简化后的等效直流调速系统如图2-3所示。
图2-3简化后的等效直流调速系统2.2按转子磁链定向的基本方程异步电动机在两相同步旋转坐标系上的数学模型包括电压方程、磁链方程和电磁转矩方程。
分别如下:⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+-+--+=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡rq rd sq sd r r r s m m s r s r r m m m m s s s m m ss s rq rd sq sd i i i i P L R L P L L L P L R L P L P L L P L R L L P L L P L R u u u u ωωωωωωωω11111 （2-1）⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡rq rd sq sd r mr m m s m s rq rd sq sd i i i i L L L L L L L L 00000000ψψψψ （2-2）)(rq sd rd sq m p e i i i i L n T -= （2-3）当两相同步旋转坐标系按转子磁链定向时,应有rd rm r ψψψ== （2-4） 0rq rt ψψ== （2-5）得到dq 坐标系的状态方程2221222121p mp sq r L r m r r sd r sd m s r r m sd r sd sq s r r s rs sq sq m s r r mr sq sd s r s r s n L n dw i T dt JL JL d i dt T T di L R L R L u i w i dt L L T L L L di u L R L R L w i w i dt L L L L L ψψψψσσσψσσσ⎫=-⎪⎪⎪=-+⎪⎪⎬+⎪=-++⎪⎪+⎪=---+⎪⎭（2-6）得到旋转角速度：1msq r rL i T ωωψ=+ （2-7） 得到电磁转矩表达式：r st rmpe i L L n T ψ= （2-8） 得到转子磁链表达式：sm r mr i PT L +=1ψ （2-9）式中: 1ω为同步转速；ω为转子转速； u 为电压；ψ为磁链；i 为电流；R 电阻；L 为电感；p n 为极对数；r T 为转子时间常数且rr rL T R =；σ为电动机漏磁系数且21m s r L L L σ=-；rd P dtψ=为微分因子。
s 表示定子；r 表示转子；d 表示d 轴；q 表示q 轴；m 表示同轴定、转子间的互感。
3 坐标变换3.1坐标变换原理由于异步电动机三相原始动态数学模型相当复杂，分析和求解这组非线性方程十分困难。
在实际应用中必须予以简化，由于直流电动机的主磁通基本上由励磁绕组的励磁电流决定，这是直流电动机的数学模型及其控制系统比较简单的根本原因。
如果能将交流电动机的物理模型等效地变换成类似直流电动机的模式，分析和控制就可以大大简化。
所以，三相绕组可以用相互独立的两相正交对称绕组等效代替，等效的原则是产生的磁动势相等。
其中图3-1和图3-2 分别为三相坐标系和两相坐标系物理模型和静止两相正交坐标系和旋转正交坐标系的物理模型。
图3-1 三相坐标系和两相坐标系物理模型图3-2 静止两相正交坐标系和旋转正交坐标系的物理模型三相绕组A 、B 、C 和两相绕组之间的变换，称作三相坐标系和两相正交坐标系间的变换，简称3/2变换。
图3-3中绘出ABC 和两个坐标系中的磁动势矢量，将两个坐标系原点重合，并使A 轴和α轴重合。
设三相绕组每相有效匝数为3N ，两相绕组每相有效匝数为2N 按磁动势相等的原则，三相合成磁动势与两相合成磁动势相等，故两套绕组在α，β轴上的投影都应相等。
图3-3 三相坐标系和两相正交坐标系中的磁动势矢量因此，2333311cos cos()3322A B C A B C N i N i N i N i N i i i αππ=--=-- （3-1） 23333sinsin()332B C B C N i N i N i N i i βππ=-=- （3-2） 写成矩阵形式，得3211122330A B C i i N i i N i αβ⎡⎤⎡⎤--⎢⎥⎡⎤⎢⎥⎢=⎢⎥⎢⎥⎢⎣⎦⎢⎥⎣⎦⎢⎣ （3-3） 根据变换前后总功率不变，得3223N N =0A B C i i i ++=，最终得到坐标变换式为 30222A B i i i i αβ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦⎣⎦⎢⎣（3-4） 相应的逆变换为20362A B ii i i αβ⎡⎤⎢⎥⎡⎤⎡⎤⎢⎥=⎢⎥⎢⎥⎢⎣⎦⎣⎦⎢⎣（3-5） 从静止两相正交坐标系αβ到旋转正交坐标系dq 的变换，称作静止两相-旋转正交变换，简称2s/2r 变换，其中s 表示静止，r 表示旋转，变换的原则同样是产生的磁动势相等。
其静止两相正交坐标系和旋转正交坐标系中的磁动势矢量图如图3-4所示。
图3-4 静止两相正交坐标系和旋转正交坐标系中的磁动势矢量旋转正交变换为（3-6）静止两相正交坐标系到旋转正交坐标系的变换阵为（3-7） 对(3-6)式进行逆变换可以得到两相静止到两相旋转的变换矩阵为：⎥⎦⎤⎢⎣⎡-==-ϕϕϕϕcos sin sin cos 12222sr rsCC （3-8） 电压和磁链的旋转变换阵与电流旋转变换阵相同。
3.2建立坐标变换模型3.2.1 2r/3s 变换模型根据式子（3-3）和（3-8）可以建立3s/2r 的电路模型结构图如图3-5所示。
图3-5 dqo_to_abc 模块2r/3s 变换为()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡++--=13/2cos 3/2sin 13/2cos 3/2sin 1cos sin 32pi pi pi pi C srϕϕϕϕϕϕ （3-9） 3.2.2 3s/2r 变换模型如图3-6为3s/2r 变换模型电路图。
图3-6 abc_to_dq03s/2r 变换为()()()()⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+-+-=3/13/13/13/2cos 3/23/2cos 3/2cos 3/23/2sin 3/23/2sin 3/2sin 3/232pi pi pi pi C srϕϕϕϕϕϕ （3-10）4 矢量控制系统设计4.1 矢量控制系统的电流闭环控制方式思想图4-1为电流闭环控制后的系统结构图，转子磁链环节为稳定的惯性环节，对转子可以采用闭环控制，也可以采用开环控制方式；而转速通道存在积分环节，为不稳定结构，必须加转速外环。
常用的电流闭环控制有两种方法：一个是将定子电流两个分量的给定置*smi 和*st i 施行2/3变换，得到三相电流给定值，再经过PWM 控制逆变器输出三相电压，采用电流滞环控制型PWM 变频器，在三相定子坐标系中完成电流闭环控制，如图4-2。
另一个是将检测到得三相电流施行3/2变换和旋转变换得到ist 和ism 。
本次MATLAB 仿真系统设计也是采用的这种控制方法。
图4-1 电流闭环控制后的系统结构图图4-2 带转矩环和磁链闭环矢量控制系统的电气原理图4.2 MATLAB 系统仿真系统设计本次MATLAB 系统结构仿真模型如图4-3所示，其中SVPWM 用惯性环节等效代替，若采用实际的SVPWM 方法仿真，将大大增加仿真计算时间，对计算机的运行速度和存容量要求较高，转速，转子磁链和两个电流调节器均采用带有积分和输出限幅的PI 调节器，两相磁链有电动机模型直接得到，其中转子磁链的幅值也直接有电动机模型直接得到。
