机器人学- 坐标转换分解

机器人坐标变换原理机器人坐标变换是机器人控制中的一个重要概念，它涉及到机器人在不同坐标系下的定位和运动控制。

机器人通常使用多个坐标系来描述其运动和操作，如世界坐标系、基座坐标系、工具坐标系等。

机器人坐标变换的原理基于坐标系之间的关系和变换矩阵的计算。

下面从多个角度来解释机器人坐标变换的原理。

1. 机器人坐标系，机器人通常由多个关节组成，每个关节都有自己的坐标系。

机器人的末端执行器也有自己的坐标系。

这些坐标系之间通过关节运动相互连接，形成了机器人的整体坐标系。

2. 坐标系关系，机器人的坐标系之间存在着一定的关系，如基座坐标系与世界坐标系之间的关系、工具坐标系与末端执行器坐标系之间的关系等。

这些关系可以通过变换矩阵来描述。

3. 变换矩阵，变换矩阵是用于描述坐标系之间关系的数学工具。

对于二维情况，变换矩阵是一个2x2的矩阵，对于三维情况，变换矩阵是一个4x4的矩阵。

变换矩阵包含了平移、旋转和缩放等变换信息。

4. 坐标变换过程，机器人坐标变换的过程可以分为两个步骤，前向变换和逆向变换。

前向变换是从基座坐标系到末端执行器坐标系的变换，逆向变换是从末端执行器坐标系到基座坐标系的变换。

5. 坐标变换公式，机器人坐标变换的公式可以通过矩阵乘法来表示。

对于前向变换，可以使用连续的变换矩阵相乘的方式计算末端执行器坐标系相对于基座坐标系的变换。

对于逆向变换，可以使用逆矩阵的方式计算基座坐标系相对于末端执行器坐标系的变换。

总结起来，机器人坐标变换的原理是基于坐标系之间的关系和变换矩阵的计算。

通过变换矩阵的乘法和逆矩阵的运算，可以实现机器人在不同坐标系下的定位和运动控制。

这种坐标变换的原理在机器人控制中起着重要的作用，能够帮助机器人实现复杂的任务和精确的定位。

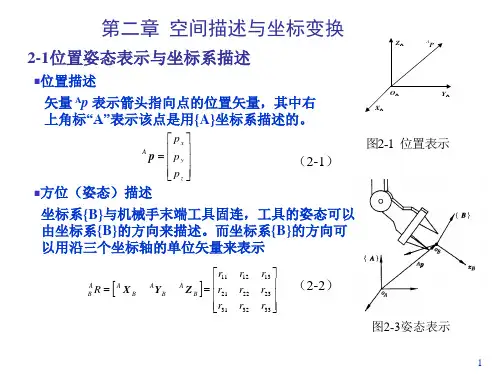
移动机器人坐标系转世界坐标系的原理移动机器人坐标系与世界坐标系之间的转换原理主要涉及三个坐标系：物体坐标系、惯性坐标系和世界坐标系。

物体坐标系是与机器人本身固连的一个参考坐标系，用于描述机器人的运动状态。

机器人上的各个关节和传感器都相对于这个物体坐标系进行定位和描述。

惯性坐标系是为了简化世界坐标系到机器人坐标系的转换而引入的中间坐标系。

它的原点与物体坐标系的原点重合，惯性坐标系的轴平行于世界坐标系的轴。

物体坐标系转换到惯性坐标系只需旋转，而从惯性坐标系转换到世界坐标系只需平移。

世界坐标系是一个特殊的坐标系，它建立了描述其他坐标系所需要的参考系。

世界坐标系是固定的，而机器人在世界坐标系中的位置和姿态会随着移动而改变。

机器人坐标系与世界坐标系之间的转换需要综合考虑平移和旋转的影响。

具体来说，当机器人移动时，其物体坐标系的原点在惯性坐标系中会发生平移，而当机器人进行旋转时，惯性坐标系相对于世界坐标系会发生旋转。

这种转换可以通过一系列的矩阵变换来实现，包括平移矩阵和旋转变换矩阵。

要完成从机器人坐标系到世界坐标系的转换，首先需要将机器人当前的状态表示为相对于物体坐标系的齐次变换矩阵（包括平移和旋转）。

然后，将这个齐次变换矩阵与从世界坐标系到物体坐标系的齐次变换矩阵相乘，即可得到从世界坐标系到机器人当前状态的齐次变换矩阵。

通过这个矩阵，可以找到机器人在世界坐标系中的位置和姿态。

同时，如果机器人在运行过程中引入了外部行走轴或旋转轴，还需要通过测量一些机械参数将机器人基坐标系变换到外部行走轴上，这种变换也称为D-H变换。

以上内容仅供参考，如需更多信息，建议查阅移动机器人相关书籍或咨询该领域专家。

坐标系变换和分解速度控制方法一个机器人是由关节连接着的连杆组成，在运动学分析中，它被描述为连杆的铰链和关节。

在它的一端的铰链起着支撑作用，另一端是末端效应器或机械手。

机器人控制要求末端的效应器或机械手能够精确地移动到空间指定点，完成任务。

在执行任务时，机器人的末端效应器必须通过规划好的特殊路径。

这一部分将来讨论一种简单的数学方法在描述末端效应器和基坐标之间关系中的应用。

机器人的末端效应器在空间的位置和方位及方向必须得以描述和控制。

在机器人中许多关节的位置和方位，需要通过其他关节与基准的坐标变换来决定。

如果这个机器人有六个关节或者六个自由度，那么机器人必须设定六次坐标变换，对于每一个关节，坐标变换涉及到这一关节的坐标与前一连杆关节的坐标。

1坐标变换1.1 关节—球坐标变换球坐标是定义为机器人的基坐标，这些坐标是通过机器人的基准关节或已知的一段距离。

我们通常习惯把基坐标定义为X0轴、Y0轴和Z0轴在坐标原点O处构成。

关节坐标是定义为坐标中心设置在一个特殊的关节，一个滑动关节或者是移动关节上，沿着移动方向一个坐标一个坐标的设置。

在转动关节上，一坐标轴线是平行于关节轴线。

如图6.23所示，在一个机器人上连续关节之间的关系。

关节I可以认为是一个基准关节。

下一个向着末端效应器的关节已被标记物1号，每相连的关节都标有数码，用于与前一关节相互区别开了。

连杆的标记方法与关节的标记方法是相同的。

它们的标记方法如图6.23所示，在这种特殊情况下，使用笛卡尔坐标系（x,y,z）表示，如果，我们选择把I定义为 1.那么第一根连杆为1号，第一个关节的坐标为（x0,y0,z0），我们把它认为是固定在基准上。

1.2 坐标系参数每一个坐标系通常是由四个参数所决定的，这些参数是用来对这一坐标系与前一坐标系之间的相互关系进行描述，这种数学方法是由Denavit和Hartenbery与1955年首次提出，这一方法提供了在同一基体上的必要参数，是坐标变换的一种简单的方法。

其余的比较简单，大家可以自己考虑。

3. 坐标系}B {的位置变化如下：初始时，坐标系}A {与}B {重合，让坐标系}B {绕B Z 轴旋转θ角；然后再绕B X 旋转φ角。

给出把对矢量P B 的描述变为对P A描述的旋转矩阵。

解： 坐标系}B {相对自身坐标系（动系）的当前坐标系旋转两次，为相对变换，齐次变换顺序为依次右乘。

∴对P A 描述有 P T P BA B A = ；其中 ),(),(φθx Rot z Rot T AB = 。

9. 图2-10a 示出摆放在坐标系中的两个相同的楔形物体。

要求把它们重新摆放在图2-10b 所示位置。

（1）用数字值给出两个描述重新摆置的变换序列，每个变换表示沿某个轴平移或绕该轴旋转。

（2）作图说明每个从右至左的变换序列。

（3）作图说明每个从左至右的变换序列。

解：（1）方法1:如图建立两个坐标系}{1111z y x o 、}{2222z y x o ，与2个楔块相固联。

图1：楔块坐标系建立（方法1）对楔块1进行的变换矩阵为：)90,()90,(1z Rot y Rot T = ；对楔块2进行的变换矩阵为：)180,()90,()90,()4,0,3(oo 02o 2z Rot x TRot z Rot Trans T --= ；其中 ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=100001005010000102T ； 所以 ：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=10000010000101001T ；⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=10004010000121002T 对楔块2的变换步骤：① 绕自身坐标系X 轴旋转︒90； ② 绕新形成的坐标系的Z 轴旋转︒180； ③ 绕定系的Z 轴旋转︒-90； ④ 沿定系的各轴平移)4,0,3(-。

方法2：如图建立两个坐标系}{1111z y x o 、}{2222z y x o 与参考坐标系重合，两坐标系与2个楔块相固联。

图1：楔块坐标系建立（方法2）对楔块1进行的变换矩阵为：)90,()90,(1z Rot y Rot T = ； 对楔块2进行的变换矩阵为：)90,()180,()90,()0,0,4()9,0,2(o o o 2--=z Rot x Rot y Rot Trans Trans T ；所以 ：⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡=10000010000101001T ；⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡--=10009010000121002T 。

浅谈当前机器人坐标转换在机器人的应用中，可以使用不同的坐标系来定义机器人，传感器和其他物体的位置。

通常,对象在三维空间中的位置可以通过位置和方向值指定。

这些值有多个可能的表示形式应用于某些特定应用程序。

平移和旋转是位置和方向的替代术语。

Robotics System Toolbox 机器人系统工具箱支持机器人中常用的表示形式，并允许您在它们之间进行转换。

将这些表示应用于三维点时,可以在坐标系之间进行变换。

1、坐标系标识统一一般机器人通常使用右手坐标系,ROS里面用的也是右手坐标系。

左:左手坐标系,右:右手坐标系。

记忆:大拇指是z轴,食指是x轴(右手指往内转动)。

我们说旋转多少度时,都以右手手指往内攥的方向为正方向。

2、坐标变换习惯上,我们表示一个物体的三维位置和朝向时,都会在其身上附一个随动的坐标系。

所以描述一个物体在坐标系中的位置和朝向,总是可以等效为描述物体自身坐标系和别的坐标系之间的关系。

旋转矩阵:表示两个坐标系之间的旋转关系。

举例:表示导航小车自身的坐标系和地图坐标系之间的旋转关系。

如上所述,我们描述机器人在地图中的姿态,一般不会讲机器人在地图坐标系中的坐标,而是讲机器人自身的坐标系和地图坐标系之间的旋转平移关系。

(虽然它和机器人的坐标在数值上是一样的)连续的旋转变换:比如从C旋转成B,再从B旋转成A,那么从C到A的旋转矩阵就是按顺序从后往前直接连乘。

前面我们说了旋转,而平移很简单,就是向量之间的加减。

目前,我们平移加旋转一个物体,想得物理世界一个固定点在移动后的物体的坐标系里的坐标,我们得先计算平移,再计算旋转。

而齐次坐标变换的作用就是将两者统一成一个矩阵,矩阵左上角是旋转矩阵,右侧为平移向量。

齐次坐标转换矩阵统一了平移和旋转,方便了坐标变换的逆运算、多坐标系的连续变换,运算规则和旋转矩阵类似。

3、机器人运动学机器人运动学包括正向运动学和逆向运动学，正向运动学即给定机器人各关节变量，计算机器人末端的位置姿态； 逆向运动学即已知机器人末端的位置姿态，计算机器人对应位置的全部关节变量机器人运动学包括正向运动学和逆向运动学，正向运动学即给定机器人各关节变量，计算机器人末端的位置姿态； 逆向运动学即已知机器人末端的位置姿态，计算机器人对应位置的全部关节变量。

其余的比较简单，大家可以自己考虑。

3. 坐标系{B}的位置变化如下：初始时，坐标系{A}与{B}重合，让坐标系{B}绕描述AB的描述变为对PZ轴旋转角；然后再绕X B旋转角。

给出把对矢量PB的旋转矩阵。

解：坐标系{B}相对自身坐标系（动系）的当前坐标系旋转两次，为相对变换，齐次变换顺序为依次右乘。

A；对P A A B描述有P T PBA其中T Rot(z,)Rot(x,)B。

9. 图2-10a 示出摆放在坐标系中的两个相同的楔形物体。

要求把它们重新摆放在图2-10b 所示位置。

（1）用数字值给出两个描述重新摆置的变换序列，每个变换表示沿某个轴平移或绕该轴旋转。

（2）作图说明每个从右至左的变换序列。

（3）作图说明每个从左至右的变换序列。

解：（1）方法1:如图建立两个坐标系{1x y z}o2x y z，与2个楔块相固联。

o、{}111222图1：楔块坐标系建立（方法1）对楔块1进行的变换矩阵为：T1Rot(y,90)Rot(z,90)；对楔块2进行的变换矩阵为：o0o o T2Trans(3,0,4)Rot(z,90)TRot(x,90)Rot(z,180)；21000其中01052T；0010000100100012所以：1000T；10100T2114 00010001对楔块2的变换步骤：①绕自身坐标系X轴旋转90；②绕新形成的坐标系的Z轴旋转180；③绕定系的Z轴旋转90；④沿定系的各轴平移(3,0,4)。

方法2：如图建立两个坐标系{o1x y z}、{o2x2y2z2}与参考坐标系重合，两坐标系111与2个楔块相固联。

图1：楔块坐标系建立（方法2）对楔块1进行的变换矩阵为：T1Rot(y,90)Rot(z,90)；对楔块2进行的变换矩阵为：o o oT2Trans(2,0,9)Trans(4,0,0)Rot(y,90)Rot(x,180)Rot(z,90)；00100012所以：1000T；101001000T。