实验四 多重共线性模型的检验和处理

多重共线性的检验与修正【实验目的】掌握多重共线性的检验方法和补救措施。

【实验要求】选择习题4.7，运用EViews 软件进行解答。

【实验内容】一、 利用EViews 软件，输入654321,X X X X X X Y ，，，，， 等数据，采用这些数据对模型进行OLS 回归，结果如下表所示由此可见，该模型2R =0.9810,2R =0.9677可决系数很高，F 检验值73.8081，明显显著，但是当228.2)818()(025.02/=-=-t k n t α，不仅所有解释变量系数t 检验不显著，而且654321X X X X X X ，，，，，系数符号与预期相反，这表明它们之间很可能存在严重多重共线性；二、计算各解释变量的相关系数，的相关系数矩阵如下由相关系数矩阵可以看出，各解释变量相互之间相关系数较高，证实确实存在严重的多重共线性。

三、修正多重共线性采用逐步回归的办法，去检验和解决多重共线性问题。

分别做lny对lnxi(i=1……7)的一元回归，结果如下表：其中，加入lnx1的方程修正拟合度最大，以lnx1为基础，顺次加入其它变量逐步回归，结果如下表：这里说明：对于两个解释变量标准T 分布为：1312318302502.)(t )(n t .α/=-=-，加入各解释变量后，要么2R 下降，要么ln i X （i=1……7）参数的T 检验不显著，这说明765432,X X X X X X ，，，，引起严重多重共线性，应予以剔除。

最后，修正后的回归结果为：1ln 2359.01631.9ˆln X Y t+= T= (73.1914) (19.7895)2R =0.9607 2R =0.9583 F=391.6234 DW=0.5038 这说明,在其他因素不变的情况下，当国民总收入增加e 单位，能源消费标准煤总量增加2359.0e单位。

此案例存在问题是样本容量过小，其可靠性受到影响，如果增大样本容量，效果会好一些； 【练习解答】1) 所建立的对数线性多元回归模型为1ln 2359.01631.9ˆln X Y t+= 2) 会，从表中的解释变量比如“国民总收入”与“GDP ”的本身意义，我们知道这两个变量之间存在很大的联系；3)存在多重共线性，通过逐步回归方法：①简单线性回归分析，找出基本解释变量②逐步进行二次，三次回归分析，直到出现回归系数不显著或者变量系数符号与预期不相符，以及修正拟合度不高的情况，即可认为该解释变量会引起严重多重共线性，应予以剔除，最后得出所需要的回归模型。

【实验名称】：多重共线性的检验方法和处理【实验目的】：掌握多重共线性的原理【实验原理】：综合统计检验法、相关系数矩阵检验法、逐步回归法【实验步骤】：一、创建一个新的工作文件：二、输入样本数据：三、用普通最小二乘法估计模型：由于解释变量个数较多，并且解释变量之间可能存在相关性，为了降低这种相关性以减弱序列相关性对模型的影响，我们先对各个解释变量和被解释变量取对数：即在Eviews软件的命令框执行：genr lnY=log（Y），genr lnX1=log（X1）,genr lnX2=log （X2）……genr lnX5=log（X5）我们设粮食生产函数为：LnY=β0+β1lnX1+β2lnX2+β3lnX3+β4lnX4+β5lnX5+μ用运普通最小二乘法估计：下表给出了采用Eviews软件对表一的数据进行回归分析的统计结果：Dependent Variable: LNYMethod: Least SquaresDate: 12/19/13 Time: 10:05Sample: 1983 2007C -4.173174 1.923624 -2.169434 0.0429LNX1 0.381145 0.050242 7.586182 0.0000 LNX2 1.222289 0.135179 9.042030 0.0000 LNX3 -0.081110 0.015304 -5.300024 0.0000 LNX4 -0.047229 0.044767 -1.054980 0.3047R-squared 0.981597 Mean dependent var 10.70905 Adjusted R-squared 0.976753 S.D. dependent var 0.093396 S.E. of regression 0.014240 Akaike info criterion -5.459968 Sum squared resid 0.003853 Schwarz criterion -5.167438 Log likelihood 74.24960 F-statistic 202.6826 Durbin-Watson stat 1.791427 Prob(F-statistic) 0.000000根据上表估计出的参数，可以得到如下普通最小二乘法估计模型：lnY=‐4.17+0.381lnX1+1.222lnX2‐0.081lnX3‐0.047lnX4‐0.101lnX5四、模型检验：1、数学检验：由于R2为0.9816接近于一，且F=202.68>F0.05（5，9）=2.74，故认为粮食产量和上述解释变量之间的总体线性关系显著；但是就X4,X5来说，其t检验的参数较小，尚不能通过t检验，因此怀疑模型中存在多重共线性。

多重共线性模型的检验与处理一、 研究的目的和要求 1）研究的目的中国钢材工业自新中国成立以来，历经起伏，虽然目前中国钢铁工业已形成具有相当规模，布局比较合理，大、中、小型企业相结合，行业比较完整的工业体系，但是钢材行业在现在有进入低速增长的趋势，面临供大于求，同质无序竞争，效益下滑的严峻局面。

在此背景下，寻找正确的钢材产量的预测模型，改变追求规模和产量的观念，给如何控制产量，优化产品提供了一定的参考。

本实验的目的在于建立并检验我国钢材产量预测模型，检验其多重共线性，并加以补救并得出正确的预测模型。

2）研究的具体内容本实验主要研究并建立检验我国钢材产量预测模型，检验其多重共线性，并加以补救并得出正确的预测模型。

二、 模型设定经分析，影响我国的钢材产量的主要因素除了生铁产量和发电量外，还可能和固定资产投资、国内生产总值、铁路运输量有关。

为此，为考虑的影响因素主要有生铁产量X1和发电量X2、固定资产投资X3、国内生产总值X4、铁路运输量X5，为此设定了如下形式的计量经济模型：12132435465t Y X X X X X ββββββμ=++++++其中Yt 为第t 年的钢材产量（万吨）；生铁产量X1（万吨）;发电量X2（亿千瓦时）;固定资产投资X3（亿元）;国内生产总值X4（亿元）;铁路运输量X5（万吨）。

为估计模型中的参数，收集1978－1997年我国钢材产量及其它相关经三、 估计参数利用Eviews 软件，生成Yt 、X1、X2、X3、X4、X5等数据，采用这些数据对模型进行OLS 回归，输入命令：LS Yt C X1 X2 X3 X4 X5 可得到如下回归表格如下表2：表2 OLS 回归结果Dependent Variable: YT Method: Least Squares Date: 05/20/15 Time: 10:16 Sample: 1978 1997 Included observations: 20Variable Coefficient Std. Error t-Statistic Prob. C 354.5884 435.6968 0.813842 0.4294 X1 0.026041 0.120064 0.216892 0.8314 X2 0.994536 0.136474 7.287380 0.0000 X3 0.392676 0.086468 4.541271 0.0005 X4 -0.085436 0.016472 -5.186649 0.0001 X5-0.0059980.006034-0.9940190.3371R-squared 0.999098 Mean dependent var 5153.450 Adjusted R-squared 0.998776 S.D. dependent var 2512.131 S.E. of regression 87.87969 Akaike info criterion 12.03314 Sum squared resid 108119.8 Schwarz criterion 12.33186 Log likelihood -114.3314 Hannan-Quinn criter. 12.09145 F-statistic 3102.411 Durbin-Watson stat 1.919746 Prob(F-statistic)0.000000由此可见2R =0.999098，2R =0998776可决系数很高，F 检验值3102.411，明显显著。

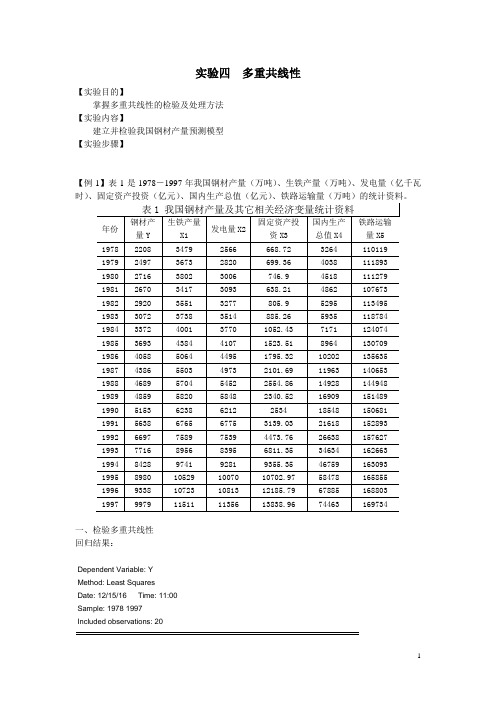
实验四多重共线性【实验目的】掌握多重共线性的检验及处理方法【实验内容】建立并检验我国钢材产量预测模型【实验步骤】【例1】表1是1978－1997年我国钢材产量（万吨）、生铁产量（万吨）、发电量（亿千瓦时）、固定资产投资（亿元）、国内生产总值（亿元）、铁路运输量（万吨）的统计资料。

一、检验多重共线性回归结果：Dependent Variable: YMethod: Least SquaresDate: 12/15/16 Time: 11:00Sample: 1978 1997Included observations: 20Coefficient Std. Error t-Statistic Prob.C 354.5884 435.6968 0.813842 0.4294X1 0.026041 0.120064 0.216892 0.8314X2 0.994536 0.136474 7.287380 0.0000X3 0.392676 0.086468 4.541271 0.0005X4 -0.085436 0.016472 -5.186649 0.0001X5 -0.005998 0.006034 -0.994019 0.3371R-squared 0.999098 Mean dependent var 5153.450Adjusted R-squared 0.998776 S.D. dependent var 2512.131S.E. of regression 87.87969 Akaike info criterion 12.03314Sum squared resid 108119.8 Schwarz criterion 12.33186Log likelihood -114.3314 Hannan-Quinn criter. 12.09145F-statistic 3102.411 Durbin-Watson stat 1.919746Prob(F-statistic) 0.000000⒈相关系数检验Y X1 X2 X3 X4 X5Y 1 0.99722268494996170.99770290227705490.96444194528244830.96921953429264450.9377357298079813X1 0.9972226849499617 10.99518313725376320.9696451991579440.97310363132347510.9303828192971817X2 0.99770290227705490.9951831372537632 10.959616056441480.96963746168774820.9454416018907617X3 0.96444194528244830.9696451991579440.95961605644148 10.99610097741545820.8276429550478994X4 0.96921953429264450.97310363132347510.96963746168774820.9961009774154582 10.8470479268267548X5 0.93773572980798130.93038281929718170.94544160189076170.82764295504789940.8470479268267548 1由相关系数矩阵可以看出，各解释变量之间的相关系数较高，解释变量之间确实存在严重的多重共线性。

计量经济学实验报告题目：关于多重共线性模型的检验和处理方法姓名：张飞飞学号：2008163050专业：工商管理指导教师：崔海燕实验时间： 2010-12-22二○一○年十二月二十五日关于多重共线性模型的检验和处理的方法一、实验目的：掌握多重共线性模型检验和处理的方法二、实验原理：判定系数检验法、逐步回归法、解释变量、相关系数检验三、实验步骤：1.创建一个新的工作文件：打开Eviews软件，点击File下的New File,创建一个新的工作文件，选择Annual,在Start Date栏中输入1983，在End date栏中输入2000，点击OK,点击保存，完成创建新的工作文件。

2.输入数据：点击Quick下的Empty Group,导入中国粮食生产函数模型的具体数据，命名被解释变量为Y,解释变量为X1、X2、X3、X4、X5，其中：Y表示粮食产量；X1表示农业化肥施用量；X2表示粮食播种面积；X3表示成灾面积；X4表示农业机械总动力；X5表示农业劳动力.点击Name保存数据，命名为Group01。

3.采用普通最小二乘法估计模型参数：点击Quick下的Estimate Equation,输入方程y c x1 x2 x3 x4 x5.点击OK,生成EQ1. 如下表所示：从结果可以看出：R-squared的值为0.982798，拟合优度比较高（一般为0.9以上），F-statistic 的值为137.1164，也比较大，说明模型上存在多重共线性，但无法看出变量之间的关系。

4.进行多重共线性检验：主要运用综合统计检验和采用解释变量之间的相关系数进行检验。

由综合统计检验法（步骤3)，可以看出存在多重共线性，继而进行解释变量之间的相关下系数检验。

点击Quick下的Groupstatistics,选择Correlations,打开Series List界面，输入X1 X2 X3 X3 X4 X5,点击OK,生成Group02,结果如下图：从结果可以看出：X1和X4之间的相关系数为0.960278，最接近1，说明X1和X4之间存在高度相关性。

山西大学实验报告实验报告题目：多重共线性问题的检验和处理学院：专业：课程名称：计量经济学学号：学生姓名：教师名称：崔海燕上课时间：一、实验目的：熟悉和掌握Eviews在多重共线性模型中的应用，掌握多重共线性问题的检验和处理。

二、实验原理：1、综合统计检验法；2、相关系数矩阵判断；3、逐步回归法；三、实验步骤：（一）新建工作文件并保存打开Eviews软件，在主菜单栏点击File\new\workfile，输入start date1978和end date 2006并点击确认，点击save键，输入文件名进行保存。

（二）输入并编辑数据在主菜单栏点击Quick键，选择empty\group新建空数据栏，根据理论和经验分析，影响粮食生产（Y）的主要因素有农业化肥施用量（X1）、粮食播种面积（X2）、成灾面积（X3）、农业机械总动力（X4）和农业劳动力（X5），其中成灾面积的符号为负，其余均应为正。

下表给出了1983——2000中国粮食生产的相关数据。

点击name键进行命名，选择默认名称Group01,保存文件。

Y X1 X2 X3 X4 X5 1983 38728 1660 114047 16209 18022 31151 1984 40731 1740 112884 15264 19497 30868 1985 37911 1776 108845 22705 20913 31130 1986 39151 1931 110933 23656 22950 31254 1987 40208 1999 111268 20393 24836 31663 1988 39408 2142 110123 23945 26575 32249 1989 40755 2357 112205 24449 28067 33225 1990 44624 2590 113466 17819 28708 38914 1991 43529 2806 112314 27814 29389 39098 1992 44264 2930 110560 25895 30308 38669 1993 45649 3152 110509 23133 31817 37680 1994 44510 3318 109544 31383 33802 36628 1995 46662 3594 110060 22267 36118 35530 1996 50454 3828 112548 21233 38547 34820 1997 49417 3981 112912 30309 42016 34840 1998 51230 4084 113787 25181 45208 35177 1999 50839 4124 113161 26731 48996 35768 2000 46218 4146 108463 34374 52574 36043 2001 45264 4254 106080 31793 55172 36513 2002 45706 4339 103891 27319 57930 36870 2003 43070 4412 99410 32516 60387 365462004 46947 4637 101606 16297 64028 35269 2005 48402 4766 104278 19966 68398 33970 2006 49804 4928 104958 24632 72522 32561 2007 50160 5108 105638 25064 76590 31444 （三）用普通最小二乘法估计模型参数用最小二乘法估计模型参数。

一、实训背景多重共线性是指回归模型中存在两个或两个以上的自变量高度相关，导致回归系数估计不准确、显著性检验失效等问题。

为了解决多重共线性问题，我们进行了一次多重共线性实训，通过实际操作，了解和掌握多重共线性的检验方法和解决策略。

二、实训目的1. 理解多重共线性的概念和产生原因；2. 掌握多重共线性的检验方法；3. 学习解决多重共线性的策略；4. 培养实际操作能力和问题解决能力。

三、实训内容1. 数据收集与整理本次实训选用某地区居民消费支出数据作为研究对象，数据包括居民收入、教育支出、医疗支出、娱乐支出等变量。

2. 数据分析（1）多重共线性检验采用方差膨胀因子（VIF）和条件指数（CI）对数据进行多重共线性检验。

VIF值越大，表示多重共线性程度越高；CI值越小，表示多重共线性程度越低。

（2）解决多重共线性策略针对检验出的多重共线性问题，采取以下策略进行解决：1）剔除高度相关的变量：通过VIF和CI筛选出高度相关的变量，并将其剔除。

2）主成分分析（PCA）：将高度相关的变量通过主成分分析转换为低维变量，降低多重共线性。

3）岭回归：在回归模型中引入岭参数，对回归系数进行惩罚，降低多重共线性。

四、实训过程1. 数据导入与预处理首先，将数据导入统计软件（如SPSS、R等），然后进行数据清洗，包括处理缺失值、异常值等。

2. 多重共线性检验（1）计算VIF和CI通过软件中的相关系数矩阵，计算每个变量的VIF和CI值。

（2）筛选出高度相关的变量根据VIF和CI值，筛选出高度相关的变量。

3. 解决多重共线性问题（1）剔除高度相关的变量根据筛选结果，将高度相关的变量从模型中剔除。

（2）主成分分析对剩余变量进行主成分分析，将高度相关的变量转换为低维变量。

（3）岭回归在回归模型中引入岭参数，对回归系数进行惩罚。

4. 结果分析通过上述处理，多重共线性问题得到有效解决。

对比处理前后的回归系数，发现回归系数估计更加准确，显著性检验更加有效。

《计量经济学》实验报告四开课实验室：财经科学实验室年月日班级：学号：姓名：实验项目名称：多重共线性的检验与修正成绩：实验性质：验证性□综合性□设计性指导教师签字：【实验目的】掌握多重共线性的检验与修正方法并能运用Eviews软件进行实现【实验要求】能根据OLS的估计结果判断是否存在多重共线性，熟悉逐步回归法修正模型的基本操作步骤，读懂各项上机榆出结果的含义并能进行分析【实验软件】 Eviews 软件【实验内容】根据给定的案例数据按实验要求进行操作【实验方案与进度】实验：设蔬菜销售量Y与人口（X1）、价格（X2）、粮食（X3）、收入（X4）、副食（X5）Dependent Variable: Y Method: Least Squares Date: 06/03/13 Time: 16:48 Sample: 1978 1996 Included observations: 19Variable Coefficient Std. Error t-Statistic Prob. C -1.530260 6.006901 -0.254750 0.8032 X1 0.014649 0.002923 5.012107 0.0003 X2 -0.702775 0.254521 -2.761169 0.0172 X3 0.060321 0.027575 2.187545 0.0492 X4 0.119825 0.036991 3.239290 0.0071 X5 0.018081 0.026022 0.694816 0.5004 X60.0922660.0542651.7003020.1148 R-squared0.986169 Mean dependent var 9.091579 Adjusted R-squared 0.979254 S.D. dependent var 1.717935 S.E. of regression 0.247442 Akaike info criterion 0.322027 Sum squared resid 0.734730 Schwarz criterion 0.669979 Log likelihood 3.940740 F-statistic 142.6067 Durbin-Watson stat2.292164 Prob(F-statistic)0.000000123456-1.5300.0150.7030.0600.120.0180.092t t t t t t t t Y X X X X X X u =+-+++++（2）方程线性显著性检验由（1）表中的数据可知F 统计量的值为142.6067，查表得0.05(6,12)F =3，显然142.6067>0.05(6,12)F =3，说明方程具有线性显著性。

实验名称：多重共线性的检验与处理实验时间：2011.12.10实验要求：主要是学习多重共线性的检验与处理，主要是研究解释变量与其余解释变量之间有严重多重共线性的模型，分析变量之间的相关系数。

通过具体案例建立模型，然后估计参数，求出相关的数据。

再对模型进行检验，看数据之间是否存在多重共线性。

最后利用所求出的模型来进行修正。

实验内容：实例：我国钢材供应量分析通过分析我国改革开放以来（1978－1997）钢材供应量的历史资料，可以建立一个单一方程模型。

根据理论及对现实情况的认识，影响我国钢材供应量 Y（万吨）的主要因素有：原油产量X1（万吨），生铁产量X2（万吨），原煤产量X3（万吨），电力产量X4（亿千瓦小时），固定资产投资X5(亿元)，国内生产总值X6(亿元)，铁路运输量X7（万吨）。

（一）建立我国钢材供应量的计量经济模型：（二）估计模型参数，结果为：Dependent Variable: YMethod: Least SquaresDate: 11/02/09 Time: 16:09Sample: 1978 1997Included observations: 20Variable Coefficient Std. Error t-Statistic Prob.C 139.2362 718.2493 0.193855 0.8495X1 -0.051954 0.090753 -0.572483 0.5776X2 0.127532 0.132466 0.962751 0.3547X3 -24.29427 97.48792 -0.249203 0.8074X4 0.863283 0.186798 4.621475 0.0006X5 0.330914 0.105592 3.133889 0.0086X6 -0.070015 0.025490 -2.746755 0.0177X7 0.002305 0.019087 0.120780 0.9059R-squared 0.999222 Mean dependent var 5153.350Adjusted R-squared 0.998768 S.D. dependent var 2511.950S.E. of regression 88.17626 Akaike info criterion 12.08573Sum squared resid 93300.63 Schwarz criterion 12.48402Log likelihood -112.8573 F-statistic 2201.081Durbin-Watson stat 1.703427 Prob(F-statistic) 0.000000由此可见，该模型可绝系数很高，F检验值2201.081，明显显著。

多重共线性诊断及处理⼀、定义多重共线性（Multicollinearity）是指线性回归模型中的解释变量之间由于存在较精确相关关系或⾼度相关关系⽽使模型估计失真或难以估计准确。

完全共线性的情况并不多见，⼀般出现的是在⼀定程度上的共线性，即近似共线性。

⼆. ⽬前常⽤的多重共线性诊断⽅法 1.⾃变量的相关系数矩阵R诊断法：研究变量的两两相关分析，如果⾃变量间的⼆元相关系数值很⼤，则认为存在多重共线性。

但⽆确定的标准判断相关系数的⼤⼩与共线性的关系。

有时，相关系数值不⼤，也不能排除多重共线性的可能。

R实现：画协⽅差矩阵图 2.⽅差膨胀因⼦（the variance inflation factor，VIF)诊断法：⽅差膨胀因⼦表达式为：VIFi=1/（1-R2i)。

其中Ri为⾃变量xi对其余⾃变量作回归分析的复相关系数。

当VIFi很⼤时，表明⾃变量间存在多重共线性。

该诊断⽅法也存在临界值不易确定的问题，在应⽤时须慎重。

判断：VIF j>10时，说明⾃变量x与其余⾃变量之间存在严重的多重共线关系，这种多重共线性可能会过度地影响最⼩⼆乘估计值 3.容忍值（Tolerance，简记为Tol）法：容忍值实际上是VIF的倒数，即Tol＝1/VIF。

其取值在0～1之间，Tol越接近1，说明⾃变量间的共线性越弱。

在应⽤时⼀般先预先指定⼀个Tol值，容忍值⼩于指定值的变量不能进⼊⽅程，从⽽保证进⼊⽅程的变量的相关系数矩阵为⾮奇异阵，计算结果具有稳定性。

但是，有的⾃变量即使通过了容忍性检验进⼊⽅程，仍可导致结果的不稳定。

4.多元决定系数值诊断法：假定多元回归模型p个⾃变量，其多元决定系数为R2y（X1，X2,…，Xp）。

分别构成不含其中某个⾃变量（Xi,i=1,2,…，p）的p个回归模型，并应⽤最⼩⼆乘法准则拟合回归⽅程，求出它们各⾃的决定系数R2i（i=1,2,…，p）。

如果其中较⼤的⼀个R2k与R2y很接近，就表明该⾃变量在模型中对多元决定系数的影响不⼤，说明该变量对Y总变异的解释能⼒可由其他⾃变量代替。