顺层岩质路堑边坡稳定性有限元分析

0引言近年来,随着公路、铁路建设的飞速发展,工程建设中,由顺层岩质路堑边坡失稳造成的滑坡灾害越来越多,给工程建设、经济建设和人民生命财产造成了巨大损失。

要对潜在的顺层岩质路堑边坡滑坡灾害进行防治就必须先弄清影响其稳定性的因素及影响规律,因此,研究顺层岩质路堑边坡稳定性影响因素及影响规律对我国的道路建设事业有着非常重要的意义和价值。

1顺层岩质路堑边坡的破坏模式顺层岩质路堑边坡是指岩面和坡面的走向、倾向二者产状要素基本相同的层状结构岩体路堑边坡[1]。

实践证明,边坡的破坏与其自身岩土体的结构类型存在着密切的联系,边坡的变形与破坏可概括为多种模式[2]。

本文总结出顺层岩质路堑边坡的几种变形破坏模式,可为顺层岩质路堑边坡稳定性分析与评价提供依据。

1.1滑移-拉裂破坏模式这类变形破坏主要发生在开挖坡角大于岩层倾角的缓倾和中等倾角顺层岩质路堑边坡中。

斜坡岩体沿下伏软弱层面向临空面方向滑动,并使滑移体拉裂解体(见图1。

当滑移面向临空面方向的倾角已足以使上覆岩体的下滑力超过该面的实际抗剪阻力时,则该面一经揭露临空,一旦后缘拉裂面出现即会迅速滑落。

1.2塑流-拉裂破坏模式基于MIDAS/GTS的顺层岩质路堑边坡稳定性影响因素及影响规律分析胡佐平1,牟锐2(1.湖州市交通规划设计院,浙江湖州313000;2.中国华西工程设计建设有限公司武汉分公司,湖北武汉430074摘要:总结顺层岩质路堑边坡的破坏模式,并利用MIDAS/GTS岩土工程数值分析软件,选取典型的顺层岩质路堑边坡模型进行详细的数值模拟,得出各岩土参数对顺层岩质路堑边坡稳定性的影响规律,具有一定的工程价值。

关键词:顺层岩质路堑边坡;稳定性;影响因素中图分类号:U416.14文献标识码:A文章编号:1002-4786(201009-0010-04DOI:10.3869/j.issn.1002-4786.2010.09.001Influencing Factors and Rules of Stability of Bedding RockCutting Slope Based on MIDAS/GTSHU Zuo-ping1,MOU Rui2(1.Huzhou Traffic&Plan Design Institute,Huzhou313000,China;2.China Huaxi Engineering Design&ConstructionCo.,Ltd.,Wuhan Branch,Wuhan430074,ChinaAbstract:By summing up the failure modes of bedding rock cutting slope,it executes numerical simulation to a typical bedding rock cutting slope model usingMIDAS/GTS,which is a numerical analysis software for geotechnical engineer.Thus the influence rule of each rock parameter on the sta-bility of bedding rock cutting slope is obtained,which has a certain engineering value.Key words:bedding rock cutting slope;stability;influencing factor10TRANSPORT STANDARDIZATION.1HALF OF Sep.,2010(No.228 TRANSPORT STANDARDIZATION.1HALF OF Sep.,2010(No.228abcd图4弯曲-拉裂变形破坏过程示意图A BA ′B ′CC ′图5顺层滑移型破坏过程示意图abcd图2塑流-拉裂变形破坏过程示意图(b(c①②100mm 100mm1260mm 950mm图3滑移-弯曲变形破坏过程示意图①-原地面线;②-变形的坡面或开挖坡面;③-页岩夹层(滑移面①②510③图1滑移-拉裂破坏形态(以自然边坡为例这类变形主要发生在开挖坡角大于岩层倾角且含有中至厚层软弱基座的水平或缓倾顺层岩质边坡中。

基于有限元法的顺层岩质边坡锚杆加固稳定性分析
汪勇;皮崇斌
【期刊名称】《土工基础》
【年(卷),期】2013(0)6
【摘要】结合某道路顺层岩质高切边坡实例,运用大型有限元软件MIDAS/GTS建立顺层岩质边坡的平面应变二维模型,基于有限元强度折减法,对锚杆加固前后的边坡稳定性进行了研究,主要分析了锚杆加固前后边坡位移、塑性破坏区以及安全系数的变化;同时着重讨论了锚固长度、锚杆间距、倾角等因素对边坡整体稳定性的影响,对影响边坡整体稳定性的因素进行了敏感性研究,分析了各因素与边坡安全系数之间的函数曲线关系。

【总页数】6页(P41-46)
【关键词】顺层岩质边坡;锚杆加固;稳定性;强度折减;有限元分析
【作者】汪勇;皮崇斌
【作者单位】武汉市市政工程质量监督站;武汉市建筑市场管理站
【正文语种】中文
【中图分类】TU472
【相关文献】
1.岩质边坡锚杆框架梁加固的有限元分析 [J], 李书兵;苏骏;毕辉
2.顺层岩质边坡稳定性及预应力锚杆加固研究 [J], 廖峻;李江腾;郝瑞卿;刘博
3.格构梁联合锚杆在顺层岩质边坡加固中的数值模拟分析 [J], 张勇;吴礼浩;方龙建
4.格构梁联合锚杆在顺层岩质边坡加固中的数值模拟分析 [J], 周敏
5."串层锚杆"加固的反倾层状岩质边坡稳定性分析 [J], 屈新;徐兴倩;吕谦;娄高中因版权原因，仅展示原文概要，查看原文内容请购买。

顺层岩质边坡岩层倾角的稳定性研究摘要：工程中常遇到不同边坡情况，边坡的地质条件直接决定工程的经济投入与经济效益.岩质边坡的稳定性受诸多因素影响，本文采用GEO-Studio软件进行对顺层岩质边坡不同倾角情况下的静力稳定性情况，进行多次有限元分析，着重探讨了顺层岩质边坡的静力稳定性与岩层倾角的关系，并深入分析岩层倾角对边坡稳定性的影响原因，同时对比三种安全系数分析方法在边坡稳定性分析中的分析结果。

关键词：顺层岩质边坡；倾角；静力稳定性；影响原因；安全系数；1 引言近年来，随着基础工程建设的快速推进，许多大型建设项目相继完成建设。

边坡治理工程受到越来越多的重视。

由于边坡治理工程受安全要求高，造价高，工程进度要求快等因素的限制，国内外学者对其的研究从未停止。

但由于边坡工程影响因素较多，影响机理较为复杂，因此未能对其进行全面深入系统分析。

岩质边坡因其岩层走向不同，划分为顺层岩质边坡与切层岩质边坡。

其中，顺层岩质边坡是一种易于导致安全事故的地质情况，顺层岩质边坡在其自重作用下，产生顺层滑移力，从而导致边坡失稳破坏。

而顺层岩质边坡稳定性受结构面倾角、岩层走向、岩层的力学特征等影响，已经引起很多学者的关注，并对经顺层岩质边坡稳定性进行了分析研究，取得了一定成果。

其中郑洁等探究了边坡坡脚与边坡稳定性系数的关系。

郭光威对岩质边坡与土质边坡稳定性评价方式进行了深入研究。

陈鹏等人进行了边坡高度，坡顶荷载以及相应工程措施对边坡稳定性的影响研究。

然而，现阶段顺层岩质边坡稳定性分析还存在一些问题亟待解决，如岩质边坡的失稳破坏规律只能依靠工程经验进行判别，而对岩质边坡失稳破坏的影响因素及影响规律的系统研究较少。

因此，需要对各影响因素进行系统分析，从而得出一套可以指导工程建设的科学理论。

本文主要研究顺层岩质边坡岩层倾角对边坡稳定性的影响，采用有限元数值模拟对不同岩层倾角情况下边坡稳定性情况及其影响原因进行分析汇总。

2岩质边坡稳定性影响因素岩质边坡的稳定性因素受诸多因素的影响，如：岩层走向、岩层倾角、岩层结构面强度，结构面数量、边坡坡脚、坡顶堆载、边坡高度，地下水位、岩体密度等。

岩质边坡稳定性有限元分析及监测方法研究的开题报告一、选题背景岩质边坡是指边坡整体或部分由岩体构成的边坡。

它们在水库、铁路、公路、隧道等工程中广泛存在，对工程的建设和运营安全造成威胁。

岩质边坡稳定性问题一直是岩土工程领域的研究重点之一。

目前，岩质边坡稳定性分析方法主要有解析法和数值法两种。

其中，解析法适用于规则边坡和简单几何形状的边坡，但对边坡的复杂形状和变化较大的岩体力学参数缺乏适用性；而数值法则能够更好地刻画岩质边坡复杂变形和破坏过程，能够适用于各类岩石边坡的稳定性分析。

随着数字化技术的不断发展，基于有限元法的岩质边坡稳定性分析方法逐渐得到广泛应用。

然而，由于各种因素的影响，有限元方法在岩质边坡稳定性分析中仍面临着精确度、可靠性、时效性等方面的挑战。

因此，如何通过优化有限元分析方法，提高其精度和可靠性，成为了研究的重点之一。

二、研究内容本研究将以一具体岩质边坡为研究对象，开展有限元分析和监测方法研究。

具体研究内容如下：1.岩体力学参数测试与分析通过对现场采集的岩体样品进行力学实验，获取岩体的杨氏模量、泊松比、抗压强度等力学参数。

结合有限元分析，分析不同岩体力学参数对边坡稳定性的影响。

2.有限元分析方法优化基于岩体力学参数测试结果，对有限元分析方法进行优化。

采用不同网格密度、材料本构模型等参数，比较分析不同分析方案的精度和可靠性，找到最优方案。

3.边坡监测方法研究采用激光扫描和三维数字化技术，建立岩质边坡的数字模型。

结合物理模型试验，开展边坡变形和位移的现场监测，掌握边坡变形规律和变形量，对比有限元分析结果，验证模型的可靠性。

三、研究意义本研究将针对实际工程中常见的岩质边坡问题，开展有限元分析与监测方法研究。

该研究有重要的理论和应用意义：1.优化有限元分析方法，提高稳定性分析精度和可靠性，为工程建设提供科学依据。

2.建立数字模型和开展现场监测，获知边坡变形规律和变形量，为预测和控制边坡稳定性提供依据。

基于极限平衡法及有限元法的边坡稳定性综合分析边坡稳定性是岩土工程中一个非常重要的问题，直接关系到边坡的安全运营和人民生命财产的安全。

为了研究边坡的稳定性，可以采用极限平衡法和有限元法进行综合分析。

极限平衡法是一种常用的边坡稳定性分析方法，它基于边坡在达到稳定状态时受到的平衡力原理。

其基本思想是，在边坡稳定过程中，边坡的抗滑力应该大于或等于外力作用在边坡上的附加抗滑力，从而实现边坡的稳定。

通过极限平衡法可以计算边坡的安全系数，如果安全系数大于1，则说明边坡稳定；否则，需要采取相应的加固措施。

有限元法是一种数值计算方法，可以对边坡进行力学分析。

有限元法将边坡划分成许多小的单元，通过对单元进行应力分析，然后再将各个单元的结果进行耦合，得到边坡整体的稳定性。

有限元法能够考虑材料的非线性、边坡的复杂形状以及边坡上的各种工况，具有较高的精确度和灵活性。

在边坡稳定性综合分析中，可以结合极限平衡法和有限元法的优点，进行更加精确的分析。

可以利用极限平衡法对边坡的整体稳定性进行初步评估，得到边坡的安全系数。

然后，可以使用有限元法对边坡进行更加详细的力学计算，考虑材料的非线性特性以及复杂的边界条件，得到边坡的应力、变形等参数。

将有限元法得到的结果与极限平衡法的结果进行对比，验证极限平衡法的合理性，并根据需要进行相应的修正。

综合分析可以更全面地评估边坡的稳定性，为边坡的设计和加固提供科学依据。

可以根据有限元法的分析结果，确定边坡上的最不稳定部位，并进行有针对性的加固措施，提高边坡的安全性。

基于极限平衡法和有限元法的边坡稳定性综合分析能够结合两种方法的优点，提高边坡稳定性分析的精确度和可靠性，对于岩土工程的设计和施工具有重要意义。

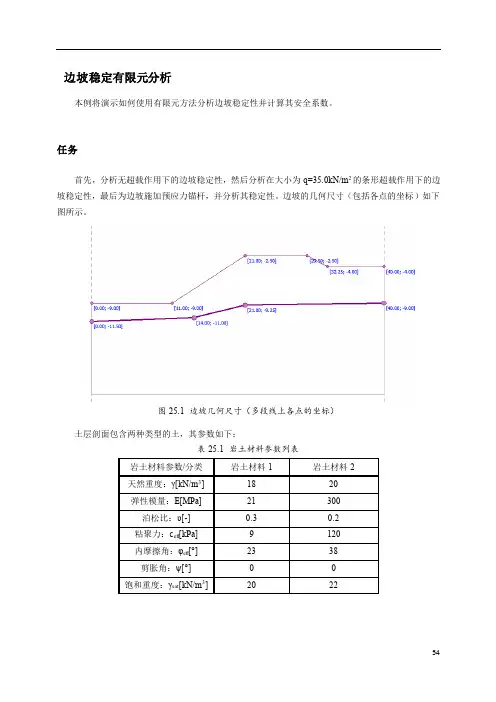
边坡稳定有限元分析本例将演示如何使用有限元方法分析边坡稳定性并计算其安全系数。

任务首先，分析无超载作用下的边坡稳定性，然后分析在大小为q=35.0kN/m2的条形超载作用下的边坡稳定性，最后为边坡施加预应力锚杆，并分析其稳定性。

边坡的几何尺寸（包括各点的坐标）如下图所示。

图25.1 边坡几何尺寸（多段线上各点的坐标）土层剖面包含两种类型的土，其参数如下：表25.1 岩土材料参数列表计算我们使用“GEO5岩土工程有限元分析计算模块”（以下简称“有限元模块”）（v18版）来分析该问题。

下面为建模和分析步骤：-建模阶段：分析设置和几何建模-工况阶段[1]：分析边坡无超载作用时的稳定性-工况阶段[2]：分析加入超载后边坡的稳定性-工况阶段[3]：分析加入锚杆后边坡的稳定性-结论建模阶段：分析设置和几何建模在分析设置界面中设置“分析类型”为“边坡稳定分析”，保持其他选项不变。

图25.2 【分析设置】界面注：选择“边坡稳定分析”时和选择“应力应变分析”时的设置以及建模过程几乎完全一样。

在【分析】界面点击“开始分析”按钮即可以分析并计算边坡的安全系数。

在“有限元-边坡稳定分析”模块中，各个工况阶段之间是相互独立的，即当前工况阶段的分析结果不受上一工况阶段分析结果的影响。

下一步，设置全局坐标范围。

设置的坐标范围要足够大，这样才能使得所要分析的区域不受边界条件的影响。

对于该算例，设置全局坐标范围<0m, 40m>，设置底边界距离多段线最低点距离为10m。

设置各个多段线和土层剖面，其参数如下表所示。

图25.3 全局坐标对话框表25.2各多段线及其节点的坐标列表设置各个岩土材料的参数并将其指定到相应的分区。

在本算例中，我们选择Drucker-Prager（DP）模型（见注）。

设置两种岩土材料的剪胀角ψ均为0°，即当材料受到剪力作用时，其体积不发生改变。

注：分析边坡稳定性时，必须选择非线性弹塑性模型作为岩土材料的本构模型，因为在边坡稳定分析过程中岩土材料会产生塑性应变，且塑性应变的产生是和岩土材料的强度参数c和φ相关的。

贵州某高速公路顺层岩质边坡稳定性分析与支护措施探讨随着西部地区大规模工程建设的开展，在施工过程中不可避免的形成了大量的路堑顺层岩质边坡，文章将从地层岩性、岩体结构、工程环境等方面对贵州某高速公路顺层岩质边坡的稳定性进行分析，并结合工程实际提出支护措施，结论对顺层边坡的开挖防护有一定的参考价值。

标签：顺层边坡；岩体结构；稳定性近年来，随着我国加大对西部地区高速公路建设的步伐，在建设过程中出现了大量的顺层岩质路堑边坡，如何评价其稳定性对公路的顺利建设至关重要。

但由于边坡的变形破坏模式与地层岩性、岩体结构、地质构造、地形地貌、水文地质特征及人类工程活动等密切相关。

根据前人的研究经验，顺层岩质边坡可分为缓倾角顺层边坡（岩层倾角40°）。

缓倾角顺层边坡开挖后边坡的自稳性较好，在贵州的山区道路建设中，较多出现的是以中等倾角的顺层边坡，偶尔会出现“夹心饼干”式的边坡结构，而陡倾角顺层边坡由于岩层倾角大于坡角，常发生弯折-溃曲破坏。

文章选取贵州某高速公路某段顺层岩质边坡，在对其工程地质环境条件及边坡基本特征分析的基础上，对边坡稳定性进行分析并提出支护措施。

1 某高速公路工程地质条件1.1 地形地貌该高速公路场区为低中山溶蚀洼地地貌，东南高，北西低，边坡范围内地形标高889.23～968.75m，相对高差79.52m，地形坡度较陡，一般为20～45°，最大坡度54°。

1.2 地层岩性根据地质调绘、钻探、物探资料，该段公路出露的地层为第四系灰褐色耕植土，结构松散；第四系残坡积粉质粘土，褐黄色，硬塑，含砾石5%～11%；寒武系牛蹄塘组页岩，强-中风化，泥质结构，块状构造，局部节理发育，见有方解石充填；震旦系灯影组白云岩，强-中风化，隐晶质结构，中厚层构造，节理发育，裂隙面见水质侵染。

1.3 水文地质条件边坡区位于溶蚀洼地，地表无长年性水流，仅在雨季有短暂地表径流；地下水由上部土层孔隙潜水和深部基岩裂隙水组成，含水量较小，其补给来源主要靠大气降水的入渗补给，排泄基准面为两岔河河面，根据现场钻孔测得地下水位0.5m。

有限元法在边坡稳定性分析中的应用摘要：本文系统地介绍了边坡稳定性分析有限元法的基本原理和计算模型，然后应用有限元法对某滑坡实例进行稳定性分析，再用极限平衡法对其计算结果进行验证，证明了利用有限元法进行边坡稳定性分析结果的可靠性，并充分体现了利用有限元法进行边坡稳定性分析的优越性。

关键词：边坡稳定；Mohr-Coulomb准则；有限元法；极限平衡法边坡稳定性分析是岩土工程中一项十分重要的工作，也是经典土力学最早试图解决而至今仍未圆满解决的课题[1]。

常用的边坡稳定性分析方法有各种极限平衡条分法、有限元法等[2]。

极限平衡条分法把土体作为刚体来处理，能给出土坡稳定性安全系数及其相应的滑动面，但是它仅从静力平衡角度出发，没有考虑边坡土体异于弹性体材料的特点，如土体材料的非线性本构关系等，因此，不管做何种巧妙的假定，都不可能对计算结果有很大的改进，也很难肯定其结果的正确程度如何[3]；随着计算机技术的不断提高，边坡稳定性分析中越来越多地使用有限元法。

有限元法是将连续介质离散为一组通过节点传递相互作用的单元集合，由于单元能够以不同的方式进行组合，且单元本身可以有不同的形状，用来模拟对象形状的复杂性，因而有限元法是边坡稳定性分析中一种较为理想的方法。

笔者先用有限元法对一实际工程进行边坡稳定性分析，再用极限平衡法对其进行验证，并通过比较，展示出利用有限元法进行边坡稳定性分析的优越性。

1 边坡稳定性分析的有限元计算模型1.1 有限元法基本原理本文主要针对二维平面问题进行研究，以节点位移为基本未知量。

若边坡结构离散后总结点数为n，则整个结构的节点位移向量为，单元节点位移向量为。

根据所选单元类型，确定单元位移模式，将外荷载转化为等效节点荷载列阵，导出单元的应变、应力矩阵及刚度矩阵[4]，通过推导可以得出单元节点力与节点位移和单元刚度矩阵之间的关系[5]（1）式中：，，，，将任意节点i的平衡方程改为节点位移（2）式中：为单元刚度矩阵的元素，是该单元上在n节点发生单位位移时所对应的i节点产生的节点力；为i节点的等效荷载。

探讨边坡稳定性有限元分析的处理技巧本文从边坡结构稳定性分析的角度着手，首先研究了有限元分析方法的基本原理，从理论层面介绍了边坡结构有限元分析的基本方法与特点，然后从施工角度围绕边坡结构稳定性问题进行研究，总结了边坡稳定性的影响因素，提出了施工过程中边坡稳定性问题的处理技术要点，望能够引起业内人士的关注与重视。

标签：边坡；稳定性；有限元0 引言对于我国而言，受到地质条件复杂因素的影响，滑坡等地质灾害发生几率高，所导致的经济损失是非常巨大的。

现阶段，边坡失稳已经发成成为仅次于地震的第二大地质灾害。

如何预先通过合理方法研究并判断边坡结构稳定性，已成为各行业领域人员高度重视的课题之一。

目前针对边坡稳定性的分析方法包括定量、定性两类。

有限元分析法作为应用最为广泛的数值定量分析方法之一，可以满足静力许可、应变相容以及应力-应变作用间的本构关系，故在近年来岩土工程结构稳定性分析中应用广泛。

1 边坡稳定性有限元分析有限元分析方法是指将待求解分析区域内以及边界面通过离散处理的方式形成有限个仅在节点部位联系的单元以及子域，然后引入单元形函数作为试函数项，将单元節点未知量作为待定系数，经计算得到加权残数关系。

在以有限元分析方法对岩土结构边坡稳定性问题进行研究的过程中，充分考虑了边坡岩体结构存在的非连续性以及非均质性特点，能够以量化数值的方式给出岩体结构在应力、应变大小以及分布上的具体关系。

相较于常规意义上的极限平衡分析方法而言，有限元分析方法从最先、最可能出现屈服破坏的部位以及最迫切需要进行加固处理的部位入手展开研究，能够近似的从应力-应变角度研究边坡结构的变形破坏机理。

但，在有关边坡结构位移不连续性问题的研究方面还存在一定局限性。

在对边坡结构稳定性问题进行有限元分析的过程中，为确保分析结果的可靠性，必须特别重视考虑以下几个方面的问题：第一，边坡结构应当为半无限体，且荷载以重力荷载为主；第二，在有限元分析过程中必须充分考虑对本构关系的选择问题，所选择的本构关系不但需要与待分析的边坡坡面受力情况相符合，还需要以最简化的方式反应边坡边界受力情况。

四川建筑　第卷5期　1顺层岩质边坡稳定性影响因素综合分析牛双建1,东兆星1,李顺波1,杨大方2(11中国矿业大学建筑工程学院,江苏徐州210008;21河南理工大学土木工程学院,河南焦作454003) 【摘　要】　基于正交试验设计方法,采用极限平衡法借助理正岩土分析软件中的岩质边坡稳定性分析模块,分析了边坡高度H 、结构面倾角α、结构面粘聚力c 、结构面摩擦角φ、张裂隙距坡顶距离L 、裂隙水的埋深H w 、地震作用E 、水平外荷载P x 、竖向外荷载P y 等9种因素对顺层岩质边坡稳定性的影响,每个因素考虑了4个水平,利用理正岩土分析软件计算出各种组合下的安全系数,最后利用极差分析得出各影响因素的影响程度由大到小排序为:H >φ>α>L >H w >c >E >P x >P y 。

【关键词】　顺层岩质边坡;　安全系数;　正交试验设计;　极限平衡法 【中图分类号】　T U432 【文献标识码】　A 倾斜的地面称为坡或斜坡,露天矿开采形成的斜坡构成采矿区的边界也称为边坡;在铁路、公路建筑施工中,所形成的路堤斜坡称为路堤边坡;开挖路堑所形成的斜坡为路堑边坡;在水利建设中开挖所形成的斜坡也是边坡。

因此,边坡工程在国民经济建设中具有重要的意义。

在边坡工程中有许多属于岩质边坡,因此研究岩质边坡的稳定性有重要的实际应用价值[1]。

影响顺层岩质边坡稳定性的因素很多,如结构面数量、性质和强度、层面倾角、自然坡角、开挖坡角、岩层走向与边坡走向夹角等[2]～[5]。

本文综合前人研究分析的基础上综合分析了几乎所有可以定量确定的各种影响因素对顺层岩质边坡稳定性的影响程度。

1　正交试验设计方法及理论 正交试验设计是利用“正交表”进行科学地安排与分析多因素试验的方法。

其主要优点是能在很多试验方案中挑选出代表性强的少数几个试验方案,并且通过这少数试验方案的试验结果的分析,推断出最优方案。

边坡稳定性分析中的有限元强度折减法安全系数
边坡稳定性分析中的有限元强度折减法安全系数
算方法、与传统极限平衡法相比所具有的优势、边坡失稳判据以及计算结果的影响因素。

采用有限元分析软件Plaxis进行强度折减计算，直至满足位移不收敛，从而得到边坡稳定安全系数。

论文关键词：边坡稳定,有限元强度折减法,失稳判据,安全系数
0.引言
边坡稳定性分析是岩土工程中一个十分重要的问题。

常用的边坡稳定性分析方法很多，如传统边坡稳定分析方法有:极限平衡法,极限分析法,滑移线场法等。

到目前极限平衡法已经日趋完善,基于该原理的新方法的不同仅是在条间力的假设上不同。

该法简单易用，为实际工程中广泛采用。

但是它没有考虑土体的应力应变特性,还要假设潜在滑面(如面、折线形、圆弧滑动面、对数螺线柱面等),对同一工程问题算不出一致的解。

极限分析法中的上限法虽然对真实解提供了一个严格的上限,但上限法中采用相关联流动法则，过大地考虑了土的剪胀性。

有限元法由于能反映边坡岩土体的应力-应变关系，考虑实际边坡体的复杂边界条件和采用一般土的材料模型，因而是一种较好的研究边坡稳定性的方法。

1.强度折减原理
在有限元静力稳态计算中,如果模型为不稳定状态,有限元计算将不收敛。

那么反过来,通过调整参数,使有限元计算从收敛变得不收敛,就表征边坡模型从稳
定状态向不稳定状态发生了转变。