运筹学教程(第三版)清华大学出版社出版 郭耀煌 胡远权编著 习题答案习题答案(第七章)

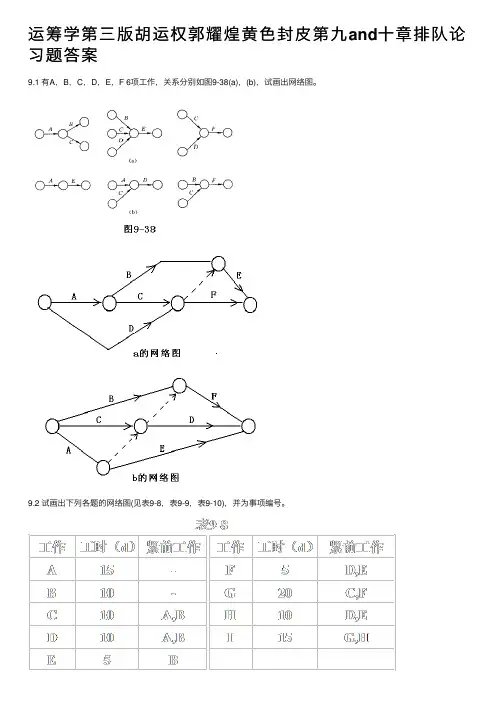
运筹学第三版胡运权郭耀煌黄⾊封⽪第九and⼗章排队论习题答案9.1 有A，B，C，D，E，F 6项⼯作，关系分别如图9-38(a)，(b)，试画出⽹络图。

9.2 试画出下列各题的⽹络图(见表9-8，表9-9，表9-10)，并为事项编号。

9.3 设有如图9-39，图9-40⽹络图，⽤图上计算法计算时间参数，并求出关键路线。

9.4 绘制表9-11，表9-12所⽰的⽹络图，并⽤表上计算法计算⼯作的各项时间参数、确定关键路线。

9.5 某⼯程资料如表9-13所⽰。

要求：(1)画出⽹络图。

(2)求出每件⼯作⼯时的期望值和⽅差。

(3)求出⼯程完⼯期的期望值和⽅差。

(4)计算⼯程期望完⼯期提前3天的概率和推迟5天的概率。

解：每件⼯作的期望⼯时和⽅差见表9-13的左部。

⼯程完⼯期的期望值为32个⽉，⽅差为5（1+1+1+1+1）。

⼯程期望完⼯期提前3天的概率为0.09，推迟5天的概率为0.987。

9.6 对图9-41所⽰⽹络，各项⼯作旁边的3个数分别为⼯作的最乐观时间、最可能时间和最悲观时间，确定其关键路线和最早完⼯时间的概率。

根据关键线路，再考虑到其他线路上的时差很多，可知最早完⼯时间应该等于关键线路上各个⼯作最早完⼯时间之和:4+2+6+2+3=2=19 。

概率为0.005 。

9.7 某项⼯程各道⼯序时间及每天需要的⼈⼒资源如图9-42所⽰。

图中，箭线上的英⽂字母表⽰⼯序代号，括号内数值是该⼯序总时差，箭线下左边数为⼯序⼯时，括号内为该⼯序每天需要的⼈⼒数。

若⼈⼒资源限制每天只有15⼈，求此条件下⼯期最短的施⼯⽅案。

解:最短⼯期还是15天。

各个⼯作的开始时间如下图所⽰：9.8 已知下列⽹络图有关数据如表9-14，设间接费⽤为15元／天，求最低成本⽇程。

解：将①→②缩短两天，总⼯期为25天，直接费⽤7420元，间接费⽤375元，最⼩总费⽤为7795元。

⽹络图和关键线路如下：9.9 ⼀项⼩修计划包括的⼯作如表9-15所⽰。

运筹学教程(第二版)习题解答8.1 证明在9座工厂之间，不可能每座工厂只与其他3座工厂有业务联系，也不可能只有4座工厂与偶数个工厂有业务联系。

解：将有联系的工厂做一条连线。

如果仅有9座工厂只与其他3座工厂有业务联系，说明顶点次数之和为27，矛盾如果只有4座工厂与偶数个工厂有业务联系，其他5个工厂一定与奇数个工厂有业务联系，说明顶点次数之和还是奇数，矛盾。

8.2 有八种化学药品A、B、C、D、E、F、G、H 要放进贮藏室。

从安全角度考虑，下列各组药品不能贮存在同一室内：A—C，A—F，A—H，B—D，B—F，B—H，C—D，C—G，D—E，D—G，E—G，E—F，F—G，G—H，问至少需要几间贮藏室存放这些药品。

解：能贮存在同一室内的两种药品之间作一条连线。

贮存在同一室内的药品应该构成一个完全图。

ABG，CFH ，DE构成完全图。

故，存放这些药品最少需要 3 间储藏室。

8.36个人围成圆圈就座，每个人恰好只与相邻者不相识，是否可以重新就座，使每个人都与邻座认识?解：两个人认识作一条连线。

8.4判定图8-50中的两个图能否一笔画出，若能，则用图形表示其画法。

解：(a)图都是偶点，可以一笔画出。

(b)图只有两个奇点，一个奇点为起点，另一个奇点为终点。

8.5求解如图8-51所示的中国邮路问题，A点是邮局8.6分别用深探法、广探法、破圈法找出图8-52所示图的一个生成树。

8.7设计如图5-53所示的锅炉房到各座楼铺设暖气管道的路线，使管道总长度最（单位：m）。

8.8分别用避圈法和破圈法求图8-54所示各图的最小树8.9 给定权数1，4，9，16，25，36，49，64，81，构造—棵霍夫曼树。

8.10 如图8-55，v0是一仓库，v9是商店，求一条从v0到v9的最短路。

8.11 求图8-56中v1到各点的最短路8.12 求图8-57网络中各顶点间的最短路8.13 某设备今后五年的价格预测分别是（5，5，6，7，8），若该设备连续使用，其第j 年的维修费分别为（1，2，3，5，6），某单位今年购进一台，问如何确定更新方案可使5年里总支出最小（不管设备使用了多少年，其残值为0）解：最优解为：先使用两年，更新后再使用三年。

运筹学第三版课后习题答案第一章：引论1.1 课后习题习题1a)运筹学是一门应用数学的学科，旨在解决实际问题中的决策和优化问题。

它包括数学模型的建立、问题求解方法的设计等方面。

b)运筹学可以应用于各个领域，如物流管理、生产计划、流程优化等。

它可以帮助组织提高效率、降低成本、优化资源分配等。

c)运筹学主要包括线性规划、整数规划、指派问题等方法。

习题2运筹学的应用可以帮助组织提高效率、降低成本、优化资源分配等。

它可以帮助制定最佳的生产计划，优化供应链管理，提高运输效率等。

运筹学方法的应用还可以帮助解决紧急情况下的应急调度问题，优化医疗资源分配等。

1.2 课后习题习题1运筹学方法可以应用于各个领域，如物流管理、生产计划、供应链管理、流程优化等。

在物流管理中，可以使用运筹学方法优化仓储和运输的布局，提高货物的运输效率。

在生产计划中，可以使用运筹学方法优化产品的生产数量和生产周期，降低生产成本。

在供应链管理中，可以使用运筹学方法优化订单配送和库存管理，提高供应链的效率。

在流程优化中，可以使用运筹学方法优化业务流程，提高整体效率。

习题2在物流管理中，可以使用运筹学方法优化车辆的调度和路线规划，以提高运输效率和降低成本。

在生产计划中，可以使用运筹学方法优化生产线的安排和产品的生产量，以降低生产成本和提高产能利用率。

在供应链管理中，可以使用运筹学方法优化供应链各个环节的协调和调度，以提高整体效率和减少库存成本。

在流程优化中，可以使用运筹学方法优化业务流程的排布和资源的分配，以提高流程效率和客户满意度。

第二章：线性规划基础2.1 课后习题习题1线性规划是一种数学优化方法，用于解决包含线性约束和线性目标函数的优化问题。

其一般形式为：max c^T*xs.t. Ax <= bx >= 0其中，c是目标函数的系数向量，x是决策变量向量，A是约束矩阵，b是约束向量。

习题2使用线性规划方法可以解决许多实际问题，如生产计划、供应链管理、资源分配等。

第一章习题解答1.1 用图解法求解下列线性规划问题。

并指出问题具有惟一最优解、无穷多最优解、无界解还是无可行解。

+=32min 21x x Z +=23max 21x x Z ⎪⎩⎪⎨⎧≥≥+≥+0,422664.)1(212121x x x x x x st ⎪⎩⎪⎨⎧≥≥+≤+0,124322.)2(212121x x x x x x st ⎪⎩⎪⎨⎧≤≤≤≤≤++=85105120106.max )3(212121x x x x st x x Z ⎪⎩⎪⎨⎧≥≤+−≥−+=0,23222.65max )4(21212121x x x x x x st x x Z 第一章习题解答无穷多最优解，,422664.32min )1(21212121⎪⎩⎪⎨⎧≥≥+≥++=x x x x x x st x x Z 是一个最优解3,31,121===Z x x 该问题无解⎪⎩⎪⎨⎧≥≥+≤++=0,124322.23max )2(21212121x x x x x x st x x Z 第一章习题解答85105120106.max )3(212121⎪⎩⎪⎨⎧≤≤≤≤≤++=x x x x st x x Z 唯最优解16,6,1021===Z x x 唯一最优解，该问题有无界解⎪⎩⎪⎨⎧≥≤+−≥−+=0,23222.65max )4(21212121x x x x x x st x x Z 第一章习题解答1.2 将下述线性规划问题化成标准形式。

1422245243min )1(432143214321⎪⎪⎧≤+−+−=−+−+−+−=x x x x x x x x x x x x Z .,0,,23243214321⎪⎪⎩⎨≥≥−++−无约束x x x x x x x x st ⎪⎩⎪⎨⎧≥≤≤−+−=++−+−=无约束321321321321,0,0624322min )2(x x x x x x x x x st x x x Z 第一章习题解答.2321422245243min )1(4321432143214321⎪⎪⎪⎨⎧≥−++−≤+−+−=−+−+−+−=x x x x x x x x x x x x st x x x x Z ,0,,4321⎪⎩≥无约束x x x x ⎪⎪⎩⎪⎪⎨⎧≥=−+−++−=+−+−+=−+−+−+−+−=0,,,,,232142222455243max 64241321642413215424132142413214241321x x x x x x x x x x x x x x x x x x x x x x x st x x x x x Z 第一章习题解答⎪⎪⎨⎧≥≤≤−+−=++−+−=无约束321321321321,0,0624322min)2(x x x x x x x x x st x x x Z ⎩⎪⎩⎪⎨⎧≥=++−+=−++−+−+=0,,,,6243322max 43231214323121323121323121x x x x x x x x x x x x x x st x x x x Z第一章习题解答634334max )3(3212121⎪⎪⎧=−+=++=x x x x x st x x Z 517,0,1,59,524,,1,0424321421=====⎪⎪⎩⎨=≥=++Z x x x x j x x x x j 该题是唯一最优解：）（"第一章习题解答⎪⎧≤++−≤++++=151565935121510max 321321x x x x x x x x x Z 该题无可行解。

运筹学第三版课后习题答案运筹学是一门研究如何在有限资源下做出最优决策的学科。

它涉及到数学、统计学、经济学等多个学科的知识，可以应用于各个领域，如物流管理、生产调度、供应链优化等。

而《运筹学》第三版是一本经典的教材，它系统地介绍了运筹学的基本概念、方法和应用。

本文将针对该教材的课后习题进行解答，帮助读者更好地理解和掌握运筹学的知识。

第一章：线性规划1. 习题1.1：求解线性规划问题的常用方法有哪些？答：求解线性规划问题的常用方法包括单纯形法、对偶理论、整数规划等。

其中，单纯形法是最常用的方法，它通过迭代寻找目标函数值最小（或最大）的解。

2. 习题1.2：什么是线性规划的对偶问题？如何求解线性规划的对偶问题？答：线性规划的对偶问题是指通过原始问题的约束条件构造一个新的问题，该问题的目标是最大化（或最小化）原始问题的目标函数值。

求解线性规划的对偶问题可以使用对偶理论，通过将原始问题转化为对偶问题的等价形式，再利用对偶问题的特性进行求解。

第二章：整数规划1. 习题2.1：什么是整数规划问题？与线性规划问题有何不同？答：整数规划问题是指决策变量的取值必须为整数的线性规划问题。

与线性规划问题相比，整数规划问题的解空间更为有限，求解难度更大。

整数规划问题在实际应用中常常涉及到资源的离散分配、路径选择等问题。

2. 习题2.2：列举几个整数规划问题的应用场景。

答：整数规划问题的应用场景包括生产调度、物流路径优化、设备配置等。

例如，在生产调度中，需要确定每个生产批次的数量和时间，以最大化产能利用率和最小化生产成本。

第三章：动态规划1. 习题3.1：什么是动态规划？它的基本思想是什么？答：动态规划是一种通过将问题划分为多个子问题，并保存子问题的解来求解原问题的方法。

其基本思想是利用子问题的解构建全局最优解，从而避免重复计算和提高求解效率。

2. 习题3.2：动态规划在哪些问题中有应用？答：动态规划在最短路径问题、背包问题、序列比对等问题中有广泛的应用。

1. 某饲养场饲养动物出售，设每头动物每天至少需700g 蛋白质、30g 矿物质、100mg 维生素。

现有五种饲料可供选用，各种饲料每kg 营养成分含量及单价如表1所示。

表1要求确定既满足动物生长的营养需要，又使费用最省的选用饲料的方案。

解：设总费用为Z 。

i=1,2,3,4,5代表5种饲料。

i x 表示满足动物生长的营养需要时，第i 种饲料所需的数量。

则有：⎪⎪⎩⎪⎪⎨⎧=≥≥++++≥++++≥++++++++=5,4,3,2,1,01008.022.05.0305.022.05.07008623..8.03.04.07.02.0min 54321543215432154321i x x x x x x x x x x x x x x x x t s x x x x x Z i2. 某医院护士值班班次、每班工作时间及各班所需护士数如表2所示。

每班护士值班开始时间向病房报道，试决定：（1） 若护士上班后连续工作8h ，该医院最少需要多少名护士，以满足轮班需要； （2） 若除22:00上班的护士连续工作8h 外（取消第6班），其他班次护士由医院排定上1～4班的其中两个班，则该医院又需要多少名护士满足轮班需要。

表2解：（1）设i x 第i 班开始上班的人数，i=1,2,3,4,5,6⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=≥≥+≥+≥+≥+≥+≥++++++=且为整数6,5,4,3,2,1,0302050607060..min 655443322161654321i x x x x x x x x x x x x x t s x x x x x x Z i 解：（2）在题设情况下，可知第五班一定要30个人才能满足轮班需要。

则设设i x 第i 班开始上班的人数，i=1,2,3,4。

⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧=≥=+++=≥+++=+++=≥+++=+++=≥+++=+++=≥+++++++=4,3,2,1,1002150216021702,160..30min i44434241444443342241143433323133443333223113242322212244233222211214131211114413312211114321j i y x y y y y y x y x y x y x y y y y y y x y x y x y x y y y y y y x y x y x y x y y y y y y x y x y x y x y t s x x x x Z ij 变量，—是，，，第四班约束，，第三班约束，，第二班约束，第一班约束3. 要在长度为l 的一根圆钢上截取不同长度的零件毛坯，毛坯长度有n 种，分别为ja （j=1,2，…n ）。

Ｐ66： 8.某部门有３个生产同类产品的工厂（产地），生产的产品由4个销售点出售,各工厂A １， Ａ2,A 3的生产量、各销售点B 1,B 2,Ｂ3，B 4的销售量(假定单位为t )以及各工厂到销售点的单位运价(元/t )示于下表中，问如何调运才能使总运费最小？表解：一、该运输问题的数学模型为:可以证明:约束矩阵的秩为r (A) ＝ 6． 从而基变量的个数为 6.34333231242322213141141312116115893102114124min x x x x x x x x x x x x x c z i j ij ij +++++++++++==∑∑==⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎨⎧==≥=++=++=++=++=+++=+++=+++4,3,2,1;3,2,1,01412148221016342414332313322212312111343332312423222114131211j i x x x x x x x x x x x x x x x x x x x x x x x x x ij 111213142122232431323334x x x x x x x x x x x x 712111111111111111111111111⨯⎛⎫ ⎪⎪⎪ ⎪⎪⎪ ⎪⎪ ⎪⎝⎭二、给出运输问题的初始可行解(初始调运方案)1. 最小元素法思想：优先满足运价（或运距)最小的供销业务。

此时得到一个初始调运方案(初始可行解）:其余（非基）变量全等于零。

此解满足所有约束条件,且基变量（非零变量）的个数为6(等于m ＋n-1=３+４-1＝6).,1013=x ,821=x ,223=x ,1432=x ,834=x ,614=x总运费为（目标函数值） 2. 伏格尔（Vogel)法伏格尔法的基本思想：运输表中各行各列的最小运价与次小运价之差值（罚数)应尽可能地小。

或者说：优先供应罚数最大行(或列）中最小运费的方格,以避免将运量分配到该行（或该列）次小运距的方格中。