固定床流体力学概要

fluent固定床的一种模拟方法Fluent是一种流体力学仿真软件，可用于模拟各种工程问题，
包括气体和液体在固定床中的流动。

在固定床模拟中，Fluent可以提供准确的流体流动和质量传递解决方案。

固定床模拟是指在固定位置上的颗粒床中流体的运动。

它在许
多工程领域中都有广泛的应用，例如化工工艺、废水处理、碳捕
集和催化剂反应工程等。

通过模拟流体在固定床中的流动，可以
优化床层设计，改善传质效率，并提高工艺的可持续性和经济性。

实现固定床模拟的方法之一是使用Fluent软件。

Fluent提供了
一系列的物理模型和数值算法，可以准确地描述颗粒床中的流动
行为。

该软件允许用户定义床层的几何形状、颗粒属性和边界条件，并将其输入模拟中。

随后，Fluent会根据所选的模拟方案，对床层中的流体运动进行计算，并提供关于压降、速度分布和质量
传递等参数的详细结果。

为了准确模拟固定床流动，用户需要正确选择和定义模拟参数。

这些参数包括颗粒属性（如密度、粒径和形状）、流体特性（如
粘度和密度）、床层几何形状和边界条件。

用户还可以选择适当
的物理模型和数值方法，以便更准确地模拟床层中的流动。

根据
不同的应用需求，用户可以通过调整这些参数来优化模拟结果。

Fluent是一种用于模拟固定床流动的强大工具。

通过正确选择
和定义模拟参数，使用者可以准确地模拟床层中的流体运动，并
获得有关压降、速度分布和质量传递等参数的详细结果。

这种模
拟方法对于优化床层设计、改善传质效率和改进工艺可持续性非
常有益。

第一章绪论表面力：又称面积力，是毗邻流体或其它物体，作用在隔离体表面上的直接施加的接触力。

它的大小与作用面积成比例。

剪力、拉力、压力质量力：是指作用于隔离体内每一流体质点上的力，它的大小与质量成正比。

重力、惯性力流体的平衡或机械运动取决于：1.流体本身的物理性质（内因）2.作用在流体上的力（外因）流体的主要物理性质：密度：是指单位体积流体的质量。

单位：kg/m3 。

重度：指单位体积流体的重量。

单位： N/m3 。

流体的密度、重度均随压力和温度而变化。

流体的流动性：流体具有易流动性，不能维持自身的形状，即流体的形状就是容器的形状。

静止流体几乎不能抵抗任何微小的拉力和剪切力，仅能抵抗压力。

流体的粘滞性：即在运动的状态下，流体所产生的阻抗剪切变形的能力。

流体的流动性是受粘滞性制约的，流体的粘滞性越强，易流动性就越差。

任何一种流体都具有粘滞性。

牛顿通过著名的平板实验，说明了流体的粘滞性，提出了牛顿内摩擦定律。

τ=μ(du/dy)τ只与流体的性质有关，与接触面上的压力无关。

动力粘度m：反映流体粘滞性大小的系数，单位：N•s/m2运动粘度n：ν=μ/ρ第二章流体静力学流体静压强具有特性1.流体静压强既然是一个压应力，它的方向必然总是沿着作用面的内法线方向，即垂直于作用面，并指向作用面。

2.静止流体中任一点上流体静压强的大小与其作用面的方位无关，即同一点上各方向的静压强大小均相等。

静力学基本方程: P=Po+pgh等压面：压强相等的空间点构成的面绝对压强：以无气体分子存在的完全真空为基准起算的压强 Pabs相对压强：以当地大气压为基准起算的压强 PP=Pabs—Pa（当地大气压）真空度：绝对压强不足当地大气压的差值，即相对压强的负值 PvPv=Pa-Pabs= -P测压管水头：是单位重量液体具有的总势能基本问题：1、求流体内某点的压强值：p = p0 +γh；2、求压强差：p – p0 = γh ；3、求液位高：h = （p - p0）/γ平面上的净水总压力：潜没于液体中的任意形状平面的总静水压力P，大小等于受压面面积A与其形心点的静压强pc之积。

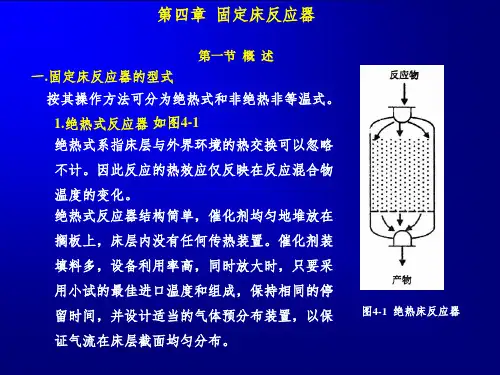
列管式固定床床层高度计算公式列管式固定床床层高度计算公式概述列管式固定床是一种常见的化工设备，在设计和操作中需要考虑床层的高度。

床层高度的合理选择对设备的效率和操作的安全性都有重要影响。

本文将列举几种常用的床层高度计算公式，并举例解释说明。

1. 简化公式床层高度计算的一种简化公式为：H = (V / (A * φ))^(1/3)其中，H为床层高度，V为床层体积，A为床层横截面积，φ为床层孔隙率。

示例假设某固定床的体积为1000 m^3，横截面积为10 m^2，孔隙率为。

H = (1000 / (10 * ))^(1/3) ≈ m因此，该固定床的合理床层高度约为 m。

2. 经验公式除了简化公式外，还存在一些经验公式可供参考。

Ergun公式Ergun公式是一种常用的床层压降计算公式，可用于估算床层高度。

ΔP/L = 150 * (1 - ε)^2 * ( * u / dp + 150 * (1 - ε)* u^2 / dp^2)其中，ΔP/L为单位长度床层压降，ε为床层孔隙率，u为气体流速，dp为颗粒直径。

示例假设某固定床的床层孔隙率为，气体流速为 m/s，颗粒直径为 m。

根据Ergun公式计算床层压降：ΔP/L = 150 * (1 - )^2 * ( * / + 150 * (1 - ) * ^2/ ^2)≈ Pa/m因此，在满足操作要求的最大床层压降为5000 Pa/m的情况下，该固定床的合理床层高度约为：H ≈ 5000 / ≈ m3. 其他因素在实际应用中，床层高度的选择还需考虑其他因素，如颗粒的堆积特性、气力输送性、液固分布、物料反应等。

结论本文列举了几种常用的床层高度计算公式，并给出了相关示例。

在实际应用中，需要综合考虑各种因素来确定合理的床层高度，以确保设备的效率和操作的安全性。

列管式固定床床层高度计算公式（续）4. 质量传递公式在某些情况下，为了满足质量传递的需求，床层高度的计算可以采用质量传递公式。

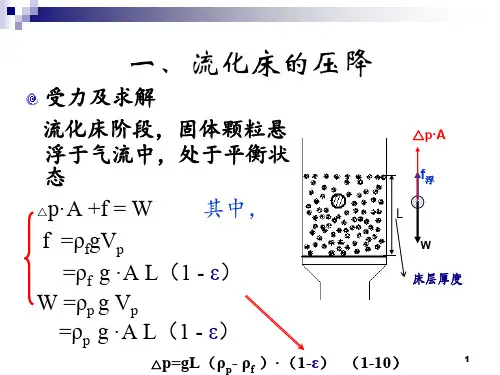
反应器设计中的流体力学模型研究第一章：引言在化学工程领域中，反应器是一种用于进行化学反应的设备。

流体力学的研究在反应器设计中发挥着重要的作用，因为反应器中的反应需要流体的不断混合和传热现象。

流体力学模型可以帮助工程师了解流体在反应器内的行为，优化反应器的设计，并提高反应器的性能。

本文将介绍反应器设计中的流体力学模型研究。

我们将从不同类型的反应器开始，分析不同的流体力学模型，并讨论流体力学模型对反应器性能的影响。

同时，我们还将介绍一些工程实践中的案例，以说明流体力学模型研究在反应器设计中的实际应用。

第二章：批式反应器批式反应器是最简单的反应器之一。

在批式反应器中，化学反应在一个封闭的容器中进行，当反应达到预定程度时，反应混合料被排空。

批式反应器的设计取决于许多因素，包括化学反应速率和混合要求。

在批式反应器中，流体力学模型主要关注混合。

有许多混合模型可用于批式反应器，常见的有完全混合模型和不完全混合模型。

完全混合模型假设反应物在反应器内均匀地分布，混合完全。

该模型通常适用于低粘度液体。

与之相对，不完全混合模型得出的结果更加逼近实际操作中的情况，因为在真实反应器中，混合程度是不同的。

混合程度可以通过混合时间和混合系数来表示。

混合时间是指反应物达到均匀状态所需的时间。

混合系数是指反应物通过流体在反应器内混合的程度。

流体力学模型可以帮助工程师确定反应器设计参数，例如流动方式和叶片类型。

这些参数对混合时间和混合系数具有很大的影响。

第三章：连续流反应器与批式反应器相比，连续流反应器具有更高的流量、不间断的生产和更好的混合，因此被广泛应用。

在连续流反应器中，反应物和产物在反应过程中不断流过反应器，直到反应完成。

不同于批式反应器，连续流反应器的混合不是均匀的。

流体在反应器内的流动模式和速度分布对反应成分转换率和转化效率有很大影响。

在连续流反应器中，通常使用计算流体力学模型。

这些模型可以帮助工程师确定流体在反应器内的流动模式和速度分布。

颗粒床固定床的新型结构优化
颗粒床固定床是一种常见的反应器结构，其主要特点是将反应物料放置在固定的床层中，通过床层内的颗粒物料进行反应。

然而，传统的颗粒床固定床结构存在一些问题，如反应效率低、传质不均等。

因此，新型结构优化成为了研究的热点。

新型结构优化主要包括以下几个方面：
一、床层结构优化
传统的颗粒床固定床结构中，床层的颗粒物料通常是均匀分布的，这样会导致反应物料在床层中的传质不均，从而影响反应效率。

因此，优化床层结构是提高反应效率的关键。

一种常见的优化方法是采用多层床层结构，通过不同颗粒物料的分布，实现反应物料在床层中的均匀分布，从而提高反应效率。

二、颗粒物料优化
颗粒物料的大小、形状、密度等因素都会影响反应效率。

因此，优化颗粒物料的性质也是提高反应效率的重要手段。

一种常见的优化方法是采用多种颗粒物料混合，通过不同颗粒物料的互相作用，实现反应物料在床层中的均匀分布，从而提高反应效率。

三、流体力学优化
流体力学是颗粒床固定床反应器中的重要因素，其影响着反应物料
在床层中的传质和传热。

因此，优化流体力学也是提高反应效率的关键。

一种常见的优化方法是采用多孔介质，通过孔隙的大小和分布，实现反应物料在床层中的均匀分布，从而提高反应效率。

新型结构优化是提高颗粒床固定床反应器反应效率的重要手段。

通过优化床层结构、颗粒物料和流体力学等因素，可以实现反应物料在床层中的均匀分布，从而提高反应效率。

未来，随着科技的不断发展，新型结构优化将会得到更加广泛的应用。