湖北省荆州市沙市第五中学高中数学第一章导数及其应用章末检测新人教版选修2_2

湖北省荆州市沙市第五中学高中数学 1.1.2 导数的概念导学案（无 答案）新人教版选修 2导学案 1.了解瞬时速度、瞬时变化率的概念; 2.理解导数的概念,知道瞬时变化率就是导数,体会导数的思想及 学习目标： 其内涵; 3.会求函数在某点的导数. 学习重点： 学习难点： 学法指导： 知识链接 一、创设情景 (一)平均变化率 (二)探究 探究: 计算运动员在 0  t  h 瞬时速度、瞬时变化率的概念、导数的概念. 导数的概念.65 这段时间里的平均速度,并思考以下问题: 49(1)运动员在这段时间内使静止的吗？ (2)你认为用平均速度描述运动员的运动状态有什么问题吗？ 探究过程: 如图是函数 h(t )  4.9t 2  6.5t  10 的图像, 结合图形可知, h(65 )  h(0) , 49ot65 )  h(0) 49 所以 v   0( s / m) 65 0 49 65 虽然运动员在 0  t  这段时间里的平均速度为 0(s / m) , 49 h(但实际情况是运动员仍然运动,并非静止, 可以说明用平均速度不能精确描述运动员的运动状态. 自主学习 1.瞬时速度 我们把物体在某一时刻的速度称为瞬时速度.运动员的平均速度不能反映他在某一时刻的 瞬时速度,那么,如何求运动员的瞬时速度呢？比如, t  2 时的瞬时速度是多少？考察 t  2 附近的情况:1思考: 当 t 趋近于 0 时,平均速度 v 有什么样的变化趋势？ 结论: 当 t 趋近于 0 时,即无论 t 从小于 2 的一边,还是从大于 2 的一边趋近于 2 时,平均速 度 v 都趋近于一个确定的值 13.1 . 从物理的角度看 , 时间 t 间隔无限变小时 , 平均速度 v 就无限趋近于史的瞬时速度 . 因 此,运动员在 t  2 时的瞬时速度是 13.1m / s 为了表述方便,我们用 limt  0h(2  t )  h(2)  13.1 t表示“当 t  2 , t 趋近于 0 时,平均速度 v 趋近于定值 13.1 ” 小结: 局部以匀速代替变速,以平均速度代替瞬时速度,然后通过取极限,从瞬时速度的近似 值过渡到瞬时速度的精确值. 2.导数的概念 从函数 y  f ( x) 在 x  x0 处的瞬时变化率是:f ( x0  x)  f ( x0 ) f  lim  x  0 x x ' 我们称它为函数 y  f ( x) 在 x  x0 出的导数,记作 f ( x0 ) 或 y' |x x0x 0lim即 f ( x0 )  limx 0f ( x0  x)  f ( x0 ) x说明: (1)导数即为函数 y  f ( x) 在 x  x0 处的瞬时变化率; (2) x  x  x0 ,当 x  0 时, x  x0 ,所以 f ( x0 )  limx 0f ( x)  f ( x0 ) . x  x0合作探究 三、典例分析2 例 1 (1)求函数 y  3x 在 x  1 处的导数.(2)求函数 f ( x)   x  x 在 x  1 附近的平均变化率,并求出该点处的导数.22分析: 先求 f  y  f ( x0  x)  f ( x0 ) ,再求 解: (1)法一 定义法(略)y y ,最后求 lim .  x  0 x x3x 2  3 12 3( x 2  12 )  lim  lim3( x  1)  6 x 1 x 1 x 1 x 1 x 1 2 y  (1  x)  (1  x)  2   3  x (2) x x y (1  x)2  (1  x)  2 f (1)  lim   lim (3  x)  3 x 0 x x 0 x法二 y |x 1  lim 例 2 将原油精炼为汽油、柴油、塑胶等各种不同产品,需要对原油进行冷却和加热,如果第xh 时,原油的温度(单位: C )为 f ( x)  x2  7 x  15(0  x  8) ,计算第 2 h 时和第 6 h 时,原油温度的瞬时变化率,并说明它们的意义. 解: 在第 2 h 时和第 6 h 时,原油温度的瞬时变化率就是 f ' (2) 和 f ' (6) f (2  x)  f ( x0 ) f  根据导数定义 x x (2  x)2  7(2  x)  15  (22  7  2  15)   x  3 x f  lim (x  3)  3 同理可得: f (6)  5 所以 f (2)  lim x 0 x x 0在第 2 h 时和第 6 h 时,原油温度的瞬时变化率分别为 3 和 5 , 说明在第 2 h 附近,原油温度大约以 3 C / h 的速率下降 在第 6 h 附近,原油温度大约以 5 C / h 的速率上升. 注: 一般地, f ' ( x0 ) 反映了原油温度在时刻 x0 附近的变化情况. 四、课堂练习2 1.质点运动规律为 s  t  3 ,求质点在 t  3 的瞬时速度为.2.求曲线 y  f ( x)  x 在 x  1 时的导数.333.例 2 中,计算第 3h 时和第 5h 时,原油温度的瞬时变化率,并说明它们的意义.五、回顾总结 1.瞬时速度、瞬时变化率的概念. 2.导数的概念.4。

学科：数学学段：高二年级课题：§1.3.1函数的单调性与导数（2课时）教学目标：1．了解可导函数的单调性与其导数的关系；2．能利用导数研究函数的单调性，会求函数的单调区间，对多项式函数一般不超过三次；教学重点：利用导数研究函数的单调性，会求不超过三次的多项式函数的单调区间教学难点：利用导数研究函数的单调性，会求不超过三次的多项式函数的单调区间教学过程与设计：详细过程一．创设情景函数是客观描述世界变化规律的重要数学模型，研究函数时，了解函数的赠与减、增减的快与慢以及函数的最大值或最小值等性质是非常重要的．通过研究函数的这些性质，我们可以对数量的变化规律有一个基本的了解．下面，我们运用导数研究函数的性质，从中体会导数在研究函数中的作用．二．新课讲授1．问题：图 3.3-1（1），它表示跳水运动中高度h随时间t变化的函数2() 4.9 6.510h t t t=-++的图像，图3.3-1（2）表示高台跳水运动员的速度v随时间t变化的函数'()()9.8 6.5v t h t t==-+的图像．运动员从起跳到最高点，以及从最高点到入水这两段时间的运动状态有什么区别？通过观察图像，我们可以发现：（1）运动员从起点到最高点，离水面的高度h随时间t的增加而增加，即()h t是增函数．相应地，'()()0v t h t=>．（2）从最高点到入水，运动员离水面的高度h随时间t的增加而减少，即()h t是减新建教案函数．相应地，'()()0v t h t =<．2．函数的单调性与导数的关系观察下面函数的图像，探讨函数的单调性与其导数正负的关系．如图3.3-3，导数'0()f x 表示函数()f x 在 点00(,)x y 处的切线的斜率．在0x x =处，'0()0f x >，切线是“左下右上”式的，这时，函数()f x 在0x 附近单调递增；在1x x =处，'0()0f x <，切线是“左上右下”式的，这时，函数()f x 在1x 附近单调递减．结论：函数的单调性与导数的关系在某个区间(,)a b 内，如果'()0f x >，那么函数()y f x =在这个区间内单调递增；如果'()0f x <，那么函数()y f x =在这个区间内单调递减．说明：（1）特别的，如果'()0f x =，那么函数()y f x =在这个区间内是常函数．3．求解函数()y f x =单调区间的步骤：（1）确定函数()y f x =的定义域；（2）求导数''()y f x =；（3）解不等式'()0f x >，解集在定义域内的部分为增区间；（4）解不等式'()0f x <，解集在定义域内的部分为减区间．三．典例分析例1．已知导函数'()f x 的下列信息：（3）做出结论：()'0f x >为增函数，()'0f x <为减函数．例5 已知函数 232()4()3f x x ax x x R =+-∈在区间[]1,1-上是增函数，求实数a 的取值范围．解：'2()422f x ax x =+-，因为()f x 在区间[]1,1-上是增函数，所以'()0f x ≥对[]1,1x ∈-恒成立，即220x ax --≤对[]1,1x ∈-恒成立，解之得：11a -≤≤ 所以实数a 的取值范围为[]1,1-．说明：已知函数的单调性求参数的取值范围是一种常见的题型，常利用导数与函数单调性关系：即“若函数单调递增，则'()0f x ≥；若函数单调递减，则'()0f x ≤”来求解，注意此时公式中的等号不能省略，否则漏解．四．课堂练习1．求下列函数的单调区间1.f (x )=2x 3－6x 2+72.f (x )=x1+2x 3. f (x )=sin x , x ]2,0[π∈ 4. y=xlnx 2．课本 练习五．回顾总结（1）函数的单调性与导数的关系（2）求解函数()y f x =单调区间（3）证明可导函数()f x 在(),a b 内的单调性六．布置作业。

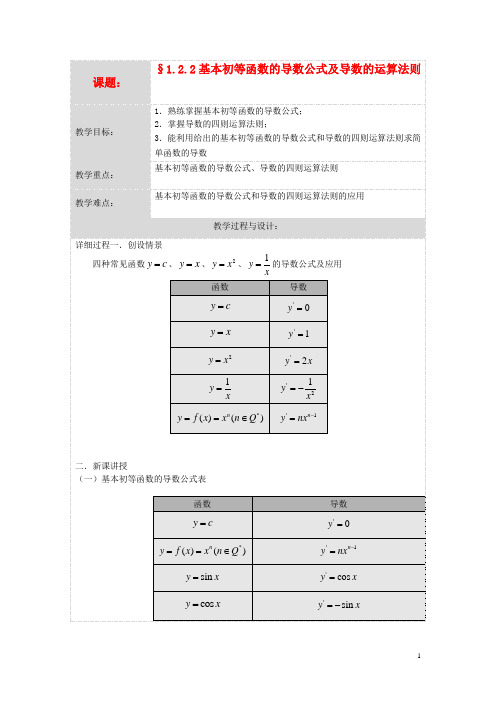
解：根据基本初等函数导数公式表，有'() 1.05ln1.05tp t =所以'10(10) 1.05ln1.050.08p =≈（元/年）因此，在第10个年头，这种商品的价格约为0.08元/年的速度上涨． 例2．根据基本初等函数的导数公式和导数运算法则，求下列函数的导数． （1）323y x x =-+ （2）y ＝xx --+1111；（3）y ＝x · sin x · ln x ；（4）y ＝x x 4； （5）y ＝xxln 1ln 1+-．（6）y ＝（2 x 2－5 x ＋1）e x（7） y ＝xx x xx x sin cos cos sin +-【点评】① 求导数是在定义域内实行的．② 求较复杂的函数积、商的导数，必须细心、耐心． 例3日常生活中的饮水通常是经过净化的．随着水纯净度的提高，所需净化费用不断增加．已知将1吨水净化到纯净度为%x 时所需费用（单位：元）为5284()(80100)100c x x x=<<-求净化到下列纯净度时，所需净化费用的瞬时变化率：（1）90% （2）98% 解：净化费用的瞬时变化率就是净化费用函数的导数．''''252845284(100)5284(100)()()100(100)x x c x x x ⨯--⨯-==--20(100)5284(1)(100)x x ⨯--⨯-=-25284(100)x =-（1）因为'25284(90)52.84(10090)c ==-，所以，纯净度为90%时，费用的瞬时变化率是52.84元/吨．（2）因为'25284(98)1321(10090)c ==-，所以，纯净度为98%时，费用的瞬时变化率是1321元/吨．函数()f x 在某点处导数的大小表示函数在此点附近变化的快慢．由上述计算可知，''(98)25(90)c c =．它表示纯净度为98%左右时净化费用的瞬时变化率，大约是纯净度为90%左右时净化费用的瞬时变化率的25倍．这说明，水的纯净度越高，需要的净化费用就越多，而且净化费用增加的速度也越快．四．课堂练习1．课本P92练习2．已知曲线C：y＝3 x4－2 x3－9 x2＋4，求曲线C上横坐标为1的点的切线方程；（y＝－12 x＋8）五．回顾总结（1）基本初等函数的导数公式表（2）导数的运算法则六．布置作业。

湖北省荆州市沙市第五中学高中数学 1.6微积分基本定理导学案（无答案）新人教版选修2导学案学习目标：1. 通过实例直观了解微积分基本定理的含义;2. 熟练地用微积分积分定理计算微积分.学习重点：微积分基本定理的含义; 学习难点：用微积分积分定理计算微积分. 学法指导：知识链接1.基本初等函数地求导公式:2.导数运算法则:3.连续函数)(x f 在[]b a ,上的定积分定义:4.定积分的性质:自主学习看课本57—59得出微积分基本定理:如果)(x f 是区间[]b a ,上的连续函数并且)()(/x f x F =,那么=⎰ba dx x f )(__________合作探究例1.计算下列定积分:(1)⎰211dx x (2)dx xx ⎰-312)12(例2.计算下列定积分:⎰π0sin xdx ,⎰ππ2sin xdx ,⎰π20sin xdx . 由计算结果你能发现什么结论?试利用曲边梯形的面积表示所发现的结论.例3.计算下列定积分:(1)⎰--202)4)(24(dx x x (2)dx xx x ⎰--21232 (3)dx x x 232)1(⎰+ (4)dx x x )1(41⎰- (5)⎰+20)sin 3(πdx x x (6)⎰-21)2(dx xe x (7)⎰102dx e x (8)⎰462cos ππxdx(9)⎰312dx x (10)⎰+1021dx x x (11)dx x ⎰202)2(sin π(12)⎰-a dx x a 022 (13)dx x x ⎰+1011.下列各式中,正确的是 A.)()()(///a f b f dx x f ba -=⎰ B. )()()(///b f a f dx x f b a-=⎰ C. )()()(/a f b f dx x f ba -=⎰ D. )()()(/b f a f dx x f ba -=⎰ 2.已知自由落体的运动速度g gt v (=为常数),则当[]2,1∈t 时,物体下落的距离是 A.g 21 B.g C.g 23 D.g 2 3.若,2ln 3)12(1+=+⎰a dx x x 则a 的值是 A.6 B.4 C.3 D.24.dx x ⎰--1121等于 A.4π B.2π C.π D.π2 5.)(x f 是一次函数,且⎰⎰==1010617)(,5)(dx x xf dx x f ,那么)(x f 的解析式是 A.34+x B.43+xC.24+-xD.43+-x6.已知⎰--=-aa dx x 8)12(,则a =( )7.设)(x f 是奇函数,求⎰-aa dx x f )(=( )8.设[][]⎩⎨⎧∈-∈=2,1,21,0,)(2x x x x x f ,求⎰20)(dx x f 9.求dx x x )1(11+⎰-。

导数及其应用全章微型检测1．(2013·高考辽宁卷)设函数f (x )满足x 2f ′(x )＋2xf (x )＝e x x ，f (2)＝e 28，则x ＞0时，f (x )( )A ．有极大值，无极小值B ．有极小值，无极大值C ．既有极大值又有极小值D ．既无极大值也无极小值2．(2012·高考湖南卷)设定义在R 上的函数f (x )是最小正周期为2π的偶函数，f ′(x )是f (x )的导函数，当x ∈[0，π] 时，0＜f (x )＜1；当x ∈(0，π) 且x ≠π2时，(x －π2)f′(x )＞0.则函数y ＝f (x )－sin x 在[－2π，2π]上的零点个数为( )A ．2B ．4C ．5D ．8 3．(2013·石家庄高三检测)已知等比数列{a n }，且a 4＋a 8＝⎠⎛024－x 2dx ，则a 6(a 2＋2a 6＋a 10)的值为________．4．已知函数f (x )＝e x －a e －x ，若f ′(x )≥23恒成立，则实数a 的取值范围是________．5．(2012·高考北京卷)已知函数f (x )＝ax 2＋1(a >0)，g (x )＝x 3＋bx .(1)若曲线y ＝f (x )与曲线y ＝g (x )在它们的交点(1，c )处具有公共切线，求a ，b 的值；(2)当a ＝3，b ＝－9时，若函数f (x )＋g (x )在区间[k ,2]上的最大值为28，求k 的取值范围．6．设函数f (x )＝x e x .(1)求f (x )的单调区间与极值；(2)是否存在实数a ，使得对任意的x 1、x 2∈(a ，＋∞)，当x 1＜x 2时恒有f x 2－f a x 2－a＞f x 1－f a x 1－a成立？ 若存在，求a 的取值范围；若不存在，请说明理由．参考答案1、解析：选D.由题意知f ′(x )＝e x x 3－2f x x ＝e x －2x 2f x x 3. 令g(x )＝e x －2x 2f (x )，则g ′(x )＝e x －2x 2f′(x)－4xf(x)＝e x －2(x 2f ′(x )＋2xf (x ))＝e x －2e x x ＝e x ⎝ ⎛⎭⎪⎫1－2x . 由g ′(x )＝0得x ＝2，当x ＝2时，g(x )min ＝e 2－2×22×e 28＝0，即g (x )≥0，则当x ＞0时，f ′(x )＝g x x 3≥0， 故f (x )在(0，＋∞)上单调递增，既无极大值也无极小值．2、解析：选B.∵⎝⎛⎭⎪⎫x －π2f ′(x )＞0， 当π2＜x ＜π时，f ′(x )＞0， ∴f (x )在⎝ ⎛⎭⎪⎫π2，π上是增函数．当0＜x ＜π2时，f ′(x )＜0， ∴f (x )在⎝⎛⎭⎪⎫0，π2上是减函数． 设π≤x ≤2π，则0≤2π－x ≤π.由f(x)是以2π为最小正周期的偶函数知f (2π－x )＝f (x )．故π≤x ≤2π时，0＜f (x )＜1.依题意作出草图可知，y 1＝f (x )与y 2＝sin x 在[－2π，2π]上有四个交点．3、解析：由定积分的几何意义知⎠⎛024－x 2d x ＝π，∴a 4＋a 8＝π，∴a 6(a 2＋2a 6＋a 10)＝a 6a 2＋2a 26＋a 6a 10＝a 24＋2a 4a 8＋a 28＝(a 4＋a 8)2＝π2.答案：π24、解析：由题意可知，f ′(x )＝e x ＋a e －x ≥23恒成立，分离参数可得，a ≥(23－e x )e x恒成立，令e x ＝t (t ＞0)，问题等价于a ≥(－t 2＋23t )max ＝3.所以a ∈[3，＋∞)．答案：[3，＋∞)5、解：(1)∵f (x )＝ax 2＋1，∴f ′(x )＝2ax ，∴f ′(1)＝2a .又f (1)＝c ＝a ＋1，∴f (x )在点(1，c )处的切线方程为y －c ＝2a (x －1)，即y －2ax ＋a －1＝0.∵g (x )＝x 3＋bx ，∴g ′(x )＝3x 2＋b ，∴g ′(1)＝3＋b .又g (1)＝1＋b ＝c ，∴g (x )在点(1，c )处的切线方程为y －(1＋b )＝(3＋b )(x －1)，即y －(3＋b )x ＋2＝0.依题意知3＋b ＝2a ，且a －1＝2，即a ＝3，b ＝3.(2)记h (x )＝f (x )＋g (x )．当a ＝3，b ＝－9时，h (x )＝x 3＋3x 2－9x ＋1，h ′(x )＝3x 2＋6x －9.令h ′(x )＝0，得x 1＝－3，x 2＝1.当k ≤－3时，函数h (x )在区间[k ,2]上的最大值为h (－3)＝28；当－3<k <2时，函数h (x )在区间[k ,2]上的最大值小于28.因此，k 的取值范围是(－∞，－3]．6、解：(1)f ′(x )＝(1＋x )e x .令f ′(x )＝0，得x ＝－1. f ′(x )的变化情∴f (x )f (x )极小值＝f (－1)＝－1e. (2)设g (x )＝f x －f a x －a，由题意，对任意的x 1、x 2∈(a ，＋∞)，当x 1＜x 2时恒有g (x 2)＞g (x 1)，即y ＝g (x )在(a ，＋∞)上是单调递增函数．又g ′(x )＝f x x －a －[f x －f a x －a 2＝＋x x x －a －x e x ＋a e ax －a 2＝x2＋x－ax－a x－x e x＋a e ax －a2＝x2e x－ax e x－a e x＋a e ax －a2，∴∀x∈(a，＋∞)，g′(x)≥0.令h(x)＝x2e x－ax e x－a e x＋a e a，h′(x)＝2x e x＋x2e x－a(1＋x)e x－a e x＝x(x＋2)e x－a(x＋2)e x＝(x＋2)(x－a)e x.若a≥－2，当x＞a时，h′(x)＞0，h(x)为(a，＋∞)上的单调递增函数，∴h(x)＞h(a)＝0，不等式成立．若a＜－2，当x∈(a，－2)时，h′(x)＜0，h(x)为(a，－2)上的单调递减函数，∴∃x0∈(a，－2)，h(x0)＜h(a)＝0，与∀x∈(a，＋∞)，h(x)≥0矛盾．综上，a的取值范围为[－2，＋∞)．。

第一章导数及其应用综合检测时间120分钟，满分150分。

一、选择题(本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．(2010·全国Ⅱ文，7)若曲线y＝x2＋ax＋b在点(0，b)处的切线方程是x－y＋1＝0，则( )A．a＝1，b＝1B．a＝－1，b＝1C．a＝1，b＝－1D．a＝－1，b＝－1[答案] A[解析] y′＝2x＋a，∴y′|x＝0＝(2x＋a)|x＝0＝a＝1，将(0，b)代入切线方程得b＝1.2．一物体的运动方程为s＝2t sin t＋t，则它的速度方程为( ) A．v＝2sin t＋2t cos t＋1B．v＝2sin t＋2t cos tC．v＝2sin tD．v＝2sin t＋2cos t＋1[答案] A[解析] 因为变速运动在t0的瞬时速度就是路程函数y＝s(t)在t0的导数，S′＝2sin t＋2t cos t＋1，故选A.3．曲线y＝x2＋3x在点A(2,10)处的切线的斜率是( )A．4B．5C ．6D ．7 [答案] D[解析] 由导数的几何意义知，曲线y ＝x 2＋3x 在点A (2,10)处的切线的斜率就是函数y ＝x 2＋3x 在x ＝2时的导数，y ′|x ＝2＝7，故选D.4．函数y ＝x |x (x －3)|＋1( ) A ．极大值为f (2)＝5，极小值为f (0)＝1 B ．极大值为f (2)＝5，极小值为f (3)＝1 C ．极大值为f (2)＝5，极小值为f (0)＝f (3)＝1 D ．极大值为f (2)＝5，极小值为f (3)＝1，f (－1)＝－3 [答案] B[解析] y ＝x |x (x －3)|＋1＝⎩⎪⎨⎪⎧x 3－3x 2＋1 (x <0或x >3)－x 3＋3x 2＋1 (0≤x ≤3)∴y ′＝⎩⎪⎨⎪⎧3x 2－6x (x <0或x >3)－3x 2＋6x (0≤x ≤3)x 变化时，f ′(x )，f (x )变化情况如下表：极大极小故应选B.5．(2009·安徽理，9)已知函数f(x)在R上满足f(x)＝2f(2－x)－x2＋8x－8，则曲线y＝f(x)在点(1，f(1))处的切线方程是( ) A．y＝2x－1B．y＝xC．y＝3x－2D．y＝－2x＋3[答案] A[解析] 本题考查函数解析式的求法、导数的几何意义及直线方程的点斜式．∵f(x)＝2f(2－x)－x2＋8x－8，∴f(2－x)＝2f(x)－x2－4x＋4，∴f(x)＝x2，∴f′(x)＝2x，∴曲线y＝f(x)在点(1，f(1))处的切线斜率为2，切线方程为y －1＝2(x－1)，∴y＝2x－1.6．函数f(x)＝x3＋ax2＋3x－9，已知f(x)在x＝－3时取得极值，则a等于( )A．2B．3C．4D．5[答案] D[解析] f′(x)＝3x2＋2ax＋3，∵f(x)在x＝－3时取得极值，∴x＝－3是方程3x2＋2ax＋3＝0的根，∴a＝5，故选D.7．设f(x)，g(x)分别是定义在R上的奇函数和偶函数．当x<0时，f′(x)g(x)＋f(x)g′(x)>0，且g(－3)＝0，则不等式f(x)g(x)<0的解集是( )A．(－3,0)∪(3，＋∞)B．(－3,0)∪(0,3)C．(－∞，－3)∪(3，＋∞)D．(－∞，－3)∪(0,3)[答案] D[解析] 令F(x)＝f(x)·g(x)，易知F(x)为奇函数，又当x<0时，f′(x)g(x)＋f(x)g′(x)>0，即F′(x)>0，知F(x)在(－∞，0)内单调递增，又F(x)为奇函数，所以F(x)在(0，＋∞)内也单调递增，且由奇函数知f(0)＝0，∴F(0)＝0.又由g(－3)＝0，知g(3)＝0∴F(－3)＝0，进而F(3)＝0于是F(x)＝f(x)g(x)的大致图象如图所示∴F(x)＝f(x)·g(x)<0的解集为(－∞，－3)∪(0,3)，故应选D.8．下面四图都是同一坐标系中某三次函数及其导函数的图象，其中一定不正确的序号是( )A ．①②B ．③④C ．①③D ．①④ [答案] B[解析] ③不正确；导函数过原点，但三次函数在x ＝0不存在极值；④不正确；三次函数先增后减再增，而导函数先负后正再负．故应选B.9．(2010·湖南理，5)⎠⎜⎛241xd x 等于( )A ．－2ln2B ．2ln2C ．－ln2D ．ln2 [答案] D[解析] 因为(ln x )′＝1x，所以 ⎠⎜⎛241x dx ＝ln x |42＝ln4－ln2＝ln2. 10．已知三次函数f (x )＝13x 3－(4m －1)x 2＋(15m 2－2m －7)x ＋2在x ∈(－∞，＋∞)是增函数，则m 的取值范围是( )A ．m <2或m >4B ．－4<m <－2C ．2<m <4D ．以上皆不正确 [答案] D[解析] f ′(x )＝x 2－2(4m －1)x ＋15m 2－2m －7，由题意得x 2－2(4m －1)x ＋15m 2－2m －7≥0恒成立，∴Δ＝4(4m －1)2－4(15m 2－2m －7)＝64m 2－32m ＋4－60m 2＋8m ＋28 ＝4(m 2－6m ＋8)≤0， ∴2≤m ≤4，故选D.11．已知f (x )＝x 3＋bx 2＋cx ＋d 在区间[－1,2]上是减函数，那么b ＋c ( )A ．有最大值152B ．有最大值－152C ．有最小值152D ．有最小值－152[答案] B[解析] 由题意f ′(x )＝3x 2＋2bx ＋c 在[－1,2]上，f ′(x )≤0恒成立．所以⎩⎪⎨⎪⎧f ′(－1)≤0f ′(2)≤0即⎩⎪⎨⎪⎧2b －c －3≥04b ＋c ＋12≤0令b ＋c ＝z ，b ＝－c ＋z ，如图过A ⎝⎛⎭⎪⎫－6，－32得z 最大，最大值为b ＋c ＝－6－32＝－152.故应选B.12．设f (x )、g (x )是定义域为R 的恒大于0的可导函数，且f ′(x )g (x )－f (x )g ′(x )<0，则当a <x <b 时有( )A ．f (x )g (x )>f (b )g (b )B ．f (x )g (a )>f (a )g (x )C ．f (x )g (b )>f (b )g (x )D ．f (x )g (x )>f (a )g (x ) [答案] C[解析] 令F (x )＝f (x )g (x )则F ′(x )＝f ′(x )g (x )－f (x )g ′(x )g 2(x )<0 f (x )、g (x )是定义域为R 恒大于零的实数∴F (x )在R 上为递减函数，当x ∈(a ，b )时，f (x )g (x )>f (b )g (b )∴f (x )g (b )>f (b )g (x )．故应选C.二、填空题(本大题共4个小题，每小题4分，共16分．将正确答案填在题中横线上)13.⎠⎜⎛－2－1d x(11＋5x )3＝________. [答案]772[解析] 取F (x )＝－110(5x ＋11)2，从而F ′(x )＝1(11＋5x )3则⎠⎜⎛－2－1d x(11＋5x )3＝F (－1)－F (－2)＝－110×62＋110×12＝110－1360＝772.14．若函数f (x )＝ax 2－1x的单调增区间为(0，＋∞)，则实数a 的取值范围是________．[答案] a ≥0[解析] f ′(x )＝⎝⎛⎭⎪⎫ax －1x ′＝a ＋1x 2，由题意得，a ＋1x2≥0，对x ∈(0，＋∞)恒成立，∴a ≥－1x2，x ∈(0，＋∞)恒成立，∴a ≥0.15．(2009·陕西理，16)设曲线y ＝x n ＋1(n ∈N *)在点(1,1)处的切线与x 轴的交点的横坐标为x n ，令a n ＝lg x n ，则a 1＋a 2＋…＋a 99的值为________．[答案] －2[解析] 本小题主要考查导数的几何意义和对数函数的有关性质．k ＝y ′|x ＝1＝n ＋1，∴切线l ：y －1＝(n ＋1)(x －1)， 令y ＝0，x ＝nn ＋1，∴a n ＝lgnn ＋1，∴原式＝lg 12＋lg 23＋…＋lg 99100＝lg 12×23×…×99100＝lg 1100＝－2.16．如图阴影部分是由曲线y ＝1x，y 2＝x 与直线x ＝2，y ＝0围成，则其面积为________．[答案] 23＋ln2[解析]由⎩⎪⎨⎪⎧y 2＝x ，y ＝1x，得交点A (1,1)由⎩⎪⎨⎪⎧x ＝2y ＝1x得交点B ⎝⎛⎭⎪⎫2，12.故所求面积S ＝⎠⎜⎛01x d x ＋⎠⎜⎛121x d x ＝23x 32| 10＋ln x | 21＝23＋ln2. 三、解答题(本大题共6个小题，共74分．解答应写出文字说明、证明过程或演算步骤)17．(本题满分12分)(2010·江西理，19)设函数f (x )＝ln x ＋ln(2－x )＋ax (a >0)．(1)当a ＝1时，求f (x )的单调区间；(2)若f (x )在(0,1]上 的最大值为12，求a 的值．[解析] 函数f (x )的定义域为(0,2)， f ′(x )＝1x －12－x＋a ，(1)当a ＝1时，f ′(x )＝－x 2＋2x (2－x )，所以f (x )的单调递增区间为(0，2)，单调递减区间为(2，2)；(2)当x ∈(0,1]时，f ′(x )＝2－2xx (2－x )＋a >0，即f (x )在(0,1]上单调递增，故f (x )在(0,1]上的最大值为f (1)＝a ，因此a ＝12.18．(本题满分12分)求曲线y ＝2x －x 2，y ＝2x 2－4x 所围成图形的面积．[解析] 由⎩⎪⎨⎪⎧y ＝2x －x 2，y ＝2x 2－4x得x 1＝0，x 2＝2.由图可知，所求图形的面积为S ＝⎠⎜⎛02(2x －x 2)d x ＋|⎠⎜⎛02(2x 2－4x )d x |＝⎠⎜⎛02(2x －x 2)d x －⎠⎜⎛02(2x 2－4x )d x . 因为⎝⎛⎭⎪⎫x 2－13x 3′＝2x －x 2，⎝ ⎛⎭⎪⎫23x 3－2x 2′＝2x 2－4x ， 所以S ＝⎝ ⎛⎭⎪⎫x 2－13x 3⎪⎪⎪⎪2－⎝ ⎛⎭⎪⎫23x 3－2x 2⎪⎪⎪⎪2＝4.19．(本题满分12分)设函数f (x )＝x 3－3ax ＋b (a ≠0)． (1)若曲线y ＝f (x )在点(2，f (2))处与直线y ＝8相切，求a ，b 的值；(2)求函数f (x )的单调区间与极值点．[分析] 考查利用导数研究函数的单调性，极值点的性质，以及分类讨论思想．[解析] (1)f ′(x )＝3x 2－3a .因为曲线y ＝f (x )在点(2，f (2))处与直线y ＝8相切，所以⎩⎪⎨⎪⎧f ′(2)＝0，f (2)＝8.即⎩⎪⎨⎪⎧3(4－a )＝0，8－6a ＋b ＝8.解得a ＝4，b ＝24.(2)f ′(x )＝3(x 2－a )(a ≠0)．当a <0时，f ′(x )>0，函数f (x )在(－∞，＋∞)上单调递增，此时函数f (x )没有极值点．当a >0时，由f ′(x )＝0得x ＝±a .当x ∈(－∞，－a )时，f ′(x )>0，函数f (x )单调递增； 当x ∈(－a ，a )时，f ′(x )<0，函数f (x )单调递减； 当x ∈(a ，＋∞)时，f ′(x )>0，函数f (x )单调递增． 此时x ＝－a 是f (x )的极大值点，x ＝a 是f (x )的极小值点． 20．(本题满分12分)已知函数f (x )＝12x 2＋ln x .(1)求函数f (x )的单调区间； (2)求证：当x >1时，12x 2＋ln x <23x 3.[解析] (1)依题意知函数的定义域为{x |x >0}， ∵f ′(x )＝x ＋1x，故f ′(x )>0，∴f (x )的单调增区间为(0，＋∞)． (2)设g (x )＝23x 3－12x 2－ln x ，∴g ′(x )＝2x 2－x －1x，∵当x >1时，g ′(x )＝(x －1)(2x 2＋x ＋1)x>0，∴g (x )在(1，＋∞)上为增函数， ∴g (x )>g (1)＝16>0，∴当x >1时，12x 2＋ln x <23x 3.21．(本题满分12分)设函数f (x )＝x 3－92x 2＋6x －a .(1)对于任意实数x, f ′(x )≥m 恒成立，求m 的最大值； (2)若方程f (x )＝0有且仅有一个实根，求a 的取值范围． [分析] 本题主要考查导数的应用及转化思想，以及求参数的范围问题．[解析] (1)f ′(x )＝3x 2－9x ＋6＝3(x －1)(x －2)．因为x ∈(－∞，＋∞)．f ′(x )≥m ，即3x 2－9x ＋(6－m )≥0恒成立．所以Δ＝81－12(6－m )≤0，得m ≤－34，即m 的最大值为－34.(2)因为当x <1时，f ′(x )>0；当1<x <2时，f ′(x )<0；当x >2时f ′(x )>0.所以当x ＝1时，f (x )取极大值f (1)＝52－a ，当x ＝2时，f (x )取极小值f (2)＝2－a .故当f (2)>0或f (1)<0时，方程f (x )＝0仅有一个实根，解得a <2或a >52.22．(本题满分14分)已知函数f (x )＝－x 3＋ax 2＋1(a ∈R )．(1)若函数y ＝f (x )在区间⎝ ⎛⎭⎪⎫0，23上递增，在区间⎣⎢⎡⎭⎪⎫23，＋∞上递减，求a 的值；(2)当x ∈[0,1]时，设函数y ＝f (x )图象上任意一点处的切线的倾斜角为θ，若给定常数a ∈⎝ ⎛⎭⎪⎫32，＋∞，求θ的取值范围；(3)在(1)的条件下，是否存在实数m ，使得函数g (x )＝x 4－5x 3＋(2－m )x 2＋1(m ∈R )的图象与函数y ＝f (x )的图象恰有三个交点．若存在，请求出实数m 的值；若不存在，试说明理由．[解析] (1)依题意f ′⎝ ⎛⎭⎪⎫23＝0，由f ′(x )＝－3x 2＋2ax ，得－3⎝ ⎛⎭⎪⎫232＋2a ·23＝0，即a ＝1.(2)当x ∈[0,1]时，tan θ＝f ′(x )＝－3x 2＋2ax ＝－3⎝⎛⎭⎪⎫x －a 32＋a23.由a ∈⎝ ⎛⎭⎪⎫32，＋∞，得a 3∈⎝ ⎛⎭⎪⎫12，＋∞.①当a 3∈⎝ ⎛⎦⎥⎤12，1，即a ∈⎝ ⎛⎦⎥⎤32，3时，f ′(x )max ＝a 23，f (x )min ＝f ′(0)＝0.此时0≤tan θ≤a 23.②当a3∈(1，＋∞)，即a ∈(3，＋∞)时，f ′(x )max ＝f ′(1)＝2a－3，f ′(x )min ＝f ′(0)＝0，此时，0≤tan θ≤2a －3.又∵θ∈[0，π)，∴当32<a ≤3时，θ∈⎣⎢⎡⎦⎥⎤0，arctan a 23，当a >3时，θ∈[0，arctan(2a －3)]．(3)函数y ＝f (x )与g (x )＝x 4－5x 3＋(2－m )x 2＋1(m ∈R )的图象恰有3个交点，等价于方程－x 3＋x 2＋1＝x 4－5x 3＋(2－m )x 2＋1恰有3个不等实根，∴x 4－4x 3＋(1－m )x 2＝0，显然x ＝0是其中一个根(二重根)，方程x 2－4x ＋(1－m )＝0有两个非零不等实根，则⎩⎪⎨⎪⎧Δ＝16－4(1－m )>01－m ≠0∴m >－3且m ≠1故当m >－3且m ≠1时，函数y ＝f (x )与y ＝g (x )的图象恰有3个交点．。

高中数学第一章导数及其应用A章末测试新人教A版选修2-2编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（高中数学第一章导数及其应用A章末测试新人教A版选修2-2）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为高中数学第一章导数及其应用A章末测试新人教A版选修2-2的全部内容。

高中数学 第一章 导数及其应用A 章末测试 新人教A 版选修2—2（基础过关卷）（时间:90分钟 满分:100分) 第Ⅰ卷（选择题 共50分)一、选择题(本大题共10小题，每小题5分，共50分．在每小题给出的四个选项中，只有一项是符合题目要求的)1．已知f （x )＝ln xx 2，则f ′(e）＝( ）A ．错误!B ．错误!C ．－错误!D ．－错误!2．曲线f (x ）＝e x＋x 在(1,f (1））的切线方程为( ） A ．（1＋e ）x －y ＝0 B ．e x －y ＋1＝0C ．（1＋e ）x ＋y －2（1＋e)＝0D ．x －（1＋e)y ＝03．函数f (x ）＝a ln x ＋x 在x ＝1处取得极值,则a 的值为( ) A ．错误! B ．－1 C ．0 D ．－错误! 4．函数f （x )＝错误!（ ) A ．在（0，2）上单调递减B ．在(－∞,0)和(2，＋∞)上单调递增C ．在(0，2)上单调递增D ．在（－∞，0）和（2，＋∞)上单调递减5．已知函数f （x ）的导函数为f ′(x ）＝2x 2，x ∈(－1,1)．如果f （x ）＜f (1－x )，则实数x 的取值范围为( )A ．错误!B ．(－1，1)C ．（）－112D ．错误!6．错误!π4π4-⎰cos 2x d x＝( )A．错误! B．错误!C．错误! D．－错误!7．已知函数y＝f(x),其导函数y＝f′（x)的图象如图所示,则y＝f（x）（)A．在(－∞,0）上为减函数B．在x＝0处取极小值C．在(4，＋∞）上为减函数D．在x＝2处取极大值8．已知函数f（x）的导数f′（x)＝a(x＋1)(x－a)，且f（x)在x＝a处取得极大值,则实数a的取值范围是（）A．a＞－1 B．－1＜a＜0C．0＜a＜1 D．a＞19．如果圆柱的轴截面的周长l为定值，则体积的最大值为（)A．错误!3π B．错误!3πC．错误!3π D．错误!错误!3π10．若f（x）＝－错误!x2＋b ln(x＋2）在（－1,＋∞)上是减函数,则实数b的取值范围是（）A．[－1，＋∞) B．(－1，＋∞)C．（－∞,－1］ D．(－∞，－1)第Ⅱ卷（非选择题共50分)二、填空题（本大题共5小题，每小题5分，共25分．把答案填在题中的横线上)11．由曲线y＝e x＋x与直线x＝0，x＝1,y＝0所围成图形的面积等于__________．12．在平面直角坐标系xOy中，点P在曲线C：y＝x3－10x＋3上,且在第二象限内，已知曲线C在点P处的切线的斜率为2，则点P的坐标为__________．13．函数f（x）＝（x2－3)e x在［0,2］上的最大值为__________．14．若f(x）＝错误!则11-⎰f(x)d x＝__________.15．函数f（x)＝x3－3ax＋b(a＞0)的极大值为6，极小值为2，则f（x)的减区间是__________．三、解答题（本大题共4小题，共25分．解答时应写出文字说明、证明过程或演算步骤)16．（本小题6分）已知函数f(x)＝x3＋ax2＋bx在x＝－错误!与x＝1处都取得极值．(1）求函数f(x)的解析式；(2）求函数f（x)在区间[－2，2］的最大值与最小值．17．（本小题6分）已知函数f（x）＝ax3＋bx2的图象过点M（1,4)，曲线在点M处的切线恰好与直线x＋9y＝0垂直．(1）求实数a,b的值;(2)若函数f（x）在区间[m,m＋1]上单调递增，求m的取值范围．18．（本小题6分)已知函数f（x)＝ln x x。

§1.1.2 导数的概念 课题：1．了解瞬时速度、瞬时变化率的概念； 2．理解导数的概念，知道瞬时变化率就是导数，体会导数的思想 及其内涵； 3．会求函数在某点的导数 瞬时速度、瞬时变化率的概念、导数的概念； 导数的概念． 教学过程与设计： 详细过程一．创设情景 （一）平均变化率 （二）探究：计算运动员在 0  t 教学目标：教学重点： 教学难点：65 这段时间里的平均速度，并思考以下问题： 49⑴运动员在这段时间内使静止的吗？ ⑵你认为用平均速度描述运动员的运动状态有什么问题吗？ 探究过程：如图是函数 h(t)= -4.9t +6.5t+10 的图像，结合图形可知， h(265 )  h(0) ， 4965 )  h(0) 所以 v  49  0( s / m) ， 65 0 49 65 虽然运动员在 0  t  这段时间里的平均速度为 0(s / m) ，但实际 49 h(h情况是运动员仍然运动，并非静止，可以说明用平均速度不能精确描 述运动员的运动状态． o t 二．新课讲授 1．瞬时速度 我们把物体在某一时刻的速度称为瞬时速度。

运动员的平均速度不能反映他在某一时刻的瞬时速度，那么，如何求运动员的瞬时速度呢？比如， t  2 时的瞬时速度是多 少？考察 t  2 附近的情况：思考：当 t 趋近于 0 时，平均速度 v 有什么样的变化趋势？ 结论：当 t 趋近于 0 时，即无论 t 从小于 2 的一边，还是从大于 2 的一边趋近于 2 时， 平均速度 v 都趋近于一个确定的值 13.1 ． 从物理的角度看，时间 t 间隔无限变小时，平均速度 v 就无限趋近于史的瞬时速度， 因此，运动员在 t  2 时的瞬时速度是 13.1m / s 为了表述方便，我们用 limh(2  t )  h(2)  13.1 t  0 t表示“当 t  2 ， t 趋近于 0 时，平均速度 v 趋近于定值 13.1 ” 小结：局部以匀速代替变速，以平均速度代替瞬时速度，然后通过取极限，从瞬时速度的近 似值过渡到瞬时速度的精确值。