判别分析作业

聚类分析与判别分析的例题1、某超市经销十种品牌的饮料，其中有四种畅销，三种滞销，三种平销。

下表是这十种品牌饮料的销售价格（元）和顾客对各种饮料的口味评分、信任度评分的平均数。

（1）根据数据建立贝叶斯判别函数，并根据此判别函数对原样本进行回判。

（2)现有一新品牌的饮料再该超市试销，其销售价格为3.0，顾客对其口味的评分平均分为8，信任评分为5，试预测该饮料的销售情况。

2、银行的贷款部门需要判别每个客户的信用好坏（是否未履行还贷责任），以决定是否给予贷款。

可以根据贷款申请人的年龄、受教育程度、现从事工作的年龄、未变更住址的年数、收入，负债收入比例、信用卡债务、其他债务等来判断其信用情况。

下表是某银行的客户资料中抽取的部分数据，（1）根据样本资料分别用距离判别法、贝叶斯判别法和费系尔判别法建立判别函数和判别规则。

(2)某客户的如上情况资料为（53，1，9，18，50，11，20，2.02，3.58），对其进行信用好坏的判别。

目前信用好坏客户序号已履行还贷责任1 23 1 7 2 31 6.6 0.34 1.712 34 1 173 59 8.0 1.81 2.913 42 2 7 23 41 4.6 0.94 0.944 39 1 195 48 13.1 1.93 4.365 35 1 9 1 34 5.0 0.40 1.30未履行还贷责任6 37 1 1 3 24 15.1 1.80 1.827 29 1 13 1 42 7.4 1.46 1.658 32 2 11 6 75 23.3 7.76 9.729 28 2 2 3 23 6.4 0.19 1.2910 26 1 4 3 27 10.5 2.47 0.363、从胃癌患者、萎缩性胃炎患者和非胃炎患者中分别抽取五个病人进行思想生化指标的化验：血清铜蛋白、蓝色反应、尿吲哚乙酸和中性硫化物，数据见下表。

试用距离判别法建立判别函数，并根据此判别函数对原样本进行回判。

图1由前面分析发现，协方差矩阵不等，可以考虑采用Separate-groups协方差矩阵。

输出结果表1-10：分類結果a被解释变量預測的群組成員資格總計Setosa 鸢尾花Versico-lor 鸢尾花Virginica 鸢尾花原始計數Setosa 鸢尾花50 0 0 50 Versico-lor 鸢尾花0 47 3 50Virginica 鸢尾花0 1 49 50 %Setosa 鸢尾花100.0 .0 .0 100.0 Versico-lor 鸢尾花.0 94.0 6.0 100.0 Virginica 鸢尾花.0 2.0 98.0 100.0a. 97.3% 個原始分組觀察值已正確地分類。

图2分類處理摘要已處理31 已排除遺漏或超出範圍群組代碼0至少一個遺漏識別變數0已在輸出中使用31群組的事前機率地区在前分析中使用的觀察值未加權加權1 .3332 2.0002 .333 2 2.0003 .333 1 1.000總計 1.000 5 5.000分類函數係數地区1 2 3人均食品支出.014 -.004 .021 人均衣着支出-.058 .024 -.092 （常數）-10.708 -3.645 -19.157 費雪 (Fisher) 線性區別函數图4 分類結果a地区預測的群組成員資格總計1 2 3原始計數 1 2 0 0 22 0 2 0 23 1 0 0 1未分組的觀察值8 18 0 26% 1 100.0 .0 .0 100.02 .0 100.0 .0 100.03 100.0 .0 .0 100.0未分組的觀察值30.8 69.2 .0 100.0a. 80.0% 個原始分組觀察值已正確地分類。

由表1-10可以看出，通过判别函数预测，有146个观测是分类正确的，其中，y=1组50个观测全部被判对，y=2组50个观测中有47个被判对，y=3组50个观测中有49个被判对，从而有97.3%的原始观测被判对。

应用多元统计分析习题解答_判别分析第四章判别分析4.1 简述欧几里得距离与马氏距离的区别和联系。

答：设p维欧几里得空间中的两点X=和Y=。

则欧几里得距离为。

欧几里得距离的局限有①在多元数据分析中，其度量不合理。

②会受到实际问题中量纲的影响。

设X,Y是来自均值向量为，协方差为的总体G中的p维样本。

则马氏距离为D(X,Y)=。

当即单位阵时，D(X,Y)==即欧几里得距离。

因此，在一定程度上，欧几里得距离是马氏距离的特殊情况，马氏距离是欧几里得距离的推广。

4.2 试述判别分析的实质。

答：判别分析就是希望利用已经测得的变量数据，找出一种判别函数，使得这一函数具有某种最优性质，能把属于不同类别的样本点尽可能地区别开来。

设R1，R2，…，Rk是p维空间R p 的k个子集，如果它们互不相交，且它们的和集为，则称为的一个划分。

判别分析问题实质上就是在某种意义上，以最优的性质对p 维空间构造一个“划分”，这个“划分”就构成了一个判别规则。

4.3 简述距离判别法的基本思想和方法。

答：距离判别问题分为①两个总体的距离判别问题和②多个总体的判别问题。

其基本思想都是分别计算样本与各个总体的距离（马氏距离），将距离近的判别为一类。

①两个总体的距离判别问题设有协方差矩阵∑相等的两个总体G 1和G 2，其均值分别是μ1和μ 2，对于一个新的样品X ，要判断它来自哪个总体。

计算新样品X 到两个总体的马氏距离D 2（X ，G 1）和D 2（X ，G 2），则X，D 2（X ，G 1）D 2（X ，G 2）X，D 2（X ，G 1）> D 2（X ，G 2， 具体分析，2212(,)(,)D G D G -X X111122111111111222*********()()()()2(2)2()-----------''=-----''''''=-+--+'''=-+-X μΣX μX μΣX μX ΣX X ΣμμΣμX ΣX X ΣμμΣμX ΣμμμΣμμΣμ11211212112122()()()2()22()2()---''=-++-'+⎛⎫=--- ⎪⎝⎭''=--=--X ΣμμμμΣμμμμX ΣμμX μααX μ记()()W '=-X αX μ 则判别规则为X，W(X)X，W(X)<0②多个总体的判别问题。

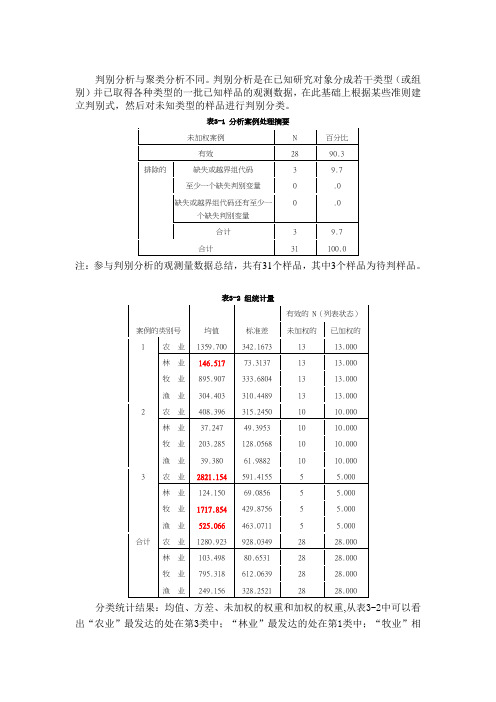
判别分析与聚类分析不同。

判别分析是在已知研究对象分成若干类型（或组别）并已取得各种类型的一批已知样品的观测数据，在此基础上根据某些准则建立判别式，然后对未知类型的样品进行判别分类。

表3-1 分析案例处理摘要未加权案例N 百分比有效28 90.3排除的缺失或越界组代码 3 9.7至少一个缺失判别变量0 .0缺失或越界组代码还有至少一个缺失判别变量0 .0合计 3 9.7合计31 100.0注：参与判别分析的观测量数据总结，共有31个样品，其中3个样品为待判样品。

表3-2 组统计量案例的类别号均值标准差有效的 N（列表状态）未加权的已加权的1 农业1359.700 342.1673 13 13.000林业146.517 73.3137 13 13.000牧业895.907 333.6804 13 13.000渔业304.403 310.4489 13 13.0002 农业408.396 315.2450 10 10.000林业37.247 49.3953 10 10.000牧业203.285 128.0568 10 10.000渔业39.380 61.9882 10 10.0003 农业2821.154 591.4155 5 5.000林业124.150 69.0856 5 5.000牧业1717.854 429.8756 5 5.000渔业525.066 463.0711 5 5.000合计农业1280.923 928.0349 28 28.000林业103.498 80.6531 28 28.000牧业795.318 612.0639 28 28.000渔业249.156 328.2521 28 28.000 分类统计结果：均值、方差、未加权的权重和加权的权重,从表3-2中可以看出“农业”最发达的处在第3类中；“林业”最发达的处在第1类中；“牧业”相对比较发达的处在第3类中；“渔业”比较发达的处在第3类中.表3-3 汇聚的组内矩阵a农业林业牧业渔业协方差农业147937.808 32.329 53946.036 38237.523林业32.329 4221.968 763.564 5011.382牧业53946.036 763.564 88914.814 -1202.757渔业38237.523 5011.382 -1202.757 81954.578相关性农业 1.000 .001 .470 .347林业.001 1.000 .039 .269牧业.470 .039 1.000 -.014渔业.347 .269 -.014 1.000a. 协方差矩阵的自由度为 25。

判别分析实验报告判别分析实验报告一、引言判别分析是一种常用的统计分析方法，广泛应用于数据挖掘、模式识别、生物信息学等领域。

本实验旨在通过对一个真实数据集的分析，探讨判别分析在实际问题中的应用效果。

二、数据集介绍本实验使用的数据集是一份关于肿瘤患者的临床数据，包括患者的年龄、性别、肿瘤大小、转移情况等多个变量。

我们的目标是根据这些变量，建立一个判别模型，能够准确地预测患者是否患有恶性肿瘤。

三、数据预处理在进行判别分析之前，我们首先对数据进行预处理。

这包括数据清洗、缺失值处理、异常值检测等步骤。

通过对数据的观察和分析，我们发现有部分数据存在缺失值，需要进行处理。

我们选择使用均值替代缺失值的方法进行处理，并对替代后的数据进行了异常值检测。

四、判别模型建立在本实验中，我们选择了线性判别分析（LDA）作为判别模型的建立方法。

LDA 是一种经典的判别分析方法，通过将数据投影到低维空间中，使得不同类别的样本在投影后的空间中能够更好地区分开来。

我们使用Python中的scikit-learn 库来实现LDA算法。

五、模型评估为了评估建立的判别模型的性能，我们将数据集划分为训练集和测试集。

使用训练集对模型进行训练，并使用测试集进行模型的评估。

我们选择了准确率、精确率、召回率和F1值等指标来评估模型的性能。

经过多次实验和交叉验证，我们得到了一个较为稳定的模型，并对其性能进行了详细的分析和解释。

六、结果与讨论经过模型评估，我们得到了一个在测试集上准确率为85%的判别模型。

该模型在预测恶性肿瘤时具有较高的精确率和召回率，说明了其在实际应用中的可行性和有效性。

但同时我们也发现，该模型在预测良性肿瘤时存在一定的误判率，可能需要进一步优化和改进。

七、结论本实验通过对一个真实数据集的判别分析，验证了判别分析方法在预测恶性肿瘤的应用效果。

通过建立判别模型，并对其性能进行评估，我们得到了一个在测试集上具有较高准确率的模型。

然而，我们也发现了该模型在预测良性肿瘤时存在一定的误判率，需要进一步的改进和优化。

《多元统计分析》实验报告实验名称: 判别分析及正态检验专业：统计学班级：120802姓名：指导教师：2014 年6 月26 日给出血友病基因携带者数据1，共分2组，第一组为非携带者（1π），第二组为必然携带者（2π），分组变量为g ，变量x1表示()10log AHF 活性，变量x2表示()10log AHF 抗原，利用上述数据： （1）对两个组检查二元正态性假定；一通过菜单系统实现 二运行结果第一组的正态性检验一运行程序proc princomp data=sasuser.zu1 out=prin prefix=z standard;var x1 x2;run;proc univariate data=work.prin normal plot;var z1 z2;run;二运行结果三结论分析第二组的正态性检验一运行程序proc princomp data=sasuser.zu2 out=prin1 prefix=z standard; var x1 x2;run;proc univariate data=work.prin1 normal plot;var z1 z2;run;二运行结果三结论分析（2）假定两组先验概率相等，求样本线性判别函数，并估计误判概率；一运行程序proc discrim data=sasuser.liangzu listerr crosslisterr;class g;var x1-x2;run;二运行结果三结论分析（3）将血友病基因携带者数据2中的10个新事例用（2）得到的判别函数进行分类；一运行程序proc discrim data=sasuser.liangzu testdata=sasuser.daipan listerr crosslisterr testlist;class g;var x1-x2;run;二运行结果三结论分析（3）假定必然携带者（组2）的先验概率为0.25。

数理统计大作业（二）全国各省发展程度的聚类分析及判别分析指导教师院系名称材料科学与工程院学号学生姓名2015 年 12 月21 日目录全国各省发展程度的聚类分析及判别分析 (1)摘要： (1)引言 (1)1实验方案 (2)1.1数据统计 (2)1.2聚类分析 (3)1.3判别分析 (4)2结果分析与讨论 (5)2.1聚类分析结果 (5)2.2聚类分析结果分析： (8)2.3判别分析结果 (9)2.4 Fisher判别结果分析： (11)参考文献： (16)全国各省发展程度的聚类分析及判别分析摘要：利用SPSS软件对全国31个省、直辖市、自治区(浙江、安徽、甘肃除外)的主要经济指标进行多种聚类分析，分析选择最佳聚类类数，并对浙江、湖南、甘肃进行类型判别分析。

通过这两个方法对全国各省进行发展分类。

本文选取了7项社会发展指标作为决定发展程度的影响因素，其中经济因素为主要因素，同时评估城镇化率和人口素质因素。

各项数据均来自2014年国家统计年鉴。

分析结果表明：北京市和上海市和天津市为同一类；江苏省和山东省和广东省为同一类型；河北、湖北、河南、湖南、四川、辽宁为同一类；其余的为另一类。

关键词：聚类分析、判别分析、发展引言聚类分析是根据研究对象的特征对研究对象进行分类的多元统计分析技术的总称。

它直接比较各事物之间的性质，将性质相近的归为一类，将性质差别较大的归入不同的类。

系统聚类分析又称集群分析，是聚类分析中应用最广的一种方法，它根据样本的多指标（变量）、多个观察数据，定量地确定样品、指标之间存在的相似性或亲疏关系，并据此连结这些样品或指标，归成大小类群，构成分类树状图或冰柱图。

判别分析是根据多种因素(指标)对事物的影响来实现对事物的分类，从而对事物进行判别分类的统计方法。

判别分析适用于已经掌握了历史上分类的每一个类别的若干样品，希望根据这些历史的经验（样品），总结出分类的规律性（判别函数）来指导未来的分类。

判别分析练习题判别分析练习题在统计学中，判别分析是一种用于分类和预测的方法。

它通过对不同类别的样本进行分析，构建一个分类模型，以便将未知样本分配到正确的类别中。

判别分析在各个领域都有广泛的应用，如医学诊断、金融风险评估等。

下面我将给大家提供一些判别分析的练习题，希望能够帮助大家更好地理解和应用这一方法。

1. 假设有两个类别的样本，每个样本都有两个变量。

已知两个类别的样本均值和协方差矩阵如下：类别1：均值为(1, 2)，协方差矩阵为[[2, 1], [1, 2]]类别2：均值为(3, 4)，协方差矩阵为[[3, 1], [1, 3]]现有一个未知样本(2, 3)，请利用判别分析方法判断该样本属于哪个类别。

解答：首先，我们需要计算两个类别的判别函数值。

对于类别1，判别函数为：g1(x) = -0.5 * (x - μ1) * Σ1^-1 * (x - μ1)T - 0.5 * ln(|Σ1|) + ln(P1)其中，x为未知样本，μ1为类别1的均值，Σ1为类别1的协方差矩阵，P1为类别1的先验概率。

类似地，对于类别2，判别函数为：g2(x) = -0.5 * (x - μ2) * Σ2^-1 * (x - μ2)T - 0.5 * ln(|Σ2|) + ln(P2)其中，μ2为类别2的均值，Σ2为类别2的协方差矩阵，P2为类别2的先验概率。

根据给定的均值和协方差矩阵，我们可以计算出：μ1 = (1, 2), Σ1 = [[2, 1], [1, 2]]μ2 = (3, 4), Σ2 = [[3, 1], [1, 3]]假设两个类别的先验概率相等，即P1 = P2 = 0.5。

将未知样本(2, 3)代入判别函数中，可以计算出：g1(2, 3) = -4.5g2(2, 3) = -5.5由于g2(2, 3)的值较小，所以未知样本更有可能属于类别2。

2. 现有一个三类别的样本，每个样本有三个变量。

已知三个类别的样本均值和协方差矩阵如下：类别1：均值为(1, 2, 3)，协方差矩阵为[[2, 1, 1], [1, 2, 1], [1, 1, 2]]类别2：均值为(4, 5, 6)，协方差矩阵为[[3, 1, 2], [1, 3, 2], [2, 2, 3]]类别3：均值为(7, 8, 9)，协方差矩阵为[[4, 1, 2], [1, 4, 2], [2, 2, 4]]现有一个未知样本(3, 4, 5)，请利用判别分析方法判断该样本属于哪个类别。

利用SPSS对全国各省进行经济类型聚类和判别分析摘要：本文利用SPSS统计软件对中国大陆（除港、澳、台之外）的31个省、市、自治区2000年到2009年的经济总量进行聚类分析，将这31个省、市、自治区分为了三大类，即经济发达地区、中等水平区、经济落后区。

并以这31个省级行政区10年的经济数据为样本，进行判别分析，建立了Fisher判别模型。

从判回代统计表可以看出该判别模型有着很高的正确率。

关键词：SPSS 聚类分析判别分析Fisher判别法一、引言利用各省以往经济数据对各省进行经济类型的划分，有助于了解各省的经济发展的状况,特别是能有助于了解全国各区域经济发展状况。

这对于相关部门制定相应的经济政策有一定的参考意义。

本文利用SPSS统计软件对全国31个省级行政区近10年的经济总量进行了聚类分析，把这31个地区划分为三个大类，即经济发达地区、中等水平区、经济落后区，然后对分好的类进行了判别分析，建立了判别函数。

从结果可以看出，其判别效果较好。

二、聚类分析和判别分析简介1、聚类分析法俗话说：“物以类聚，人以群分”。

对研究对象进行适当的分类，进而发现其规律性，是人们认识世界的一种基本方法。

研究怎样对事物进行合理分类（归类）的统计方法称为聚类分析。

依据分类对象的不同可以把聚类分析再分成Q型聚类和R型聚类，Q聚类是对样品进行聚类，R聚类是指对变量进行聚类。

聚类分析的基本原理是把某种性质相似的对象归于同一类，而不同的类之间则存在较大的差异。

为此，首先需要能刻画各个变量之间或者各个样本点之间的相似性，Q聚类一般使用“距离”度量样本点之间的相似性，R聚类则使用“相似系数”作为变量相似性的度量。

定义样本之间的距离可以采用欧氏距离、明考夫斯基距离、马氏距离、兰氏距离等测度；定义各变量之间的相似系数则多采用样本相关系数、夹角余弦等测度。

系统聚类法（Hierarchical Clustering Method ）是最常用的一种聚类方法。