概率统计实验报告
- 格式:docx
- 大小:30.00 KB
- 文档页数:6

《概率统计》实验报告专业 数学 班级 ** 姓名 **学号20120402444 实验地点 电教楼五号机房 实验时间 2014。
06。
03一、实验目的1.学会用matlab 计算常见分布的概率。
2.熟悉matlab 中用于描述性统计的基本操作与命令3。
学会matlab 进行参数估计与假设检验的基本命令与操作二、实验内容:(给出实验程序与运行结果)实验一:1. 在50个产品中有18个一级品,32个二级品,从中任意抽取30个,求其中恰有20个二级品的概率;解:由题可知:p=2096.0305020321018=C C C 程序如下:>>p=nchoosek(18,10)*nchoosek(32,20)/nchoosek (50,30)p = 0.20962、设随机变量()23,2X N ,求()25P X <<;()2P X >解:p (2〈X<5)=5328.0)2()5(=-F F程序如下:〉>p=normcdf (5,3,2)—normcdf(2,3,2)p =0。
5328P (|X |〉2)=6977.0)2()2(1=-+-F F程序如下:〉>p=1-[normcdf (2,3,2)—normcdf(-2,3,2)]p = 0.69773、一批产品的不合格率为0。
02,现从中任取40件进行检查,若发现两件或两件以上不合格品就拒收这批产品,求拒收的概率。
解: 1905.0)98.0()02.0()98.0()02.0(1391140400040=--=C C P程序如下:〉>p=1-binopdf(0 ,40,0。
02)—binopdf(1 ,40,0。
02)p = 0.1905实验二:1、在同一个坐标系中画出均值为6,方差为1,2,3的正态分布概率密度图形。
解:程序如下:>>x=-20:0。
01:20;〉〉y1=normpdf(x ,6,1);y2=normpdf(x ,6,2^(1/2));y3=normpdf(x,6,3^(1/2)); >〉 plot(x ,y1,x ,y2,x ,y3)2、根据调查,某集团公司的中层管理人员的年薪(单位:万元)数据如下:40.6 39.6 37。


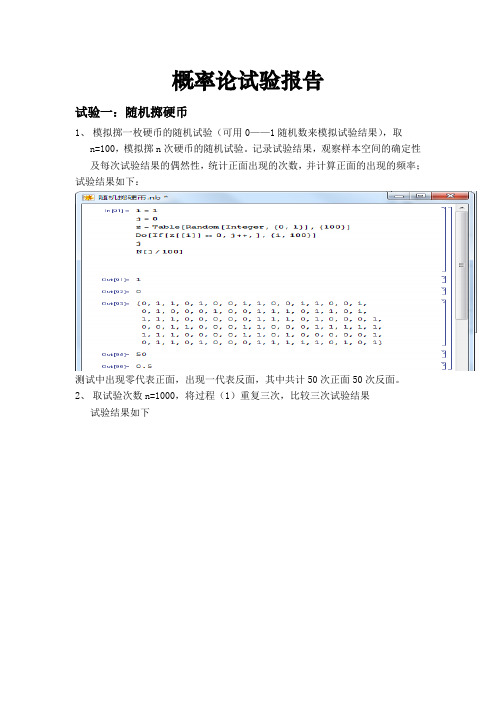
概率论试验报告试验一:随机掷硬币1、模拟掷一枚硬币的随机试验(可用0——1随机数来模拟试验结果),取n=100,模拟掷n次硬币的随机试验。
记录试验结果,观察样本空间的确定性及每次试验结果的偶然性,统计正面出现的次数,并计算正面的出现的频率;试验结果如下:测试中出现零代表正面,出现一代表反面,其中共计50次正面50次反面。
2、取试验次数n=1000,将过程(1)重复三次,比较三次试验结果试验结果如下3、三次结果分别是0.501,0.503,0.521 。
这充分说明模拟情况接近真实情况,频率接近概率0.5。
试验二:高尔顿钉板试验1、自高尔顿钉板上端放一个小球, 任其自由下落. 在其下落过程中,当小球碰到钉子时从左边落下的概率为p , 从右边落下的概率为,1p -碰到下一排钉子又是如此, 最后落到底板中的某一格子. 因此任意放入一球, 则此球落入哪个格子事先难以确定. 设横排共有20=m 排钉子, 下面进行模拟实验:(1) 取,5.0=p 自板上端放入一个小球, 观察小球落下的位置; 将该实验重复作5次, 观察5次实验结果的共性及每次实验结果的偶然性;(2) 分别取,85.0,5.0,15.0=p 自板上端放入n 个小球, 取,5000=n 观察n 个小球落下后呈现的曲线我们分析可知,这是一个经典的古典概型试验问题2、具体程序:3、我们分析实验结果可知,若小球碰钉子后从两边落下的概率发生变化, 则高尔顿钉板实验中小球落入各个格子的频数发生变化, 从而频率也相应地发生变化. 而且, 当,5.0p曲线峰值的格子位置向右偏; 当><p曲线峰值的格子位置向左偏。
,5.0试验三:抽签试验1、我们做模拟实验,用1-10的随机整数来模拟实验结果。
在1-10十个随机数中,假设10代表抽到大王,将这十个数进行全排,10出现在哪个位置,就代表该位置上的人摸到大王。
每次随机排列1-10共10个数,10所在的位置随机变化,分别输出模拟实验10次, 100次,1000次的结果, 将实验结果进行统计分析, 给出分析结果。

概率统计实验报告班级16030学号*****姓名2018 年1 月3 日1、 问题概述和分析 (1) 实验内容说明:题目12、(综合性实验)分析验证中心极限定理的基本结论: “大量独立同分布随机变量的和的分布近似服从正态分布”。
(2) 本门课程与实验的相关内容大数定理及中心极限定理; 二项分布。
(3) 实验目的分析验证中心极限定理的基本结论。
2、实验设计总体思路 2.1、引论在很多实际问题中,我们会常遇到这样的随机变量,它是由大量的相互独立的随机因素的综合影响而形成的,而其中每一个个别因素在总的影响中所起的作用是微小的,这种随机变量往往近似的服从正态分布。
2.2、 实验主题部分 2.2.1、实验设计思路1、 理论分析设随机变量X1,X2,......Xn ,......独立同分布,并且具有有限的数学期望和方差:E(Xi)=μ,D(Xi)=(k=1,2....),则对任意x ,分布函数满足该定理说明,当n 很大时,随机变量近似地服从标准正态分布N(0,1)。
因此,当n 很大时, 近似地服从正态分布N(n,n).2、实现方法(写清具体实施步骤及其依据)(1) 产生服从二项分布),10(p b 的n 个随机数, 取2.0=p , 50=n , 计算n 个随机数之和y 以及)1(1010p np np y --;依据:n 足够大,且该二项分布具有有限的数学期望和方差。
(2) 将(1)重复1000=m 组, 并用这m 组)1(1010p np np y --的数据作频率直方图进行观察.依据:通过大量数据验证随机变量的分布,且符合极限中心定理。
2.2.2、实验结果及分析注:实验所涉及的程序单列,本段只给出你认为有用的实验结果和对结果的分析或所得的结论,可以出现必要的图形、文字和数学公式,不出现Matlab程序代码,所有的程序请单列一节。
结论:大量独立同分布随机变量序列,近似的服从正态分布。
2.2.3、程序及其说明要求:此处使用数学符号给出相关算法需结合算法对程序相关变量进行说明关键程序段应给出相关的注释性说明。

《概率统计》实验报告实验人员:系(班):矿业工程系机械设计制造及其自动化1404班 学号:20141804408 姓名:李君阳 实验地点:电教楼四层三号机房实验名称:《概率统计》实验时间:2016.5.10,2016.5.17 16:30——18:30.实验目的:1.加强学生的动手能力,让学生掌握对MATLAB 软件的应用。
2.为以后的数学计算节省时间,提高精确度,准确度,合理的利用科学技术。
实验内容:(给出实验程序与运行结果)一、古典概型2、在50个产品中有18个一级品,32个二级品,从中任意抽取30个,求其中恰有20个二级品的概率.解:p=C 3220C 1810c 5030=0.2096>> p=nchoosek(32,20)*nchoosek(18,10)/nchoosek(50,30)p =0.2096二、计算概率1、某人进行射击,设每次射击的命中率为0.02,独立射击200次,试求至少击中两次的概率.2、一铸件的砂眼(缺陷)数服从参数为0.5的泊松分布,求此铸件上至多有1个砂眼的概率和至少有2个砂眼的概率. 解:1.p=1-c 2000∗0.98400-c 2001*0.98199*0.02=0.1458>> p=binopdf(2,200,0.02)p =0.1458 2.P(ζ=0)= 5.00*!05.0-e P(ζ=1)= 5.01*!15.0-e P(ζ1)=0.9098P(ζ)=0.09024、设随机变量()23,2X N ,求()25P X <<;()2P X >解:P(2<X<5)=F(5)-F(2)= )5(1,0σa F -=)235(1,0-F -)232(1,0-F = -=0.08413-(1-0.6915)=0.5328P(|X |>2)=P(X<-2)+P(X>2)=P(X<-2)+1-P(X<2)=0.6977normcdf(5,3,2)-normcdf(2,3,2) ≤2≥吕梁学院《概率统计》实验报告ans =0.5328>> normcdf(-2,3,2)-normcdf(2,3,2)+1ans =0.6977三、作图1、画出N(2,9),N(4,9),N(6,9)的图像进行比较;(图1)画出N(0,1),N(0,4),N(0,9)的图像进行比较.解:y1=normpdf(x,2,3);y2=normpdf(x,4,3);y3=normpdf(x,6,3);plot(x,y1,x,y2,x,y3)>> x=-40:0.01:40;y1=normpdf(x,0,1);y2=normpdf(x,0,2);y3=normpdf(x,0,3);plot(x,y1,x,y2,x,y3)(图2)四、常见统计量的计算1、根据调查,某集团公司的中层管理人员的年薪(单位:万元)数据如下:42 41 39.2 37.6 40.2 40 41 41.4 36.1 43.140.3 39.3 38.4 36.5 38.1 38.5 39.1 40.6 38.3 39.7求其公司中层管理人员年薪的样本均值、样本方差、样本标准差,绘制直方图。
2.(1)BINOMDIST(2,15,0.05,FALSE)=0.13475BINOMDIST(2,15,0.05,TRUE)=0.9638(2)EXPONDIST(1,0.1,FALSE)=0.09048EXPONDIST(4,0.1,TRUE)=0.32968(3)NORMDIST(2,0,1, TRUE)=0.97725NORMSDIST(2)-- NORMSDIST(--2)=0.9545=NORMINV(0.98,0,1)=2.05NORMSDIST(0.1)-- NORMSDIST(--1)=0.3812=NORMINV(0.05,5,100)=--159.49(4)POISSON(4,2,FALSE)=0.090POISSON(4,2,TRUE)=0.9473(5) BINOMDIST(2,15,0.05,FALSE)=0.13475营业税金与社会商品总额关系(1)打开EXCEL,建立数据文件如下图:税收Y 销售X3.93 142.085.96 177.307.85 204.689.82 242.6812.50 316.2415.55 341.9915.79 332.6916.39 389.2918.45 453.40调用线性回归分析程序:单击工具/数据分析/回归/确定,填写对话框,确定后输出结果,分析结果知回归方程为:Y=-2.258+0.0487X(2)对数据调用相关分析程序:依次单击工具/数据分析/相关系数/确定,填写对话框后,单击确定得到下面表格:所以,Y与X的皮尔逊相关系数为: 0.981069(3)建立假设H0:b=0 ,H1:b=/0,统计检验量F=(SSR/k)/(SSE/n-k-1)有数据分析结果知:F=179.6507P(F(1,7)>179.6507)=3.02E-06<<0.05所以认为回归方程是显著有效的。
(4)在(1)中表的B11中补充数据X=320在A11中输入公式=-2.258+0.0487X320运行课的到X=320的点预测值y=13.326。
大学概率统计实验报告引言在概率统计学中,实验是一种重要的数据收集方法。
通过实验,我们可以收集到一系列随机变量的观测值,然后利用统计方法对这些观测值进行分析和推断。
本实验旨在通过一个简单的骰子实验来介绍概率统计的基本理论和方法。
实验目标本实验的目标是通过投掷骰子的实验,验证骰子的随机性,并研究骰子的概率分布。
实验步骤1.准备一个六面骰子和一张记录表格。
2.将骰子投掷20次,并记录每次投掷的结果。
将结果按照出现的次数填入表格中。
3.统计记录表格中每个数字出现的频数,并计算频率。
4.绘制柱状图展示各个数字的频率分布情况。
实验结果与分析根据实验记录表格,我们统计得到了每个数字出现的频数如下:数字 1 2 3 4 5 6频数 4 3 6 2 4 1根据频数,我们可以计算出每个数字的频率。
频率是指某个数字出现的次数与总次数的比值。
通过计算,我们得到了每个数字的频率如下:数字 1 2 3 4 5 6频率0.2 0.15 0.3 0.1 0.2 0.05通过绘制柱状图,我们可以更直观地观察到各个数字的频率分布情况。
柱状图如下所示:0.3 | █| █| █| █0.25 | █| █| █| █0.2 | █ █ █| █ █ █ █| █ █ █ █| █ █ █ █0.15 | █ █ █ █| █ █ █ █| █ █ █ █| █ █ █ █0.1 | █ █ █ █| █ █ █ █| █ █ █ █| █ █ █ █0.05 | █ █ █ █| █ █ █ █| █ █ █ █| █ █ █ █----------------1 2 3 4 5 6根据实验结果,我们可以观察到以下现象和结论: - 各个数字的频率接近于理论概率,表明骰子的结果具有一定的随机性。
- 数字3的频率最高,约为0.3,而数字6的频率最低,约为0.05。
这说明骰子的结果并不完全均匀,存在一定的偏差。
结论与讨论通过本次实验,我们了解了概率统计的基本理论和方法,并通过投掷骰子的实验验证了骰子的随机性。
概率统计实验报告结论引言概率统计是数学中非常重要的一个分支,它利用统计方法对一定的随机现象进行描述、分析和预测。
本次实验中我们通过模拟实验的方式,利用概率统计的方法对一些实际问题进行了研究和分析。
实验一:骰子实验我们进行了一系列的骰子实验,通过投掷骰子并记录点数的方式来研究骰子的概率分布。
实验结果表明,投掷骰子时,每个面出现的概率是均等的,即每个面的概率是1/6。
这符合理论预期,也验证了概率统计中的等概率原理。
实验二:扑克牌实验通过抽取一副扑克牌中的若干张牌,并记录其点数和花色,我们研究了扑克牌中各个点数和花色的概率分布情况。
实验结果表明,52张扑克牌中各个点数和花色的概率分布近似均等,并且点数和花色之间是相互独立的。
这进一步验证了概率统计中的等概率原理和独立事件的性质。
实验三:掷硬币实验通过进行大量的抛硬币实验,我们研究了硬币正反面出现的概率分布情况。
实验结果表明,掷硬币时正面和反面出现的概率非常接近,都是1/2。
这也符合理论预期,并且进一步验证了概率统计中的等概率原理。
实验四:随机数生成器实验通过计算机程序生成随机数,并对其进行统计分析,我们研究了随机数生成器的质量问题。
实验结果表明,一个好的随机数生成器应该具备均匀分布、独立性和不可预测性等特征。
我们的实验结果显示,所使用的随机数生成器满足这些条件,从而可以被广泛应用于概率统计领域。
实验五:二项分布实验通过进行大量的二项分布实验,我们研究了二项分布的特性。
实验结果表明,二项分布在一定条件下可以近似成正态分布,这是概率统计中的重要定理之一。
实验结果还显示,二项分布的均值和方差与试验的次数和成功的概率有关,进一步验证了概率统计中与二项分布相关的理论。
总结通过本次概率统计实验,我们对骰子、扑克牌、硬币、随机数和二项分布等与概率统计相关的问题进行了研究和分析。
实验结果与理论预期基本一致,验证了概率统计中的一些重要原理和定理。
这些实验结果对我们的概率统计学习和应用有着重要的意义,同时也为我们在探索更深层次的概率统计问题提供了一定的启示和思路。
概率统计实验报告
班级1403018
学号***********
姓名张可心
2015年12月28日
1、问题概述和分析
(1)实验内容说明
(验证性实验)使用Matlab软件绘制正态分布、指数分布、均匀分布密度函数图像。
(2)本门课程与实验的相关内容
本实验与教材中第二章“随机变量及其分布”相关,通过Matlab中的函数来绘制第二章中学过的几种重要的连续型随
机变量概率密度函数图像。
(3)实验目的
通过本实验学习一些经常使用的统计数据的作图命令,提高进行实验数据处理和作图分析的能力。
2、实验设计总体思路
2.1、引论
利用教材中的相关知识,通过Matlab来绘制正态分布、指数分布、均匀分布密度函数图像,从而加深对概率统计知识的理解,并提高进行实验数据处理和作图分析的能力。
2.2、实验主题部分
2.2.1、实验设计思路
1、理论分析
(1)参数为μ和σ2的正态分布的概率密度函数是:
可以用函数normpdf计算正态分布的概率密度函数值,调用格式:y=normpdf(x, mu, sigma) %输入参数可以是标量、向量、矩阵。
(2)参数为μ的指数分布的概率密度函数是:
可以用函数exppdf计算指数分布的概率密度函数值,调用格式:y=exppdf(x, mu) %输入参数可以是标量、向量或矩阵。
(3)参数为a, b的均匀分布的概率密度函数是:
可以用函数exppdf计算均匀分布的概率密度函数值,调用格式:y=unifpdf(x, a, b) %输入参数可以是标量、向量、矩阵。
最后调用plot函数绘制图像。
2、实现方法
(1)x=a:0.1:b %将区间[a,b]以0.1为步长等分, 赋给变量x。
(2)通过调用函数normpdf、exppdf、unifpdf分别计算出对应的概
率密度函数。
(3)调用函数plot绘制图像。
2.2.2、实验结果及分析
绘制分别服从均值是0, 标准差分别是0.5,1, 1.5的正态分布概率密度函数图像:
绘制分别服从参数μ为0.5 ,1,2的指数分布概率密度函数图像:
绘制分别服从参数a,b分别为1,2;0.5,2.5;0.2,2.8的均匀分布概率密度函数图像
2.2.3、程序及其说明
%%正态分布
x=-5:0.1:5;
y1=normpdf(x, 0, 0.5);
y2=normpdf(x, 0, 1);
y3=normpdf(x, 0,1.5);
plot(x, y1, 'r-', x, y2, 'g-', x, y3, 'b-') %yn是服从期望为0,方差为σn的正态分布的密度函数
title('正态分布概率密度图像(红:σ=0.5;绿:σ=1;蓝:σ=1.5)')
%%指数分布
x=0:0.1:5;
y1=exppdf(x,0.5);
y2=exppdf(x,1);
y3=exppdf(x,2);
plot(x, y1, 'r-', x, y2, 'g-', x, y3, 'b-') %yn是服从参数为μn的指数分布的密度函数
title('指数分布概率密度图像(红:μ=0.5;绿:μ=1;蓝:μ=2)')
%%均匀分布
x=0:0.0001:5;
y1=unifpdf(x, 1, 2);
y2=unifpdf(x, 0.5, 2.5);
y3=unifpdf(x, 0.2, 2.8);
plot(x, y1, 'r-', x, y2, 'g-', x, y3, 'b-') %yn是区间为[0,5]的均匀分布的密度函数
title('均匀分布概率密度图像(红:1,2;绿:0.5,2.5;蓝:0.2,2.8)') 2.3、对教材正文的深入理解和创新性说明
2.3.1、对教材正文的深入理解
通过本次试验加深对概率密度函数的理解,特别是概率密度的相关性质的理解,比如:f(x)≥0等,可以从图像中直观的反映出来。
2.3.2、对论文中探索性内容或创新点说明
2.4、体会
体会:
通过本次实验基本掌握了MATLAB软件的关于统计作图的基本操作,会进行常用的概率密度函数的作图,提高了观察实验现象或处理数据方面的能力。
通过本次实验,使我觉得要想掌握课堂上所学的知识结合实践是极为关键的。
同时,实验还可以加深我们对于书中一些抽象的概念的理解,也能增加学生的兴趣。
建议:
由于进入大二以来课时多,时间繁忙,所以我认为自己对于本次实验准备的还是不够充足,感觉还有很多东西需要去探索,但同时也激发了我对概率论的兴趣。
让我意识到实践对于学习的重要性,希望学校能多搞一些实践性的实验,作为课堂理论知识的拓展。