驻波 东北大学 大学物理

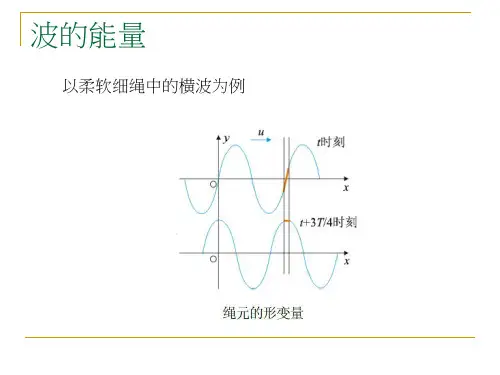
以柔软细绳中的横波为例
⏹波的能量密度w:波传播时,单位体积介质中所
储存的波的能量.
⏹波的能流密度I:波传播时,单位时间内通过垂
直于波的传播方向单位面积的
体积介质中所波的能量.
⏹对于简谐波,两者关系为:I=uw
简谐波的能量密度和能流密度
⏹机械波的平均能量密度和平均能流密度:
都与振幅平方成正比,与频率平方成正比.
⏹电磁波的平均能量密度和平均能流密度:
都与振幅平方成正比,与频率无关.
⏹在介质中任意一点,简谐机械波的动能与势能都是同相位振动的;在真空中传播的简谐电磁波的电场能和磁场能在任意一点都是同相位振动的.
波的叠加原理
当几列波在介质中某点相遇时,该点的振动位移是各列波单独存在时在该点引起的位移的叠加
波的叠加原理举例驻波(standing waves)
122cos cos x y y y A t u
ωω=+=1cos ()x y A t u ω=-2cos ()x y A t u
ω=+
驻波
⏹形成驻波的条件:两列简谐波
✓频率相同;
✓振幅相同;
✓振动方向相同;
✓在同一媒介中相向传播,叠加而形成逐波.⏹驻波的现象:
✓相邻波节(或波腹)的间距为二分之一波长;✓相邻波节与波腹的间距为四分之一波长;
✓相邻两波节之间各点(称为一段)同相位振动;✓相邻两段的振动相位差为π.
驻波举例
位于A,B两点的两个简谐波源的振幅相同,频率都是100Hz,相位差为π.若A,B相距30m,波速为400m/s,求AB连线上因叠加而静止的各点的位置.
波的叠加原理举例驻波(standing waves)
拍(beats)。

第9章 振动 作 业一、教材：选择填空题 １~5；计算题:13，14,１8 二、附加题 （一)、选择题1、一沿x 轴作简谐振动的弹簧振子，振幅为A ，周期为T ,振动方程用余弦函数表示，如果该振子的初相为π34,则ｔ＝０时,质点的位置在:D(A)过A x 21=处，向负方向运动； (B) 过A x 21=处,向正方向运动;(C ）过A x 21-=处，向负方向运动； (D)过A x 21-=处，向正方向运动。

2、一质点作简谐振动,振动方程为:ｘ＝A ｃｏs(ωt ＋φ ）在t=T/2（T 为周期)时刻,质点的速度为:B(A ） sin A ωϕ-. (B ） sin A ωϕ. （C) cos A ωϕ-. (D)cos A ωϕ.3、一质点沿x 轴做简谐运动,振动方程为:21410cos(2)3x t ππ-=⨯+。

从t = ０时刻起,到x =-2c ｍ处，且向x 轴正方向运动的最短时间间隔为:C (A)1s 8. (Ｂ) 1s 4. (Ｃ) 1s 2. （D) 1s 3. （Ｅ） 1s 6. (二）、计算题1、一物体沿x 轴做简谐运动,振幅Ａ = ０.12m ，周期Ｔ = 2s.当t = 0时,物体的位移x 0= ０.０６ｍ,且向x 轴正向运动．求:（１）此简谐运动的运动方程;(2)ｔ = T ／４时物体的位置、速度和加速度;解:(1）0.12cos 3x t ππ⎛⎫=- ⎪⎝⎭m（2)0.12sin 3v t πππ⎛⎫=-- ⎪⎝⎭m ／s 20.12cos 3a t πππ⎛⎫=-- ⎪⎝⎭m ／ｓ2 t = Ｔ／4时0.12cos 0.106x π==≈m0.12sin0.060.196v πππ=-=-≈-ｍ/s20.12cos 0.06 1.026a πππ=-=-≈-m ／s 22、一物体沿x 轴做简谐运动,振幅A = 10.0cm,周期T ＝ 2.０ｓ.当t ＝ 0时，物体的位移x 0= -５cm ，且向x 轴负方向运动．求：(1)简谐运动方程;(2）t = 0.5ｓ时,物体的位移;（3)何时物体第一次运动到x = 5ｃm 处?(4)再经过多少时间物体第二次运动到x = 5ｃm 处?解:(１)20.1cos 3x t ππ⎛⎫=+⎪⎝⎭ｍ(2）t = 0.5ｓ时,270.1cos 0.1cos 0.087236x πππ⎛⎫=+=≈- ⎪⎝⎭m (3)利用旋转矢量法，第一次运动到x =5ｃm 处，相位是15233t πππ=+所以11t =s(３）利用旋转矢量法，第二次运动到x =5ｃm 处,相位是27233t πππ=+所以253t =s 215210.6733t t t s ∆=-=-==３、若简谐振动方程为m ]4/20cos[1.0ππ+=t x ,求：（1）振幅、频率、角频率、周期和初相；（2)t =2s 时的位移、速度和加速度．解：(１）可用比较法求解．据]4/20cos[1.0]cos[ππϕω+=+=t t A x得:振幅0.1A m =,角频率20/rad s ωπ=,频率1/210s νωπ-==, 周期1/0.1T s ν==,/4rad ϕπ=(2）2t s =时，振动相位为:20/4(40/4)t rad ϕππππ=+=+ 据cos x A ϕ=，sin A νωϕ=-,22cos a A x ωϕω=-=-得20.0707, 4.44/,279/x m m s a m s ν==-=-4、如图所示，质量为10g 的子弹以1000m ．s －1的速度射入木块并嵌在木块中,并使弹簧压缩从而作简谐振动，若木块质量为4.99kg ，弹簧的劲度系数31810N m -⨯⋅，求振动的振幅。

大学物理驻波（一）引言概述：驻波是在介质中传播的波在与逆向传播的波相遇时形成的一种特殊波动现象。

它在大学物理中有着重要的应用和理论意义。

本文将从驻波的基本概念和特点入手，详细介绍了驻波的形成条件，驻波的数学描述以及驻波的实验观察等。

正文：1. 驻波的基本概念和特点- 驻波是由两个相同频率、振幅相等而方向相反的波在空间中相遇而形成的。

- 驻波的震动节点是固定不动的，而虚节点一直在不断地交替出现。

- 驻波是由于波的干涉而形成的，不会传输能量或物质。

2. 驻波的形成条件- 驻波形成的必要条件是波的传播速度相同，波长相等且频率相同。

- 在一维情况下，驻波形成的充分条件是两波的幅值、频率、相位相同。

3. 驻波的数学描述- 驻波可以用数学方程来描述，常用的方程为y(x,t) = Acos(kx)cos(ωt + φ)，其中A为振幅，k为波数，ω为角频率，φ为初相位。

- 驻波方程中的k和ω与波长λ和周期T之间有着确定的关系：k = 2π/λ，ω = 2π/T。

4. 驻波的实验观察- 驻波可以通过在一定条件下的波的传播介质中观察到，如绳上的驻波、声管中的驻波等。

- 在实验观察中，可以通过调节波的频率、振幅、传播介质的长度等参数来观察驻波的形成与特性。

5. 驻波的应用- 驻波在声学、光学、电磁学以及其他物理学领域中有着广泛的应用，如乐器共鸣现象、干涉仪的工作原理等。

- 驻波还可以用于测量波的参数，如测量波速、波长等。

总结：驻波是在介质中传播的波在与逆向传播的波相遇时形成的一种特殊波动现象。

它具有震动节点固定、虚节点不断交替出现的特点，是由波的干涉形成的。

驻波的形成需要满足波的传播速度相等、波长相等且频率相同的条件。

驻波可以通过实验观察到，并可用数学方程进行描述，有着广泛的应用价值。

大学物理驻波实验报告一、实验目的1、观察弦线上驻波的形成，了解驻波的特点和规律。

2、测量弦线振动的频率、波长和波速，验证驻波的相关理论。

3、掌握利用驻波测量物理量的实验方法和数据处理技巧。

二、实验原理当两列振幅相同、频率相同、传播方向相反的简谐波在同一直线上相向传播时，叠加形成驻波。

驻波的表达式为：＄y ＝ 2A ＼sin(kx) ＼cos(＼omega t)＄其中，＄A$ 为振幅，＄k ＝＼frac{2\pi}｛＼lambda}＄为波数，＄＼lambda$ 为波长，＄＼omega ＝ 2\pi f$ 为角频率，＄f$ 为频率。

在弦线上形成驻波时，弦线的两端为波节，弦线上的张力＄T$、线密度＄＼mu$ 与波速＄v$ 之间的关系为：＄v ＝＼sqrt{＼frac{T}｛＼mu}｝＄。

又因为＄v ＝＼lambda f$ ，所以可以通过测量弦线的张力、线密度、振动频率和波长来研究驻波的特性。

三、实验仪器弦音计、砝码、米尺、电子天平、信号发生器等。

四、实验步骤1、安装实验仪器将弦线的一端固定在弦音计的可移动刀口上，另一端通过砝码盘悬挂一定质量的砝码，以提供弦线的张力。

调整弦音计的位置，使弦线处于水平状态。

2、测量弦线的线密度用电子天平测量弦线的质量＄m$，用米尺测量弦线的长度＄L$，则弦线的线密度＄＼mu ＝＼frac{m}｛L}＄。

3、调节信号发生器的频率打开信号发生器，调节输出频率，使弦线产生振动。

观察弦线上的振动情况，当出现稳定的驻波时，记录此时信号发生器的频率＄f$ 。

4、测量驻波的波长通过移动弦音计的可移动刀口，改变弦线的长度，使弦线上出现不同阶数的驻波。

记录相邻两个波节之间的距离，即为半波长＄＼frac{＼lambda}｛2}＄。

测量多个数据，计算波长的平均值。

5、改变弦线的张力在砝码盘中增加或减少砝码，改变弦线的张力，重复步骤 3 和 4，测量不同张力下的频率和波长。

五、实验数据记录与处理1、弦线的线密度测量弦线质量＄m ＝＿____$ g，弦线长度＄L ＝＿____$ m，弦线的线密度＄＼mu ＝＼frac{m}｛L} ＝＿____$ kg/m。

大学物理驻波实验报告大学物理驻波实验报告引言：驻波是物理学中一个重要的现象，它在很多领域都有广泛的应用。

本次实验旨在通过观察和测量驻波的特性，深入了解驻波现象及其相关的物理原理。

实验目的：1. 理解驻波的定义和基本特性；2. 学习使用仪器测量驻波的参数；3. 掌握驻波的数学表达式及其物理解释。

实验原理：驻波是由两个同频率、同振幅的相向传播的波叠加形成的。

当两个波相遇时，它们会相互干涉，形成驻波。

在一维情况下，驻波的表达式为y(x, t) = 2Asin(kx)sin(ωt)，其中A为振幅，k为波数，x为位置，ω为角频率。

实验装置：1. 信号发生器：用于产生驻波的信号；2. 波形发生器：用于产生驻波所需的波形；3. 波形显示器：用于观察和测量驻波的参数；4. 测量工具：如尺子、计时器等。

实验步骤：1. 将信号发生器和波形发生器连接，并设置相同的频率和振幅；2. 将波形发生器的输出连接到波形显示器，并调整显示器的位置和角度，以便观察到驻波的现象；3. 通过调节波形发生器的相位差，观察驻波的变化，并记录下相应的数据；4. 使用尺子测量波形显示器上相邻两个节点（波峰或波谷）之间的距离，并记录下来；5. 重复步骤3和步骤4，直到获得足够的数据。

实验结果与分析：通过实验观察和测量，我们得到了一系列驻波的数据。

根据这些数据，我们可以计算出驻波的波长、频率和相速度等参数。

首先，我们可以通过测量相邻两个节点之间的距离来计算驻波的波长。

根据驻波的定义，相邻两个节点之间的距离应该等于波长的一半。

因此，我们可以将测得的距离乘以2，得到驻波的波长。

其次，我们可以通过测量信号发生器的频率和波长，计算出驻波的频率。

根据频率的定义，频率等于波速除以波长。

由于我们已经测得了波长，所以可以将波速除以波长，得到驻波的频率。

最后，我们可以通过测量两个相邻节点之间的时间间隔，计算出驻波的相速度。

相速度定义为波长除以周期。

由于周期等于时间间隔的倒数，所以可以将波长除以时间间隔，得到驻波的相速度。

一、 填空题1．已知某简谐运动的振动曲线如图所示， 则此简谐运动的运动方程为 __________________。

2. 一声源以20m/s 的速率向静止的观察者运动，观察者接收到声波的频率是1063Hz,则该声源的 振动频率为 Hz .(声速为:340m/s)3． 在驻波中，两个相邻波节之间各质点的振动相位___ _____ 。

4．一束光强为I 0的自然光依次通过三个偏振片P 1、P 2、P 3，其中P 1与P 3的偏振化方向相互垂直，P 2与P 3的偏振化方向之间的夹角为450，则通过三个偏振片后透射光强为_________________________。

5．一容器内储有氧气（视为理想气体），其压强为1.01×10 5 Pa ，温度为27 0C ，则氧气系统的分子数密度为_251044.2⨯__3m - ；氧分子的平均平动动能为_______J 。

6．1mol 理想气体由平衡态1（P 1，V 1，T ）经一热力学过程变化到平衡态2（P 2，V 2，T )，始末状态温度相同，此过程中的系统熵变△S = S 2－S 1 = ________ 。

7．在描述原子内电子状态的量子数l m l n ,,中，当4=l 时，n 的最小可能取值为___________。

8．在康普顿效应实验中，波长为0λ的入射光子与静止的自由电子碰撞后反向弹回，而散射光子的波长为λ，反冲电子获得的动能为 ______ 。

9．激光与普通光源所发出的光相比具有方向性好、单色性好、 和能量集中的特性。

二、 选择题（单选题，每小题2分，共10分）（将正确答案前的字母填写到右面的【 】中）1．当质点以频率ν作简谐运动时，它的动能变化频率为 【 】（A ）2/ν （B ）ν （C ）ν22．处于平衡态的一瓶氦气和一瓶氮气(均可视为理想气体)的分子数密度相同，分子的平均平动动能也相同，则它们 【 】 （A ）温度，压强均不相同 （B ）温度相同但压强不同 （C ）温度，压强都相同3．下列物体哪个是绝对黑体 【 】 （A ）不能反射任何光线的物体 （B ）不辐射任何光线的物体 （C ）不辐射可见光的物体4．以下说法正确的是： 【 】 （A ）任何过程总是沿着熵增加的方向进行； （B ）自然界中的一切自发过程都是不可逆的； （C ）不可逆过程就是不能向相反方向进行的过程；5．一束自然光自空气射向一块平板玻璃，如图： 【 】 设入射角等于布儒斯特角，则在界面2的反射光 （A ）是自然光； （B ）是部分偏振光；（C ）是线偏振光且光矢量的振动方向垂直于 入射面。