和与积的奇偶性 课件
- 格式：pptx
- 大小：103.49 KB
- 文档页数：17
下载文档原格式
合集下载
和与积的奇偶性
和与积的奇偶性一、创设情境，引发探究 1、回顾激活。
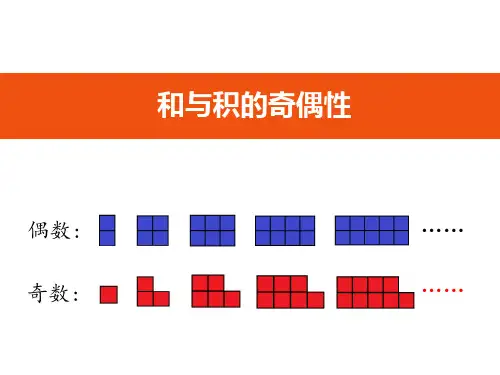
提问：我们已经认识了奇数和偶数。
想一想，奇数和偶数各有什么特点？说明：自然数按是不是2的倍数分为奇数和偶数两类。
是2的倍数就是偶数，不是2的倍数就是奇数。
2、创设问题情境。
出示：1+3+5+……+29。
提问：如果不计算，你能直接判断1+3+5+……+29的和是奇数还是偶数吗？你是怎么想的？引导：研究算式的和是奇数还是偶数，是和的奇偶性问题。
（板书：奇偶性）这里加数比较多，又都是奇数，得数到底是怎样的数呢？如果加数更多会怎样呢？这样的计算有没有什么规律呢？像这样复杂的问题，我们可以从简单的问题入手开始研究，看看有没有什么规律。
（板书：解决复杂的问题从简单入手）二、主动探究，发现规律 1、探究两个数和的奇偶性。
（1）引导：现在，我们从最简单的开始，先研究两个数相加的和是奇数还是偶数，大家自己举例看一看：每次任意选几个不是0的自然数，算出它们的和，填在表格里，看看和是奇数还是偶数。
生自己举例后，与同桌交流自己的发现。
集体交流：仔细观察、比较得数和算式，想一想两个数相加，什么情况下和是奇数？什么情况下和是偶数？看一看，自己的计算结果符合刚才交流的结论吗？小结：刚才我们研究了两个数的和的奇偶性情况，通过举例子，再观察比较，发现两个数相加的和的奇偶性，与加数是奇数还是偶数有关。
如果一个奇数加一个偶数，和是奇数；两个偶数或两个奇数相加，和是偶数。
（板书：一个奇数加一个偶数，和是奇数两个偶数或两个奇数相加，和是偶数）（2）判断：任意打开数学书，左右两边页码的和是奇数还是偶数？为什么是奇数？追问：任意两个自然数相加，和是奇数还是偶数？为什么？说明：两个加数中只有一个奇数，和是奇数。
2、探究几个数连加的和的奇偶性。
（1）引导：我们已经发现了两个不是0的自然数的和的奇偶性的特征。
那要是任意3个、4个，或5个以上的不是0的自然数连加，和是奇数还是偶数呢？请大家分别选几个写成连加算式，填在表格里。
和与积的奇偶性
苏教版数学五年级（下册）
和与积的奇偶性
灌云县杨集中心小学 徐洪玲
81+3+675+7+8+11+814+19
？ +15+121= ？ 81×3×675×7×8×11×814
×19×15×121=
探究一：
任意选两个不是0的自然数，求出它 们的和，再看看和是奇数还是偶数。
加数
加数
和
和是奇数 还是偶数
3 5 1 2 4
加数中偶 和的奇 数的个数 偶性
1
奇数
2
奇数
2
奇数
3
偶数
2
偶数
和是奇数还是偶数，与加 数中奇数的个数有什么关系？
算式
1+3+4+5=13 2+3+7+3+6+5+3=29 2+3+4=9 1+8+2+9+4=24 2+3+5+1+3+2=16
加数中奇 数的个数
3 5 1 2 4
加数中偶 和的奇 数的个数 偶性
加数中偶 和的奇 数的个数 偶性
1
奇数
2
奇数
2
奇数
3
偶数
2
偶数
1+2+3+4+5+6+7+8+9+10 奇数 和是奇数还是偶数？为什么？
1+2+3+4+5+6+......+99+100 偶数 和是奇数还是偶数？为什么？
1+3+5+7+9+......+99 偶数 和是奇数还是偶数？为什么？
和与积的奇偶性
灌云县杨集中心小学 徐洪玲
81+3+675+7+8+11+814+19
？ +15+121= ？ 81×3×675×7×8×11×814
×19×15×121=
探究一：
任意选两个不是0的自然数，求出它 们的和，再看看和是奇数还是偶数。
加数
加数
和
和是奇数 还是偶数
3 5 1 2 4
加数中偶 和的奇 数的个数 偶性
1
奇数
2
奇数
2
奇数
3
偶数
2
偶数
和是奇数还是偶数，与加 数中奇数的个数有什么关系？
算式
1+3+4+5=13 2+3+7+3+6+5+3=29 2+3+4=9 1+8+2+9+4=24 2+3+5+1+3+2=16
加数中奇 数的个数
3 5 1 2 4
加数中偶 和的奇 数的个数 偶性
加数中偶 和的奇 数的个数 偶性
1
奇数
2
奇数
2
奇数
3
偶数
2
偶数
1+2+3+4+5+6+7+8+9+10 奇数 和是奇数还是偶数？为什么？
1+2+3+4+5+6+......+99+100 偶数 和是奇数还是偶数？为什么？
1+3+5+7+9+......+99 偶数 和是奇数还是偶数？为什么？
苏教版五下和与积的奇偶性
偶数的特点：
是2的倍数，个位上的数字是2、4、6、8、0。
奇数的特点： 不是2的倍数，个位上的数字是1、3、5、7、9.
探索与发现
偶数+偶数=偶数 奇数+奇数=偶数 奇数+偶数=奇数
讨论： 1、你写的连加算式中，有几个加数是偶数？有 几个加数是奇数？ 2、和是奇数还是偶数，与加数中奇数的个数有 什么关系？
思维训练
一班学生，人数在30至5，总是有一行少1个人， 这班学生有多少人？
解决问题 1、有50个梨,75个橘子和100个苹 果,要把这些水果平均放在若干个 袋子里,并且每个袋里的三 种水果 的个数也相等,最多可以装几袋?每 袋中梨子,橘子和苹果各是几个?
2、两个连续偶数的积是224，这两个数分 别是多少？它们的最小公倍数是多少？最 大公因数是多少？
练习
一、求出每组数的最大公因数 和最小公倍数： 14和30 18、16 和19 25 15和50
1+2+3+……+29和是奇数还 是偶数？
解决复杂问题要从简单入手，寻 找规律解决复杂问题。找规律时， 可以先举出一类例子，再观察、 比较，找找有什么特点，从中发 现规律，从而解决复杂问题。
1×2×3×……×99的积是奇 数还是偶数？你能直接判断吗？
乘数都是奇数，积是奇数；乘数 中只要有一个偶数，积就是偶数。
是2的倍数，个位上的数字是2、4、6、8、0。
奇数的特点： 不是2的倍数，个位上的数字是1、3、5、7、9.
探索与发现
偶数+偶数=偶数 奇数+奇数=偶数 奇数+偶数=奇数
讨论： 1、你写的连加算式中，有几个加数是偶数？有 几个加数是奇数？ 2、和是奇数还是偶数，与加数中奇数的个数有 什么关系？
思维训练
一班学生，人数在30至5，总是有一行少1个人， 这班学生有多少人？
解决问题 1、有50个梨,75个橘子和100个苹 果,要把这些水果平均放在若干个 袋子里,并且每个袋里的三 种水果 的个数也相等,最多可以装几袋?每 袋中梨子,橘子和苹果各是几个?
2、两个连续偶数的积是224，这两个数分 别是多少？它们的最小公倍数是多少？最 大公因数是多少？
练习
一、求出每组数的最大公因数 和最小公倍数： 14和30 18、16 和19 25 15和50
1+2+3+……+29和是奇数还 是偶数？
解决复杂问题要从简单入手，寻 找规律解决复杂问题。找规律时， 可以先举出一类例子，再观察、 比较，找找有什么特点，从中发 现规律，从而解决复杂问题。
1×2×3×……×99的积是奇 数还是偶数？你能直接判断吗？
乘数都是奇数，积是奇数；乘数 中只要有一个偶数，积就是偶数。
和与积的奇偶性 (1)
加数
加数
和
和是奇数还是偶数
奇数+奇数=（ 偶 ）数
Hale Waihona Puke 偶数+偶数=（ 偶 ）数
奇数+偶数=（ 奇 ）数
想一想：
1、任意打开数学书， 左、右两边页码 的和是奇数还是偶数？
2、任意两个相邻自然数的和是奇数还 是偶数？为什么？
任意选3个、4个，甚至更多个非0的 自然数，写成连加算式，写在练习本上。 先想想和是奇数还是偶数，再通过计算 验证自己的猜想。
1+3+5+7+……+29的和是奇数还是 偶数？为什么？
任意选2个、3个、4个，甚至更多个非 0的自然数，在练习本上写出乘法算式求出 它们的积，再看看积是奇数还是偶数,写在 算式的右边。
算 式 积是奇数 还是偶数
2个数相乘
3个或4个数连乘 更多个数连乘
小组交流：
你能把同学们写的算式按积是奇数 还是偶数分成两类吗? 再分类观察和比 较，并说说自己的发现。
奇数×奇数=（ 奇 ）数 奇数×偶数=（ 偶 ）数 偶数×偶数=（ 偶 ）数 几个数相乘，乘数都是奇数，积 一定是奇数；乘数中只要有一个是偶 数，积一定是偶数。
81×3×675×7×8×11×814×19×121 的积是奇数还是偶数？
1、这节课我们探索了什么？说说都发 现了什么？ 2、通过今天的探索，你们学会了发现 规律的方法了吗？
在加法和乘法中，我们找到了 和与积的奇偶性，那其它的运算中 也有一定的规律吗？
苏教版五年级数学下册
想一想： 奇数和偶数各有什么特征？
快速抢答：
判断下列数是奇数，还是偶数。
1 778
99
3455
70
《函数的奇偶性》函数 PPT教学课件
∴f(x)是偶函数.
解:(1)∵由
课堂篇
探究学习
探究一
探究二
探究三
(4)设 f(x)=(x-2)
∵由
+2
-2
≥ 0,
思维辨析
当堂检测
+2
.
-2
得 x≤-2 或 x>2,
-2 ≠ 0,
∴函数的定义域为(-∞,-2]∪(2,+∞),
不关于原点对称.
∴f(x)=(x-2)
+2
既不是奇函数也不是偶函数.
课前篇
自主预习
一
二
3.做一做
(1)下列函数是偶函,2]
B.y=x3-x2
C.y=x3
D.y=x2,x∈[-1,0)∪(0,1]
答案:D
(2)下列函数中,既是奇函数又是减函数的为(
A.y=x-1
B.y=3x2
1
C.y=2
答案:D
D.y=-x|x|
)
课前篇
探究三
思维辨析
当堂检测
4.已知函数f(x)是定义在R上的偶函数,当x∈(-∞,0)时,f(x)=x-x4;当
x∈(0,+∞)时,f(x)=
.
解析:方法一:由于是填空题,故可采用直接代换法,将x用-x代替,
D.f(x)=x2+x4
答案:AD
当堂检测
)
课堂篇
探究学习
探究一
探究二
探究三
思维辨析
当堂检测
2.有下列说法:
①偶函数的图像一定与y轴相交;
②若y=f(x)是奇函数,则由f(-x)=-f(x)可知f(0)=0;
③既是奇函数也是偶函数的函数一定是f(x)=0,x∈R;
解:(1)∵由
课堂篇
探究学习
探究一
探究二
探究三
(4)设 f(x)=(x-2)
∵由
+2
-2
≥ 0,
思维辨析
当堂检测
+2
.
-2
得 x≤-2 或 x>2,
-2 ≠ 0,
∴函数的定义域为(-∞,-2]∪(2,+∞),
不关于原点对称.
∴f(x)=(x-2)
+2
既不是奇函数也不是偶函数.
课前篇
自主预习
一
二
3.做一做
(1)下列函数是偶函,2]
B.y=x3-x2
C.y=x3
D.y=x2,x∈[-1,0)∪(0,1]
答案:D
(2)下列函数中,既是奇函数又是减函数的为(
A.y=x-1
B.y=3x2
1
C.y=2
答案:D
D.y=-x|x|
)
课前篇
探究三
思维辨析
当堂检测
4.已知函数f(x)是定义在R上的偶函数,当x∈(-∞,0)时,f(x)=x-x4;当
x∈(0,+∞)时,f(x)=
.
解析:方法一:由于是填空题,故可采用直接代换法,将x用-x代替,
D.f(x)=x2+x4
答案:AD
当堂检测
)
课堂篇
探究学习
探究一
探究二
探究三
思维辨析
当堂检测
2.有下列说法:
①偶函数的图像一定与y轴相交;
②若y=f(x)是奇函数,则由f(-x)=-f(x)可知f(0)=0;
③既是奇函数也是偶函数的函数一定是f(x)=0,x∈R;
《和与积的奇偶性》公开课件教学课件
奇数乘偶数结果为偶数
任何奇数与一个偶数相乘，结果仍为偶 数。例如，3x4=12，12是偶数。
特殊数字积的奇偶性
0的积的奇偶性
任何数字与0相乘，结ຫໍສະໝຸດ 都为0，即 0是唯一的偶数。1的积的特殊性
任何数字与1相乘，结果都等于原 数字，即1既不是奇数也不是偶数 。
04
和与积的奇偶性在数学中的应用
在代数中的应用
积的奇偶性
两个整数相乘结果的奇偶性取决于两个乘数的奇偶 性。
教学目标
掌握判断整数和与积的 奇偶性的方法。
通过实例分析，培养学 生的数学思维和逻辑推 理能力。
激发学生对数学的兴趣 和好奇心，提高其自主 学习和探究能力。
理解奇偶性的概念及其 在整数中的表现。
02
和的奇偶性
偶数和的性质
80%
偶数和的定义
03
积的奇偶性
偶数积的性质
偶数乘偶数结果为偶数
任何偶数与另一个偶数相乘，结果仍为偶数。例如，2x4=8，8是偶 数。
偶数乘奇数结果为偶数
任何偶数与一个奇数相乘，结果仍为偶数。例如，2x5=10，10是偶 数。
奇数积的性质
奇数乘奇数结果为奇数
任何奇数与另一个奇数相乘，结果仍 为奇数。例如，3x7=21，21是奇数。
请证明以下结论：如果两个整数a和b满足a+b为偶数，那么a和b 的奇偶性必须相同。
进阶练习题2
请证明以下结论：如果两个整数a和b满足a*b为偶数，那么a和b中 至少有一个数为偶数。
进阶练习题3
请举出一些整数，使得它们的和为偶数，积为奇数。
思考题
思考题1
请思考整数和与积的奇偶性之间的关系，并尝试 总结规律。
《和与积的奇偶性》公开课件 教学课件
任何奇数与一个偶数相乘，结果仍为偶 数。例如，3x4=12，12是偶数。
特殊数字积的奇偶性
0的积的奇偶性
任何数字与0相乘，结ຫໍສະໝຸດ 都为0，即 0是唯一的偶数。1的积的特殊性
任何数字与1相乘，结果都等于原 数字，即1既不是奇数也不是偶数 。
04
和与积的奇偶性在数学中的应用
在代数中的应用
积的奇偶性
两个整数相乘结果的奇偶性取决于两个乘数的奇偶 性。
教学目标
掌握判断整数和与积的 奇偶性的方法。
通过实例分析，培养学 生的数学思维和逻辑推 理能力。
激发学生对数学的兴趣 和好奇心，提高其自主 学习和探究能力。
理解奇偶性的概念及其 在整数中的表现。
02
和的奇偶性
偶数和的性质
80%
偶数和的定义
03
积的奇偶性
偶数积的性质
偶数乘偶数结果为偶数
任何偶数与另一个偶数相乘，结果仍为偶数。例如，2x4=8，8是偶 数。
偶数乘奇数结果为偶数
任何偶数与一个奇数相乘，结果仍为偶数。例如，2x5=10，10是偶 数。
奇数积的性质
奇数乘奇数结果为奇数
任何奇数与另一个奇数相乘，结果仍 为奇数。例如，3x7=21，21是奇数。
请证明以下结论：如果两个整数a和b满足a+b为偶数，那么a和b 的奇偶性必须相同。
进阶练习题2
请证明以下结论：如果两个整数a和b满足a*b为偶数，那么a和b中 至少有一个数为偶数。
进阶练习题3
请举出一些整数，使得它们的和为偶数，积为奇数。
思考题
思考题1
请思考整数和与积的奇偶性之间的关系，并尝试 总结规律。
《和与积的奇偶性》公开课件 教学课件
苏教版数学五年级下册《和与积的奇偶性》说课稿(附反思、板书)课件
《和与积的奇偶性》说课
苏教版小学数学五年级下册
大家好，今天我说课的内容是苏教版小学数学五年 级下册《因数和倍数》单元的探索规律活动《和与积的 奇偶性》。下面我将从说教材、说学情、说教学目标、 说教学重难点、说教法、说教学过程和板书设计及教学 反思这八个方面展开。接下来开始我的说课。恳请大家 批评指正。
一、说教材
《和与积的奇偶性》是苏教版数学五年级下册《因数和倍数》 的探索计算规律的活动。本课是在学生已经认识奇数、偶数、质数、 合数等概念，并在已经积累较多探索数的特征的活动经验的基础上 安排的。通过活动，一方面能使学生感受数学规律的多样性和趣味 性，感受数学知识之间的广泛联系；另一方面则有利于他们从新的 角度进一步丰富对奇数、偶数的认识，从而提升数学思考的水平。
二、说教学目标
1. 尝试运用举例和验证等方法探索和与积的奇偶性,逐步掌握发现规 律的方法。 2. 经历探索加法与乘法中数的奇偶性变化的过程,在活动中发现计算 中数的奇偶性的变化规律,在活动中体验研究方法,提高推理能力。 3. 在学习“和与积的奇偶性”的活动中,能组织学生积极参与数学学 习活动,用我的情感塑造学生的情感。
总之，在整个教学过程中，我始终立足让学生在玩中学会， 在动手中提高技能，学生学得轻松愉快。我将继续努力，让 我的数学课堂教学更高效，更精彩。
八、教学反思
1. 创设问题情境,激发学生学习兴趣。创设问题情境的目的在于 上课时创设一种学生探索的氛围,以激发学生的学习兴趣,为学生 提供自我表现的机会,培养学生的问题意识,根据小学生对实物、 色彩、游戏更感兴趣的特点,我设计了游戏活动引入教学。在几 个学生试过之后,同学们的学习情绪逐步高涨。这时,学生就会产 生一种疑问,教师抓住学生好奇的时机,充分肯定学生的提问,表扬 他们问题提得好,有思考价值,让学生尝到成功的喜悦。
苏教版小学数学五年级下册
大家好，今天我说课的内容是苏教版小学数学五年 级下册《因数和倍数》单元的探索规律活动《和与积的 奇偶性》。下面我将从说教材、说学情、说教学目标、 说教学重难点、说教法、说教学过程和板书设计及教学 反思这八个方面展开。接下来开始我的说课。恳请大家 批评指正。
一、说教材
《和与积的奇偶性》是苏教版数学五年级下册《因数和倍数》 的探索计算规律的活动。本课是在学生已经认识奇数、偶数、质数、 合数等概念，并在已经积累较多探索数的特征的活动经验的基础上 安排的。通过活动，一方面能使学生感受数学规律的多样性和趣味 性，感受数学知识之间的广泛联系；另一方面则有利于他们从新的 角度进一步丰富对奇数、偶数的认识，从而提升数学思考的水平。
二、说教学目标
1. 尝试运用举例和验证等方法探索和与积的奇偶性,逐步掌握发现规 律的方法。 2. 经历探索加法与乘法中数的奇偶性变化的过程,在活动中发现计算 中数的奇偶性的变化规律,在活动中体验研究方法,提高推理能力。 3. 在学习“和与积的奇偶性”的活动中,能组织学生积极参与数学学 习活动,用我的情感塑造学生的情感。
总之，在整个教学过程中，我始终立足让学生在玩中学会， 在动手中提高技能，学生学得轻松愉快。我将继续努力，让 我的数学课堂教学更高效，更精彩。
八、教学反思
1. 创设问题情境,激发学生学习兴趣。创设问题情境的目的在于 上课时创设一种学生探索的氛围,以激发学生的学习兴趣,为学生 提供自我表现的机会,培养学生的问题意识,根据小学生对实物、 色彩、游戏更感兴趣的特点,我设计了游戏活动引入教学。在几 个学生试过之后,同学们的学习情绪逐步高涨。这时,学生就会产 生一种疑问,教师抓住学生好奇的时机,充分肯定学生的提问,表扬 他们问题提得好,有思考价值,让学生尝到成功的喜悦。
和与积的奇偶性课件
《和与积的奇偶性课件ppt》xx年xx月xx日•引言•和的奇偶性•积的奇偶性•例子目•结论录01引言和与积的奇偶性是数学中的重要概念，是进一步学习数论和代数的基础。
学生在学习该课程之前已经了解整数和基本运算性质。
课程背景让学生掌握和与积的奇偶性基本概念和性质。
提高学生数学素养和逻辑思维能力，为后续数学学习和实际应用打下基础。
课程目标和意义教学方法和内容概述内容概述：本课程将分为以下几个部分2. 和的奇偶性；4. 应用举例。
教学方法：讲解、演示、练习、互动。
1. 和与积的奇偶性基本概念；3. 积的奇偶性；010*********02和的奇偶性和的奇偶性是指，对于两个整数相加，其结果的奇偶性取决于两个整数奇偶性的不同情况。
如果两个整数同为奇数或同为偶数，则它们的和为偶数；如果一个整数为奇数，另一个整数为偶数，则它们的和为奇数。
和的奇偶性的定义1两个数的和的奇偶性规则23如果两个数都是偶数，则它们的和也是偶数。
如果两个数都是奇数，则它们的和也是奇数。
如果一个数是偶数，另一个数是奇数，则它们的和是奇数。
多个数的和的奇偶性规则如果多个数中只有偶数，则它们的和是偶数。
如果多个数中有奇数也有偶数，则它们的和是奇数。
如果多个数中只有奇数，则它们的和是奇数。
对于任意多个数的和，我们可以将它们分成两部分：偶数和奇数，然后根据上述规则得出和的奇偶性。
03积的奇偶性对于任意两个整数a和b，它们的积ab的奇偶性，是指ab除以2的余数的奇偶性。
如果余数为0，则ab为偶数；如果余数为1，则ab为奇数。
定义$2 \times 3 = 6$，因为6除以2的余数为0，所以2和3的积为偶数。
$3 \times 4 = 12$，因为12除以2的余数为0，所以3和4的积为偶数。
例子积的奇偶性的定义两奇数之积为奇数如果a和b都是奇数，那么它们的积ab一定是奇数。
例如：$3 \times 5 = 15$，因为15是奇数，所以3和5的积是奇数。
和与积的奇偶性课件
详细描述
根据奇偶数的定义，奇数可以表示为2n+1，偶数可以表示为2n，其中n是整数。两个 奇数相加时，(2n+1)+(2m+1)=2(n+m)+2=2(n+m+1)，结果为偶数；两个偶数相加
时，2n+2m=2(n+m)，结果为偶数；一个奇数和一个偶数相加时， (2n+1)+2m=2(n+m)+1，结果为奇数。
如果两个数都是奇数或都是偶数 ，那么它们的积一定是奇数；如 果一个数是奇数，另一个数是偶 数，那么它们的积一定是偶数。
多数之积的奇偶性
总结词
多个数的乘积的奇偶性可以通过判断每个数的奇偶性和乘积 的个数来得出。
详细描述
当乘积中有偶数个奇数时，乘积为偶数；当乘积中有奇数个 奇数时，乘积为奇数。
特殊数的积的奇偶性
和与积的奇偶性课件
contents
目录
• 奇偶性的基本概念 • 和的奇偶性 • 积的奇偶性 • 和与积的奇偶性的应用 • 习题与解答
01
奇偶性的基本概念
奇数和偶数的定义
奇数
不能被2整除的整数，如1、3、5、7等。
偶数
能被2整除的整数，如2、4、6、8等。
奇偶性的性质
奇数与奇数相加得偶数： 如3+5=8。
决策制定
在制定决策时，可以利用 和与积的奇偶性来分析问 题，从而做出更加明智的 决策。
在计算机科学中的应用
数据处理
在计算机科学中，可以利用和与 积的奇偶性来进行数据处理和分
析。
加密算法
在加密算法中，可以利用和与积的 奇偶性来设计更加安全的加密算法 。
软件测试
在软件测试中，可以利用和与积的 奇偶性来测试软件的正确性和稳定 性。
根据奇偶数的定义，奇数可以表示为2n+1，偶数可以表示为2n，其中n是整数。两个 奇数相加时，(2n+1)+(2m+1)=2(n+m)+2=2(n+m+1)，结果为偶数；两个偶数相加
时，2n+2m=2(n+m)，结果为偶数；一个奇数和一个偶数相加时， (2n+1)+2m=2(n+m)+1，结果为奇数。
如果两个数都是奇数或都是偶数 ，那么它们的积一定是奇数；如 果一个数是奇数，另一个数是偶 数，那么它们的积一定是偶数。
多数之积的奇偶性
总结词
多个数的乘积的奇偶性可以通过判断每个数的奇偶性和乘积 的个数来得出。
详细描述
当乘积中有偶数个奇数时，乘积为偶数；当乘积中有奇数个 奇数时，乘积为奇数。
特殊数的积的奇偶性
和与积的奇偶性课件
contents
目录
• 奇偶性的基本概念 • 和的奇偶性 • 积的奇偶性 • 和与积的奇偶性的应用 • 习题与解答
01
奇偶性的基本概念
奇数和偶数的定义
奇数
不能被2整除的整数，如1、3、5、7等。
偶数
能被2整除的整数，如2、4、6、8等。
奇偶性的性质
奇数与奇数相加得偶数： 如3+5=8。
决策制定
在制定决策时，可以利用 和与积的奇偶性来分析问 题，从而做出更加明智的 决策。
在计算机科学中的应用
数据处理
在计算机科学中，可以利用和与 积的奇偶性来进行数据处理和分
析。
加密算法
在加密算法中，可以利用和与积的 奇偶性来设计更加安全的加密算法 。
软件测试
在软件测试中，可以利用和与积的 奇偶性来测试软件的正确性和稳定 性。
和与积的奇偶性-五年级数学优秀课件
【课堂练习】 判断奇偶性： 1、奇+偶+奇+奇+偶+偶=（ ）；
2、23+89+54+65+999+146的和是（ ）；
3、3+5+7+9+11+13+15+17+19+21的和是（ ）。
【课堂练习】 判断奇偶性：
1、奇+偶+奇+奇+偶+偶=（奇）；
2、23+89+54+65+999+146的和是（ 偶）；
五个连续的偶数的和是320，这五个数中最小的是？
【课后作业】
谢谢观看！
和与积的奇偶性
偶数2. 经典例题 3. 课堂练习 4. 课堂小结 5. 课后作业
【知识点梳理】
【经典例题】
【经典例题】
【经典例题】
？ ？
【经典例题】
偶数 奇数
【知识梳理】
偶数: 奇数:
奇+奇=偶 偶+偶=偶 奇+偶=奇
…… ……
【经典例题】
3、3+5+7+9+11+13+15+17+19+21的和是（偶 ）。
【课堂练习】
【课堂练习】
5个奇数相加，结果是奇数！
【课堂练习】
【课堂练习】
50个奇数相加，结果是偶数！
【课堂练习】
【课堂练习】
（1000÷2+1）个奇数相加，结果是寄数！
【比赛真题】
【奥数真题】
【经典例题】
3×5×11×7
1387+276+24+360+389的结果是奇数还是偶数？
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
加数
加数
和
和是奇数还是偶数
偶数+偶数=（ 偶 ）数
奇数+奇数=（ 偶 ）数 奇数+偶数=（ 奇 ）数
打开数学书到任意一页，左、右两边页 码的和是奇数还是偶数？
你知道这是为什么吗？
下面的 里藏着几？
算式236+67 的和是偶数， 下 面可能藏着几？
2、4、6、8或0
想一想
116+522+120的结果是奇数还是偶数？
1×2×3×4= 积是（ ）偶数
1×3×5×7×9×11······×1000001=
积是（ 奇）数
通过本节课的学习，你们学到了哪 些知识?
在学习的过程中，你们学会了什么 方法?
规则：掷筛子，按掷到的数相加，得到的和是
几，对应的奖励就归你。
1 笔记本
2 谢谢
3 钢笔一支
4 谢谢
5 免一次作业
6 谢谢
7
做一周 班长
8 谢谢
9
去邹老师家 吃一次饭
10 谢谢
11 奖金20元
12 谢谢
探究一 两个数和的奇偶性
要求：任意选两个不是0的自然数，求出它们的和。 再看看和是奇数还是偶数。
任意选几个不是0的自然数，求出它们的积。积的奇偶 性，也会出现像上面这样的一些规律吗？
算式
乘数中偶数的个数 积是奇数还是偶数
几个数相乘，只要有一个乘数是偶数，它们的积 一定是偶数。
不计算，判断下列算式的积是奇数还是偶数
偶 奇 863×24 （ ）数 125×367 （ ）数 976×324 （ ）数 偶 偶 奇 521×234 （ ） 数 765×789（ ）数 966×992 （ ）数 偶
举例
算式中奇数的个数 和是奇数还是偶数
算式
举例 算式中奇数的个数 和是奇数还是偶数
偶数+奇数
1
奇数
偶数+奇数+奇数
2
偶数
偶数+奇数+奇数+奇数奇数+奇数+奇数
4
偶数
偶数+奇数+奇数+奇数+奇数+ 奇数
5
奇数
……
……
……
和的奇偶性——只看奇数个数
和的奇偶性，与加数中奇数的个数有什么关系？
再加1个偶数呢？ 再加10个偶数呢？
……
和的奇偶性 与偶数的个数无关
再加一个奇数呢？
探究二 几个数相加和的奇偶性
用两个数和的奇偶性规律推想，几个数相加和是奇 数还是偶数
算式 偶数+奇数 偶数+奇数+奇数 偶数+奇数+奇数+奇数 偶数+奇数+奇数+奇数+奇数 偶数+奇数+奇数+奇数+奇数+
奇数 ……
当加数中有（ 奇数 ）个奇数时，和一定是（ 奇数 ）数；
当加数中有（ 偶数 ）个奇数时，和一定是（ 偶数 ）数。
下面算式的和是奇数还是偶数？ 16+113+1055+2058+1567+521=
下面算式的和是奇数还是偶数？ 16+113+1055+2058+1567+524=奇数
下面算式的和是奇数还是偶数？ 16+113+1055+2058+1567+524=奇数 48+1159+176+145+1861+1755=
下面算式的和是奇数还是偶数？ 16+113+1055+2058+1567+524=奇数 48+1159+176+145+1861+1755=偶数
1+2+3+4+……+48的和是奇数 还是偶数？为什么？
1+2+3+4+……+48里一共有个 24 奇数， 所以它们的和是 偶 数
探究三 几个数相乘积的奇偶性