第四节反常积分无穷限广义积分无界函数的广义积分习题例题小结

考研广义积分

2 +∞ x dx = d x , 并求其值 . 例题试证例题试证 ∫ 4 ∫0 4 0 1+ x 1+ x 1 t= 令 x 0 1 (− 1 ) d t ∫+∞ 1 t2 解: 1+ 4 2 2 t +∞ t +∞ x =∫ d t= ∫ dx 4 4 0 1+ t 0 1+ x 2 +∞ d x +∞ x 1 +∞ d x ∴ ∫ = ∫ + d x 4 4 ∫0 4 0 1+ x 2 0 1+ x 1+ x +∞
a
ε →0
a+ε
这时称反常积分就称反常积分
如果上述极限不存在, 收敛 ; 如果上述极限不存在发散 .
类似地 , 若 f (x) ∈C[a, b), 而在 b 的左邻域内无界的左邻域内无界, 则定义
而在点而在点 c 的邻域内无界 , 则定义
∫a f (x)dx + ∫c f (x)dx b c−ε1 f (x) dx = lim ∫ f (x) dx + lim ∫ ε →0 c+ε ε →0+ a

(b − a)1−q ; 所以当 q < 1 时, 该广义积分收敛 , 其值为 1− q 当 q ≥ 1 时, 该广义积分发散 .
d x. 求 I = ∫−1 2 1+ f (x) 的无穷间断点, 解： x = 0与x = 2为f (x) 的无穷间断点故 I 为 Q 反常积分. 反常积分 0 2 f ′(x) 3 f ′(x) f ′(x) I =∫ d x+ ∫ d x+ ∫ dx 2 2 2 −11+ f (x) 01+ f (x) 21+ f (x)

高等数学@5-4反常积分

( x)dx
发散
.
y f (x)
s
a
b
x
b
定义
b
f ( x)dx lim f ( x)dx .

a a
右端极限存在,
则称反广常义积分
b

f
( x)dx
收敛
,
否则
,
则称
b

f
( x)dx
发散
.
2

f ( x)dx
定义
0
f ( x)dx
F () lim F (x) ; F () lim F (x)
x
x
则有类似牛 – 莱公式的计算表达式 :

a f (x) dx F (x)
F () F (a)
b
f (x) dx F (x)

f (x) dx F (x)
F (b) F () F () F ()
(a 0)
解.
x
3a 是
x 3a2
x
2
的无穷间断点
.
3a x dx
0
3a2 x2

( 3a)
3a2 x2
0
(0 3a) 3a . #
上限 (
3 a)
代入的含义是
lim
x( 3 a)

3a2 x2 .
13
例6.
1 1 1 x
解:
[ arctan x ]|0

[ arctan x ]|

0 22
思考:
分析:
原积分发散 !

高教社2024高等数学第五版教学课件-5.4 反常积分

解
0
计算反常积分‫׬‬−∞ − 。
0
‫׬‬−∞

−
0 −
‫ ׬‬
→−∞
=
= (− − )|0 = (−1 + − ) = +∞
→−∞
→−∞
0
所以，反常积分‫׬‬−∞ − 发散。
例3
解
+∞ 1
计算反常积分‫׬‬−∞
。
→0+
→0+
1
1
计算反常积分‫׬‬0
。
1− 2
解因为
1
→1− 1− 2
1
1
‫׬‬0 1− 2
=
= +∞，所以 = 1是瑕点。故有
1−
1
‫׬‬0

2
1−
→0+
=
|1−
0
= = ( 1 − ) =
→0+

2
3
2
‫ ׬‬2
=
2 1
(

−
1
).

2
,
2
当 → +∞时,其极限就是火箭无限远离地球需作的功.
我们很自然地会把这个极限写作上限为+∞的“积分”:
+∞ 2

‫׬‬
2
=
2
‫׬‬

→+∞ 2
=
2 1
(

→+∞
1
− ).

1
最后,由机械能守恒定律可求得初速度0 至少应使 0 2
2
用 = 9.81/ 2 , = 6.371 × 106 代入得0 =

第四节反常积分

f ( x) dx lim
f ( x ) dx a a
a
v.p. f ( x) dx (c 为瑕点, a c b)
a
c b lim f ( x ) dx f ( x ) dx c a 0
注意: 主值意义下反常积分存在不等于一般意义下反

Biblioteka x 1 x2
dx lim
A
x 1 x
2
A A
dx 0
解: 不正确因为
x 1 x
2
dx lim
2 b
a a b

b
x 1 x2
dx lim
b
1 2 1 x2
a a b
d 1 x 2
lim 1 x lim 1 b 2 lim 1 a 2 a a a b
例9 解
计算广义积分

0
dx . 3 x( x 1)
此题为混合型广义积分, 积分上限为 ,
下限 x 0 为被积函数的瑕点. 令 x t , 则 x t 2 , x 0 时 t 0, x 时
t , 于是 dx 2 tdt dt . 2 0 x( x 1)3 0 t (t 2 1)3 / 2 0 (t 2 1)3 / 2

1 1 x2 0 x2 1 x2
1
dt
1
d( x 1 ) x 2
0 ( x 1)2 x
dt 2 t 2 (2) 当一题同时含两类反常积分时, 应划分积分区间,
0
分别讨论每一区间上的反常积分.
(3) 有时需考虑主值意义下的反常积分. 其定义为

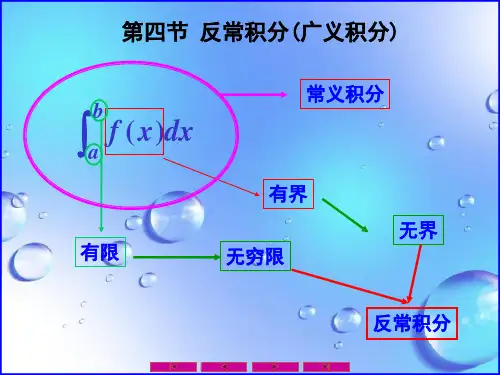
课件：反常积分

dx发
散,
1
1
1 x
dx也
发
散.
思考题(2)
求位于x轴上方,直线x 1右侧,曲线y 2 1 x2
下方的平面图形的面积.
解
所求面积
1
1
2 x
2
dx
2arctan
x 1
22
4
.
2
三、小结与教学要求:
◆掌握无穷限的广义积分
a
f
( x)dx,
b
f
( x)dx,
f
(
x
)dx.
◆掌握无界函数的广义积分（瑕积分）
若lim b ta t
f
( x)dx存在,
则称此极限为f ( x)在(a,b]上的反常积分, 记作ab f ( x)dx,
即
b
a
f ( x)dx
b
lim
ta t
f ( x)dx,
此时,也称广义积分收敛; 否则,称广义积分发散.
类似地, 设f ( x)在[a,b)上连续, 点b为f ( x)的瑕点,
若lim t tb a
f
( x)dx存在,
则称此极限为f ( x)在[a,b)上的反常积分, 记作ab f ( x)dx,
即
b
a
f ( x)dx
t
lim
tb a
f ( x)dx.
此时,也称广义积分收敛; 否则,称广义积分发散.
若f ( x)在[a,b]上除c点外处处连续,且c为瑕点,则定义
b
a
x
1
,
(2) p 1,
1 1 x p dx
x1 1
p
p
1

第四节广义积分

1
lim t0 t
dx x2
tl im 0[x1]t1tl im 0[x1]1t
lim (11)lim (11)
t t 0
t 0
t
如果忽视了被积函数在积分区间内有瑕点
而作出
1 dx 1 x2

[
1 x
]11
2
就全错了。
1 ln x
y
1
y

1
பைடு நூலகம்
1 x2
x
ln x 1
(6) 1 x 2 d x
解： 1lnxx21dx1(1lnx)d(1x)
[1xlnx]1
1dx 1x x
xl im 1xlnx1[1x]1
1 lim 110
x x
y
x

x
(1
)dxa
0
x2 a2
(8)
dx
2a (x2 a2)32
(a0)
解：令 xasect d xasecttantd t
则

dx
π2

1 asecttantdt
2a(x2a2)32 π3a3tan3t

1 a2
π π
2 3
cos tdt sin 2 t

t0
1 t0
1 t0
⑶
1 d x
1 x 2
t
50
t2
50 40
解：被积函数 1 在区 x2
间 [1,1]上有无穷间断
点 x0，
f (x)
0 4
5
30 20 10
2
0
2
x
4 5
1

反常积分法课件

3、
0
x ne xdx（
n 为自然数
）；4、
2 dx 0 (1 x)2
；
5 、 2 xdx ； 1 x1
6 、
x ln x 0 (1 x 2 )2
dx
；
7 、
1
ln
n
xdx
.
0
三、求当 k 为何值时
，广义积分 b dx a (x a)k
(b a)
收敛？又 k 为何值时，这广义积分发散？
的瑕点是哪几点？
01
02
思考题解答
1
ln
x
0
x
dx 1
积分
x0,可能x 的瑕1 点是
lim lnx lim1 1, x1
x014x 1 x1 x
03
的瑕1点l是nx dx
0 x1
x0.
不是瑕点,
练习题
一、填空题：
1、广义积分 dx 当_______时收敛；当______ 时
1 xp 发散；
0 1x2
6、广义积分x f(t)d的 t 几何意义是 ______________
________________________.
二、判别下列各广义积分的收敛性，如果收敛，则计
算广义积分的值：
1、 e pt cosh tdt 0
( p 1) ； 2、 dx
；
x2 2x 2
1
因此当q 1时反常积分收敛，其值为 1 ； 1q
当q 1时反常积分发散.
例6 计算反常积分
2 dx .
1 x ln x
2
1
dx x ln x

广义反常积分简单提

a
dx
a
lim
dx
0 a2 x2 0 0 a2x2
l im 0arcsaxina0 l im 0arcas ain0
2
.
例 6证明广义积分 01x1qd当 xq1时收敛，当
q1时发散 .
证 (1)q1,
11
0 x q
dx
1
0
1 x
dx
lnx10
,
(2)q1,
1
0
1 xq
1
dx x2
.
解
dx 1 x2
0 dx 1 x2
dx 0 1 x2
al ima011x2dxbl im0b11x2dx
al im arctxa 0 anbl im arctxab0n
al im arctaanbl im arctban22.
例2
计算广义积分
2
1 x2
c
b
l i0a m f(x )d x l i0c m f(x )dx
否则，就称广义积分 a b f ( x ) d 发散 . x
定义中C为瑕点，以上积分称为瑕积分.
a dx
例5
计算广义积分 0
a2x2
(a0).
解
lim 1 , xa0 a2x2
x a 为被积函数的无穷间断点 .
第四节广义（反常）积分
• 一、无穷限的广义积分 • 二、无界函数的广义积分 • 三、小结
一、无穷限的广义积分
定义 1 设函数f (x)在区间[a,)上连续，取
ba，如果极限lim b b a
f
(x)dx存在，则称此极

高等数学反常积分(同济六版)

p >1
+∞,
机动目录
q ≥1
上页下页返回结束
说明: 说明 (1) 有时通过换元 , 反常积分和常义积分可以互相转化 . 例如 ,
=∫
1 x2 0 x2 + 1 x2
1 1+
dt = ∫
1
d(x − 1) x +2
0 (x − 1)2 x
dt =∫ −∞ 2 + t 2 (2) 当一题同时含两类反常积分时, 应划分积分区间,
机动
目录
上页
下页
返回
结束
例6. 证明反常积分时发散 . 证: 当 q = 1 时, 当 q≠1 时
当 q < 1 时收敛 ; q≥1
= [ ln x − a ]
1−q
b a
+
= +∞
(x − a) = 1− q
(b − a)1−q , q <1 b 1− q a+= +∞, q >1
+∞
b
机动
目录
上页
下页
返回
结束
例1. 计算反常积分解:
= [ arctan x ] −∞
=
+∞
y
y=
π
− (− ) = π 2 2
π
1 1+x2
o
x
思考: 思考分析: 分析原积分发散 !
注意: 注意对反常积分, 只有在收敛的条件下才能使用 “奇偶函数积分” 的性质, 否则会出现错误 .
机动目录上页下页返回结束
1
A= ∫
+∞ dx
1 y= 2 x A

5(4)反常积分

反常积分
注为了方便起见, 规定:
f ( x) C(a, b], 如a为瑕点, F( x) f ( x),
由N—L公式, 则反常积分
b
a f ( x)dx F (b) F (a ) F(b)
lim F( x)
xa
[F
(
x
)]
b a
f ( x) C[a, b),如b为瑕点,
边梯形的面积可记作
A
dx 1 x2
其含义可理解为
A
lim
b
b 1
dx x2

lim b

1 x
b 1

lim 1 b

1 b

1
y

1 x2
A
1b
7
机动目录上页下页返回结束
反常积分
定义1 (1) 设f ( x)在[a,)上连续, 取t a,

2

lim cos 1 cos
x
x
2
1.
13
反常积分
例
讨论积分

sin
xdx的敛散性.

解考虑由于被积函数为奇函数,
积分区间又为对称区间, 因而

sin xdx 0

由定义可知

sin xdx

[
cos
x
]

lim cos x lim cos x
dx
dx
1
4. 当 x 为何值时，函数 I x x tet2 dt有极值。 0 解 Ix xex2 令 Ix 0 得唯一驻点 x 0 当x 0时I x 0, 当x 0时I x 0, 故 x 0 为函数 I x的惟一的极值点（极小值点）。

高等数学第四节反常积分-精品文档

2. ( 1 0 ) ( 0 1 )
dx arctan x 1 x2

. 2 2
3

(k0 ) 例 2 .I x dx e sin
0
kx
kx 1 e cos x

D ekx
第四节反常积分
P 250
a

f (x)dx lim ) dx . f(x
a b

定义
b
右端极限存在 , 则称反常积分 ( x ) dx 收敛 , 广义积分 f
a
否则 ,则称 ( x ) dx 发散 . f
a
y f( x )
b 此曲边梯形右端无限延伸 ,其面积 s为有限值 .

y f( x )
a
y f( x )
s b s
s
b

f(x )dx
x
s

f(x )dx
2
a
b
x
例 1 .
e
x
0 x dx edx ex dx 0

x0 x e e 0
0 x x 0 e lim e lim e e x x
a 0 3
0
( 0 3 a ) 3 a .#
2 2 上限 a 代入的含义 lim 3 a x . 3 x 0 3
9
a

1 1 例 6 . dx ln x 0 . x 1 1
1
错 !
1
忽视了 x0是被积函数的无穷间点 .

第四节反常积分

xa
1 1q
(x
a)1q
1 (b a)1q 1q
,q 1
,q 1
b a
(x
1 a)q
dx
收敛，且其值为 1 1q
发散
(b
a )1 q
,q 1 ,q 1
类似地，有
b a
1 (b x)q
dx
收敛，且其值为 1 1q
发散
(b a)1q
,q 1 ,q 1
例8 讨论反常积分 2 dx 的收敛性 1 x ln x
设x a为 f ( x) 的瑕点, 在(a, b]上F'( x) f ( x), 则反常积分
b
b
f ( x)dx lim f ( x)dx
a
ta t
lim[F(b) F(t)] t a
F(b) lim F(t) t a
F(b) F(a )
[F ( x)]ba
b a
f
( x)dx
( )
x
x
2
2
f
(
x)
1
1 x
2
上述反常积分表示：曲线无限延伸与x 轴所围图形的面积。
例2
计算反常积分
2
1 x2
sin
1 x
dx.
解
2
1 x2
sin
1 x
dx
2
(
sin
1 x
)d
1 x
cos
1 x 2
lim cos 1 cos
x
x
2
10 1
例3
证明反常积分 1
1 dx 0 x2
0 1
dx x2
[
1 x

高数反常积分知识点与例题精讲

例1
计算广义积分

2
1 x2
sin
1 x
dx.
解

2
1 x2
sin
1 x
dx

2

sin
1 x
d

1 x

lim b
b
2
sin
1 x
d

1 x

lim
b
cos
1b x 2

lim
b
cos
1 b

cos
2

1.
例2
计算广义积分

1
dx x
2
.
解法1:
dx 1 x2

0
dx 1 x2

dx 0 1 x2
lim a
0
a1
1 x2
dx

lim
b
b1 0 1 x2 dx

lim arctan
1 p

0

e
pt
d
t
机动目录上页下页返回结束
二、无界函数的广义积分
引例:曲线
与 x 轴, y 轴和直线
开口曲边梯形的面积可记作
所围成的
其含义可理解为
A

lim
0
1
dx x

lim
0
2
1 x

lim 2(1 ) 2
0

机动目录上页下页返回结束
注意: 对反常积分, 只有在收敛的条件下才能使用 “偶倍奇零” 的性质否, 则会出现错误 .

第四节反常积分

第四节定积分的近似计算（略）第五节广义积分㈠．本课的基本要求掌握无穷区间和无界函数的广义积分的定义并运用㈡．本课的重点、难点无穷区间的广义积分为重点，无界函数的广义积分为难点㈢．教学内容前面讨论的定积分有二个前提：一是积分区间是有限的；二是被积函数在该区间是有界的。

而实际问题中往往要突破这两个限制，这就需要把定积分的概念加以推广而为反常积分。

一．无穷限的反常积分先考察位于曲线A x x x xy ===,112轴之上而夹在之下，直线之间的区域的面积。

1)(11)(lim12=+∞→-==+∞→⎰A I A A x dx A I A A时，有，当自然，可以把这一极限理解为位于曲线112==x x xy 轴之上，直线之下，之右向右无限延展的区域的面积。

但是，如果对,1,1>=x xy 考察同样的问题，有)(ln 11+∞→+∞→=⎰A A dx xA在这种情形下，无限延展的区域就没有有限的面积了。

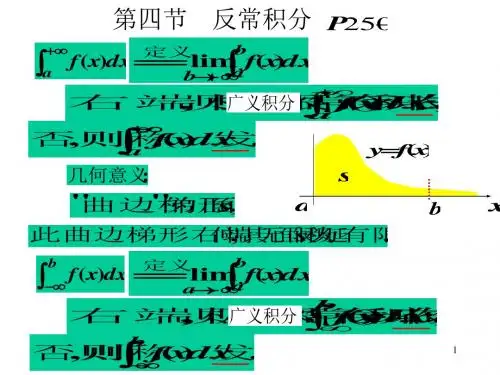
一般地：定义1设⎰+∞→>+∞tat dxx f a t a x f )(,),[)(lim极限上连续，取在区间称为),[)(+∞a x f 在区间上的反常积分，记为⎰⎰+∞→+∞=tat adx x f dx x f )()(lim。

如果等号右端的极限存在，则反常积分⎰+∞adx x f )(收敛；如果等号右端的极限不存在，则称此反常积分发散。

类似地，可以定义],()(b x f -∞在上的反常积分为⎰⎰-∞→∞-=btt bdx x f dx x f )()(lim对于),()(+∞-∞在x f 上的反常积分定义为=⎰+∞∞-dx x f )(+⎰-∞→ctt dx x f )(lim ⎰+∞→tct dx x f )(lim其中c 为介于a,b 之间的任意实数，a,b 各自独立地趋向于负、正无穷大，且仅当右端两个极限都存在时，反常积分⎰+∞∞-dx x f )(才收敛，否则是发散的。

第四节反常积分无穷限广义积分无界函数的广义积分

例 3 证明广义积分当 p 1 时发散.

1 x
p
1
dx 当 p 1 时收敛，
证 (1) p 1,1

1 x
dx p
1

1 x
dx ln x 1 ,

, p 1 1 x ( 2) p 1, dx p 1 , p1 1 x 1 p 1 p1 1 因此当 p 1 时广义积分收敛，其值为； p1 当 p 1 时广义积分发散.
即当 p 0 时收敛，当 p 0 时发散.
二、无界函数的广义积分
定义 2 设函数 f ( x ) 在区间( a , b] 上连续，而在点 a 的右邻域内无界．取 0 ，如果极限
0 a
lim
b
f ( x )dx 存在，则称此极限为函数 f ( x )
2
sin
1 x
dx .

1 x
2
sin 2
b
1 x
dx 2 sin

1 1 d x x
b
lim
b

2
1 1 1 sin d lim cos b x2 x x

1 lim cos cos 1. b b 2
a
f ( x )dx .
a

f ( x )dx lim
a f ( x )dx b
b
当极限存在时，称广义积分收敛；当极限不存在时，称广义积分发散.
类似地，设函数 f ( x ) 在区间( , b] 上连续，取

第四节反常积分无穷限广义积分无界函数的广义积分习题例题小结

合集下载

考研广义积分

高等数学@5-4反常积分

高教社2024高等数学第五版教学课件-5.4 反常积分

第四节反常积分

课件：反常积分

第四节广义积分

反常积分法课件

广义反常积分简单提

高等数学反常积分(同济六版)

5(4)反常积分

高等数学第四节反常积分-精品文档

第四节反常积分

高数反常积分知识点与例题精讲

第四节反常积分

第四节反常积分无穷限广义积分无界函数的广义积分

文档推荐

最新文档

第四节反常积分无穷限广义积分无界函数的广义积分习题例题小结

合集下载

考研广义积分

高等数学@5-4反常积分

高教社2024高等数学第五版教学课件-5.4 反常积分

第四节 反常积分

课件：反常积分

第四节 广义积分

反常积分法课件

广义反常积分简单提

高等数学 反常积分(同济六版)

5(4)反常积分

高等数学第四节反常积分-精品文档

第四节反常积分

高数 反常积分 知识点与例题精讲

第四节 反常积分

第四节 反常积分 无穷限广义积分 无界函数的广义积分

文档推荐

最新文档

第四节反常积分

第四节广义积分

高等数学反常积分(同济六版)

高数反常积分知识点与例题精讲

第四节反常积分

第四节反常积分无穷限广义积分无界函数的广义积分