山东省莱芜五中2013届高三4月模拟数学(理)试题 Word版含答案

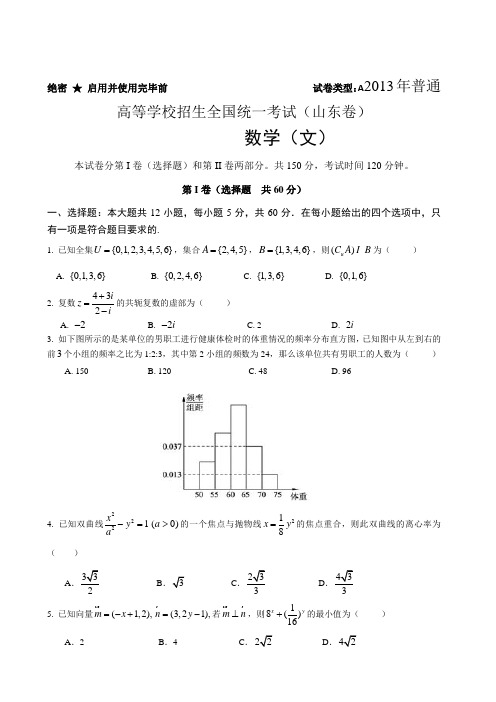
绝密 ★ 启用并使用完毕前试卷类型：A 2013年普通高等学校招生全国统一考试（山东卷）数学（文）本试卷分第I 卷（选择题）和第II 卷两部分。

共150分，考试时间120分钟。

第I 卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知全集{0,1,2,3,4,5,6}U =，集合{2,4,5}A =，{1,3,4,6}B =，则()u C A B 为（ ）A. {0,1,3,6}B. {0,2,4,6}C. {1,3,6}D. {0,1,6} 2. 复数432iz i+=-的共轭复数的虚部为（ ） A. 2- B. 2i - C. 2 D. 2i3. 如下图所示的是某单位的男职工进行健康体检时的体重情况的频率分布直方图，已知图中从左到右的前3个小组的频率之比为1:2:3，其中第2小组的频数为24，那么该单位共有男职工的人数为（ ）A. 150B. 120C. 48D. 964. 已知双曲线2221x y a -=(0)a >的一个焦点与抛物线218x y =的焦点重合，则此双曲线的离心率为（ ）A ．2BC ．3D ．35. 已知向量(1,2),m x =-+(3,21),n y =-若m n ⊥，则18()16xy+的最小值为（ ）A ．2B ．4C ．D ．6. 已知变量,x y 满足约束条件2823y x x y x y ≤⎧⎪-≤⎨⎪+≥⎩，则目标函数62z x y =-的最小值为（ ）A ．32B ．4C ．8D ．2 7. 已知数列{},{}n n a b 满足113a b ==，113n n n nb a a b ++-==，n N +∈，若数列{}n c 满足n n a c b =，则2013c =（ ）A. 20129B ．201227C ．20139D. 2013278. 已知函数()f x 的定义域为[3,6]，则函数y =）A ．3[,)2+∞B ．3[,2)2C ．3(,)2+∞D ．1[,2)29. 执行如图所示的程序框图，则输出的结果为（ ）A ．2B ．1C ．21D ．1- 10. 已知四面体S ABC -的正方形；则四面体S ABC -外接球的表面积为（ ）A. 6πB. 4πC. 8πD. 3π11. 在△ABC 中，内角A ，B ，C 的对边分别是a ，b ，c ，若22245b c b c +=+-且222a b c bc =+-，则△ABC 的面积为（ ）A.B.2C. 2D.12. 定义域为R 的函数()f x 满足()()22f x f x +=，当[)0,2x ∈时，()[)[)232,0,1,1,1,2,2x x x x f x x -⎧-∈⎪⎪=⎨⎛⎫⎪-∈ ⎪⎪⎝⎭⎩则当[)4,2x ∈--时，函数()f x 的最小值为（ ） A. 116-B. 14- C. 12-D. 18-第II 卷（非选择题 共90分）二、填空题：本大题共4小题，每小题4分，共16分．13. 若函数22()1xf x x =+在点(2,(2))f 处的切线为l ，则直线l 与y 轴的交点坐标为_____________.14. 已知函数4log ,0()2,0x x x f x x ->⎧=⎨≤⎩，则21((4))(log )6f f f -+=_____________.15. 容易计算2510,22551210,222555123210,2222555512343210⨯=⨯=⨯=⨯=；根据此规律猜想9922225555⋅⋅⋅⨯⋅⋅⋅位位所得结果由左向右的第八位至第十位的三个数字依次为 .16. 对于函数lg |3|y x =-和sin2xy π=(410)x -≤≤，下列说法正确的是 .（1）函数lg |3|y x =-的图像关于直线3x =-对称； （2）sin2xy π=(410)x -≤≤的图像关于直线3x =对称；（3）两函数的图像一共有10个交点；（4）两函数图像的所有交点的横坐标之和等于30； （5）两函数图像的所有交点的横坐标之和等于24.三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．17.（本小题满分12分）已知函数21()sin cos sin cos cos cos()(0)2f x x x x ϕϕπϕϕπ=+++<<，其图象过点1(,).34π （1）求ϕ的值；（2）将函数)(x f y =图象上各点向左平移6π个单位长度，得到函数)(x g y =的图象，求函数)(x g 在2[,]43ππ-上的单调递增区间.18.（本小题满分12分）中国共产党第十八次全国代表大会期间，某报刊媒体要选择两名记者去进行专题采访，现有记者编号分别为1,2,3,4,5的五个男记者和编号分别为6,7,8,9的四个女记者．要从这九名记者中一次随机选出取两名，每名记者被选到的概率是相等的，用符号(,)x y 表示事件“抽到的两名记者的编号分别为x 、y ，且x y <”． （1）共有多少个基本事件？并列举出来；（2）求所抽取的两记者的编号之和小于17但不小于11或都是男记者的概率．19. （本小题满分12分）如图所示，PA ^平面ABC ，点C 在以AB 为直径的⊙O 上，30CBA??，2PA AB ==，点E 为线段PB 的中点，点M 在弧AB 上，且OM ∥AC ．（1）求证：平面MOE ∥平面P AC ； （2）求证：平面P AC ^平面PCB ； （3）求三棱锥O PBC -的体积.ME BOCAP20. （本小题满分12分）在等差数列{}n a 中，345842,30a a a a ++==. （1）求数列{}n a 的通项公式； （2）若数列{}n b满足2n a n b λ+=+（R λ∈），则是否存在这样的实数λ使得{}n b 为等比数列； （3）数列{}n c 满足112,1,2n n n n n c T a n --⎧⎪=⎨⎪⎩为奇数，为偶数为数列{}n c 的前n 项和，求2n T .21.（本小题满分13分）在平面直角坐标系xOy 中，椭圆E 的中心为原点，焦点12,F F 在y 轴上，离过F 1的直线l 交E 于,A B 两点，且2ABF ∆的周长为（1）求椭圆E 的方程；（2）过圆22:5O x y +=上任意一点P 作椭圆E 的两条切线，若切线都存在斜率，求证两切线斜率之积为定值.22.（本题满分13分）已知函数()ln (1)ln 2e f x x f x '=-⋅+，32()()2x g x f x x=--. （1）求()f x 的单调区间；（2）设函数2()4h x x mx =-+，若存在1(0,1]x ∈，对任意的2[1,2]x ∈，总有12()()g x h x ≥成立，求实数m 的取值范围.参考答案CADCC BDBCA BB13. 32(0,)25； 14. 8； 15. 898； 16.（2）（3）（4）； 17. 解：（1）11cos 21()sin 2sin cos cos 222x f x x ϕϕϕ+=+-11sin 2sin cos 2cos 22x x ϕϕ=+1(sin 2sin cos 2cos )2x x ϕϕ=+1cos(2).2x ϕ=-……3分 又函数图象过点1(,).34π，所以11cos(2)423πϕ=⨯-，即21cos(),32πϕ-=又0ϕπ<<，所以.3πϕ=……6分（2）由（1）知1()cos(2)23f x x π=-，将函数()y f x =图象上各点向左平移6π个单位长度后，得到函数()y g x =的图象，可知1()cos 22g x x =.……9分因为2[,]43x ππ∈-，所以42[,]23x ππ∈-，由202x π-≤≤和423x ππ≤≤知函数)(x g 在2[,]43ππ-上的单调递增区间为[,0]4π-和2[,]23ππ.……12分18. 解:（1）共有36个基本事件，列举如下：)2,1(，)3,1(，)4,1(，)5,1(，)6,1(，)7,1(，)8,1(,)9,1(，)3,2(，)4,2(，)5,2(，)6,2(，)7,2(，)8,2(,)9,2(，)4,3(，)5,3(，)6,3(，)7,3(，)8,3(,)9,3(，)5,4(，)6,4(，)7,4(，)8,4(,)9,4(，)6,5(，)7,5(，)8,5(,)9,5(，)7,6(，)8,6(,)9,6(，)8,7(,)9,7(，)9,8(，共36个.（2）记事件“所抽取的记者的编号之和小于17但不小于11”为事件A ，即事件A 为“{},1,2,3,4,5,6,7,8,9x y ∈，且1117x y ≤+<，其中y x <”，由（1）可知事件A 共含有15个基本事件，列举如下：)9,2(，)8,3(,)9,3(，)7,4(，)8,4(,)9,4(，)6,5(，)7,5(，)8,5(,)9,5(，)7,6(，)8,6(,)9,6(，)8,7(,)9,7( 共15个；其中“都是男记者”记作事件B ，则事件B 为“5x <且5y <，y x <”，包含：)2,1(，)3,1(，)4,1(，)5,1(，)3,2(，)4,2(，)5,2(，)4,3(，)5,3(，)5,4(，共10个；故151025()()363636P A P B +=+=. 19.（1）证明：因为点E 为线段PB 的中点，点O 为线段AB 的中点， 所以 OE ∥PA . 因为 PA Ì平面PAC ，OE Ë平面PAC ， 所以 OE ∥平面P AC . ……2分又因为 OM ∥AC ，AC Ì平面PAC ， OM Ë平面PAC ，所以 OM ∥平面P AC . ……3分因OE Ì平面MOE ，OM Ì平面MOE ，OE OM O =，所以平面MOE ∥平面P AC . ……5分（2）证明：因为 点C 在以AB 为直径的⊙O 上，所以 90ACB??，即BC AC ⊥.因为 PA ^平面ABC ，BC Ì平面ABC ，所以 PA BC ⊥.……8分 因为 AC Ì平面PAC ，PA Ì平面PAC ，PAAC A =，所以 BC ^平面PAC .因为 BC Ì平面PBC ， 所以 平面P AC ^平面PCB .…10分 （3）011211sin120326O PBC P OBC V V --==⨯⨯⨯⨯⨯=三棱锥三棱锥.……12分 20. 解：（1）因为{}n a 是一个等差数列，所以34544342,14a a a a a ++==∴=.设数列{}n a 的公差为d ，则84416d a a =-=，故4d =；故4(4)42n a a n d n =+-=-.……3分 （2）29n a n n b λλ+=+=+.假设存在这样的λ使得{}n b 为等比数列，则212n n n b b b ++=⋅，即122(9)(9)(9)n n n λλλ+++=+⋅+，整理可得0λ=. 即存在0λ=使得{}n b 为等比数列.……7分（3）∵12,23,n n n c n n -⎧=⎨-⎩为奇数为偶数，∴242221(223)2(243)22(223)n n T n -=+⨯-++⨯-++++⨯-……9分242212224(12)3n n n -=++++++++-214(1)414321423n n n n n n n -+-=+⨯-=+--. ……12分 21. 解：（1）设椭圆E 的方程为22221y x a b+=（0a b >>），因AB 过1F 且,A B 在椭圆上，则2ABF ∆的周长为221212||||||||||||||AB AF BF AF AF BF BF ++=+++4a ==，故a =又离心率3c e a ==，2221,2c b a c ∴=∴=-=. 故椭圆E 的方程为22132y x +=.（2）设点00(,)P x y ，过点P 的椭圆E 的切线0l 的方程为00()y y k x x -=-.故0022()132y y k x x y x -=-⎧⎪⎨+=⎪⎩，可得2220000(32)4()2()60k x k y kx x kx y ++-+--=. 因0l 与椭圆E 相切，故2220000[4()]4(32)[2()6]0k y kx k kx y ∆=--+--=. 整理可得2220000(2)2(3)0x k kx y y -+--=.设满足题意的椭圆E 的两条切线的斜率分别为12,k k ，则20122032y k k x -⋅=--. 因点P 在圆O 上，22005x y ∴+=，2012205312x k k x --∴⋅=-=--.故两条切线的斜率之积为常数1-. 22. 解：（1）1()(1)f x f x ''=-，1(1)1(1),(1)2f f f '''∴=-∴=， 1()ln ln ,(0)22e f x x x x ∴=-+>，故112()22xf x x x-'=-=. ∴当02x <<时，()0f x '>；当2x >时，()0f x '<. ∴()f x 的单调增区间为(0,2)，单调减区间为(2,)+∞.……5分（2）2()2ln ln 2eg x x x x =---，则2221222()2x x g x x x x -+'=-+=， 而22115222()048x x x -+=-+>，故在(0,1]上()0g x '>，即函数()g x 在(0,1]上单调递增，∴max ()(1)ln 21g x g ==-.……7分而“存在1(0,1]x ∈，对任意的2[1,2]x ∈，总有12()()g x h x ≥成立”等价于“()g x 在(0,1]上的最大值不小于()h x 在[1,2]上的最大值”.……9分而()h x 在[1,2]上的最大值为(1),(2)h h 中的最大者，记为max{(1),(2)}h h .所以有(1)ln 21(1)(1)ln 21(2)g h g h =-≥⎧⎨=-≥⎩，(1)ln 215(1)ln 2182g mg m =-≥-⎧∴⎨=-≥-⎩，6ln 2,6ln 21(9ln 2)2m m m ≥-⎧⎪∴∴≥-⎨≥-⎪⎩.-+∞.……13分故实数m的取值范围为[6ln2,)。

2013年某校高考数学四模试卷（理科）一、选择题：本大题共10小题，每小题5分，共50分.在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知全集U ={−1, 1, 2, 3, 4}，集合A ={1, 2, 3}，B ={2, 4}，则(∁U A)∪B 为（ ） A {1, 2, 4} B {2, 3, 4} C {−1, 2, 4} D {−1, 2, 3, 4}2. 如果复数z = 2 − 1 + i，则（ ）A |z|＝2B z 的实部为1C z 的虚部为−1D z 的共轭复数为1+i 3. 已知双曲线x 2a 2−y 2b 2=1的一个焦点与抛物线y 2=4x 的焦点重合，且双曲线的离心率等于√5，则该双曲线的方程为（ ） A 5x 2−45y 2=1 B x 25−y 24=1 C y 25−x 24=1 D 5x 2−54y 2=14. 已知(x 2+1x )n 的二项展开式的各项系数和为32，则二项展开式中x 4的系数为（ ） A 5 B 10 C 20 D 405. 采用系统抽样方法从960人中抽取32人做问卷调查为此将他们随机编号为1，2...960，分组后在第一组采用简单随机抽样的方法抽到的号码为9，抽到的32人中，编号落入区间[1, 450]的人做问卷A ，编号落人区间[451, 750]的人做问卷B ，其余的人做问卷C ．则抽到的人中，做问卷C 的人数为（ ） A 15 B 10 C 9 D 76. 把函数y =cos2x +1的图像上所有点的横坐标伸长到原来的2倍（纵坐标不变），然后向左平移1个单位长度，再向下平移1个单位长度，得到的图像是( )A B C D7. 在区间[−π, π]内随机取两个数分别记为a ，b ，则使得函数f(x)＝x 2+2ax −b 2+π有零点的概率为（ ） A 78B 34C 12D 148. 如果执行如图的程序框图，那么输出的值是（ ）A 0B 12C −12D −19. 已知实数a ，b ，c ，d 成等比数列，且函数y =ln(x +2)−x ，当x =b 时取到极大值c ，则ad 等于( )A −1B 0C 1D 210. 定义在R 上的函数y =f(x)是减函数，且函数y =f(x −1)的图象关于(1, 0)成中心对称，若s ，t 满足不等式f(s 2−2s)≤−f(2t −t 2)．则当1≤s ≤4时，ts 的取值范围是（ ）A [−12，1)B [−14，1)C [−12，1]D [−14，1]二、填空题：本大题共7小题，每小题5分，共25分.将答案填写在题中的横线上. 11. 已知等差数列{a n }的前n 项和为S n ，a 5=5，S 5=15，则数列{1a n a n+1}的前100项和为________．12. 已知函数f(x)满足：x ≥4，则f(x)=(12)x ；当x <4时f(x)=f(x +1)，则f(2+log 23)=________．13. 一个几何体的三视图如图π×12×1=π所示，则该几何体的体积为________．14. 已知a →=(λ, 2λ)，b →=(3λ, 2)，如果a →与b →的夹角为锐角，则λ的取值范围是________． 15. （不等式选做题）若不存在实数x 使|x −3|+|x −1|≤a 成立，则实数a 的取值集合是________．16. 如图，已知AB 和AC 是圆的两条弦，过点B 作圆的切线与AC 的延长线相交于点D ，过点C 作BD 的平行线与圆相交于点E ，与AB 相交于点F ，AF =3，FB =1，EF =32，则线段CD 的长为________．17. （坐标系与参数方程选做题） 已知直线l 1:{x =1+tcosαy =tsinα（t 为参数）与圆C 2:{x =cosθy =sinθ（θ为参数）的位置关系不可能是________．三、解答题：本大题共6小题，共75分.解答应写出文字说明、证明过程或演算步骤. 18. 已知△ABC 的三个内角A 、B 、C 的对边分别为a 、b 、c ，且b 2+c 2=a 2+bc ，求： （1）2sinBcosC −sin(B −C)的值； （2）若a =2，求△ABC 周长的最大值．19. 已知函数f(x)=x 2−2(n +1)x +n 2+5n −7．（1）设函数y =f(x)的图象的顶点的纵坐标构成数列{a n }，求证：{a n }为等差数列； （2）设函数y =f(x)的图象的顶点到x 轴的距离构成数列{b n }，求{b n }的前n 项和S n ． 20. 如图，四棱锥P −ABCD 的底面ABCD 为直角梯形，其中BA ⊥AD ，CD ⊥AD ，CD =AD =2AB ，PA ⊥底面ABCD ，E 是PC 的中点．(1)求证：BE // 平面PAD ；(2)若BE ⊥平面PCD ，求平面EBD 与平面BCD 夹角的余弦值．21. 某品牌的汽车4S 店，对最近100位采用分期付款的购车者进行统计，统计结果如右表所示：已知分3期付款的频率为0.2，4S 店经销一辆该品牌的汽车，顾客分1期付款，其利润为1万元；分2期或3期付款其利润为1.5万元；分4期或5期付款，其利润为2万元．用η表示经（1）求表中的a ，b 值；（2）若以频率作为概率，求事件A ：“购买该品牌汽车的3位顾客中，至多有1位采用3期付款”的概率P(A)；（3）求η的分布列及数学期望Eη．22.如图，F 1，F 2是离心率为√22的椭圆C:x 2a2+y 2b 2=1(a >b >0)的左、右焦点，直线l:x =−12将线段F 1F 2分成两段，其长度之比为1:3．设A ，B 是C 上的两个动点，线段AB 的中垂线与C 交于P ，Q 两点，线段AB 的中点M 在直线l 上． （1） 求椭圆C 的方程； （2） 求F 2P →⋅F 2Q →的取值范围．23. 已知函数f(x)=12ax 2−(2a +1)x +2lnx(a ∈R)．（1）若曲线y =f(x)在x =1和x =3处的切线互相平行，求a 的值； （2）求f(x)的单调区间；（3）设g(x)=x 2−2x ，若对任意x 1∈(0, 2]，均存在x 2∈(0, 2]，使得f(x 1)<g(x 2)，求a 的取值范围．2013年某校高考数学四模试卷（理科）答案1. C2. C3. D4. B5. D6. A7. B8. D9. A 10. C 11.10010112. 124 13. π+√3314. (−∞, −43)∪(0, 13)∪(13, +∞) 15. {a|a <2} 16. 4317. 相离18. 解：（1）∵ b 2+c 2=a 2+bc ，∴ a 2=b 2+c 2−bc ， 结合余弦定理知cosA =b 2+c 2−a 22bc=b 2+c 2−(b 2+c 2−bc)2bc=12，又A ∈(0, π)，∴ A =π3，∴ 2sinBcosC −sin(B −C)=sinBcosC +cosBsinC =sin(B +C)=sin[π−A]=sinA =√32； （2）由a =2，结合正弦定理得： asinA =bsinB =csinC =√32=4√33， ∴ b =4√33sinB ，c =4√33sinC ， 则a +b +c =2+4√33sinB +4√33sinC=2+4√33sinB +4√33sin(2π3−B)=2+2√3sinB +2cosB =2+4sin(B +π6)，可知周长的最大值为6．19. （1）证明：∵ f(x)=x 2−2(n +1)x +n 2+5n −7=[x −(n +1)]2+3n −8， ∴ a n =3n −8，---------∴ a n+1−a n =3(n +1)−8−(3n −8)=3， ∴ 数列{a n }为等差数列．---------（2）解：由题意知，b n =|a n |=|3n −8|，--------- ∴ 当1≤n ≤2时，b n =8−3n ，S n =b 1+⋯+b n =n(b 1+b n )2=n[5+(8−3n)]2=13n−3n 22；----当n ≥3时，b n =3n −8，S n =b 1+b 2+b 3+...+b n =5+2+1+...+(3n −8)=7+(n−2)[1+(3n−8)]2=3n 2−13n+282．---------∴ S n ={13n−3n 22，1≤n ≤23n 2−13n+282，n ≥3．---------20. (1)证明：设AB =a ，PA =b ，以A 为坐标原点，AB 为x 轴，AD 为y 轴，AP 为z 轴，建立空间直角坐标系， 则A(0, 0, 0)，B(a, 0, 0)，P(0, 0, b)， C(2a, 2a, 0)，D(0, 2a, 0)，E(a, a, b2)． BE →=(0,a,b2)，AD →=(0,2a,0)，AP →=(0,0,b)，∴ BE →=12AD →+12AP →． 又∵ BE ⊄平面PAD ， ∴ BE // 平面PAD ．(2)解：∵ BE ⊥平面PCD ，∴ BE ⊥PC ，即BE →⋅PC →=0． 又∵ PC →=(2a,2a,−b)， ∴ BE →⋅PC →=2a 2−b 22=0．即b =2a ，在平面BDE 和平面BDC 中，BE →=(0,a,a)，BD →=(−a,2a,0)，BC →=(a,2a,0)， ∴ 平面BDE 的一个法向量为n 1→=(2,1,−1)， 平面BDC 的一个法向量为n 2→=(0,0,1)， ∴ cos <n 1→，n 2→>=√6．∴ 平面EBD 与平面CBD 夹角的余弦值为√66．21. 解：（1）由a 100=0.2得a =20∵ 40+20+a +10+b =100∴ b =10（2）记分期付款的期数为ξ，则ξ的可能取值是1，2，3，4，5， 依题意得：P(ξ=1)=40100=0.4，P(ξ=2)=20100=0.2，P(ξ=3)=0.2， P(ξ=4)=10100=0.1，P(ξ=5)=10100=0.1 则“购买该品牌汽车的3位顾客中至多有1位采用3期付款”的概率P(A)=0.83+C 310.2×(1−0.2)2=0.896（3）∵ η的可能取值为：1，1.5，2（单位万元） P(η=1)=P(ξ=1)=0.4P(η=1.5)=P(ξ=2)+P(ξ=3)=0.4P(η=2)=P(ξ=4)+P(ξ=5)=0.1+0.1=0.2∴ η的分布列为：∴ η的数学期望Eη=1×0.4+1.5×0.4+2×0.2=1.4（万元）22. 解：（1）设F 2(c, 0)，则c−12c+12=13，所以c =1．因为离心率e =√22，所以a =√2，所以b =1所以椭圆C 的方程为x 22+y 2=1． …（2）当直线AB 垂直于x 轴时，直线AB 方程为x =−12，此时P(−√2, 0)、Q(√2, 0)，F 2P →⋅F 2Q →=−1．当直线AB 不垂直于x 轴时，设直线AB 的斜率为k ，M(−12, m) (m ≠0)，A(x 1, y 1)，B(x 2, y 2)．由{x 122+y 12=1x 222+y 22=1得(x 1+x 2)+2(y 1+y 2)⋅y 1−y2x 1−x 2=0，则−1+4mk =0，∴ k =14m．此时，直线PQ 斜率为k 1=−4m ，PQ 的直线方程为y −m =−4m(x +12)，即y =−4mx −m ． 联立{y =−4mx −mx 22+y 2=1消去y ，整理得(32m 2+1)x 2+16m 2x +2m 2−2=0．所以x 1+x 2=−16m 232m 2+1，x 1x 2=2m 2−232m 2+1．于是F 2P →⋅F 2Q →=(x 1−1)(x 2−1)+y 1y 2=x 1x 2−(x 1+x 2)+1+(4mx 1+m)(4mx 2+m) =(1+16m 2)x 1x 2+(4m 2−1)(x 1+x 2)+1+m 2 =(1+16m 2)(2m 2−2)32m 2+1+(4m 2−1)(−16m 2)32m 2+1+1+m 2=19m 2−132m 2+1． 令t =1+32m 2，1<t <29，则F 2P →⋅F 2Q →=1932−5132t．又1<t <29，所以−1<F 2P →⋅F 2Q →<125232． 综上，F 2P →⋅F 2Q →的取值范围为[−1, 125232)．…23. 解：（1）∵ 函数f(x)=12ax 2−(2a +1)x +2lnx(a ∈R)， ∴ f′(x)=ax −(2a +1)+2x (x >0)．∵ 曲线y =f(x)在x =1和x =3处的切线互相平行， ∴ f ′(1)=f ′(3)，即a −(2a +1)+2=3a −(2a +1)+23，解得a =23．（2）f′(x)=(ax−1)(x−2)x(x >0)．①当a ≤0时，x >0，ax −1<0， 在区间(0, 2)上，f ′(x)>0； 在区间(2, +∞)上f ′(x)<0， 故f(x)的单调递增区间是(0, 2)， 单调递减区间是(2, +∞)．②当0<a <12时，1a>2，在区间(0, 2)和(1a，+∞)上，f ′(x)>0；在区间(2,1a )上f ′(x)<0，故f(x)的单调递增区间是(0, 2)和(1a，+∞)，单调递减区间是(2,1a)③当a =12时，f′(x)=(x−2)22x，故f(x)的单调递增区间是(0, +∞)．④当a >12时，0<1a <2，在区间(0,1a )和(2, +∞)上，f ′(x)>0； 在区间(1a ，2)上f ′(x)<0，故f(x)的单调递增区间是(0,1a)和(2, +∞)，单调递减区间是(1a，2)．（3）由已知，在(0, 2]上有f(x)max <g(x)max ． 由已知，g(x)max =0，由（2）可知， ①当a ≤12时，f(x)在(0, 2]上单调递增，故f(x)max =f(2)=2a −2(2a +1)+2ln2=−2a −2+2ln2， 所以，−2a −2+2ln2<0，解得a >ln2−1， 故ln2−1<a ≤12．②当a >12时，f(x)在(0,1a]上单调递增，在[1a ，2]上单调递减，故f(x)max =f(1a )=−2−12a −2lna ． 由a >12可知lna >ln 12>ln 1e=−1，2lna >−2，−2lna <2，所以，−2−2lna <0，f(x)max <0， 综上所述，a >ln2−1．。

山东省2014届理科数学一轮复习试题选编38：算法初步一、选择题 1 ．（山东省潍坊市2013届高三第一次模拟考试理科数学）运行右面框图输出的S 是254,则①应为（ ）A ．n ≤5B ．n ≤6C ．n ≤7D ．n ≤8【答案】C 本程序计算的是212(12)2222212n nn S +-=+++==-- ,由122254n +-=,得12256n +=,解得7n =.此时18n +=,不满足条件,输出,所以①应为7n ≤,选C ． 2 ．（2013年山东临沂市高三教学质量检测考试理科数学）执行如图所示的程序框图,输出的S 值为（ ）A ．4B ．32 C．23D ．-1 【答案】 【答案】A 41,124i S ===--;222,2(1)3i S ===--;233,2223i S ===-;24,4322i S ===-;25,124i S ===--;所以S 的取值具有周期性,周期为 4.由12013i +≥时,得2012i ≥,所以当2012i =时,输出S ,此时20124034i ==⨯,所以输出S 的值和4i =时,相同,所以4S =,选 C ．3 ．（山东省济宁市2013届高三第一次模拟考试理科数学 ）如果右边程序框图的输出结果是6,那么在判断框中①表示的“条件”应该是（ ）A ．i≥3B ．i≥4C ．i≥5D ．i≥6 【答案】D【解析】第一次循环,264,6410,2m s i =-+==+==;第二次循环,2262,10212,3m s i =-⨯+==+==;第三次循环,2360,12,4m s i =-⨯+===;第四次循环,2462,12210,5m s i =-⨯+=-=-==;第五次循环,2564,1046,6m s i =-⨯+=-=-==;此时满足条件输出6s =,所以条件应为,6i ≥选D ．4 ．（山东省泰安市2013届高三第二次模拟考试数学（理）试题）已知数列{}11,1,n n n a a a a n +==+中,若利用如图所示的程序框图计算并输出该数列的第10项,则判断框内的条件可以是（ ）A ．11?n ≤B ．10?n ≤C ．9?n ≤D ．8?n ≤【答案】C 5 ．（山东省临沂市2013届高三5月高考模拟理科数学）执行如图所示的程序框图,输出的结果是（ ）A ．11B ．12C ．13D ．14【答案】C 第一次循环,1,2,123x y z ===+=;第二次循环,2,3,235x y z ===+=;第三次循环,3,5,358x y z ===+=;第四次循环,5,8,5813x y z ===+=,此时满足条件,输出13z =,选 C ． 6 ．（山东省泰安市2013届高三第一轮复习质量检测数学（理）试题）若程序框图如图所示,则该程序运行后输出k 的值是（ ）A ．4B ．5C ．6D ．7【答案】B第一次35116,1n k =⨯+==;第二次168,22n k ===;第三次84,32n k ===;第四次42,42n k ===;第五次21,52n k ===此时满足条件输出5k =,选 B ． 7 ．（山东省济南市2013届高三4月巩固性训练数学（理）试题）定义某种运算⊗,a b ⊗的运算原理如图 所示.设x x f ⊗=1)(.()f x 在区间[2,2]-上的最大值为. （ ）A ．-2B ．-1C ．0D ．2【答案】D 8 ．（山东省济宁市2013届高三4月联考理科数学）左图是某高三学生进入高中三年来的数学考试成绩茎叶图,第1次到14次的考试成绩依次记为1214,,,.A A A 右图是统计茎叶图中成绩在一定范围内考试次数的一个算法流程图.那么算法流程图输出的结果是7．98．6 3 89．3 9 8 8 4 1 5 10．3 1 11．4 （ ）A ．7B ．8C ．9D ．10【答案】D9 ．（山东省滨州市2013届高三第一次（3月）模拟考试数学（理）试题）执行如图所示的程序框图,若输出结果为3,则可输入的实数x 值的个数为（ ）A ．1B ．2C ．3D ．4【答案】C 由题意知221,2log ,2x x y x x ⎧-≤=⎨>⎩.当2x ≤时,由213x -=,得24x =,解得2x =±.当2x >时,由2log 3x =,得8x =,所以输入的实数x 值的个数为3个,选 C ．10．（山东省德州市2013届高三第二次模拟考试数学（理）试题）执行如图所示的程序框图,若输入n 的值为≤≥16,则输出s 的值为（ ）A ．17B ．16C ．10D ．9【答案】C 11．（山东省2013届高三高考模拟卷（一）理科数学）执行如图所示的程序框图,若输入5=p ,6=q ,则输出a ,i 的值分别为（ ）A ．5,1B ．30,3C ．15.3D ．30.6【答案】D 【解析】执行程序框图可知,当1=i 时,15⨯=a ;当2=i 时,25⨯=a ;;当6=i 时,65⨯=a ,即a 能被q 整除,退出循环,输出i a ,的值分别为30,6. 12．（山东省德州市2013届高三3月模拟检测理科数学）如图所示,程序框图运行后输出k 的值是（ ）A ．4B ．5C ．6D ．7【答案】B 第一次循环,35116,1n k =⨯+==;第二次循环,168,22n k ===; 第三次循环,84,32n k ===;第四次循环,42,42n k ===;第五次循环,21,52n k ===,此时输出5k =,选B ． 13．（山东省菏泽市2013届高三第二次模拟考试数学（理）试题）阅读程序框图,若输出的S 的值等于16,那么在程序框图中的判断框内应填写的条件是（ ）A ．i>5?B ．i>6?C ．i>7?D ．i>8?【答案】A14．（山东省兖州市2013高三9月入学诊断检测数学(理)试题）右图给出的是计算111124620++++ 的值的一个框图,其中菱形判断框内应填入的条件是 （ ）A ．10>iB ．10<iC ．11>iD ．11<i【答案】A15．（山东省莱钢高中2013届高三4月模拟检测数学理试题 ）若右边的程序框图输出的S 是254,则条件①可为（ ）A ．5n ≤B ．6n ≤C ．7n ≤D ．8n ≤【答案】C16．（山东省枣庄市2013届高三3月模拟考试数学（理）试题）如图是一个算法的流程图,若输出的结果是31,则判断框中整数M 的值是（ ）A ．3B ．4C ．5D ．6【答案】B本程序计算的是21222AS =++++ ,即11122112A A S ++-==--,由121=31A +-得12=32A +,解得4A =,则15A +=时,条件不成立,所以4M =,选B ． 17．（山东省莱芜五中2013届高三4月模拟数学（理）试题）执行如图所示的程序框图,则输出的结果为（ ）A ．2B ．1C ．21 D ．1-【答案】C 18．（山东省凤城高中2013届高三4月模拟检测数学理试题 ）阅读如图所示的程序框图,运行相应的程序,则输出的结果是（ ）ABC．D．【答案】A19．（山东省文登市2013届高三3月二轮模拟考试数学（理））右面的程序框图中,若输出S 的值为126,则图中应填上的条件为（ ） A ．5n ≤ B ．6n ≤C ．7n ≤D ．8n ≤【答案】B 20．（2012年山东理）(6)执行下面的程序图,如果输入a=4,那么输出的n 的值为（ ）C ．4D ．5【答案】:312,140,00=+==+==q p n ;716,541,11=+==+==q p n ;15114,2145,22=+==+==q p n ,q p n >=,3.答案应选 B ．21．（山东省枣庄市2013届高三4月（二模）模拟考试数学(理)试题）右图是某算法的程序框图,则程序运行后输出的结果是（ ）A ．6B ．27C ．124D ．168【答案】B 22．（山东省潍坊市2013届高三第二次模拟考试理科数学）运行如图所示的程序,若结束时输出的结果不小于3,则t 的取值范围为（ ）A ．14t ≥B ．18t ≥C ．14t ≤D ．18t ≤ 【答案】B 第一次循环,2,2,211n x t a ===-=;第二次循环,4,4,413n x t a ===-=;第三次循环,6,8,633n x t a ===-=,此时满足条件输出83x t a =,由题意知833x t a =≥,解得81t ≥,即18t ≥,选B ．23．（山东省济南市2013届高三3月高考模拟理科数学）阅读右边的程序框图,运行相应的程序,输出的结果为（ ）A ．1311B ．2113C ．813D ．138【答案】D第7题图第一次循环,112,1,2z x y =+===;第二次循环,123,2,3z x y =+===;第三次循环,235,3,5z x y =+===;第四次循环,358,5,8z x y =+===;第五次循环,5813,8,13z x y =+===;第六次循环,81321z =+=,不满足条件输出138y x =,选 D ． 24．（山东省夏津一中2013届高三4月月考数学（理）试题）如图给出的是计算20121614121+⋅⋅⋅+++的值的程序框图,其中判断框内应填入的是（ ）A ．2012i ≤B ．i >2012C ．1006≤iD ．i >1006【答案】A 25．（山东省青岛即墨市2013届高三上学期期末考试数学（理）试题）如果执行下面的程序框图,输出的S=110,则判断框处为（ ）A ．10<k ?B ．11≥k ?C ．10≤k ?D ．11>k ?【答案】C【 解析】由程序可知该程序是计算(22)242(1)2k k S k k k +=+++==+ ,由(1)110S k k =+=得10k =,则当10k =时,110111k k =+=+=不满足条件,所以条件为10k ≤,选 C ．26．（山东省莱芜市莱芜二中2013届高三4月模拟考试数学（理）试题）右图给出了一个程序框图,其作用是输入x 的值,输出相应的y 值.若要使输入的x 值与输出的y 值相等,则这样的x 值有（ ）A ．1个B ．2个C ．3个D ．4个【答案】C27．（山东威海市2013年5月高三模拟考试数学（理科））一算法的程序框图如右图所示,若输出的12y =,则输入的x 可能为 （ ）A ．1－B ．1C ．1或5D ．1－或1【答案】 B ． 二、填空题 28．（2013届山东省高考压轴卷理科数学）执行如右图的程序框图,那么输出S 的值是________.第5题图【答案】1-【解析】由框图知:12,1;1,2;,3;2S k S k S k ===-===2,4;1,5,S k S k ===-=不满足条件,输出S 的值是1-.29．（2013山东高考数学（理））执行右图的程序框图,若输入的ε的值为0.25,则输出的n 的值为_____.,10123,312,2F F n =+==-==,此时1110.253F =≤不成立.第二次循环,10235,523,3F F n =+==-==,此时1110.255F =≤成立,输出3n =. 30．（山东省济南市2013届高三上学期期末考试理科数学）已知程序框图如右图所示,则输出的i =________;【答案】9【 解析】第一次循环,133,5S i =⨯==;第二次循环,3515,7S i =⨯==;第三次循环,157105,9S i =⨯==;第四次循环,满足条件输出9i =. 31．（山东省德州市2013届高三上学期期末校际联考数学（理））执行如图所示程序框图,输出结果S=.【答案】1【解析】第一次循环1(1)2,3,2S T n =--===;第二次循环23(1)21,5,3S T n =--⨯===;第三次循环35(1)6,7,4S T n =--===;第四次循环47(1)61,9,5S T n =--⨯===,第五次循环,满足条件,输出1S =. 32．（2011年高考（山东理））执行右图所示的程序框图,输入2,3,5l m n ===,则输出的y 的值是______.【答案】解析:1406375278,y =++=278105173,17310568y y =-==-=.答案应填:68. 33．（山东省烟台市2013届高三3月诊断性测试数学理试题）执行如右图所示的程序框图,输出的S 值为___________【答案】10第一次循环,1,1,2i S i ==-=;第二次循环,22,123,3i S i ==-+==; 第三次循环,23,336,4i S i ==-=-=;第四次循环,24,6410,5i S i ==-+==,此时不满足条件,输出10S =. 34．（山东省菏泽市2013届高三5月份模拟考试数学（理）试题）执行如图所示的程序框图,输出S 的值为__________.【答案】-2 35．（山东省淄博市2013届高三复习阶段性检测（二模）数学（理）试题）执行如图所示的程序框图,若输出的结果是8,则输入的数是______.【答案】2或22- 由a b ≥得23x x ≥,解得1x ≤.所以当1x ≤时,输出2a x =,当1x >时,输出3b x =.所以当1x ≤时,由28a x ==,解得822x =-=-.若1x >,由38b x ==,得2x =,所以输入的数为2或22-. 36．（2010年高考（山东理））执行右图所示的程序框图,若输入10x =,则输出y 的值为_____________.【答案】54-【解析】当x=10时,y=110-1=42⨯,此时|y-x|=6; 当x=4时,y=14-1=12⨯,此时|y-x|=3;当x=1时,y=111-1=-22⨯,此时|y-x|=32;当x=12-时,y=115-1=-224⨯-（）,此时|y-x|=3<14,故输出y 的值为54-.【命题意图】本题考查程序框图的基础知识,考查了同学们的试图能力.37．（山东省济南市2012届高三3月高考模拟题理科数学（2012济南二模））如果执行右面的程序框图,那么输出的S =______.【答案】 20【解析】第一次循环:2,220==+=k S ;第二次循环:3,642==+=k S ;第三次循环:4,1266==+=k S ;第四次循环:5,20812==+=k S ;第五次循环:输出20=S .38．（山东省莱芜市莱芜十七中2013届高三4月模拟数学（理）试题）执行如图的程序框图,如果输入的n 是4,则输出的p 是______【答案】3 39．（山东省青岛市2013届高三第一次模拟考试理科数学）某程序框图如右图所示,若3a=,则该程序运行后,输出的x 值为【答案】31 第一次循环,2317,2x n =⨯+==;第二次循环,27115,3x n =⨯+==;第三次循环,215131,4x n =⨯+==.此时不满足条件,输出31x =. 40．（2009高考(山东理)）执行右边的程序框图，输入的T= .【答案】【解析】:按照程序框图依次执行为S=5,n=2,T=2; S=10,n=4,T=2+4=6;S=15,n=6,T=6+6=12;S=20,n=8,T=12+8=20;S=25,n=10,T=20+10=30>S,输出T=30 答案:30。

山东省莱芜市莱芜二中2013届高三4月模拟考试数学试题（理）一、选择题：本大题共12小题；每小题5分，共60分，在每小题给出的四个选项中，只有一个选项 符合题目要求，把正确选项的代号涂在答题卡上．1.设全集{}9,8,7,6,5,4,3,2,1=U ，[{}3,1)(=B A U ,{}[4,2)(=B A U ,则集合B= Ａ．{}4,3,2,1 B ．{}5,4,3,2,1 Ｃ．{}9,8,7,6,5 D ．{}9,8,72．若复数3i()12ia z a +=∈+R 实部与虚部相等，则a 的值等于 Ａ．-1 Ｂ．3 Ｃ．-9 Ｄ．9 3.一个几何体的三视图如图所示，则该几何体的体积为Ａ．1 B ．13 Ｃ．12 D ．324．设向量(1,sin )θ=a ，(3sin ,1)θ=b ，且//a b ，则cos2θ等于Ａ．31- B ．32- Ｃ．32 D ．315. 下列推理是归纳推理的是Ａ．A ，B 为定点，动点P 满足|PA|＋|PB|＝2a ＞|AB|，则P 点的轨迹为椭圆 B ．由a 1＝1，a n ＝3n －1，求出S 1，S 2，S 3，猜想出数列的前n 项和S n 的表达式Ｃ．由圆x 2＋y 2＝r 2的面积πr 2，猜想出椭圆x 2a 2＋y 2b2＝1的面积S ＝πabD ．科学家利用鱼的沉浮原理制造潜艇6. 右图给出了一个程序框图，其作用是输入x 的值，输出相应的y 值．若要使输入的x 值与输出的y 值相等，则这样的x 值有 A ．1个 B ．2个 C ．3个 D ．4个7．若直线x －y ＝2被圆(x －a)2＋y 2＝4所截得的弦长为22，则实数a 的值为Ａ．－1或 3 B ．1或3 Ｃ．－2或6 D ．0或4 8．下列四个判断： ①2,10x R x x ∃∈-+≤；②已知随机变量X 服从正态分布N （3，2σ），P （X ≤6）=0．72，则P （X ≤0）=0．28; ③已知21()nx x+的展开式的各项系数和为32，则展开式中x 项的系数为20；④11e dx x>⎰⎰其中正确的个数有：A ．1个B ．2个C ．3个D ．4个9.已知A ，B ，C ，D 是函数sin()(0,0)2y x πωω=+Φ><Φ<一个周期内的图象上的四个点，如图所示，(,0),6A π-B 为y 轴上的点，C 为图像上的最低点，E 为该函数图像的一个对称中心，B 与D 关于点E 对称，CD在x 轴上的投影为12π，则,ωΦ的值为 Ａ．2,3πω=Φ= B ． 2,6πω=Φ= Ｃ． 1,23πω=Φ= D ．1,26πω=Φ=10.已知R 上可导函数()f x 的图象如图所示，则不等式2(23)()0x x f x '-->的解集为A ．(,1)(1,0)(2,)-∞-⋃-⋃+∞B ．(,1)(1,1)(3,)-∞-⋃-⋃+∞C ．(,2)(1,2)-∞-⋃D ．(,2)(1,)-∞-⋃+∞11．已知O 为坐标原点，双曲线22221x y a b-=(0,0)a b >>的右焦点F ，以OF 为直径作圆交双曲线的渐近线于异于原点的两点A 、B ，若()0AO AF OF +⋅=，则双曲线的离心率e 为Ａ．2 B ．3D12．等差数列{}n a 前n 项和为n S ，已知310061006(1)2013(1)1,a a -+-=310081008(1)2013(1)1,a a -+-=-则Ａ．2013100810062013,S a a => B ．2013100810062013,S a a =< Ｃ．2013100810062013,S a a =-> D ．2013100810062013,S a a =-<二、填空题：本大题共4个小题，每小题4分，共16分.请把答案填在答题纸的相应位置. 13.若存在实数x 使|||1|3x a x -+-≤成立，则实数a 的取值范围是 . 14. 指数函数xa b y ⋅=在[]2,b 上的最大值与最小值的和为6，则=a .15．如图，已知边长为8米的正方形钢板有一个角锈蚀，其中4AE =米，6CD =米. 为了合理利用这块钢板,将在五边形ABCDE 内截取一个矩形10题A MEPDCB N F块BNPM ，使点P 在边DE 上. 则矩形BNPM 面积的最大值为____ 平方米 .16.设点(1,0)A ，(2,1)B ，如果直线1ax by +=与线段AB 有一个公共点，那么22a b +的最小值为 三、解答题：本大题共6个小题，共74分．解答时要求写出必要的文字说明、证明过程或推理步骤。

山东省2013届高三最新理科模拟试题精选（17套）分类汇编12：圆锥曲线一、选择题1 ．（山东省枣庄市2013届高三4月（二模）模拟考试数学(理)试题）12,F F 为双曲线22221(0,0)x y a b a b -=>>的左右焦点,过点2F 作此双曲线一条渐近线的垂线,垂足为M ,满足12||2||MF MF =（ ）A ．2y x =±B ．12y x =±C ．y =D ．2y x =±【答案】A2 ．（山东省文登市2013届高三3月二轮模拟考试数学（理））方程22123x y m m -=--表示双曲线,则m 的取值范围是 （ ） A ．23m << B ．30m -<< 或02m <<或3m > C ．3>m 或23<<-m D ．23m <<或3m <- 【答案】D 3 ．（山东省潍坊市2013届高三第二次模拟考试数学理试题（word 版））已知双曲线22221x y a b-=的实轴长为2,焦距为4,则该双曲线的渐近线方程是 （ ）A ．3y x =±B ．y x =C ．y =D ．2y x =±【答案】C4 ．（山东省泰安市2013线22221x y a b-=恒有两个公共点,则双曲线离心率的取值范围是 （ ）A ．[)2,+∞B ．()2,+∞C ．(D ．)+∞【答案】B5 ．（山东省莱芜五中2013届高三4月模拟数学（理）试题）已知双曲线2221x y a-=(0)a >的一个焦点与抛物线218x y =的焦点重合,则此双曲线的离心率为 （ ）A B C D 【答案】C6 ．（山东省莱芜市莱芜四中2013届高三4月月考数学试题）过双曲线22x a -22y b=1(a>0,b>0)的左焦点1F (-c,0)(c>0),作圆22x y +=24a 的切线,切点为E,直线1F E 交双曲线右支于点P,若OE =12(1OF +OP ),则双曲线的离心率为 （ ）A B C D 【答案】C 7 ．（山东省莱芜市莱芜二中2013届高三4月模拟考试数学（理）试题）已知O 为坐标原点,双曲线22221x y a b-=(0,0)a b >>的右焦点F,以OF 为直径作圆交双曲线的渐近线于异于原点的两点（ ） A ．B,若()0AO AF OF +⋅=,则双曲线的离心率e 为 （ ）A ．2B ．3C D 【答案】C8 ．（山东省莱钢高中2013届高三4月模拟检测数学理试题 ）设1F 、2F 分别为双曲线22221(0,0)x y a b a b-=＞＞的左、右焦点.若在双曲线右支上存在点P ,满足212P F F F =,且2F 到直线1PF的距离等于双曲线的实轴长,则该双曲线的离心率为 （ ）A ．45B ．56 C ．35 D ．23 【答案】C9 ．（山东省济宁市2013届高三4月联考理科数学）已知椭圆方程22143x y +=,双曲线22221(0,0)x y a b a b-=>>的焦点是椭圆的顶点,顶点是椭圆的焦点,则双曲线的离心率为 （ ）ABC ．2D ．3【答案】C 10．（山东省济南市2013届高三4月巩固性训练数学（理）试题）若椭圆1C :1212212=+b y a x (011>>b a )和椭圆2C :1222222=+b y a x (022>>b a )的焦点相同且12a a >.给出如下四个结论:① 椭圆1C 和椭圆2C 一定没有公共点; ②1122a b a b >; ③ 22212221b b a a -=-; ④1212a a b b -<-.其中,所有正确结论的序号是 （ ） A ．①③ B①③④ C ．①②④ D ．②③④ 【答案】B 11．（山东省菏泽市2013届高三第二次模拟考试数学（理）试题）已知中心在原点的椭圆与双曲线有公共焦点,左、右焦点分别为F 1、F 2,且两条曲线在第一象限的交点为P ,△PF 1F 2是以PF 1为底边的等腰三角形,若|PF 1|=10,椭圆与双曲线的离心率分别为1e ,2e ,则12e e +1的取值范围是（ ）A ．(1,+∞)B ．(43,+∞) C ．(65,+∞) D ．(109,+∞) 【答案】B12．（山东省凤城高中2013届高三4月模拟检测数学理试题 ）已知抛物线y 2=4x 的焦点为F ,准线为222,1(0)x l l y a a-=>与双曲线交于A ,B 两点,若△FAB 为直角三角形,则双曲线的离心率是 （ ）ABC ．2D1【答案】B 13．（山东省德州市2013届高三第二次模拟考试数学（理）试题）已知双曲线22221x y a b-=(a>0,b>0)的离心率为2,该双曲线与抛物线y 2= 16x 的准线交于A,B 两点,若则双曲线的方程为（ ）A ．2213y x -=B．22126x y -= C ．23x -y 2 =1 D ．221412x y -= 【答案】A 二、填空题 14．（山东省淄博市2013届高三复习阶段性检测（二模）数学（理）试题）若双曲线()222210x y a b a b-=>>的左、右焦点分别为F 1,F 2,线段F 1F 2被抛物线22y bx =的焦点分成5:3两段,则此双曲线的离心率为______. 【答案】332 15．（山东省夏津一中2013届高三4月月考数学（理）试题）给出下列四个命题:①若直线l过抛物线22x y =的焦点,且与这条抛物线交于A 、B 两点,则AB 的最小值为2;②双曲线1916:22-=-y x C 的离心率为35;③若⊙,02:221=++x y x C ⊙012:222=-++y y x C ,则这两圆恰有2条公切线;④若直线06:21=+-y x a l 与直线()0934:2=+--y a x l 互相垂直,则.1-=a 其中正确命题的序号是______.(把你认为正确命题的序号都填上) 【答案】②③ 16．（山东省潍坊市2013届高三第二次模拟考试数学理试题（word 版））如图,椭圆22221(0)x y a b a b +=>>的左、右焦点为12,F F ,上顶点为A,离心率为12,点P 为第一象限内椭圆上的一点,若112:S PF A S PF F ∆∆=2:1,则直线1PF 的斜率为______________.【答案】517．（山东省泰安市2013届高三第二次模拟考试数学（理）试题）过抛物线24y x =的焦点F 的直线交抛物线于A,B 两点,点O 是坐标原点,则AF EF ⋅的最小值是____. 【答案】418．（山东省济宁市2013届高三4月联考理科数学）若圆C 以抛物线y 2=4x 的焦点为圆心, 截此抛物线的准线所得弦长为6,则该圆 的标准方程是______________________________【答案】()13122=+-y x19．（山东省济南市2013届高三4月巩固性训练数学（理）试题）如图,F 1,F 2是双曲线C:22221x y a b-=(a >0,b >0)的左、右焦点,过F 1的直线与双曲线的左、右两支分别交于A ,B 两点.若 | AB | : | BF 2 | : | AF 2 |=3 : 4 : 5,则双曲线的离心率为____________.20．（山东省济南市2012届高三3月高考模拟题理科数学（2012济南二模））过双曲线2222x y a b -=1(a >0,b >0)的左焦点F,作圆2224a x y +=的切线,切点为E ,延长FE 交双曲线右支于点P ,若E 为PF 的中点,则双曲线的离心率为__________. 【答案】【答案】210【解析】设双曲线的右焦点为M ,连接PM,因为E 为PF 的中点,所以OE 为三角形FPM 的中位线,所以PM=2OE=a ,所以PF=3a ,EF=23a,又FE 为切线,所以有2222410)2()23(a a a c =+=,所以210==a c e .三、解答题21．（山东省淄博市2013届高三复习阶段性检测（二模）数学（理）试题）已知抛物线24y x=的焦点为F 2,点F 1与F 2关于坐标原点对称,直线m 垂直于x 轴(垂足为T),与抛物线交于不同的两点P,Q 且125F P F Q ⋅=-. (I)求点T 的横坐标0x ;(II)若以F 1,F 2为焦点的椭圆C过点1,2⎛⎝⎭. ①求椭圆C 的标准方程;②过点F 2作直线l 与椭圆C 交于A,B 两点,设22F A F B λ=,若[]2,1,TA TB λ∈--+求的取值范围.【答案】解:(Ⅰ)由题意得)0,1(2F ,)0,1(1-F ,设),(00y x P ,),(00y x Q -, 则),1(001y x F +=,),1(002y xF --=. 16题图由521-=⋅F F ,得512020-=--y x 即42020-=-y x ,① 又),(00y x P 在抛物线上,则0204x y =,② 联立①、②易得20=x(Ⅱ)(ⅰ)设椭圆的半焦距为c ,由题意得1=c ,设椭圆C 的标准方程为)0(12222>>=+b a by a x ,则121122=+b a ③ 122+=b a ④将④代入③,解得12=b 或212-=b (舍去) 所以2122=+=b a故椭圆C 的标准方程为1222=+y x (ⅱ)方法一:容易验证直线l 的斜率不为0,设直线l 的方程为1x ky =+将直线l 的方程代入2212x y +=中得:22(2)210k y ky ++-= 设112212(,),(,),00A x y B x y y y ≠≠且,则由根与系数的关系, 可得:12222ky y k +=-+ ⑤ 12212y y k =-+ ⑥ 因为B F A F 22λ=,所以12y y λ=,且0λ<. 将⑤式平方除以⑥式,得:221222214142222y y k k y y k k λλ++=-⇒++=-++ 由[]51112,1+22022λλλλλ∈--⇒-≤≤-⇒-≤++≤2214022k k ⇒-≤-≤+所以 7202≤≤k 因为1122(2,),(2,)TA x y TB x y =-=-,所以1212(4,)TA TB x x y y +=+-+,又12222k y y k +=-+,所以2121224(1)4()22k x x k y y k ++-=+-=-+, 故2222221212222216(1)4||(4)()(2)(2)k k TA TB x x y y k k ++=+-++=+++ 2222222216(2)28(2)828816(2)2(2)k k k k k +-++==-++++, 令212t k =+,所以2207k ≤≤ 所以27111622k ≤≤+,即71[,]162t ∈, 所以222717||()828168()42TA TB f t t t t +==-+=--.而71[,]162t ∈,所以169()[4,]32f t ∈.所以||TA TB +∈ 方法二:【D 】1．)当直线l 的斜率不存在时,即1-=λ时,)22,1(A ,)22,1(-B , 又T )0,2(,所以(1,(1,)222TA TB +=-+--= 【D 】2．)当直线l 的斜率存在时,即[)1,2--∈λ时,设直线l 的方程为)1(-=x k y由⎪⎩⎪⎨⎧=+-=1222y x kkx y 得0224)21(2222=-+-+k x k x k 设()()1122,,,A x y B x y ,显然120,0y y ≠≠,则由根与系数的关系,可得:2221214k k x x +=+,22212122k k x x +-=⋅ 221212122)(k kk x x k y y +-=-+=+ ⑤22212122121)1)((k k x x x x k y y +-=++-=⋅ ⑥因为B F A F 22λ=,所以12y y λ=,且0λ<. 将⑤式平方除以⑥式得:221421k +-=++λλ由[)1,2--∈λ得⎪⎭⎫⎢⎣⎡--∈+2,251λλ即⎪⎭⎫⎢⎣⎡-∈++0,2121λλ 故0214212<+-≤-k ,解得272≥k 因为1122(2,),(2,)TA x y TB x y =-=-, 所以1212(4,)TA TB x x y y +=+-+,又222121)1(44k k x x ++-=-+,2222222221221)21(4)21()1(16)()4(k k k k y y x x ++++=++-+=+ 22222222)21(221104)21(2)21(10)21(4k k k k k ++++=+++++=令2211k t +=,因为272≥k 所以8121102≤+<k ,即⎥⎦⎤ ⎝⎛∈81,0t ,所以22251721042()22TA TB t t t+=++=+-1694,32⎛⎤∈ ⎥⎝⎦.⎥⎦⎤⎝⎛+8213,2 综上所述:||[2,8TA TB +∈ 22．（山东省枣庄市2013届高三4月（二模）模拟考试数学(理)试题）已知抛物线22x py=上点(2,2)处的切线经过椭圆2222:1(0)x y E a b a b+=>>的两个顶点.(1)求椭圆E 的方程;(2)过椭圆E 的上顶点A 的两条斜率之积为4-的直线与该椭圆交于,B C 两点,是否存在一点D,使得直线BC恒过该点?若存在,请求出定点D的坐标;若不存在,请说明理由;∆的重心为G,当边BC的端点在椭圆E上运动时,求(3)在(2)的条件下,若ABC222++的取值范围.||||||GA GB GC【答案】23．（山东省夏津一中2013届高三4月月考数学（理）试题）已知两点F1(-1,0)及F2(1,0),点P在以F1、F2为焦点的椭圆C上,且|PF1|、|F1F2|、|PF2|构成等差数列.(1)求椭圆C的方程;(2)如图7,动直线l:y=kx+m与椭圆C有且仅有一个公共点,点M,N是直线l上的两点,且F1M⊥l,F2N⊥l.求四边形F1MNF2面积S的最大值.【答案】解:(1)依题意,设椭圆C 的方程为22221x y a b+=.1122PF FF PF 、、构成等差数列, ∴1122224a PF PF F F =+==, 2a =.又1c =,23b ∴=.∴椭圆C 的方程为22143x y += (2) 将直线l 的方程y k xm =+代入椭圆C 的方程223412x y +=中,得01248)34(222=-+++m kmx x k由直线l 与椭圆C 仅有一个公共点知,2222644(43)(412)0k m k m ∆=-+-=, 化简得:2243m k =+设11d F M ==,2d =(法一)当0k ≠时,设直线l 的倾斜角为则12tan d d MN θ-=⨯,12d dMN k-∴=221212121()22d d d d S d d k k --=+==m m 14++2243m k =+,∴当0k ≠时,3>m ,3343131=+>+m m ,32<S . 当0=k 时,四边形12F MNF 是矩形,S = 所以四边形12F MNF 面积S的最大值为(法二)222222212222()2(53)11m k k d d k k +++=+==++, 222122233311m k k d d k k -+====++. MN ∴===四边形12F MNF 的面积121()2S MN d d =+)(11212d d k ++=,22221222122)1(1216)2(11++=+++=k k d d d d k S12)211(41622≤-+-=k 当且仅当0k =时,212,S S ==故max S =所以四边形12F MNF 的面积S的最大值为24．（山东省文登市2013届高三3月二轮模拟考试数学（理））设点(,)P x y 到直线2x =的距离与它到定点(1,0),并记点P 的轨迹为曲线C . (Ⅰ)求曲线C 的方程;(Ⅱ)设(2,0)M -,过点M 的直线与曲线C 相交于,E F 两点,当线段EF 的中点落在由四点1212(1,0),(1,0),(0,1),(0,1)C C B B --构成的四边形内(包括边界)时,求直线斜率的取值范围.=整理得2212x y +=,所以曲线C 的方程为2212x y +=(Ⅱ)显然直线的斜率k 存在,所以可设直线的方程为(2)y k x =+.设点,E F 的坐标分别为1122(,),(,),x y x y 线段EF 的中点为G 00(,)x y ,由22(2)12y k x x y =+⎧⎪⎨+=⎪⎩ 得2222(12)8820k x k x k +++-=由2222(8)4(12)(82)0k k k ∆=-+->解得k <<.(1) 由韦达定理得2122812k x x k -+=+,于是1202x x x +==22412k k -+,0022(2)12k y k x k =+=+ 因为2024012k x k =-≤+,所以点G 不可能在y 轴的右边,又直线1211,C B C B ,方程分别为1,1y x y x =+=-- 所以点G 在正方形内(包括边界)的充要条件为000011y x y x ≤+⎧⎨≥--⎩ 即22222224112122411212k k k kk k k k ⎧-≤+⎪⎪++⎨⎪≥-⎪++⎩ 亦即222210,2210.k k k k ⎧+-≤⎪⎨--≤⎪⎩解得k ≤≤,(2) 由(1)(2)知,直线斜率的取值范围是[25．（山东省潍坊市2013届高三第二次模拟考试数学理试题（word 版））已知定点(,0)2pA (p 为常数,p>O),B 为z 轴负半轴七的一个动点,动点M 使得AM AB =,且线段BM 的中点在y 轴上(I)求动点脚的轨迹C 的方程;(Ⅱ)设EF 为曲线C 的一条动弦(EF 不垂直于x 轴),其垂直平分线与x 轴交于点 T(4,0),当p=2时,求EF 的最大值. 【答案】26．（山东省泰安市2013届高三第二次模拟考试数学（理）试题）已知椭圆()2222:10x y E a b a b+=>>的左、右焦点分别为F 1、F 2,点()11,P x y 是椭圆上任意一点,且124PF PF +=,椭圆的离心率1.2e = (I)求椭圆E 的标准方程;(II)直线1PF 交椭圆E 于另一点()12,Q x y ,椭圆右顶点为A,若3AP AQ ⋅=,求直线1PF 的方程;(III)过点11,04M x ⎛⎫⎪⎝⎭作直线1PF 的垂线,垂足为N,当1x 变化时,线段PN 的长度是否为定值?若是,请写出这个定值,并证明你的结论;若不是,请说明理由.【答案】27．（山东省莱芜五中2013届高三4月模拟数学（理）试题）如图,设A 是圆226x y +=上的动点,点B 是A 在x 轴上投影,M 为AB 上一点,且||||3MB AB =.当A 在圆上运动时,点M 的轨迹为曲线G . 过点(,0)m (m 且倾斜角为56π的直线l 交曲线G 于,C D 两点.(1)求曲线G 的方程;(2)若点F 是曲线G 的右焦点且[,]32CFD ππ∠∈,求m 的取值范围.【答案】解:(1)设点M 的坐标是(,)x y ,A 的坐标是(,)A A x y ,因为点B 是A 在x 轴上投影,M 为AB 上一点,且||||MB AB =,所以A x x =,且A y =,∵A 在圆226x y +=上,∴22)6x +=,整理得22162x y +=. 即G 的方程是22162x y +=. (2)如下图,直线l 交曲线G 于,C D 两点,且[,]32CFD ππ∠∈.由题意得直线l的方程为)3y x m =--(m >.由22162()3x y y x m ⎧+=⎪⎪⎨⎪=--⎪⎩,消去y 得222260x mx m -+-=.由2248(6)0m m ∆=-->解得m -<.又m >m <<.设1122(,),(,)C x y D x y ,则212126,2m x x m x x -+==,2121212121[)][)]()333m m y y x m x m x x x x ∴=-⋅-=⋅-++. 1122(2,),(2,)FC x y FD x y =-=-.2212121212462(3)(2)(2)()43333m m m m FC FD x x y y x x x x +-∴⋅=--+=-+++=.又由椭圆方程可知2263x y -=,1||()FC xx ===-,2||()FD x x ====-,2121212221||||(3)(3)[3()9](612)333FC FD x x x x x x m m ∴⋅=--=-++=-+,22222(3)2(3)3cos 1612||||(612)3m m FC FD m m CFD m m FC FD m m -⋅-∴∠===-+⋅-+. 因[,]32CFD ππ∠∈,2212(3)1cos [0,],026122m m CFD m m -∴∠∈∴≤≤-+, 22032(3)0,24011m m m m m mm ≤≥⎧⎧-≥⎪⎪∴∴⎨⎨--≤≤≤+⎪⎪⎩⎩或,故10m ≤≤或31m ≤≤m <<故31m ≤≤28．（山东省莱芜市莱芜四中2013届高三4月月考数学试题）如图所示,设抛物线1C :2y =4mx(m>0)的准线与x 轴交于1F ,焦点为2F ;以1F , 2F 为焦点,离心率e=12的椭圆2C与抛物线1C 在x 轴上方的交点为P,延长P 2F 交抛物线于点Q,M 是抛物线1C 上一动点,且M 在P 与Q 之间运动. (1)当m=1时,求椭圆2C 的方程;(2)当△P 1F 2F 的边长恰好是三个连续的自然数时,求△MPQ 面积的最大值.【答案】解:(1)当m=1时, 2y =4x,则1F (-1,0), 2F (1,0),设椭圆方程为22a x +22by =1(a>b>0),则c=1,又e=a c =21, 所以a=2, 2b =3,所以椭圆2C 的方程为42x +32y =1.(2)设P(p x ,p y )(p x >0, p y >0),Q(Q x ,Q y )(Q x >0, Q y <0), 因为c=m,e=a c =21,则a=2m, 2b =32m 故椭圆方程为224m x +223m y =1,由⎪⎩⎪⎨⎧==+mx y m y m x 413422222,得32x +16mx-122m =0, 即(x+6m)(3x-2m)=0,得p x =32m, 代入抛物线方程得p y =362m, 即P(32m ,362m),|P 2F |=p x +m=35m , |P 1F |=2a-|P 2F |=4m-35m =37m ,|1F 2F |=2m, 因为△P 1F 2F 的边长恰好是三个连续的自然数, 所以m=3,此时抛物线方程为2y =12x,P(2,26), 直线PQ 方程为y=-26(x-3).联立⎪⎩⎪⎨⎧=--=xy x y 12)3(622,得22x -13x+18=0, 即(x-2)(2x-9)=0, 所以Q x =29, 代入抛物线方程得Q y =-36, 即Q(29,-36), ∴|PQ|=22)6362()292(++-=225. 设M(122t ,t)到直线PQ 的距离为d,t∈(-36,26),则d=124|6666|2+-+t t =306|(t+26)2-275|, ∵t∈(-36,26)∴当t=-26时,dmax=306×275=465,即△MPQ 面积的最大值为21×225×465=166125.29．（山东省莱芜市莱芜十七中2013届高三4月模拟数学（理）试题）已知椭圆)0(12222>>=+b a by a x 的左右焦点分别为21,F F ,短轴两个端点为B A ,,且四边形B AF F 21是边长为2的正方形.(Ⅰ) 求椭圆方程;(Ⅱ) 若D C ,分别是椭圆长轴的左右端点,动点M 满足CD MD ⊥,连接CM ,交椭圆于点P ,证明:→→⋅OP OM 为定值;(Ⅲ)在(Ⅱ)的条件下,试问x 轴上是否存在异于点C 的定点Q ,使得以MP 为直径的圆恒过直线MQ DP ,的交点,若存在,求出点Q 的坐标;若不存在,请说明理由. 【答案】解:(1)222,,2c b a c b a +===,22=∴b ,∴椭圆方程为12422=+y x (2))0,2(),0,2(D C -,设),(),,2(110y x P y M ,则),2(),,(011y OM y x OP ==→→. 直线CM :42y y y x -=-,即00214y x y y +=, 将00214y x y y +=代入椭圆4222=+y x 得 042121)81(2020220=-+++y x y x y由韦达定理有8)8(2,8)8(4)2(2020120201+--=∴+-=-y y x y y x ,882001+=∴y y y . )88,8)8(2(2002020++--=∴→y y y y OP ,48324888)8(4202020202020=++=+++--=⋅∴→→y y y y y y OM OP (定值)(3)设存在)0,(m Q 满足条件,则DP MQ ⊥.),2(0y m MQ --=→,)88,84(2002020++-=→y yy y DP ,则由0=⋅→→DP MQ 得 088)2(8420202020=+--+-y y m y y ,从而得0=m .∴存在)0,0(Q 满足条件.30．（山东省莱芜市莱芜二中2013届高三4月模拟考试数学（理）试题）如图,椭圆22122:1(0)x y C a b a b +=>>x 轴被曲线22:C y x b =-截得的线段长等于1C 的短轴长.2C 与y 轴的交点为M ,过坐标原点O 的直线l 与2C 相交于点A B 、,直线,MA MB 分别与1C 相交于点D E 、. (1)求1C 、2C 的方程; (2)求证:M A M B ⊥.(3)记,MAB MDE ∆∆的面积分别为12S S 、,若12S S λ=,求λ的取值范围.【答案】(1)22222c a b a =∴= 又2b b =,得1b =22221:1,:12x C y x C y ∴=-+= (2)设直线1122:,(,),(,)AB y kx A x y B x y =则22101y kxx kx y x =⎧⇒--=⎨=-⎩ 211221212(,1)(,1)(1)()1MA MB x y x y k x x k x x ⋅=+⋅+=++++=0M A M B ∴⊥(3)设直线1212:1;:1,1MA y k x MB y k x k k =-=-=-1121122110,(,1)111x k y k x x A k k y y k y x ==-⎧⎧=⎧⎪∴-⎨⎨⎨=-=-=-⎪⎩⎩⎩解得或,同理可得222(,1)B k k - MABOD11212S MA MB k =1212111222221112141120421,(,)11212211212k x y k x k x k k D x y k k k y y k ⎧==-⎧⎪+=⎧-⎪⎪∴⎨⎨⎨=-++-+=⎩⎪⎪=⎩⎪+⎩解得或 同理可得2222222421(,)1212k k E k k -++212S MD ME ∴=212211212152()(12)(12)9161616k S k k k S λ++++===≥31．（山东省莱钢高中2013届高三4月模拟检测数学理试题 ）已知椭圆E 的中心在坐标原点,焦点在坐标轴上,且经过(2,0)A -、(2,0)B 、三点. (1)求椭圆E 的方程:(2)若点D 为椭圆E 上不同于A 、B 的任意一点,(1,0),(1,0)F H -,当DFH ∆内切圆的面积最大时.求内切圆圆心的坐标;(3)若直线:(1)(0)l y k x k =-≠与椭圆E 交于M 、N 两点,证明直线AM 与直线BN 的交点在定直线上并求该直线的方程.【答案】【解析】:(1)设椭圆方程为)0,0(1m 22>>=+n m ny x 将(2,0)A -、(2,0)B、E 的方程,得.∴椭圆E 的方程(2)||2FH =,设DFH 边上的高为DFHS =当点D 在椭圆的短轴顶点时,h 所以DFHS的最大值为设DFH 的内切圆的半径为R ,因为DFH ∆的周长为定值6.所以DFH S R ∆=⨯621,所以R 的最大值为所以内切圆圆心的坐标为），（33,0±(3)将直线:(1)l y k x =-代入椭圆E 的方程.得 2222(34)84(3)0k x k x k +-+-=.设直线l 与椭圆E 的交点1122(,),(,)M x y N x y ,由根系数的关系,得2221222143)3(4,438k k x x k k x x +-=+=+直线AM 的方程为它与直线4x =的交点坐标为 同理可求得直线BN 与直线4x =的交点坐标为下面证明P 、Q 两点重合,即证明P 、Q 两点的纵坐标相等:1122(1),(1)y k x y k x =-=-,因此结论成立.综上可知.直线AM 与直线BN 的交点住直线4x =上32．（山东省济宁市2013届高三4月联考理科数学）已知椭圆C:222210xy (a b )a b+=>>的离心率与等轴双曲线的离心率互为倒数关系,直线0l :x y -=与以原点为圆心,以椭圆C 的短半轴长为半径的圆相切. (1)求椭圆C 的方程;(2)设M 是椭圆的上顶点,过点M 分别作直线MA,MB 交椭圆于A,B 两点,设两直线的斜率分别为k 1,k 2,且k 1+k 2=4,证明:直线AB 过定点(12-,-l). 【答案】33．（山东省济南市2013届高三4月巩固性训练数学（理）试题）设),(),,(2211y x Q y x P 是抛物线px y 22=)0(>p 上相异两点,P Q 、到y 轴的距离的积为4且0=⋅. (1)求该抛物线的标准方程.(2)过Q 的直线与抛物线的另一交点为R ,与x 轴交点为T ,且Q 为线段RT 的中点,试求弦PR 长度的最小值.【答案】解:(1)∵ OP →·OQ →=0,则x 1x 2+y 1y 2=0,又P 、Q 在抛物线上,故y 12=2px 1,y 22=2px 2,故得y 122p ·y 222p+y 1y 2=0, y 1y 2=-4p 2222212144)(||p py y x x ==∴ 又|x 1x 2|=4,故得4p 2=4,p =1. 所以抛物线的方程为: 22y x =(2)设直线PQ 过点E (a ,0)且方程为x =my +a 联立方程组⎩⎨⎧=+=xy amy x 22消去x 得y 2-2my -2a =0∴ ⎩⎨⎧-==+ay y m y y 222121 ①设直线PR 与x 轴交于点M (b ,0),则可设直线PR 方程为x =ny +b ,并设R (x 3,y 3), 同理可知,⎩⎨⎧-==+by y n y y 223131 ②由①、②可得32y b y a= 由题意,Q 为线段RT 的中点,∴ y 3=2y 2,∴b =2a 分 又由(Ⅰ)知, y 1y 2=-4,代入①,可得 -2a =-4 ∴ a =2.故b =4 ∴831-=y y∴3123123124)(1||1|PR |y y y y n y y n -+⋅+=-+=2481222≥+⋅+=n n .当n =0,即直线PQ 垂直于x 轴时|PR |取最小值2434．（山东省济南市2012届高三3月高考模拟题理科数学（2012济南二模））已知椭圆的焦点坐标为1F (-1,0),2F (1,0),过2F 垂直于长轴的直线交椭圆于P 、Q 两点,且|PQ |=3, (1) 求椭圆的方程;(2) 过2F 的直线l 与椭圆交于不同的两点M 、N ,则△1F MN 的内切圆的面积是否存在最大值?若存在求出这个最大值及此时的直线方程;若不存在,请说明理由.【答案】【答案】解:(1) 设椭圆方程为2222x y a b +=1(a>b >0),由焦点坐标可得c =1由PQ |=3,可得22b a=3,解得a =2,b,故椭圆方程为2243x y +=1(2) 设M 11(,)x y ,N 22(,)x y ,不妨1y >0, 2y <0,设△1F MN 的内切圆的径R , 则△1F MN 的周长=4a =8,112F MNS =(MN +1F M +1F N )R =4R 因此1F MNS最大,R 就最大,1212121()2AMN S F F y y y y =-=-, 由题知,直线l 的斜率不为零,可设直线l 的方程为x =my +1,由221143x my x y =+⎧⎪⎨+=⎪⎩得22(34)m y ++6my -9=0,得1y =,2y =则12AMNS=AB (12y y -)=12y y -令则t≥1,则212121313AMNt St t t===++,令f (t )=3t +1t ,则f ′(t ) =3-21t , 当t ≥1时,f ′(t )≥0,f (t)在[1,+∞)上单调递增,有f (t )≥f (1)=4, AMN S≤123=3, 即当t =1,m =0时,AMN S ≤123=3, AMN S =4R ,∴max R =34,这时所求内切圆面积的最大值为916π.故直线l :x =1,△AMN 内切圆面积的最大值为916π35．（山东省菏泽市2013届高三第二次模拟考试数学（理）试题）如图,已知直线l 与抛物线y x 42=相切于点P(2,1),且与x 轴交于点A,O 为坐标原点,定点B 的坐标为(2,0). (I) 若动点M 满足0||2=+⋅,求点M 的轨迹C;(II)若过点B 的直线l ′(斜率不等于零)与(I)中的轨迹C 交于不同的两点E 、F(E 在B 、F 之间),试求△OBE 与△OBF 面积之比的取值范围.【答案】解:(I)由22414x y y x ==得,.21x y ='∴∴直线l 的斜率为1|2='=x y ,故l 的方程为1-=x y ,∴点A 坐标为(1,0)设),(y x M 则),1(),,2(),0,1(y x y x -=-==, 由0||2=+⋅AM BM AB 得 .0)1(20)2(22=+-⋅+⋅+-y x y x整理,得.1222=+y x∴点M 的轨迹为以原点为中心,焦点在x 轴上,长轴长为22,短轴长为2的椭圆 (II)如图,由题意知直线l 的斜率存在且不为零,设l 方程为y=k (x -2)(k ≠0)①将①代入1222=+y x ,整理,得 0)28(8)12(2222=-+⋅-+k x k x k ,由△>0得0<k 2<21. 设E (x 1,y 1),F (x 2,y 2) 则⎪⎪⎩⎪⎪⎨⎧+-=+=+.1228,12822212221k k x x k k x x ② 令||||,BF BE S S OBF OBE ==∆∆λλ则,由此可得 .10,22,21<<--=⋅=λλλ且x x 由②知,124)2()2(221+-=-+-k x x 121212222)(2)2()4.21x x x x x x k -⋅-=-++=+（222141,(1)8(1)2k k λλ+∴==-++即2214110,0,332(1)2201,k λλλλ<<∴<-<-<<++<<解得又1223<<-∴λ.∴△OBE 与△OBF 面积之比的取值范围是(3-22,1)36．（山东省凤城高中2013届高三4月模拟检测数学理试题 ）椭圆2222:1(0)x y G a b a b+=>>的两个焦点为12(,0),(,0)F c F c -,M 是椭圆上的一点,且满足120FM F M ⋅=. (Ⅰ)求离心率的取值范围;(Ⅱ)当离心率e 取得最小值时,椭圆上的点到焦点的最近距离为)12(4-.①求此时椭圆G 的方程;②设斜率为k (k ≠0)的直线l 与椭圆G 相交于不同的两点A 、B ,Q 为AB 的中点,问A 、B两点能否关于过点(0,P 、Q 的直线对称?若能,求出k 的取值范围;若不能,请说明理由.【答案】解:(1)设M (x ,y ),则由又M 在椭圆上,∴∴,又0≤x 2≤a 2,∴,∵, ∴(2)①依题意得:()⎪⎩⎪⎨⎧=-=-22124ac c a ∴⎩⎨⎧==424b a ∴椭圆方程是: ②.设l :y =kx +m,由而△>0可得m 2<32k 2+16又A 、B 两点关于过点、Q 的直线对称 ∴,设A(x 1,y 1),B(x 2,y 2),则 ∴ ∴又k≠0,∴或 ∴需求的k 的取值范围是或37．（山东省德州市2013届高三第二次模拟考试数学（理）试题）已知中心在原点,焦点在x 轴上的椭圆C 的离心率为12,其中一个顶点是抛物线x 2=-的焦点. (I)求椭圆C 的标准方程;(Ⅱ)是否存在过点P(2,1)的直线l 与椭圆C 交于不同的两点A,B 满足PA ·54PB =,若存在,求出直线l 的方程;若不存在,请说明埋由 【答案】解:(1)设椭圆C 的标准方程为22221(0)x y a b a b+=>>,由题意得b =由12c a =得2,1a c == 故椭圆C 的标准方程为22143x y +=.(2)若存在过点P(2,1)的直线l满足条件,则l的斜率存在。

莱芜一中2013年4月高三教学质量调研考试数学（理）试题本试题分为第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分，共4页．训练时间120分钟，满分150分，考试结束后，将本试卷和答题卡一并交回．一、选择题：本大题共12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

1、已知11mni i=-+，其中,m n R ∈，i 为虚数 单位，则m ni += （ ） A 、12i + B 、2i + C 、12i - D 、2i -2、如果执行右边的程序框图，那么输出的S 等于 （ ）A 、2550B 、2500C 、2450D 、26523、若有直线m 、n 和平面α、β，下列四个命题中，正确的是 （ ） A 、若//m α，//n α，则//m nB 、若m α⊂，n α⊂，//m β，//n β则//αβC 、若αβ⊥，m α⊂，则m β⊥D 、若αβ⊥，m β⊥，m α⊄，则//m α4.如图所示的韦恩图中，A 、B 是非空集合，定义A *B 表示阴影部分集合．若,x y R ∈，{}A x y ==，{}3,0x B yy x ==>，则A *B =（ ）．A ．(2,)+∞B ．[)0,1(2,)⋃+∞C ．[]0,1(2,)⋃+∞D ．[]0,1[2,)⋃+∞ 5.下列命题正确的个数 （ ） A ．1B ．2C ．3D ．4（1） 命题“2000,13x R x x ∃∈+>”的否定是“2,13x R x x ∀∈+≤”； （2）函数22()cos sin f x ax ax =-的最小正周期为π”是“1a =”的必要不充分条件； （3）．22x x ax +≥在[]1,2x ∈上恒成立⇔max min 2)()2(ax x x ≥+在[]1,2x ∈上恒成立 （4）．“平面向量a 与b 的夹角是钝角”的充分必要条件是“0a b ⋅<”。

6.已知各项为正数的等差数列{}n a 的前20项和为100，那么714a a ⋅的最大值为 ( )A ．25B ．50C ．100D ．不存在7、在ABC ∆中，“sin A (2sin sin )C A -cos A =(2cos cos )C A +”是 “角A 、B 、C 成等差数列”的 （ ）A 、充分非必要条件B 、充要条件C 、必要非充分条件D 、既不充分也不必要条件8、已知实数x 、y 满足222242(1)(1)(0)y x x y y x y r r ≤⎧⎪+≤⎪⎨≥-⎪⎪++-=>⎩则r 的最小值为（ ）A 、1 BC9、设a 、,,,(0,)b R a b x y +∈≠∈+∞，则222()a b a b x y x y ++≥+，当且仅当a bx y=时取等号，利用以上结论，可以得到函数291()((0,))122f x x x x =+∈-的最小值为 （ ）A 、169B 、121C 、25D 、1610．设函数()2xf x =，则如图所示的函数图象（ ）A ．(||)y f x =B ．|()|y f x =-C ．|)|(x f y --=D ．|)|(x f y -= 11、函数11y x =-的图像与函数2sin (24)y x x π=-≤≤的图像所有交点的横坐标之和等于 （ ） A 、2 B 、3 C 、4 D 、612、在直角坐标平面中，ABC ∆的两个顶点A 、B 的坐标分别为A （－1，0），B （1，0），平面内两点G 、M 同时满足下列条件：（1）GA GB GC O ++= （2）||||||MA MB MC ==（3）//GM AB 则ABC ∆的顶点C 的轨迹方程为（ ）A 、2213x y += (0)y ≠ B 、2213x y -= (0)y ≠ C 、2213y x += (0)y ≠ D 、2213y x -= (0)y ≠二、填空题：本大题共4小题，每小题4分，共26分。

山东省莱芜市第五职业中学高三数学理模拟试卷含解析一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有是一个符合题目要求的1. 在△ABC中，“A＜B＜C”是“cos2A＞cos2B＞cos2C”的（）A．充分不必要条件B．必要不充分条件C．充要条件D．既不充分也不必要条件参考答案：C【考点】必要条件、充分条件与充要条件的判断．【分析】在△ABC中，“A＜B＜C”?a＜b＜c，再利用正弦定理、同角三角函数基本关系式、倍角公式即可得出．【解答】解：在△ABC中，“A＜B＜C”?a＜b＜c?sinA＜sinB＜sinC?sin2A＜sin2B＜sin2C1﹣2sin2A＞1﹣2sin2B＞1﹣2sin2C?“cos2A＞cos2B＞cos2C”．∴在△ABC中，“A＜B＜C”是“cos2A＞cos2B＞cos2C”的充要条件．故选：C．2. 某校100名学生的数学测试成绩分布直方图如图所示，分数不低于即为优秀，如果优秀的人数为20人，则的估计值是（）A．130 B．140 C ．134D．137高考资源网w。

w-w*k&s%5￥u参考答案：C 略3. （2009江西卷理）展开式中不含的项的系数绝对值的和为，不含的项的系数绝对值的和为，则的值可能为A． B．C． D．参考答案：D解析：，，则可取，选D4.已知是定义在R上的单调函数，实数，，，若，则（）A. B. C. D.参考答案：答案：A5. 已知集合A＝{1，a}，B＝{1，2，3}，则“a＝3”是“A? B”的A．充分而不必要条件 B．必要而不充分条件C．充要条件 D．既不充分也不必要条件参考答案：【知识点】必要条件、充分条件与充要条件的判断．A2【答案解析】A 解析：当a=3时，A={1，3}所以A?B，即a=3能推出A?B；反之当A?B时，所以a=3或a=2，所以A?B成立，推不出a=3故“a=3”是“A?B”的充分不必要条件,故选A．【思路点拨】先有a=3成立判断是否能推出A?B成立，反之判断“A?B”成立是否能推出a=3成立；利用充要条件的题意得到结论．6. 已知集合，集合，则为A. B. C. D.参考答案：C略7. 某程序的框图如图所示，运行该程序时，若输入的x=0.1，则运行后输出的y值是（）A．﹣1 B．0.5 C． 2 D．10参考答案：考点：程序框图．专题：算法和程序框图．分析：按照程序框图的流程，判断输入的值是否满足判断框中的条件，“是”按y=lgx求出y．解答：解：当x=0.1时，满足第一个判断框中的条件，执行“是”，也满足第二个判断框中的条件，执行“是”，将x=0.1代入y=lgx得y=﹣1故选A．点评：本题考查解决程序框图的选择结构时，关键是判断出输入的值是否满足判断框中的条件．8. 若集合，全集，则=（）A． B．C． D．参考答案：A因为，所以,所以，选A.9. 设函数f（x）在R上可导，其导函数为f′（x），且函数y=（1﹣x）f′（x）的图象如图所示，则下列结论中一定成立的是（）A．函数f（x）有极大值f（2）和极小值f（1）B．函数f（x）有极大值f（﹣2）和极小值f（1）C．函数f（x）有极大值f（2）和极小值f（﹣2）D．函数f（x）有极大值f（﹣2）和极小值f（2）参考答案：D【考点】函数在某点取得极值的条件；函数的图象．【分析】利用函数的图象，判断导函数值为0时，左右两侧的导数的符号，即可判断极值．【解答】解：由函数的图象可知，f′（﹣2）=0，f′（2）=0，并且当x＜﹣2时，f′（x）＞0，当﹣2＜x＜1，f′（x）＜0，函数f（x）有极大值f（﹣2）．又当1＜x＜2时，f′（x）＜0，当x＞2时，f′（x）＞0，故函数f（x）有极小值f（2）．故选D．10. （5分）设A是整数集的一个非空子集，对于k∈A，如果k﹣1?A且k+1?A，那么称k是集合A的一个“好元素”．给定集合S={1，2，3，4，5，6，7，8}，由S的3个元素构成的所有集合中，不含“好元素”的集合共有（）A． 2个 B． 4个 C． 6个 D． 8个参考答案：C【考点】：元素与集合关系的判断．【专题】：集合．【分析】：根据题意，要使S的三个元素构成的集合中不含好元素，只要这三个元素相连即可，所以找出相连的三个数构成的集合即可．解：根据好元素的定义，由S的3个元素构成的集合中，不含好元素的集合为：{1，2，3}，{2，3，4}，{3，4，5}，{4，5，6}，{5，6，7}，{6，7，8}．故选C．【点评】：考查对好元素概念的理解，以及子集的概念，元素与集合的关系．二、填空题:本大题共7小题,每小题4分,共28分11. 如图，∠ACB=90°，DA⊥平面ABC，AE⊥DB交DB于E，AF⊥DC交DC于F，且AD=AB=2，则三棱锥D﹣AEF体积的最大值为．参考答案：考点：棱柱、棱锥、棱台的体积．专题：空间位置关系与距离．分析：由于S△ADE是定值．因此要求三棱锥D﹣AEF体积的最大值，只要求出点F到平面ABD的距离的最大值即可．由题意可得：取AB的中点O，连接CO，当CO⊥AB时，点F到平面PBD的距离最大，设为h．利用即可得出h．解答：解：∵DA⊥平面ABC，∴AD⊥AB．∵AD=AB=2，AE⊥DB，∴S△ADE==1．因此要求三棱锥D﹣AEF体积的最大值，只要求出点F到平面ABD的距离的最大值即可．由题意可得：取AB的中点O，连接CO，当CO⊥AB时，点F到平面PBD的距离最大，设为h．此时：OA=OC=OB=1，AC=，．=．FD=．∴=，∴．∴三棱锥D﹣AEF体积的最大值===．故答案为：．点评：本题考查了线面垂直的判定与性质定理、三棱锥的体积计算公式、三角形的面积计算公式、三角形相似的性质、圆的性质、射影定理，考查了推理能力与计算能力，属于中档题．12. 若点P(1,1)为圆的弦MN的中点，则弦MN所在直线的方程为．参考答案：因为为圆的弦的中点，所以圆心坐标为，，所在直线方程为，化简为，故答案为.13. 已知，若平面内三点共线，则．参考答案：解析：本小题主要考查三点共线问题。

山东省2013届高三高考模拟卷（四）数学（理科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，全卷满分150分，考试时间120分钟第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．已知集合，，若，则的值为A．2 B．1 C．D．2．定义运算，则符合条件的复数是A．B．C．D．3．“”是“”成立的A．充分不必要条件 B．必要不充分条件C．充分必要条件 D．既不充分也不必要条件4.定义某种运算，运算原理如图所示，则式子的值为A．13 B．11 C．8 D．45.已知三棱锥的俯视图与侧视图如图所示，俯视图是边长为2的正三角形，侧视图是有一直角边为2的直角三角形，则该三棱锥的正视图可能为6．已知圆C的方程为，当圆心C到直线的距离最大时，的值为A．B．C．D．57.如果在一周内（周一至周日）安排三所学校的学生参观某展览馆，每天最多只安排一所学校，要求甲学校的学生连续参观两天，其余学校的学生均只参观一天，则不同的安排方法共有A．50种 B．60种 C．120种 D．210种8．设两个向量和，其中为实数，若，则的取值范围是A．B．[4，8] C．D．9．设，函数的图象可能是10．已知斜率为2的直线过抛物线的焦点F，且与轴相交于点A，若△OAF(O为坐标原点)的面积为4，则抛物线方程为A．B．C．或D．或11.在△ABC中，已知，，且最大角为，则这个三角形的最大边等于A．4 B．14 C．4或14 D．2412．已知是奇函数，且满足，当时，，当时，的最大值为，则A．B．C．D．1第Ⅱ卷二、填空题：本大题共4小题，每小题4分，共16分．把答案填写在答题纸的相应位置．13．由曲线和直线围成的封闭图形的面积为_______。

14．已知变量满足约束条件，且目标函数的最小值为，则常数_______．15.已知四棱柱中，侧棱底面ABCD，且，底面ABCD的边长均大于2，且，点P在底面ABCD内运动，且在AB，AD上的射影分别为M，N，若|PA|=2，则三棱锥体积的最大值为______．16．对大于或等于2的正整数的幂运算有如下分解方式：……根据上述分解规律，若，的分解中最小的正整数是21，则________．三、解答题：本大题共6个小题，共74分．解答应写文字说明、证明过程或演算步骤，把答案填写在答题纸的相应位置．17．（本小题满分12分）已知△ABC的三个内角A、B、C所对的边分别为，且，．(1)求cosC的值；(2)当时，求函数的最大值．18.(本小题满分12分)已知数列满足：，，．数列的前项和为，且，．(1)求数列，的通项公式；(2)令数列满足，求数列的前项和．19．(本小题满分12分)甲、乙两人参加某电视台举办的答题闯关游戏，按照规则，甲先从6道备选题中一次性抽取3道题独立作答，然后由乙回答剩余3题，每人答对其中2题就停止答题，即闯关成功．已知在6道备选题中，甲能答对其中的4道题，乙答对每道题的概率都是．(1)求甲、乙至少有一人闯关成功的概率；(2)设甲答对题目的个数为，求的分布列及数学期望．20.（本小题满分12分）如图，在四棱锥P-ABCD中，底面是直角梯形ABCD，其中AD⊥AB，CD∥AB，AB=4，CD=2，侧面PAD是边长为2的等边三角形，且与底面ABCD垂直，E为PA的中点．(1)求证：DE∥平面PBC；(2)求二面角的余弦值．21.（本小题满分13分）已知椭圆C：的离心率，左、右焦点分别为，抛物线的焦点F恰好是该椭圆的一个顶点．(1)求椭圆C的方程；(2)已知圆M：的切线与椭圆相交于A、B两点，那么以AB为直径的圆是否经过定点？如果是，求出定点的坐标；如果不是，请说明理由，22．(本小题满分13分)设函数，．(1)当且时，直线与函数和函数的图象相切于同一点，求直线的方程．(2)若函数在区间[2，4]上为单调函数，求实数的取值范围．山东省2013届高三高考模拟卷（四）数学（理科）参考答案一、1．B【解析】因为，所以．又因为，而B中最多有两个元素，所以，所以．选B．2.A【解析】设．根据定义运算得，即，根据复数相等的定义得得所以．3．B【解析】由得，；由得．因此“”是“”成立的必要不充分条件，所以选B．4．A 【解析】原式1) =13．5．C【解析】由于空间几何体的正视图和侧视图“高平齐”，故正视图的高一定是2，由于正视图和俯视图“长对正”，故正视图的底面边长为2，又根据侧视图可知这个空间几何体最前面的面垂直于底面，这个面遮住了后面的一个侧棱，综上可知，这个空间几何体的正视图可能是C．6．A【解析】圆C的方程可化为，所以圆心C的坐标为，又直线恒过点，所以当圆心C到直线的距离最大时，直线CA应垂直于直线，因为直线CA的斜率为，所以，．7.C【解析】先安排甲学校的参观时间，一周内两天连排的方法共有6种，甲任选一种为，然后在剩下的五天中任选两天有序地安排其余两所学校参观，安排方法有种，按照分步乘法计数原理可知共有不同的安排方法种，故选C．8．A【解析】根据已知条件得，又，所以，，于是，即，故，即，解得，故，故选A．9．C【解析】由解析式可知，当时，，由此可以排除A、B选项．又当时，，从而可以排除D．故选C．10．D【解析】抛物线的焦点坐标是，直线的方程是，令，得，故，所以△OAF的面积为，由题意，得，解得．故抛物线方程是或．故选D．11．B 【解析】因为，所以，所以，又，所以，所以大于，则，由余弦定理得，所以，所以或（舍去）．12．D【解析】由题意知，所以，所以．当时，，则，，令0，得，又，所以．当0时，，在上单调递增；当时，，在上单调递减．所以，所以得．二、13．【解析】由，得或，则曲线与直线围成的图形的面积．14．9【解析】先根据约束条件画出变量满足的可行域如图中阴影部分所示．易知直线与的交点为，观察图形可知目标函数在点处取得最小值，即，解得．15．【解析】由条件可得，A、M、P、N四点在以PA为直径的圆上，所以由正弦定理得，所以、在△PMN中，由余弦定理可得，当且仅当PM= PN时取等号，所以，所以底面△PMN的面积，当且仅当PM= PN时取最大值，故三棱锥的体积．16．11【解析】由，，，…，可知．由，可知，易知，则21是53的分解中最小的正整数，可得．故．三、17．【解析】(1)在△ABC中，因为，所以．（2分）又，，所以，或（舍），（4分）所以．（6分）(2)由(1)知，（7分）所以，（10分）又，所以．（12分）18．【解析】(1)由已知可知数列为等差数列，且首项为1，公差为1．∴数列的通项公式为．（2分）∵，∴，∴，∴数列为等比数列，（4分）又，∴，∴数列的通项公式为．（6分）(2)由已知得：．∴，∴，（8分）∴两式相减得．（10分）∴数列的前项和．（12分）19．【解析】(1)设甲、乙闯关成功分别为事件A、B，则，（3分）事件相互独立，则甲、乙至少有一人闯关成功的概率是．（6分）(2)由题知的所有可能取值是1，2．，，（9分）则的分布列为所以．（12分）20．【解析】(1)法一如图，取AB的中点F，连接DF，EF．在直角梯形ABCD中，CD∥AB，且AB=4，CD=2，所以，所以四边形BCDF为平行四边形，所以DF∥BC．（2分）在△PAB中，PE=EA，AF=FB，所以EF//PB．又因为DFEF=F，PBBC=B，所以平面DEF∥平面PBC．因为DE平面DEF，所以DE∥平面PBC．（4分）法二取PB的中点M，连接CM，ME．在△PAB中，PE=EA，PM=MB，所以．在直角梯形ABCD中，CD∥AB，且AB=4，CD=2，故，所以，（2分）所以四边形CDEM为平行四边形，故DE∥CM．因为CM平面PBC，DE平面PBC，所以DE∥平面PBC．（4分）(2)取AD的中点O，BC的中点N，连接ON，则ON∥AB．在△PAD中，PA=PD=AD=2，所以PO⊥AD，，又因为平面PAD⊥平面ABCD，平面PAD平面ABCD=AD，所以PO⊥平面ABCD．（6分）如图，以O为坐标原点；分别以OA，ON，OP所在直线为轴建立空间直角坐标系，则，，，，．因为E为PA的中点，所以，故，．（8分）因为平面PAD⊥平面ABCD，平面PAD平面ABCD=AD，PO⊥AD，所以PO⊥平面ABD，故为平面ABD的一个法向量．设平面EBD的法向量为，由，得，即，令，则，，所以为平面EBD的一个法向量．（10分）所以．设二面角的大小为，由图可知，所以．（12分）21．【解析】(1)因为椭圆C的离心率，所以，即．（4分）因为抛物线的焦点恰好是该椭圆的一个顶点，所以，所以，．所以椭圆C的方程为．（6分）(2)(i)当直线的斜率不存在时．因为直线与圆M相切，故其中的一条切线方程为．由不妨设，，则以AB为直径的圆的方程为．（6分）(ii)当直线的斜率为零时．因为直线与圆M相切，所以其中的一条切线方程为．由不妨设，，则以AB为直径的圆的方程为．显然以上两圆都经过点O(0，0)．（8分）(iii)当直线的斜率存在且不为零时．设直线的方程为．由消去，得，所以设，，则，．所以．所以．①（11分）因为直线和圆M相切，所以圆心到直线的距离，整理，得， ②将②代入①，得，显然以AB为直径的圆经过定点O(0，0)综上可知，以AB为直径的圆过定点(0，0)．（13分）22．【解析】(1)由题易得，，因为直线与函数的图象相切于同一点，则令，解得，或，或(舍去)．（2分）易得，，；，．，；，．（3分）①当时，，易知直线的斜率为2，且直线过点(1，1)，则直线的方程为；（4分）②当时，因为，则，即，(*)令，则，易得方程(*)在且上一定有解，且直线以为斜率，过点，所以直线的方程为．综上所述，直线的方程为或．（6分）(2)由题易知，，要使在区间[2，4]上为单调递增函数，需在[2，4]时恒成立，即在时恒成立，即在时恒成立，即．（9分）设，则，易知当时，，所以在[2,4]上单调递减，则，即，所以，所以当时，在区间[2，4]上为单调递增函数．（11分）要使在区间[2，4]上为单调递减函数，需在[2，4]时恒成立，易得．综上所述，若在区间[2，4]上为单调函数，则的取值范围为．（13分）。

山东省2013届高三高考模拟卷（三）数学（理科）本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分，全卷满分150分，考试时间120分钟第Ⅰ卷一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．集合P={3，4，5}，Q={6，7}，定义},|),{(*Q b P a b a Q P ∈∈=，则Q P *的子集个数为A ．7B ．12C ．32D ．642．已知20<<a ，复数z 的实部为a ，虚部为1，则||z 的取值范围是 A ．(1，5) B ．(1，3) C ．)5,1( D ．)3,1( 3．若命题“p 或q ”与命题“非p ”都是真命题，则A ．命题p 不一定是假命题B ．命题q 一定是真命题C ．命题q 不一定是真命题D ．命题p 与命题q 同真同假4．已知数阵⎪⎪⎪⎪⎪⎪⎪⎭⎫⎝⎛333231232221131211aa aa a aa a a中，每行的3个数依次成等差数列，每列的3个数也依次成等差数列，若822=a ，则这9个数的和为A ．16B ．32C ．36D ．725．某几何体的三视图如右图所示，其中正视图是腰长为2的等腰三角形，侧视图是半径为1的半圆，该几何体的体积为A ．63π B ．33π C ．23π D ．π3 6．执行如右图所示的程序框图，如果输入的n 是4，则输出的p的值是 A．8 B ．5 C ．3 D ．2 7．函数()cos(2)f x x x π=-的图象大致为8．连接球面上两点的线段称为球的弦，半径为4的球的两条弦AB 、CD 的长度分别为72、34，M 、N 分别为AB 、CD 的中点，每条弦的两端都在球面上运动，有下列四个命题：①弦AB 、CD 可能相交于点M ；②弦AB 、CD 可能相交于点N ；③MN 的最大值为5；④MN 的最小值为1．其中真命题的个数为A ．1B ．2C ．3D ．49．在直角坐标系中，若不等式组⎪⎩⎪⎨⎧--≤≤≥1)1(,2,0x k y x y y 表示一个三角形区域，则实数k 的取值范围是A ．)1,(--∞B ．),0(+∞C ．),2()2,0(+∞D ．),2()2,0()1,(+∞--∞ 10．将“你能HOlD 住吗”8个汉字及英文字母填人5×4的方格内，其中“你”字填入左上角，“吗”字填入右下角，将其余6个汉字及英文字母依次填入方格，要求只能横读或竖读成一句原语，如图所示为一种填法，则共有不同的填法种数是A.35B.15C.20D.7011．过抛物线)0(22>=p px y 的焦点F ，斜率为34的直线交抛物线于A ，B 两点，若)1(>=λλFB AF ，则λ的值为A ．5B ．4C ．34 D ．25 12．对任意实数y x ,，定义运算cxy by ax y x ++=*，其中c b a ,,为常数，等号右边的运算是通常意义的加、乘运算．现已知1*2=4，2*3=6，且有一个非零实数m ，使得对任意实数x ，都有x m x =*，则=mA ．2B ．3C ．4D ．5第Ⅱ卷二、填空题：本大题共4小题，每小题4分，共16分．把答案填写在答题纸的相应位置．13．若非零向量,满足||||=，0)2(=⋅+，则a 与b 的夹角为______． 14．已知26()k x x+（k 是正整数）的展开式中，常数项小于120，则=k _______． 15．若关于x 的不等式3|||1|>++-m x x 的解集为R ，则实数m 的取值范围是_______． 16．过双曲线的一个焦点的直线垂直于一条渐近线，且与双曲线的两支相交，则该双曲线离心率的取值范围是_________．三、解答题：本大题共6个小题，共74分．解答应写文字说明、证明过程或演算步骤，把答案填写在答题纸的相应位置．17．(本小题满分12分)已知函数1)sin (cos cos 2)(+-=x x x x f ，R x ∈． (1)求函数)(x f 的最小正周期；(2)求函数)(x f 在区间]43,8[ππ上的最小值与最大值．18．(本小题满分12分)某学校的一间功能室统一使用某种节能灯管，已知这种灯管的使用寿命ξ(单位：月)服从正态分布),(2σμN ，且使用寿命不少于12个月的概率为0．8，使用寿命不少于24个月的概率为0．2．(1)求这种灯管的平均使用寿命μ；(2)假设一间功能室一次性换上2支这种新灯管，使用12个月时进行一次检查，将已经损坏的灯管换下(中途不更换)，设需要更换的灯管数为η，求η的分布列和数学期望． 19．（本小题满分12分）如图甲，△ABC 是边长为6的等边三角形，E ，D 分别为AB ，AC 靠近B ，C 的三等分点，点G 为BC 边的中点，线段AG 交线段ED 于点F ．将△AED 沿ED 翻折，使平面AED ⊥平面BCDE ，连接AB ，AC ，AG ，形成如图乙所示的几何体．(1)求证：BC ⊥平面AFG ；(2)求二面角D AE B --的余弦值． 20．(本小题满分12分)已知常数0>p 且1=/p ，数列}{n a 的前n 项和)1(1n n a ppS --=，数列}{n b 满足121l o g -+=-n p n n a b b 且11=b ．(1)求证：数列}{n a 是等比数列；(2)若对于在区间[0，1]上的任意实数λ，总存在不小于2的自然数k ，当k n ≥时，)23)(1(--≥n b n λ恒成立，求k 的最小值．21．（本小题满分13分）已知椭圆C ：)0(12222>>=+b a b y a x 的长轴长为4，离心率22=e(1)求椭圆的方程；(2)设椭圆C 的左顶点为A ，右顶点为B ，点S 是椭圆C 上位于x 轴上方的动点，直线AS ，BS 与直线l ：3=x 分别交于M ，N 两点，求线段MN 的长度的最小值．22．（本小题满分13分）已知函数⎩⎨⎧≥<+++-=)1(ln )1()(23x x a x c bx x x x f ，的图象过点)2,1(-，且在点))1(,1(--f 处的切线与直线-x 015=+y 垂直．(1)求实数c b ,的值；(2)求)(x f 在e e ](,1[-为自然对数的底数）上的最大值；(3)对任意给定的正实数a ，曲线)(x f y =上是否存在两点P ，Q ，使得△POQ 是以O 为直角顶点的直角三角形，且此三角形斜边的中点在y 轴上？山东省2013届高三高考模拟卷（三）数学（理科）参考答案一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．1．D 【解析】集合Q P *中的元素为(3，6)，(3，7)，(4，6)，(4，7)，(5，6)，(5，7)共6个，故Q P *的子集个数为6426=．2．C 【解析】由于复数z 的实部为a ，虚部为1，且20<<a ，故由21||a z +=得5||1<<z ． 3．B 【解析】由题可知“非p ”是真命题，所以p 是假命题，又因为“p 或q ”是真命题，所以q 是真命题．故选B ．4．D 【解析】依题意得+++++++31232221131211a a a a a a a 3332a a +72933322322212==++=a a a a ．5．B 【解析】由三视图可知该几何体是圆锥沿轴截面截成两部分，然后把截面放在平面上，底面相对接的图形（如图）．圆锥的底面半径为1，母线长为2，故圆锥的高=h 31222=-．易知该几何体的体积就是整个圆锥体的体积，即3331313122πππ=⨯⨯=h r ． 6．C 【解析】由题知，第一次进入循环，满足1<4，循环后1=p ，1=s ，1=t ，2=k ；第二次进入循环，满足2<4，循环后2=p ，=s 1，2=t ，3=k ；第三次进入循环，满足3<4，循环后3=p ，2=s ，3=t ，4=k ，因为4=4，不满足题意，所以循环结束．输出p 的值为3，选C ．7．A 【解析】因为()cos(2)cos f x x x x x π=-=，)(cos )cos()()(x f x x x x x f -=-=--=-，所以函数x x x f cos )(=为奇函数，排除B ，C ；又因为当20π<<x 时，=)(x f 0cos >x x ，故选择A ．8．C 【解析】设球的球心O 到直线AB 、CD 的距离分别为d d 、'，利用勾股定理可求出3='d ，2=d ，所以CD 可以经过M ，而AB 不会经过N ，所以①正确，②不正确；又5='+d d ，1=-'d d ，所以③④正确．故选C ．9．A 【解析】 由题意可知，直线1)1(--=x k y 过定点)1,1(-．当这条直线的斜率为负值时，如图1所示，若不等式组表示一个三角形区域，则该直线的斜率)1,(--∞∈k ；当这条直线的斜率为正值时，如图2所示，1)1(--≤x k y 所表示的区域是直线1)1(--=x k y 及其右下方的半平面，这个区域和另外两个半平面的交集是一个无界区域，不能构成三角形．因此k 的取值范围是)1,(--∞．10．A 【解析】要把6个汉字及英文字母依次填入6个方格中，按照规则分为两类：一类是4个字横向2个字纵向，有26C 种填法；另一类是3个字横向3个字纵向，有36C 种填法：所以共有3520153626=+=+C C 种填法．11．B 【解析】 根据题意设),(11y x A ，),(22y x B ．由FB AF λ=得),2(),2(2211y p x y x p -=--λ，故21y y λ=-，即=λ21y y -．设直线AB 的方程为)2(34p x y -=，联立直线与抛物线方程，消元得02322=--p py y ．故p y y 2321=+，=21y y 2p -，492)(122121221-=++=+y y y y y y y y ，即=+--21λλ49-．又1>λ，故4=λ．12．D 【解析】由定义可知，⎩⎨⎧=++==++=66323*24222*1c b a c b a ，解得⎩⎨⎧+=-=226c b ca ，又对任意实数x ，都有x m x =*，即++-=+++-=c x c cm cxm m c cx m x 2()6()22(6*x m =)2恒成立，则⎩⎨⎧=+=-0)22(16m c c cm ，解得⎩⎨⎧=-=51m c 或⎪⎩⎪⎨⎧=-=061m c （舍）． 第Ⅱ卷13．︒120【解析】由题意得⋅=+⋅=⋅+22||22)2(a b b a b b a 0,cos 2=+><a b a ，所以21,cos ->=<b a ，所以,的夹角为︒120． 14．1【解析】二项展开式的通项为r rrr xk x C T )()(6261-+=rr r x k C 3126-=，令0312=-r ，得4=r ，故常数项为446k C ，由常数项小于120，即<446k C 120，得84<k ．又k 是正整数，故1=k ．15．),2()4,(+∞--∞ 【解析】由题意知，不等式+-|1|x 3||>+m x 恒成立，即函数|||1|)(m x x x f ++-=的最小值大于3，根据不等式的性质可得--≥++-)1(||||1|x m x x |1||)(+=+m m x ，故只要3|1|>+m 即可，所以31>+m 或31-<+m ，即得m 的取值范围是),2()4,(+∞--∞ ．16． ),2(+∞【解析】不妨设双曲线的方程为)0,0(12222>>=-b a by a x ，焦点,(c F 0)，渐近线x ab y =，则过点F 的直线方程为)(c x b ay --=，与双曲线联立，消去y 得02)(42244244=--+-b a c a a x a b α，由⎪⎩⎪⎨⎧<-->∆020444ab c a 得44a b >，即a b >，故2>e ． 三、17．【解析】(1)1)sin (cos cos 2)(+-=x x x x f 1sin cos 2cos 22+-=x x x)432sin(2222sin 2cos π++=+-=x x x ．（4分） 因此，函数)(x f 的最小正周期为π．（6分） (2)由题易知)432sin(22)(π++=x x f 在区间]83,8[ππ上是减函数， 在区间]43,83(ππ上是增函数，（8分） 又2)8(=πf ，22)83(-=πf ，3)43(=πf ，（10分）所以，函数)(x f 在区间]43,8[ππ上的最大值为3，最小值为22-．（12分） 18．【解析】(1)因为),(~2σμξN ，8.0)12(=≥ξP ，2.0)24(=≥ξP ， 所以2.0)12(=<ξP ，显然)24()12(≥=<ξξP P ．（3分） 由正态分布密度曲线的对称性可知，1822412=+=μ， 即这种灯管的平均使用寿命是18个月．（6分）(2)这种灯管的使用寿命少于12个月的概率为2.08.01=-． 由题意知，η的可能取值为0，1，2，（8分） 则64.08.02.0)0(22=⨯==C P η，⨯==1122.0)1(C P η32.08.01=，04.08.02.0)2(0222=⨯==C P η．（10分） 所以η的分布列为所以4.004.0232.0164.00=⨯+⨯+⨯=ηE ．（12分）19．【解析】(1)在图甲中，由△ABC 是等边三角形，E ，D 分别为AB ，AC 的三等分点，点G为BC 边的中点，易知DE ⊥AF ，DE ⊥GF ，DE//BC ．（2分）在图乙中，因为DE ⊥AF ，DE ⊥GF ，AF FG=F ，所以DE ⊥平面AFG ． 又DE//BC ，所以BC ⊥平面AFG ．（4分）(2)因为平面AED ⊥平面BCDE ，平面AED 平面BCDE=DE ，DE ⊥AF ，DE ⊥GF ，所以FA ，FD ，FG 两两垂直．以点F 为坐标原点，分别以FG ，FD ，FA 所在的直线为z y x ,,轴，建立如图所示的空间直角坐标系xyz F -．则)32,0,0(A ，)0,3,3(-B ，)0,2,0(-E ，所以)32,3,3(--=AB ，,1,3(-=BE 0)．（6分） 设平面ABE 的一个法向量为),,(z y x n =．则⎪⎩⎪⎨⎧=⋅=⋅0BE n ，即⎪⎩⎪⎨⎧=+-=--0303233y x z y x ，取1=x ，则3=y ，1-=z ，则)1,3,1(-=n ．（8分） 显然)0,0,1(=m 为平面ADE 的一个法向量， 所以55||||,cos =⋅>=<n m n m ．（10分） 又由图知二面角D AE B --为钝角，所以二面角D AE B --的余弦值为55-．（12分） 20．【解析】(1)当2≥n 时，-----=-=-1(1)1(11ppa p p S S a n n n n )1-n a ，整理得1-=n n pa a ．（3分） 由)1(1111a p p S a --==，得=1a 0>p ，则恒有0>=n n p a ，从而p a an n =-1．所以数列}{n a 为等比数列．（6分）(2)由(1)知nn p a =，则12log 121-==--+n a b b n P n n ，所以=+-++-+-=---112211)()()(b b b b b b b b n n n n n 222+-n n ，（8分）所以)23)(1(222--≥+-n n n λ，则+-+-n n n 5)23(2λ04≥在]1,0[∈λ时恒成立．记45)23()(2+-+-=n n n f λλ，由题意知，⎩⎨⎧≥≥0)1(0)0(f f ，解得4≥n 或1≤n ．（11分）又2≥n ，所以4≥n ．综上可知，k 的最小值为4．（12分） 21．【解析】(1)由题意得42=a ，故2=a ，（1分） 因为22==a c e ，所以2=c ，2)2(2222=-=b ，（3分） 所以所求的椭圆方程为12422=+y x ．（4分） (2)依题意，直线AS 的斜率k 存在，且0>k ，故可设直线AS 的方程为)2(+=x k y ，从而)5,3(k M ，由⎪⎩⎪⎨⎧=++=124)2(22y x x k y 得+1(0488)22222=-++k x k x k ．（6分）设),(11y x S ，则2212148)2(k k x +-=⨯-，得2212142k k x +-=，从而21214k ky +=， 即)214,2142(222k kk k S ++-，（8分）又由B(2，0)可得直线SB 的方程为22142202140222-+--=-+-k k x k k y ， 化简得)2(21--=x ky ， 由⎪⎩⎪⎨⎧=--=3)2(21x x k y 得⎪⎩⎪⎨⎧-==k y x 213，所以)21,3(k N -， 故|215|||kk MN +=，（11分） 又因为0>k ，所以102152215||=∙≥+=kk k k MN ， 当且仅当k k 215=，即1010=k 时等号成立， 所以1010=k 时，线段MN 的长度取最小值10．（13分） 22．【解析】(1)当1<x 时，b x x x f ++-='23)(2，（2分）由题意，得⎩⎨⎧-=-'=-,5)1(,2)1(f f 即⎩⎨⎧-=+--=+-,523,22b c b 解得0==c b ．（4分）(2)由(1)，知⎩⎨⎧≥<+-=),1(ln ),1()(23x x a x x x x f （5分）①当11<≤-x 时，)23()(--='x x x f ，由0)(>'x f ，得320<<x ；由0)(<'x f ，得01<≤-x 或132<<x ．所以)(x f 在)0,1[-和)1,32(上单调递减，在)32,0(上单调递增． 因为2)1(=-f ，274)32(=f ，0)0(=f ，所以)(x f 在)1,1[-上的最大值为2．②当e x ≤≤1时，x a x f ln )(=，当0≤a 时，0)(≤x f ；当0>a 时，)(x f 在],1[e 上单调递增．（7分）所以)(x f 在],1[e 上的最大值为a ．所以当2≥a 时，)(x f 在],1[e -上的最大值为a ； 当2<a 时，)(x f 在],1[e -上的最大值为2．（8分）(3)假设曲线)(x f y =上存在两点P ，Q 满足题意，则P ，Q 只能在y 轴两侧， 因为△POQ 是以O 为直角顶点的直角三角形，所以0=∙OQ OP ，不妨设)0))((,(>t t f t P ，则由△POQ 斜边的中点在y 轴上知,(t Q -)23t t +，且 1≠t ．所以0))((232=++-t t t f t ．（*） 是否存在两点P ，Q 满足题意等价于方程(*)是否有解．若10<<t ，则23)(t t t f +-=，代入方程(*)，得++-+-3232)((t t t t 0)2=t ， 即0124=+-t t ，而此方程无实数解；当1>t 时，则t a t f ln )(=，代入方程(*)，得0)(ln 232=+∙+-t t t a t ，即t t aln )1(1+=。

绝密 ★ 启用并使用完毕前 试卷类型：A2013年普通高等学校招生全国统一考试（山东卷）数学（理）本试卷分第I 卷（选择题）和第II 卷两部分。

共150分，考试时间120分钟。

第I 卷（选择题 共60分）一、选择题：本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的.1. 已知全集{0,1,2,3,4,5,6}U =，集合{2,4,5}A =，{1,3,4,6}B =，则()u C A B 为（ ）A. {0,1,3,6}B. {0,2,4,6}C. {0,1,6}D. {1,3,6} 2. 复数432iz i+=-的共轭复数的虚部为（ ） A. 2- B. 2i - C. 2 D. 2i3. 某单位安排2013年春节期间7天假期的值班情况，7个员工每人各值一天. 已知某员工甲必须排在前两天，员工乙不能排在第一天，员工丙必须排在最后一天，则不同的值班顺序有（ ） A. 120种B. 216种C. 720种D. 540种4. 已知向量(1,2),m x =-+(3,21),n y =-若m n ⊥，则18()16xy+的最小值为（ ） A ．2 B ．4 C． D．5. 已知双曲线2221x y a-=(0)a >的一个焦点与抛物线218x y =的焦点重合，则此双曲线的离心率为（ ）ABCD6. 已知变量,x y 满足约束条件2823y x x y x y ≤⎧⎪-≤⎨⎪+≥⎩，则目标函数62z x y =-的最小值为（ ）A ．32B ．4C ．8D ．2 7. 已知数列{},{}n n a b 满足113a b ==，113n n n nb a a b ++-==，n N +∈，若数列{}n c 满足n n a c b =，则2013c =（ ）A. 20129B ．201227C ． 20139D. 2013278. 已知函数()f x 的定义域为[3,6]，则函数y =）A ．3[,)2+∞B ．3[,2)2C ．3(,)2+∞D ．1[,2)29. 执行如图所示的程序框图，则输出的结果为（ ）A ．2B ．1C ．21D ．1- 10. 已知四面体S ABC -四面体S ABC -外接球的表面积为（ ）A. 6πB. 4πC. 8πD. 3π11. 在△ABC 中，内角A ，B ，C 的对边分别是a ，b ，c ，若22245b c b c +=+-且222a b c bc =+-，则△ABC 的面积为（ ）A.B.C. 2D.12. 定义域为R 的函数()f x 满足()()22f x f x +=，当[)0,2x ∈时，()[)[)232,0,1,1,1,2,2x x x x f x x -⎧-∈⎪⎪=⎨⎛⎫⎪-∈ ⎪⎪⎝⎭⎩则当[)4,2x ∈--时，函数()2142t f x t ≥-+恒成立，则实数t 的取值范围为（ ）A. 23t ≤≤B. 13t ≤≤C. 14t ≤≤D. 24t ≤≤第II 卷（非选择题 共90分）二、填空题：本大题共4小题，每小题4分，共16分．13. 若函数22()1xf x x =+在点(2,(2))f 处的切线为l ，则直线l 与y 轴的交点坐标为_________.14. 已知1(2)xa e x d x =+⎰（e 为自然对数的底数），函数l n ,0()2,0xx xf x x ->⎧=⎨≤⎩，则21()(l og )6f a f +=__________. 15. 若31()n x x-展开式中的所有二项式系数和为512，则该展开式中3x 的系数为______.16. 对于函数lg |3|y x =-和sin 2xy π=(410)x -≤≤，下列说法正确的是 . （1）函数lg |3|y x =-的图像关于直线3x =-对称； （2）sin2xy π=(410)x -≤≤的图像关于直线3x =对称；（3）两函数的图像一共有10个交点；（4）两函数图像的所有交点的横坐标之和等于30； （5）两函数图像的所有交点的横坐标之和等于24.三、解答题：本大题共6小题，共74分．解答应写出文字说明、证明过程或演算步骤．17.（本小题满分12分）已知函数21()sin cos sin cos cos cos()(0)2f x x x x ϕϕπϕϕπ=+++<<，其图象过点1(,).34π （1）求ϕ的值；（2）将函数)(x f y =图象上各点向左平移6π个单位长度，得到函数)(x g y =的图象，求函数)(x g 在2[,]43ππ-上的单调递增区间.18.（本小题满分12分）2012年10月莫言获得诺贝尔文学奖后，其家乡山东高密政府准备投资6.7亿元打造旅游带，包括莫言旧居周围的莫言文化体验区，红高粱文化休闲区，爱国主义教育基地等；为此某文化旅游公司向社会公开征集旅游带建设方案，在收到的方案中甲、乙、丙三个方案引起了专家评委的注意，现已知甲、乙、丙三个方案能被选中的概率分别为231,,543，且假设各自能否被选中是无关的. （1）求甲、乙、丙三个方案只有两个被选中的概率；（2）记甲、乙、丙三个方案被选中的个数为ξ，试求ξ的期望.19. （本小题满分12分）如图1， 在直角梯形A B C D 中， 90ADC ∠=︒， //CD AB ，4,2AB AD CD ===，M 为线段AB 的中点. 将ADC ∆沿AC 折起，使平面ADC ⊥平面ABC ，得到几何体D ABC -，如图2所示. （1）求证:BC ⊥平面ACD ；（2）求二面角A CD M --的余弦值.20. （本小题满分12分）在等差数列{}n a 中，345842,30a a a a ++==. （1）求数列{}n a 的通项公式； （2）若数列{}n b满足2n a n b λ+=+（R λ∈），则是否存在这样的实数λ使得{}n b 为等比数列； （3）数列{}n c 满足112,1,2n n n n n c T a n --⎧⎪=⎨⎪⎩为奇数，为偶数为数列{}n c 的前n 项和，求2n T .21. （本小题满分13分）如图，设A 是圆226x y +=上的动点，点B 是A 在x 轴上投影，M 为AB 上一点，且||||3MB AB =．当A 在圆上运动时，点M 的轨迹为曲线G . 过点(,0)m (m >且倾斜角为56π的直线l 交曲线G 于,C D 两点. （1）求曲线G 的方程；（2）若点F 是曲线G 的右焦点且[,]32CFD ππ∠∈，求m 的取值范围.22. （本小题满分13分）已知函数()ln (1)2ex f x f x '=-⋅，32()()2x ag x f x x=--（其中a R ∈）. （1）求()f x 的单调区间；（2）若函数()g x 在区间[2,)+∞上为增函数，求a 的取值范围；（3）设函数2()4h x x mx =-+，当1a =时，若存在1(0,1]x ∈，对任意的2[1,2]x ∈，总有12()()g x h x ≥成立，求实数m 的取值范围.参考答案DABCC BDBCA BB13. 32(0,)25； 14. 7； 15. 84； 16.（2）（3）（4）； 17. 解：（1）11cos 21()sin 2sin cos cos 222x f x x ϕϕϕ+=+- 11sin 2sin cos 2cos 22x x ϕϕ=+1(sin 2sin cos 2cos )2x x ϕϕ=+1cos(2).2x ϕ=-……3分 又函数图象过点1(,).34π，所以11cos(2)423πϕ=⨯-，即21cos(),32πϕ-= 又0ϕπ<<，所以.3πϕ=……6分 （2）由（1）知1()cos(2)23f x x π=-，将函数()y f x =图象上各点向左平移6π个单位长度后，得到函数()y g x =的图象，可知1()cos 22g x x =.……9分因为2[,]43x ππ∈-，所以42[,]23x ππ∈-，由202x π-≤≤和423x ππ≤≤知函数)(x g 在2[,]43ππ-上的单调递增区间为[,0]4π-和2[,]23ππ.……12分 18. 解：记甲、乙、丙三个方案被选中的事件分别为,,A B C ，则231(),(),()543P A P B P C ===.（1）“只有两个方案被选中”可分为三种情形：①甲未被选中，乙、丙被选中，概率为3313()()()()54320P A B C P A P B P C ⋅⋅=⋅⋅=⨯⨯=.……1分 ②乙未被选中，甲、丙被选中，概率为2111()()()()54330P A B C P A P B P C ⋅⋅=⋅⋅=⨯⨯=.……2分③丙未被选中，甲、乙被选中，概率为2321()()()()5435P A B C P A P B P C ⋅⋅=⋅⋅=⨯⨯=.……3分以上三种情况是互斥的. 因此只有两个方案被选中的概率为：311232030560P =++=.……5分 （2）由题意可知ξ的可能取值为0，1，2，3.……6分3121(0)()()()()54310P P A B C P A P B P C ξ==⋅⋅=⋅⋅=⨯⨯=；(1)()()()P P A B C P A B C P A B C ξ==⋅⋅+⋅⋅+⋅⋅()()()()()()()()()P A P B P C P A P B P C P A P B P C =⋅⋅+⋅⋅+⋅⋅2123323112554354354360=⨯⨯+⨯⨯+⨯⨯=； 由（1）知23(2)60P ξ==；2311(3)()()()()54310P P A B C P A P B P C ξ==⋅⋅=⋅⋅=⨯⨯=.……10分故1252318901231060601060E ξ=⨯+⨯+⨯+⨯=.……12分19. 解析：（1）在图1中，可得AC BC ==， 从而222AC BC AB +=， 故AC BC ⊥.取AC 中点O 连结DO ， 则DO AC ⊥， 又面ADC ⊥面ABC ， 面ADC面ABC AC =， DO ⊂面ACD ， 从而OD ⊥平面ABC .∴OD BC ⊥，又AC BC ⊥， AC OD O =.∴BC ⊥平面ACD .（2）建立空间直角坐标系O xyz -如图所示，则M ，(C ，D，(2,CM =，(2,0,CD =.设1(,,)n x y z =为面CDM 的法向量，则1100n CM n CD ⎧⋅=⎪⎨⋅=⎪⎩即00==， 解得y x z x =-⎧⎨=-⎩. 令1x =-，可得1(1,1,1)n =-.又2(0,1,0)n =为面ACD的一个法向量，∴121212cos ,||||3n n n n n n ⋅<>===∴二面角A CDM --（法二）如图，取AC 的中点N ，DC 的中点G ，连结,,MN NG GM .易知//MN BC ，又BC ACD ⊥面，MN ACD ∴⊥面，又CD ACD ⊂面，MN CD ∴⊥.又NG 为ACD ∆的中位线，因AD DC ⊥，NG DC ∴⊥，NG MN N =，且,N G M N 都在面MNG 内，故CD MNG ⊥面，故NGM ∠即为二面角A CD M --的平面角. 在Rt ADC ∆中，易知AC = 在Rt ABC ∆中，易知BC =MN ∴=在Rt MNG ∆中1,NG MN MG ==故cos 3NG NGM MG ∠===∴二面角A CD M --20. 解：（1）因为{}n a 是一个等差数列，所以34544342,14a a a a a ++==∴=.设数列{}n a 的公差为d ，则84416d a a =-=，故4d =；故4(4)42n a a n d n =+-=-.……3分 （2）29n a n n b λλ+=+=+.假设存在这样的λ使得{}n b 为等比数列，则212n n n b b b ++=⋅，即122(9)(9)(9)n n n λλλ+++=+⋅+， 整理可得0λ=. 即存在0λ=使得{}n b 为等比数列.……7分（3）∵12,23,n n n c n n -⎧=⎨-⎩为奇数为偶数，∴242221(223)2(243)22(223)n n T n -=+⨯-++⨯-++++⨯-……9分242212224(12)3n n n -=++++++++-214(1)414321423n n n n n n n -+-=+⨯-=+--. ……12分 21. 解：（1）设点M 的坐标是(,)x y ，A 的坐标是(,)A A x y ，因为点B 是A 在x 轴上投影，Ｍ为AB 上一点，且||||MB AB =，所以A x x =，且A y =，∵A 在圆226x y +=上，∴22)6x +=，整理得22162x y +=. 即G 的方程是22162x y +=. （2）如下图，直线l 交曲线G 于,C D 两点，且[,]32CFD ππ∠∈.由题意得直线l的方程为)y x m =-(m >.由22162)x y y x m ⎧+=⎪⎪⎨⎪=-⎪⎩，消去y 得222260x mx m -+-=. 由2248(6)0m m ∆=-->解得m -<<.又mm <设1122(,),(,)C x y D x y ，则212126,2m x x m x x -+==，2121212121[)][)]()333m m y y x m x m x x x x ∴=-⋅-=⋅-++. 1122(2,),(2,)FC x y FD x y =-=-.2212121212462(3)(2)(2)()43333m m m m FC FD x x y y x x x x +-∴⋅=--+=-+++=.又由椭圆方程可知2263x y -=，1||()FC xx ====-，2||()FD x x ===-，2121212221||||(3)(3)[3()9](612)333FC FD x x x x x x m m ∴⋅=--=-++=-+，22222(3)2(3)3cos 1612||||(612)3m m FC FD m m CFD m m FC FD m m -⋅-∴∠===-+⋅-+. 因[,]32CFD ππ∠∈，2212(3)1cos [0,],026122m m CFD m m -∴∠∈∴≤≤-+，22032(3)0,24011m m m m m m m ≤≥⎧⎧-≥⎪⎪∴∴⎨⎨--≤≤+⎪⎪⎩⎩或10m ≤≤或31m ≤≤m <31m ≤≤22. 解：（1）1()(1)f x f x ''=-，1(1)1(1),(1)2f f f '''∴=-∴=， 1()ln ,(0)22ex f x x x ∴=->，故112()22xf x x x-'=-=.∴当02x <<时，()0f x '>；当2x >时，()0f x '<. ∴()f x 的单调增区间为(0,2)，单调减区间为(2,)+∞.……3分（2）2()2ln 2a ex g x x x =--，则2221222()2a x x a g x x x x -+'=-+=，由题意可知22220x x ax -+≥在[2,)+∞上恒成立，即2220x x a -+≥在[2,)+∞上恒成立，因函数2()22u x x x a =-+开口向上，且对称轴为14x =，故()u x 在[2,)+∞上单调递增，因此只需使(2)0u ≥，解得3a ≥-； 易知当3a =-时，()0g x '≥且不恒为0. 故3a ≥-.……7分（3）当1a =时，2()2ln 2ex g x x x =--，22221152()2248()0x x x g x x x-+-+'==>，故在(0,1]上()0g x '>，即函数()g x 在(0,1]上单调递增，∴max ()(1)ln 21g x g ==-.……9分而“存在1(0,1]x ∈，对任意的2[1,2]x ∈，总有12()()g x h x ≥成立”等价于“()g x 在(0,1]上的最大值不小于()h x 在[1,2]上的最大值”.而()h x 在[1,2]上的最大值为(1),(2)h h 中的最大者，记为max{(1),(2)}h h .所以有(1)ln 21(1)(1)ln 21(2)g h g h =-≥⎧⎨=-≥⎩，(1)ln 215(1)ln 2182g m g m =-≥-⎧∴⎨=-≥-⎩，6ln 2,6ln 21(9ln 2)2m m m ≥-⎧⎪∴∴≥-⎨≥-⎪⎩. 故实数m 的取值范围为[6ln 2,)-+∞.……13分。